Mixed Convection in a Horizontal Channel–Cavity Arrangement with Different Heat Source Locations
Abstract
1. Introduction
2. Problem Formulation and Numerical Approach
2.1. The Governing Equations
- (i).
- U = Ui = ±1 and V = 0 at the intake (going either right or left).
- (ii).
- θ = 0 at the inlet and cold wall; θ = 1 at the hot wall.
- (iii).
- Under outlet constant pressure, P = 0.
- (iv).
- U = V= 0 at all walls.
Nusselt Number
2.2. Procedures for Simulation and Numerical Testing [40]
- (1)
- To reduce the amount of inaccuracy present in the numerical findings, two techniques may be used: establishing the grids and doing an examination of the density of each individual grid component.
- (2)
- Assessing the accuracy of the findings produced by the numerical model.
2.3. Grid Independency Test
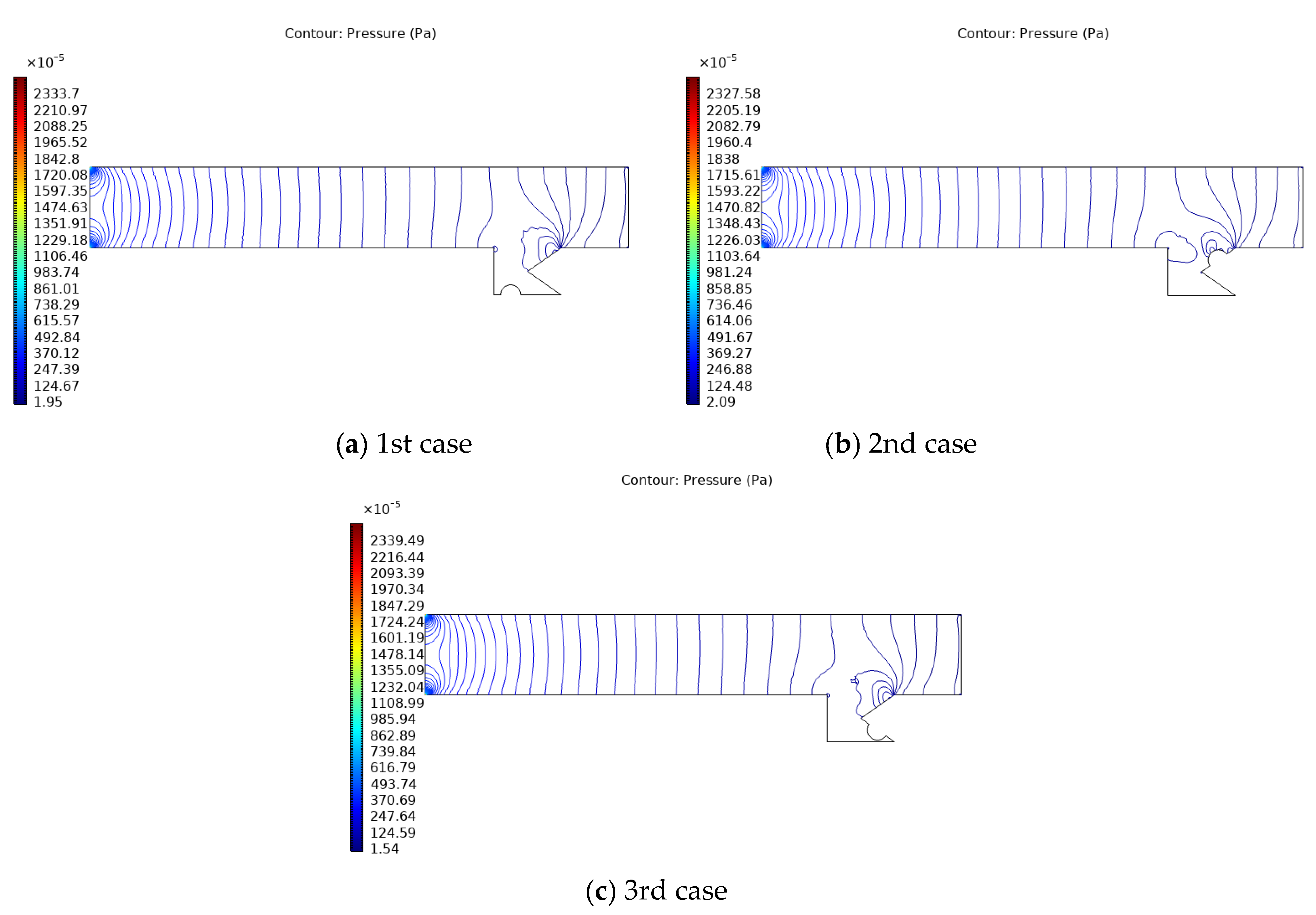
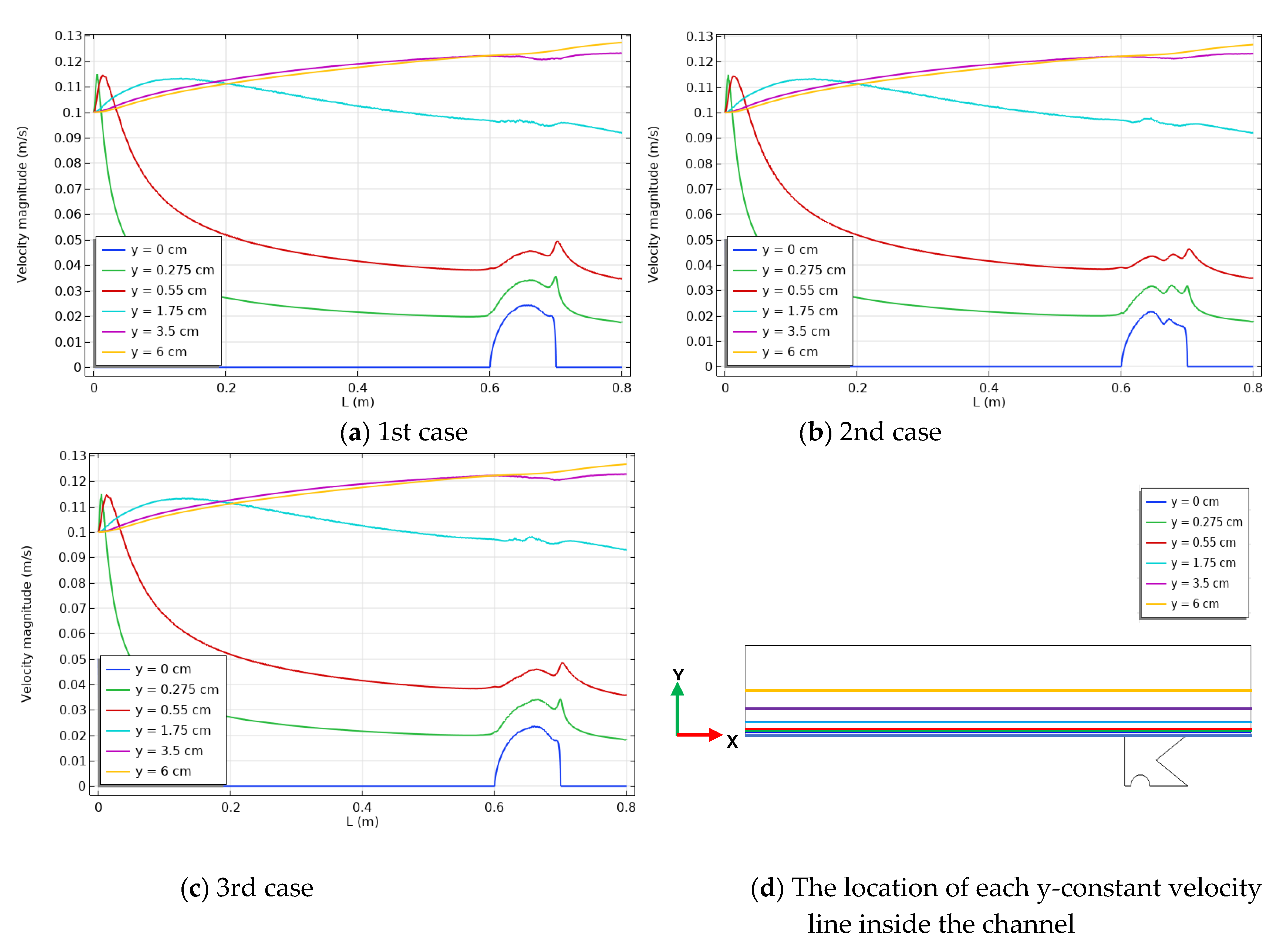
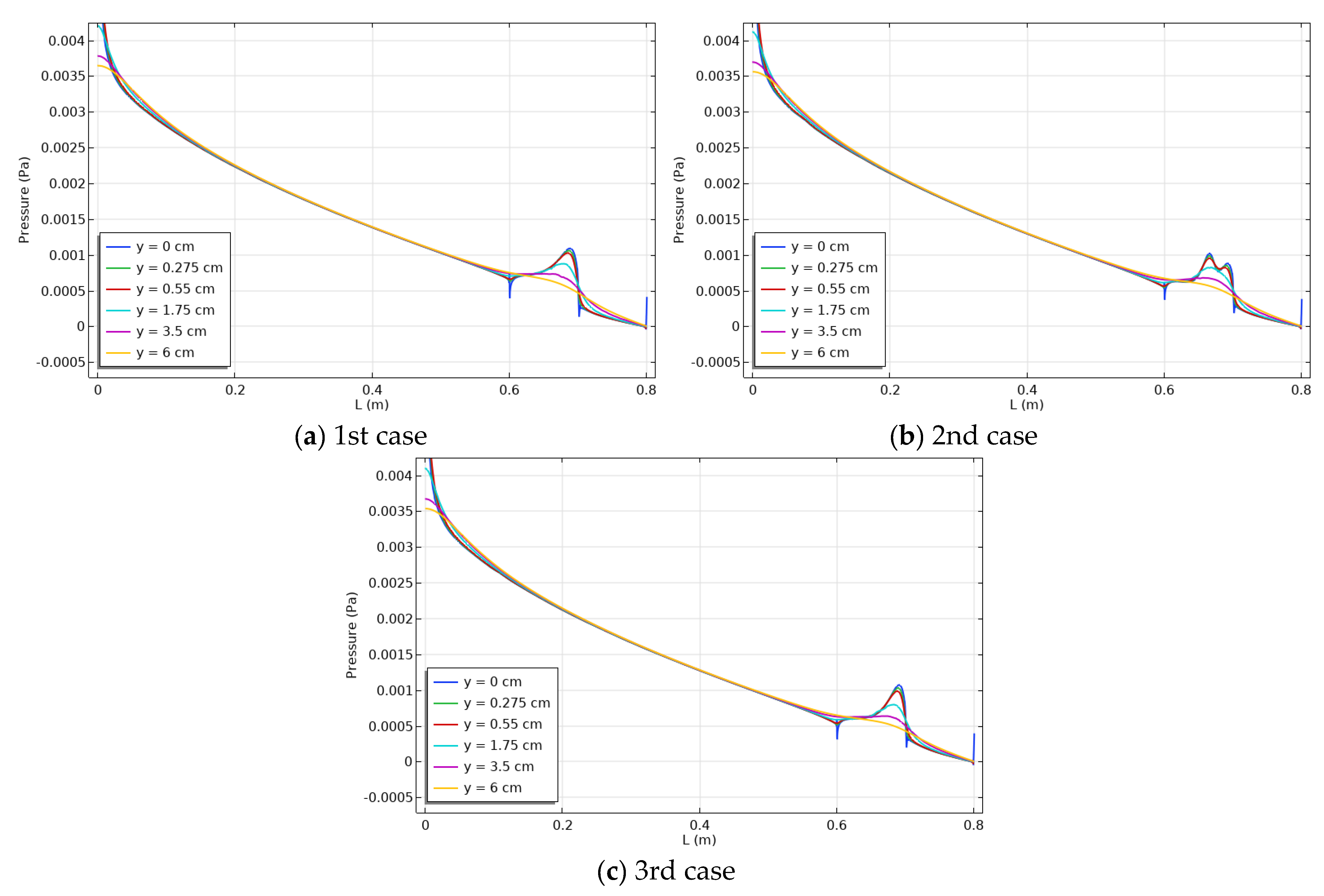
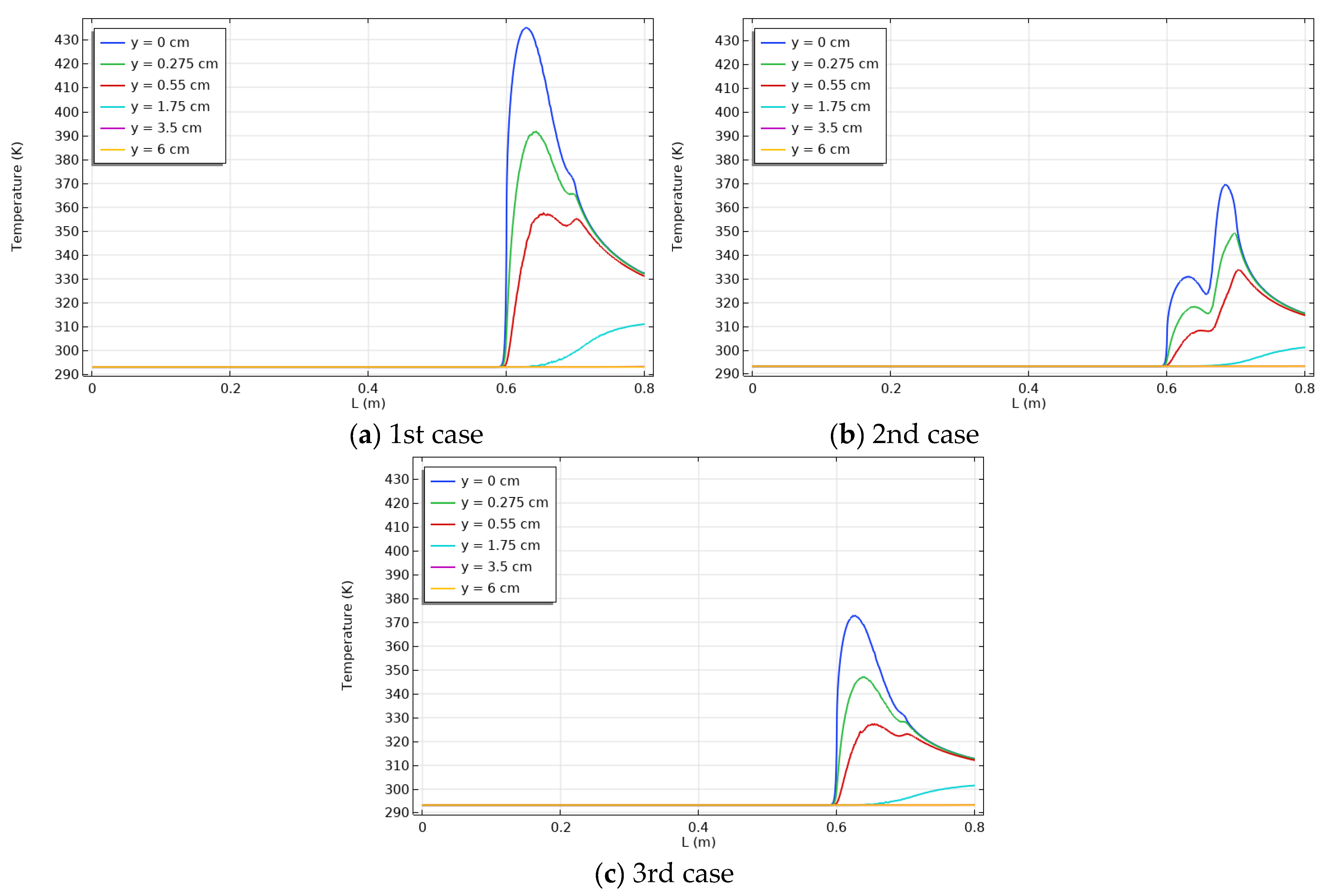
3. Results and Discussion
4. Conclusions
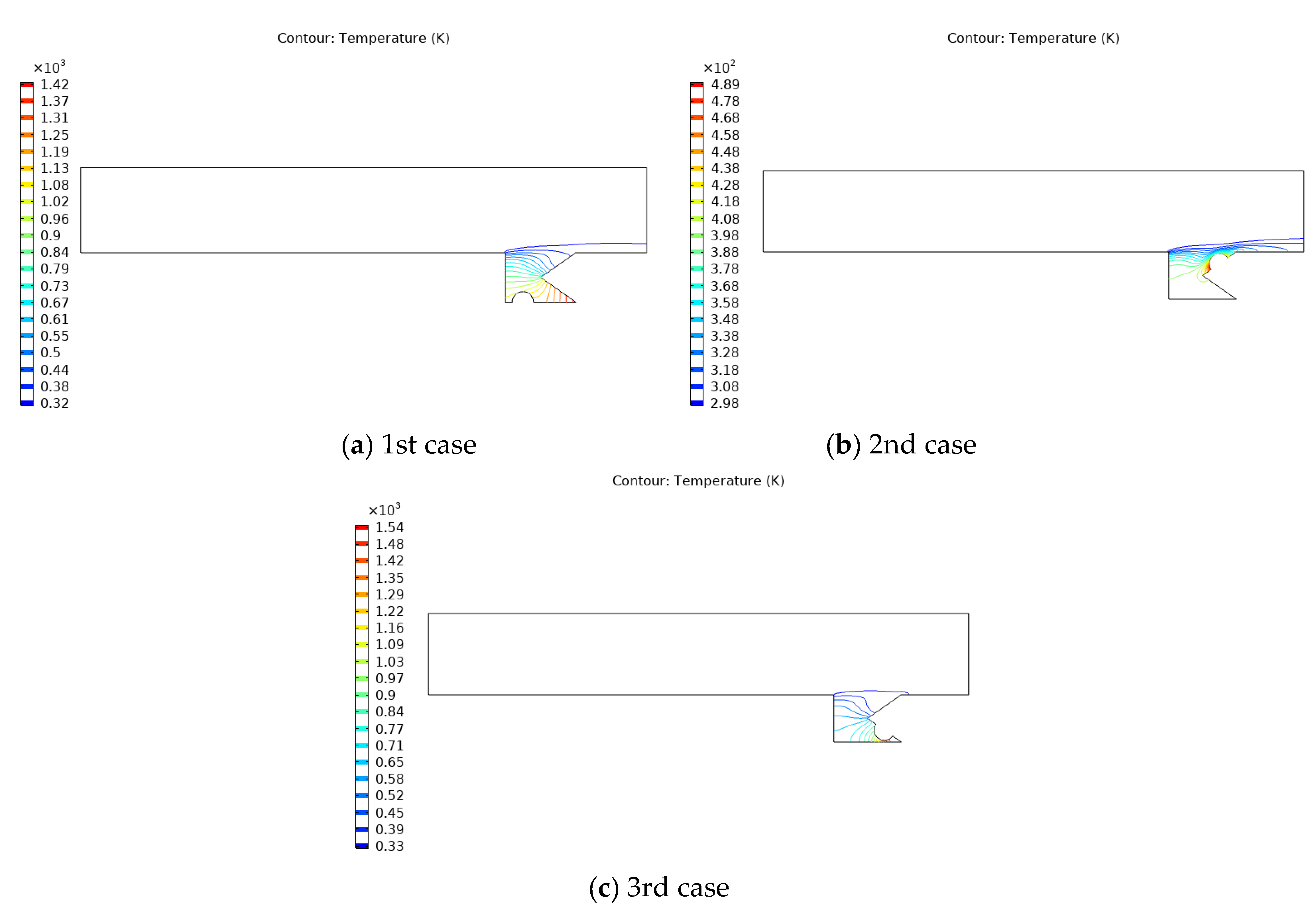
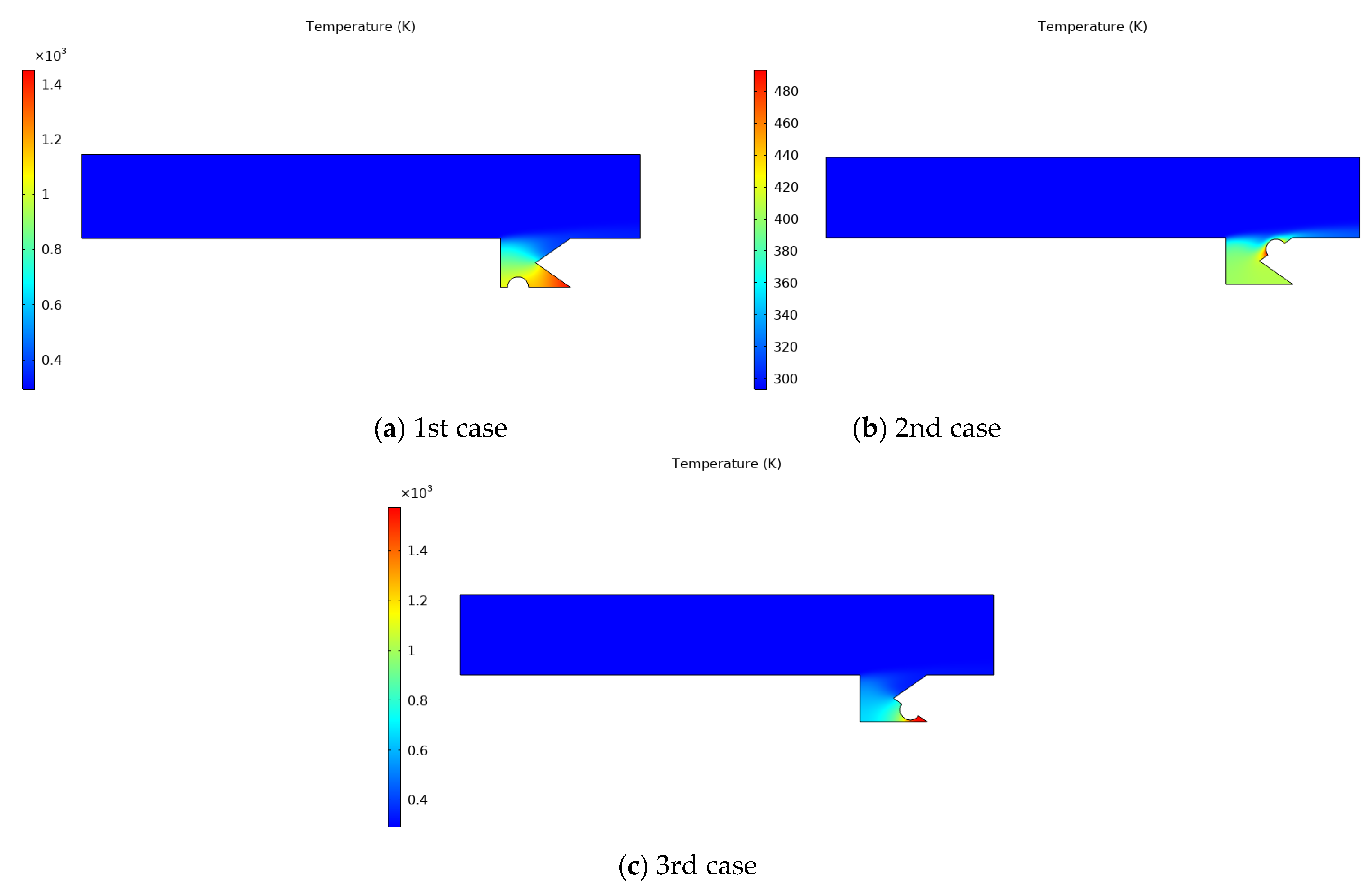
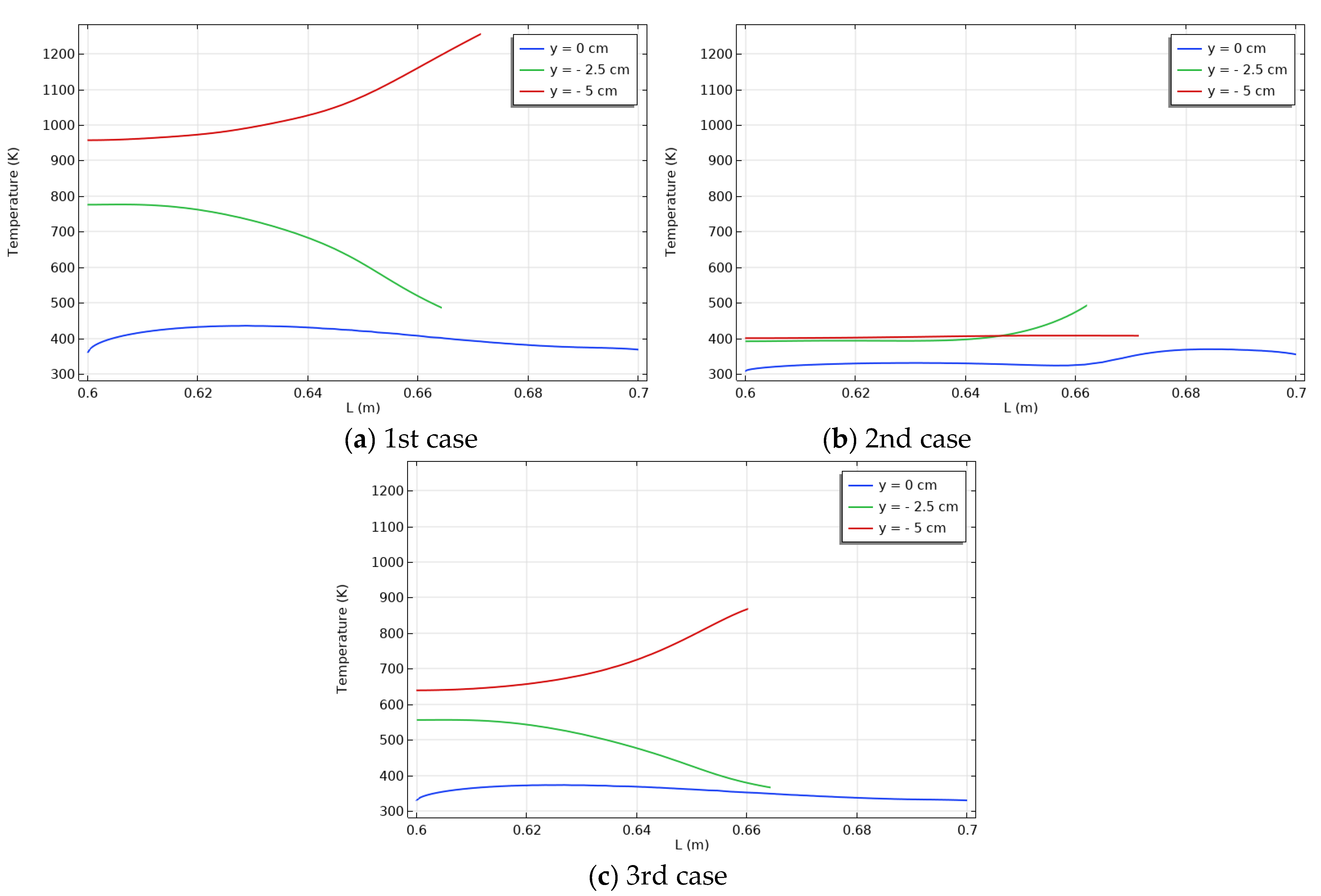
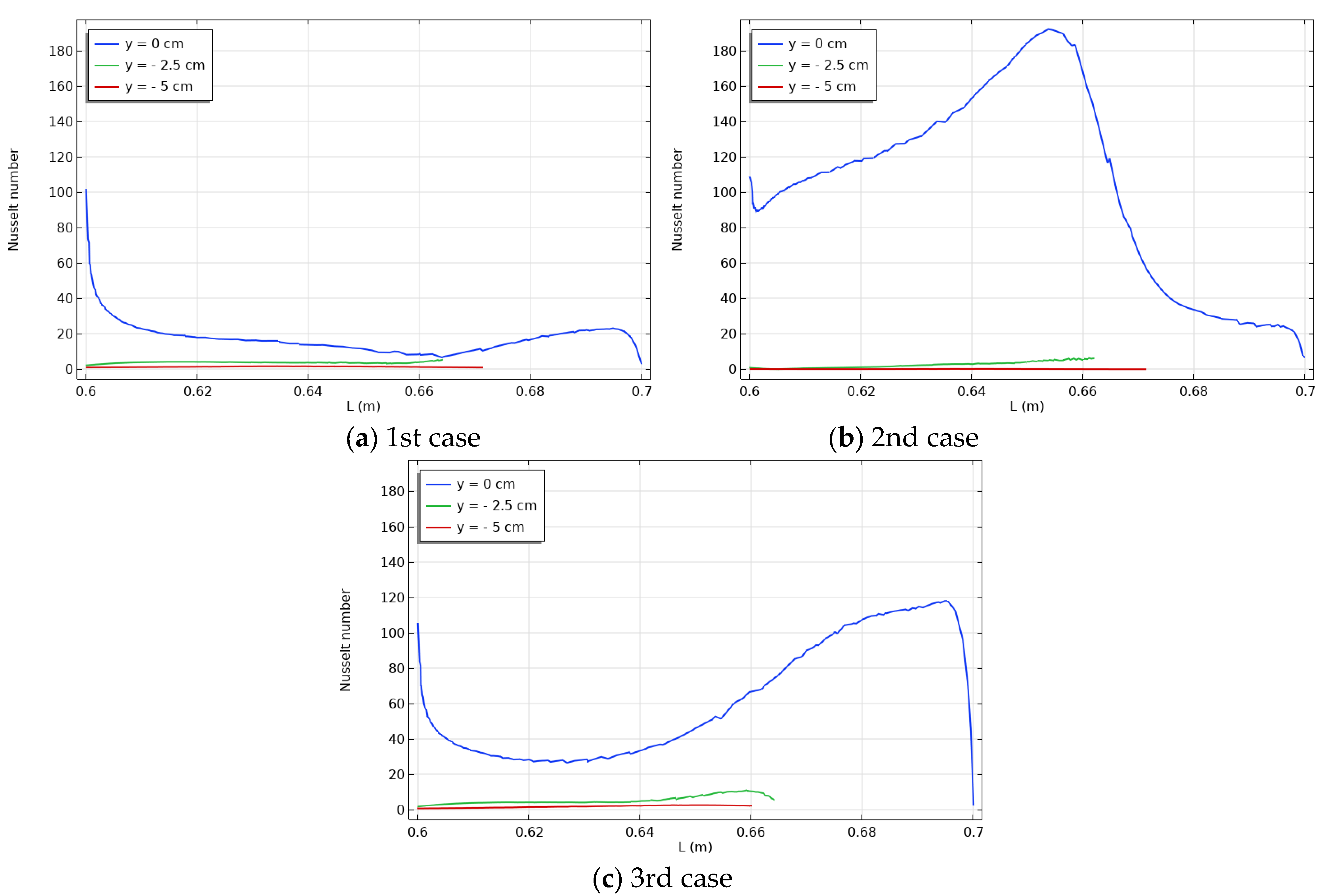
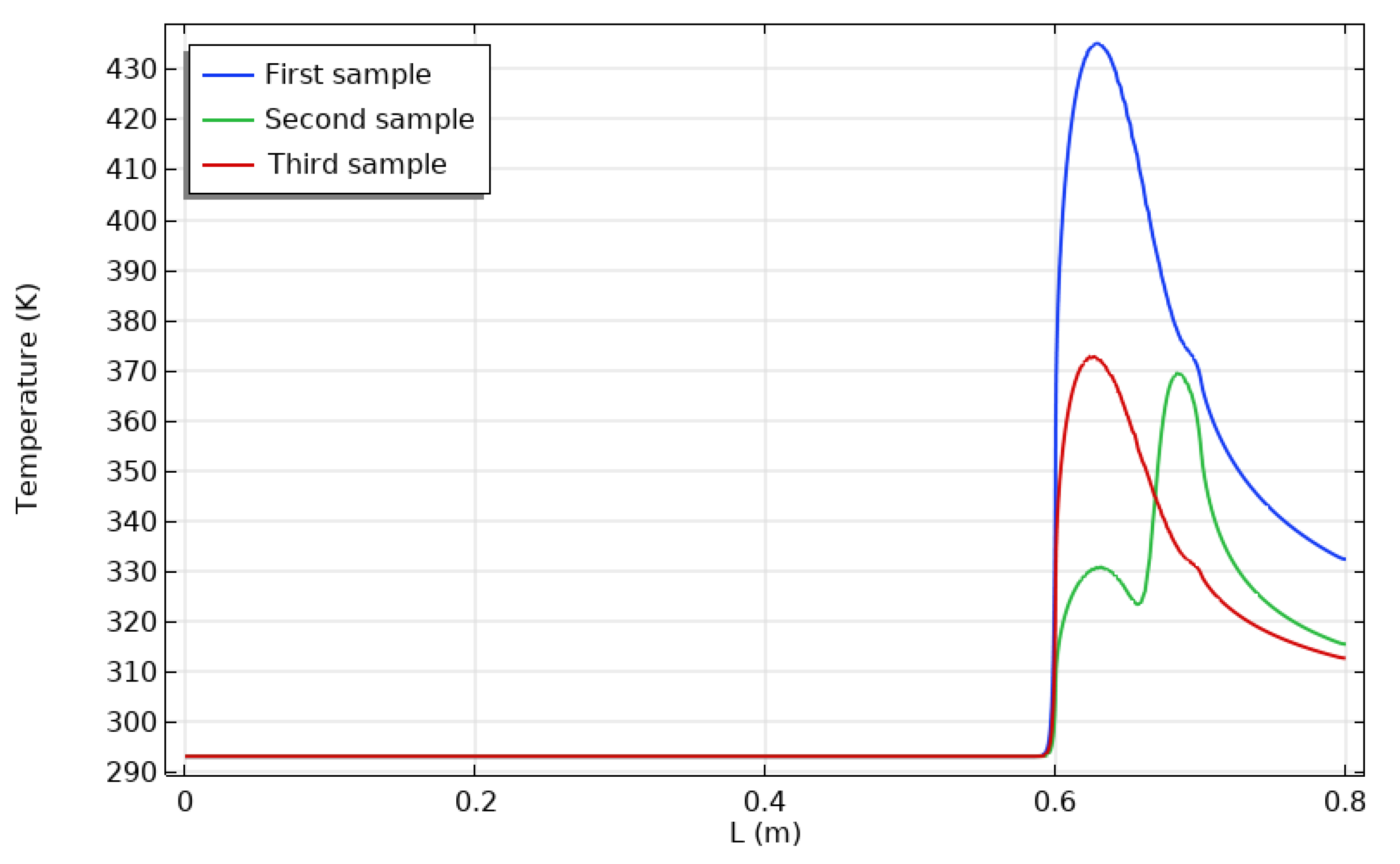
- The higher heat transmission was performed in case two because the heat source was near the contact surface between the channel and the cavity.
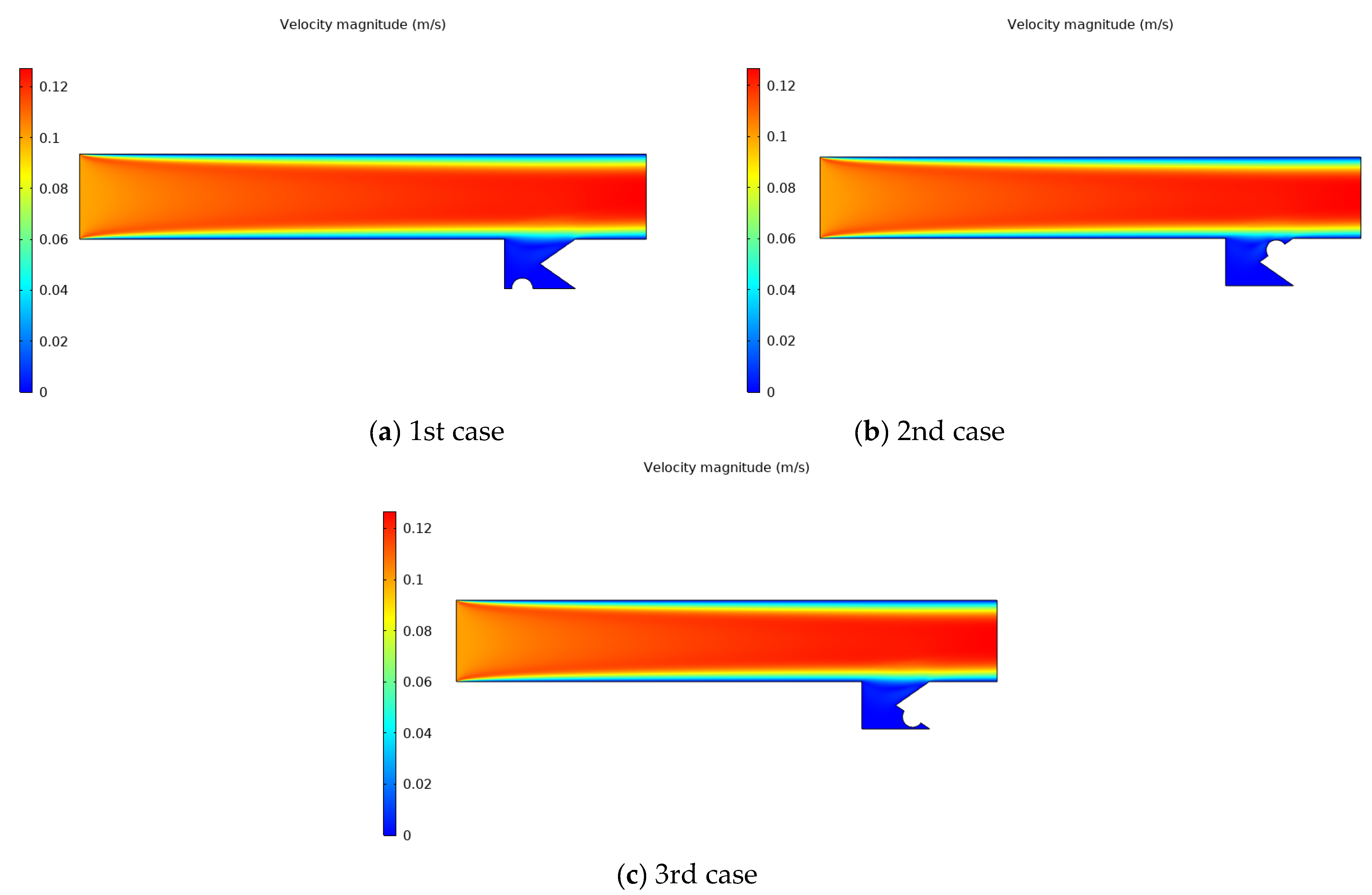
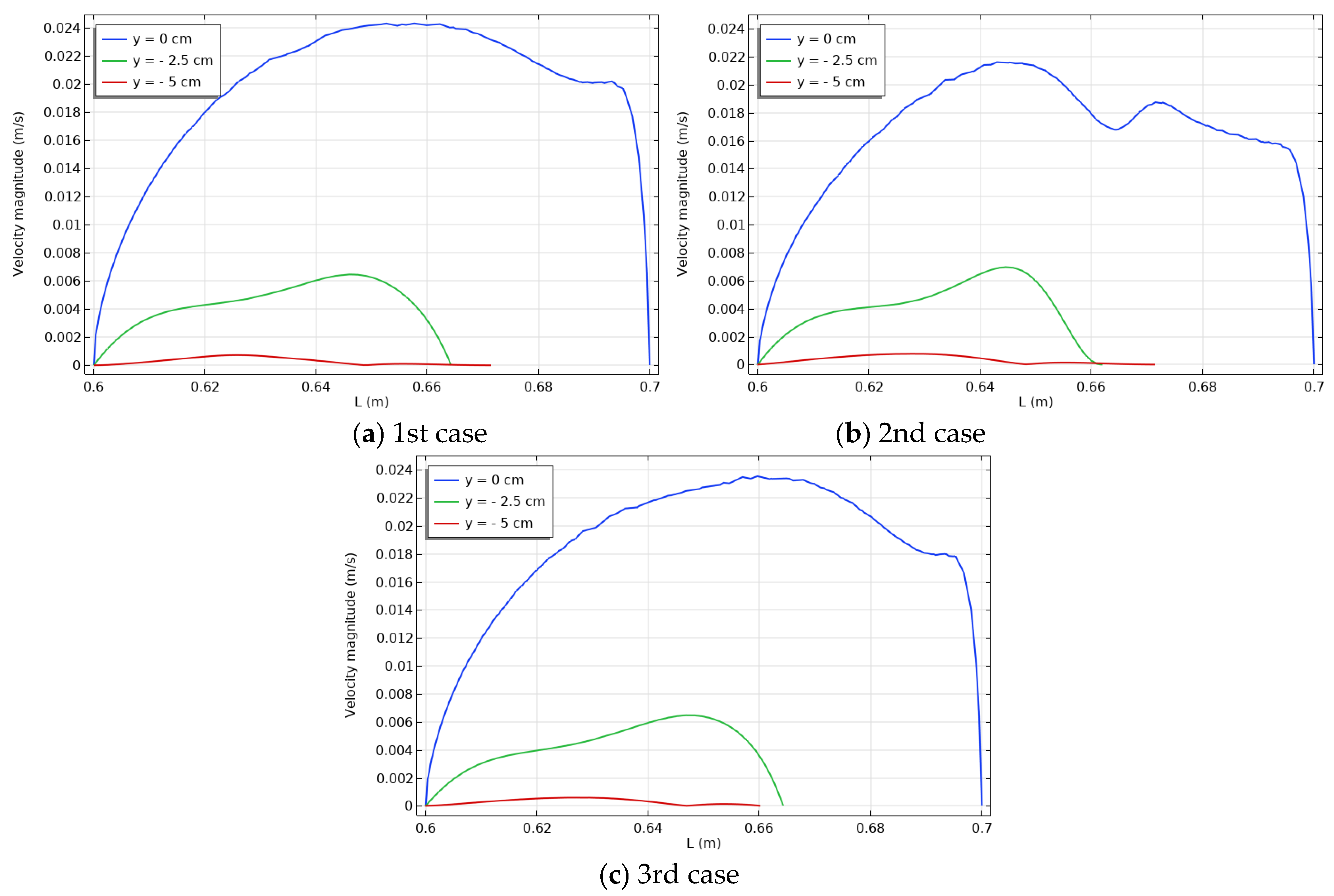
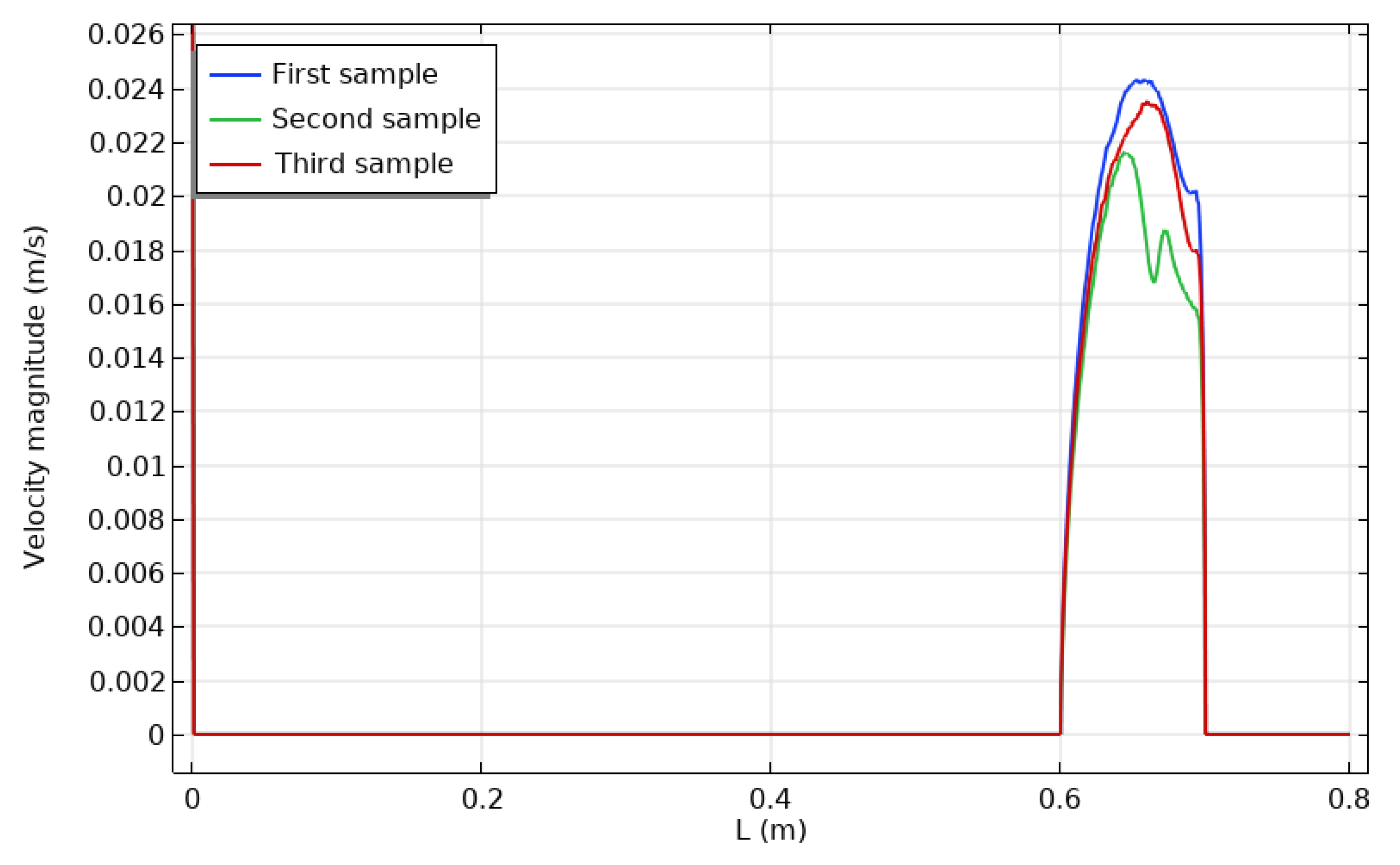
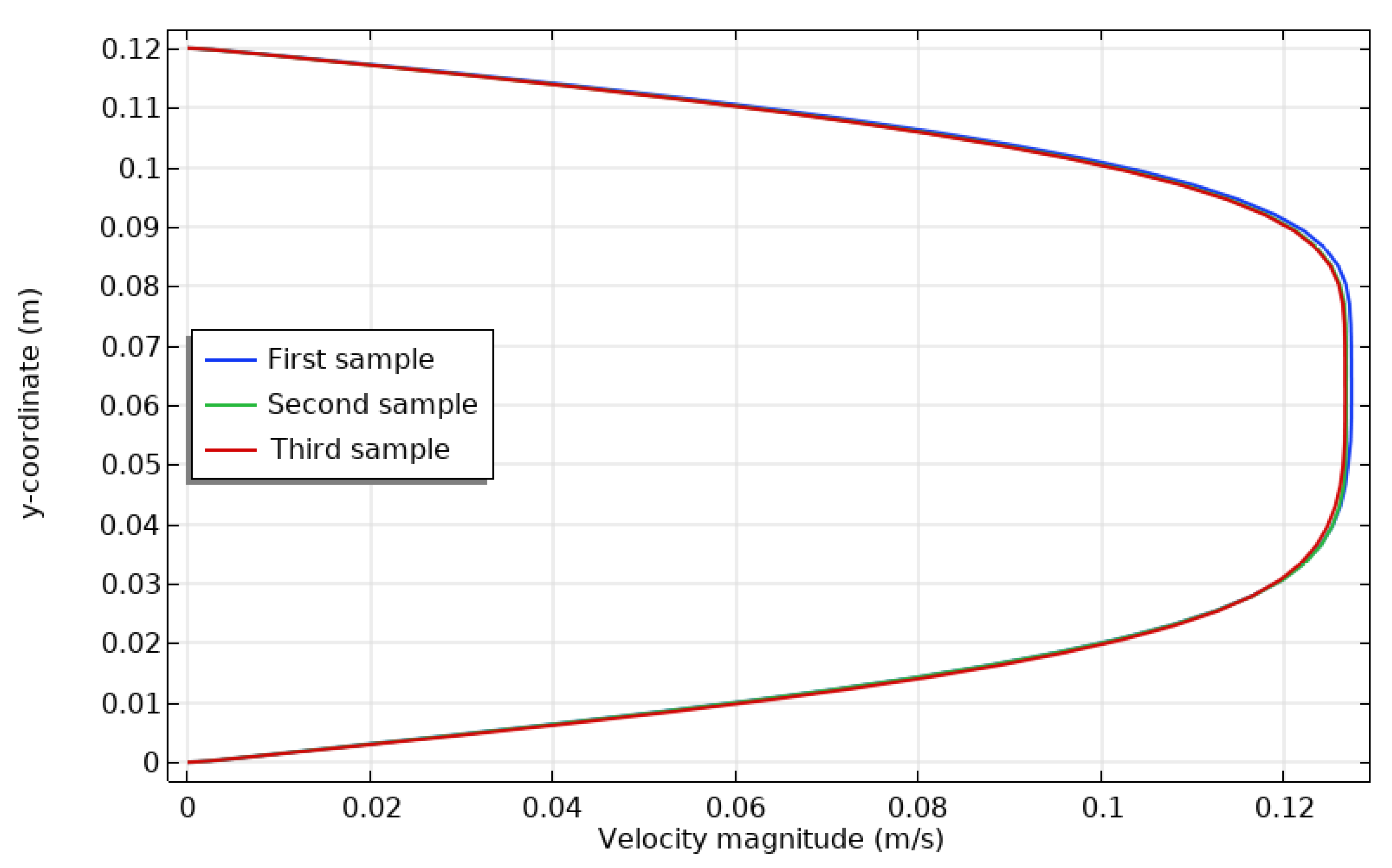
- The velocity distribution seems unaffected by changing the location of heated sources.
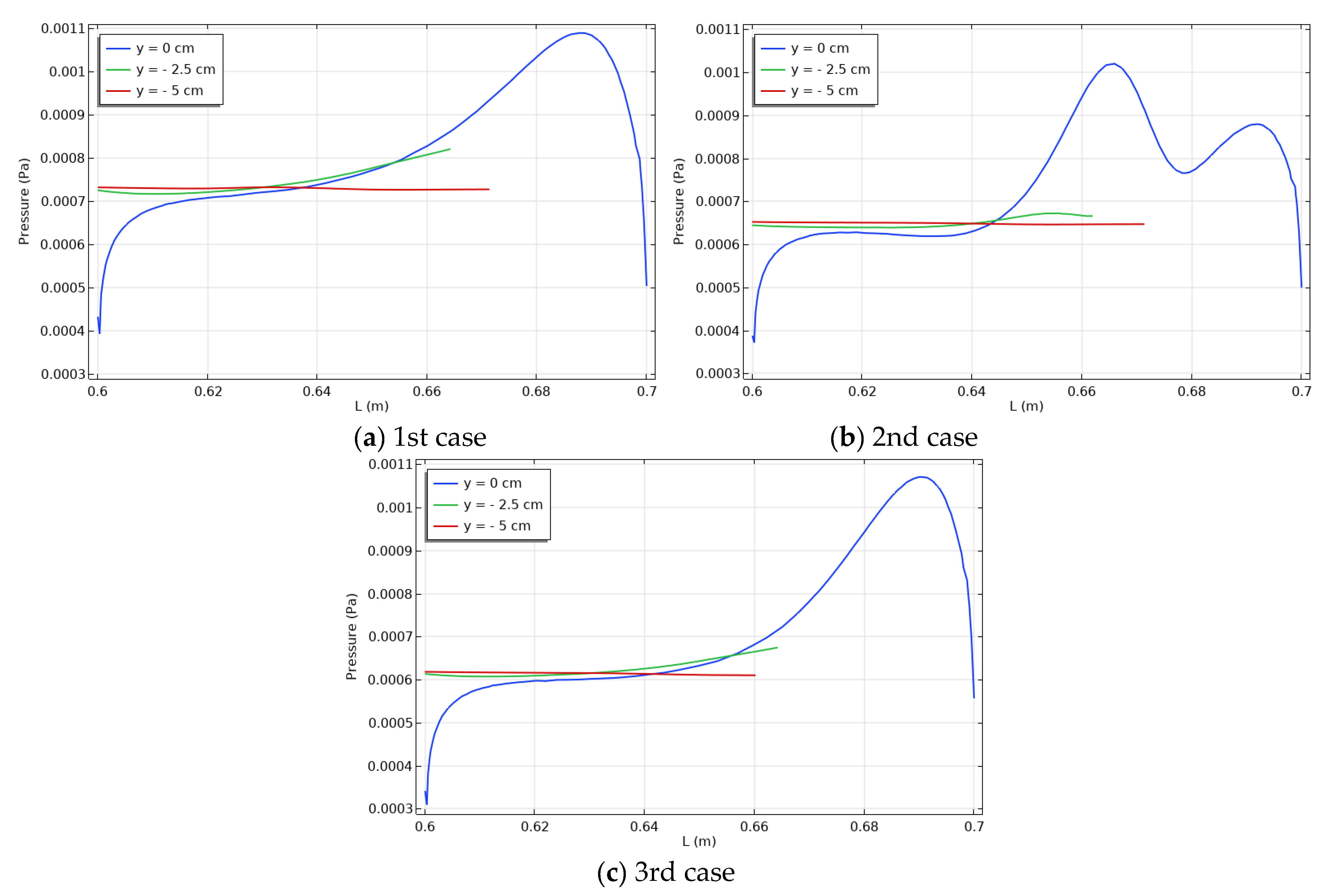
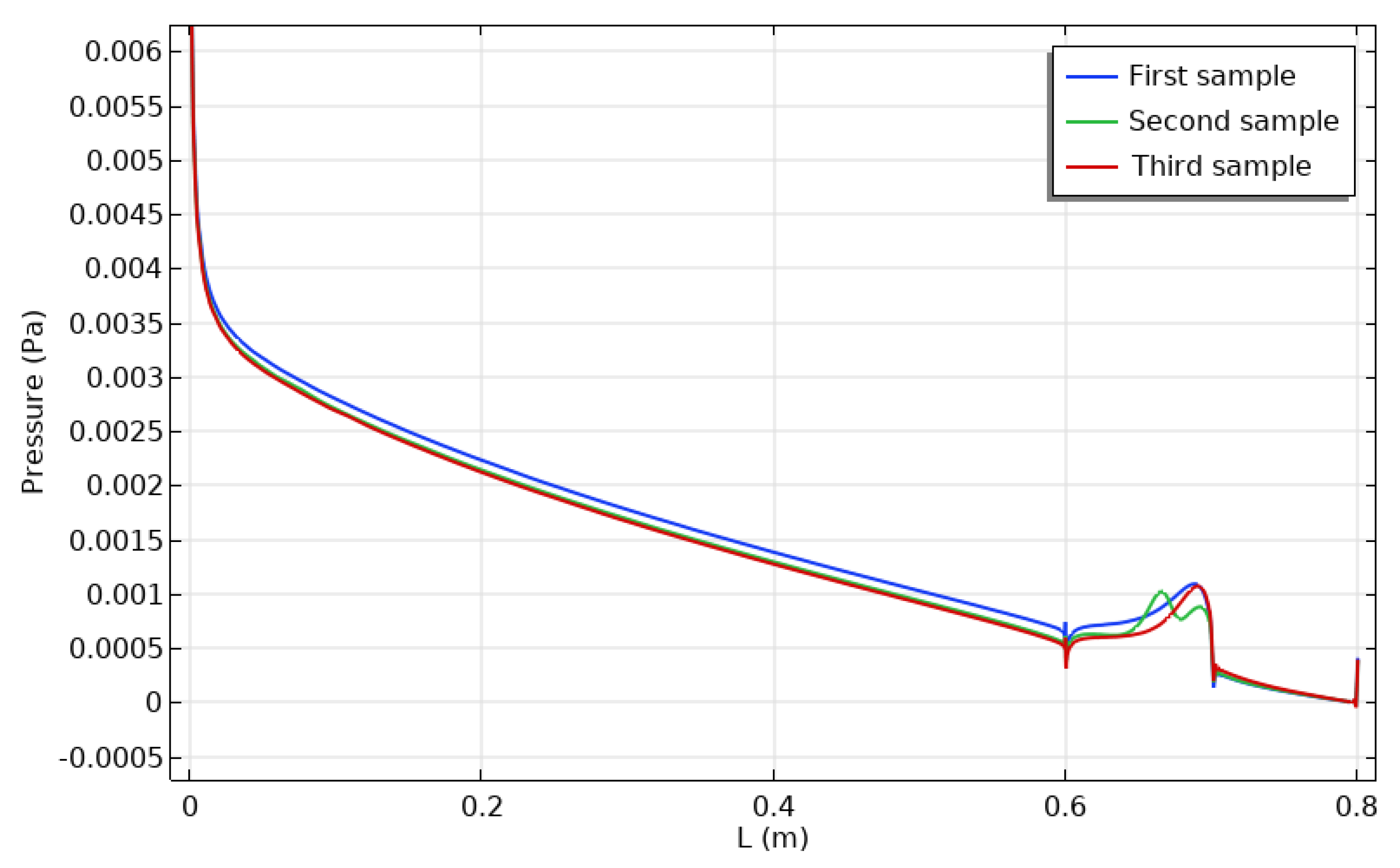
- The pressure distribution along the channel was unaffected by the rise in the positive y axis.
- The pressure distribution seems unaffected by changing the location of the heated source.
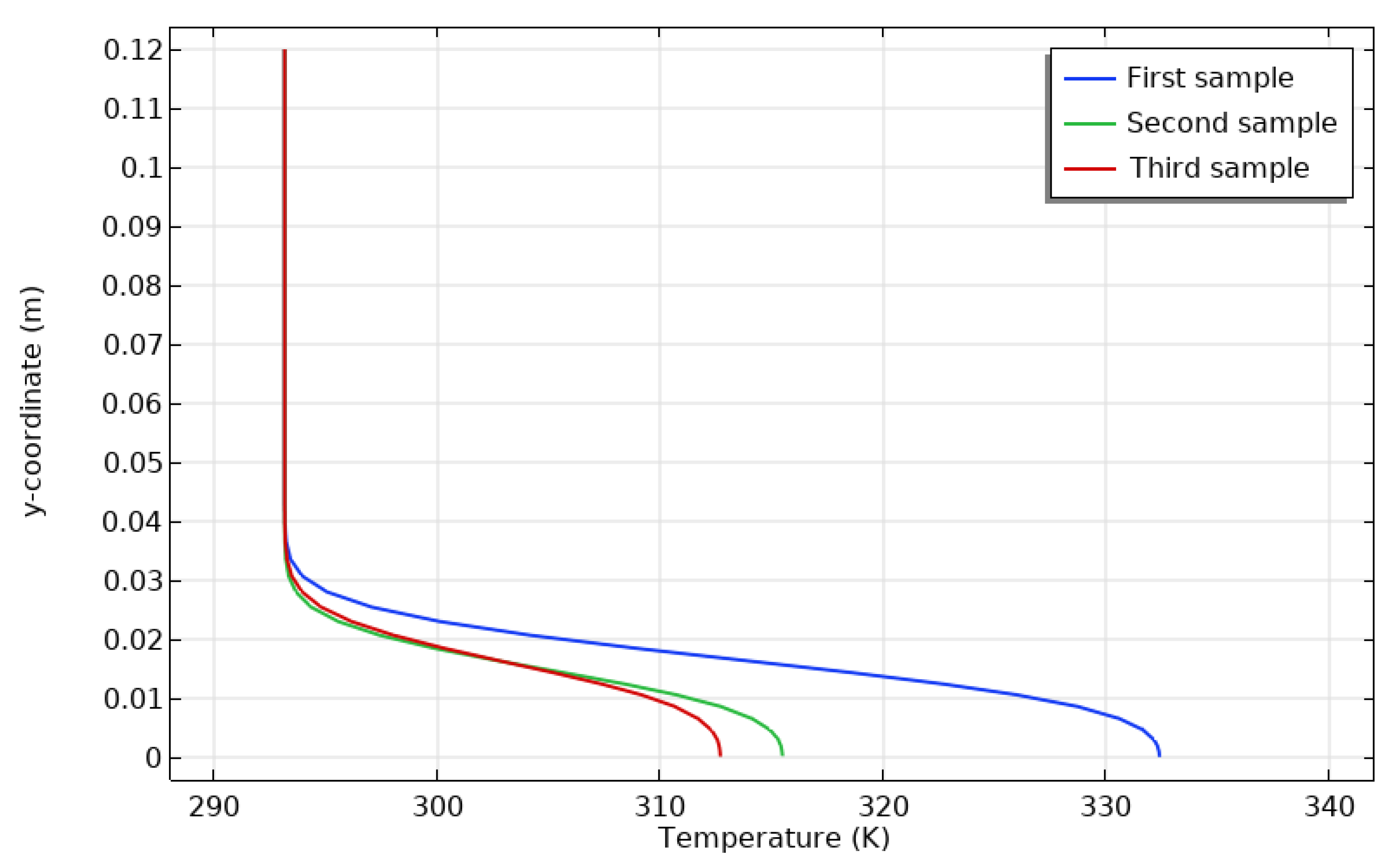
- At y = 0.035 m, the air density profile began to differ from one case to another, the third case had the largest value than the second, and the latter had the largest value in density distribution than the first case.
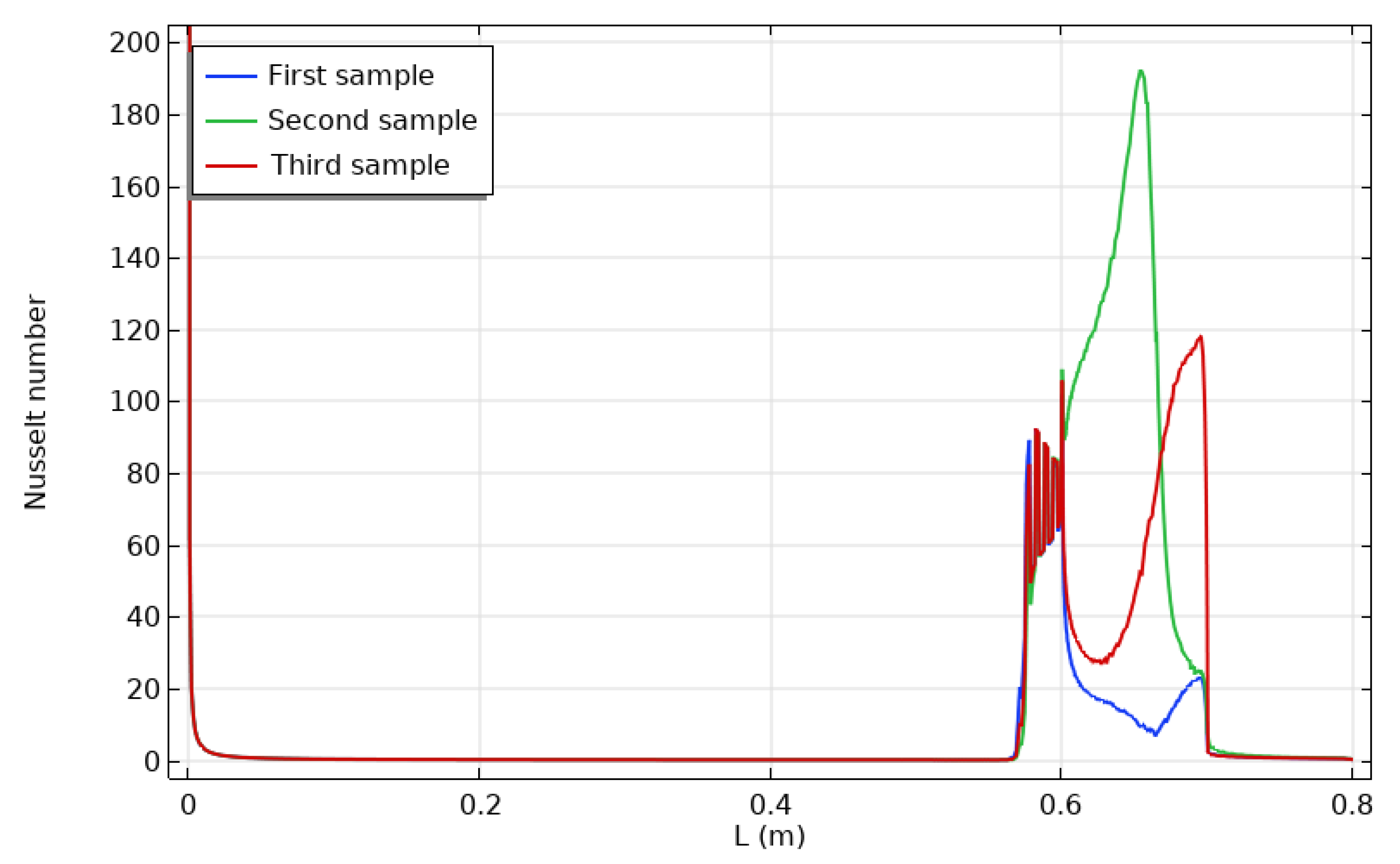
- The highest heat transmission occurred at the interface between the enclosure and the channel (y = 0), where the maximum Nusselt number also occurred. As y increased in absolute value, the maximum Nusselt number decreased.
- First and third cases had the same pressure distribution, while the second case caused more recirculating streamlines than the other cases because the air stream impinged with the heat source and thus increased the recirculation of the air stream at this zone.
- The three cases had the same local velocity distribution, except at the first half of the enclosure, where the first case had a larger local velocity than the third case, and the second case had the lowest local velocity.
- The investigation of the influence of magnetic field, tilt angle, vibration, and oscillation on mixed convection heat transfer in a channel–cavity assembly will be the focus of future work related to this research project.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Definition (unit) |
| D | Tube diameter (m) |
| L | Tube length (m) |
| W | Cavity width (m) |
| H | Cavity height (m) |
| r | Spherical radius of heat source in cavity (m) |
| Tin | Inlet temperature of flow (K) |
| V | Flow velocity (m/s) |
| Pw | Heat power source in cavity (W) |
| Re | Reynolds number (--) |
| Ri | Richardson number (--) |
| Pr | Prandtl number (--) |
| Nu | Nusselt number (--) |
| g | Gravitational acceleration (m/s2) |
| P | Pressure (Pa) |
| Q | Heat flux (W/m2) |
| Greek Symbols | |
| Symbol | Definition |
| Air Density (kg/m3) | |
| Viscosity (kinematic) of air (m2/s) | |
| viscosity (dynamic) of air (kg/m.s) | |
| Localized heat source Dimensionless length | |
| Dimensionless temperature | |
| Thermal expansion coefficient (1/K) | |
| Air thermal diffusivity (m2/s) | |
| Subscripts | |
| Symbol | Definition |
| in | Inlet |
| h | Hot |
| c | Cold |
| avg | Average |
References
- Mebarek-Oudina, F.; Bessaïh, R. Oscillatory mixed convection flow in a cylindrical container with rotating disk under axial magnetic field and various wall electrical conductivity. Int. Rev. Phys. 2010, 4, 45–51. [Google Scholar]
- Mebarek-Oudina, F.; Bessaïh, R. Numerical modeling of MHD stability in a cylindrical configuration. J. Frankl. Inst. 2014, 351, 667–681. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Qasem, N.A.A.; Younis, O.; Marzouki, R.; Mourad, A.; Shah, N.A.; Chung, J.D. MHD Hybrid Nanofluid Mixed Convection Heat Transfer and Entropy Generation in a 3-D Triangular Porous Cavity with Zigzag Wall and Rotating Cylinder. Mathematics 2022, 10, 769. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Kumar, M.D.; Raju, C.S.K.; Sajjan, K.; El-Zahar, E.R.; Shah, N.A. Linear and quadratic convection on 3D flow with transpiration and hybrid nanoparticles. Int. Commun. Heat Mass Transfer 2022, 134, 105995. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F. Convective heat transfer of Titania nanofluids of different base fluids in cylindrical annulus with discrete heat source. Heat Transfer—Asian Res. 2019, 48, 135–147. [Google Scholar] [CrossRef]
- Younis, O.; Rashid, F.; Khalaf, A.; Hussein, A.; Ben Hamida, M.; Ali, B. Thermal-hydraulic analysis of transient conjugate heating between hemi-spherical body and air. Front. Heat Mass Transf. (FHMT) 2022, 19, 21. [Google Scholar] [CrossRef]
- Salhi, J.E.; Amghar, K.; Bouali, H.; Salhi, N. Combined Heat and Mass Transfer of Fluid Flowing through Horizontal Channel by Turbulent Forced Convection. Model. Simul. Eng. 2020, 2020, 1453893. [Google Scholar] [CrossRef]
- Younis, O.; Rashid, F.; Fakhrulddin, S.; Eleiwi, M.; Hussein, A.; Tahseen, T.; Ahmed, M. CFD Simulation In Thermal-Hydraulic Analysis of Air Flow on Different Attack Angles of Row Flat Tube. Front. Heat Mass Transf. (FHMT) 2022, 19, 6. [Google Scholar] [CrossRef]
- Ahmadinejad, M.; Soleimani, A.; Gerami, A. Performance enhancement of a photovoltaic thermal (PVT) system with sinusoidal fins: A quasi-transient energy-exergy analysis. Int. J. Green Energy 2022, 2131, 434. [Google Scholar] [CrossRef]
- Al-Jibory, M.W.; Rashid, F.L.; Talib, S.M. Numerical Investigation of Heat Transfer Enhancement in Ribbed Elliptical Passage. J. Eng. Appl. Sci. 2018, 13, 7223–7234. [Google Scholar]
- Cha, C.K.; Jaluria, Y. Recirculating mixed convection flow for energy extraction. Int. J. Heat Mass Transf. 1984, 27, 1801–1810. [Google Scholar] [CrossRef]
- Imberger, J.; Hamblin, P.F. Dynamics of lake reservoirs and cooling ponds, Annu. Rev. Fluid Mech. 1982, 14, 153–187. [Google Scholar] [CrossRef]
- Ideriah, F.J.K. Prediction of turbulent cavity flow driven by buoyancy and shear. J. Mech. Engng. Sci. 1980, 22, 287–295. [Google Scholar] [CrossRef]
- Pilkington, L.A.B. Review lecture: The float glass process. Proc. R. Soc. Lond. A 1969, 314, 1–25. [Google Scholar]
- Schriber, R.; Keller, H.B. Driven cavity flows by efficient numerical techniques. J. Comput. Phys. 1983, 49, 310–333. [Google Scholar] [CrossRef]
- Thompson, M.C.; Ferziger, J.H. An adaptive multigrid technique for the incompressible Navier–Stokes equations. J. Comput. Phys. 1989, 82, 94–121. [Google Scholar] [CrossRef]
- Abd Al-Hassan, A.Q.; Ismael, M.A. Numerical Study of Double Diffusive Mixed Convection in Horizontal Channel with Composite Opeb Porous Cavity. Spec. Top. Rev. Porous Media Int. J. 2019, 10, 401–419. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Niroumand, A.H.; Yan, W.M.; Karimipour, A. Mixed convection heat transfer from surface-mounted block heat sources in a horizontal channel with nanofluids. Int. J. Heat Mass Transf. 2015, 89, 783–791. [Google Scholar] [CrossRef]
- Rahul, K.C. Numerical Simulations of Mixed Convection from a Horizontal Channel with Radiating Heat Sources. Int. J. Eng. Res. Technol. 2017, 6, 49–57. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Janagi, K. Numerical Study on Mixed Convection Flow and Energy Transfer in an Inclined Channel Cavity: Effect of Baffle Size. Math. Comput. Appl. 2022, 27, 9. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Laouira, H.; Aissa, A.; Hussein, A.K.; El Ganaoui, M. Convection Heat Transfer Analysis in a Channel with an Open Trapezoidal Cavity: Heat Source Locations effect. MATEC Web Conf. 2020, 330, 01006. [Google Scholar] [CrossRef]
- Bahlaoui, A.; Raji, A.; Hasnaoui, M.; Ouardi, C.; Naïmi, M.; Makayssi, T. Height Partition Effect on Combined Mixed Convection and Surface Radiation in a Vented Rectangular Cavity. J. Appl. Fluid Mech. 2011, 4, 89–96. [Google Scholar]
- Rajamohan, G.; Ramesh, N.; Kumar, P. Mixed convection and radiation studies on thermally developing laminar flow in a horizontal square channel with variable side heated wall. Int. J. Therm. Sci. 2019, 140, 298–307. [Google Scholar] [CrossRef]
- Gangawane, K.M.; Gupta, S. Mixed convection characteristics in rectangular enclosure containing heated elliptical block: Effect of direction of moving wall. Int. J. Therm. Sci. 2018, 130, 100–115. [Google Scholar] [CrossRef]
- Ding, G.; Li, N.; Liu, B.; Li, J.; Xiao, Y.; Gu, H. Numerical study of mixed and free convection heat transfer under ocean conditions. Int. J. Heat Mass Transf. 2023, 203, 123811. [Google Scholar] [CrossRef]
- Everts, M.; Mahdavi, M.; Meyer, J.P.; Sharifpur, M. Development of the hydrodynamic and thermal boundary layers of mixed convective laminar flow through a horizontal tube with a constant heat flux. Int. J. Therm. Sci. 2023, 187, 108178. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, F.; Wang, J. Mixed convection heat transfer and transient flow of high-pressure gas in a large-scale cavity with rotating blade. Int. J. Therm. Sci. 2023, 187, 108205. [Google Scholar] [CrossRef]
- Moradi, R.; Mahyari, A.; Gerdroodbary, M.B.; Abdollahi, A.; Amini, Y. Shape effect of cavity flameholder on mixing zone of hydrogen jet at supersonic flow. Int. J. Hydrogen Energy 2018, 43, 16364–16372. [Google Scholar] [CrossRef]
- Yaseen, D.T.; Ismael, M.A. Effect of Deformable Baffle on the Mixed Convection of Non-Newtonian Fluids in a Channel-Cavity. Basrah J. Eng. Sci. 2020, 20, 18–26. [Google Scholar] [CrossRef]
- Li, Z.; Li, C. Non-Gaussian non-stationary wind pressure forecasting based on the improved empirical wavelet transform. J. Wind Eng. Ind. Aerodyn. 2018, 179, 541–557. [Google Scholar] [CrossRef]
- Perna, R.; Abela, M.; Mameli, M.; Mariotti, A.; Pietrasanta, L.; Marengo, M.; Filippeschi, S. Flow characterization of a pulsating heat pipe through the wavelet analysis of pressure signals. Appl. Therm. Eng. 2020, 171, 115128. [Google Scholar] [CrossRef]
- Ota, T.; Nishiyama, H.; Taoka, Y. Heat transfer and flow around an elliptic cylinder. Int. J. Heat Mass Transf. 1984, 27, 1771–1779. [Google Scholar]
- Howard, F.; Goodman, W. Axisymmetric bluff-body drag reduction through geometrical modification. J. Aircr. 1985, 22, 516–522. [Google Scholar] [CrossRef]
- Selby, G.V.; Lin, J.C.; Howard, F.G. Turbulent Flow Separation Control Over a Backward-Facing Ramp Via Transverse and Swept Grooves. J. Fluids Eng. 1990, 112, 238–240. [Google Scholar] [CrossRef]
- Ota, T.; Aiba, S.; Tsuruta, T.; Kaga, M. Forced convection heat transfer from an elliptical cylinder with axis ratio 1:3. Bull. JSME 1983, 26, 262–267. [Google Scholar] [CrossRef]
- Moallemi, M.K.; Jang, K.S. Prandtl number effects on laminar mixed convection heat transfer in a lid-driven cavity. Int. J. Heat Mass Transf. 1992, 35, 1881–1892. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Siginer, D.A.; Wang, H.P. Enhancing Thermal Conductivity of Fluids with Nanoparticles Development and Applications of Non-Newtonian Flows; The American Society of Mechanical Engineers: New York, NY, USA, 1995; Volume 231, pp. 99–105. [Google Scholar]
- Liang, H.; You, S.; Zhang, H. Comparison of three optical models and analysis of geometric parameters for parabolic trough solar collectors. Energy 2016, 96, 37–47. [Google Scholar] [CrossRef]
- Bortolato, M.; Dugaria, S.; Col, D.D. Experimental study of a parabolic trough solar collector with flat bar-and-plate absorber during direct steam generation. Energy 2016, 116, 1039–1050. [Google Scholar] [CrossRef]

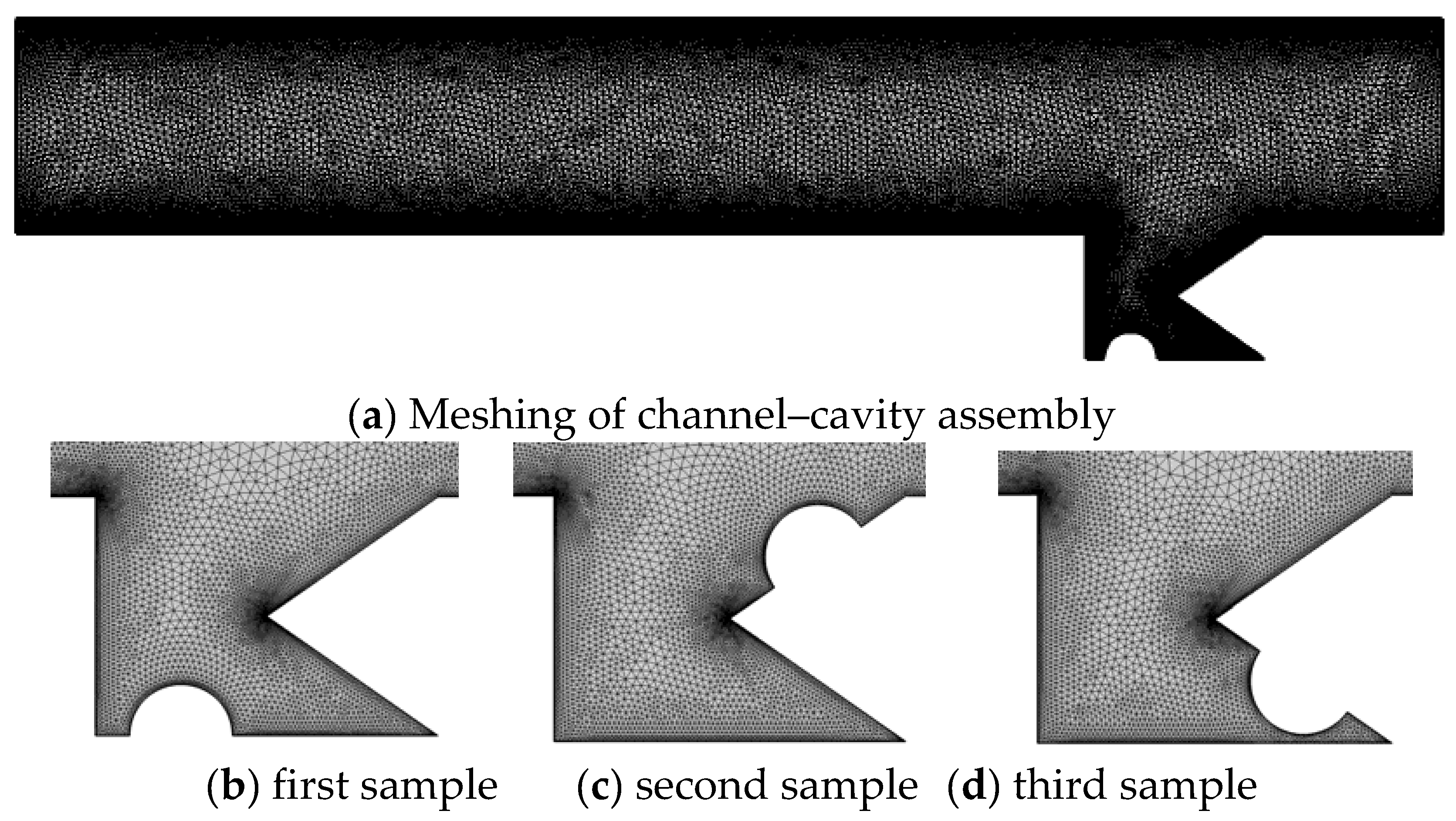

| Symbol | Value | Description |
|---|---|---|
| D | 12 cm | Tube diameter |
| L | 80 cm | Tube length |
| W | 10 cm | Cavity width |
| H | 7 cm | Cavity height |
| r | 1.5 cm | Spherical radius of heat source in cavity |
| Tin | 20 °C | Inlet temperature of flow |
| Vin | 0.1 m/s | Inlet velocity (Reynolds number = 2.8814) |
| Pw | 20 W | Heat power source in cavity |
| Density of Component | Case | Number of Total Cell | Velocity Magnitude (m/s) | |
|---|---|---|---|---|
| 0.1 | 1 | 43,157 | 0.082 | -- |
| 2 | 160,050 | 0.092 | 12.195 | |
| 3 | 211,300 | 0.094 | 2.174 | |
| 4 | 292,500 | 0.095 | 1.064 | |
| 0.2 | 1 | 34,220 | 0.062 | -- |
| 2 | 78,340 | 0.072 | 16.129 | |
| 3 | 137,550 | 0.074 | 2.778 | |
| 4 | 212,200 | 0.075 | 1.351 | |
| 0.3 | 1 | 41,170 | 0.072 | -- |
| 2 | 61,550 | 0.082 | 13.889 | |
| 3 | 112,200 | 0.084 | 2.439 | |
| 4 | 182,000 | 0.084 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, F.L.; Al-Gaheeshi, A.M.R.; Alhwayzee, M.; Ali, B.; Shah, N.A.; Chung, J.D. Mixed Convection in a Horizontal Channel–Cavity Arrangement with Different Heat Source Locations. Mathematics 2023, 11, 1428. https://doi.org/10.3390/math11061428
Rashid FL, Al-Gaheeshi AMR, Alhwayzee M, Ali B, Shah NA, Chung JD. Mixed Convection in a Horizontal Channel–Cavity Arrangement with Different Heat Source Locations. Mathematics. 2023; 11(6):1428. https://doi.org/10.3390/math11061428
Chicago/Turabian StyleRashid, Farhan Lafta, Asseel M. Rasheed Al-Gaheeshi, Mohammed Alhwayzee, Bagh Ali, Nehad Ali Shah, and Jae Dong Chung. 2023. "Mixed Convection in a Horizontal Channel–Cavity Arrangement with Different Heat Source Locations" Mathematics 11, no. 6: 1428. https://doi.org/10.3390/math11061428
APA StyleRashid, F. L., Al-Gaheeshi, A. M. R., Alhwayzee, M., Ali, B., Shah, N. A., & Chung, J. D. (2023). Mixed Convection in a Horizontal Channel–Cavity Arrangement with Different Heat Source Locations. Mathematics, 11(6), 1428. https://doi.org/10.3390/math11061428






