Computational and Stability Analysis of MHD Time-Dependent Thermal Reaction Flow Impinging on a Vertical Porous Plate Enclosing Magnetic Prandtl Number and Thermal Radiation Effect
Abstract
1. Introduction
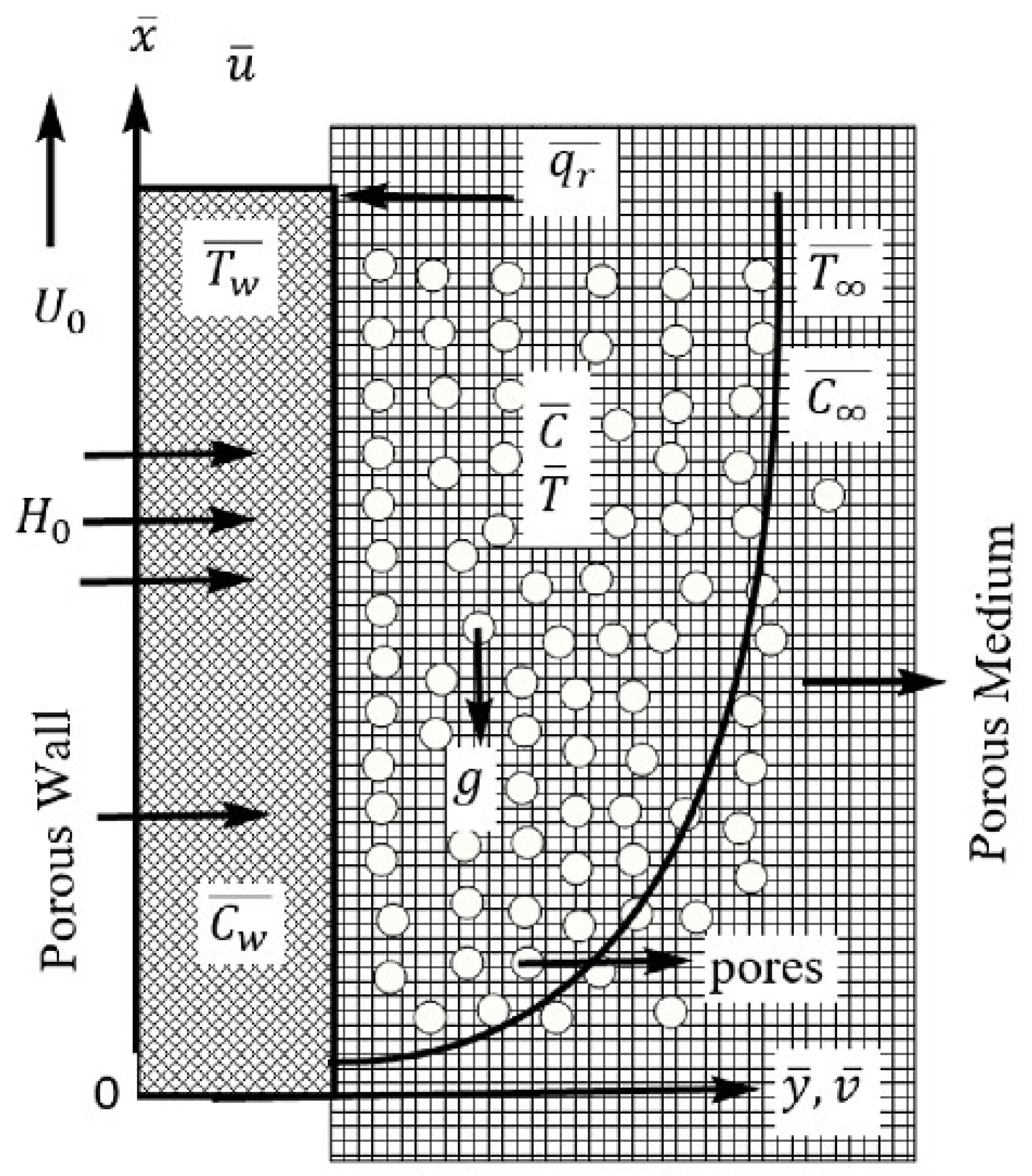
2. Mathematical Modeling
- From the accustomed Boussinesq’s approximation, the physical proper ties of the liquid cosidered are constants and body force terms include density variation with temperature.
- If the liquid flow is at high speed, the energy equation contains terms of viscous dissipation and Joule heating.
- Between foreign mass and fluid there is no chemical reaction reflected. To notice the Soret number’s effect on the liquid flow, the concentration of foreign mass is believed to be very high.
3. Mathematical Formulation
3.1. Local Shear Stress and Average Shear Stress
3.2. Local Current Density and Average Current Density
3.3. Local and Average Nusselt Number
3.4. Local and Average Sherwood Number
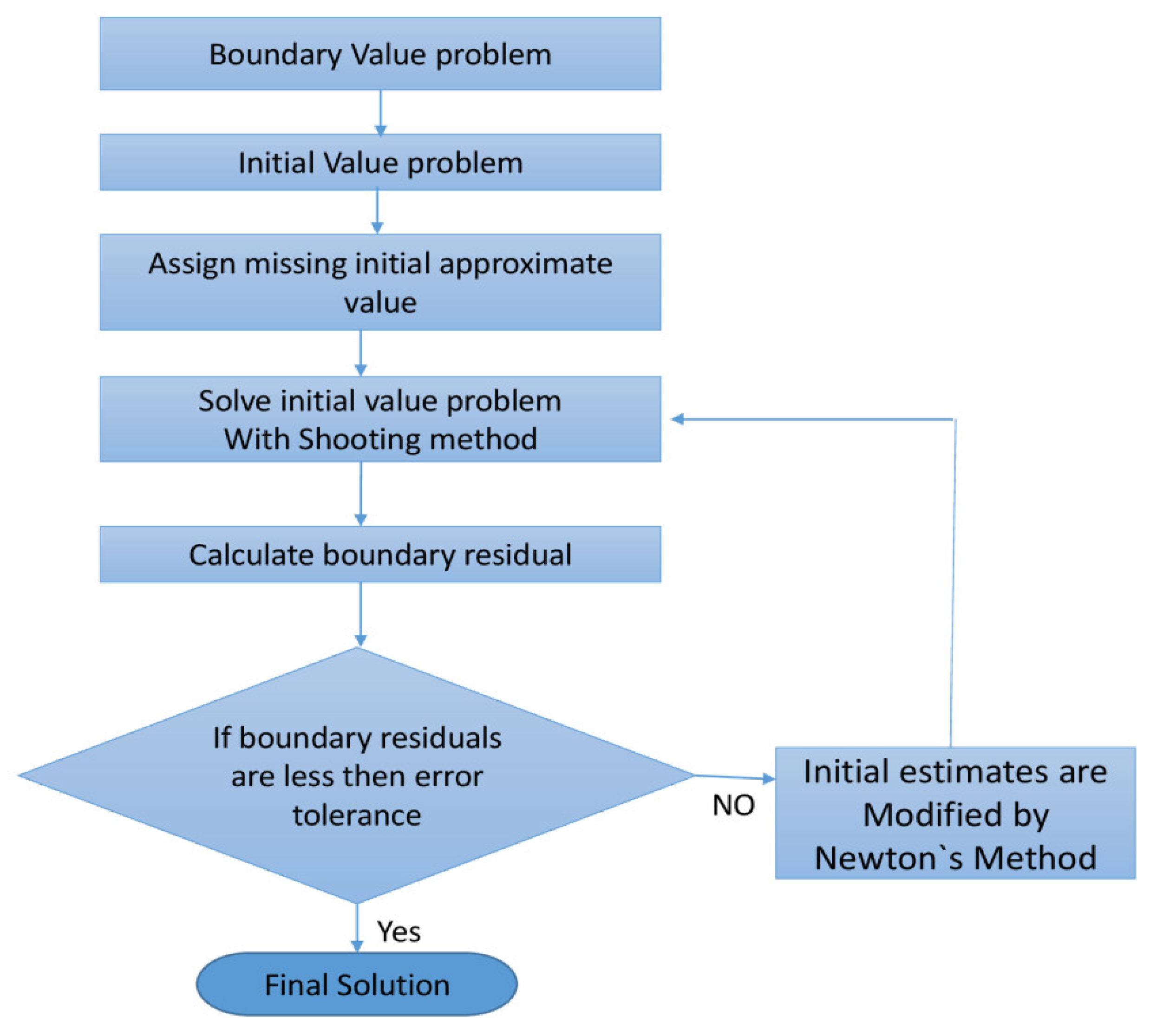
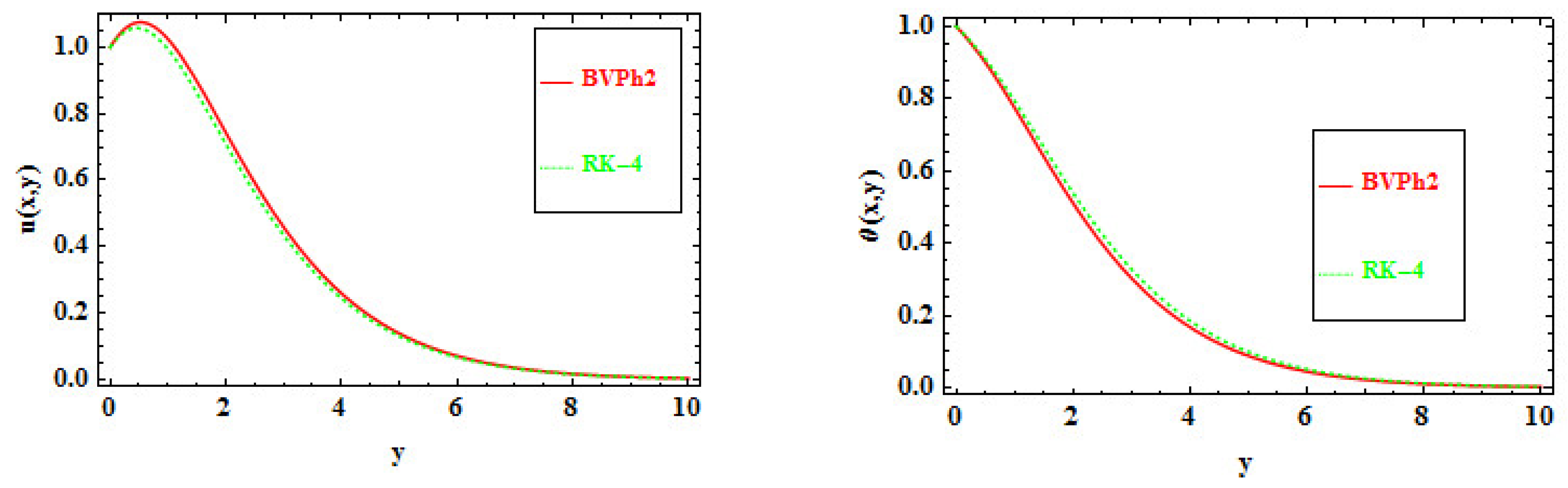
4. Numerical Solution and Confirmation of the Code
5. Stability Analysis
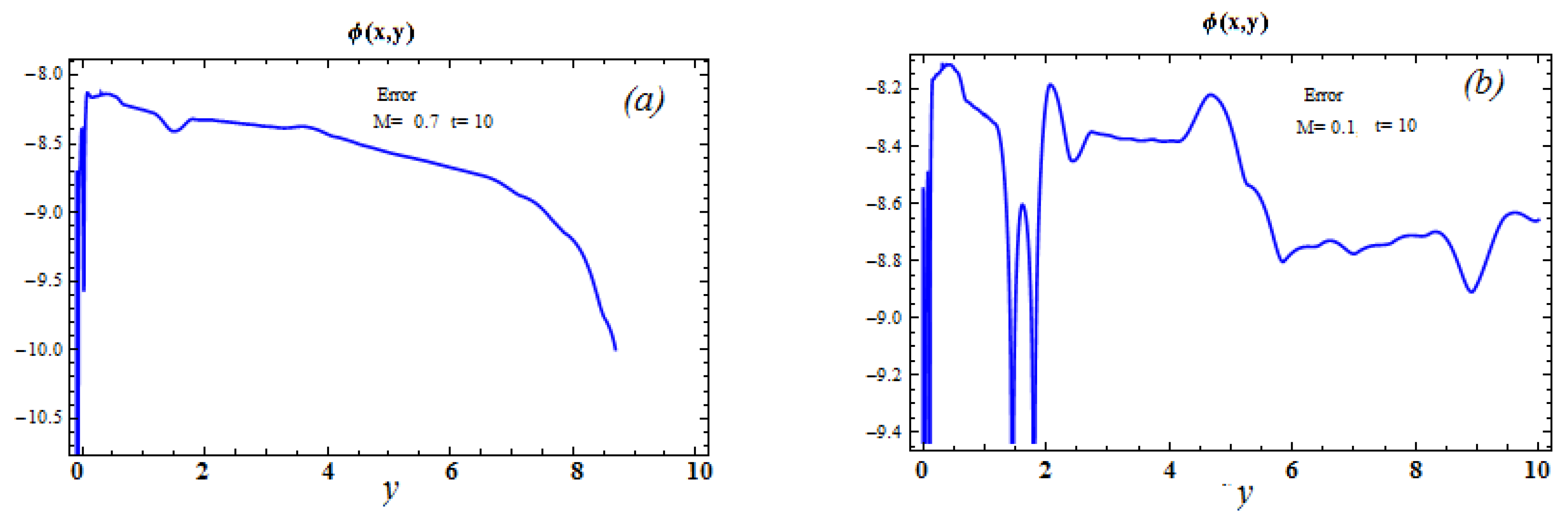
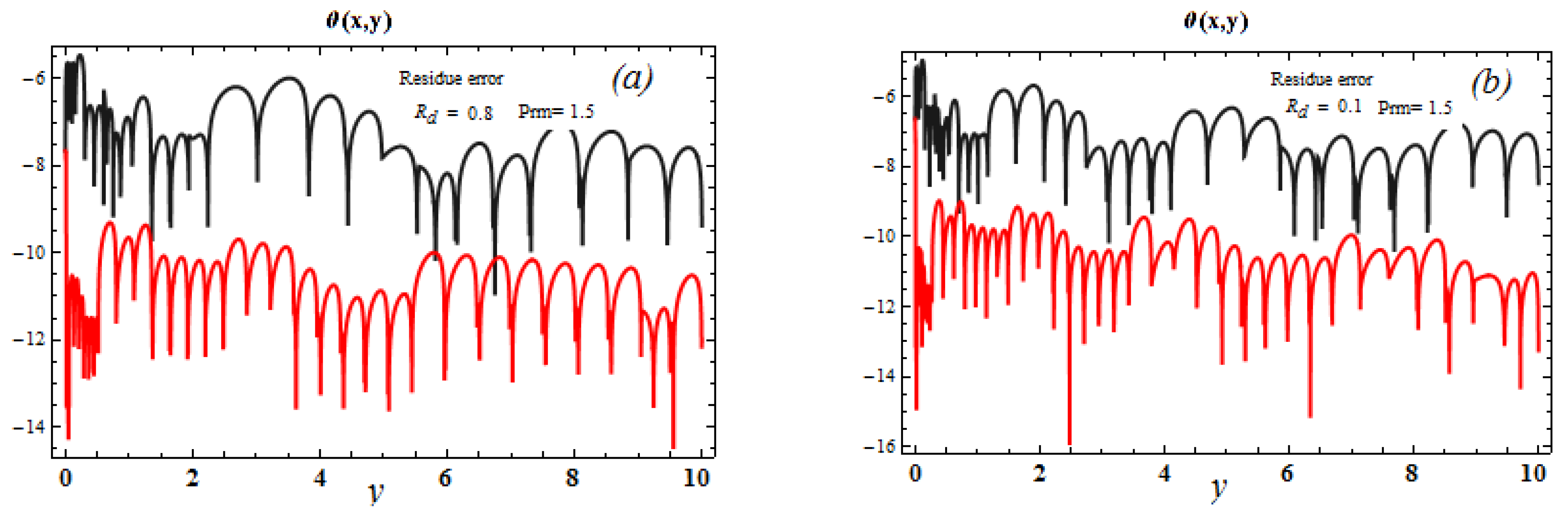
6. Error Explanation
7. Results and Discussion
8. Conclusions
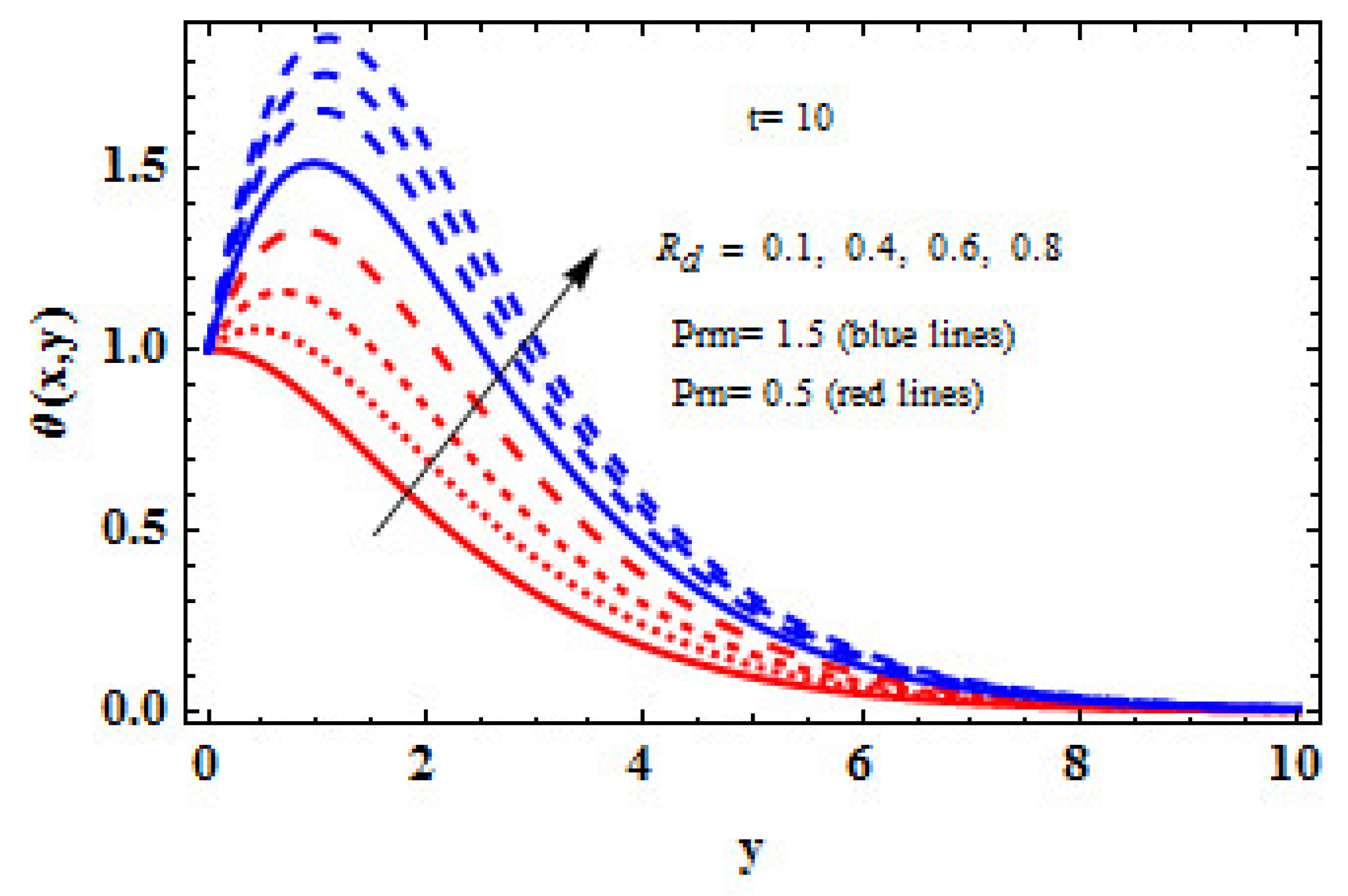
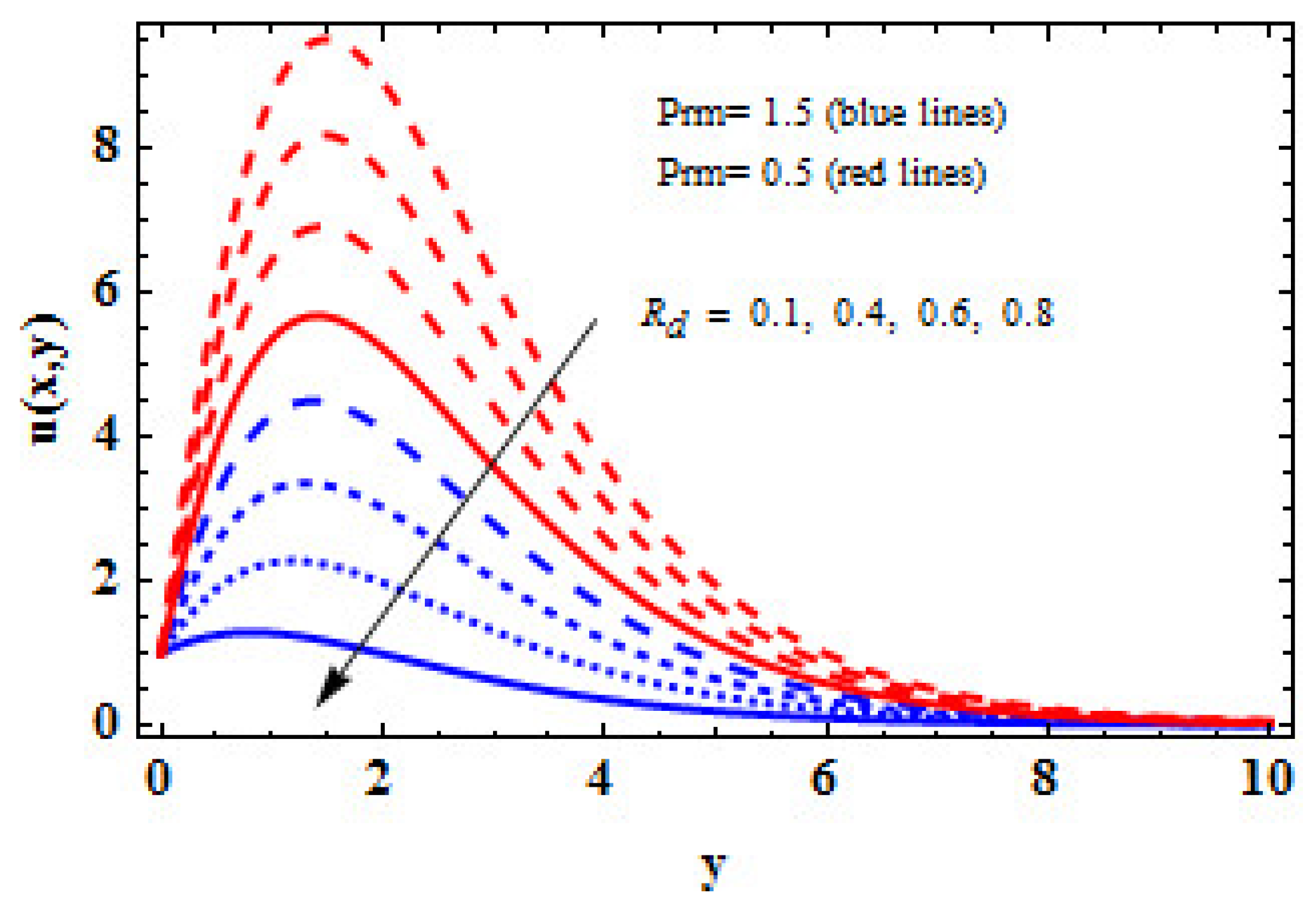
- The temperature profile of the viscous liquid appears to be enhancing as the thermal radiation factor is increased in the presence of MPN. Additionally, larger MPN corresponds to higher temperatures.
- Due to the existence of a radiation influence in the fluid flow, an upsurge in magnetic field enhances temperature distribution. It is also observed that as time passes, additional electromagnetic waves are released and the temperature rises.
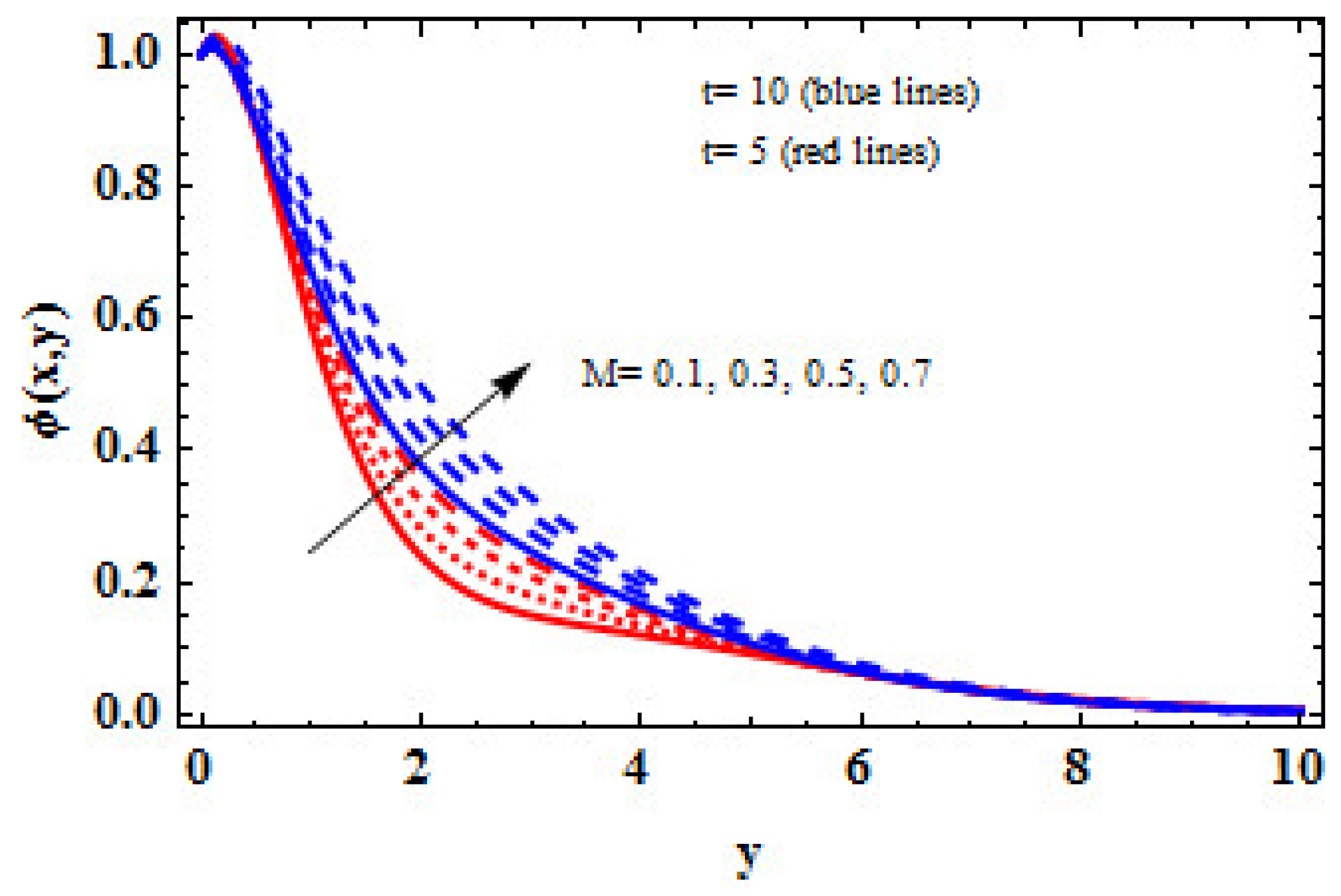
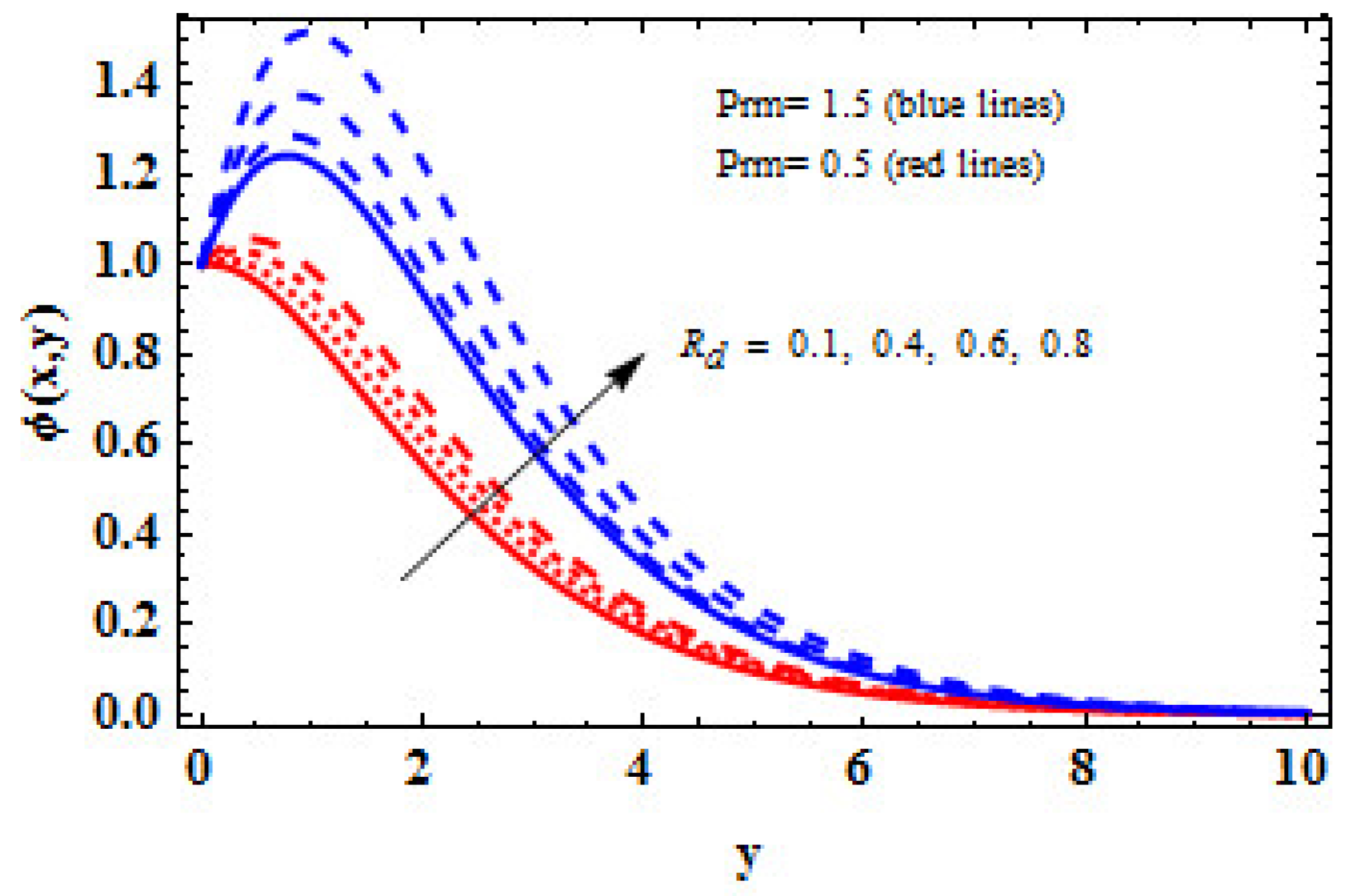
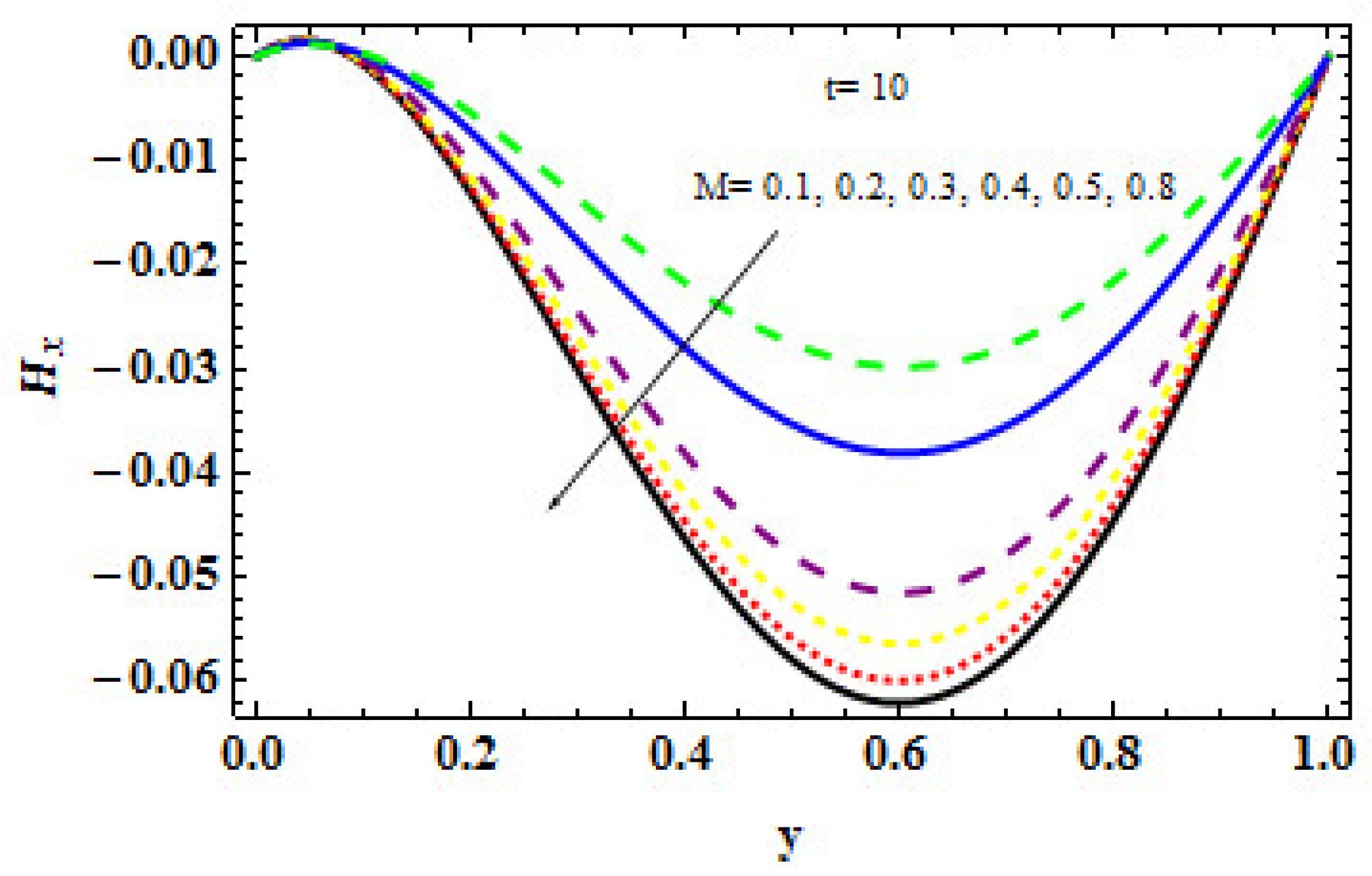
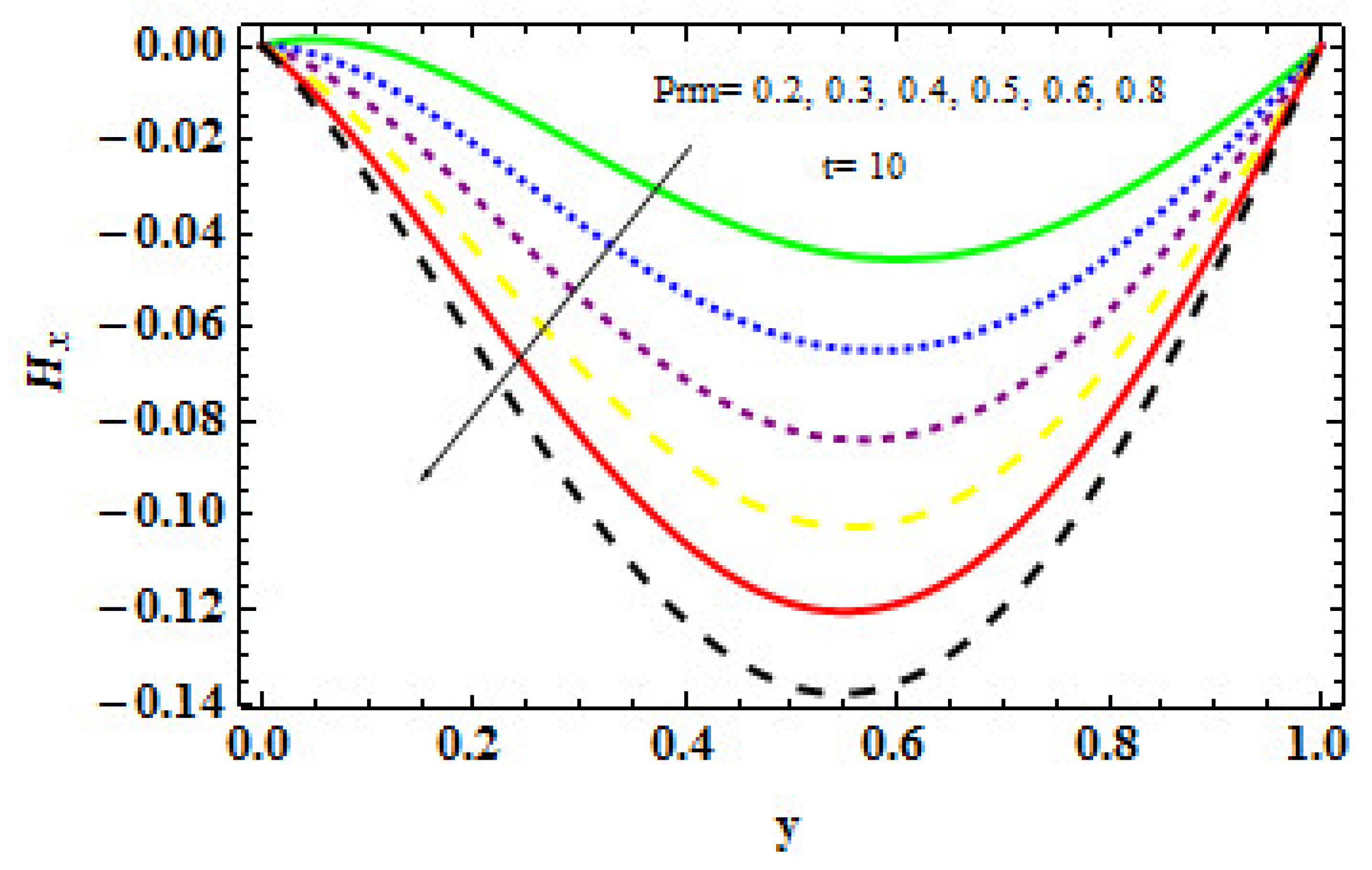
- The occurrence of magnetic field in the channel and the developing magnetic effect cause a rapid movement in the electric charge produced by the magnetic parameter, leading to a high concentration in the fluid.
- The point of interest is that the liquid flow velocity rises as the heat source parameter increases. However, as the channel progresses, velocity decreases owing to the applied magnetic field.
- It is witnessed that if the magnetic effect is enhanced for a prolonged period, an electric charge is released, which improves the concentration in the fluid.
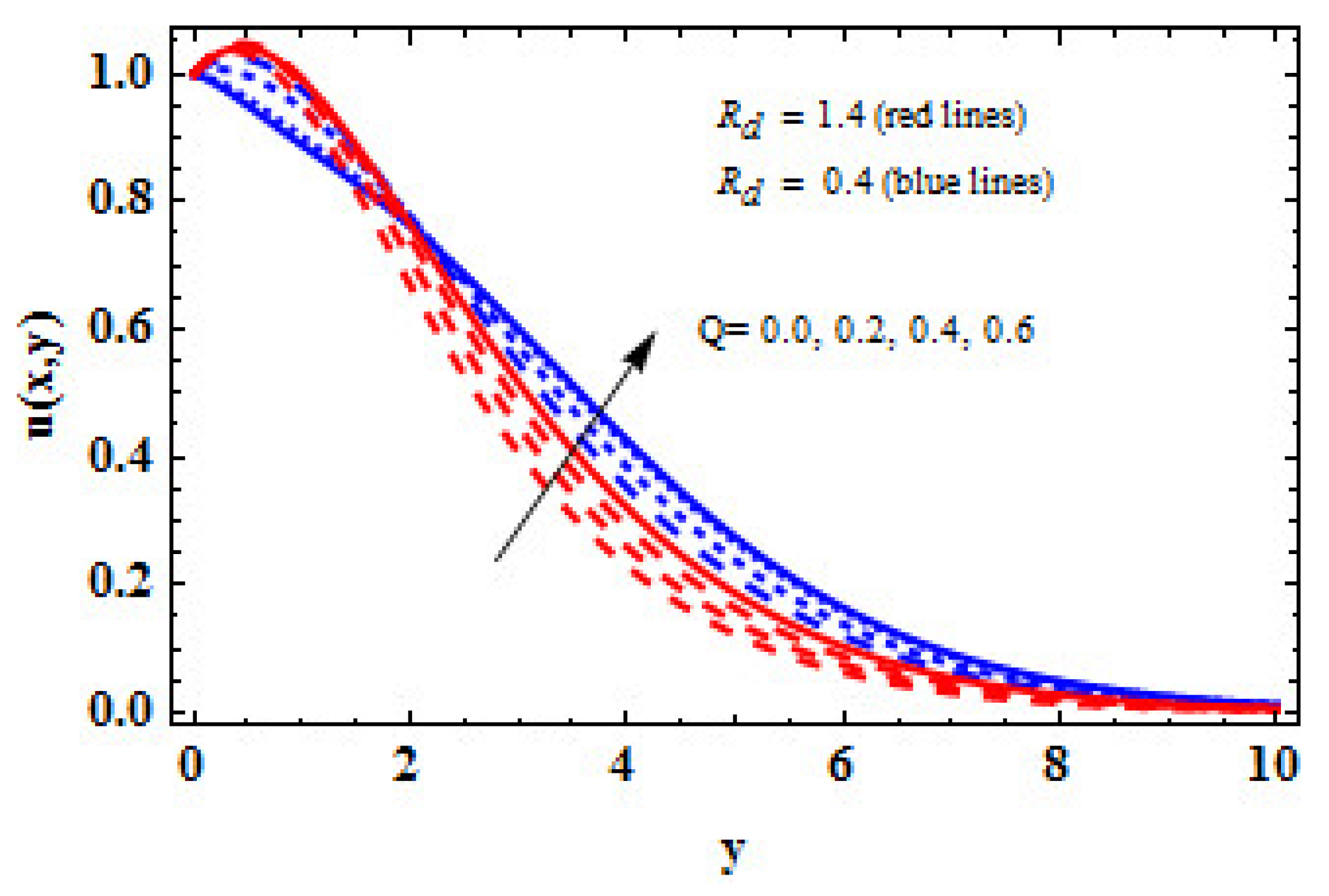
- In the existence of a high MPN, an increment in TR causes an increase in the concentration, indicating that the fluid is a good observer but a poor emitter.
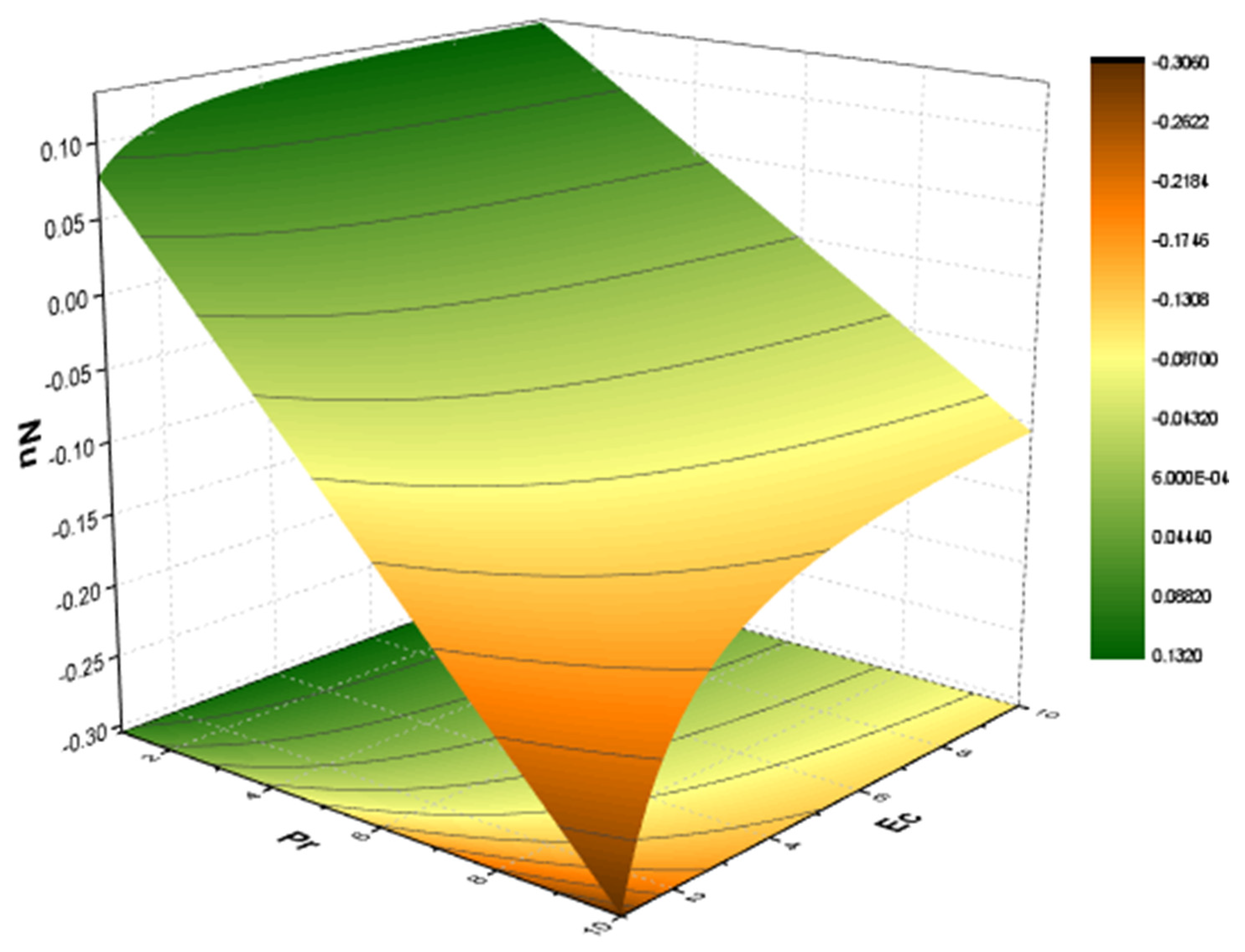
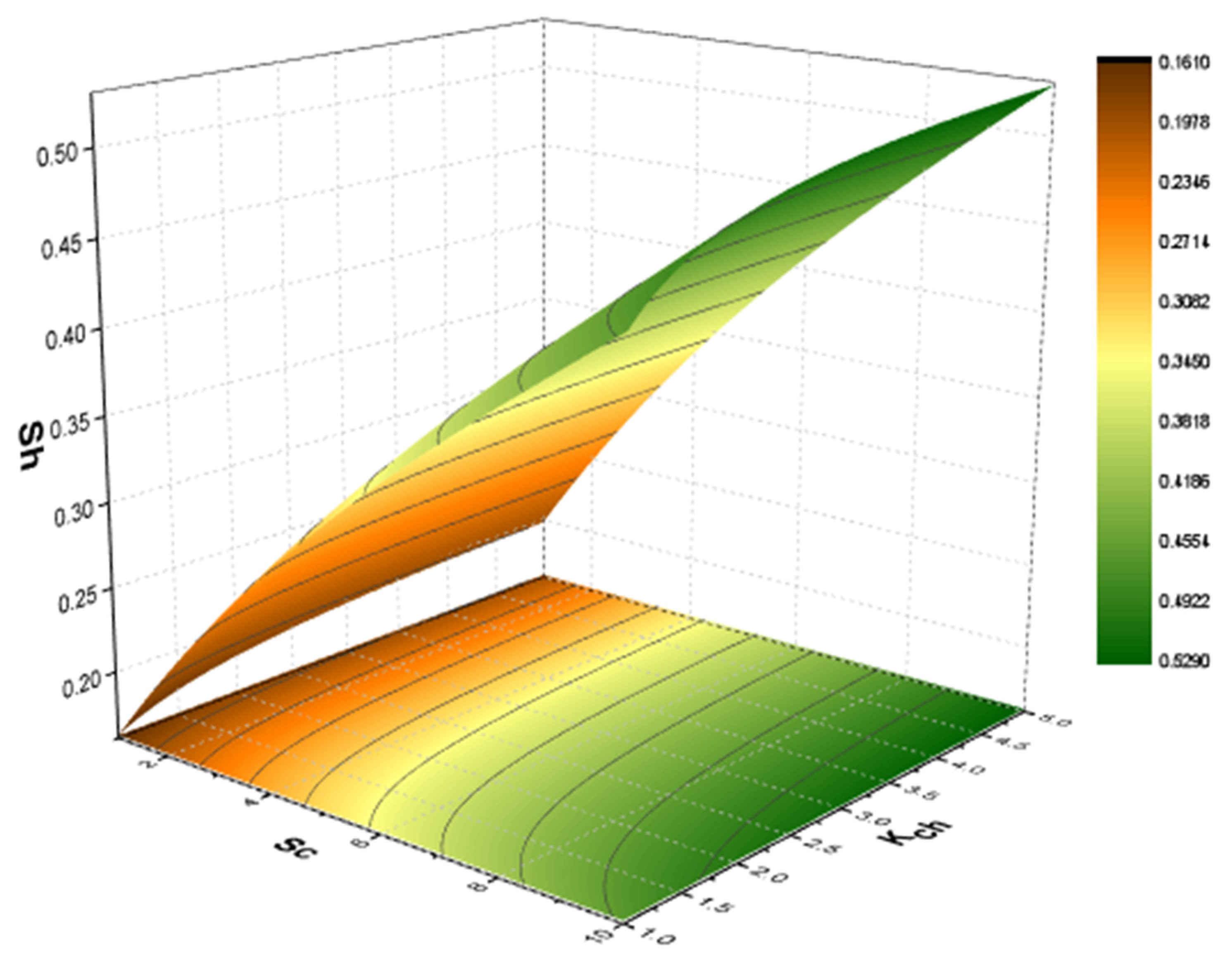
- It is observed that the SF declines with the increasing values of , and the opposite behavior is perceived for the growing values of .
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| uniform magnetic field vector | |
| concentration variable of species | |
| specific heat | |
| concentration near the wall | |
| concentration away from the plate | |
| coefficient of mass diffusivity | |
| electric field intensity | |
| charge of the electron | |
| body force per unit mass | |
| induced magnetic field vector | |
| induced magnetic field vector | |
| induced magnetic field component | |
| induced magnetic field at the wall | |
| dimensionless induced magnetic field | |
| current density vector | |
| fluid pressure | |
| velocity vector | |
| fluid temperature | |
| mean fluid temperature | |
| temperature near the wall | |
| temperature away from the plate | |
| dimensionless time | |
| dimensionless velocity components | |
| thermal expansion coefficient | |
| thermal conductivity | |
| coefficient of viscosity | |
| dissipation function | |
| dimensionless concentration |
References
- Olanrewaju, P.O.; Adesanya, A.O.; Olanrewaju, M.A. Boundary layer flow of nanofluids over a moving surface in a flowing fluid in the presence of radiation. Int. J. Appl. Sci. Technol. 2012, 2, 274–285. [Google Scholar]
- Poornima, T.; Reddy, N.B. Radiation effects on MHD free convective boundary layer flow of nanofluids over a nonlinear stretching sheet. Adv. Appl. Sci. Res. 2013, 4, 190–202. [Google Scholar]
- Turkyilmazoglu, M.; Pop, I. Heat and mass transfer of unsteady natural convection flow of some nanofluids pasta vertical infinite flat plate with radiation effect. Int. J. Therm. Sci. 2013, 59, 167–171. [Google Scholar]
- Gireesha, B.J.; Umeshaiah, M.; Prasannakumara, B.C.; Shashikumar, N.S.; Archana, M. Impact of nonlinear thermal radiation on magnetohydrodynamic three-dimensional boundary layer flow of Jeffrey nanofluid over a nonlinearly permeable stretching sheet. Phys. A Stat. Mech. Its Appl. 2020, 549, 124051. [Google Scholar]
- Sohail, M.; Ali, U.; Zohra, F.T.; Al-Kouz, W.; Chu, Y. Thounthong, Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application. Open Phys. 2021, 19, 100–110. [Google Scholar] [CrossRef]
- Kejela, S.B.; Daba, M.; Girum, A. Investigation of effects of thermal radiation, magnetic field, Eckert number and thermal slip on MHD Hiemenz flow by optimal homotopy asymptotic method. J. Math. 2021, 2021, 5590657. [Google Scholar] [CrossRef]
- Koriko, O.K.; Adegbie, K.S.; Animasaun, I.L.; Olotu, M.A. Numerical solutions of the partial differential equations for investigating the significance of partial slip due to lateral velocity and viscous dissipation: The case of blood-gold Carreau nanofluid and dusty fluid. Numer. Methods Part. Differ. Equ. 2021, 7, 1–15. [Google Scholar] [CrossRef]
- Song, Y.; Khan, S.A.; Imran, M.; Waqas, H.; Khan, S.U.; Khan, M.I.; Qayyum, S.; Chu, Y. Applications of modified Darcy law and nonlinear thermal radiation in bioconvection flow of micropolar nanofluid over an off centered rotating disk. Alex. Eng. J. 2021, 60, 4607–4618. [Google Scholar] [CrossRef]
- Ijaz, M.; Nadeem, S.; Ayub, M.; Mansoor, S. Simulation of magnetic dipole on gyrotactic ferromagnetic fluid flow with nonlinear thermal radiation. J. Therm. Anal. Calorim. 2021, 143, 2053–2067. [Google Scholar] [CrossRef]
- Muhammad, T.; Waqas, H.; Khan, S.A.; Ellahi, R.; Sait, S.M. Significance of nonlinear thermal radiation in 3D Eyring-Powell nanofluid flow with Arrhenius activation energy. J. Therm. Anal. Calorim. 2021, 143, 929–944. [Google Scholar] [CrossRef]
- Wakif, A.; Chamkha, A.; Thumma, T.; Animasaun, I.L.; Sehaqui, R. Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina–Copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2021, 143, 1201–1220. [Google Scholar] [CrossRef]
- Kumar, M.A.; Reddy, Y.D.; Rao, V.S.; Goud, B.S. Thermal radiation impact on MHD heat transfer natural convective nano fluid flow over an impulsively started vertical plate. Case Stud. Therm. Eng. 2021, 24, 100826. [Google Scholar] [CrossRef]
- Pouzesh, A.; Hajmohammadi, M.R.; Poozesh, S. Investigations on the internal shape of constructal cavities intruding a heat generating body. Therm. Sci. 2015, 19, 609–618. [Google Scholar] [CrossRef]
- Gul, R.; Khan, Z.H.; Khan, W.A. Heat transfer from solids with variable thermal conductivity and uniform internal heat generation using homotopy perturbation method. In Proceedings of the ASME 2008 Heat Transfer Summer Conference, Jacksonville, FL, USA, 10–14 August 2008; pp. 311–319. [Google Scholar]
- Ahmed, S.E.; Hussein, A.K.; Mohammed, H.A.; Sivasankaran, S. Boundary layer flow and heat transfer due to permeable stretching tube in the presence of heat source/sink utilizing nanofluids. Appl. Math. Comput. 2014, 238, 149–162. [Google Scholar] [CrossRef]
- Akilu, S.; Narahari, M. Effects of heat generation or Absorption on free convection flow of a nanofluid past an isothermal inclined plate. Adv. Mater. Res. 2014, 970, 267–271. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, A.K.; Kumar, D. Influence of heat source/sink on MHD flow between vertical alternate conducting walls with Hall effect. Phys. A Stat. Mech. Its Appl. 2020, 544, 123562. [Google Scholar] [CrossRef]
- Nagaraju, G.; Garvandha, M.; Murthy, J.V.R. MHD flow in a circular horizontal pipe under heat source/sink with suction/injection on wall. Front. Heat Mass Transf. 2019, 13, 1–8. [Google Scholar] [CrossRef]
- Yusuf, T.S.; Gambo, D. Role of heat source/sink on time dependent free convective flow in a coaxial cylinder filled with porous material: A semi analytical approach. Int. J. Appl. Power Eng. 2020, 8, 67–77. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Kuman, P.; Alrabaiah, H.; Khan, W.; Islam, S.; Shaheen, N. Chemically reactive MHD micropolar nanofluid flow with velocity slips and variable heat source/sink. Sci. Rep. 2020, 10, 20926. [Google Scholar] [CrossRef]
- Shaheen, S.; Bég, O.A.; Gul, F.; Maqbool, K. Electro-Osmotic propulsion of Jeffrey fluid in a ciliated channel under the effect of nonlinear radiation and heat source/sink. J. Biomech. Eng. 2021, 143, 051008. [Google Scholar] [CrossRef]
- Thumma, T.; Mishra, S.R. Effect of nonuniform heat source/sink, and viscous and Joule dissipation on 3D Eyring–Powell nanofluid flow over a stretching sheet. J. Comput. Des. Eng. 2020, 7, 412–426. [Google Scholar] [CrossRef]
- Harada, N. Applications of magnetohydrodynamics (MHD) and recent research trends. IEEJ Trans. Power Energy 2007, 127, 447–450. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. The effects of thermal radiation and non-uniform heat source/sink on MHD boundary layer flow and heat transfer past a stretching sheet embedded in non-Darcian porous medium. Front. Heat Mass Transf. 2016, 7, 37. [Google Scholar] [CrossRef]
- Priyadharshini, P.; Archana, M.V.; Ahammad, N.A.; Raju, C.S.K.; Yook, S.J.; Shah, N.A. Gradient descent machine learning regression for MHD flow: Metallurgy process. Int. Commun. Heat Mass Transf. 2022, 138, 106307. [Google Scholar] [CrossRef]
- Hasen, S.S.; Abdulhadi, A.M. MHD effect on peristaltic transport for Rabinowitsch fluid through a porous medium in cilia channel. Iraqi J. Sci. 2020, 61, 1461–1472. [Google Scholar] [CrossRef]
- Elazem, N.Y.A. Numerical results for influence the flow of MHD nanofluids on heat and mass transfer past a stretched surface. Nonlinear Eng. 2021, 10, 28–38. [Google Scholar] [CrossRef]
- Salahuddin, T.; Khan, M.; Saeed, T.; Ibrahim, M.; Chu, Y. Induced MHD impact on exponentially varying viscosity of Williamson fluid flow with variable conductivity and diffusivity. Case Stud. Therm. Eng. 2021, 25, 100895. [Google Scholar] [CrossRef]
- Alghamdi, W.; Alsubie, A.; Kumam, P.; Saeed, A.; Gul, T. MHD hybrid nanofluid flow comprising the medication through a blood artery. Sci. Rep. 2021, 11, 11621. [Google Scholar] [CrossRef] [PubMed]
- Taiwo, Y.S.; Gambo, D.; Olaife, A.H. Effect of heat source/sink on MHD start-up natural convective flow in an annulus with isothermal and isoflux boundaries. Arab J. Basic Appl. Sci. 2020, 27, 365–374. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, D.; Singh, J. Analytical study for MHD flow of Williamson nanofluid with the effects of variable thickness, nonlinear thermal radiation and improved Fourier’s and Fick’s Laws. SN Appl. Sci. 2020, 2, 438. [Google Scholar] [CrossRef]
- Ahmad, S.; Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 987–991. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ziabakhsh, Z.; Ganji, D.D. Transport of magnetohydrodynamic nanofluid in a porous media. Coll. Surf. A Phys. Eng. Asp. 2017, 520, 201–212. [Google Scholar] [CrossRef]
- Bakar, S.A.; Arifin, N.; Ali, F.M.; Bachok, N.; Nazar, R.; Pop, I. A stability analysis on mixed convection boundary layer flow along a permeable vertical cylinder in a porous medium filled with a nanofluid and thermal radiation. Appl. Sci. 2018, 8, 483. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Velocity slip and entropy generation phenomena in thermal transport through metallic porous channel. J. Non-Equil Thermodyn. 2020, 45, 247–256. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Qasem, N.A.A.; Younis, O.; Marzouki, R.; Mourad, A.; Shah, N.A.; Chung, J.D. MHD Hybrid Nanofluid Mixed Convection Heat Transfer and Entropy Generation in a 3-D Triangular Porous Cavity with Zigzag Wall and Rotating Cylinder. Mathematics 2022, 10, 769. [Google Scholar] [CrossRef]
- Kumar, M.D.; Raju, C.S.K.; Sajjan, K.; El-Zahar, E.R.; Shah, N.A. Linear and quadratic convection on 3D flow with transpiration and hybrid nanoparticles. Int. Commun. Heat Mass 2022, 134, 105995. [Google Scholar] [CrossRef]
- Fetecau, C.; Shah, N.A.; Vieru, D. General Solutions for Hydromagnetic Free Convection Flow over an Infinite Plate with Newtonian Heating, Mass Diffusion and Chemical Reaction. Commun. Theor. Phys. 2017, 68, 768–782. [Google Scholar] [CrossRef]
- Shah, N.A.; Zafar, A.A.; Akhtar, S. General solution for MHD-free convection flow over a vertical plate with ramped wall temperature and chemical reaction. Arab. J. Math. 2018, 7, 49–60. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Influence of heat and chemical reactions on Walter’s B fluid model for blood flow through a tapered artery. J. Taiwan Inst. Chem. Eng. 2011, 42, 67–75. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z. Channel flow of a Maxwell fluid with chemical reaction. Z. Angew. Math. Phys. 2008, 59, 124–144. [Google Scholar] [CrossRef]
- Kameswaran, P.K.; Shaw, S.; Sibanda, P.; Murthy, P.V.S.N. Homogeneous–heterogeneous reactions in a nanofluid due to a porous stretching sheet. Int. J. Heat Mass Transf. 2013, 57, 465–472. [Google Scholar] [CrossRef]
- Uddin, M.J.; Khan, W.A.; Ismail, A.I. Lie group analysis and numerical solutions for magneto convective slip flow along a moving chemically reacting radiating plate in porous media with variable mass diffusivity. Heat Transf. Asian Res. 2015, 93, 1501–1509. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Momoniat, E.; Ferdows, M.; Basiriparsa, A. Lie group solution for free convective flow of a nanofluid past a chemically reacting horizontal plate in porous media. Math. Probl. Eng. 2014, 2014, 239082. [Google Scholar] [CrossRef]
- Srinivas, S.; Reddy, A.S.; Ramamohan, T. Mass transfer effects on viscous flow in an expanding or contracting porous pipe with chemical reaction. Heat Transf. Asian Res. 2015, 44, 552–567. [Google Scholar] [CrossRef]
- Uddin, M.J.; Beg, O.A.; Aziz, A.; Ismail, A.I.M. Group analysis of free convection flow of a magnetic nanofluid with chemical reaction. Math. Probl. Eng. 2015, 2015, 621503. [Google Scholar] [CrossRef]
- Wijayanta, A.T. A localized meshless approach using radial basis functions for conjugate heat transfer problems in a heat exchanger. Int. J. Refrig. 2020, 110, 38–46. [Google Scholar] [CrossRef]
- Makarim, D.A.; Suami, A.; Wijayanta, A.T.; Kobayashi, N.; Itaya, Y. Marangoni convection within thermosolute and absorptive aqueous LiBr solution. Int. J. Heat Mass Transf. 2022, 188, 122621. [Google Scholar]
- Tyurenkova, V.V.; Smirnova, M.N. Material combustion in oxidant flows: Self-similar solutions. Acta Astronaut. 2016, 120, 129–137. [Google Scholar] [CrossRef]
- Smirnov, N.N. Heat and mass transfer in a multi-component chemically reactive gas above a liquid fuel layer. Int. J. Heat Mass Transf. 1985, 28, 929–938. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Betelin, V.B.; Nikitin, V.F.; Stamov, L.I.; Altoukhov, D.I. Accumulation of errors in numerical simulations of chemically reacting gas dynamics. Acta Astronaut. 2015, 117, 338–355. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Betelin, V.B.; Shagaliev, R.M.; Nikitin, V.F.; Belyakov, I.M.; Deryuguin, Y.N.; Aksenov, S.V.; Korchazhkin, D.A. Hydrogen fuel rocket engines simulation using LOGOS code. Int. J. Hydrog. Energy 2014, 39, 10748–10756. [Google Scholar] [CrossRef]
- Sodeifian, G.; Nikooamal, H.R.; Yousefi, A.A. Molecular dynamics study of epoxy/clay nanocomposites: Rheology and molecular confinement. J. Polym. Res. 2012, 19, 9897. [Google Scholar] [CrossRef]
- Sodeifian, G. Non-Linear Rheology of Polymer Melts: Constitutive Equations, Rheological Properties of Polymer Blends, Shear Flow, Sliding Plate Rheometers; Lambert Academic Publishing: Saarbruecken, Germany, 2021. [Google Scholar]
- Ramakrishna, S.B.; Thavada, S.K.; Venkatachala, G.M.; Bandaru, M. Impacts of chemical reaction, diffusion-thermo and radiation on unsteady natural convective flow past an inclined vertical plate under aligned magnetic field. Biointerface Res. Appl. Chem. 2021, 11, 13252–13267. [Google Scholar]



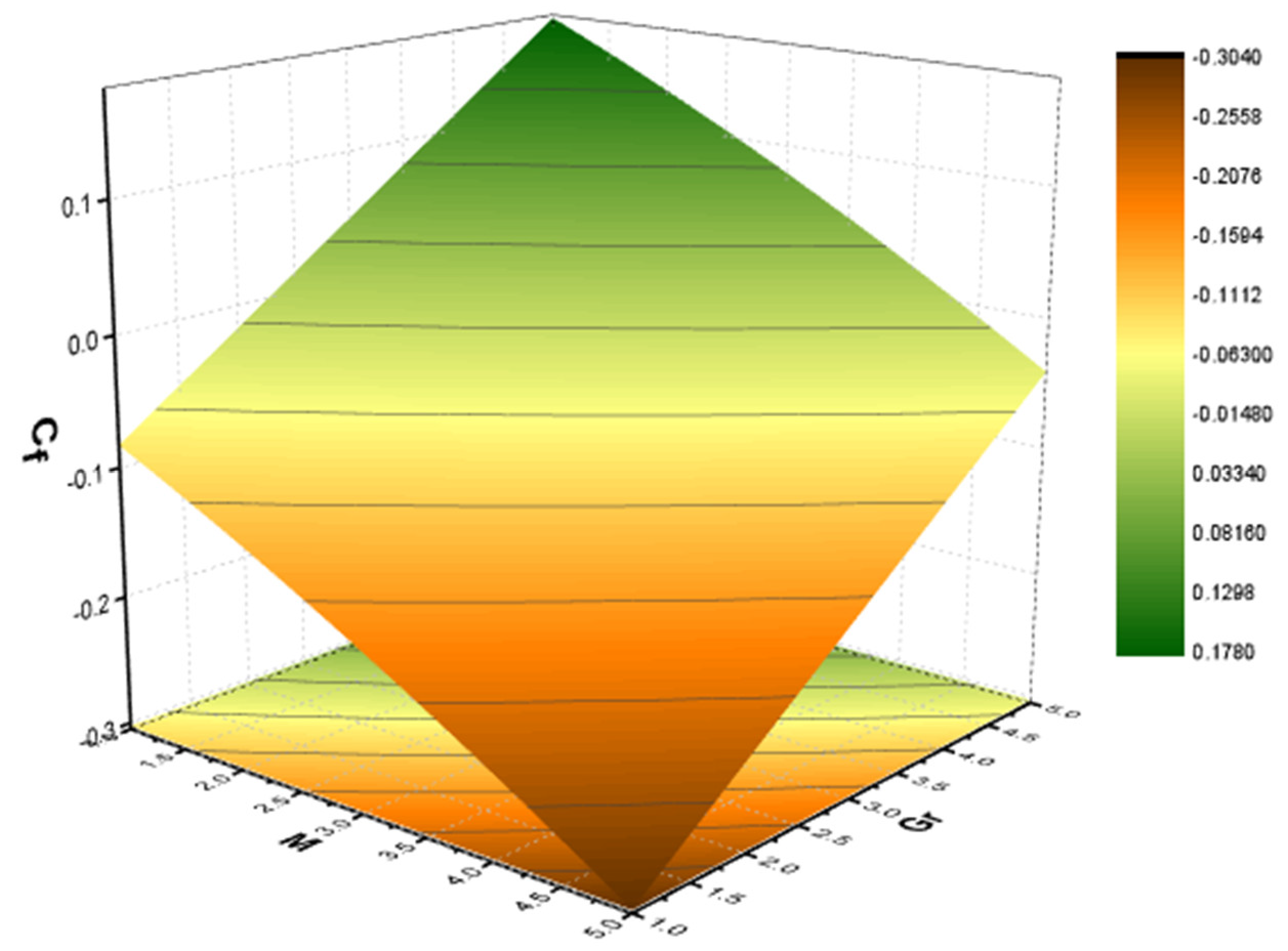
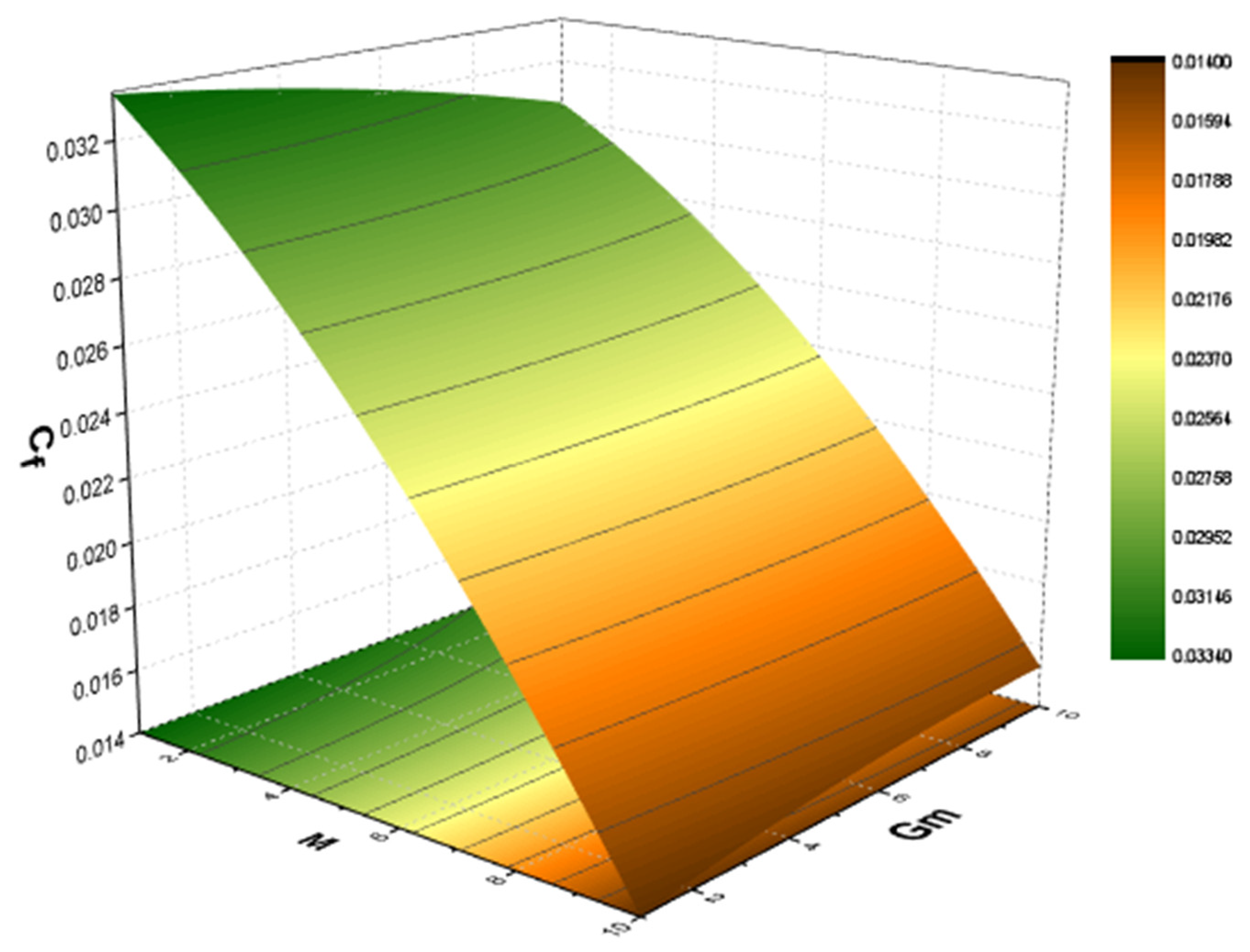
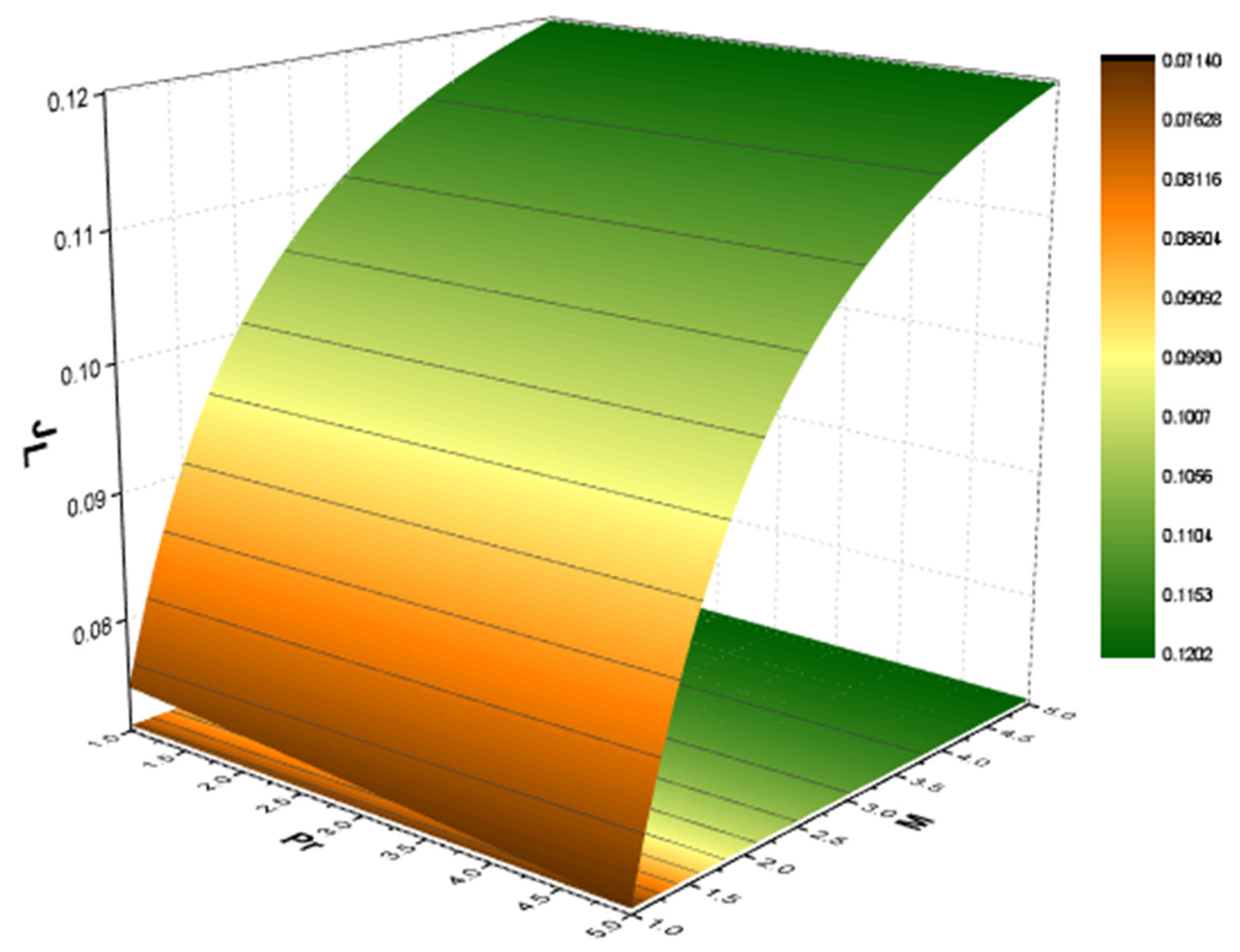
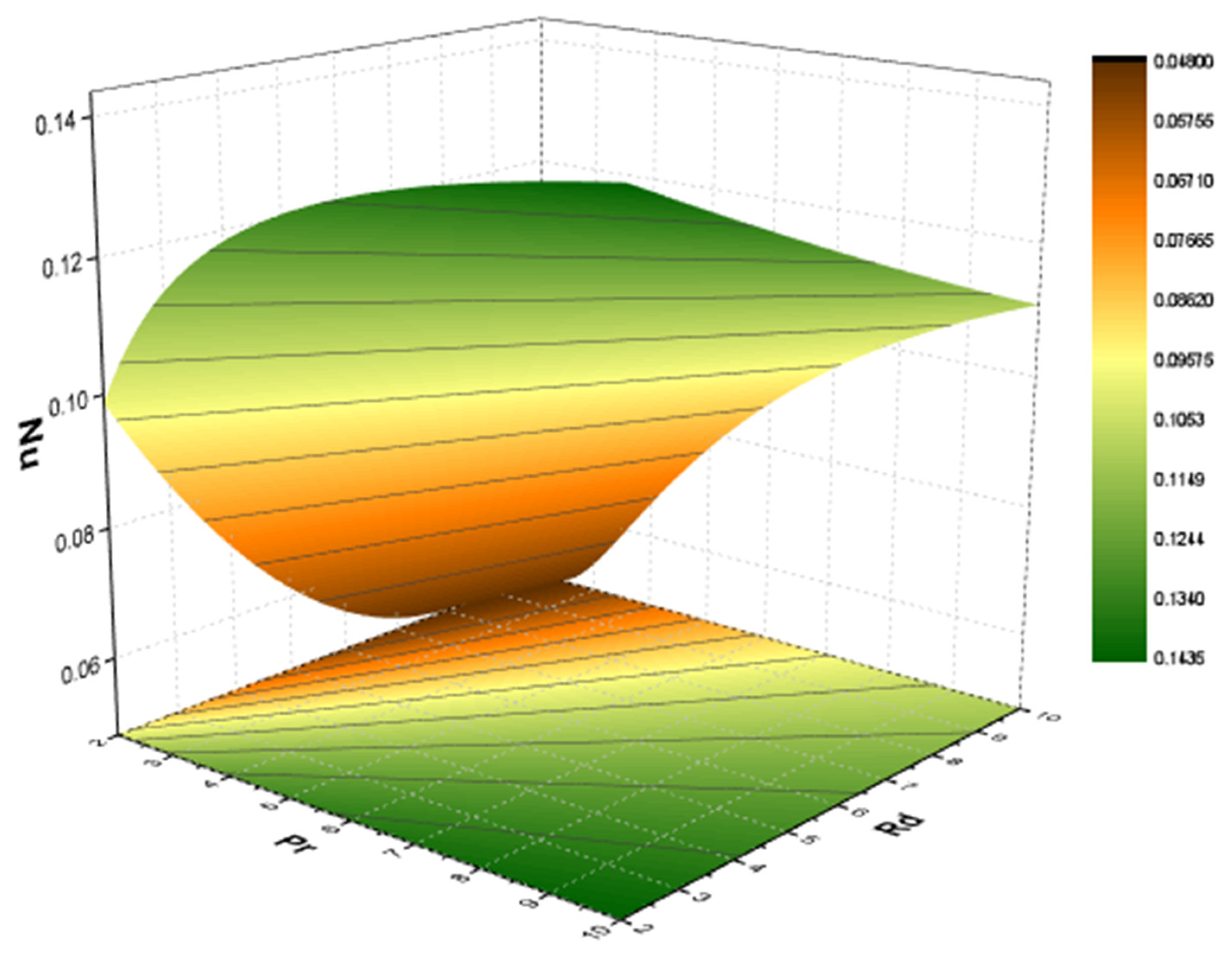
| Present Work | Ramakrishna [55] | Absolute Error | Ramakrishna [55] | Absolute Error | CPU Time | ||
|---|---|---|---|---|---|---|---|
| 0.2 | −0.056534 | −0.056525 | 2.30244 | 2.30228 | 0.236152 | ||
| 0.4 | −0.069844 | −0.069832 | 2.14910 | 2.14951 | 0.335419 | ||
| 0.8 | −0.087808 | −0.087815 | 1.88910 | 1.88932 | 0.587210 | ||
| 1.5 | −0.090382 | −0.090390 | 1.74336 | 1.74347 | 0.023903 | ||
| 2.0 | −0.238020 | −0.238031 | 1.43678 | 1.43660 | 0.556721 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeeshan; Ahammad, N.A.; Shah, N.A.; Chung, J.D.; Khan, M.S. Computational and Stability Analysis of MHD Time-Dependent Thermal Reaction Flow Impinging on a Vertical Porous Plate Enclosing Magnetic Prandtl Number and Thermal Radiation Effect. Mathematics 2023, 11, 1376. https://doi.org/10.3390/math11061376
Zeeshan, Ahammad NA, Shah NA, Chung JD, Khan MS. Computational and Stability Analysis of MHD Time-Dependent Thermal Reaction Flow Impinging on a Vertical Porous Plate Enclosing Magnetic Prandtl Number and Thermal Radiation Effect. Mathematics. 2023; 11(6):1376. https://doi.org/10.3390/math11061376
Chicago/Turabian StyleZeeshan, N. Ameer Ahammad, Nehad Ali Shah, Jae Dong Chung, and Muhammad Shoaib Khan. 2023. "Computational and Stability Analysis of MHD Time-Dependent Thermal Reaction Flow Impinging on a Vertical Porous Plate Enclosing Magnetic Prandtl Number and Thermal Radiation Effect" Mathematics 11, no. 6: 1376. https://doi.org/10.3390/math11061376
APA StyleZeeshan, Ahammad, N. A., Shah, N. A., Chung, J. D., & Khan, M. S. (2023). Computational and Stability Analysis of MHD Time-Dependent Thermal Reaction Flow Impinging on a Vertical Porous Plate Enclosing Magnetic Prandtl Number and Thermal Radiation Effect. Mathematics, 11(6), 1376. https://doi.org/10.3390/math11061376






