Measures of Extropy Based on Concomitants of Generalized Order Statistics under a General Framework from Iterated Morgenstern Family

Abstract

In this work, we reveal some distributional characteristics of concomitants of generalized order statistics (GOS) with parameters that are pairwise different, arising from iterated Farlie–Gumbel–Morgenstern (IFGM) family of bivariate distributions. Additionally, the joint distribution and product moments of concomitants of GOS for this family are discussed. Moreover, some well-known information measures, i.e., extropy, cumulative residual extropy (CRJ), and negative cumulative extropy (NCJ), are derived. Applications of these results are given for order statistics, record values, and progressive type-II censored order statistics with uniform marginals distributions. Additionally, the issue of estimating the CRJ and NCJ is looked into, utilizing the empirical technique and the concomitant of GOS. Finally, bivariate real-world data sets have been analyzed for illustrative purposes, and the performance of the proposed method is quite satisfactory.

1. Introduction

In recent decades, statisticians have become increasingly interested in modeling bivariate data. Bivariate distributions can be found in many forms, but it is important to find those that are based on marginal distributions. By using families of bivariate distributions, we are able to model a large number of datasets easily. In this regard, the Farlie-Gumbel-Morgenstern (FGM) family of bivariate distributions is the most useful and widely used. With this family, it is easy to see the marginals’ dependence structure. As a result, many researchers have modified this model in order to achieve better correlations between variables. This model and its generalizations have been the subject of many remarkable works. Among these researchers are [1,2,3,4,5,6], among others.

The generalized FGM denoted by IFGM$(\lambda ,\eta )$ with a single iteration has the cumulative distribution function (CDF) and probability density function (PDF), which are given by [5] as

$$\begin{array}{c}\hfill F_{X,Y}(x,y)=F_X(x)F_Y(y)\left[1+\lambda {\overline{F}}_X(x){\overline{F}}_Y(y)+\eta F_X(x)F_Y(y){\overline{F}}_X(x){\overline{F}}_Y(y)\right],\end{array}$$

(1)

$$\begin{array}{c}\hfill f_{X,Y}(x,y)=f_X(x)f_Y(y)\left[1+\lambda (1-2F_X(x))(1-2F_Y(y))+\eta (2F_X(x)-3F_X^2(x))(2F_Y(y)-3F_Y^2(y))\right],\end{array}$$

(2)

where $f_X,f_Y,$ and $F_X,F_Y$ are the marginal PDF and CDF of random variables (RVs) X and Y, respectively, while ${\overline{F}}_X=1-F_X$ and ${\overline{F}}_Y=1-F_Y$ are the survival functions (SFs). The natural parameter space $\mathsf{\Omega }=\{(\lambda ,\eta ):-1\le \lambda \le 1;-1\le \lambda +\eta ;\eta \le \frac{3-\lambda +\sqrt{9-6\lambda -3{\lambda }^2}}{2}\}$ is convex (cf. [5]). Applications of the family IFGM$(\lambda ,\eta )$ in the reliability theory were described by [4] who demonstrated that utilizing IFGM distributions, rather than FGM distributions, for these applications yields more accurate findings. It is important to note that the IFGM model is more tractable and adaptable. As a result, there are a number of compelling arguments in favor of employing the model IFGM$(\lambda ,\eta ).$

Tests on materials and their strength, reliability, lifetime, and other factors are carried out in a non-descending order; thus, we must take into account numerous models of ascendingly ordered RVs. The model of generalized order statistics (GOS) was introduced by [7] as a unified model for ascendingly ordered RVs. The GOS model contains many important models of ordered RVs, such as order statistics (OS), record values, sequential OS, and progressive type-II censored OS (POS-II). The RVs $X(r,n,\tilde{m},k),r=1,2,\dots ,n$ are called GOS based on absolutely continuous CDF $F_X$ with the PDF $f_X,$ if their joint PDF (JPDF) has the form

$$f_{1,\dots ,n:n}^{(\tilde{m},k)}(x_1,\dots ,x_n)=\left(\prod _{j=1}^n{\gamma }_j\right)\left(\prod _{j=1}^{n-1}{\overline{F}}_X^{{\gamma }_j-{\gamma }_{j+1}-1}(x_j)f_X(x_j)\right){\overline{F}}_X^{{\gamma }_n-1}(x_n)f_X(x_n),$$

where $F_{}^{-1}(0)\le x_1\le \dots \le x_n\le F_{}^{-1}(1).$ The parameters ${\gamma }_1,\dots ,{\gamma }_n$ are defined by ${\gamma }_n=k>0,{\gamma }_r=k+n-r+{\sum }_{j=r}^{n-1}{m}_j,r=1,\dots ,n-1\mathrm{and}\tilde{m}=(m_1,m_2,\dots ,m_{n-1})\in \mathbb{R}.$

In this work, we focus only on the parameters ${\gamma }_1,\dots ,{\gamma }_n$, which are pairwise different, i.e., ${\gamma }_i\ne {\gamma }_j,i\ne j,i,j=1,2,\dots ,n-1.$ With this assumption, we obtain a very wide subclass of GOS, which contains m-GOS (when $m_1=\cdots =m_{n-1}=m$), OS, and record values. The PDF of the rth GOS and the JPDF of rth and sth GOS, $1\le r<s\le n,$ respectively, are given by

$$f_{X(r,n,\tilde{m},k)}(x)=C_{r-1}\sum _{i=1}^r{a}_i(r){\overline{F}}_X^{{\gamma }_i-1}(x)f_X(x),x\in \mathbb{R},1\le r\le n,$$

(3)

$$\begin{array}{c}\hfill f_{X(r,n,\tilde{m},k),X(s,n,\tilde{m},k)}(x,y)=C_{s-1}\left[\sum _{i=r+1}^s{a}_i^{(r)}(s){\left(\frac{{\overline{F}}_Y(y)}{{\overline{F}}_X(x)}\right)}^{{\gamma }_i}\right]\left[\sum _{i=1}^r{a}_i^{}(r){\overline{F}}_X^{{\gamma }_i}(x)\right]\frac{f_X(x)}{{\overline{F}}_X(x)}\frac{f_Y(y)}{{\overline{F}}_Y(y)},x<y,\end{array}$$

(4)

where $C_{r-1}={\displaystyle \prod _{i=1}^r}{\gamma }_i,a_i(r)={\displaystyle \prod _{\genfrac{}{}{0pt}{}{j=1}{j\ne i}}^r}\frac{1}{{\gamma }_j-{\gamma }_i},1\le i\le r\le n,$ and $a_i^{(r)}(s)={\displaystyle \prod _{\genfrac{}{}{0pt}{}{j=r+1}{j\ne i}}^s}\frac{1}{{\gamma }_j-{\gamma }_i},r+1\le i\le s\le n$ (cf. [8]).

The concept of concomitants of OS was introduced by [9] for the first time. In problems of selection and prediction, the concomitants are of interest. [10] provided a comprehensive review of the concomitants of OS. One of the most critical applications of concomitants of OS and record value is the sampling approach known as ranking set sampling. Particularly, when the primary RV Y is expensive and complex to measure, while the secondary RV X is inexpensive and straightforward. Let $(X_i,Y_i),i=1,2,\dots ,n,$ be a random sample from a bivariate CDF $F_{X,Y}(x,y).$ The concomitant of the rth GOS, $Y_{[r,n,\tilde{m},k]},r=1,2,\dots ,n$ is the Y value associated with $X(r,n,\tilde{m},k).$ There are many works on the concomitants of m-GOS (see [3,11,12,13,14,15]). However, only a few studies have been looked at the concomitants of GOS in a general setting. Accordingly, [16] investigated the distribution of concomitants of GOS from FGM bivariate distributions. In addition, various information measures for concomitant GOS were established under a general framework by [1]. Lastly, the concomitants of dual GOS in the Bairamov–Kotz–Becki FGM family were examined by [2]. In this paper, we will extend the recent work of [12] to concomitants of GOS under a general framework of the family IFGM$(\lambda ,\eta ).$

The idea of information–theoretic entropy was first introduced by [17], and it is essential in a number of disciplines, including financial analysis, data compression, molecular biology, hydrology, meteorology, computer science, and information theory. There are clear relationships between the measurement uncertainty of RVs, which is used in many fields, and other key data and reliability measurements. Extropy (J), a dual function that complements Shannon entropy, was proposed by [18]. This measure of uncertainty has received a lot of attention over the last five years (see [6]).

$$J(X)=-\frac{1}{2}{\int }_0^{\infty }{f}_X^2(x)dx=-\frac{1}{2}{\int }_0^1{f}_X(F_X^{-1}(u))du\le 0.$$

(5)

Recently, a number of authors have become interested in the J measure and its uses. The lower bounds for the J measure of OS and record values, monotone qualities, and certain characterization results were all covered by [19]. In addition, [20] concentrated on the leftover J measure of OS. The J measure estimators were examined by [21] with applications in testing uniformity. In the FGM family, [12] looked at the measurements of J for concomitants of m-GOS. Moreover, [22,23] nonparametric’s calculation of the residual J measure of concomitants of m-GOS using actual and simulated COVID-19 viral data is presented. Finally, [24] provided a description of compressive sensing utilizing ranked set sampling’s J measure.

The cumulative residual extropy (CRJ) was proposed by [25] in analogy with (5) as a measure of the uncertainty of RVs. The CRJ is defined as

$${\xi }^{*}(X)=-\frac{1}{2}{\int }_0^{\infty }{\overline{F}}_X^2(x)dx\le 0.$$

(6)

It is clear that ${\xi }^{*}(X)$ is always non-positive. Hence, the negative CRJ (NCRJ) can be presented as (cf. [26])

$$\xi (X)=\frac{1}{2}{\int }_0^{\infty }{\overline{F}}_X^2(x)dx.$$

(7)

Recently, [27] discussed some properties and applications of negative cumulative extropy (NCE) in analogy with (5), defined as

$$\mathcal{C}\xi (X)=\frac{1}{2}{\int }_0^{\infty }\left(1-F_X^2(x\right)dx=\frac{1}{2}{\int }_0^1\frac{1-u^2}{f_X(F_X^{-1}(u))}du.$$

(8)

Allowing some of the important models in many branches of statistics to use some of the key models in these GOS simply in this general framework. Examining the concomitant of GOS is a crucial practical way to sort the bivariate data in this situation. Some useful models from the GOS model, such as the POSs, are not included in these submodels. The POS-II model is an essential tool for obtaining data from lifetime testing, since it enables the experimenter to save money by allowing live units to be removed early and simply by used in later tests. Additionally, it enables a balance between the time commitment and the observance of some extreme principles. One of the statistical applications of the J measure is to score the forecasting distributions using the total log scoring rule. Moreover, the aforesaid theoretical and practical importance of measure J and its related measures are defined in (5)–(8) to provide sufficient motivation to study and reveal concomitants of GOS under a general framework from the family IFGM$(\lambda ,\eta ).$

The rest of this paper is structured as follows: Section 2 reveals some distributional characteristics of concomitants of GOS based on the IFGM$(\lambda ,\eta )$ family under a general framework. As an example, POS-II under uniform distribution is given. In Section 3, the joint distribution, joint moment generating function (JMGF), and product moments of concomitants of GOS of this family are obtained. We also studied some measures such as J, CRJ, and NCJ for $Y_{[r,n,\tilde{m},k]}$ in the IFGM$(\lambda ,\eta )$ family in Section 4. Moreover, we discussed the problem of estimating the NCRJ and NCJ by employing the empirical NCRJ and NCJ for concomitants of GOS in Section 5. Additionally, for demonstrative purposes, bivariate real-world data sets are analyzed in Section 6, and the performance of the suggested strategy is extremely excellent. Finally, the conclusion is covered in Section 7.

2. Distributional Characteristics of Concomitants of GOS Based on IFGM$(\mathbf{\lambda },\mathbf{\eta })$

In this section, the distributional characteristics of concomitant GOS based on IFGM$(\lambda ,\eta )$ model with parameters that are pairwise different are obtained. Recurrence relations between single moments of concomitants are carried out. As an example, the POS-II with uniform marginal distributions is discussed.

The PDF, CDF, and SF expressions for $Y_{[r,n,\tilde{m},k]},$ for any arbitrary marginal distribution based on the IFGM$(\lambda ,\eta )$ model are obtained in the following theorem.

Theorem 1.

Let $Y_{[r,n,\tilde{m},k]}$ be the concomitant of rth GOS from IFGM$(\lambda ,\eta )$ with RV $V_i$ has the CDF $F_Y^{i+1},i=1,2.$ Then, the PDF, CDF, and SF of $Y_{[r,n,\tilde{m},k]}$ are given by

$$\begin{array}{ccc}\hfill f_{[r,n,\tilde{m},k]}(y)& =& (1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})f_Y(y)+({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})f_{V_1}(y)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{f}_{V_2}(y),\hfill \end{array}$$

(9)

$$\begin{array}{c}\hfill F_{[r,n,\tilde{m},k]}(y)=F_Y(y)\left[1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}(1-F_Y(y))+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}(F_Y(y)-F_Y^2(y))\right],\end{array}$$

(10)

$$\begin{array}{c}\hfill {\overline{F}}_{[r,n,\tilde{m},k]}(y)={\overline{F}}_Y(y)\left[1-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{F}_Y(y)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{F}_Y^2(y)\right],\end{array}$$

(11)

where ${\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}=\lambda C_{r-1}{\displaystyle \sum _{i=1}^r}{a}_i(r)\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right)$ and ${\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}=\eta C_{r-1}{\displaystyle \sum _{i=1}^r}{a}_i(r)\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right)\left(\frac{3-{\gamma }_i}{2+{\gamma }_i}\right)$.

Proof. 

First, for every positive real number $t,$ consider the integration

$$\begin{array}{ccc}\hfill I_t^{(\tilde{m},k)}& =& {\int }_{-\infty }^{\infty }{\overline{F}}_X^t(x)C_{r-1}\sum _{i=1}^r{a}_i(r){\overline{F}}_X^{{\gamma }_i-1}(x)f_X(x)dx\hfill \\ & =& C_{r-1}\sum _{i=1}^r{a}_i(r){\int }_{-\infty }^{\infty }{\overline{F}}_X^{{\gamma }_i+t-1}(x)f_X(x)dx.\hfill \end{array}$$

By using the transformation $u={\overline{F}}_X^{}(x),$ we obtain

$$\begin{array}{ccc}\hfill I_t^{(\tilde{m},k)}& =& C_{r-1}\sum _{i=1}^r{a}_i(r){\int }_0^1{u}^{{\gamma }_i+t-1}du=C_{r-1}\sum _{i=1}^r\frac{a_i(r)}{{\gamma }_i+t}.\hfill \end{array}$$

(12)

Now, by using (3) and (12), we obtain the PDF of $Y_{[r,n,\tilde{m},k]}$

$$\begin{array}{ccc}\hfill f_{[r,n,\tilde{m},k]}(y)& =& {\int }_{-\infty }^{\infty }{f}_{Y|X}(y|x)f_{X_{}(r,n,\tilde{m},k)}(x)dx\hfill \\ & =& {\int }_{-\infty }^{\infty }{f}_Y(y)\left[1+\lambda (1-2F_X(x))(1-2F_Y(y))+\eta (2F_X(x)-3F_X^2(x))(2F_Y(y)-3F_Y^2(y))\right]\hfill \\ & \times & C_{r-1}\sum _{i=1}^r{a}_i(r){\overline{F}}_X^{{\gamma }_i-1}(x)f_X(x)dx\hfill \\ & =& C_{r-1}\sum _{i=1}^r{a}_i(r){\int }_{-\infty }^{\infty }[f_Y(y)+\lambda (2{\overline{F}}_X(x)-1)(f_Y(y)-f_{V_1}(y))+\eta (4{\overline{F}}_X(x)-3{\overline{F}}_X^2(x)-1)\hfill \\ & \times & (f_{V_1}(y)-f_{V_2}(y))]{\overline{F}}_X^{{\gamma }_i-1}(x)f_X(x)dx.\hfill \end{array}$$

Then, by considering the definition of ${\mathsf{\Omega }}_{r,n:i}^{(\tilde{m},k)},i=1,2,$ and incorporating (12) in the above integrations, the required result directly follows. Finally, by some simple algebra, we can derive the CDF and SF of $Y_{[r,n,\tilde{m},k]}.$ □

Remark 1.

By using Theorem 1, the marginal hazard rate function (HRF) of $Y_{[r,n,\tilde{m},k]}$ is given by

$$\begin{array}{ccc}\hfill H_{[r,n,\tilde{m},k]}(y)& =& \frac{f_{[r,n,\tilde{m},k]}(y)}{{\overline{F}}_{[r,n,\tilde{m},k]}(y)}=\frac{f_Y(y)\left[1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}+2\left({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\right)F_Y(y)-3{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{F}_Y^2(y)\right]}{{\overline{F}}_Y(y)\left[1-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{F}_Y(y)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{F}_Y^2(y)\right]}.\hfill \end{array}$$

If the RVs stated above are taken to be the lifetime of system components or human lives at specific ages, then $H_{[r,n,\tilde{m},k]}(y)$ can be employed in reliability theory.

Using Theorem 1, we can now calculate the MGF and the moments of $Y_{[r,n,\tilde{m},k]}$, based on IFGM$(\lambda ,\eta )$ for any random distribution. Relying on (9), the MGF of $Y_{[r,n,\tilde{m},k]}$, based on IFGM$(\lambda ,\eta )$, is given by

$$\begin{array}{ccc}\hfill M_{[r,n,\tilde{m},k]}(t)& =& (1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})M_Y(t)+({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})M_{V_1}(t)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{M}_{V_2}(t),\hfill \end{array}$$

(13)

where $M_Y(t),M_{V_1}(t)$, and $M_{V_2}(t)$ are the MGFs of the RVs $Y,V_1$, and $V_2,$ respectively. Thus, by using (13) the ℓth moment of $Y_{[r,n,\tilde{m},k]}$ based on IFGM$(\lambda ,\eta )$ is given by

$$\begin{array}{ccc}\hfill {\mu }_{[r,n,\tilde{m},k]}^{(\ell )}& =& E[Y_{[r,n,\tilde{m},k]}^{\ell }]=(1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}){\mu }_Y^{(\ell )}+({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}){\mu }_{V_1}^{(\ell )}-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\mu }_{V_2}^{(\ell )},\hfill \end{array}$$

where ${\mu }_Y^{(\ell )}=E[Y^{\ell }],{\mu }_{V_1}^{(\ell )}=E[{V_1}^{\ell }]$, and ${\mu }_{V_2}^{(\ell )}=E[{V_2}^{\ell }].$

In general, if $T(y)$ is a function of y, then (9) yields

$$\begin{array}{c}\hfill E[T(Y_{[r,n,\tilde{m},k]})]=(1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})E[T(Y)]+({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})E[T(V_1)]-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}E[T(V_2)],\end{array}$$

provided the expectations exist.

The following theorem gives a useful general recurrence relation for $E[T(Y_{[r,n,\tilde{m},k]})].$

Theorem 2.

Let $T(Y_{[r,n,\tilde{m},k]})$ be a function of $Y_{[r,n,\tilde{m},k]},2\le r\le n.$ Then, we obtain

$$\begin{array}{ccc}\hfill E[T(Y_{[r,n,\tilde{m},k]})]-E[T(Y_{[r-1,n,\tilde{m},k]})]& =& C_{r-2}\sum _{i=1}^r\frac{a_i(r){\gamma }_i(1-{\gamma }_i)}{(1+{\gamma }_i)}\hfill \\ & \times & \left(\lambda E[T(Y-V_1)]+\frac{\eta (3-{\gamma }_i)}{(2+{\gamma }_i)}E[T(V_1-V_2)]\right).\hfill \end{array}$$

Proof. 

Using the relations $a_i(r-1)=({\gamma }_r-{\gamma }_i)a_i(r),C_{r-2}=\frac{C_{r-1}}{{\gamma }_r}$ and ${\displaystyle \sum _{i=1}^r}{a}_i(r)=0,$ we obtain

$$\begin{array}{ccc}\hfill E[T(Y_{[r,n,\tilde{m},k]})]-E[T(Y_{[r-1,n,\tilde{m},k]})]& =& \left({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r-1,n:1}^{(\tilde{m},k)}\right)\left(E[T(Y)]-E[T(V_1)]\right)\hfill \\ & -& \left({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r-1,n:2}^{(\tilde{m},k)}\right)\left(E[T(V_1)]-E[T(V_2)]\right),\hfill \end{array}$$

where ${\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}$(${\mathsf{\Omega }}_{r-1,n:1}^{(\tilde{m},k)}$) and ${\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}$(${\mathsf{\Omega }}_{r-1,n:2}^{(\tilde{m},k)}$) are defined via Theorem 1, then

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r-1,n:1}^{(\tilde{m},k)}& =& \lambda C_{r-1}\sum _{i=1}^r{a}_i(r)\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right)-\lambda C_{r-2}\sum _{i=1}^{r-1}{a}_i(r-1)\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right)\hfill \\ & =& \lambda C_{r-2}\sum _{i=1}^r{a}_i(r){\gamma }_i\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right).\hfill \end{array}$$

In the same manner, we obtain

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}-{\mathsf{\Omega }}_{r-1,n:2}^{(\tilde{m},k)}& =& \eta C_{r-2}\sum _{i=1}^r{a}_i(r){\gamma }_i\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right)\left(\frac{3-{\gamma }_i}{2+{\gamma }_i}\right),\hfill \end{array}$$

which completes the proof. □

In most lifetime trials, accurate product lifetime data cannot be observed due to time and money constraints, so we have suppressed data instead. The POS-II is one of the most significant censoring strategies.

Example 1.

Let $F_{X,Y}$ be a continuous bivariate CDF. Furthermore, let $X_{1:n}^{\tilde{R}},X_{2:n}^{\tilde{R}},\dots ,X_{n:n}^{\tilde{R}}$ be POS-II with general scheme $\tilde{R}=(R_1,\dots ,R_n),$ where $N=n+{\sum }_{i=1}^n{R}_i$ identical units are placed on a lifetime test. Ref. [28] derived the PDF of the concomitant $Y_{[r:n]}^{\tilde{R}}$ of the POS-II $X_{r:n}^{\tilde{R}}$ by 

$$\begin{array}{c}\hfill f_{Y_{[r:n]}^{\tilde{R}}}(y)=C_{r-1}\sum _{i=1}^r\frac{a_i(r)}{{\gamma }_i}{f}_{Y_{[1:{\gamma }_i]}}(y),\end{array}$$

where ${\gamma }_j=N-{\sum }_{i=1}^{j-1}{R}_i-j+1,1<j\le n,{\gamma }_1=N,$ $f_{1:{\gamma }_i}(x)={\gamma }_i{\overline{F}}_X^{{\gamma }_i-1}(x)f_X(x)$ and $f_{Y_{[1:{\gamma }_i]}}(y)={\int }_{-\infty }^{\infty }{f}_{Y|X}(y|x)f_{1:{\gamma }_i}(x)dx$ is the PDF of the concomitant of the minimum OS from a sample of size ${\gamma }_i.$ Now, let $F_{X,Y}$ be IFGM with uniform marginals. Then, $F_{X,Y}(x,y)=xy[1+\lambda (1-x^{})(1-y^{})+\eta xy(1-x^{})(1-y^{})],0\le x,y\le 1,$ and $f_{X,Y}(x,y)=1+\lambda (1-2x^{})(1-2y^{})+\eta (2x-3x^2)(2y-3y^2).$ Thus, we can write

$$f_{Y_{[1:{\gamma }_i]}}(y)=1+\lambda (1-2y^{})\frac{({\gamma }_i-1)}{({\gamma }_i+1)}+2\eta (2y-3y^2)\frac{({\gamma }_i-1)}{({\gamma }_i+1)({\gamma }_i+2)}.$$

Therefore, the PDF of $Y_{[r:n]}^{\tilde{R}}$ is given by

$$f_{Y_{[r:n]}^{\tilde{R}}}(y)=C_{r-1}\sum _{i=1}^r\frac{a_i(r)}{{\gamma }_i}\left\{1+\lambda (1-2y^{})\frac{({\gamma }_i-1)}{({\gamma }_i+1)}+2\eta (2y-3y^2)\frac{({\gamma }_i-1)}{({\gamma }_i+1)({\gamma }_i+2)}\right\}.$$

3. JPDF of Concomitants of GOS Based on IFGM$(\mathbf{\lambda },\mathbf{\eta })$

The following theorem gives the JPDF $f_{[r,s,n,\tilde{m},k]}(y_1,y_2)$ of the concomitants of GOS in IFGM$(\lambda ,\eta )$ under a general setting.

Theorem 3.

Let $Y_{[r,n,\tilde{m},k]}$ and $Y_{[s,n,\tilde{m},k]},r<s,$ be the concomitant of rth and sth GOS from IFGM$(\lambda ,\eta )$ with RV $V_i$ has the CDF $F_Y^{i+1},i=1,2.$ Then the JPDF of $Y_{[r,n,\tilde{m},k]}$ and $Y_{[s,n,\tilde{m},k]},$ are given by

$$\begin{array}{ccc}\hfill f_{[r,s,n,\tilde{m},k]}(y_1,y_2)& =\hfill & f_Y(y_1)f_Y(y_2)+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{f}_Y(y_2)(f_Y(y_1)-f_{V_1}(y_1))+{\mathsf{\Omega }}_{s,n:1}^{(\tilde{m},k)}{f}_Y(y_1)\hfill \\ \hfill & \times \hfill & (f_Y(y_2)-f_{V_1}(y_2))+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{f}_Y(y_2)(f_{V_1}(y_1)-f_{V_2}(y_1))+{\mathsf{\Omega }}_{s,n:2}^{(\tilde{m},k)}{f}_Y(y_1)(f_{V_1}(y_2)-f_{V_2}(y_2))\hfill \\ \hfill & +\hfill & {\mathsf{\Omega }}_{r,s,n:1}^{(\tilde{m},k)}(f_Y(y_1)-f_{V_1}(y_1))(f_Y(y_2)-f_{V_1}(y_2))+{\mathsf{\Omega }}_{r,s,n:2}^{(\tilde{m},k)}(f_Y(y_1)-f_{V_1}(y_1))\hfill \\ \hfill & \times \hfill & (f_{V_1}(y_2)-f_{V_2}(y_2))+{\mathsf{\Omega }}_{r,s,n:3}^{(\tilde{m},k)}(f_{V_1}(y_1)-f_V(y_1))(f_Y(y_2)-f_{V_1}(y_2))\hfill \\ \hfill & +\hfill & {\mathsf{\Omega }}_{r,s,n:4}^{(\tilde{m},k)}(f_{V_1}(y_1)-f_{V_2}(y_1))(f_{V_1}(y_2)-f_{V_2}(y_2)),\hfill \end{array}$$

(14)

where ${\mathsf{\Omega }}_{s,n:1}^{(\tilde{m},k)}$ and ${\mathsf{\Omega }}_{s,n:2}^{(\tilde{m},k)}$ are defined by replacing r with s in ${\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}$ and ${\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}$, respectively,

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{r,s,n:1}^{(\tilde{m},k)}={\lambda }^2\left(4I_{1,1}^{(\tilde{m},k)}-1\right)-\lambda \left({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}+{\mathsf{\Omega }}_{s,n:1}^{(\tilde{m},k)}\right),{\mathsf{\Omega }}_{r,s,n:2}^{(\tilde{m},k)}=\lambda \eta \left(8I_{1,1}^{(\tilde{m},k)}-6I_{1,2}^{(\tilde{m},k)}-2I_{1,0}^{(\tilde{m},k)}\right)-\lambda {\mathsf{\Omega }}_{s,n:2}^{(\tilde{m},k)},\end{array}$$

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{r,s,n:3}^{(\tilde{m},k)}=\lambda \eta \left(8I_{1,1}^{(\tilde{m},k)}-6I_{2,1}^{(\tilde{m},k)}-2I_{0,1}^{(\tilde{m},k)}\right)-\lambda {\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)},\end{array}$$

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{r,s,n:4}^{(\tilde{m},k)}={\eta }^2\left[\left(9I_{2,2}^{(\tilde{m},k)}-6I_{2,1}^{(\tilde{m},k)}-6I_{1,2}^{(\tilde{m},k)}+1\right)+\frac{1}{\lambda }\left({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}+{\mathsf{\Omega }}_{s,n:1}^{(\tilde{m},k)}\right)+\frac{1}{\lambda \eta }\left({\mathsf{\Omega }}_{r,s,n:2}^{(\tilde{m},k)}+{\mathsf{\Omega }}_{r,s,n:3}^{(\tilde{m},k)}\right)\right]\end{array}$$

and

$$\begin{array}{ccc}\hfill I_{p,q}^{(\tilde{m},k)}& =& \sum _{i=1}^r\frac{a_i(r)}{{\gamma }_i+p+q}\sum _{i=r+1}^s\frac{a_i^{(r)}(s)}{{\gamma }_i+q},p,qare real numbers.\hfill \end{array}$$

Proof. 

First, consider the following integration:

$$\begin{array}{c}\hfill I={\int }_{-\infty }^{\infty }{\int }_{x_1}^{\infty }{\overline{F}}_X^p(x_1){\overline{F}}_X^q(x_2)C_{s-1}\left[\sum _{i=r+1}^s{a}_i^{(r)}(s){\left(\frac{{\overline{F}}_X(x_2)}{{\overline{F}}_X(x_1)}\right)}^{{\gamma }_i}\right]\left[\sum _{i=1}^r{a}_i^{}(r){\overline{F}}_X^{{\gamma }_i}(x_1)\right]\frac{f_X(x_2)}{{\overline{F}}_X(x_2)}\frac{f_X(x_1)}{{\overline{F}}_X(x_1)}d{x}_{2}d{x}_1\end{array}$$

Taking the transformation $Z=\frac{{\overline{F}}_X(x_2)}{{\overline{F}}_X(x_1)}$, we obtain

$$\begin{array}{c}\hfill I={\int }_{-\infty }^{\infty }{\int }_0^1{C}_{s-1}\left[\sum _{i=r+1}^s{a}_i^{(r)}(s)Z^{{\gamma }_i+q-1}\right]\left[\sum _{i=1}^r{a}_i^{}(r){\overline{F}}_X^{{\gamma }_i+p+q-1}(x_1)\right]f_X(x_1)dzd{x}_1=\sum _{i=1}^r\frac{a_i(r)}{{\gamma }_i+p+q}\sum _{i=r+1}^s\frac{a_i^{(r)}(s)}{{\gamma }_i+q}=I_{p,q}^{(\tilde{m},k)}.\end{array}$$

(15)

Now, by using (2) and (4), we obtain

$$\begin{array}{ccc}\hfill f_{[r,s,n,\tilde{m},k]}(y_1,y_2)& =& {\int }_{-\infty }^{\infty }{\int }_{x_1}^{\infty }{f}_{Y|X}(y_1|x_1)f_{Y|X}(y_2|x_2)f_{X(r,n,\tilde{m},k),X(s,n,\tilde{m},k)}(x_1,x_2)d{x}_{2}d{x}_1\hfill \\ & =& {\int }_{-\infty }^{\infty }{\int }_{x_1}^{\infty }{f}_Y(y_1)[1+\lambda (1-2F_X(x_1))(1-2F_Y(y_1))+\eta F_X(x_1)F_Y(y_1)\hfill \\ \hfill & \times & (2-3F_X(x_1))(2-3F_Y(y_1))]f_Y(y_2)[1+\lambda (1-2F_X(x_2))(1-2F_Y(y_2))\hfill \\ \hfill & +& \eta F_X(x_2)F_Y(y_2)(2-3F_X(x_2))(2-3F_Y(y_2))]\hfill \\ \hfill & \times & C_{s-1}\left[\sum _{i=r+1}^s{a}_i^{(r)}(s){\left(\frac{{\overline{F}}_X(x_2)}{{\overline{F}}_X(x_1)}\right)}^{{\gamma }_i}\right]\left[\sum _{i=1}^r{a}_i^{}(r){\overline{F}}_X^{{\gamma }_i}(x_1)\right]\frac{f_X(x_2)}{{\overline{F}}_X(x_2)}\frac{f_X(x_1)}{{\overline{F}}_X(x_1)}d{x}_{2}d{x}_1.\hfill \end{array}$$

By using the obvious relations $f_Y-f_{V_1}=f_Y(1-2F_Y)$ and $f_{V_1}-f_{V_2}=f_Y{F}_Y(2-3F_Y)$ and carrying out some algebra, we obtain

$$\begin{array}{ccc}\hfill f_{[r,s,n,\tilde{m},k]}(y_1,y_2)& =& {\int }_{-\infty }^{\infty }{\int }_{x_1}^{\infty }\left\{f_Y(y_1)f_Y(y_2)+\lambda (2{\overline{F}}_X(x_1)-1)f_Y(y_2)(f_Y(y_1)-f_{V_1}(y_1))\right.\hfill \\ \hfill & +& \lambda (2{\overline{F}}_X(x_2)-1)f_Y(y_1)(f_Y(y_2)-f_{V_1}(y_2))+\eta (4{\overline{F}}_X(x_1)-3{\overline{F}}_X^2(x_1)-1)f_Y(y_2)\hfill \\ \hfill & \times & (f_{V_1}(y_1)-f_{V_2}(y_1))+\eta (4{\overline{F}}_X(x_2)-3{\overline{F}}_X^2(x_2)-1)f_Y(y_1)(f_{V_1}(y_2)-f_{V_2}(y_2))\hfill \\ \hfill & +& {\lambda }^2(4{\overline{F}}_X(x_1){\overline{F}}_X(x_2)-2{\overline{F}}_X(x_1)-2{\overline{F}}_X(x_2)+1)(f_Y(y_1)-f_{V_1}(y_1))(f_Y(y_2)-f_{V_1}(y_2))\hfill \\ \hfill & +& \lambda \eta (8{\overline{F}}_X(x_1){\overline{F}}_X(x_2)-6{\overline{F}}_X(x_1){\overline{F}}_X^2(x_2)-2{\overline{F}}_X(x_1)-4{\overline{F}}_X(x_2)-3{\overline{F}}_X^2(x_2)+1)\hfill \\ \hfill & \times & (f_Y(y_1)-f_{V_1}(y_1))(f_{V_1}(y_2)-f_{V_2}(y_2))+\lambda \eta (8{\overline{F}}_X(x_1){\overline{F}}_X(x_2)-6{\overline{F}}_X^2(x_1){\overline{F}}_X(x_2)\hfill \\ \hfill & -& 2{\overline{F}}_X(x_2)-4{\overline{F}}_X(x_1)-3{\overline{F}}_X^2(x_1)+1)(f_{V_1}(y_1)-f_{V_2}(y_1))(f_Y(y_2)-f_{V_1}(y_2))\hfill \\ \hfill & +& {\eta }^2(16{\overline{F}}_X(x_1){\overline{F}}_X(x_2)-12{\overline{F}}_X(x_1){\overline{F}}_X^2(x_2)-12{\overline{F}}_X^2(x_1){\overline{F}}_X(x_2)-4{\overline{F}}_X(x_1)\hfill \\ \hfill & -& 4{\overline{F}}_X(x_2)+9{\overline{F}}_X^2(x_1){\overline{F}}_X^2(x_2)+3{\overline{F}}_X^2(x_1)+3{\overline{F}}_X^2(x_2)+1)(f_{V_1}(y_1)-f_{V_2}(y_1))\hfill \\ \hfill & \times & (f_{V_1}(y_2)-f_{V_2}(y_2))\}{C}_{s-1}\left[\sum _{i=r+1}^s{a}_i^{(r)}(s){\left(\frac{{\overline{F}}_X(x_2)}{{\overline{F}}_X(x_1)}\right)}^{{\gamma }_i}\right]\hfill \\ \hfill & \times & \left[\sum _{i=1}^r{a}_i^{}(r){\overline{F}}_X^{{\gamma }_i}(x_1)\right]\frac{f_X(x_2)}{{\overline{F}}_X(x_2)}\frac{f_X(x_1)}{{\overline{F}}_X(x_1)}d{x}_{2}d{x}_1.\hfill \end{array}$$

Since,

$$\begin{array}{c}\hfill \left(\sum _{i=r+1}^s\frac{a_i^{(r)}(s)}{{\gamma }_i}\right)\left(\sum _{i=1}^r\frac{a_i(r)}{{\gamma }_i}\right)=\frac{1}{C_{s-1}},\sum _{i=r+1}^s\frac{a_i^{(r)}(s)}{{\gamma }_i}=\frac{C_{r-1}}{C_{s-1}},\sum _{i=1}^r\frac{a_i(r)}{{\gamma }_i}=\frac{1}{C_{r-1}}.\end{array}$$

Now, by using (15), with $p=1$ and $q=0,$ for $t=1,$ and with $p=0$ and $q=1,$ for $t=2,$ we obtain, after some algebra,

$$\begin{array}{ccc}& & {\int }_{-\infty }^{\infty }{\int }_{x_1}^{\infty }\lambda (2{\overline{F}}_X(x_t)-1)C_{s-1}\left[\sum _{i=r+1}^s{a}_i^{(r)}(s){\left(\frac{{\overline{F}}_X(x_2)}{{\overline{F}}_X(x_1)}\right)}^{{\gamma }_i}\right]\left[\sum _{i=1}^r{a}_i^{}(r){\overline{F}}_X^{{\gamma }_i}(x_1)\right]\frac{f_X(x_2)}{{\overline{F}}_X(x_2)}\frac{f_X(x_1)}{{\overline{F}}_X(x_1)}d{x}_{2}d{x}_1.\hfill \\ & & =\left\{\begin{array}{cc}\lambda \left(2I_{1,0}^{(\tilde{m},k)}-1\right)=\lambda \left(2C_{r-1}{\displaystyle \sum _{i=1}^r}\frac{a_i(r)}{{\gamma }_i+1}-1\right)=\lambda C_{r-1}{\displaystyle \sum _{i=1}^r}{a}_i(r)\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right)={\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)},\hfill & t=1,\hfill \\ \lambda \left(2I_{0,1}^{(\tilde{m},k)}-1\right)=\lambda \left(2C_{s-1}{\displaystyle \sum _{i=1}^s}\frac{a_i(s)}{{\gamma }_i+1}-1\right)=\lambda C_{s-1}{\displaystyle \sum _{i=1}^s}{a}_i(s)\left(\frac{1-{\gamma }_i}{1+{\gamma }_i}\right)={\mathsf{\Omega }}_{s,n:1}^{(\tilde{m},k)},\hfill & t=2.\hfill \end{array}\right.\hfill \end{array}$$

Finally, in the same manner, we can derive ${\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)},{\mathsf{\Omega }}_{s,n:2}^{(\tilde{m},k)},{\mathsf{\Omega }}_{r,s,n:1}^{(\tilde{m},k)},{\mathsf{\Omega }}_{r,s,n:2}^{(\tilde{m},k)},{\mathsf{\Omega }}_{r,s,n:3}^{(\tilde{m},k)}$, and ${\mathsf{\Omega }}_{r,s,n:4}^{(\tilde{m},k)},$ which completes the proof. □

As a direct consequence of Theorem 3, the JMGF of concomitants $Y_{[r,n,\tilde{m},k]}$ and $Y_{[s,n,\tilde{m},k]},$ $r<s,$ based on IFGM$(\lambda ,\eta )$ are given by

$$\begin{array}{ccc}\hfill M_{[r,s,n,\tilde{m},k]}(t_1,t_2)& =\hfill & M_Y(t_1)M_Y(t_2)+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{M}_Y(t_2)(M_Y(t_1)-M_{V_1}(t_1))+{\mathsf{\Omega }}_{s,n:1}^{(\tilde{m},k)}{M}_Y(t_1)\hfill \\ \hfill & \times \hfill & (M_Y(t_2)-M_{V_1}(t_2))+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{M}_Y(t_2)(M_{V_1}(t_1)-M_{V_2}(t_1))+{\mathsf{\Omega }}_{s,n:2}^{(\tilde{m},k)}{M}_Y(t_1)(M_{V_1}(t_2)-M_{V_2}(t_2))\hfill \\ \hfill & +\hfill & {\mathsf{\Omega }}_{r,s,n:1}^{(\tilde{m},k)}(M_Y(t_1)-M_{V_1}(t_1))(M_Y(t_2)-M_{V_1}(t_2))+{\mathsf{\Omega }}_{r,s,n:2}^{(\tilde{m},k)}(M_Y(t_1)-M_{V_1}(t_1))\hfill \\ \hfill & \times \hfill & (M_Y(t_2)-M_{V_1}(t_2))+{\mathsf{\Omega }}_{r,s,n:3}^{(\tilde{m},k)}(M_{V_1}(t_1)-M_{V_2}(t_1))(M_Y(t_2)-M_{V_1}(t_2))\hfill \\ & +\hfill & {\mathsf{\Omega }}_{r,s,n:4}^{(\tilde{m},k)}(M_{V_1}(t_1)-M_{V_2}(t_1))(M_{V_1}(t_2)-M_{V_2}(t_2)).\hfill \end{array}$$

(16)

The product moment $E\left[Y_{[r,n,\tilde{m},k]}^{\ell }{Y}_{[s,n,\tilde{m},k]}^{𝚥}\right]={\mu }_{[r,s,n,\tilde{m},k]}^{(\ell ,𝚥)},\ell ,𝚥>0$, is obtained directly from (16) as

$$\begin{array}{ccc}\hfill {\mu }_{[r,s,n,\tilde{m},k]}^{(\ell ,𝚥)})& =& {\mu }_Y^{(\ell )}{\mu }_Y^{(𝚥)}+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mu }_Y^{(𝚥)}({\mu }_Y^{(\ell )}-{\mu }_{V_1}^{(\ell )})+{\mathsf{\Omega }}_{s,n:1}^{(\tilde{m},k)}{\mu }_Y^{(\ell )}({\mu }_Y^{(𝚥)}-m{u}_{V_1}^{(𝚥)})+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\mu }_Y^{(𝚥)}({\mu }_{V_1}^{(\ell )}-{\mu }_{V_2}^{(\ell )})\hfill \\ \hfill & +& {\mathsf{\Omega }}_{s,n:2}^{(\tilde{m},k)}{\mu }_Y^{(\ell )}({\mu }_{V_1}^{(𝚥)}-{\mu }_{V_2}^{(𝚥)})+{\mathsf{\Omega }}_{r,s,n:1}^{(\tilde{m},k)}({\mu }_Y^{(\ell )}-{\mu }_{V_1}^{(\ell )})({\mu }_Y^{(𝚥)}-{\mu }_{V_1}^{(𝚥)})+{\mathsf{\Omega }}_{r,s,n:2}^{(\tilde{m},k)}({\mu }_Y^{(\ell )}-{\mu }_{V_1}^{(\ell )})\hfill \\ \hfill & \times & ({\mu }_Y^{(𝚥)}-{\mu }_{V_1}^{(𝚥)})+{\mathsf{\Omega }}_{r,s,n:3}^{(\tilde{m},k)}({\mu }_{V_1}^{(\ell )}-{\mu }_{V_2}^{(\ell )})({\mu }_Y^{(𝚥)}-{\mu }_{V_1}^{(𝚥)})+{\mathsf{\Omega }}_{r,s,n:4}^{(\tilde{m},k)}({\mu }_{V_1}^{(\ell )}-{\mu }_{V_2}^{(\ell )})({\mu }_{V_1}^{(𝚥)}-{\mu }_{V_2}^{(𝚥)}).\hfill \end{array}$$

Remark 2.

By putting $\eta =0,$ in (9) and (14), we obtain the PDF and JPDF of concomitants of GOS for FGM, which were obtained in [16].

4. Some Measures for ${\mathit{Y}}_{[\mathit{r},\mathit{n},\tilde{\mathit{m}},\mathit{k}]}$ Based on IFGM$(\mathit{\lambda },\mathit{\eta })$

In this section, the measures of J, CRJ, and NCJ for the concomitant $Y_{[r,n,\tilde{m},k]}$ of GOS based on the IFGM$(\lambda ,\eta )$ family under a general framework are derived. An application is given for the concomitants of OS and record values for some well-known distributions such as uniform, exponential, and Weibull distributions.

4.1. Measure of J for $Y_{[r,n,\tilde{m},k]}$ Based on IFGM($\lambda ,\eta$)

Let $Y_{[r,n,\tilde{m},k]}$ is the rth concomitant of GOS; then, from (5) and (9), the J measure is given by

$$\begin{array}{ccc}\hfill J(Y_{[r,n,\tilde{m},k]})& =\hfill & -\frac{1}{2}{\int }_0^{\infty }{f}_{[r,n,\tilde{m},k]}^2(y)dy\hfill \\ \hfill & =\hfill & -\frac{1}{2}{\int }_0^{\infty }{f}_Y^2(y){\left[1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}(1-2F_Y(y))+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}(2F_Y(y)-3F_Y^2(y))\right]}^{2}dy\hfill \\ & =\hfill & -\frac{1}{2}{\int }_0^{\infty }{f}_Y^2(y)dy-\frac{{\left({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\right)}^2}{2}{\int }_0^{\infty }{f}_Y^2(y){(1-2F_Y(y))}^{2}dy\hfill \\ & -\hfill & {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\int }_0^{\infty }{f}_Y^2(y)(1-2F_Y(y))dy-\frac{{\left({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}\right)}^2}{2}{\int }_0^{\infty }{f}_Y^2(y){(2F_Y(y)-3F_Y^2(y))}^{2}dy\hfill \\ \hfill & -\hfill & {\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\int }_0^{\infty }{f}_Y^2(y){(2F_Y(y)-3F_Y^2(y))}^{}dy\hfill \\ \hfill & -\hfill & {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\int }_0^{\infty }{f}_Y^2(y)(1-2F_Y(y))(2F_Y(y)-3F_Y^2(y))dy\hfill \\ \hfill & =\hfill & J(Y)-\frac{{\left({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\right)}^2}{2}E\left(\frac{{(1-2U)}^2}{q(u)}\right)-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}E\left(\frac{(1-2U)}{q(u)}\right)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}E\left(\frac{(2U-3U^2)}{q(u)}\right)\hfill \\ \hfill & -\hfill & \frac{{\left({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}\right)}^2}{2}E\left(\frac{{(2U-3U^2)}^2}{q(u)}\right)-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}E\left(\frac{(1-2U)(2U-3U^2)}{q(u)}\right),\hfill \end{array}$$

(17)

where U is a uniformly RV on $(0,1)$, $J(Y)$ is the J of the RV $Y,$ $q(u)=\frac{1}{f_Y(Q(u))}$, and $q(u)$ is the derivative of $Q(u)$, with respect to $u,$ i.e., $q(u)=Q^{\prime }(u)$.

All the results for m-GOS $(m\ge -1)$ can be considered as a special case of GOS under the general framework (see Remark 1.1 in [16]), so consider the following two cases:

• Case 1: The m-GOS become OS if $m=0$ and $k=1$. The PDF of the concomitant of the rth OS $Y_{[r:n]}$ is given by (cf. [4])

  $$f_{[r:n]}(y)=f_Y(y)\left[1+\lambda {\Delta }_{r,n:1}(1-2F_Y(y))+\eta {\Delta }_{r,n:2}(2F_Y(y)-3F_Y^2(y))\right],$$

  where ${\Delta }_{r,n:p}=\frac{p\beta (r-1+p,n-r+1)-(p+1)\beta (r+p,n-r+1)}{\beta (r,n-r+1)}$, $p=1,2$. According (17), the J of $Y_{[r:n]}$ is

  $$\begin{array}{ccc}\hfill J(Y_{[r:n]})& =\hfill & J(Y)-\frac{{\left(\lambda {\Delta }_{r,n:1}\right)}^2}{2}E\left(\frac{{(1-2U)}^2}{q(u)}\right)-\lambda {\Delta }_{r,n:1}E\left(\frac{(1-2U)}{q(u)}\right)\frac{{\left(\eta {\Delta }_{r,n:2}\right)}^2}{2}E\left(\frac{{(2U-3U^2)}^2}{q(u)}\right)\hfill \\ & -\hfill & \eta {\Delta }_{r,n:2}E\left(\frac{(2U-3U^2)}{q(u)}\right)-\lambda \eta {\Delta }_{r,n:1}{\Delta }_{r,n:2}E\left(\frac{(1-2U)(2U-3U^2)}{q(u)}\right).\hfill \end{array}$$

  (18)
• Case 2: If $m=-1$ and $k=1$, the m-GOS become upper record values. Suppose $(X_i,Y_i),i=1,2,\dots ,$ be a sequence of bivariate RVs from a continuous distribution. If $R_r,r\ge 1,$ is the sequence of upper record values in the sequence of X’s, then the Y, which corresponds with the rth record value, will be referred the concomitant of the rth record value, denoted by $R_{[r]}.$ Hence, the PDF for $R_{[r]}$ has been acquired (cf. [4])

  $$f_{[r]}(y)=f_Y(y)\left[1+\lambda {\Delta }_1(r)(1-2F_Y(y))+\eta {\Delta }_2(r)(2F_Y(y)-3F_Y^2(y))\right],$$

  where ${\Delta }_1(r)=2^{-(r-1)}-1$ and ${\Delta }_2(r)=2^{-(r-2)}-3^{-(r-1)}-1.$ According to (17), the J measure of $R_{[r]}$ is

  $$\begin{array}{ccc}\hfill J(R_{[r]})& =\hfill & J(Y)-\frac{{\left(\lambda {\Delta }_1(r)\right)}^2}{2}E\left(\frac{{(1-2U)}^2}{q(u)}\right)-\lambda {\Delta }_1(r)E\left(\frac{(1-2U)}{q(u)}\right)-\frac{{\left(\eta {\Delta }_2(r)\right)}^2}{2}E\left(\frac{{(2U-3U^2)}^2}{q(u)}\right)\hfill \\ & -\hfill & \eta {\Delta }_2(r)E\left(\frac{(2U-3U^2)}{q(u)}\right)-\lambda \eta {\Delta }_1(r){\Delta }_2(r)E\left(\frac{(1-2U)(2U-3U^2)}{q(u)}\right).\hfill \end{array}$$

  (19)

In the following examples, we present some well-known distributions, such as exponential and Weibull distributions of $J(Y_{[r,n,\tilde{m},k]}).$

Example 2.

Suppose that X and Y have exponential distributions from IFGM (IFGM-ED) (i.e., $F_Y(y)=1-exp(-\frac{y}{\theta }),y,\theta >0$. According to (17), we obtain the J in $Y_{[r,n,\tilde{m},k]}$ as follows

$$\begin{array}{ccc}\hfill J(Y_{[r,n,\tilde{m},k]})& =& -\frac{1}{2\theta }\left[\frac{1}{2}+\frac{{\left({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\right)}^2}{6}+\frac{{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}}{3}+\frac{{\left({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}\right)}^2}{30}+\frac{{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}}{6}+\frac{{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}}{10}\right].\hfill \end{array}$$

Example 3.

Suppose that X and Y have Weibull distribution from IFGM (IFGM-WD) (i.e., $F_Y(y)=1-exp\left(-{\left(\frac{y}{\beta }\right)}^{\alpha }\right),\alpha ,\beta ,y>0$). After simple algebra, we obtain the J in $Y_{[r,n,\tilde{m},k]}$ as follows

$$\begin{array}{ccc}\hfill J(Y_{[r,n,\tilde{m},k]})& =& -2^{\frac{1}{\alpha }-3}\alpha {\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{\frac{1}{\alpha }-2}{\left(\frac{1}{\beta }\right)}^{2\alpha }\mathsf{\Gamma }\left(2-\frac{1}{\alpha }\right)\hfill \\ & +& \frac{{\left({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\right)}^2}{72}\left(9\times 2^{1/\alpha }-16\times 3^{1/\alpha }+9\times 4^{1/\alpha }\right)\alpha {\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{1/\alpha }\mathsf{\Gamma }\left(2-\frac{1}{\alpha }\right)\hfill \\ & +& \frac{{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}}{36}\left(9\times 2^{1/\alpha }-8\times 3^{1/\alpha }\right)\alpha {\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{1/\alpha }\mathsf{\Gamma }\left(2-\frac{1}{\alpha }\right)-\frac{{\left({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}\right)}^2}{2}\hfill \\ & \times & \frac{\left(50\times 3^{1/\alpha }\left(9\times 2^{1/\alpha }-32\right)-17285^{1/\alpha }+225\times 2^{1/\alpha }\left(11\times 2^{1/\alpha }+2\right)\right)\alpha {\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{1/\alpha }\mathsf{\Gamma }\left(2-\frac{1}{\alpha }\right)}{1800}\hfill \\ & +& \frac{{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}}{144}\left(9\times 2^{1/\alpha }\left(3\times 2^{1/\alpha }+4\right)-64\times 3^{1/\alpha }\right)\alpha {\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{1/\alpha }\mathsf{\Gamma }\left(2-\frac{1}{\alpha }\right)\hfill \\ & -& \frac{{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}}{24}\left(3\times 2^{1/\alpha }\left(2^{1/\alpha }+2\right)-8\times 3^{1/\alpha }\right)\alpha {\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{1/\alpha }\mathsf{\Gamma }\left(2-\frac{1}{\alpha }\right).\hfill \end{array}$$

4.2. Measure of CRJ for $Y_{[r,n,\tilde{m},k]}$ Based on IFGM($\lambda ,\eta$)

For the concomitant $Y_{[r,n,\tilde{m},k]}$ of rth GOS, from (6) and (9), the CRJ measure is given by

$$\begin{array}{ccc}\hfill {\xi }^{*}(Y_{[r,n,\tilde{m},k]})& =\hfill & -\frac{1}{2}{\int }_0^{\infty }{\overline{F}}_{[r,n,\tilde{m},k]}^2(y)dy=-\frac{1}{2}{\int }_0^{\infty }{\overline{F}}_Y^2(y){\left[1-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{F}_Y(y)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{F}_Y^2(y)\right]}^2\hfill \\ \hfill & =\hfill & {\xi }^{*}(Y)-\frac{{({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})}^2}{2}{\int }_0^{\infty }{F}_Y^2(y){\overline{F}}_Y^2(y)dy-\frac{{({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)})}^2}{2}{\int }_0^{\infty }{F}_Y^4(y){\overline{F}}_Y^2(y)dy\hfill \\ \hfill & +\hfill & {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\int }_0^{\infty }{F}_Y(y){\overline{F}}_Y^2(y)dy+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\int }_0^{\infty }{F}_Y^2(y){\overline{F}}_Y^2(y)dy\hfill \\ \hfill & -\hfill & {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\int }_0^{\infty }{F}_Y^3(y){\overline{F}}_Y^2(y)dy\hfill \\ \hfill & =\hfill & {\xi }^{*}(Y)-\frac{{({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})}^2}{2}E\left(U^2{(1-U)}^{2}q(u)\right)-\frac{{({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)})}^2}{2}E\left(U^4{(1-U)}^{2}q(u)\right)\hfill \\ \hfill & +\hfill & {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}E\left(U{(1-U)}^{2}q(u)\right)+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}E\left(U^2{(1-U)}^{2}q(u)\right)\hfill \\ \hfill & -\hfill & {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}E\left(U^3{(1-U)}^{2}q(u)\right),\hfill \end{array}$$

(20)

where ${\xi }^{*}(Y)$ is the CRJ of the RV Y.

In the examples below, we show the uniform and Weibull distributions of ${\xi }^{*}(Y_{[r,n,\tilde{m},k]}).$

Example 4.

Suppose that X and Y have uniform distributions from IFGM (IFGM-UD) (i.e., $F_Y(y)=\frac{y}{{\theta }_2},0<y<{\theta }_2$). According to (20), we obtain the CRJ in $Y_{[r,n,\tilde{m},k]}$ as follows:

$$\begin{array}{c}\hfill {\xi }^{*}(Y_{[r,n,\tilde{m},k]})=-\frac{{\theta }_2}{6}-\frac{{({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})}^2}{2}\frac{{\theta }_2}{30}-\frac{{({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)})}^2}{2}\frac{{\theta }_2}{105}+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\frac{{\theta }_2}{12}+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}\frac{{\theta }_2}{30}-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}\frac{{\theta }_2}{60}.\end{array}$$

Example 5.

Suppose that X and Y have IFGM-WD, then we obtain the CRJ in $Y_{[r,n,\tilde{m},k]}$ as follows:

$$\begin{array}{ccc}\hfill {\xi }^{*}(Y_{[r,n,\tilde{m},k]})& =& -2^{-\frac{1}{\alpha }-1}{\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{-1/\alpha }\mathsf{\Gamma }\left(1+\frac{1}{\alpha }\right)\hfill \\ & -& \frac{{({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})}^2}{2}{12}^{-1/\alpha }\left(-2^{\frac{\alpha +2}{\alpha }}+3^{1/\alpha }+6^{1/\alpha }\right){\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{-1/\alpha }\mathsf{\Gamma }\left(1+\frac{1}{\alpha }\right)\hfill \\ & -& \frac{{({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)})}^2}{2}{60}^{-1/\alpha }\left(-3^{1/\alpha }{4}^{\frac{1}{\alpha }+1}+23^{\frac{1}{\alpha }+1}{5}^{1/\alpha }-4^{\frac{1}{\alpha }+1}{5}^{1/\alpha }+{10}^{1/\alpha }+{30}^{1/\alpha }\right)\hfill \\ & \times & {\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{-1/\alpha }\mathsf{\Gamma }\left(1+\frac{1}{\alpha }\right)+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{6}^{-1/\alpha }\left(3^{1/\alpha }-2^{1/\alpha }\right){\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{-1/\alpha }\mathsf{\Gamma }\left(1+\frac{1}{\alpha }\right)\hfill \\ & +& {\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{12}^{-1/\alpha }\left(-2^{\frac{\alpha +2}{\alpha }}+3^{1/\alpha }+6^{1/\alpha }\right){\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{-1/\alpha }\mathsf{\Gamma }\left(1+\frac{1}{\alpha }\right)\hfill \\ & -& {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{60}^{-1/\alpha }\left(3^{\frac{1}{\alpha }+1}{5}^{1/\alpha }-{12}^{1/\alpha }-3{20}^{1/\alpha }+{30}^{1/\alpha }\right){\left({\left(\frac{1}{\beta }\right)}^{\alpha }\right)}^{-1/\alpha }\mathsf{\Gamma }\left(1+\frac{1}{\alpha }\right).\hfill \end{array}$$

4.3. Measure of NCJ for $Y_{[r,n,\tilde{m},k]}$ Based on IFGM($\lambda ,\eta$)

For the concomitant $Y_{[r,n,\tilde{m},k]}$ of rth GOS, from (8) and (10), the NCJ measure is given by

$$\begin{array}{ccc}\hfill \mathcal{C}\xi (Y_{[r,n,\tilde{m},k]})& =& \frac{1}{2}{\int }_0^{\infty }\left(1-F_{[r,n,\tilde{m},k]}^2(y)\right)dy\hfill \\ & =& \frac{1}{2}{\int }_0^{\infty }\left(1-F_Y^2(y)\right){\left[1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}(1-F_Y(y))+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}(F_Y(y)-F_Y^2(y))\right]}^{2}dy\hfill \\ & =& \mathcal{C}\xi (Y)-\frac{{({\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)})}^2}{2}E\left(U^2{(1-U)}^{2}q(u)\right)-\frac{{({\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)})}^2}{2}E\left(U^2{(U-U^2)}^{2}q(u)\right)\hfill \\ & -& {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}E\left(U^2(1-U)q(u)\right)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}E\left(U^2(U-U^2)q(u)\right)\hfill \\ & -& {\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}E\left(U^2(1-U)(U-U^2)q(u)\right),\hfill \end{array}$$

where $\mathcal{C}{\xi }^{}(Y)$ is the NCJ of the RV Y.

5. Empirical Measures for ${\mathit{Y}}_{[\mathit{r},\mathit{n},\tilde{\mathit{m}},\mathit{k}]}$ Based on IFGM($\mathit{\lambda },\mathit{\eta }$)

In this section, we use empirical estimators to calculate the NCRJ and NCJ for concomitant $Y_{[r,n,\tilde{m},k]}.$ The mean and variance of the empirical NCRJ and NCJ of OS and record values are given.

5.1. Empirical NCRJ

We will now look at the problem of using the empirical NCRJ to estimate the NCRJ for concomitants. Let $(X_i,Y_i),i=1,2,\dots ,$ be a sequence from the IFGM family. Using the relation (7), the empirical NCRJ of $Y_{[r,n,\tilde{m},k]}$ may be calculated as follows:

$$\begin{array}{ccc}\hfill \widehat{\xi }(Y_{[r,n,\tilde{m},k]})& =\hfill & \frac{1}{2}{\int }_0^{\infty }{\left[1-{\widehat{F}}_{[r,n,\tilde{m},k]}(y)\right]}^{2}dy\hfill \\ \hfill & =\hfill & \frac{1}{2}{\int }_0^{\infty }{\left(1-{\widehat{F}}_Y(y)\right)}^2{\left[1-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\widehat{F}}_Y(y)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\widehat{F}}_Y^2(y)\right]}^{2}dy\hfill \\ \hfill & =\hfill & \frac{1}{2}{\displaystyle \sum _{j=1}^{n-1}}{\int }_{Z_j}^{Z_{j+1}}{\left(1-{\widehat{F}}_Y(y)\right)}^2{\left[1-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}{\widehat{F}}_Y(y)-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\widehat{F}}_Y^2(y)\right]}^{2}dy\hfill \\ \hfill & =\hfill & \frac{1}{2}{\displaystyle \sum _{j=1}^{n-1}}{U}_j{\left(1-\frac{j}{n}\right)}^2{\left[1-{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\frac{j}{n}-{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}{\left(\frac{j}{n}\right)}^2\right]}^2,\hfill \end{array}$$

(21)

where $U_j=Z_{j+1}-Z_j,$$j=1,2\dots ,n-1$ are sample spacings based on ordered random samples $Y_j.$

Let us consider the following examples to give the mean and variance of $\widehat{\xi }(Y_{[r:n]})$ and $\widehat{\xi }(R_{[r]}).$

Example 6.

If $(X_i,Y_i),$ $i=1,2,\dots ,n$ is a random sample from IFGM-ED, the sample spacings $U_j$ are independent and exponentially distributed, with a mean $\frac{1}{{\theta }_2(n-j)}$ (for more details, see [29]). According to [30], the empirical NCRJ mean and variance based on $Y_{[r:n]}$ are as follows:

$$\begin{array}{ccc}\hfill E\left[\widehat{\xi }(Y_{[r:n]})\right]& =& \frac{1}{2{\theta }_2}\sum _{j=1}^{n-1}\frac{1}{(n-j)}{\left(1-\frac{j}{n}\right)}^2{\left[1-\lambda {\Delta }_{r,n:1}\frac{j}{n}-\eta {\Delta }_{r,n:2}{\left(\frac{j}{n}\right)}^2\right]}^2,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill Var\left[\widehat{\xi }(Y_{[r:n]})\right]& =& \frac{1}{4{\theta }_2^2}\sum _{j=1}^{n-1}\frac{1}{{(n-j)}^2}{(1-\frac{j}{n})}^4{\left[1-\lambda {\Delta }_{r,n:1}\frac{j}{n}-\eta {\Delta }_{r,n:2}{\left(\frac{j}{n}\right)}^2\right]}^4.\hfill \end{array}$$

(23)

Example 7.

The sample spacings $U_j$ for IFGM-UD with ${\theta }_1={\theta }_2=1$ are independent of the beta distribution with parameters 1 and n. According to [30], the mean and variance of empirical NCRJ based on $R_{[r]}$ are as follows:

$$\begin{array}{ccc}\hfill E\left[\widehat{\xi }(R_{[r]})\right]& =& \frac{1}{2(n+1)}\sum _{j=1}^{n-1}{\left(1-\frac{j}{n}\right)}^2{\left[1-\lambda {\Delta }_1(r)\frac{j}{n}-\eta {\Delta }_2(r){\left(\frac{j}{n}\right)}^2\right]}^2,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Var\left[\widehat{\xi }(R_{[r]})\right]& =& \frac{n}{4{(n+1)}^2(n+2)}\sum _{j=1}^{n-1}{\left(1-\frac{j}{n}\right)}^4{\left[1-\lambda {\Delta }_1(r)\frac{j}{n}-\eta {\Delta }_2(r){\left(\frac{j}{n}\right)}^2\right]}^4.\hfill \end{array}$$

5.2. Empirical NCJ

In this subsection, using the empirical NCJ to estimate the NCJ for concomitants. Let $(X_i,Y_i),i=1,2,\dots ,$ be a sequence from IFGM family. The empirical NCJ of $Y_{[r,n,\tilde{m},k]}$ is given by

$$\begin{array}{ccc}\hfill \widehat{\mathcal{C}\xi }(Y_{[r,n,\tilde{m},k]})& =& \frac{1}{2}{\int }_0^{\infty }\left(1-{\widehat{F}}_{[r,n,\tilde{m},k]}^2(y)\right)dy\hfill \\ & =& \frac{1}{2}{\int }_0^{\infty }\left(1-{\widehat{F}}_Y^2(y)\right){\left[1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}(1-{\widehat{F}}_Y(y))+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}({\widehat{F}}_Y(y)-{\widehat{F}}_Y^2(y))\right]}^{2}dy\hfill \\ & =& \frac{1}{2}\sum _{j=1}^{n-1}{\int }_{Z_j}^{Z_{j+1}}1-{\widehat{F}}_Y^2(y){\left[1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}(1-{\widehat{F}}_Y(y))+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}({\widehat{F}}_Y(y)-{\widehat{F}}_Y^2(y))\right]}^{2}dy\hfill \\ & =& \frac{1}{2}\sum _{j=1}^{n-1}{U}_j\left\{1-{\left(\frac{j}{n}\right)}^2{\left[1+{\mathsf{\Omega }}_{r,n:1}^{(\tilde{m},k)}\left(1-\frac{j}{n}\right)+{\mathsf{\Omega }}_{r,n:2}^{(\tilde{m},k)}\left(\left(\frac{j}{n}\right)-{\left(\frac{j}{n}\right)}^2\right)\right]}^2\right\}.\hfill \end{array}$$

Example 8.

If $(X_i,Y_i),$ $i=1,2,\dots ,n$ is a random sample from IFGM-ED. The empirical NCJ mean and variance, based on $Y_{[r:n]}$, are as follows:

$$\begin{array}{c}\hfill E\left[\widehat{\mathcal{C}\xi }(Y_{[r:n]})\right]=\frac{1}{2{\theta }_2}\sum _{j=1}^{n-1}\frac{1}{(n-j)}\left\{1-{\left(\frac{j}{n}\right)}^2{\left[1+\lambda {\Delta }_{r,n:1}\left(1-\frac{j}{n}\right)+\eta {\Delta }_{r,n:2}\left(\left(\frac{j}{n}\right)-{\left(\frac{j}{n}\right)}^2\right)\right]}^2\right\},\end{array}$$

$$\begin{array}{c}\hfill Var\left[\widehat{\mathcal{C}\xi }(Y_{[r:n]})\right]=\frac{1}{4{\theta }_2^2}\sum _{j=1}^{n-1}\frac{1}{{(n-j)}^2}{\left\{1-{\left(\frac{j}{n}\right)}^2{\left[1+\lambda {\Delta }_{r,n:1}\left(1-\frac{j}{n}\right)+\eta {\Delta }_{r,n:2}\left(\left(\frac{j}{n}\right)-{\left(\frac{j}{n}\right)}^2\right)\right]}^2\right\}}^2.\end{array}$$

Example 9.

The sample spacings $U_j$ for IFGM-UD. The mean and variance of empirical NCJ, based on $R_{[r]}$, are as follows:

$$\begin{array}{c}\hfill E\left[\widehat{\mathcal{C}\xi }(R_{[r]})\right]=\frac{1}{2(n+1)}\sum _{j=1}^{n-1}\left\{1-{\left(\frac{j}{n}\right)}^2{\left[1+\lambda {\Delta }_1(r)\left(1-\frac{j}{n}\right)+\eta {\Delta }_2(r)\left(\left(\frac{j}{n}\right)-{\left(\frac{j}{n}\right)}^2\right)\right]}^2\right\},\end{array}$$

$$\begin{array}{c}\hfill Var\left[\widehat{\mathcal{C}\xi }(R_{[r]})\right]=\frac{n}{4{(n+1)}^2(n+2)}\sum _{j=1}^{n-1}{\left\{1-{\left(\frac{j}{n}\right)}^2{\left[1+\lambda {\Delta }_1(r)\left(1-\frac{j}{n}\right)+\eta {\Delta }_2(r)\left(\left(\frac{j}{n}\right)-{\left(\frac{j}{n}\right)}^2\right)\right]}^2\right\}}^2.\end{array}$$

The values of $E\left[\widehat{\xi }(Y_{[r:n]})\right]$ and Var$\left[\widehat{\xi }(Y_{[r:n]})\right]$, based on IFGM-ED by computing (22) and (23), are shown in Table 1. From Table 1, the following characteristics can be taken.

Table 1. $E\left[\widehat{\xi }(Y_{[2:n]})\right]$ and Var$\left[\widehat{\xi }(Y_{[2:n]})\right]$ from IFGM-ED.

$\mathit{E}\left[\widehat{\mathit{\xi }}({\mathit{Y}}_{[2:\mathit{n}]})\right]$ for $\mathit{\lambda }=0.99$
n	${\mathbf{\theta }}_{\mathbf{2}}$	$\mathbf{\eta }=-\mathbf{1}.\mathbf{8}$	$\mathbf{\eta }=-\mathbf{1}.\mathbf{4}$	$\mathbf{\eta }=\mathbf{0}.\mathbf{4}$	$\mathbf{\eta }=\mathbf{0}.\mathbf{8}$
5	0.5	0.3640	0.3495	0.2911	0.2796
5	1	0.1820	0.1747	0.1455	0.1398
5	2	0.0910	0.0874	0.0728	0.0700
10	0.5	0.3224	0.3109	0.2657	0.2572
10	1	0.1612	0.1555	0.1329	0.1286
10	2	0.8060	0.0777	0.0664	0.0643
15	0.5	0.3001	0.2919	0.2594	0.2532
15	1	0.1501	0.1460	0.1297	0.1266
15	2	0.070	0.0730	0.0648	0.0633
20	0.5	0.2880	0.2817	0.2580	0.2519
20	1	0.1440	0.1409	0.1284	0.1260
20	2	0.0720	0.0704	0.0642	0.0630
$Var\left[\widehat{\xi }(Y_{[2:n]})\right]$ for $\lambda =0.99$
n	${\theta }_2$	$\eta =-1.8$	$\eta =-1.4$	$\eta =0.4$	$\eta =0.8$
5	0.5	0.0391	0.0369	0.0293	0.0280
5	1	0.0098	0.0092	0.0073	0.0070
5	2	0.0024	0.0023	0.0018	0.0017
10	0.5	0.0165	0.0159	0.0137	0.0133
10	1	0.0041	0.0040	0.0034	0.0033
10	2	0.0010	0.0009	0.0008	0.0008
15	0.5	0.0103	0.0101	0.0092	0.0090
15	1	0.0026	0.0025	0.0023	0.0022
15	2	0.0006	0.0006	0.0005	0.0005
20	0.5	0.0075	0.0074	0.0070	0.0068
20	1	0.0019	0.0018	0.0017	0.0017
20	2	0.0005	0.0005	0.0004	0.0004

1.

Generally, with fixed n and ${\theta }_2,$ the values of $E\left[\widehat{\xi }(Y_{[r:n]})\right]$ and Var$\left[\widehat{\xi }(Y_{[r:n]})\right]$ decrease as the value of $\eta$ increases.

2.

In general, fixing n and ${\theta }_2$ yields $E\left[\widehat{\xi }(Y_{[r:n]})\right]$ and Var$\left[\widehat{\xi }(Y_{[r:n]})\right]$, which decreases as the value of ${\theta }_2$ increases.

The relationship between NCRJ and empirical NCRJ of $R_{[r]}$ from IFGM-UD at $n=100$ is depicted in Figure 1. The following properties can be extracted from Figure 1.

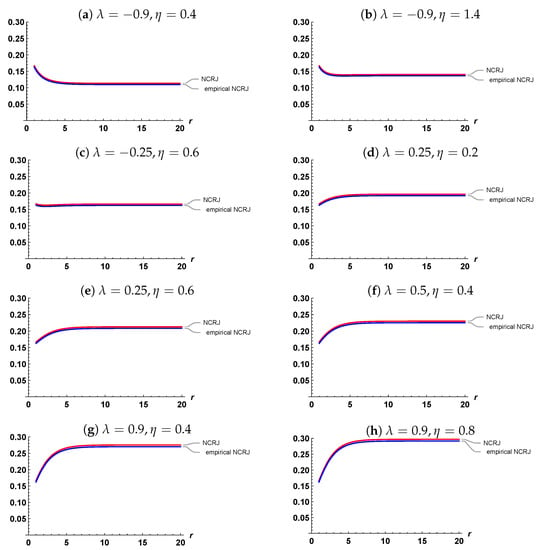
Figure 1. Representation of NCRJ and empirical NCRJ based on $R_{[r]}$ from IFGM-UD.

1.

Generally, the empirical NCRJ and NCRJ have similar values with all values of the parameter space $\mathsf{\Omega }.$

2.

The empirical NCRJ and NCRJ increase as $\lambda$ increases.

3.

With the increase in the values of r, stability occurs in the values of both NCRJ and empirical NCRJ.

6. An Application

This section examines the CRJ measure using analyses of actual data sets. Ref. [31] provide the economic data set, which comprises of 31 annual time series observations, covering the period from 1980 to 2010, on the following response variable: GDP growth Y and exports of products and services $X.$ These data were first gathered by the OECD National Accounts data and the World Bank National Accounts data. One of the key reasons for choosing to use economic data for the current study may have been the fact that economics is a significant business in many developed and developing countries. In order to increase GPA growth and exports of goods and services, the government is keen. The data is relevant to the distribution based on FGM copula and its generalizations, including IFGM, since the correlation between data is 0.2709. Here, we shall suggest three bivariate distributions to fit the data: IFGM-WD, IFGM-gamma distribution (IFGM-GD), and IFGM-generalized exponential distribution (IFGM-GED). By using the MLE method based on IFGM-WD, IFGM-GD, and IFGM-GED, we estimate the four parameters ${\alpha }_i,{\beta }_i,i=1,2,$ in the Weibull DF $F_W(w)=1-exp\left(-{\left(\frac{w}{{\beta }_i}\right)}^{{\alpha }_i}\right)$, the gamma DF $F_W(w)=\frac{1}{\mathsf{\Gamma }({\alpha }_i)}\gamma ({\alpha }_i,\frac{w}{{\beta }_i}),$ and the generalized exponential DF $F_W(w)={\left(1-exp\left(-{\beta }_{i}w\right)\right)}^{{\alpha }_i},$$w,{\alpha }_i,{\beta }_i>0,$ and $\gamma ({\alpha }_i,\frac{w}{{\beta }_i})$ is incomplete gamma function, in addition to the shape parameters $\lambda$ and $\eta .$ Moreover, the AIC and BIC are computed in Table 2, so the bivariate IFGM-GED distribution fits better the data. Table 3 examines the CRJ measure for the model estimated IFGM-WD for the concomitants $Y_{[r:31]},r=1,2,\dots ,30,$ i.e., the concomitants of the lower extreme, upper extreme, and central values. This table shows that each of the CRJ measures has a maximum value at lower extremes.

Table 2. Parameter estimation for IFGM distributions.

MLE Parameters Estimation
	${\widehat{\mathit{\alpha }}}_1$	${\widehat{\mathit{\beta }}}_1$	${\widehat{\mathit{\alpha }}}_2$	${\widehat{\mathit{\beta }}}_2$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\eta }}$	AIC	BIC
IFGM-WD	1.689	21.032	3.275	6.327	−0.8926	2.363	371.684	380.288
IFGM-GD	0.2872	21.573	0.4156	10.698	0.927	1.496	342.448	339.40
IFGM-GED	63.57	0.218	7.136	0.568	−0.592	3.491	320.32	317.58

Table 3. ${\xi }^{*}(Y_{[r:31]})$ for IFGM-WD.

r	1	2	3	4	5	6	7	8	9	10
	−2.774	−2.705	−2.642	−2.585	−2.532	−2.485	−2.441	−2.402	−2.366	−2.334
r	11	12	13	14	15	16	17	18	19	20
	−2.305	−2.279	−2.255	−2.234	−2.216	−2.200	−2.186	−2.175	−2.165	−2.158
r	21	22	23	24	25	26	27	28	29	30
	−2.154	−2.152	−2.152	−2.155	−2.162	−2.171	−2.184	−2.200	−2.145	−2.274

7. Conclusions

While the range of the correlation coefficient for the IFGM$(\lambda ,\eta )$ is similar to that of other generalizations of FGM (such as the Huang-Kotz FGM), it beats most of these generalizations, due to its flexibility and simplicity. The PDFs employed in this study were always linear combinations of other simpler distributions because of this benefit. Consequently, this fact gives a satisfactory motivation to deal with IFGM$(\lambda ,\eta )$, rather than Huang-Kotz FGM. As a result, for every arbitrary distribution, we showed a variety of distributional properties of the concomitant of GOS based on IFGM$(\lambda ,\eta )$ under the general setting. Last, but not least, the concomitant of GOS based on IFGM$(\lambda ,\eta )$ have the joint CDF and product moments. One important complementary dual measure of Shannon entropy is extropy (J), which plays a vital role in the scoring of forecasting distributions, risk measures, and independence. Moreover, some well-known information measures, i.e., J, CRJ, and NCJ, are derived. For OS, record values, and POS-II with uniform marginal distributions are used to show applications of these findings. To address the issue of calculating the CRJ and NCJ, the empirical technique is combined with concomitant of GOS. For illustrative purposes, bivariate real-world data sets have been analyzed, and the performance of the proposed method is entirely satisfactory. From these real-world data sets, we show that the IFGM is flexible in fitting, especially in the variables with the lowest correlation coefficient. We were able to obtain information related to GDP growth Y based on the exports of goods and services X by using the concomitants of OS (as an important practical kind to order the bivariate data). We show that these data are more suitable for IFGM-GED.

In discussing the potential for further research, two issues are taken into account. As a first step, we can apply the findings of this research to a weighted extropy. This shift-dependent information metric gives larger values of RVs a higher weight (see [32]). The second future research objective is to estimate these measures using classical and Bayesian methods. A significant amount of attention was paid to Bayesian methods in the literature for example [33,34,35].