Machine-Learning Approach for Risk Estimation and Risk Prediction of the Effect of Climate on Bovine Respiratory Disease
Abstract
1. Introduction
2. Materials and Methods
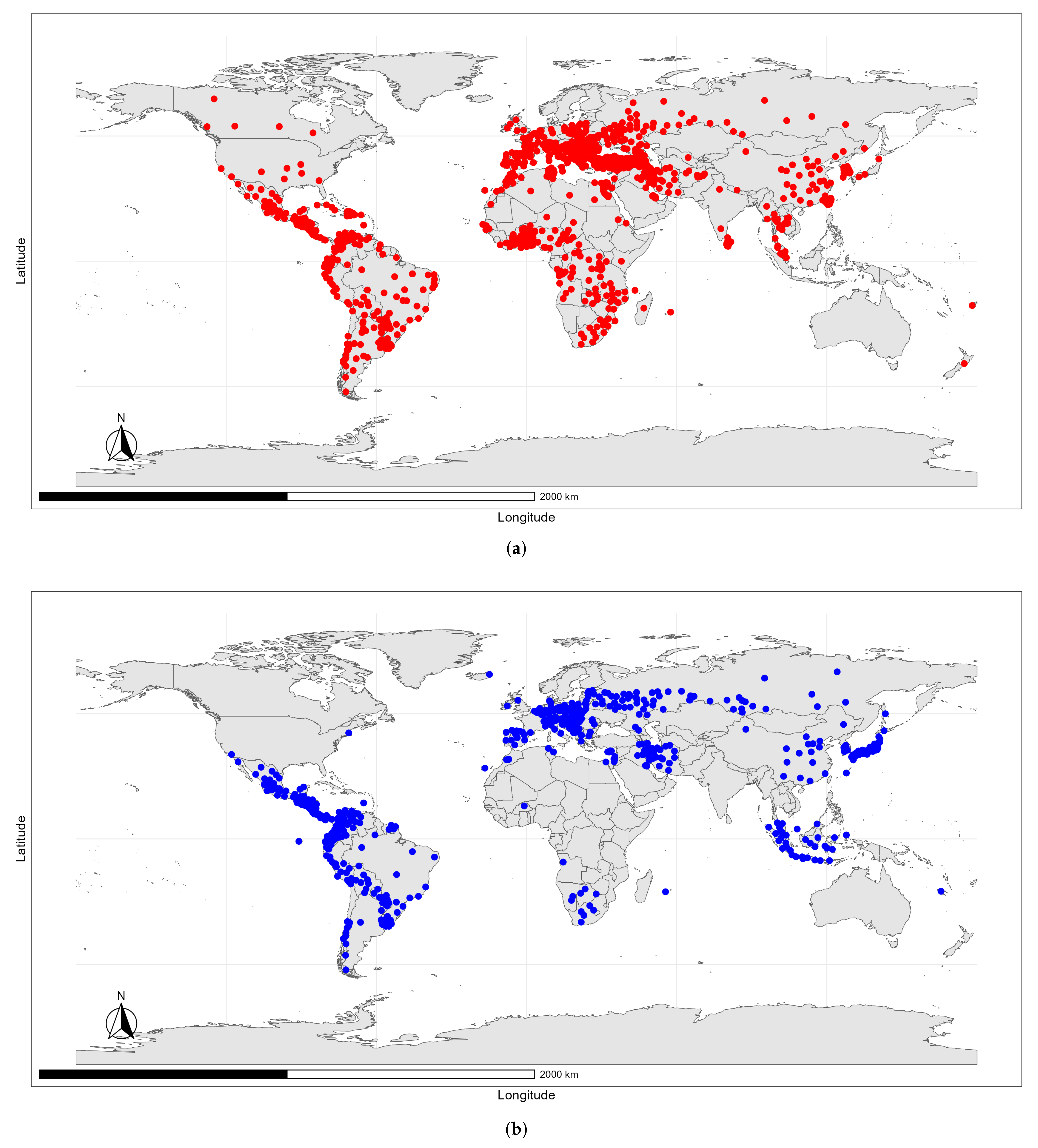
Data Sources
3. Models
3.1. Maximum Entropy Approach
3.2. Boosted Regression Tree Approach
- 1
- The training set, , where and represent the independent (features) and dependent variables, respectively.
- 2
- The loss function, . It is differentiable.
- 3
- Number of iterations/trees.
3.3. Model Predictability
3.4. Modelling Framework and Software
4. Results
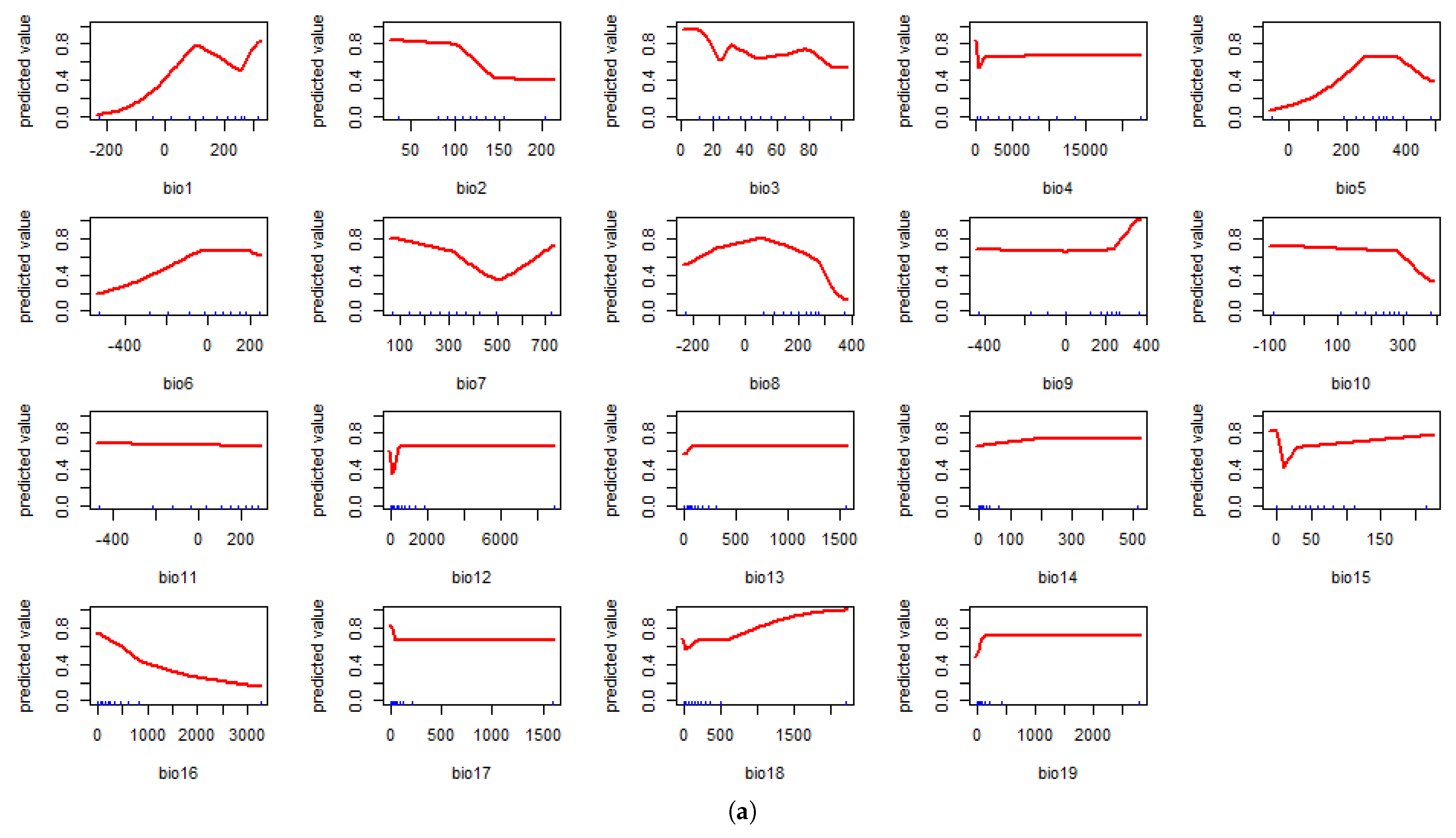
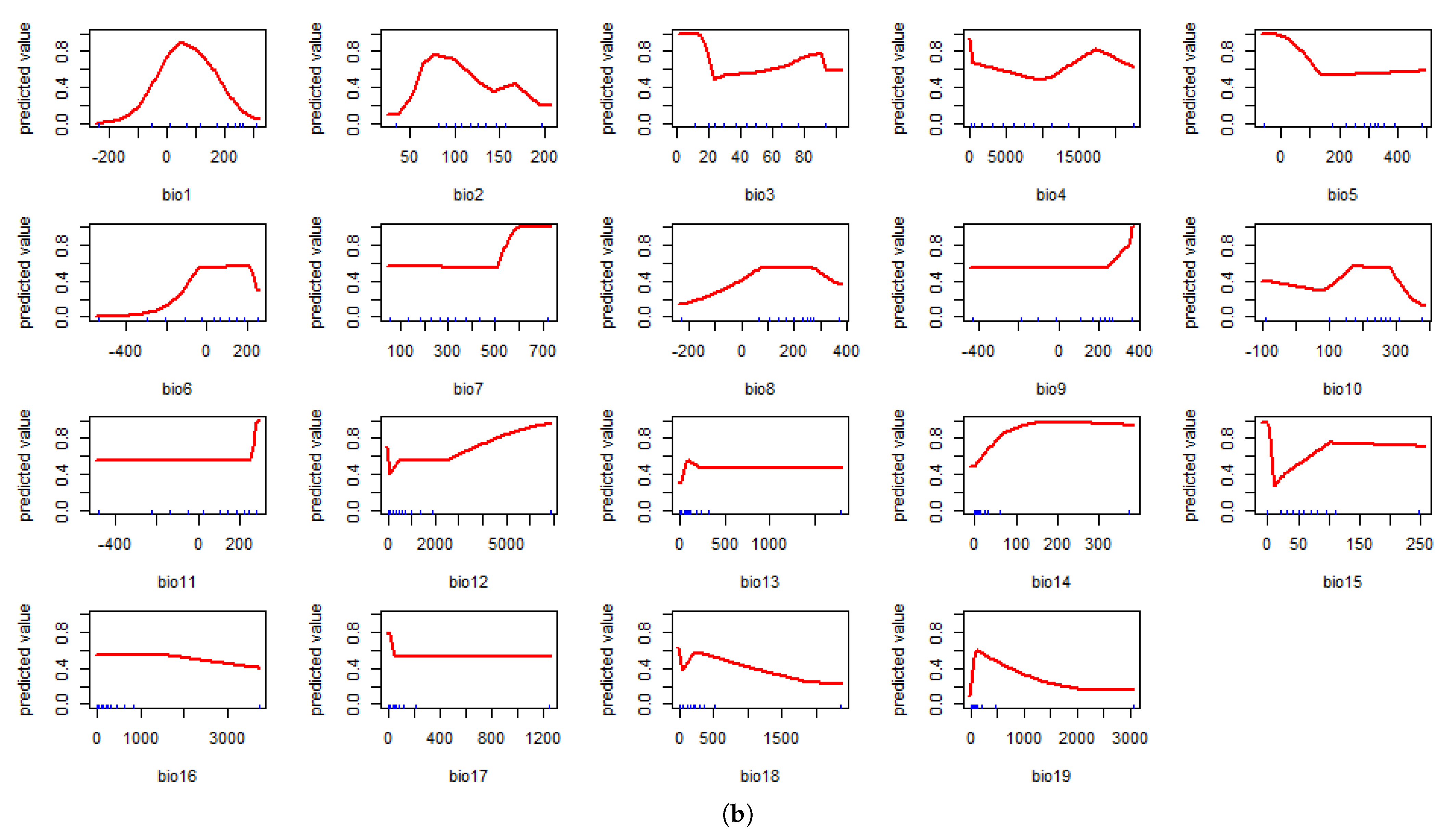
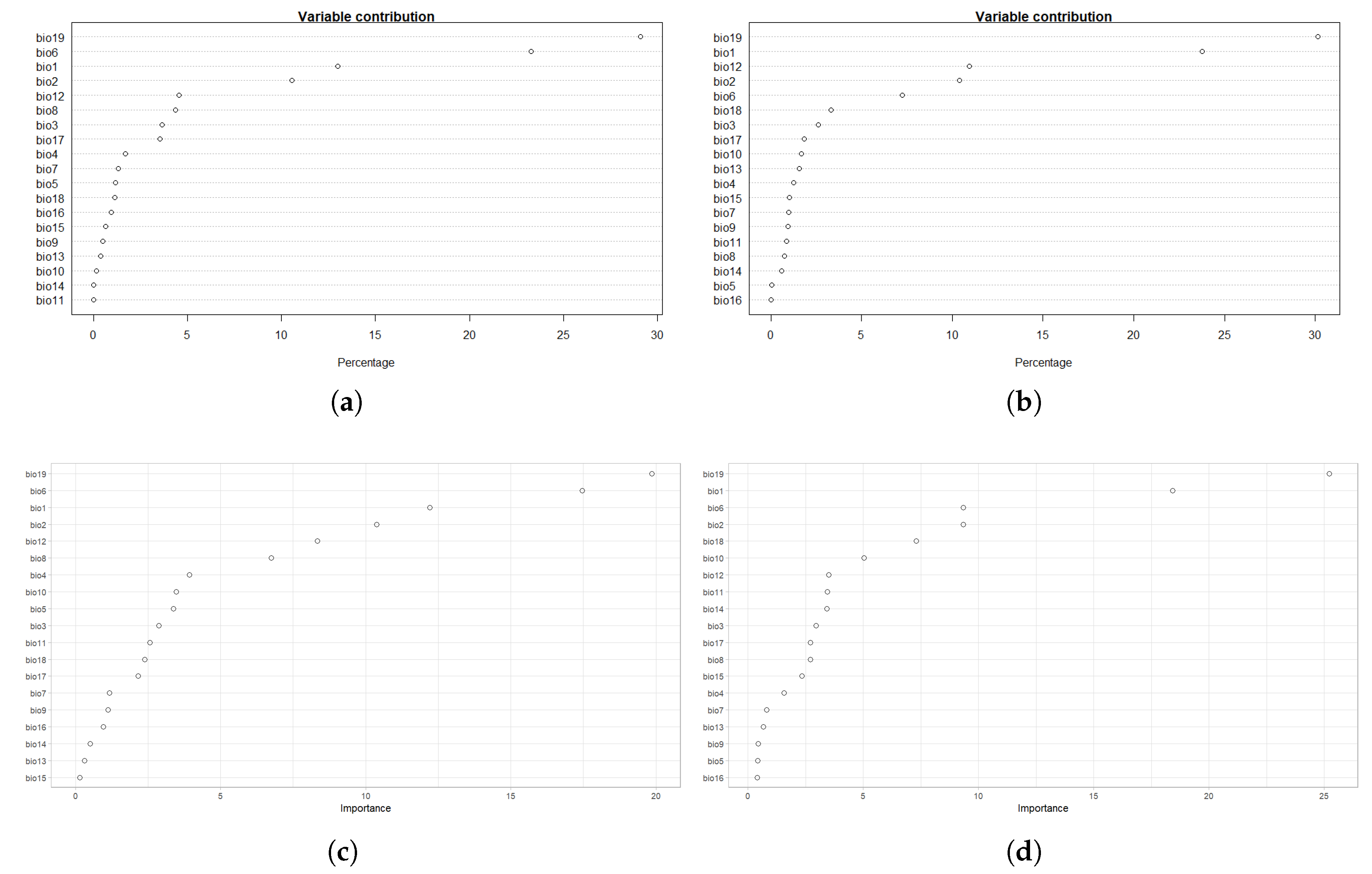
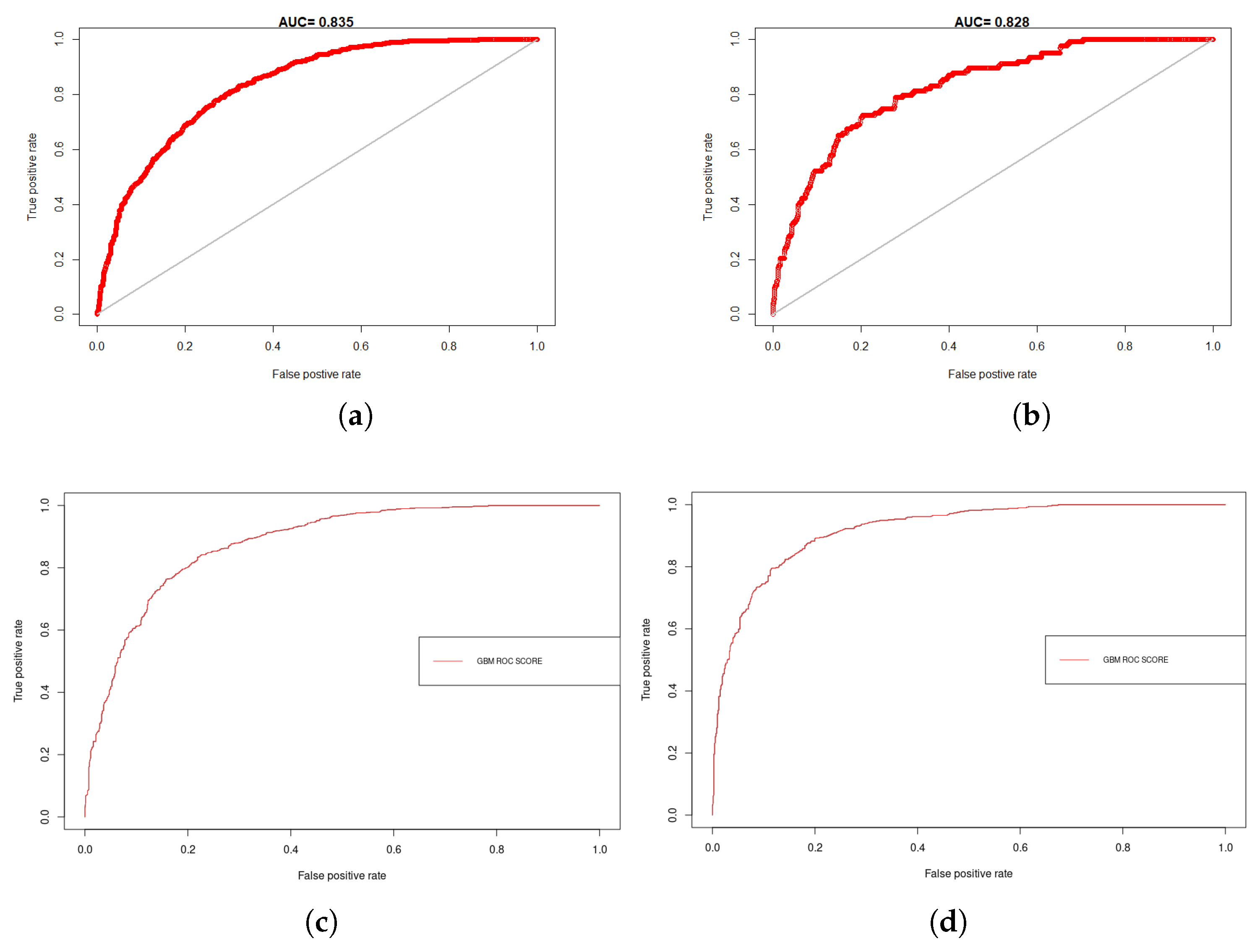
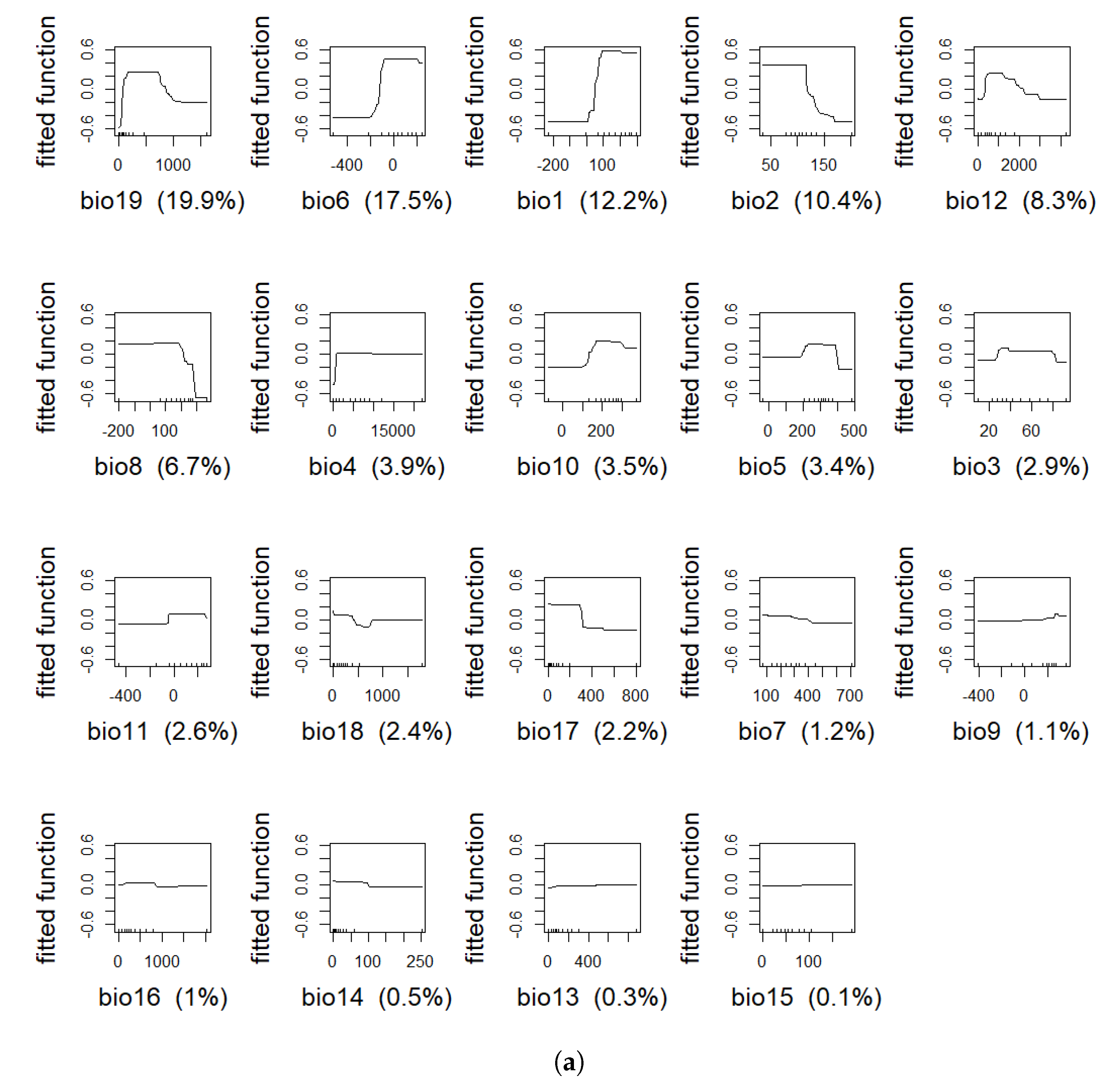
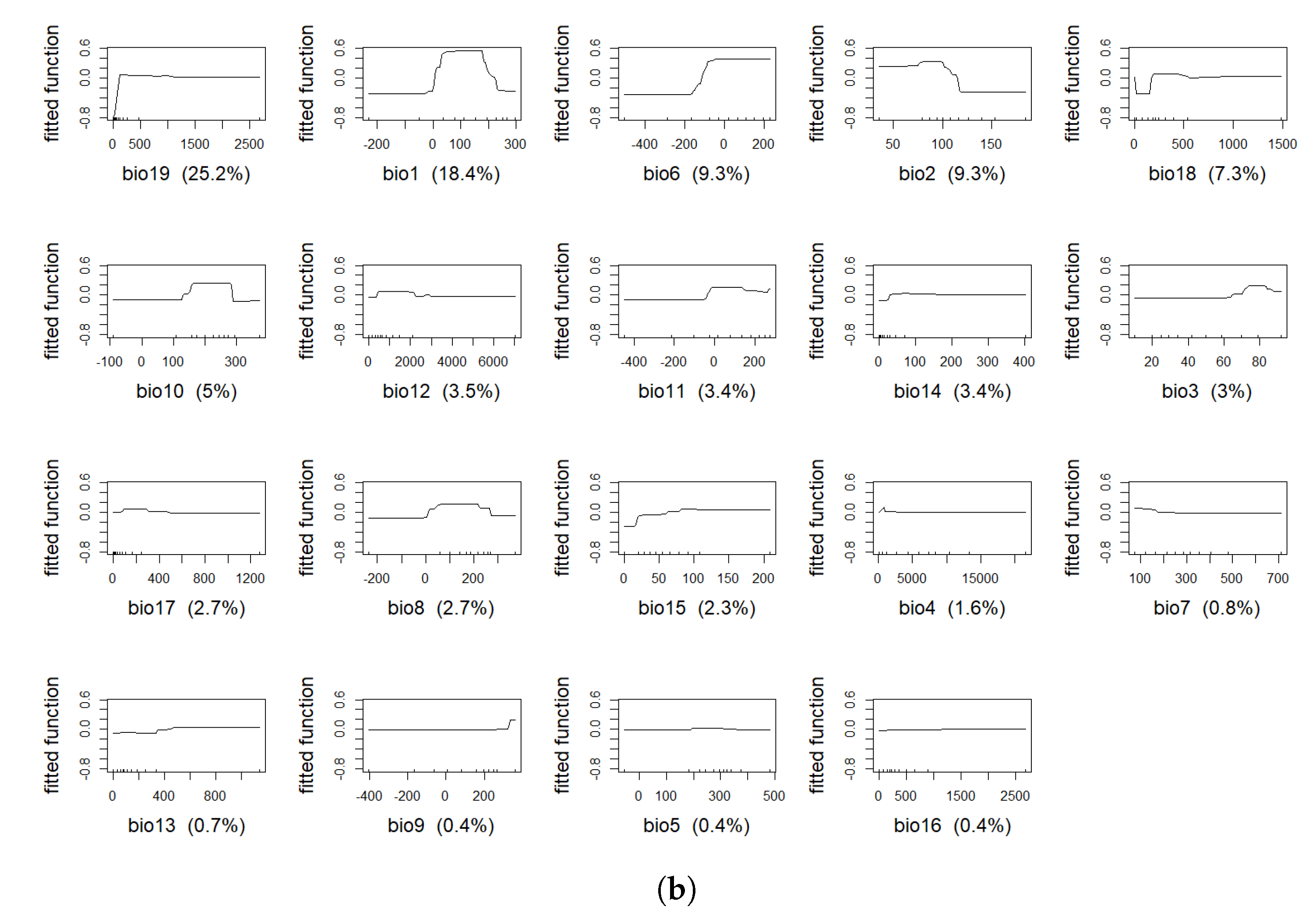
4.1. Model Assessment and Variable Importance
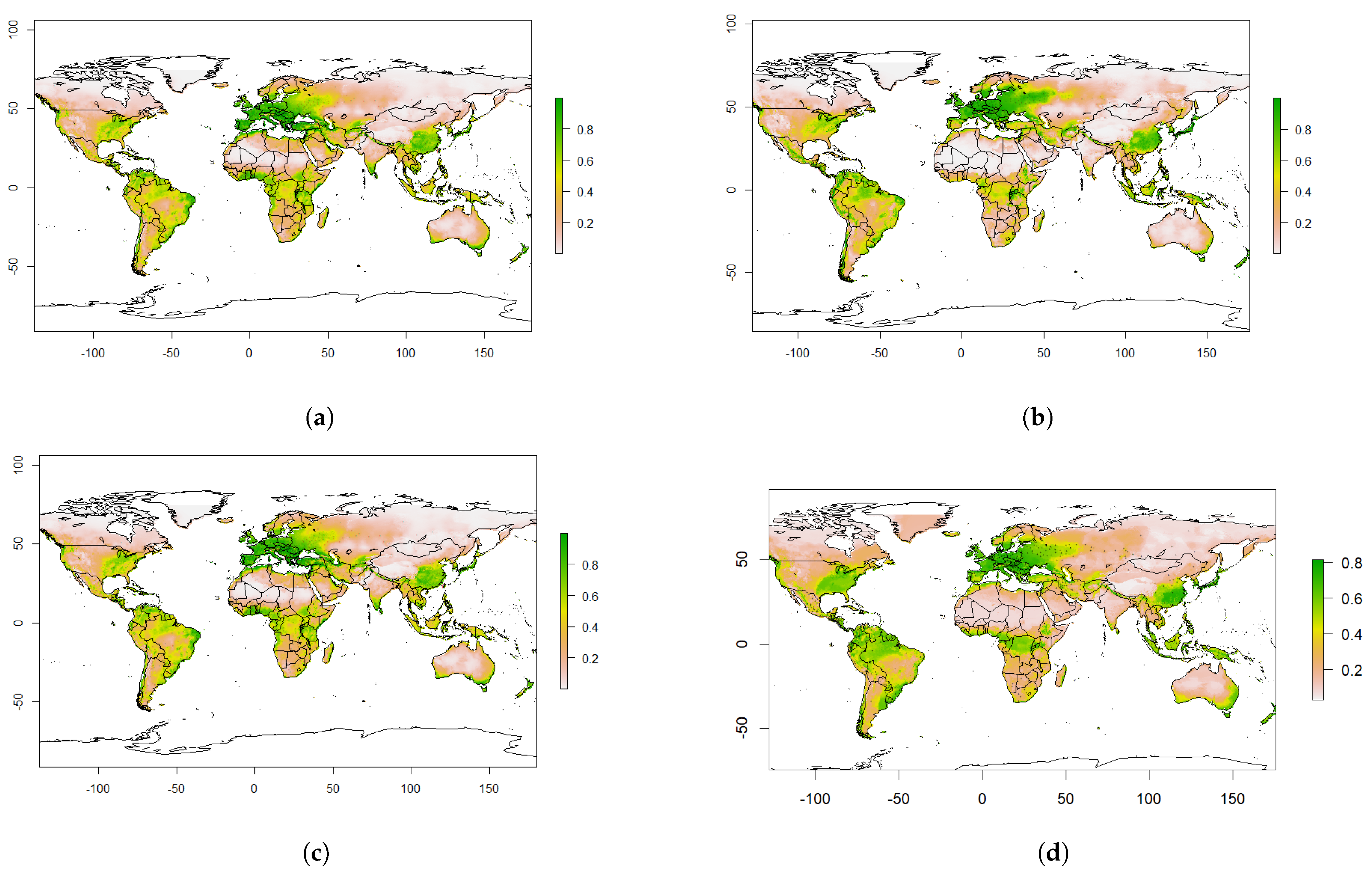
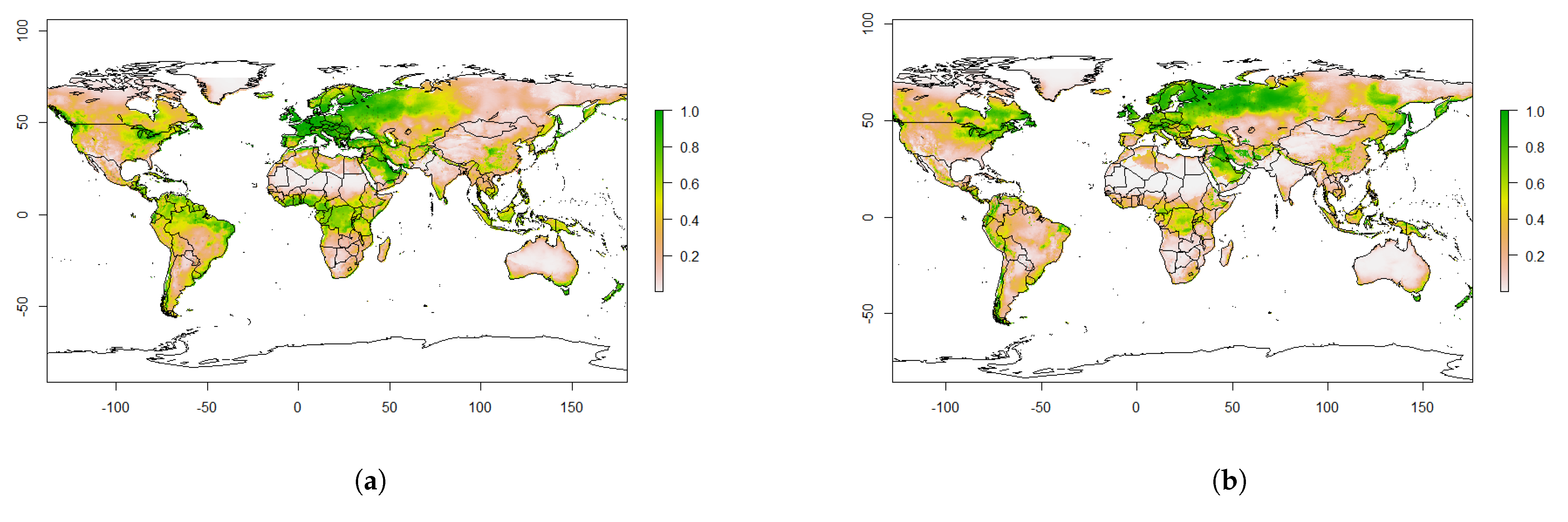
4.2. Predicted Suitability
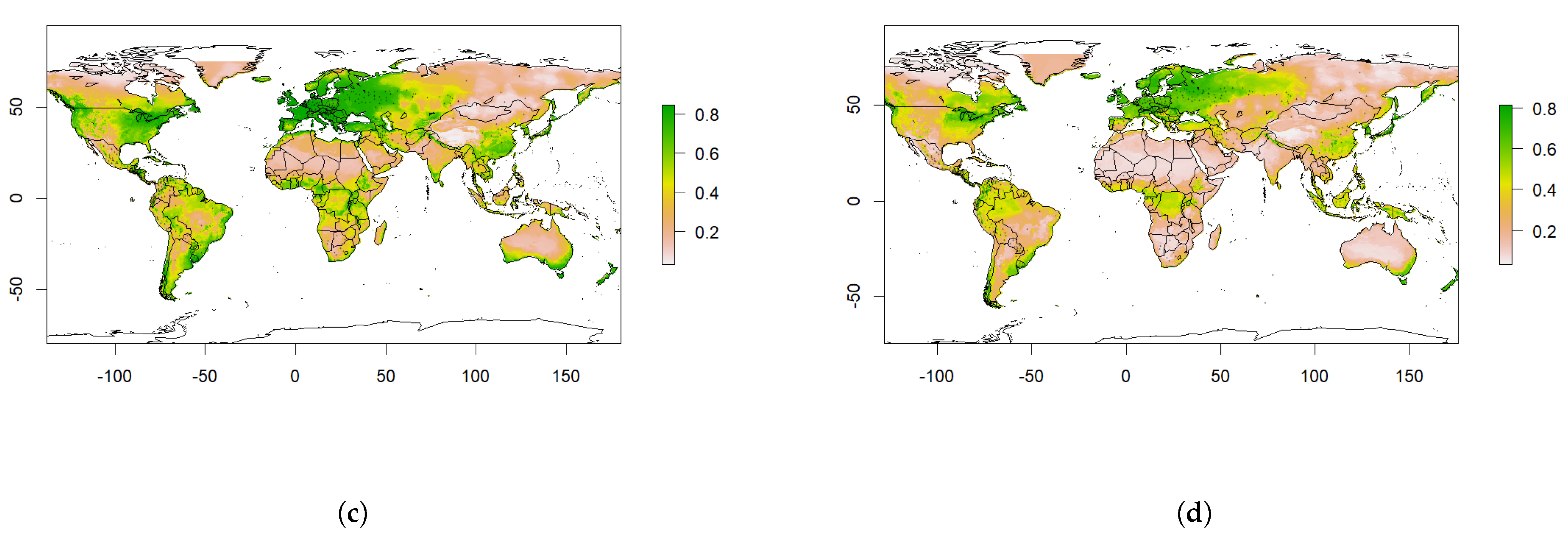
4.3. Predicted Future Suitability
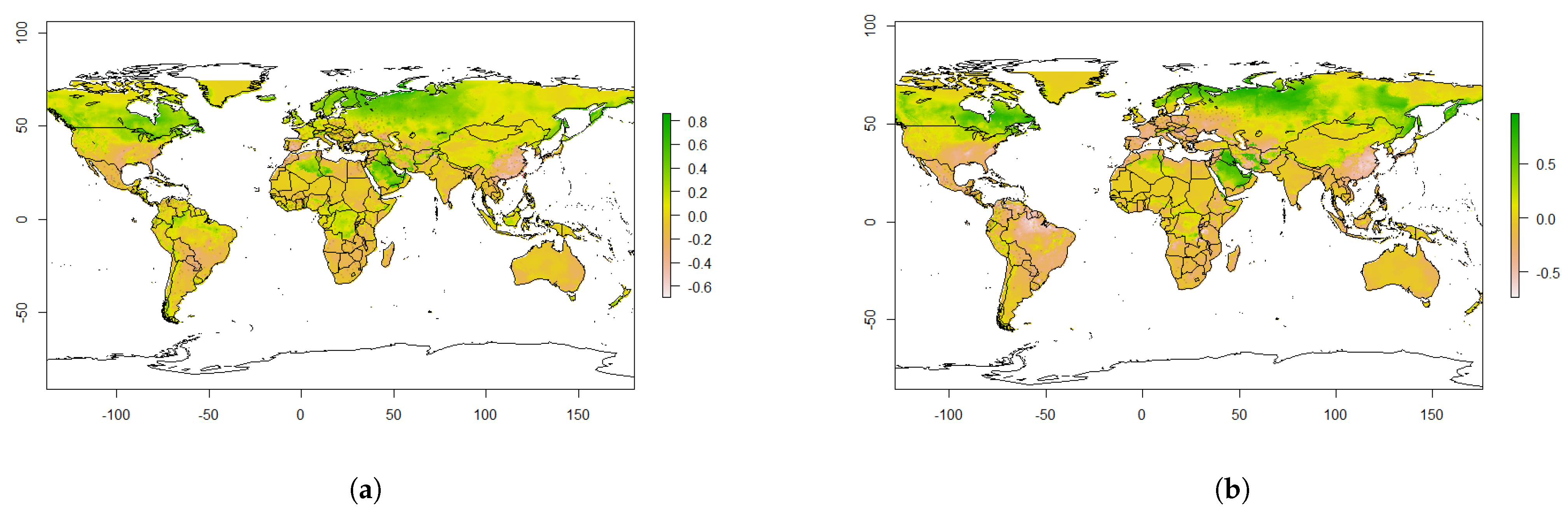
4.4. The Effect of Climate Change
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fulton, R.W. Bovine respiratory disease research (1983–2009). Anim. Health Res. Rev. 2009, 10, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Fernández, M.; Ferreras, M.d.C.; Giráldez, F.J.; Benavides, J.; Pérez, V. Production Significance of Bovine Respiratory Disease Lesions in Slaughtered Beef Cattle. Animals 2020, 10, 1770. [Google Scholar] [CrossRef]
- Taylor, J.D.; Fulton, R.W.; Lehenbauer, T.W.; Step, D.L.; Confer, A.W. The epidemiology of bovine respiratory disease: What is the evidence for preventive measures? Can. Vet. J. 2010, 51, 1351. [Google Scholar]
- Johnson, K.K.; Pendell, D.L. Market impacts of reducing the prevalence of bovine respiratory disease in United States beef cattle feedlots. Front. Vet. Sci. 2017, 4, 189. [Google Scholar] [CrossRef] [PubMed]
- Booker, C.W.; Abutarbush, S.M.; Morley, P.S.; Jim, G.K.; Pittman, T.J.; Schunicht, O.C.; Perrett, T.; Wildman, B.K.; Fenton, R.K.; Guichon, P.T.; et al. Microbiological and histopathological findings in cases of fatal bovine respiratory disease of feedlot cattle in western Canada. Can. Vet. J. 2008, 49, 473. [Google Scholar] [PubMed]
- Fentie, T.; Guta, S.; Mekonen, G.; Temesgen, W.; Melaku, A.; Asefa, G.; Tesfaye, S.; Niguse, A.; Abera, B.; Kflewahd, F.Z.; et al. Assessment of major causes of calf mortality in urban and periurban dairy production system of Ethiopia. Vet. Med. Int. 2020, 2020, 3075429. [Google Scholar] [CrossRef] [PubMed]
- Jimmy, J.; Sones, K.; Grace, D.; MacMillan, S.; Tarawali, S.; Herrero, M. Beyond milk, meat, and eggs: Role of livestock in food and nutrition security. Anim. Front. 2013, 3, 6–13. [Google Scholar]
- Thornton, P.; Herrero, M. The Inter-Linkages Between Rapid Growth in Livestock Production, Climate Change, and the Impacts on Water Resources, Land Use, and Deforestation; World Bank Policy Research Working Paper, (5178); Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Thornton, P.K.; Gerber, P.J. Climate change and the growth of the livestock sector in developing countries. Mitig. Adapt. Strateg. Glob. Chang. 2010, 15, 169–184. [Google Scholar] [CrossRef]
- Herrero, M.; Petr, H.; John, M.; Amanda, P.; Hugo, V. African Livestock Futures: Realizing the Potential of Livestock for Food Security, Poverty Reduction and the Environment in Sub-Saharan Africa; Office of the Special Representative of the UN Secretary General for Food Security and Nutrition and the United Nations System Influenza Coordination (UNSIC): Geneva, Switzerland, 2014; Available online: https://pure.iiasa.ac.at/id/eprint/11154/1/LiveStock_Report_ENG_20140725_02_web%282%29.pdf (accessed on 27 November 2022).
- Sarchet, J.J.; Pollreisz, J.P.; Bechtol, D.T.; Blanding, M.R.; Saltman, R.L.; Taube, P.C. Limitations of bacterial culture, viral PCR, and tulathromycin susceptibility from upper respiratory tract samples in predicting clinical outcome of tulathromycin control or treatment of bovine respiratory disease in high-risk feeder heifers. PLoS ONE 2022, 17, E0247213. [Google Scholar] [CrossRef]
- Hay, S.I.; Battle, K.E.; Pigott, D.M.; Smith, D.L.; Moyes, C.L.; Bhatt, S.; Brownstein, J.S.; Collier, N.; Myers, M.F.; Geoge, D.B.; et al. Global mapping of infectious disease. Philos. Trans. R. Soc. Biol. Sci. 2013, 368, 20120250. [Google Scholar] [CrossRef]
- Liu, Z.; Peng, C.; Work, T.; Candau, J.-N.; DesRochers, A.; Kneeshaw, D. Application of machine-learning methods in forest ecology: Recent progress and future challenges. Environ. Rev. 2018, 26, 339–350. [Google Scholar] [CrossRef]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecol. Model. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
- Franklin, J. Species distribution models in conservation biogeography: Developments and challenges. Divers. Distrib. 2013, 19, 1217–1223. [Google Scholar] [CrossRef]
- Elith, J.; John, R.L. Species distribution models: Ecological explanation and prediction across space and time. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar] [CrossRef]
- Naimi, B.; Hamm, N.A.S.; Groen, T.A.; Skidmore, A.K.; Toxopeus, A.G. Where is positional uncertainty a problem for species distribution modelling? Ecography 2014, 37, 191–203. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijman, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Harris, I.P.D.J.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Tyberghein, L.; Verbruggen, H.; Pauly, K.; Troupin, C.; Mineur, F.; De Clerck, O. Bio-ORACLE: A global environmental dataset for marine species distribution modelling. Glob. Ecol. Biogeogr. 2012, 21, 272–281. [Google Scholar] [CrossRef]
- Baldwin, R.A. Use of maximum entropy modeling in wildlife research. Entropy 2009, 11, 854–866. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Adegboye, O.A.; Adegboye, M. Spatially correlated time series and ecological niche analysis of cutaneous leishmaniasis in Afghanistan. Int. J. Environ. Res. Public Health 2017, 14, 309. [Google Scholar] [CrossRef] [PubMed]
- Adegboye, O.A.; Kotze, D. Epidemiological analysis of spatially misaligned data: A case of highly pathogenic avian influenza virus outbreak in Nigeria. Epidemiol. Infect. 2014, 142, 940–949. [Google Scholar] [CrossRef] [PubMed]
- Grendár, M., Jr.; Grendár, M. Maximum entropy: Clearing up mysteries. Entropy 2001, 3, 58–63. [Google Scholar] [CrossRef]
- Peterson, A.T.; Soberón, J.; Pearson, R.G.; Anderson, R.P.; Martínez-Meyer, E.; Nakamura, M.; Araújo, M.B. Ecological niches and geographic distributions (MPB-49). In Ecological Niches and Geographic Distributions (MPB-49); Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Shannon, C.E. The Best Detection of PulsesBell Laboratories Memorandum, June 22, 1944; Wiley-IEEE Press: Hoboken, NJ, USA, 1993; pp. 148–150. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Dudík, M.; Phillips, S.; Schapire, R.E. Correcting sample selection bias in maximum entropy density estimation. In Advances in Neural Information Processing Systems; Princeton University Press: Princeton, NJ, USA, 2005; p. 18. [Google Scholar]
- Fielding, A.H.; Bel, J.F. A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ. Conserv. 1997, 24, 38–49. [Google Scholar] [CrossRef]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Dudík, M.; Schapire, R.E.; Blair, M.E. Opening the black box: An open-source release of Maxent. Ecography 2017, 40, 887–893. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Mittermeier, R.A.; Myers, N.; Mittermeier, C.G.; Gil, P.R. Hotspots: Earth’s Biologically Richest and Most Endangered Terrestrial Ecoregions; CEMEX, SA, Agrupación Sierra Madre, SC: Mexico City, Mexico, 1999. [Google Scholar]
- Cusack, P.M.V.; McMeniman, N.P.; Lean, I.J. Feedlot entry characteristics and climate: Their relationship with cattle growth rate, bovine respiratory disease and mortality. Aust. Vet. J. 2007, 85, 311–316. [Google Scholar] [CrossRef]
- Robertson, J. Cattle housing: Design and management. In Bovine Medicine; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 517–524. [Google Scholar]
- Leung, N.H.L. Transmissibility and transmission of respiratory viruses. Nat. Rev. Microbiol. 2021, 19, 528–545. [Google Scholar] [CrossRef]
- Kuddus, M.A.; McBryde, E.S.; Adegboye, O.A. Delay effect and burden of weather-related tuberculosis cases in Rajshahi province, Bangladesh, 2007–2012. Sci. Rep. 2019, 9, 12720. [Google Scholar] [CrossRef]
- Adegboye, O.A.; McBryde, E.S.; Eisen, D.P. Epidemiological analysis of association between lagged meteorological variables and pneumonia in wet-dry tropical North Australia, 2006–2016. J. Expo. Sci. Environ. Epidemiol. 2020, 30, 448–458. [Google Scholar] [CrossRef] [PubMed]
- Alegbeleye, O.O.; Sant’Ana, A.S. Manure-borne pathogens as an important source of water contamination: An update on the dynamics of pathogen survival/transport as well as practical risk mitigation strategies. Int. J. Hyg. Environ. Health 2020, 227, 113524. [Google Scholar] [CrossRef] [PubMed]
- Barbet-Massin, M.; Jiguet, F.; Albert, C.H.; Thuiller, W. Selecting pseudo-absences for species distribution models: How, where and how many? Methods Ecol. Evol. 2012, 3, 327–338. [Google Scholar] [CrossRef]
- Jacob, B.G.; Novak, R.J.; Toe, L.D.; Sanfo, M.; Griffith, D.A.; Lakwo, T.L.; Habomugisha, P.; Katabarwa, M.N.; Unnasch, T.R. Validation of a remote sensing model to identify Simulium damnosum sl breeding sites in sub-Saharan Africa. PLoS Negl. Trop. Dis. 2013, 7, E2342. [Google Scholar] [CrossRef] [PubMed]
| Acronym | Description | Unit |
|---|---|---|
| bio1 | Annual Mean Temperature | °C |
| bio2 | Mean Diurnal Range (Mean of monthly (maximum temperature–minimum temperature)) | °C |
| bio3 | Isothermality (BIO2/BIO7) | °C |
| bio4 | Temperature Seasonality (SD ) | % |
| bio5 | Max Temperature of Warmest Month | °C |
| bio6 | Min Temperature of Coldest Month | °C |
| bio7 | Temperature Annual Range (BIO5-BIO6) | °C |
| bio8 | Mean Temperature of Wettest Quarter | °C |
| bio9 | Mean Temperature of Driest Quarter | °C |
| bio10 | Mean Temperature of Warmest Quarter | °C |
| bio11 | Mean Temperature of Coldest Quarter | °C |
| bio12 | Annual Precipitation | mm |
| bio13 | Precipitation of Wettest Month | mm |
| bio14 | Precipitation of Driest Month | mm |
| bio15 | Precipitation Seasonality (CV) | % |
| bio16 | Precipitation of Wettest Quarter | mm |
| bio17 | Precipitation of Driest Quarter | mm |
| bio18 | Precipitation of Warmest Quarter | mm |
| bio19 | Precipitation of Coldest Quarter | mm |
| Model | BRD | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AUC | PPP | Kappa | Sens_Spec. | AUC | PPP | Kappa | Sens_Spec. | ||
| MaxEnt | BTD | 0.835 | 0.725 | 0.377 | 0.411 | 0.910 | 0.644 | 0.285 | 0.340 |
| IBR | 0.828 | 0.573 | 0.378 | 0.415 | 0.883 | 0.616 | 0.301 | 0.281 | |
| BRT | BTD | 0.878 | 0.792 | 0.456 | 0.402 | 0.936 | 0.603 | 0.511 | 0.512 |
| IBR | 0.916 | 0.723 | 0.516 | 0.395 | 0.874 | 0.833 | 0.475 | 0.423 | |
| Variable | % BTD | % IBR |
|---|---|---|
| bio19 | 19.9 | 25.2 |
| bio6 | 17.5 | 9.3 |
| bio1 | 12.2 | 18.4 |
| bio2 | 10.4 | 9.3 |
| bio12 | 8.3 | 3.5 |
| bio8 | 6.7 | 2.7 |
| bio4 | 3.9 | 1.6 |
| bio10 | 3.5 | 5.0 |
| bio5 | 3.4 | 0.4 |
| bio3 | 2.9 | 3.0 |
| bio11 | 2.6 | 3.4 |
| bio18 | 2.4 | 7.3 |
| bio17 | 2.2 | 2.7 |
| bio7 | 1.2 | 0.8 |
| bio9 | 1.1 | 0.4 |
| bio16 | 1 | 0.4 |
| bio14 | 0.5 | 3.4 |
| bio13 | 0.3 | 0.7 |
| bio15 | 0.1 | 2.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gwaka, J.K.; Demafo, M.A.; N’konzi, J.-P.N.; Pak, A.; Olumoh, J.; Elfaki, F.; Adegboye, O.A. Machine-Learning Approach for Risk Estimation and Risk Prediction of the Effect of Climate on Bovine Respiratory Disease. Mathematics 2023, 11, 1354. https://doi.org/10.3390/math11061354
Gwaka JK, Demafo MA, N’konzi J-PN, Pak A, Olumoh J, Elfaki F, Adegboye OA. Machine-Learning Approach for Risk Estimation and Risk Prediction of the Effect of Climate on Bovine Respiratory Disease. Mathematics. 2023; 11(6):1354. https://doi.org/10.3390/math11061354
Chicago/Turabian StyleGwaka, Joseph K., Marcy A. Demafo, Joel-Pascal N. N’konzi, Anton Pak, Jamiu Olumoh, Faiz Elfaki, and Oyelola A. Adegboye. 2023. "Machine-Learning Approach for Risk Estimation and Risk Prediction of the Effect of Climate on Bovine Respiratory Disease" Mathematics 11, no. 6: 1354. https://doi.org/10.3390/math11061354
APA StyleGwaka, J. K., Demafo, M. A., N’konzi, J.-P. N., Pak, A., Olumoh, J., Elfaki, F., & Adegboye, O. A. (2023). Machine-Learning Approach for Risk Estimation and Risk Prediction of the Effect of Climate on Bovine Respiratory Disease. Mathematics, 11(6), 1354. https://doi.org/10.3390/math11061354






