Abstract
In this work, we first introduce a class of deterministic epidemic models with varying populations inspired by Arino et al. (2007), the parameterization of two matrices, demography, the waning of immunity, and vaccination parameters. Similar models have been focused on by Julien Arino, Fred Brauer, Odo Diekmann, and their coauthors, but mostly in the case of “closed populations” (models with varying populations have been studied in the past only in particular cases, due to the difficulty of this endeavor). Our Arino–Brauer models contain SIR–PH models of Riano (2020), which are characterized by the phase-type distribution , modeling transitions in “disease/infectious compartments”. The A matrix is simply the Metzler/sub-generator matrix intervening in the linear system obtained by making all new infectious terms 0. The simplest way to define the probability row vector is to restrict it to the case where there is only one susceptible class , and when matrix B (given by the part of the new infection matrix, with respect to ) is of rank one, with . For this case, the first result we obtained was an explicit formula (12) for the replacement number (not surprisingly, accounting for varying demography, waning immunity and vaccinations led to several nontrivial modifications of the Arino et al. (2007) formula). The analysis of Arino–Brauer models is very challenging. As obtaining further general results seems very hard, we propose studying them at three levels: (A) the exact model, where only a few results are available—see Proposition 2; and (B) a “first approximation” (FA) of our model, which is related to the usually closed population model often studied in the literature. Notably, for this approximation, an associated renewal function is obtained in (7); this is related to the previous works of Breda, Diekmann, Graaf, Pugliese, Vermiglio, Champredon, Dushoff, and Earn. (C) Finally, we propose studying a second heuristic “intermediate approximation” (IA). Perhaps our main contribution is to draw attention to the importance of Arino–Brauer models and that the FA approximation is not the only way to tackle them. As for the practical importance of our results, this is evident, once we observe that the Arino–Brauer models include a large number of epidemic models (COVID, ILI, influenza, illnesses, etc.).
Keywords:
epidemic models; varying population models; stability; next-generation matrix approach; basic replacement number; vaccination; waning immunity; endemic equilibria MSC:
34A34; 34A30; 37N25; 92D30; 92D25
1. Introduction
The initial motivation of this paper was to extend an outstanding formula derived in in reference ([1], [Thm 2.1]) to epidemic models with varying population sizes (linear birth rates), waning immunity, and vaccinations, expressing the replacement numbers of large classes of deterministic epidemic models as quadratic forms with respect to certain input matrices—see (15) below. Unfortunately, this formula is not well known, and particular cases of it have recently been reproved in numerous papers.
Besides achieving the initial goal, we also achieved several advances in developing the theory of the “ Arino models” with demography, waning immunity, and vaccinations. One of our main contributions is introducing (or drawing attention to) this class of models, which we view as new, as our inspiration paper [1] does not allow for changing populations, waning immunity, and vaccinations.
Remark 1.
Some confusion took place due to the fact that this paper, which was first submitted on 6 December 2021 to the Journal of Mathematical Biology (see also [2]), underwent a one-year long review process (starting with minor revisions, and ending up with a rejection based mainly on non-standard notations). Naturally, we continued our work on this fascinating model, producing already-published papers [3,4] that discuss examples of the material presented below, and creating—at a first rapid reading—the wrong impressions that preceded the current paper. On the positive side, we are now able to include updates connecting more recent works that tie the Arino models into important works [5,6,7,8,9] on the renewal model.
We will now proceed with a brief historical overview.
Deterministic mathematical epidemiology. Deterministic mathematical models have been widely adopted by epidemiologists to model the spread of diseases worldwide, starting with the Bombay plague in 1905–1906 [10], followed by measles, smallpox, chickenpox, mumps, typhoid fever, influenza, and diphtheria (see for example [11]; see [12,13,14] for comprehensive textbooks). More recently, they have been used for COVID-19 research—see for example [15,16,17,18,19,20,21,22,23,24,25,26,27].
An explanation of our title. The first foundational result in mathematical epidemiology is the “ alternative”. As already encountered in the celebrated paper, “A contribution to the mathematical theory of epidemics” [10], its final version states that the “basic replacement number” , which determines the stability of the “disease-free equilibrium”, may be computed under certain conditions (see [28,29] and Section 4.1), using only a subset of the ODE dynamics, sometimes called the “infectious equations”. The final formula identifies as the spectral radius of a matrix determined by breaking the infectious equations into two parts, one involving a constant “transfer matrix” A, and another “new infections matrix” [30]. The [1] paper that motivated our research focuses on the case of a single susceptible (new infection-producing) compartment. This allows introducing a second constant matrix B, which is part of the new infection matrix with respect to S. Under the further assumption that B has rank one, [1] shows that has an explicit simple expression in terms of the two matrices .
This intriguing result raises several questions. One that is dealt with here is the extension of the [1] result to the varying population case. Another one, as mentioned in the Conclusions section, involves the extension when B has a rank greater than one. Finally, one that we hope to deal with in the future involves proving that other fundamental quantities may be simply expressed in terms of the two matrices () as suggested by references [6,8].
References [5,6,8], i.e., “The Kermack–McKendrick epidemic model revisited” and “On the formulation of epidemic models (an appraisal of Kermack and McKendrick)” note that even experienced experts often believe that [10] is just about the SIR system, when in fact this example is just a very special case of a much more general “renewal model” (RE), also called the DDE (delay differential equation) model or KM (Kermack–McKendrick) model. Subsequently, the second paper shows that the behaviors of all infectious compartments may be dealt with by solving just one scalar renewal equation (in the cases of one-strain diseases). This may be achieved in three cases that are easier to treat separately: (a) homogeneous constant population models, (b) varying population models, and (c) models including waning immunity. The relations between the constant population SIR and SEIR models and their renewal function formulations are spelled out at the bottom of page 3 in [6]; these authors then assigned an extension as an exercise to the readers: “we leave it to our readers to elaborate this"; the general idea that delay equations with kernels defined in terms of matrix exponentials correspond to systems of ODEs, called “Linear Chain trick”. It is our impression that this “exercise” has remained unsolved to date in one direction: that of restricting “Arino models” of rank one, and showing that the row vectors of infectious classes satisfy a renewal equation, with explicit kernels involving . We provide the solution in (7), following Example 2.
The rest of our title is rather debatable. Our inspiration, the [1] paper, has five very famous authors: Arino, Brauer, van den Driessche, Watmough, and Wu, so it would have been more correct to call this the ABvdDWW model. Arino himself calls this a simple model [31], but we believe that “a deceivingly simple, but extremely challenging model” might have been more appropriate. So, after ruling out the previous two possibilities, we chose to retain only the name of the first two authors of [1]. Note also that in the previous paper [32] (where demography was not taken into account) we used the name “matrix SIR Arino models”; however, we prefer the new name, where we emphasize that there are two matrices () involved, and we added the name of Brauer, who died recently (accessed on 10 October 2022). https://math.wisc.edu/2021/10/18/in-memoriam-fred-brauer/.
Classification of the deterministic epidemic literature. The deterministic epidemic literature may be divided into three streams.
- Closed models, with no demography.
- Models in which the total population may be kept constant, by balancing births and deaths. These models are easier to study, often admit a single endemic equilibrium point, and typically obey the “ alternative”—see [33] for a review. However, as death is an essential factor of epidemics, the assumption of a constant population size (clearly an approximation that holds in the short term or for very-large populations) deserves a comment
- Finally, we arrive at the object of our paper: models with varying total populations. This introduces several challenges, the first being that varying populations typically lead to multiple endemic equilibrium points. This literature reveals the possibility of bi-stability when (absent from the previous models), even in simple examples [34,35,36] (thus, for an initial number of "infectives" being high, the trajectory may lie in the basin of attraction of a stable endemic point instead of being eradicated, a discrepancy from what is expected, which suggests that in this range, the deterministic model may be inappropriate). Despite further remarkable works—see, for example, [37,38,39,40,41,42], the literature studies on models with varying total populations, unlike the two preceding streams, have not yet reached general results. Our paper seems to be the first exception.
Contributions. The contribution of this work is three-fold. First, we introduce a class of compartmental models for epidemics that account for varying population sizes, vaccinations, and immunity losses. Secondly, we recommend studying these models at three levels, which may also be viewed as subcases, i.e., (i) the varying population epidemic models, (ii) the “first order” approximation (FA), which is recovered by ignoring certain quadratic terms from the general model proposed (induced by studying the proportions), and which is well-studied in the literature, and (iii) the “intermediate approximation” (IA), introduced here for the first time, and obtained by neglecting only the terms that are quadratic with respect to the disease/infectious compartments. Finally, we study the equilibrium points of the proposed models and their stability properties.
Organization. This paper is organized as follows. In Section 2, we introduce the Arino–Brauer matrix models with demography, vaccination, and waning immunity. Section 3 computes the ages of the infection kernels of these models, related to references [5,6,7,8,9]. Section 4 presents the stability results for the SIR–PH model—see Propositions 2–4. Section 5 provides conclusions and suggestions for future work. Finally, in Appendix A, we present the background on deterministic epidemic models, such as the basic replacement number and the next-generation matrix method.
2. Arino–Brauer Matrix Models with Demography, Waning Immunity, Vaccination, and One Susceptible Class
While can be defined as the spectral radius of a certain matrix, provided that the next-generation matrix assumptions apply, it is sometimes possible to employ models where may be explicitly expressed in terms of the matrices that define the model [1,43,44,45].
The idea behind these models is to further divide the non-infected compartments into (susceptible)/input classes, defined by producing “new non-linear infections”, and output R classes (e.g., in our example), which are fully determined by the rest, and may, therefore, be omitted from the dynamics. Furthermore, It is convenient to restrict to epidemic models the linear forces of infection, as non-linear forces of infection may lead to very complex dynamics [46,47,48,49], which are not always easy to interpret epidemiologically. This is in contrast with the Arino models already studied where one may typically establish the absence of periodic solutions (closed orbits, homoclinic loops, and oriented phase polygons) [40,42].
Below, we study the equilibrium points and the dynamical behaviors of such models, restricting to the case of one susceptible class. Our goal is to understand the effects of demography, vaccination, and waning immunity, which are missing in the original paper [1].
Definition 1.
An Arino–Brauer matrix model of type , with demography parameters (scalars), waning immunity column vector and vaccination row vector , is characterized by a set of parameters , where (in boldface) denote the column vectors of extra death rates, and denote respectively matrices of dimensions , and , respectively. This model contains one susceptible class S, a p-dimensional vector of removed states (healthy, dead, vaccinated, etc.), and an n-dimensional vector of “disease” state (latent/exposed, infective, asymptomatic, etc.). The dynamics are:
Here,
- is a row vector whose components model a set of disease states/classes.
- is the set of individuals susceptible to being infected.
- is a row vector whose components model a set of recovered states (or classes), each accounting for individuals who recover from the infection. In what follows, we will focus on the case of one recovered class.
- B is an matrix, where each entry represents the force of infection of the disease class i onto class j. We will denote by b the vector containing the sum of the entries in each row of B, namely, .
- A is an Markovian sub-generator matrix (i.e., a Markovian generator matrix for which the sum of at least one row is strictly negative), where each off-diagonal entry , , satisfies and describes the rate of transition from disease class i to disease class j; while each diagonal entry satisfies and describes the rate at which individuals in the disease class i leave toward non-infectious compartments. Alternatively, is a non-singular M-matrix [1,50]. (An M-matrix is a real matrix V with having eigenvalues whose real parts are non-negative [51]).
- are column vectors, giving the death rates in the disease and recovered compartments caused by the epidemic (and possible vaccinations), respectively.
- is a column vector describing the rates at which individuals lose immunity (i.e., transition from recovered states to susceptible states).
- is a vector describing the rates at which individuals are vaccinated (immunized).
- W is an matrix whose entries model the rates at which individuals in the disease states transfer to recovered or dead states. In what follows, we assume that the matrix satisfies (namely, the sum of the entries in each row is equal to 0), which implies mass conservation.
Remark 2.
- 1.
- Note the factorization of the first equation for the diseased compartments , which must appear in any epidemic model, to ensure the existence of a fixed point where these compartments vanish. Furthermore, this equation has two conceptual parts: the first, sometimes called “new infections”, contains all interactions of with other compartments, and the second, , contains all of the remaining terms.
- 2.
- Note that when , then W is a column vector, which completes the matrix with negative row sums A to a matrix with zero row sums. Therefore, where the last notation is standard in the theory of phase-type distributions.
- 3.
- A particular but revealing case is that when and matrix B has rank 1, the form , where is a probability row vector whose components represent the fractions of susceptibilities entering into the disease compartment j, when infection occurs. We will call this SIR-PH, following Riano [50], who emphasized its probabilistic interpretation, i.e., a SIR model where the exponential infection time is replaced by a PH-type distribution. (Some authors, including [52], similarly replace the exponential latency time in class E of SEIR by a PH-type distribution, but this is conceptually unnecessary, since all of the disease classes, may be grouped together in one group, whose phase-type will be determined by those of the components (via Kronecker product operations).). See also [53] for such models, and see Section 3 below on recent connections to the class of non-Markovian epidemic models.However, the SIR–PH model in previous works precluded important interactions between S and R, such as waning immunity and vaccination, and we amended its definition to include these interactions.
Remark 3.
We did not find any work in the literature on models with linear birth rates at this level of generality. The majority of the literature studies are dedicated to models that may be formally obtained from (1) by letting (the idea is that N is approximately constant because it is huge or it is observed only over a short period of time). We will call this model “classic/pedagogical”, where we add the last qualifier to emphasize that it is unrelated to the model we studied. This is in contrast with the FA and IA approximations introduced later, which approximate the scaled version of (1) introduced below.
It is convenient to reformulate (1) in terms of the fractions normalized by the total population
The reader may check that the following equations hold for the scaled variables:
where we let . Moreover, by letting we have
Hence, the above equation guarantees that if for some , then for all . Accordingly, in what follows, we will always assume that , which guarantees that .
The following definition places (in a common framework) the dynamics of the scaled process and two interesting approximations.
Definition 2.
Let and let
Example 1.
The SIR–PH–FA models [32,50] (in which there is only one input class and one output class ) are defined by:
Example 2.
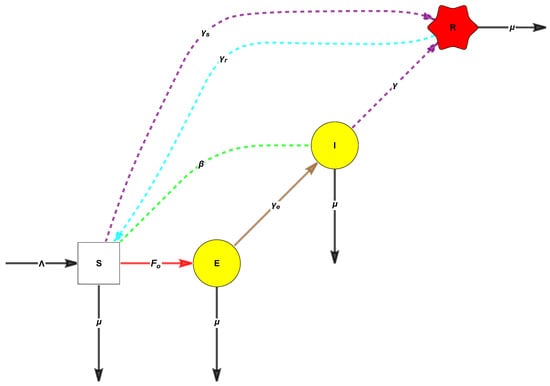
The FA-version of the SEIRS model, with , is given by:
is a particular case of the matrix Arino model obtained when
See Figure 1.

Figure 1.
Chart flow of the SEIRS model. The force of infection is The red edge corresponds to the entrance of susceptibilities into the disease classes, the dashed green edges correspond to the contacts between the diseases and susceptibilities, the brown edge is the rate of the transition matrix V, and the cyan dashed line corresponds to the rate of waning immunity. The remaining black lines correspond to the inputs and outputs of the birth and natural death rates, respectively.
Remark 4.
In this paper, we wrote the dynamical systems with the vector state variables pre-multiplying the model matrices, diverging from the dynamical systems tradition. This is because we want defined by the factorization of B (which will play an important role below) to be a row vector, following the convention in the theory of phase-type distributions.
Figure 2 below makes the case where epidemic models can be studied at three levels (the exact model, and its FA and IA approximations). The figure depicts the endemic points of an SIR-type example of the (1) model, as discussed in detail in [3].

Figure 2.
Parametric plots of the scaled epidemic and its FA and intermediate approximations for a SIR-type model with one infectious class, starting from a starting point SP with , with . are the stable endemic points of the scaled model, IA (intermediate) model, and FA model, respectively. The green vertical line denotes the immunity threshold Note that the epidemic will at first spend a long time (since births and deaths have slow rates as compared to the disease) in the vicinity of the manifold , where the three processes are indistinguishable, before turning toward the endemic equilibrium point(s).
Remark 5.
We end this section by pointing out that our scaled model (3) belongs to a class of models introduced, for different motivations, in [54]. Indeed, after dropping the first equation
and rewriting the rest as:
where , we recognize the above as a particular case of ([54], 2.1).
3. The Semi-Groups and Age of Infection Kernels Associated with SIR–PH–FA Models with of Rank One
In the case when B has rank one, SIR–PH–FA models have an associated explicit age of infection kernel, which allows obtaining via integrating.
Our attention to this subject was drawn by formulas from [6] (p. 3) for the “renewal/age of infection kernels” for particular cases of the SIR and SEIR models. These authors (as an exercise) extended their formulas to other models; determining which models to extend to was part of the exercise. Six years later, the exercise was first solved by Champredon–Dushoff–Earn [8] for the Erlang–SEIRS models. We provide below a further extension to the case of SIR–PH–FA models with B of rank one—see also [7,9] for related results.
Proposition 1.
For a SIR–PH–FA model with of rank one, the formula for the age of infection/renewal kernel (see [5,6,7,8,9] for expositions of this concept), is
where (it may be checked that this fits the formula on page 3 of [6] for SEIR when ).
Remark 6.
The beautiful decomposition (7) explicitizes the age of infection kernel as a product of the three essential factors of an epidemic: the initial proportions of infectious , the “transfer semi-group” , and the infectivity vector b. This suggests developing calibration approaches that are not model-dependent, but choose instead themselves the order of V and, subsequently, the three factors.
Proof.
Let us transform the infectious equations into an integral equation by applying the variation of the constant formula. □
The first step, the solution of the homogeneous part of the infectious equations, yields
Remark 7.
When is a probability vector, this solution has the interesting probabilistic interpretation of the survival probabilities in the various components of the semigroup generated by the Metzler/Markovian sub-generator matrix (which inherits this property from the phase-type generator A). Practically, will give the expected fractions of individuals who are still in each compartment at time t.
The variation of the constant formula implies that satisfies the integral equation:
We relate now this result to the “constituent equation” of the differential delay/renewal model Theorem 2.9 in reference [8]. In the case , (9) becomes
Denoting further by the total force of infection, and putting
our system may also be written as a system of two scalar equations
where the second equality holds if in (9) it holds that , and if on the interval is where denotes the generalized Dirac function—compare to Theorem 2.8 in reference [8]. This second form is related to Theorem 2.7b in reference [8] and Theorem 1 in reference [6]. ( In fact, these authors work with the related incidence flux between the and variables denoted by in [8], and by in [6]).
Remark 8.
- 1.
- Note that (11) is a SI system with satisfying a distributed delay (DD) equation. Such equations have been a constant preoccupation in mathematical epidemiology since the founding paper [10], see for example [55]. This is quite natural since susceptibilities become infectious only after a time after their contact. If is assumed to be a known constant, then the second equation of the SI model would involve a Dirac kernel ; however, since this is not the case, it is natural to replace the Dirac kernel by a continuous one. The fact that DD systems can be approximated by ODE systems has long been exploited in epidemic literature, under the name of “linear chain trick” (which is called Erlangization in queuing theory and mathematical finance)—see [7,9,56] for recent contributions and further references. The opposite direction, i.e., the solution of the exercise in [6] of identifying the kernels associated with ODE models, was not resolved in this generality, prior to our paper.
- 2.
- 3.
- As well-known, for DD models, the kernel may be factored as the product of with the density of the age of infection of the “intrinsic generating interval” [8,9,57]. may, thus, be obtained by integrating the kernelwith –see also (2.3) in reference [8] and (5.9) in reference [7]. A second direct proof of (12), without appealing to the first equality above (note that the kernel may be interpreted as an average time-dependent total infectivity; the fact that the disease-free equilibrium stability threshold has an integral representation that was first proved in [30]) is provided in Proposition 2 below.
- 4.
- Finally, the “intrinsic generation-interval density” is —see (2.6) in reference [8].
The Eigenstructure of the Jacobian for the Scaled Model (3)
Using , and putting , we find that the transpose of the Jacobian matrix of the scaled model (3) is given by
At the disease-free equilibrium , we have
Remark 9.
Note the structure of the second column, which is equivalent to the factorization property, and implies Proposition 2, below.
4. Stability Results for the SIR–PH Model
We consider here the particular case with a single recovered class, called the SIR–PH model, where . Notice that, in this case, we have a reduced set of parameters .
4.1. The Basic Replacement Number for SIR–PH via the Next-Generation Matrix Method [28,30]
We follow up here on a remark preceding Theorem 2.1 in reference [1], and show in the following proposition that the simplified formula for the basic replacement number still holds when waning immunity and vaccination are allowed, provided that and has rank one.
Proposition 2.
Consider a SIR–PH model (i.e., a single-recovered class), with parameters , and matrix of recovery rates .
- 1.
- (a)
- When , the unique DFE is .
- (b)
- When , exclude the case . Then, there exists a unique DFE , where satisfies the second-order equationand is given by
- 2.
- The weak alternative holds for the threshold parameter,where are defined in (21), and denotes the (dominant) Perron–Frobenius eigenvalue.
- 3.
- For rank 1, and , we further have
- (a)
- (b)
- If , and if the perturbation from linearity defined in (A3) is nonnegative, then the scalar combinationis a Lyapunov function for the DFE.
Proof.
- The disease-free system (with ) reduces toFor the fixed points, depending on , we must solve either a quadratic or a linear equationOne rootis always in and will be denoted by .The other root in the quadratic caseis strictly negative, unlessin which case it yields a second DFE point with , which we exclude (in order to apply the next-generation matrix method).
- It is enough to show here the conditions of Theorem 2 in reference [29] hold, with respect to the infectious set , and a certain splitting.The DFE and its local stability for the disease-free system are easy to check.We provide a splitting for the infectious equations:(where ). The corresponding gradients at the DFE areWe note that F has non-negative elements and that V is an M-matrix; therefore, exists and has non-negative elements, . We may check that the conditions (A2) are satisfied.For example, the last non-negativity condition in (A2)is a consequence of being an M-matrix, which implies component-wise.
- (a)
- Now if , or if has rank 1, and , the matrix F in (21) is the product of a column vector and a row vector, the dimension of its image is one, and the same holds for . Equivalently, . The “rank-nullity theorem" [58] implies that of the eigenvalues of are zero, and the Perron–Frobenius eigenvalue is the remaining one. This latter one must be equal to the trace of , which may be checked to equal . Finally, the linearity is obvious.
- (b)
- This is a particular case of [59] since the Perron–Frobenius eigenvector in our rank-one case may be taken as b.
□
Remark 10.
is continuous in , since for small,
(this approximation may be made rigorous by applying the rule of “l’Hospital").
4.2. The Classic/Pedagogical SIRS-FA Model
In this section, we present more explicit results for the disease-free equilibrium and the endemic equilibrium of the following model, referred to as SIRS-FA,
Proposition 3.
- 1.
- The pedagogical SIRS system (23) has a unique disease-free equilibrium (DFE) fixed point , whereIn the SIR–PH case, the DFE simplifies to ( this formula has appeared already in many particular cases—see for example (19–20) in reference [60]):
- 2.
- If , then the pedagogical system (23) has a unique second fixed point within its forward-invariant set. This endemic fixed point is such that is an eigenvalue of the matrix .In the SIR–PH case, it must satisfyThe disease component satisfy:( is a Perron–Frobenius eigenvector of the matrix M related to the next-generation matrix).
- 3.
- The normalization of is given by (30) below. When , this becomes:
- 4.
- The disease-free equilibrium is locally asymptotically stable if and is unstable if .
- 5.
- When , the critical vaccination defined by solving with respect to is given by
We show in Figure 3 a stream plot of the SIRS–FA model that illustrates the above properties.
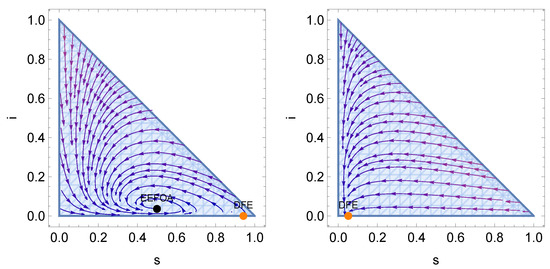
Figure 3.
Stream plots of for an example of a SIRS-FA model with one infectious class, when is smaller and bigger, respectively, than the critical vaccination defined in (27).
Proof.
The proof starts by examining the two cases that arise from factoring in the disease equations. More precisely, we will search separately in the disease-free set and in its complement . Then:
- Either and solvingfor yields the unique DFE (it may be shown by induction that the determinant is negative). Or,
- The determinant of the resulting homogeneous linear system for must be 0, which implies that satisfiesNote now that is an invertible matrix. Using , (28) may be written asDividing then by yields the characteristic polynomial of a matrixIn the SIR–PH case, noting that the rank one matrix has eigenvalues equal to zero, we conclude that the inverse of the susceptible fraction of an endemic state must equal the Perron–Frobenius eigenvalue . Note that follows from our assumption on . The other coordinates are determined starting with , which must be proportional to a Perron–Frobenius nonnegative eigenvector.
- Recall the systemSince , and is known up to the proportionality constant , it only remains to solve the last equation in (30) below:This equation may be solved numerically. When the last formula yieldsWhen , this yields (26).
- This follows from Theorem 2.1 in reference [59] (it is a consequence of the fact that a linear function proportional to the associated Perron eigenvector is a Lyapunov function when ).
- The result is immediate by solving with respect to , where is defined in (15).
□
Remark 11.
Equivalently, it is easy to check that (29) may be reformulated as saying that must satisfy
where denotes the Perron–Frobenius eigenvalue. We note that the matrices in the last formulation intervene also in the next-generation matrix approach.
4.3. A Glimpse of the Intermediate Approximation Model for Matrix SIRS, with
The intermediate approximation associated with (3) is
when , we have
and from the last equation in (32), satisfies the following third-order equation
Proposition 4.
Assume . Then:
- (a)
- The DFE points of the scaled, intermediate approximation, and FA are equal, with
- (b)
- In the SIR–PH case with scalar, they all reduce to (18).
- (c)
- The endemic point is unique. It satisfies , is an eigenvector of the matrix for the eigenvalue 0, andand it satisfies the normalization
Proof.
- (a)
- The equations determining the three DFEs coincide.
- (b)
- When is scalar, we find
- (c)
- We haveby substitution, we have
□
5. Conclusions and Further Work
We introduced a new class of matrix-parametrized models with varying populations, waning immunity, and vaccinations, and provided a few general results for the particular case of one susceptible class.
By solving the exercise of [6], we found that the Arino–Brauer models with the rank of B have a natural “intrinsic age of infection density”. Thus, these deterministic models also have associated stochastic aspects, which reveal themselves when all infectious equations are grouped into one equation.
This raises the question of whether the age of infection kernel may also be associated with
- (A, B), for which matrix B has a rank bigger than 1;
- for matrix models involving two or more susceptible classes.Other directions that are worthy of further work are:
- Determining the largest domain of attraction of the DFE, in which there exists some linear Lyapunov function that decreases (this might be approachable via linear programming).
- Calibrating real epidemic data via distributed delay models with non-monotone intrinsic generation-interval densities.
- Investigating the applicability of the Laplace transform and Laplace–Adomian decomposition approaches to our model, and extensions to fractional models—see [61,62] for possible extension directions.
We believe that studying matrix models, as opposed to individual examples, is crucial for the further development of mathematical epidemiology.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the AB Nexus seed grant from the University of Colorado.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, F.A, upon reasonable request.
Acknowledgments
We thank N. Bacaer for providing the references [63,64], and the reviewers for their thorough reviews and suggestions.
Conflicts of Interest
The authors declare no affiliation or involvement in any organization or entity with financial or non-financial interests in the subject matter or materials discussed in this manuscript.
Appendix A
Appendix A.1. Deterministic Homogeneous ODE Epidemic Models, cf. [65]
To put our work into perspective, we recall a definition of deterministic ODE epidemic models lifted from [65].
Definition A1.
A deterministic epidemic model is a dynamic system with two types of variables , where
- model the number (or density) in different compartments of infected individuals (i.e., latent, infectious, hospitalized, etc.), which should (ideally) eventually disappear if the epidemic ever ends;
- model numbers (or densities) in compartments of individuals who are not infected (i.e. susceptibilities, individuals who are immune, recovered individuals, etc.).
The system must admit an equilibrium called disease-free equilibrium (DFE) and, hence, a “quasi-triangular” linearization in the form
where is some forward-invariant subset, where “quasi-triangular” refers to the fact that the functions depend on all variables , and where N is the dimension of .
As shown in [65], any epidemic model admitting an equilibrium point admits the representation (A1), under suitable smoothness assumptions. In what follows, we will call the point a disease-free equilibrium (DFE).
Remark A1.
Note that the essential feature of (A1) is the “factorization of the disease equations".
Appendix A.2. The Basic Reproduction Number
The basic reproduction number or “net reproduction rate” is a pillar concept in demography, population dynamics, branching processes, and mathematical epidemiology—see the introduction of the book [64]. One central objective in these fields involves the stability of DFE, i.e., the conditions that ensure eradicating the sickness (or a part of the population in the population dynamics). In simple models, it was discovered that this amounts to verifying that a famous threshold parameter (called the basic reproduction number) is less than 1.
- The notation was first introduced by the mathematical demography Lotka [63,66]. In epidemiology, the basic reproduction number models the expected number of secondary cases, where one infected case would produce a homogeneous, completely susceptible stochastic population in the next generation. In the simplest setup of the branching process, this parameter—being smaller than 1—makes extinction sure. The relation to epidemiology is that epidemics are well approximated by the branching process at inception, a fact that goes back to Bartlett and Kendall.
- With more infectious classes, one deals at inception with multi-class branching processes; stability holds when the Perron–Frobenius eigenvalue of the “next-generation matrix” (NGM) means it is smaller than 1.
- For deterministic epidemic models, it seems at first that the basic reproduction number is lost due to the generation disappearing in this setup; see Chapter 3 in reference [64], who recalled a method that introduced generations, going back to Lotka, and is reminiscent of the iterative Lotka–Volterra approach in solving integrodifferential equations. At the end of the tunnel, a unified method for defining emerged only much later, via the “next generation matrix” approach [28,29,30,67]. The final result is that the local stability of the disease-free equilibrium holds off the spectral radius of a certain matrix called “next-generation matrix”, which depends only on a set of “infectious compartments” (which we aim to reduce to 0) being less than one. This approach works provided that certain assumptions listed below hold (and, thus, is undefined when these assumptions are not satisfied.).
- (C1)
- The foremost assumption is that the disease-free equilibrium is unique and locally asymptotically stable within the disease-free space , meaning that all solutions ofmust approach the point when .
- (C2)
- Other conditions are related to an “admissible splitting” as a difference between two parts , called respectively “new infections”, and “transitions”.Definition A2.A splittingwill be called admissible if satisfy the following conditions [29,59]:where the subscript j refers to the j’th component.Remark A2.The splitting of the infectious equations has its origins in epidemiology. Mathematically, it is related to the “splitting of Metzler matrices"—see, for example, [54]. Note that the splitting conditions may be satisfied for several or no subset of compartments (see for example the SEIT model, discussed in [29], Chapter 3 in reference [12]). Unfortunately, for deterministic epidemic models, there is no clear-cut definition of [13,68,69]. (One possible explanation is that several stochastic epidemiological models may correspond in the limit to the same deterministic model).
- (C3)
- We turn now to the last conditions, which concern the linearization of the infectious equations around the DFE. Using , and letting f denote the perturbation from the linearization, we may write:The “transmission and transition” linearization matrices must satisfy component-wise and V is a non-singular M-matrix, which ensures that . (The assumption (B) implies that is a “stability (non-singular) M-matrix”, which is necessary for the non-negativity and boundedness of the solutions Theorems 1–3 in reference [33].)
Under conditions (C1)–(C3), the next-generation matrix method gives an explicit expression for the basic reproduction number, given by .
The basic reproduction number is a threshold parameter in the following sense ([29], [Thm 1]):
- 1(a)
- When , the DFE is locally asymptotically stable;
- 1(b)
- When , the DFE is unstable;
- 2
- The DFE is globally asymptotically stable when , provided that the “perturbation from linearity” is non-negative Theorem 2 in reference [29]. (Note that the [70] strong alternative was only established for a general n-stage progression, which is a particular case of the model we study below, in which A is an “Erlang” upper-diagonal matrix. It is natural to expect that the result continues to hold for other non-singular Metzler matrices).
In what follows, we will call the alternative 1(a)–1(b) the “weak alternative”. In contrast, result 2 is called the “strong alternative” in [59,70].
References
- Arino, J.; Brauer, F.; van den Driessche, P.; Watmough, J.; Wu, J. A final size relation for epidemic models. Math. Biosci. Eng. 2007, 4, 159. [Google Scholar] [PubMed]
- Avram, F.; Adenane, R.; Halanay, A.; Basnarkov, L.; Bianchin, G.; Goreac, D. On matrix-SIR arino models with linear birth rate, waning immunity, disease and vaccination fatalities, and their approximations. arXiv 2021, arXiv:2112.03436. [Google Scholar]
- Avram, F.; Adenane, R.; Bianchin, G.; Halanay, A. Stability analysis of an Eight parameter SIR-type model including loss of immunity, and disease and vaccination fatalities. Mathematics 2022, 10, 402. [Google Scholar] [CrossRef]
- Avram, F.; Adenane, R.; Halanay, A. New results and open questions for SIR–PH epidemic models with linear birth rate, waning immunity, vaccination, and disease and vaccination fatalities. Symmetry 2022, 14, 995. [Google Scholar] [CrossRef]
- Brauer, F. The kermack–mckendrick epidemic model revisited. Math. Biosci. 2005, 198, 119–131. [Google Scholar] [CrossRef]
- Breda, D.; Diekmann, O.; De Graaf, W.F.; Pugliese, A.; Vermiglio, R. On the formulation of epidemic models (an appraisal of kermack and mckendrick). J. Biol. Dyn. 2012, 6 (Suppl. 2), 103–117. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Gyllenberg, M.; Metz, J.A.J. Finite dimensional state representation of linear and nonlinear delay systems. J. Dyn. Differ. Eq. 2018, 30, 1439–1467. [Google Scholar] [CrossRef]
- Champredon, D.; Dushoff, J.; Earn, D.J.D. Equivalence of the erlang-distributed seir epidemic model and the renewal equation. SIAM J. Appl. Math. 2018, 78, 3258–3278. [Google Scholar] [CrossRef]
- Diekmann, O.; Inaba, H. A systematic procedure for incorporating separable static heterogeneity into compartmental epidemic models. arXiv 2022, arXiv:2207.02339. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Earn, D.J.D. A light introduction to modelling recurrent epidemics. In Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–17. [Google Scholar]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015; Volume 61. [Google Scholar]
- Thieme, H.R. Mathematics in Population Biology; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Springer: New York, NY, USA, 2019. [Google Scholar]
- Schaback, R. On COVID-19 modelling. Jahresbericht Deutschen Mathematiker-Vereinigung 2020, 122, 167–205. [Google Scholar] [CrossRef]
- Bacaër, N. Un modèle mathématique des débuts de l’épidémie de coronavirus en france. Math. Model. Nat. Phenom. 2020, 15, 29. [Google Scholar] [CrossRef]
- Ketcheson, D.I. Optimal control of an SIR epidemic through finite-time non-pharmaceutical intervention. arXiv 2020, arXiv:2004.08848. [Google Scholar] [CrossRef] [PubMed]
- Charpentier, A.; Elie, R.; Laurière, M.; Tran, V.C. COVID-19 pandemic control: Balancing detection policy and lockdown intervention under ICU sustainability. Math. Model. Nat. Phenom. 2020, 15, 57. [Google Scholar] [CrossRef]
- Djidjou-Demasse, R.; Michalakis, Y.; Choisy, M.; Sofonea, M.T.; Alizon, S. Optimal COVID-19 epidemic control until vaccine deployment. medRxiv 2020. [Google Scholar] [CrossRef]
- Sofonea, M.T.; Reyné, B.; Elie, B.; Djidjou-Demasse, R.; Selinger, C.; Michalakis, Y.; Alizon, S. Epidemiological monitoring and control perspectives: Application of a parsimonious modelling framework to the COVID-19 dynamics in France. medRxiv 2020. [Google Scholar] [CrossRef]
- Alvarez, E.F.; Argente, D.; Lippi, F. A Simple Planning Problem for COVID-19 Lockdown; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar]
- Horstmeyer, L.; Kuehn, C.; Thurner, S. Balancing quarantine and self-distancing measures in adaptive epidemic networks. arXiv 2020, arXiv:2010.10516. [Google Scholar] [CrossRef]
- Di Lauro, F.; Kiss, I.Z.; Miller, J. Optimal timing of one-shot interventions for epidemic control. PLoS Comput Biol. 2021, 17, e1008763. [Google Scholar] [CrossRef]
- Franco, E. A feedback SIR (fSIR) model highlights advantages and limitations of infection-based social distancing. arXiv 2020, arXiv:2004.13216. [Google Scholar]
- Baker, R. Reactive social distancing in a SIR model of epidemics such as COVID-19. arXiv 2020, arXiv:2003.08285. [Google Scholar]
- Caulkins, J.; Grass, D.; Feichtinger, G.; Hartl, R.; Kort, P.M.; Prskawetz, A.; Seidl, A.; Wrzaczek, S. How long should the COVID-19 lockdown continue? PLoS ONE 2020, 15, e0243413. [Google Scholar] [CrossRef]
- Caulkins, J.P.; Grass, D.; Feichtinger, G.; Hartl, R.F.; Kort, P.M.; Prskawetz, A.; Seidl, A.; Wrzaczek, S. The optimal lockdown intensity for COVID-19. J. Math. Econ. 2021, 93, 102489. [Google Scholar] [CrossRef] [PubMed]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Further notes on the basic reproduction number. In Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; pp. 159–178. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Arino, J.; Portet, S. A simple model for COVID-19. Infect. Dis. Model. 2020, 5, 309–315. [Google Scholar] [CrossRef]
- Avram, F.; Adenane, R.; Ketcheson, D. A review of matrix SIR arino epidemic models. Mathematics 2021, 9, 1513. [Google Scholar] [CrossRef]
- De la Sen, M.; Nistal, R.; Alonso-Quesada, S.; Ibeas, A. Some formal results on positivity, stability, and endemic steady-state attainability based on linear algebraic tools for a class of epidemic models with eventual incommensurate delays. Discret. Dyn. Nat. Soc. 2019, 2019, 8959681. [Google Scholar] [CrossRef]
- Busenberg, S.; van den Driessche, P. Analysis of a disease transmission model in a population with varying size. J. Math. Biol. 1990, 28, 257–270. [Google Scholar] [CrossRef] [PubMed]
- Busenberg, S.; van den Driessche, P. A method for proving the non-existence of limit cycles. J. Math. Anal. Appl. 1993, 172, 463–479. [Google Scholar] [CrossRef]
- Derrick, W.R.; van den Driessche, P. A disease transmission model in a nonconstant population. J. Math. Biol. 1993, 31, 495–512. [Google Scholar] [CrossRef]
- Greenhalgh, D. Hopf bifurcation in epidemic models with a latent period and nonpermanent immunity. Math. Comp. Model. 1997, 25, 85–107. [Google Scholar] [CrossRef]
- Li, M.Y.; Graef, J.R.; Wang, L.; Karsai, J. Global dynamics of a SEIR model with varying total population size. Math. Biosci. 1999, 160, 191–213. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Hsieh, Y.-H. Global analysis of an SEIR model with varying population size and vaccination. Appl. Math. Model. 2010, 34, 2685–2697. [Google Scholar] [CrossRef]
- Razvan, M.R. Multiple equilibria for an SIRS epidemiological system. arXiv 2001, arXiv:0101051. [Google Scholar]
- Li, J.; Ma, Z. Qualitative analyses of SIS epidemic model with vaccination and varying total population size. Math. Comp. Model. 2002, 35, 1235–1243. [Google Scholar] [CrossRef]
- Yang, W.; Sun, C.; Arino, J. Global analysis for a general epidemiological model with vaccination and varying population. J. Math. Anal. Appl. 2010, 372, 208–223. [Google Scholar] [CrossRef]
- Ma, J.; Earn, D.J.D. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bull. Math. Biol. 2006, 68, 679–702. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z. Final and peak epidemic sizes for SEIR models with quarantine and isolation. Math. Biosci. Eng. 2007, 4, 675. [Google Scholar]
- Andreasen, V. The final size of an epidemic and its relation to the basic reproduction number. Bull. Math. Biol. 2011, 73, 2305–2321. [Google Scholar] [CrossRef]
- Liu, W.-M.; Levin, S.A.; Iwasa, Y. Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 1986, 23, 187–204. [Google Scholar] [CrossRef]
- Liu, W.-M.; Hethcote, H.W.; Levin, S.A. Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 1987, 25, 359–380. [Google Scholar] [CrossRef]
- Georgescu, P.; Hsieh, J.-H. Global stability for a virus dynamics model with nonlinear incidence of infection and removal. SIAM J. Appl. Math. 2007, 67, 337–353. [Google Scholar] [CrossRef]
- Tang, Y.; Huang, D.; Ruan, S.; Zhang, W. Coexistence of limit cycles and homoclinic loops in a SIRS model with a nonlinear incidence rate. SIAM J. Appl. Math. 2008, 69, 621–639. [Google Scholar] [CrossRef]
- Riaño, G. Epidemic models with random infectious period. medRxiv 2020. [Google Scholar] [CrossRef]
- Plemmons, R.J. M-matrix characterizations. I—Nonsingular M-matrices. Linear Algebra Its Appl. 1977, 18, 175–188. [Google Scholar] [CrossRef]
- Hurtado, P.J.; Kirosingh, A.S. Generalizations of the ‘linear chain trick’: Incorporating more flexible dwell time distributions into mean field ODE models. J. Math. Biol. 2019, 79, 1831–1883. [Google Scholar] [CrossRef] [PubMed]
- Hyman, J.M.; Li, J.; Stanley, E.A. The differential infectivity and staged progression models for the transmission of hiv. Math. Biosci. 1999, 155, 77–109. [Google Scholar] [CrossRef]
- Fall, A.; Iggidr, A.; Sallet, G.; Tewa, J.-J. Epidemiological models and Lyapunov functions. Math. Model. Nat. Phenom. 2007, 2, 62–83. [Google Scholar] [CrossRef]
- Beretta, E.; Takeuchi, Y. Global stability of an sir epidemic model with time delays. J. Math. Biol. 1995, 33, 250–260. [Google Scholar] [CrossRef]
- Andò, A.; Breda, D.; Gava, G. How fast is the linear chain trick? A rigorous analysis in the context of behavioral epidemiology. Math. Biosci. Eng. 2020, 17, 5059–5085. [Google Scholar] [CrossRef]
- Champredon, D.; Dushoff, J. Intrinsic and realized generation intervals in infectious-disease transmission. Proc. R. Soc. B Biol. Sci. 2015, 282, 20152026. [Google Scholar] [CrossRef]
- Horn, A.R.; Johnson, C.R. Matrix Analysis; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Shuai, Z.; van den Driessche, P. Global stability of infectious disease models using Lyapunov functions. SIAM J. Appl. Math. 2013, 73, 1513–1532. [Google Scholar] [CrossRef]
- De la Sen, M.; Ibeas, A. On an SE(Is)(Ih)AR epidemic model with combined vaccination and antiviral controls for COVID-19 pandemic. Adv. Diff. Eq. 2021, 2021, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Shah, K.; Din, R.U.; Deebani, W.; Kumam, P.; Shah, Z. On nonlinear classical and fractional order dynamical system addressing COVID-19. Results Phys. 2021, 24, 104069. [Google Scholar] [CrossRef] [PubMed]
- Tang, T.-Q.; Jan, R.; Bonyah, E.; Shah, Z.; Alzahrani, E. Qualitative analysis of the transmission dynamics of dengue with the effect of memory, reinfection, and vaccination. Comput. Math. Methods Med. 2022. [Google Scholar] [CrossRef]
- Lotka, A.J. Analyse Démographique Avec Application Particulière à L’espèce Humaine; Hermann: Paris, France, 1939. [Google Scholar]
- Bacaër, N. Mathématiques et Epidémies; HAL: Lyon, France, 2021. [Google Scholar]
- Claude Kamgang, J.; Sallet, G. Computation of threshold conditions for epidemiological models and global stability of the disease-free equilibrium (DFE). Math. Biosci. 2008, 213, 1–12. [Google Scholar] [CrossRef]
- Dietz, K. The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med. Res. 1993, 2, 23–41. [Google Scholar] [CrossRef]
- Perasso, A. An introduction to the basic reproduction number in mathematical epidemiology. ESAIM Proc. Surv. 2018, 62, 123–138. [Google Scholar] [CrossRef]
- Roberts, M.G. The pluses and minuses of 0. J. R. Soc. Interface 2007, 4, 949–961. [Google Scholar] [CrossRef]
- Li, J.; Blakeley, D. The failure of R0. Comput. Math. Methods Med. 2011, 2011, 527610. [Google Scholar] [CrossRef]
- Guo, H.; Li, M.Y. Global dynamics of a staged progression model for infectious diseases. Math. Biosci. Eng. 2006, 3, 513. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).