Prediction of Coal Dilatancy Point Using Acoustic Emission Characteristics: Insight Experimental and Artificial Intelligence Approaches
Abstract
1. Introduction
2. Materials and Methods
2.1. Sampling
2.2. Experimental Scheme

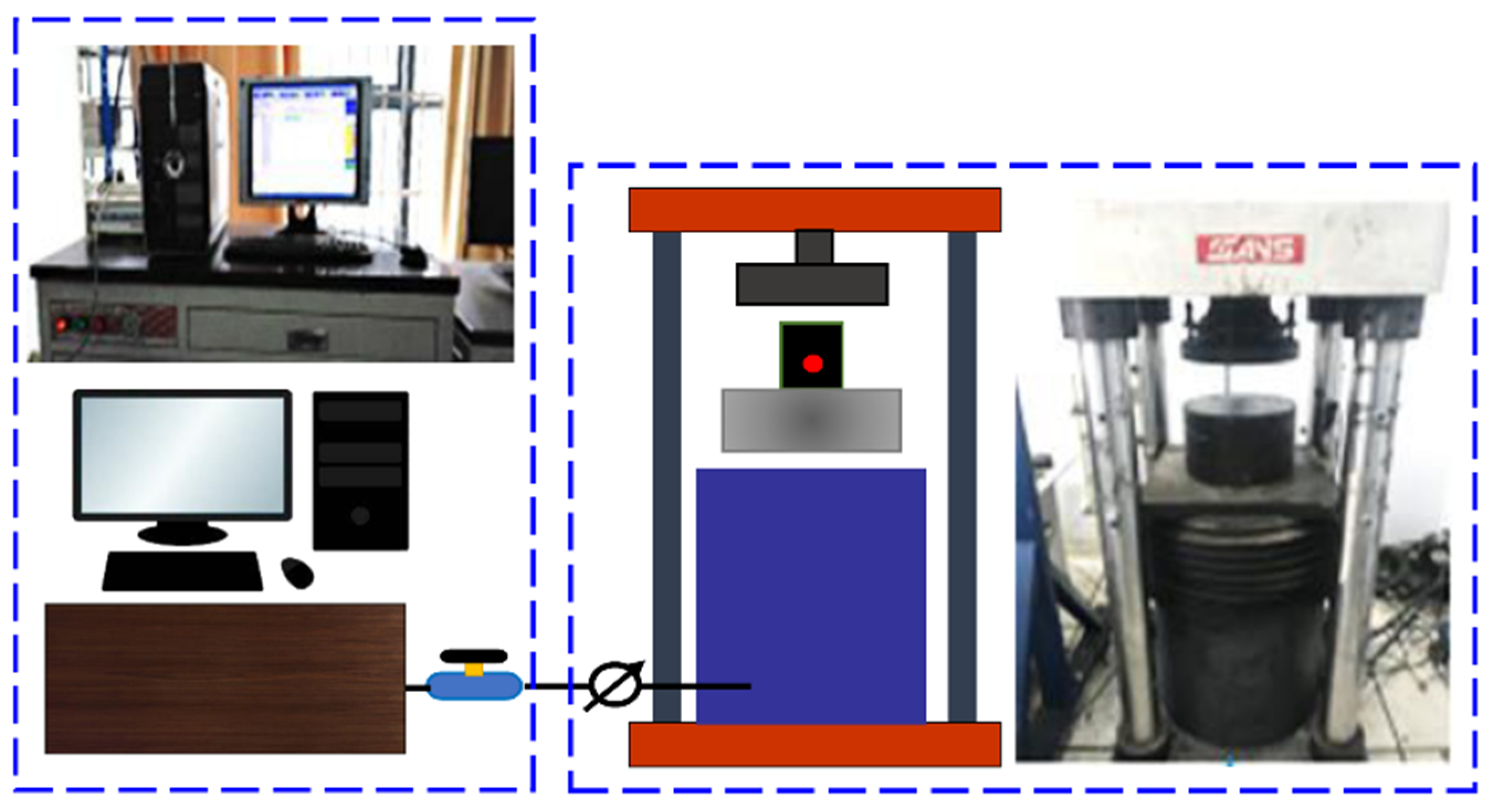
2.2.1. Loading System
2.2.2. Data Collection System
3. Intelligent Model
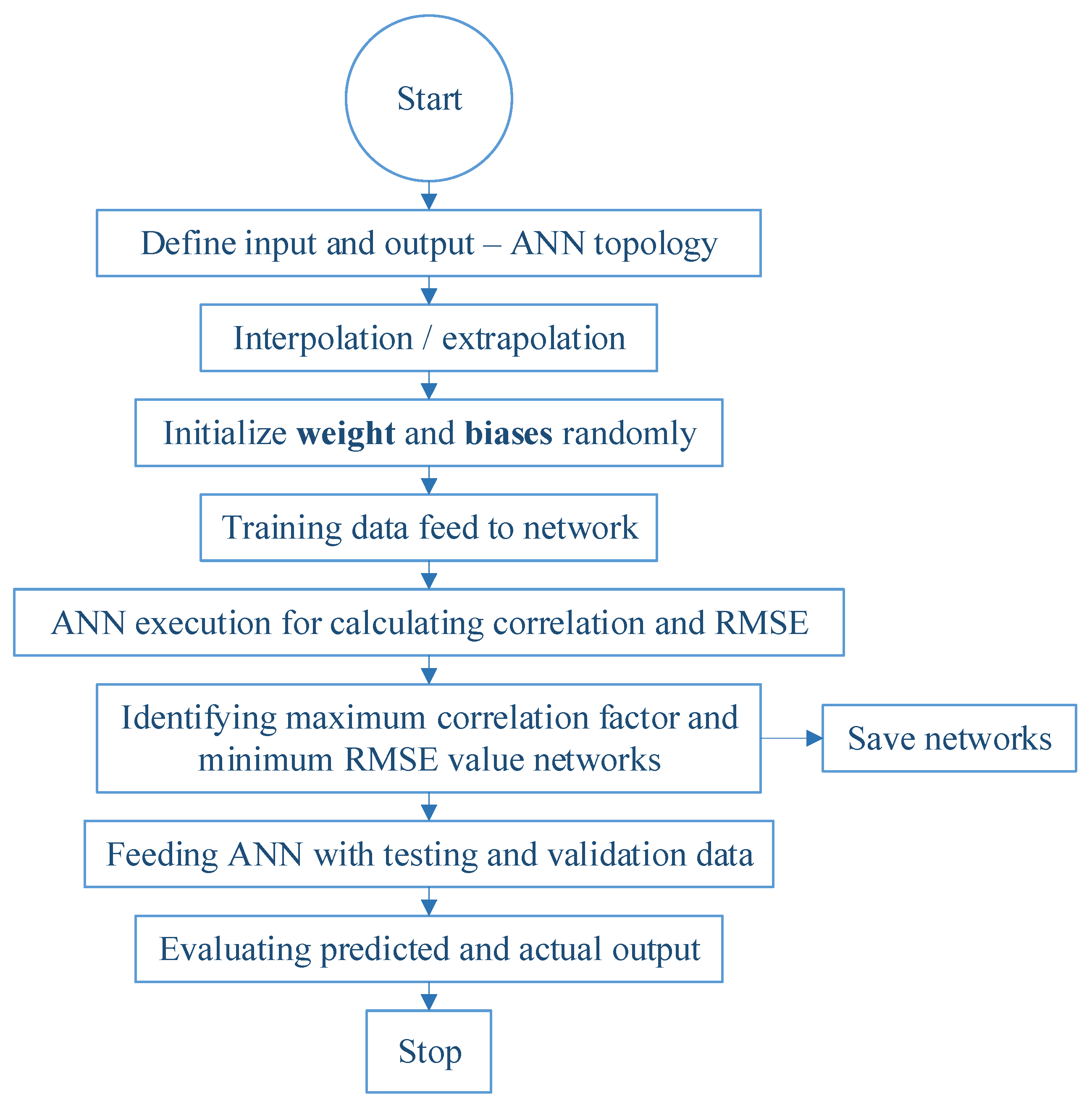
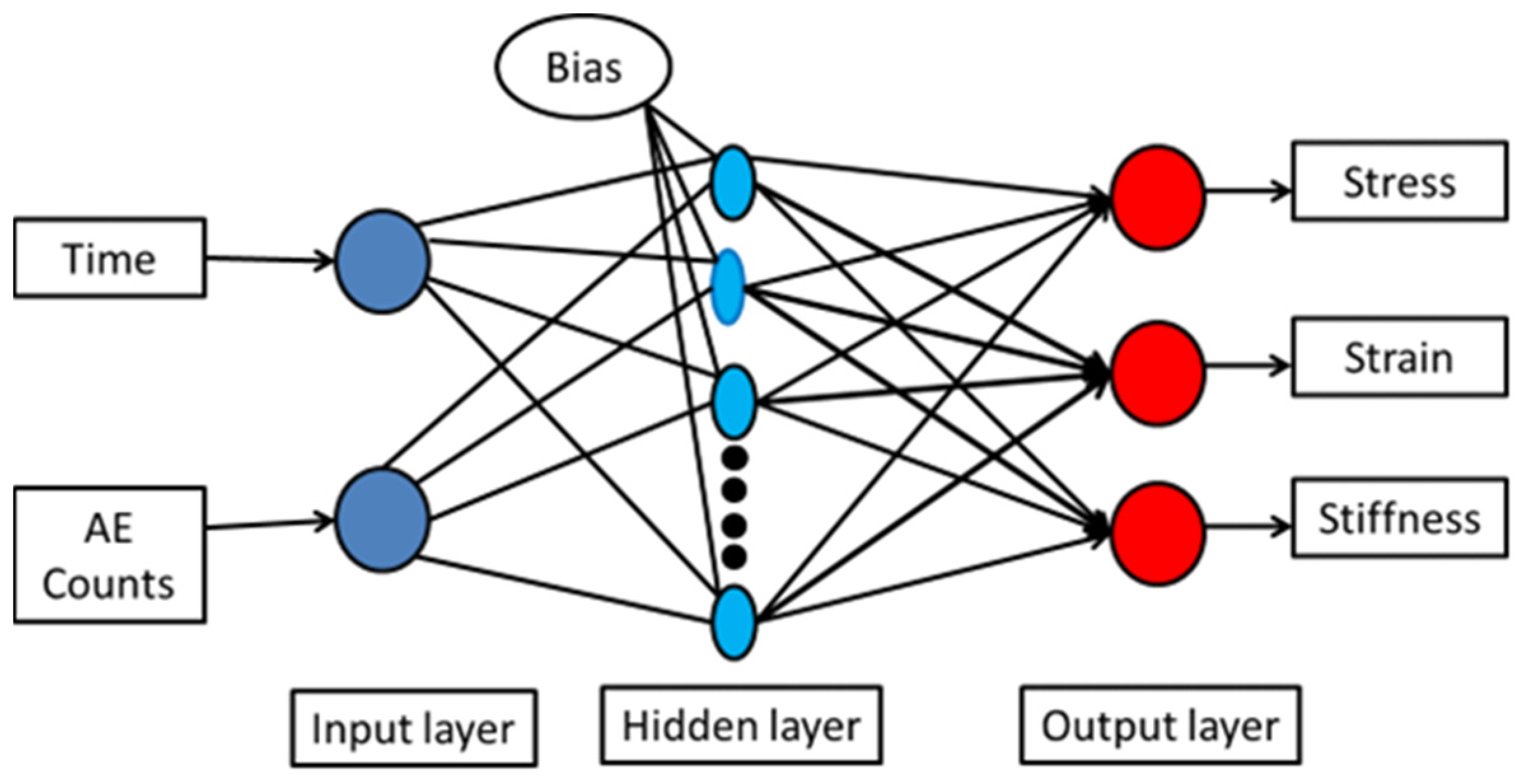
3.1. Artificial Neural Network (ANN) Model
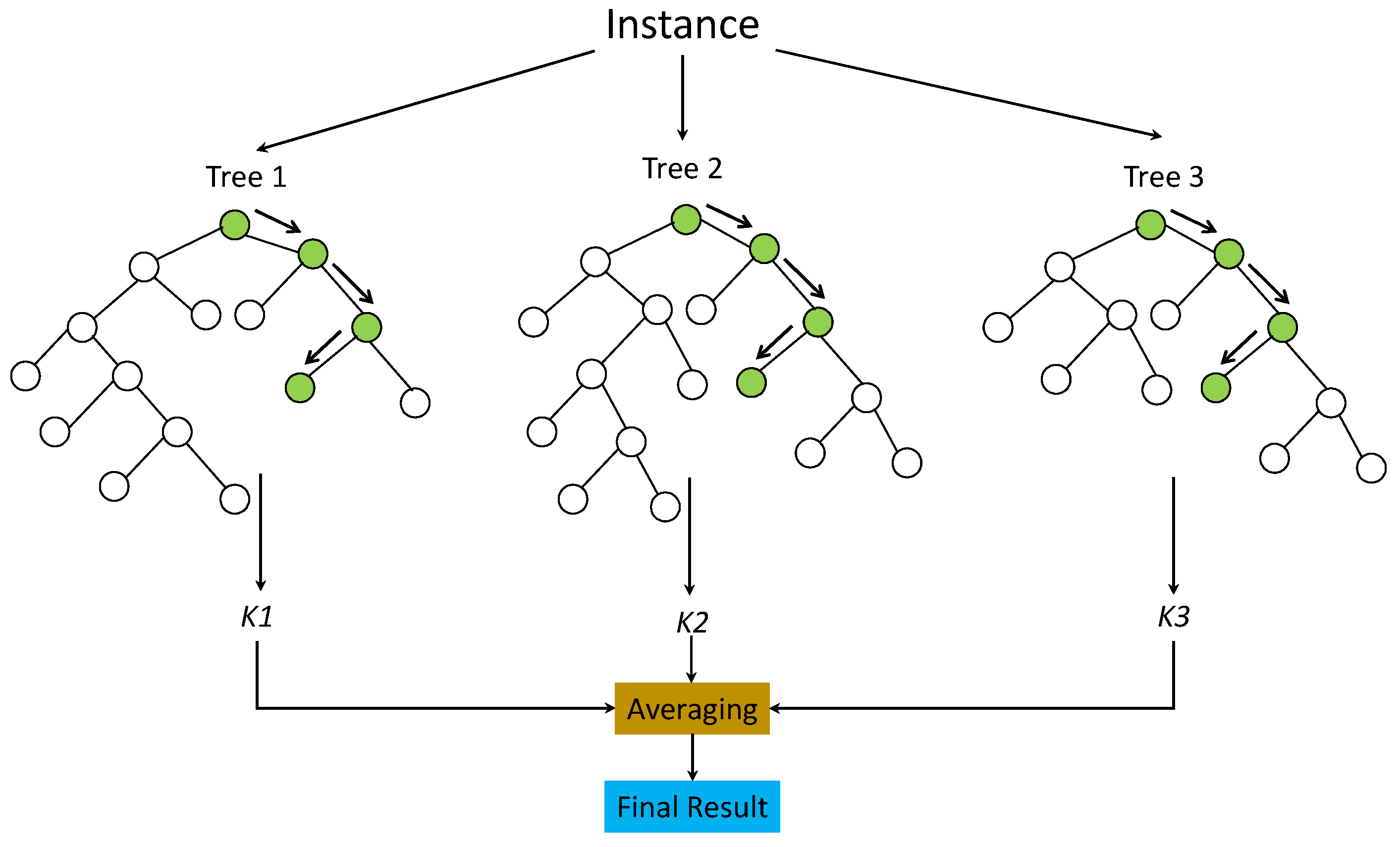
3.2. Random Forest Regression (RFR)
3.3. k-Nearest Neighbor (KNN)
4. Mechanical Characterization
4.1. Elastic Modulus
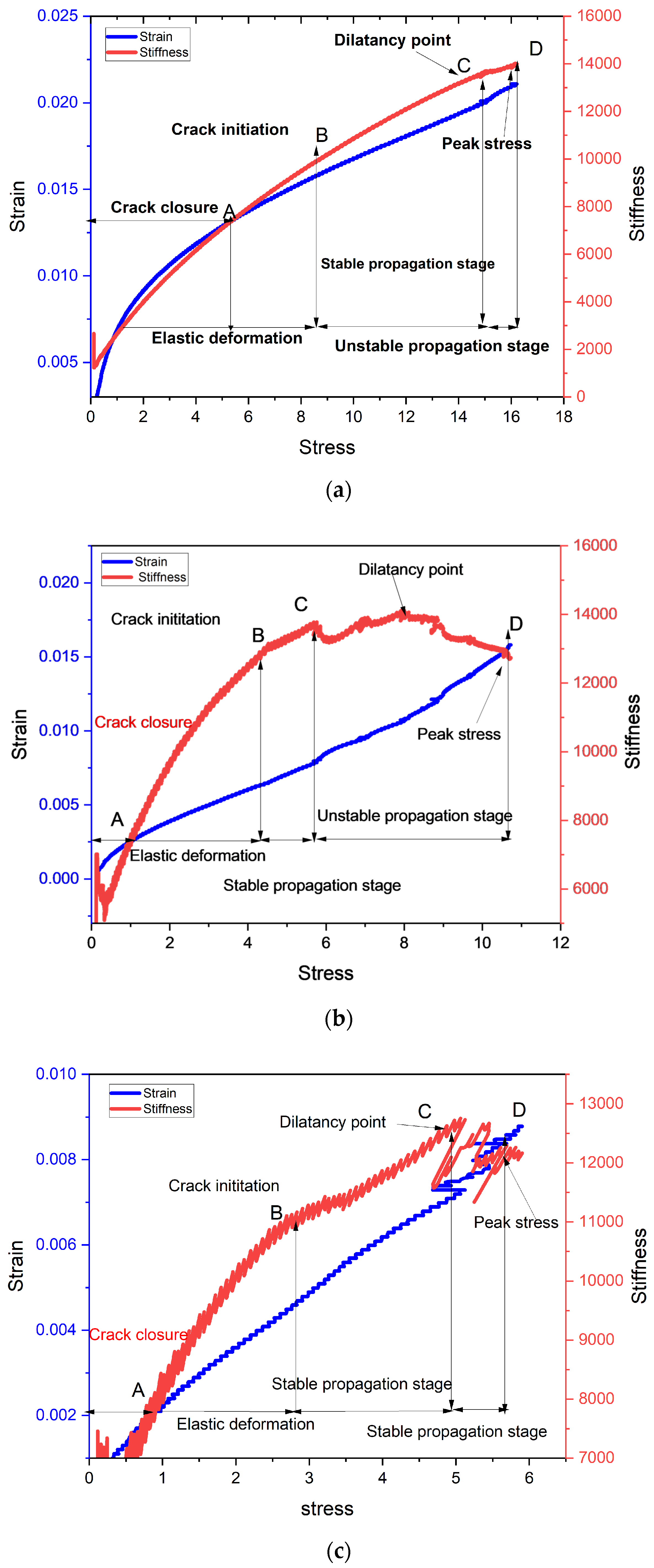
4.2. Stresses Associated with Dilatancy and Crack Initiation
4.3. Strain Energy
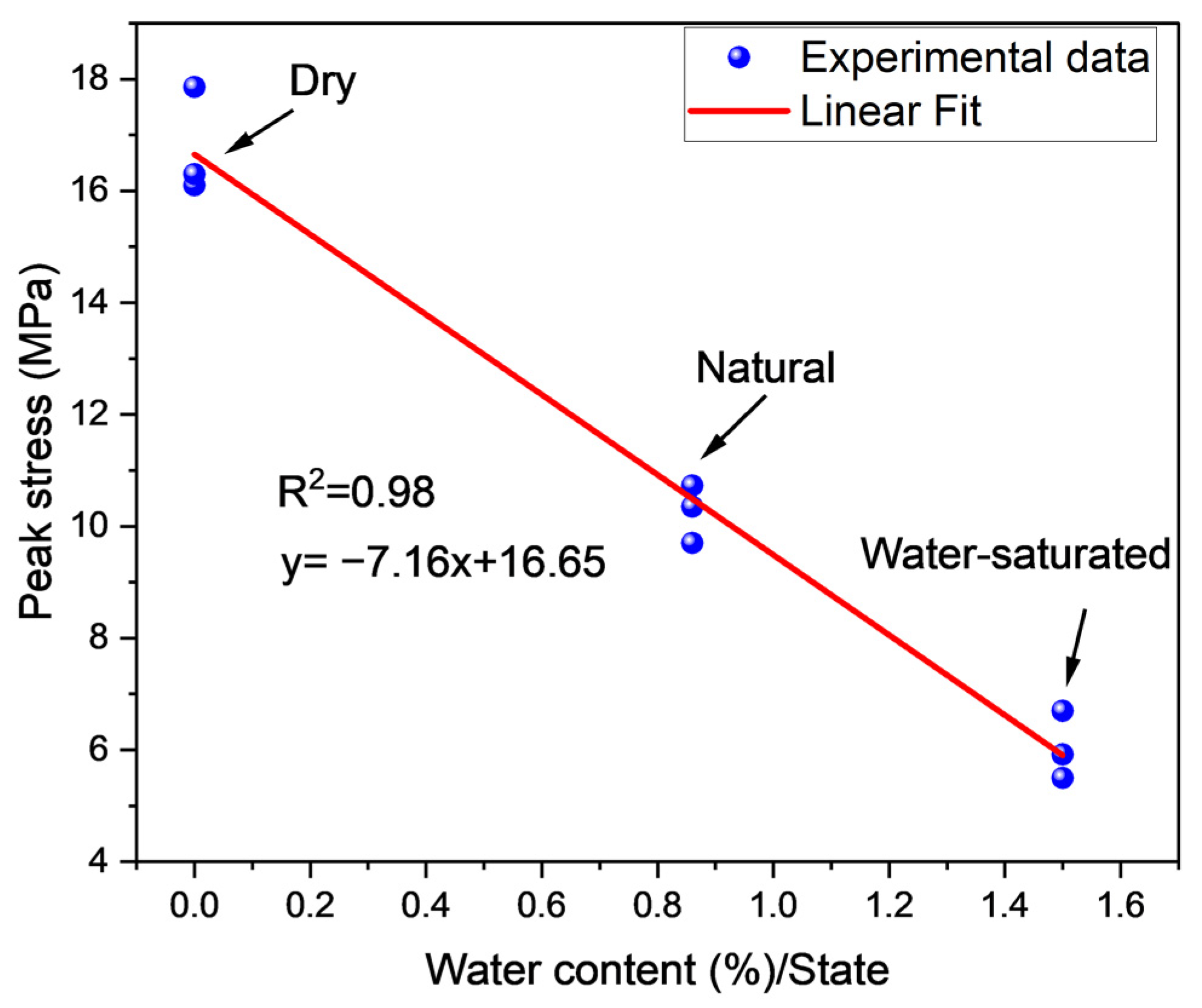
4.4. Water Content and Their Response to the Stress–Strain Curve
4.5. Strain Energy Rate
5. AE Counts Characteristics and Counts under Stress–Strain Curve Stages
6. Prediction Model
6.1. Network Phases and Regression Model
Performance of Model
6.2. Random Forest (RF)
6.3. k-Nearest Neighbor
6.4. Comparison of Statistical and Intelligent Techniquesff
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Yin, G.; Li, M.; Zhang, D.; Huang, G.; Liu, P.; Liu, C.; Zhao, H.; Yu, B. Mechanical Properties and Failure Behavior of Dry and Water-Saturated Anisotropic Coal Under True-Triaxial Loading Conditions. Rock Mech. Rock Eng. 2019, 53, 4799–4818. [Google Scholar] [CrossRef]
- Ali, M.; Wang, E.; Li, Z.; Jia, H.; Li, D.; Jiskani, I.M.; Ullah, B. Study on Acoustic Emission Characteristics and Mechanical Behavior of Water-Saturated Coal. Geofluids 2021, 2021, 5247988. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.; Yan, Y.; Gu, S.; Wang, J.; Guo, X.; Luo, C.; Suo, T. Mechanics and Acoustic Emission Fractal Characteristics of Surrounding Rock of Tantalum–Niobium Mine Under Splitting Condition. Nat. Resour. Res. 2021, 31, 149–162. [Google Scholar] [CrossRef]
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Xue, S.; Yuan, L.; Xie, J.; Wang, Y. Advances in gas content based on outburst control technology in Huainan, China. Int. J. Min. Sci. Technol. 2014, 24, 385–389. [Google Scholar] [CrossRef]
- Aguado, M.B.D.; Nicieza, C. Control and prevention of gas outbursts in coal mines, Riosa–Olloniego coalfield, Spain. Int. J. Coal Geol. 2007, 69, 253–266. [Google Scholar] [CrossRef]
- Cheng, W.; Liu, Z.; Yang, H.; Wang, W. Non-linear seepage characteristics and influential factors of water injection in gassy seams. Exp. Therm. Fluid Sci. 2018, 91, 41–53. [Google Scholar] [CrossRef]
- Zhong, C.; Zhang, Z.; Ranjith, P.G.; Lu, Y.; Choi, X. The role of pore water plays in coal under uniaxial cyclic loading. Eng. Geol. 2019, 257, 105125. [Google Scholar] [CrossRef]
- Xie, G.-X.; Hu, Z.-X. Coal mining dilatancy characteristics of high gas working face in the deep mine. J. China Coal Soc. 2014, 39, 91–96. [Google Scholar]
- Khan, N.M.; Ma, L.; Cao, K.; Hussain, S.; Liu, W.; Xu, Y.; Yuan, Q.; Gu, J. Prediction of an early failure point using infrared radiation characteristics and energy evolution for sandstone with different water contents. Bull. Eng. Geol. Environ. 2021, 80, 6913–6936. [Google Scholar] [CrossRef]
- Dong, W.; Zhao, X.; Zhou, X.; Yuan, W. Effects of moisture gradient of concrete on fracture process in restrained concrete rings: Experimental and numerical. Eng. Fract. Mech. 2019, 208, 189–208. [Google Scholar] [CrossRef]
- Tang, C.; Yao, Q.; Xu, Q.; Shan, C.; Xu, J.; Han, H.; Guo, H. Mechanical Failure Modes and Fractal Characteristics of Coal Samples under Repeated Drying–Saturation Conditions. Nat. Resour. Res. 2021, 30, 4439–4456. [Google Scholar] [CrossRef]
- Antoshchenko, M.; Tarasov, V.; Nedbailo, O.; Zakharova, O.; Yevhen, R.J.M.D. On the possibilities to apply indices of industrial coal-rank classification to determine hazardous characteristics of workable beds. Min. Miner. Deposits 2021, 15, 1–8. [Google Scholar] [CrossRef]
- Antoshchenko, M.; Tarasov, V.; Rudniev, R.; Zakharova, O.J.M.D. Using indices of the current industrial coal classification to forecast hazardous characteristics of coal seams. Min. Miner. Deposits 2022, 16, 7–13. [Google Scholar] [CrossRef]
- Bridgman, P.W. Volume Changes in the Plastic Stages of Simple Compression, in Collected Experimental Papers; Harvard University Press: Cambridge, MA, USA, 2013; Volume VII, pp. 3987–3998. [Google Scholar]
- Matsushima, S. On the Deformation and Fracture of Granite under High Confining Pressure; Bulletins-Disaster Prevention Research Institute, Kyoto University: Kyoto, Japan, 1960; Volume 36, pp. 11–19. [Google Scholar]
- Handin, J.; Hager Jr, R.V.; Friedman, M.; Feather, J.N. Experimental deformation of sedimentary rocks under confining pressure: Pore pressure tests. AAPG Bull. 1963, 47, 717–755. [Google Scholar]
- Brace, W.F.; Paulding, B.W.; Scholz, C., Jr. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Vutukuri, V.S.; Lama, R.; Saluja, S. Handbook on Mechanical Properties of Rocks: Testing Techniques and Results; Trans Tech Publications: Zürich, Switzerland, 1974; Volume 4. [Google Scholar]
- Wang, Y.; Li, X.; Ben, Y.; Wu, Y.; Zhang, B. Prediction of initiation stress of dilation of brittle rocks. Chin. J. Rock Mech. Eng. 2014, 33, 737–746. [Google Scholar]
- Hou, W.S.; Li, S.D.; Li, X.; Hao, J.M.; Pan, L.; Liu, Y.H.; Wang, R.Q. Comparison of initial and peak characteristics of rock dilatancy. Chin. J. Geotech. Eng. 2013, 35, 1478–1485. [Google Scholar]
- Ali, M.; Wang, E.; Li, Z.; Wang, X.; Khan, N.M.; Zang, Z.; Alarifi, S.S.; Fissha, Y. Analytical Damage Model for Predicting Coal Failure Stresses by Utilizing Acoustic Emission. Sustainability 2023, 15, 1236. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, E.; Zhao, D.; Zhang, L. Energy Evolution Characteristics of Water-Saturated and Dry Anisotropic Coal under True Triaxial Stresses. Sustainability 2023, 15, 1431. [Google Scholar] [CrossRef]
- Li, H.; Shen, R.; Wang, E.; Li, D.; Li, T.; Chen, T.; Hou, Z. Effect of water on the time-frequency characteristics of electromagnetic radiation during sandstone deformation and fracturing. Eng. Geol. 2020, 265, 105451. [Google Scholar] [CrossRef]
- Li, H.; Qiao, Y.; Shen, R.; He, M.; Cheng, T.; Xiao, Y.; Tang, J. Effect of water on mechanical behavior and acoustic emission response of sandstone during loading process: Phenomenon and mechanism. Eng. Geol. 2021, 294, 106386. [Google Scholar] [CrossRef]
- Ali, M.; Wang, E.; Li, Z.; Khan, N.M.; Sabri Sabri, M.M.; Ullah, B. Investigation of the acoustic emission and fractal characteristics of coal with varying water contents during uniaxial compression failure. Sci. Rep. 2023, 13, 2238. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Wang, D.; Wu, M.; Yin, G.; Li, M. Mechanical and Acoustic Emission Characteristics of Coal at Temperature Impact. Nat. Resour. Res. 2020, 29, 1755–17722. [Google Scholar] [CrossRef]
- Arcaklioğlu, E.; Erişen, A.; Yilmaz, R. Artificial neural network analysis of heat pumps using refrigerant mixtures. Energy Convers. Manag. 2004, 45, 1917–1929. [Google Scholar] [CrossRef]
- Cao, K.; Khan, N.; Liu, W.; Hussain, S.; Zhu, Y.; Cao, Z.; Bian, Y. Prediction Model of Dilatancy Stress Based on Brittle Rock: A Case Study of Sandstone. Arab. J. Sci. Eng. 2020, 46, 2165–2176. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.; Sharma, J. Energy analysis of a building using artificial neural network: A review. Energy Build. 2013, 65, 352–358. [Google Scholar] [CrossRef]
- Sharma, L.K.; Singh, T.N. Regression-based models for the prediction of unconfined compressive strength of artificially structured soil. Eng. Comput. 2018, 34, 175–186. [Google Scholar] [CrossRef]
- Singh, R.; Kainthola, A.; Singh, T.N. Estimation of elastic constant of rocks using an ANFIS approach. Appl. Soft Comput. 2012, 12, 40–45. [Google Scholar] [CrossRef]
- Sirdesai, N.N.; Singh, A.; Sharma, L.K.; Singh, R.; Singh, T. Determination of thermal damage in rock specimen using intelligent techniques. Eng. Geol. 2018, 239, 179–194. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Hu, Z.; Yu, Z.; Hao, S.; Lei, Z.; Xie, Y. Prediction of layered thermal conductivity using artificial neural network in order to have better design of ground source heat pump system. Energies 2018, 11, 1896. [Google Scholar] [CrossRef]
- Tian, H.; Shu, J.; Han, L. The effect of ICA and PSO on ANN results in approximating elasticity modulus of rock material. Eng. Comput. 2019, 35, 305–314. [Google Scholar] [CrossRef]
- Zhou, J.; Koopialipoor, M.; Li, E.; Armaghani, D.J. Prediction of rockburst risk in underground projects developing a neuro-bee intelligent system. Bull. Eng. Geol. Environ. 2020, 79, 4265–4279. [Google Scholar] [CrossRef]
- Song, D.; Wang, E.; Song, X.; Jin, P.; Qiu, L. Changes in frequency of electromagnetic radiation from loaded coal rock. Rock Mech. Rock Eng. 2016, 49, 291–302. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T. Prediction of blast-induced ground vibration using artificial neural network. Int. J. Rock Mech. Min. Sci. 2009, 46, 1214–1222. [Google Scholar] [CrossRef]
- Ma, L.; Khan, N.M.; Cao, K.; Rehman, H.; Salman, S.; Rehman, F.U. Prediction of Sandstone Dilatancy Point in Different Water Contents Using Infrared Radiation Characteristic: Experimental and Machine Learning Approaches. Lithosphere 2022, 2021, 3243070. [Google Scholar] [CrossRef]
- Lee, S.; Ha, J.; Zokhirova, M.; Moon, H.; Lee, J. Background information of deep learning for structural engineering. Arch. Comput. Methods Eng. 2018, 25, 121–129. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, I.; AlSalman, H.; Islam, S.; Asif Zahoor Raja, M.; Shoaib, M.; Gumaei, A.; Fiza, M.; Ullah, K.; Rahman, M. Levenberg–Marquardt backpropagation for numerical treatment of micropolar flow in a porous channel with mass injection. Complexity 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Wang, M.; Wan, W.; Zhao, Y. Prediction of the uniaxial compressive strength of rocks from simple index tests using a random forest predictive model. Comptes Rendus. Méc. 2020, 348, 3–32. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, W.; Jiskani, I.M.; Lu, X.; Wang, Z.; Luan, B. Slope Stability Prediction Method Based on Intelligent Optimization and Machine Learning Algorithms. Sustainability 2023, 15, 1169. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Mitri, H. Comparative performance of six supervised learning methods for the development of models of hard rock pillar stability prediction. Nat. Hazards 2015, 79, 291–316. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, X.; Niu, R.; Yang, K.; Zhao, L. The assessment of landslide susceptibility mapping using random forest and decision tree methods in the Three Gorges Reservoir area, China. Environ. Earth Sci. 2017, 76, 1–20. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Tofani, V.; Segoni, S.; Catani, F.; Casagli, N. A tool for classification and regression using random forest methodology: Applications to landslide susceptibility mapping and soil thickness modeling. Environ. Model. Assess. 2017, 22, 201–214. [Google Scholar] [CrossRef]
- Kohestani, V.R.; Hassanlourad, M.; Ardakani, A. Evaluation of liquefaction potential based on CPT data using random forest. Nat. Hazards 2015, 79, 1079–1089. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, X.; Du, K.; Qiu, X.; Li, X.; Mitri, H.S. Feasibility of random-forest approach for prediction of ground settlements induced by the construction of a shield-driven tunnel. Int. J. Géoméch. 2017, 17, 04016129. [Google Scholar] [CrossRef]
- Akbulut, Y.; Sengur, A.; Guo, Y.; Smarandache, F. NS-k-NN: Neutrosophic set-based k-nearest neighbors classifier. Symmetry 2017, 9, 179. [Google Scholar] [CrossRef]
- Chen, T.; Yao, Q.L.; Du, M.; Zhu, C.G.; Zhang, B. Experimental research of effect of water intrusion times on crack propagation in coal. Chin. J. Rock Mech. Eng. 2016, 2, 3756–3762. [Google Scholar]
- Yao, Q.; Chen, T.; Ju, M.; Liang, S.; Liu, Y.; Li, X. Effects of water intrusion on mechanical properties of and crack propagation in coal. Rock Mech. Rock Eng. 2016, 49, 4699–4709. [Google Scholar] [CrossRef]
- Liu, G.; Hu, Y.; Li, P. Behavior of soaking rock and its effects on design of arch dam. Chin. J. Rock Mech. Eng. 2006, 25, 1729–1734. [Google Scholar]
- Yao, Q.; Li, X.; Zhou, J.; Ju, M.; Chong, Z.; Zhao, B. Experimental study of strength characteristics of coal specimens after water intrusion. Arab. J. Geosci. 2015, 8, 6779–6789. [Google Scholar] [CrossRef]
- Guha Roy, D.; Singh, T.; Kodikara, J.; Das, R. Effect of water saturation on the fracture and mechanical properties of sedimentary rocks. Rock Mech. Rock Eng. 2017, 50, 2585–2600. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B.; Read, R. Identifying crack initiation and propagation thresholds in brittle rock. Can. Geotech. J. 1998, 35, 222–233. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Wu, Y.; Wang, C. Precursors for rock fracturing and failure—Part II: IRR T-Curve abnormalities. Int. J. Rock Mech. Min. Sci. 2006, 43, 483–493. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Hu, L.; Tang, C.a.; Zheng, H. Predicting rock failure with the critical slowing down theory. Eng. Geol. 2021, 280, 105960. [Google Scholar] [CrossRef]
- Wu, X.; Gao, X.; Liu, X.; Zhao, K. Abnormality of infrared temperature mutation in the process of saturated siltstone failure. J. China Coal Soc. 2015, 40, 328–336. [Google Scholar]
- Cao, K.; Ma, L.; Wu, Y.; Khan, N.; Yang, J. Using the characteristics of infrared radiation during the process of strain energy evolution in saturated rock as a precursor for violent failure. Infrared Phys. Technol. 2020, 109, 103406. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, W.; Liu, D.; Hou, Z.; Li, C. On anisotropic fracture evolution and energy mechanism during marble failure under uniaxial deformation. Rock Mech. Rock Eng. 2019, 52, 3567–3583. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, X.-T.; Yang, C.; Zhang, X.; Sharifzadeh, M.; Wang, Z. Fracturing evolution analysis of Beishan granite under true triaxial compression based on acoustic emission and strain energy. Int. J. Rock Mech. Min. Sci. 2019, 117, 150–161. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.; Jiang, Y.; Liu, P.; Guo, Y.; Liu, J.; Ma, M.; Wang, K.; Wang, S. Shear behaviour and acoustic emission characteristics of bolted rock joints with different roughnesses. Rock Mech. Rock Eng. 2018, 51, 1885–1906. [Google Scholar] [CrossRef]
- Zingg, S.; Anagnostou, G. Tunnel Face Stability and the Effectiveness of Advance Drainage Measures in Water-Bearing Ground of Non-uniform Permeability. Rock Mech. Rock Eng. 2017, 51, 187–202. [Google Scholar] [CrossRef]
- Liu, B.; Yang, R.; Guo, D.; Zhang, D. Burst-prone experiments of coal-rock combination at-1100 m level in Suncun coal mine. Chin. J. Rock Mech. Eng. 2004, 23, 2402–2408. [Google Scholar]
- Batra, D. Comparison between levenberg-marquardt and scaled conjugate gradient training algorithms for image compression using mlp. Int. J. Image Process. (IJIP) 2014, 8, 412. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]



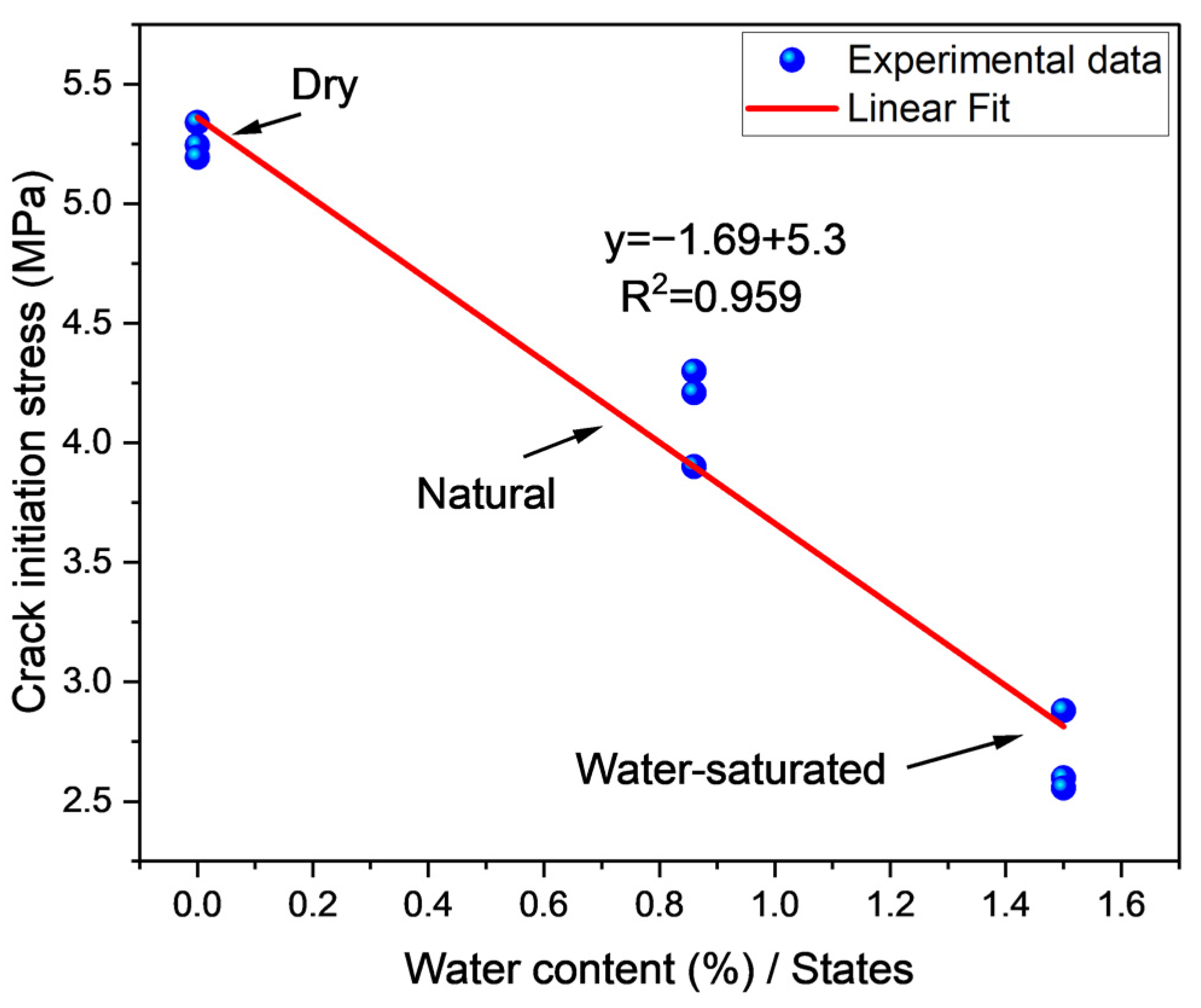


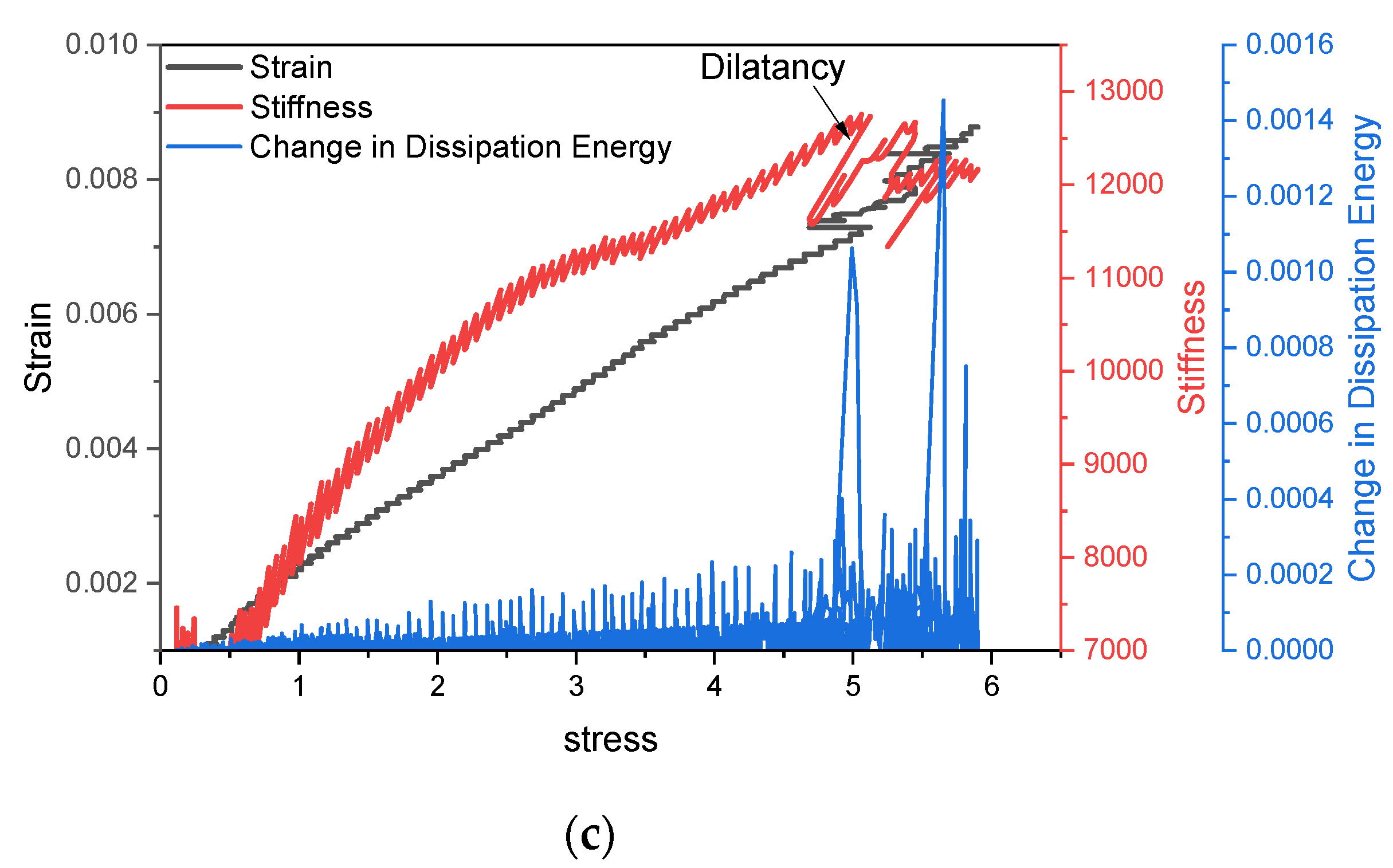

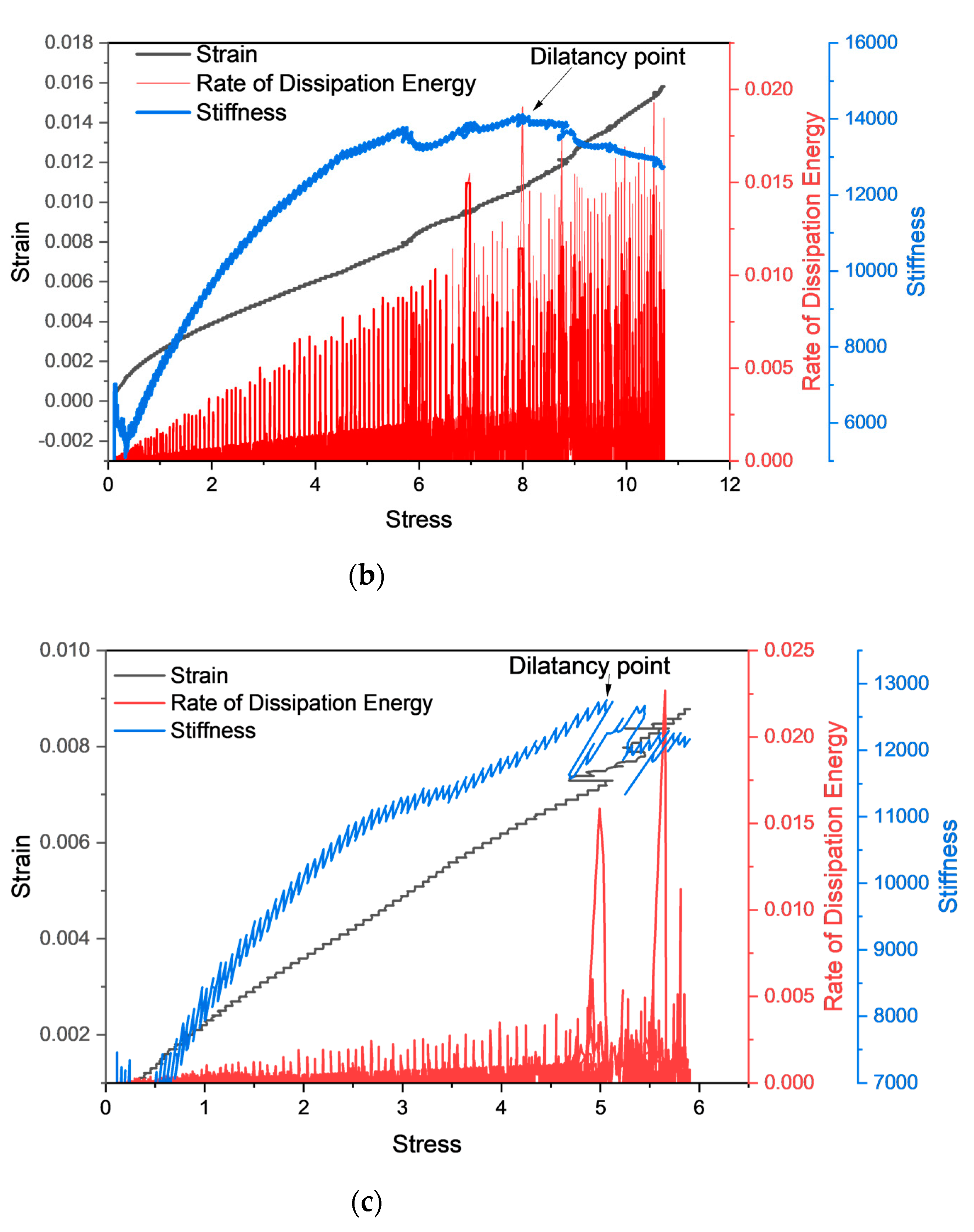
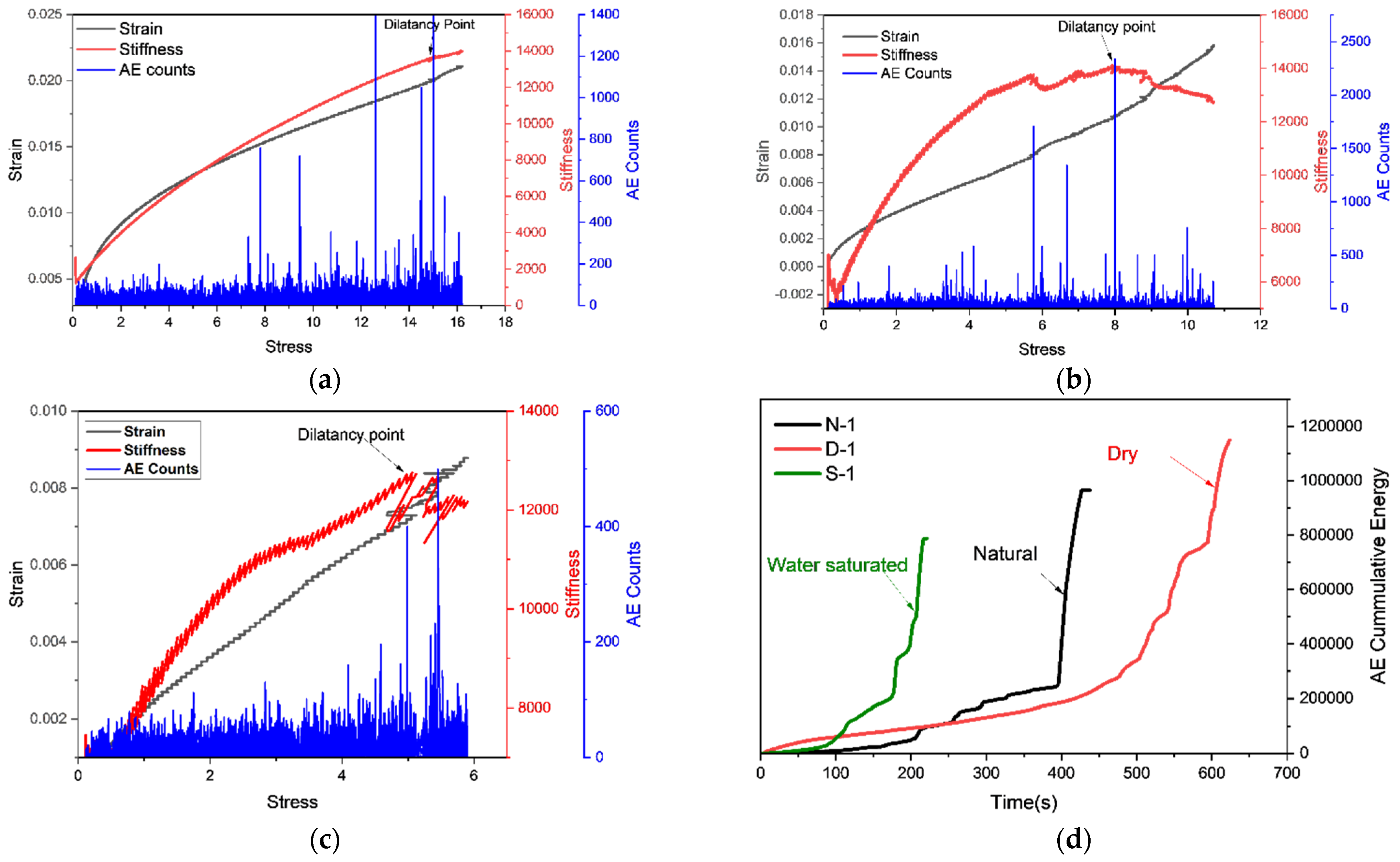
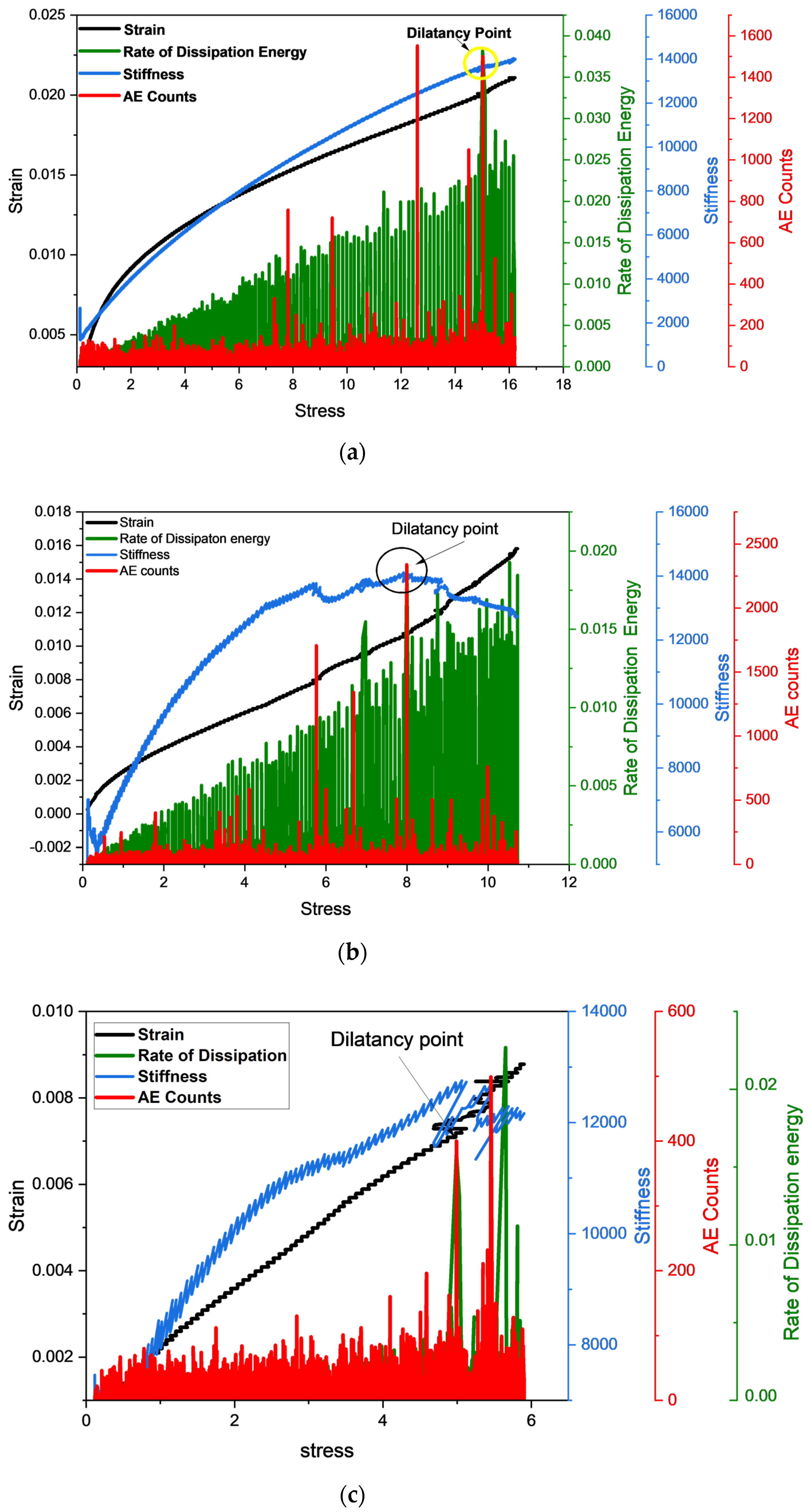

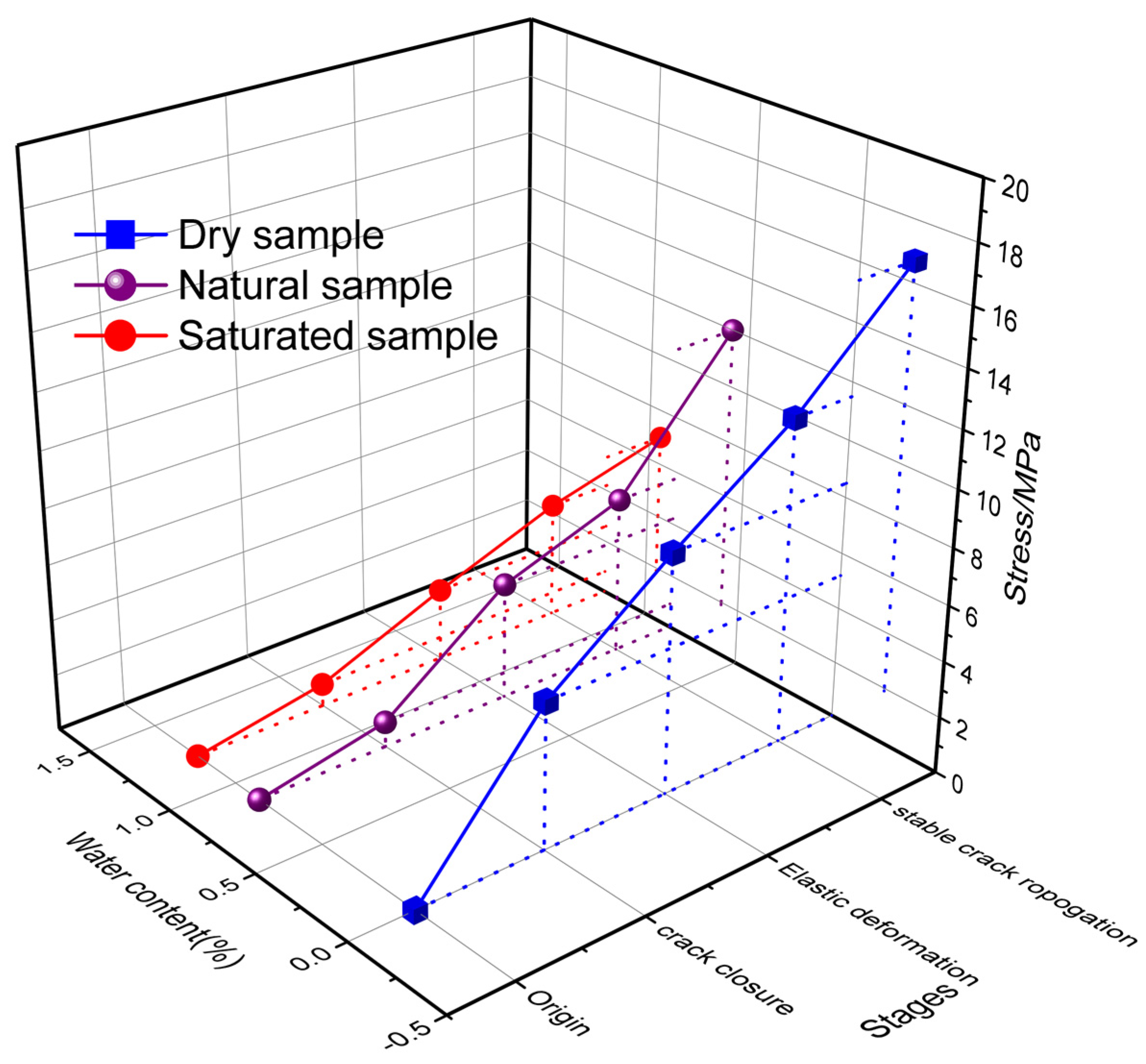



| Sample Number | State | Peak Stress (MPa) | Elastic Modulus (GPa) | Crack Initiation Stress (MPa) | Peak Strain 10−2 | Dilatancy Stress (MPa) |
|---|---|---|---|---|---|---|
| D-1 | Dry | 16.1 | 1.280 | 5.2447 | 0.02257 | 14.7 |
| D-2 | Dry | 16.3 | 1.259 | 5.194 | 0.01993 | 13.5 |
| D-3 | Dry | 17.86 | 1.330 | 5.34 | 0.0264 | 15.0 |
| N-1 | Natural | 10.73 | 0.946 | 4.3 | 0.0198 | 8.85 |
| N-2 | Natural | 10.35 | 0.882 | 4.21 | 0.0138 | 8.55 |
| N-3 | Natural | 9.70 | 0.841 | 3.9 | 0.0098 | 7.95 |
| S-1 | Saturated | 5.92 | 0.721 | 2.599 | 0.01269 | 4.9 |
| S-2 | Saturated | 5.5 | 0.683 | 2.556 | 0.01132 | 4.3 |
| S-3 | Saturated | 6.7 | 0.755 | 2.88 | 0.01352 | 5.0 |
| Parameters | Sample | Mean | Standard Deviation | Minimum | Median | Maximum |
|---|---|---|---|---|---|---|
| Time (s) | Natural | 199.77 | 115.396 | 0 | 199.73 | 399.73 |
| AE Counts | 20.35 | 44.0407 | 1 | 9 | 2339 | |
| Stiffness | 11.97 | 2342.02 | 2380.8 | 13,109.09 | 14,114.50 | |
| Strain | 0.00806 | 0.00396 | 2.2843 × 10−4 | 0.00766 | 0.0198 | |
| Stress | 5.47831 | 3.03331 | 0.11625 | 5.483 | 10.73 | |
| Time (s) | Dry | 297.435 | 171.812 | 0 | 297.32 | 595.07 |
| AE Counts | 23.6691 | 84.35789 | 1 | 10 | 4091 | |
| Stiffness | 9070.70 | 3600.09 | 842.51 | 9634.43 | 14,044.48 | |
| Strain | 0.01482 | 0.0043 | 0.00127 | 0.01552 | 0.02257 | |
| Stress | 8.21202 | 4.69204 | 0.11455 | 8.20839 | 16.35 | |
| Time (s) | Saturated | 105.73 | 61.06808 | 0 | 105.7175 | 211.502 |
| AE Counts | 15.97 | 21.60477 | 1 | 8 | 499 | |
| Stiffness | 10,476.31 | 1873.25 | 3382.03 | 11,157.28 | 14,192.85 | |
| Strain | 0.00496 | 0.00227 | 2.80717 × 10−4 | 0.00499 | 0.01269 | |
| Stress | 3.05973 | 1.65055 | 0.11565 | 3.06386 | 5.91878 |
| Output Parameters | Topology | R2 | Neuron | RMSE | Epoch | Gradient | Mu |
|---|---|---|---|---|---|---|---|
| Stiffness | 2.0-80-03 | 0.998 | 80 | 0.00703 | 5.12 × 10−2 | 246 × 10−6 | 0.01 |
| Stress’s | 2.0-80-03 | 0.999 | 80 | 0.00703 | 5.12 × 10−2 | 246 × 10−6 | 0.01 |
| Strain | 2.0-80-03 | 0.984 | 80 | 0.00703 | 5.12 × 10−2 | 246 × 10−6 | 0.01 |
| Parameters | Values | Details |
|---|---|---|
| n_estimators | 100 | Number of trees in RFR |
| max_depth | 18 | Maximum depth of tree |
| random_state | 10 | Random state |
| Parameters | Values | Descriptions |
|---|---|---|
| n_neighbors | 9 | Number neighbors |
| Metric | Minkowski | The distance metric to use |
| Predicted Parameters | Models | R2 | RMSE | MAPE (%) | VAF (%) |
|---|---|---|---|---|---|
| Strain, Stiffness, Dissipation, strain energy rate | ANN | 0.99 | 0.00703 | 1.18 | 99.23 |
| RFR | 0.97 | 1.05 | 0.25 | 97.22 | |
| KNN | 0.93 | 2.02 | 0.93 | 93.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.; Khan, N.M.; Gao, Q.; Cao, K.; Jahed Armaghani, D.; Alarifi, S.S.; Rehman, H.; Jiskani, I.M. Prediction of Coal Dilatancy Point Using Acoustic Emission Characteristics: Insight Experimental and Artificial Intelligence Approaches. Mathematics 2023, 11, 1305. https://doi.org/10.3390/math11061305
Ali M, Khan NM, Gao Q, Cao K, Jahed Armaghani D, Alarifi SS, Rehman H, Jiskani IM. Prediction of Coal Dilatancy Point Using Acoustic Emission Characteristics: Insight Experimental and Artificial Intelligence Approaches. Mathematics. 2023; 11(6):1305. https://doi.org/10.3390/math11061305
Chicago/Turabian StyleAli, Muhammad, Naseer Muhammad Khan, Qiangqiang Gao, Kewang Cao, Danial Jahed Armaghani, Saad S. Alarifi, Hafeezur Rehman, and Izhar Mithal Jiskani. 2023. "Prediction of Coal Dilatancy Point Using Acoustic Emission Characteristics: Insight Experimental and Artificial Intelligence Approaches" Mathematics 11, no. 6: 1305. https://doi.org/10.3390/math11061305
APA StyleAli, M., Khan, N. M., Gao, Q., Cao, K., Jahed Armaghani, D., Alarifi, S. S., Rehman, H., & Jiskani, I. M. (2023). Prediction of Coal Dilatancy Point Using Acoustic Emission Characteristics: Insight Experimental and Artificial Intelligence Approaches. Mathematics, 11(6), 1305. https://doi.org/10.3390/math11061305










