Darcy–Brinkman Double Diffusive Convection in an Anisotropic Porous Layer with Gravity Fluctuation and Throughflow
Abstract
1. Introduction
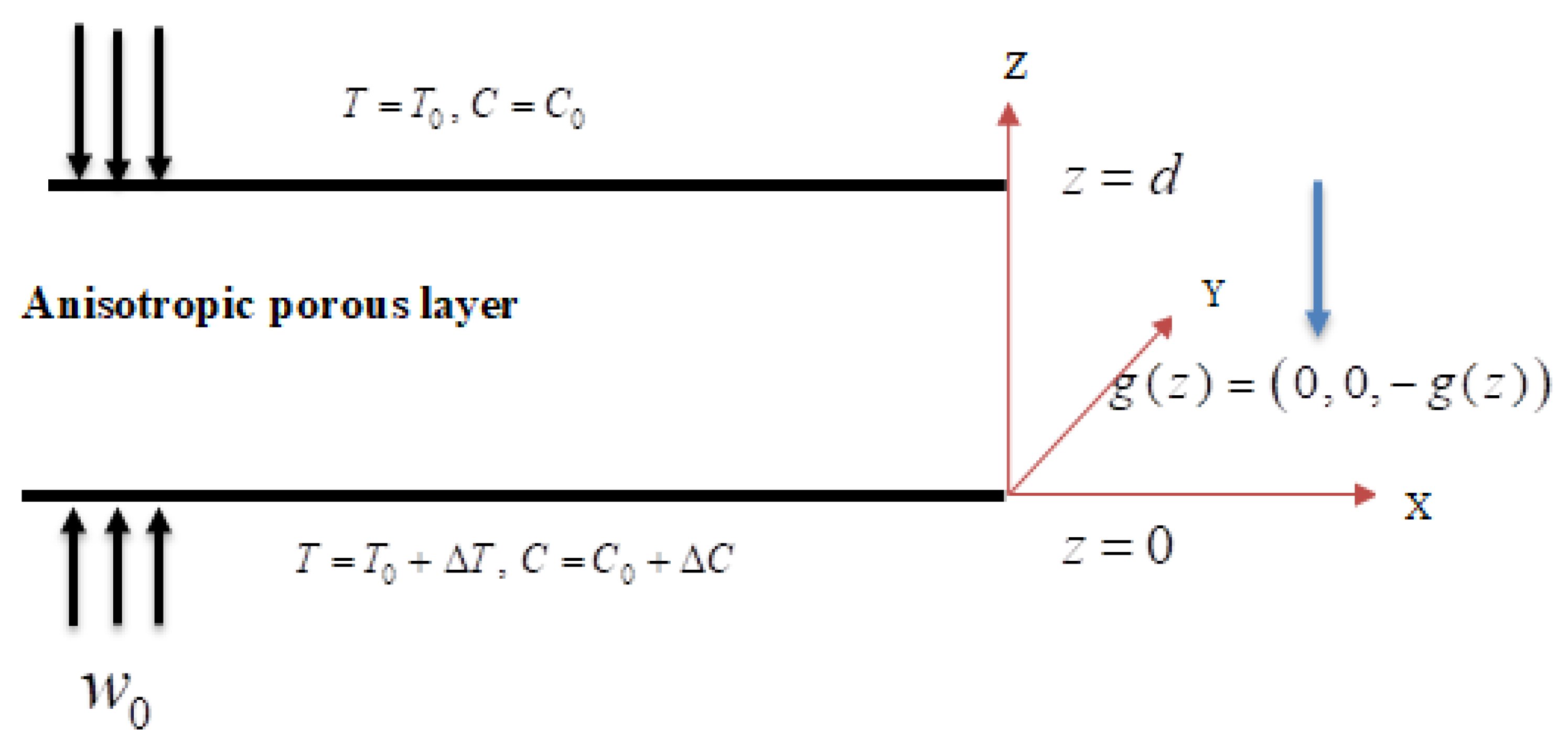
2. Materials and Methods
3. Linear Stability Analysis
4. Technique of Solution
4.1. Stationary State
4.2. Limiting Case
4.3. Oscillatory State
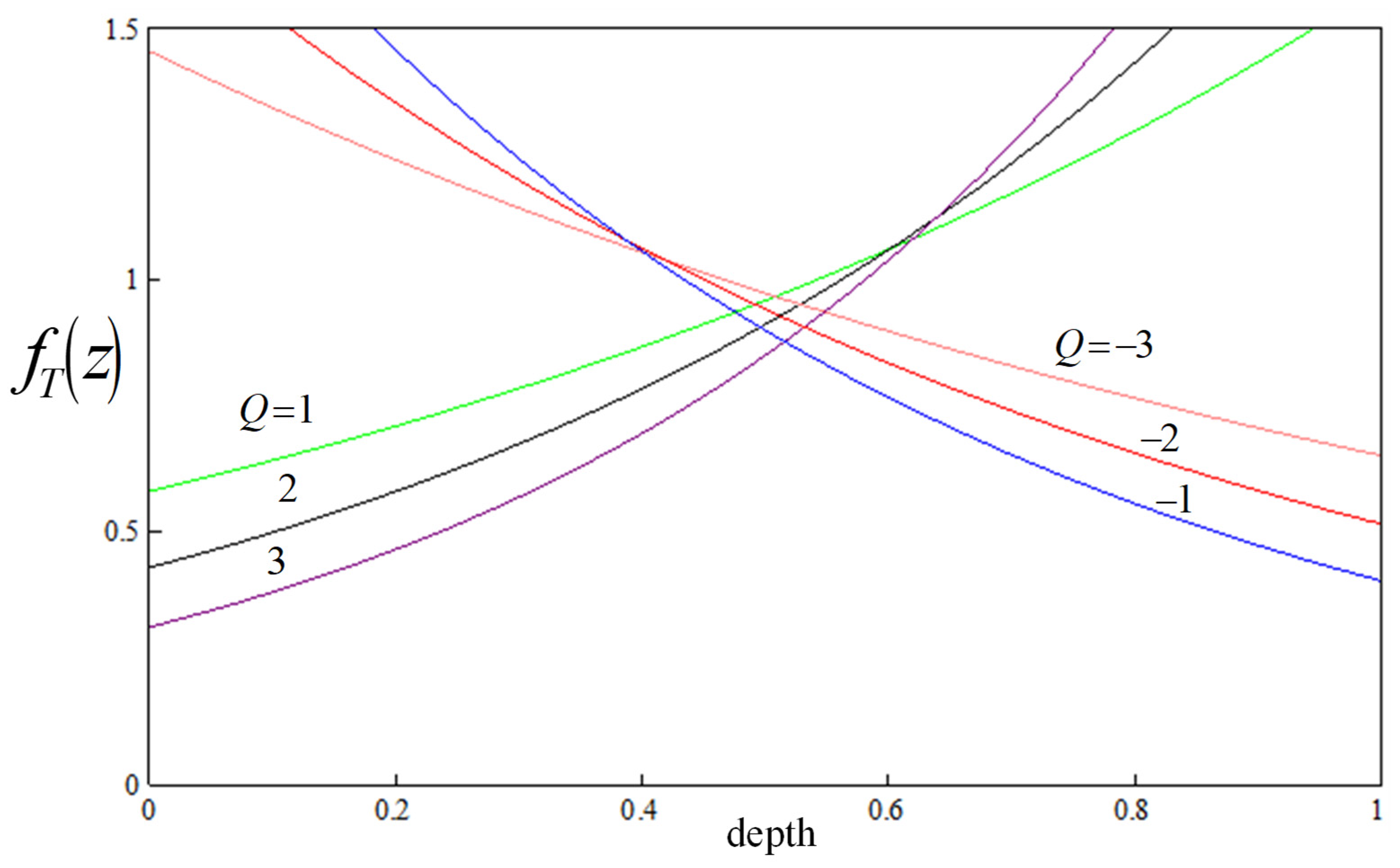
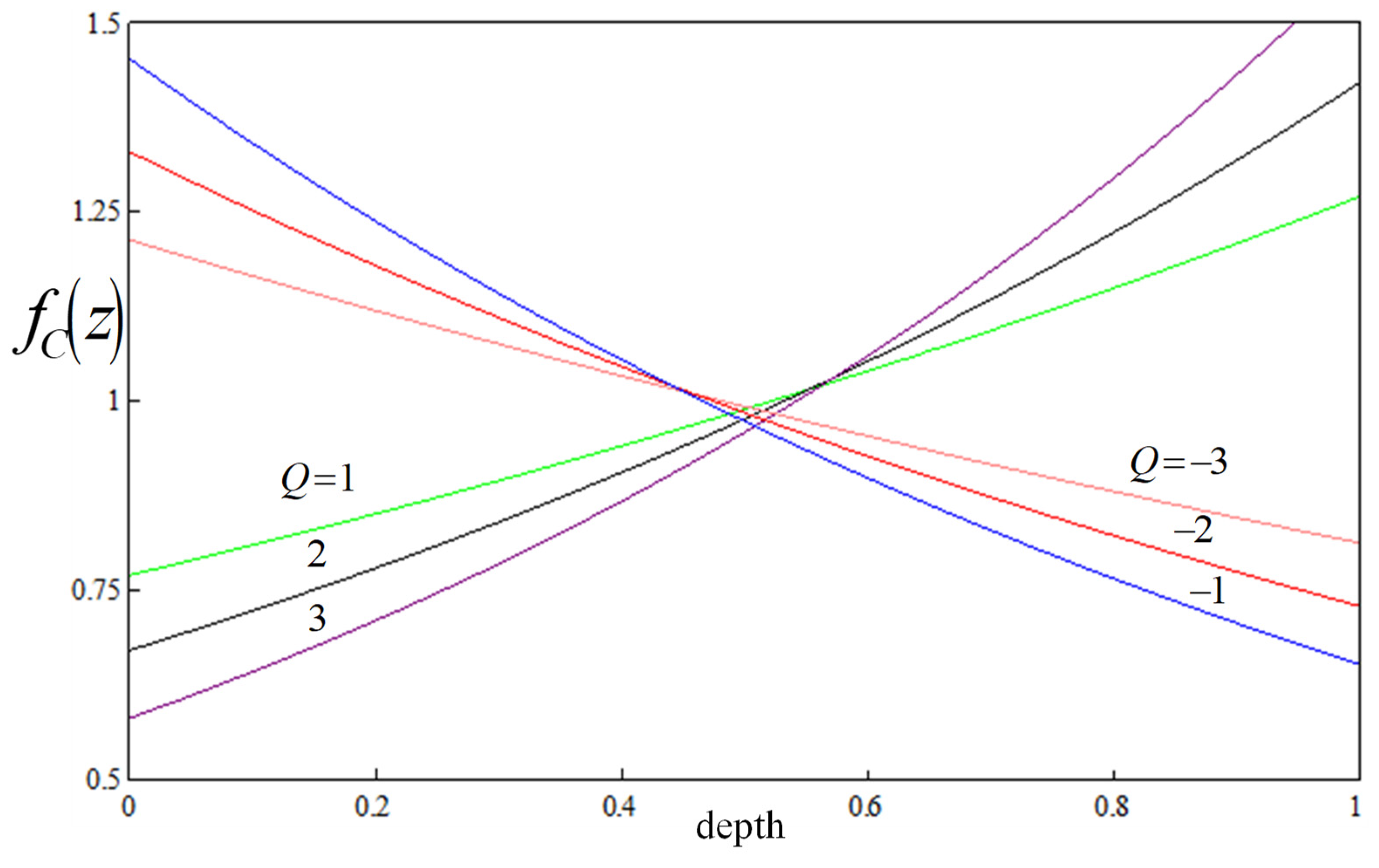
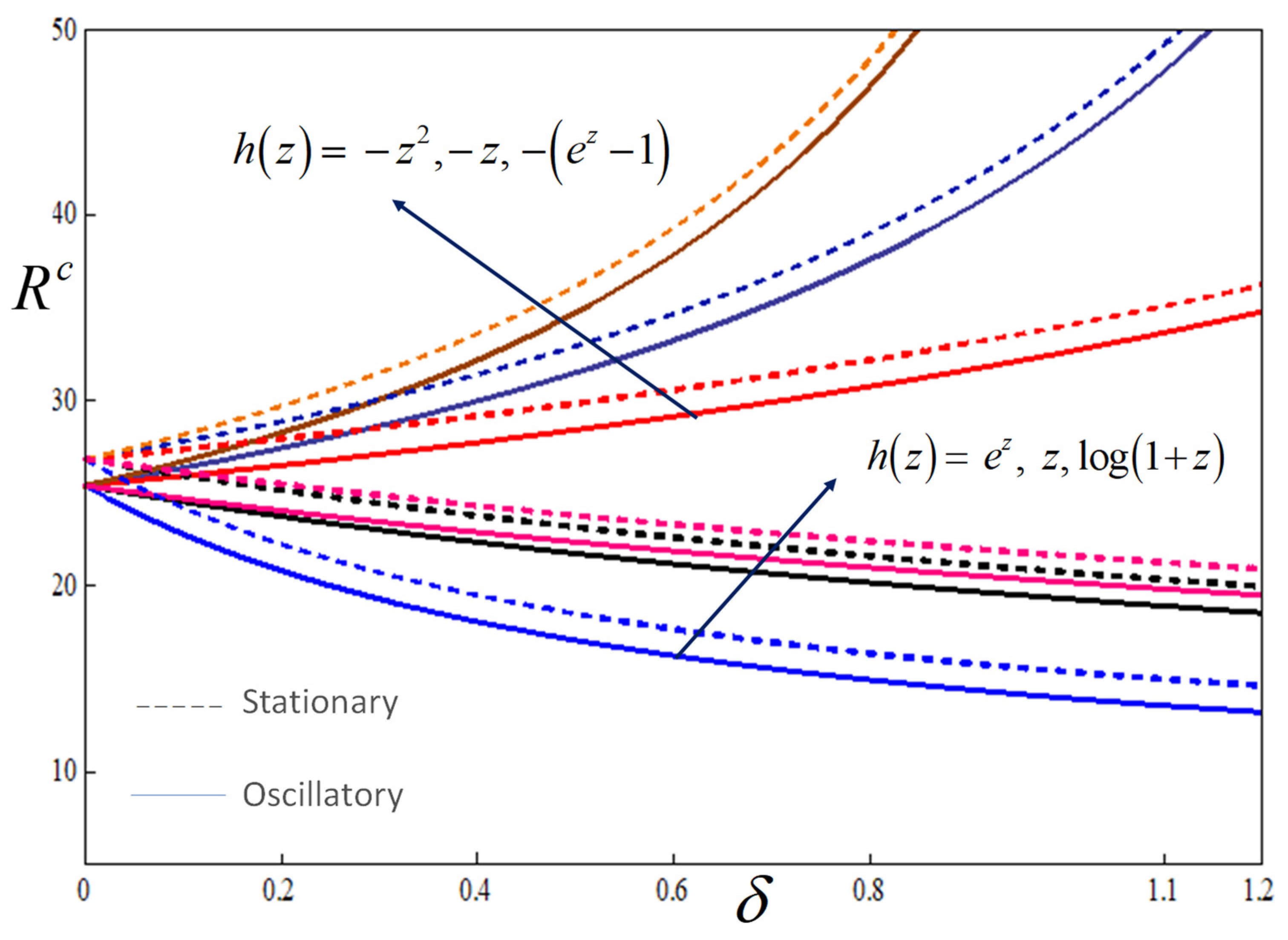
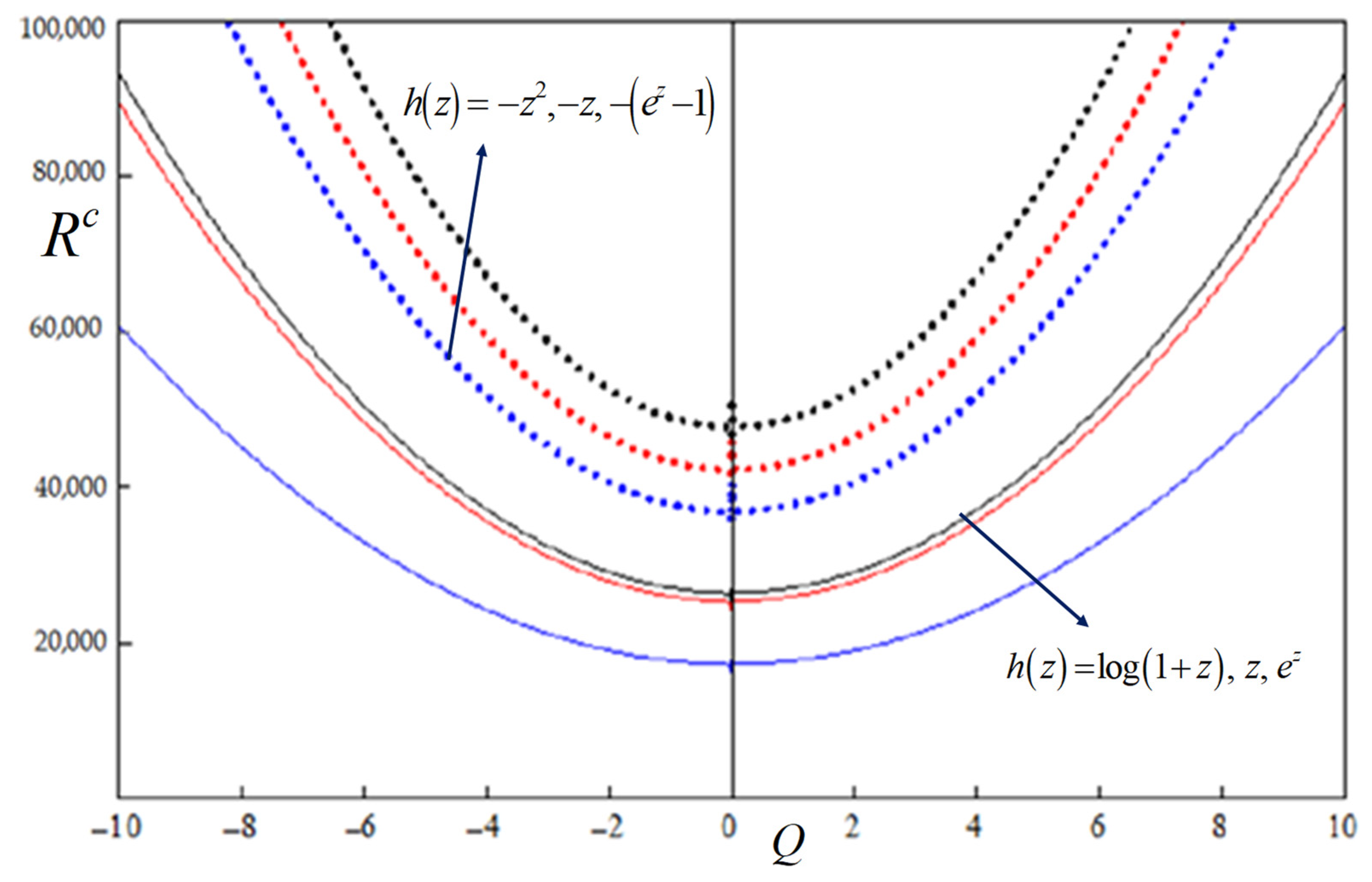
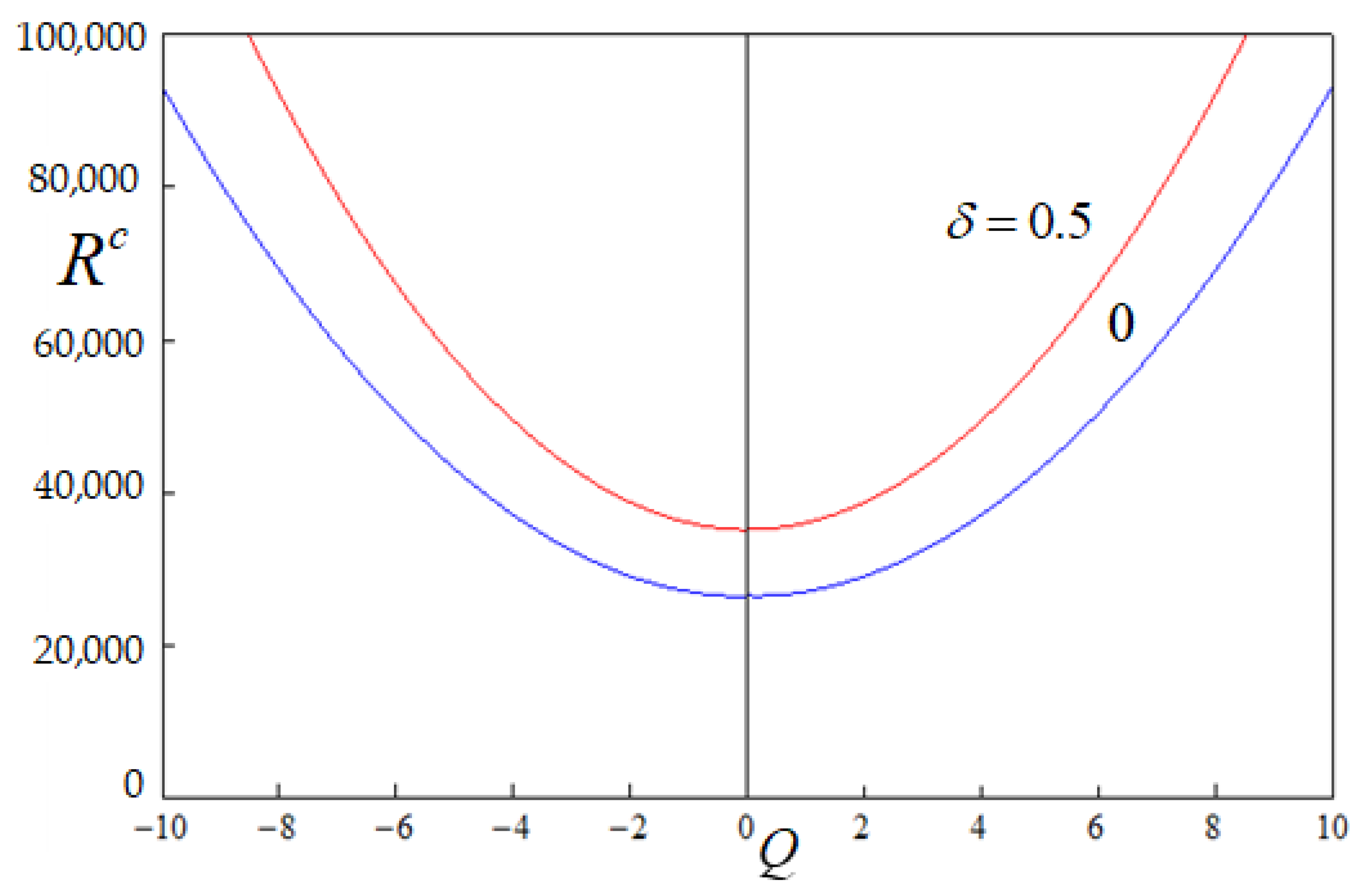
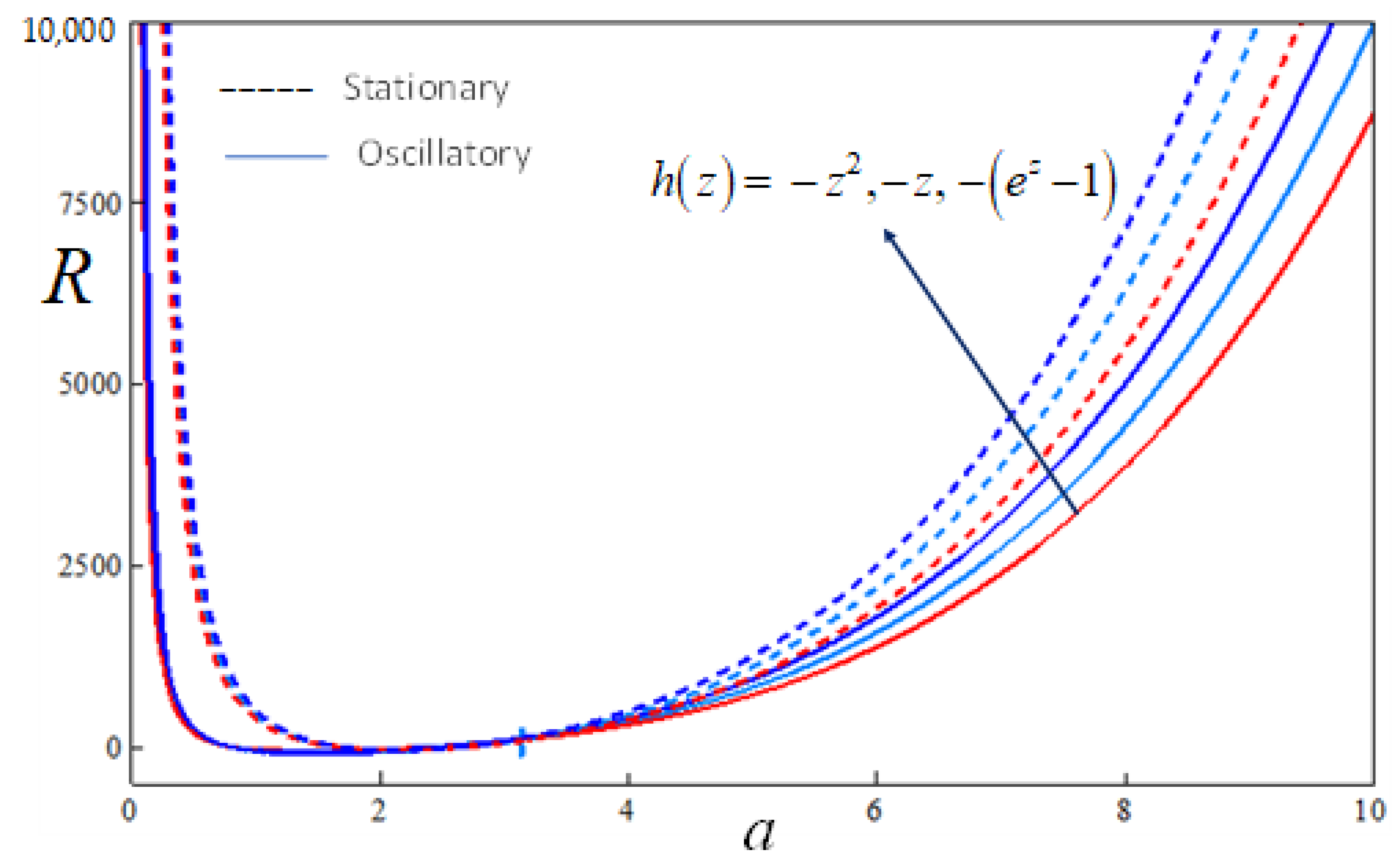
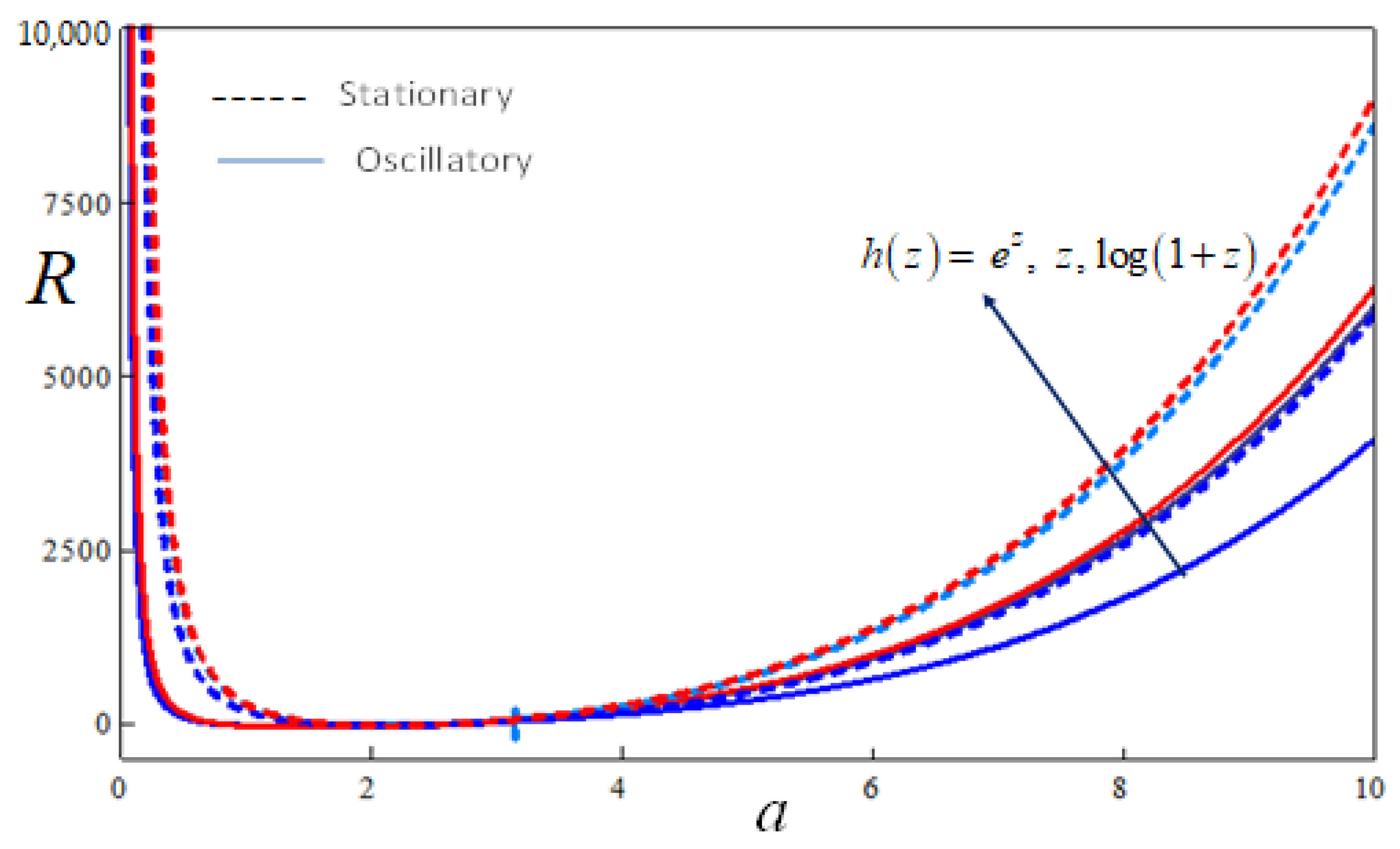
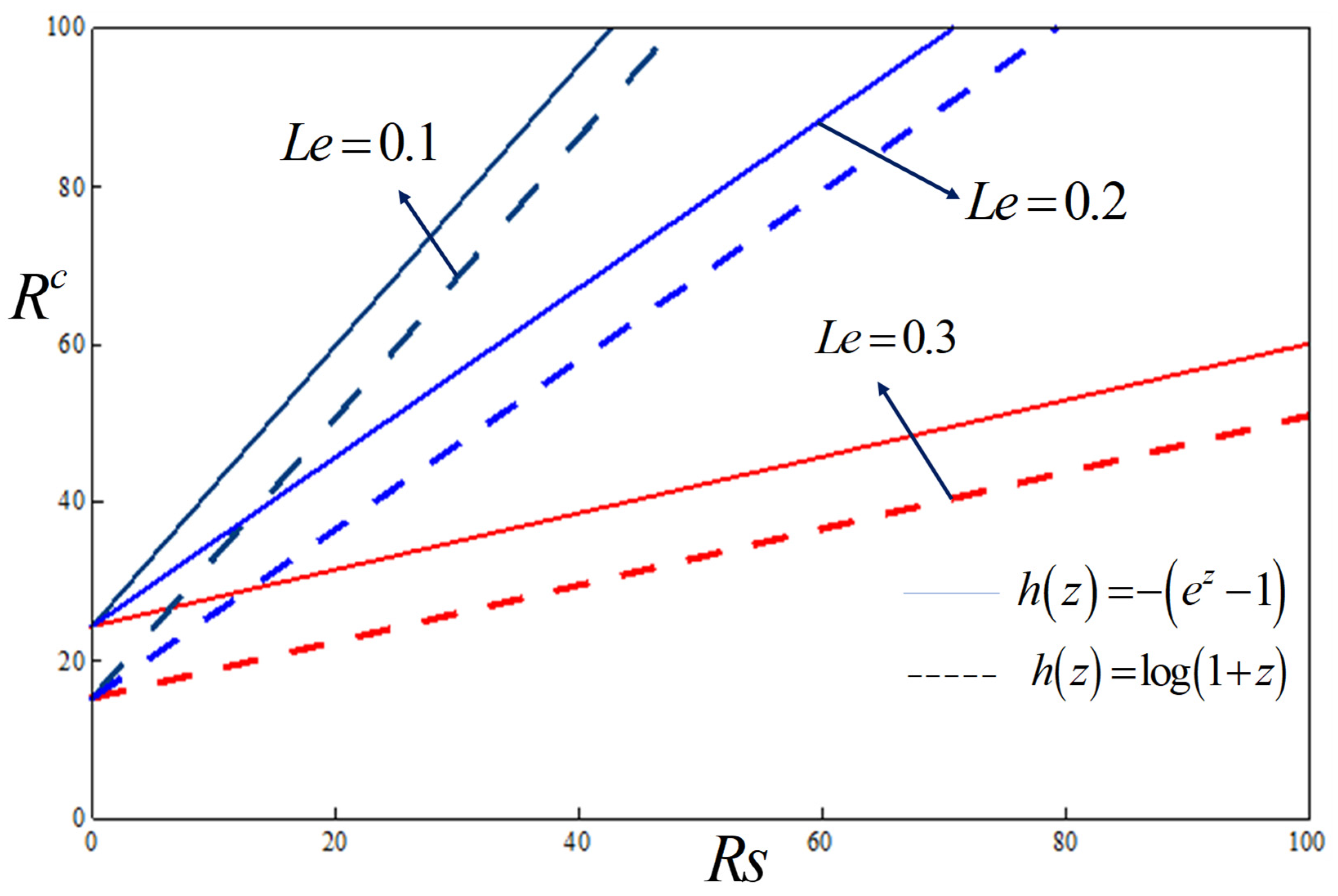
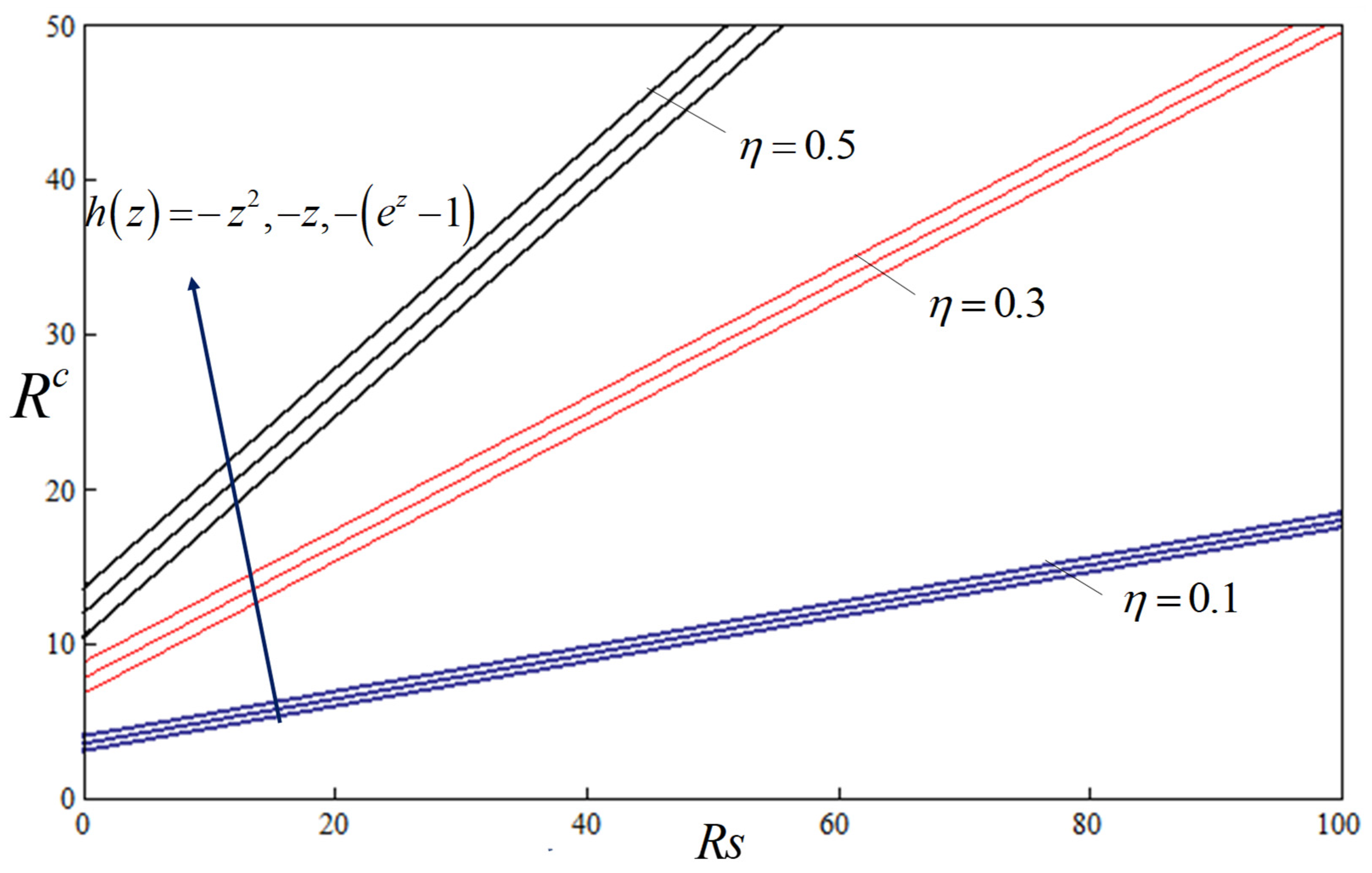
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Horizontal wave number | |
| concentration | |
| differential operator | |
| Darcy number | |
| gravity | |
| variable gravity function | |
| Gravity fluctuations | |
| Permeability | |
| Lewis number | |
| Prandtl number | |
| throughflow parameter | |
| thermal Rayleigh number | |
| solutal Rayleigh number | |
| Critical Rayleigh number | |
| Soret parameter | |
| temperature | |
| velocity vector | |
| amplitude of perturbed vertical velocity | |
| vertical throughflow velocity | |
| mechanical anisotropic parameter | |
| thermal anisotropic parameter | |
| density of the fluid | |
| reference density of the fluid | |
| solutal diffusivity | |
| μ | Fluid viscosity |
| diffusivity | |
| growth rate parameter | |
| gravity parameter | |
| characteristic Concentration difference | |
| characteristic temperature difference |
References
- Castinel, G.; Combarnous, M. Critère d’apparition de la convectiohn naturelle dans une couche poreuse anisotrope. Comptes Rendus Hebdomadaires des Sèances de l’Acadèmie des Sciences. Sèries B 1974, 278, 701–704. [Google Scholar]
- Epherre, J.F. Critere d’ apparition de la convection naturelle dans une couche poreuse anisotrope. Rev. Gen. Therm. 1975, 168, 949–950. [Google Scholar]
- Palm, E.; Tyvand, P.A. Thermal convection in a rotating porous layer. Z. Angew. Math. Phys. 1984, 35, 122–123. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Mahantesh Swamy. The onset of convection in a binary fluid-saturated anisotropic porous layer. Int. J. Therm. Sci. 2010, 49, 867–878. [Google Scholar] [CrossRef]
- Govinder, S. Coriolise effect on the stability of centrifugally driven convection in a rotating anisotropic porous layer subject to gravity. Transp. Porous Media 2007, 69, 55–66. [Google Scholar] [CrossRef]
- Shivakumara, I.S.; Mamatha, A.L.; Ravisha, M. Local thermal non-equilibrium effects on thermal convection in a rotating anisotropic porous layer. Appl. Math. Comput. 2015, 259, 838. [Google Scholar] [CrossRef]
- Degan, G.; Vasseur, P.; Bilgen, E. Convective heat transfer in a vertical anisotropic porous layer. Int. J. Heat Mass Transf. 1995, 38, 1975–1987. [Google Scholar] [CrossRef]
- Payne, L.E.; Rodrigues, J.F.; Straughan, B. Effect of anisotropic permeability on Darcy’s law. Math. Methods Appl. Sci. 2001, 24, 427–438. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Postelnicu, A. The onset of convection in an inclined anisotropic porous layer. Int. J. Heat Mass Transf. 2001, 44, 4127–4138. [Google Scholar] [CrossRef]
- Yadav, D.; Kim, M.C. Theoretical and numerical analyses on the onset and growth of convective instabilities in a horizontal anisotropic porous medium. J. Porous Media 2014, 17, 1061–1074. [Google Scholar] [CrossRef]
- Mahajan, A.; Nandal, R. Anisotropic porous penetrative convection for a local thermal non-equilibrium model with Brinkman effects. Int. J. Heat Mass Transf. 2017, 115, 235–250. [Google Scholar] [CrossRef]
- Alex, S.M.; Patil, R. Effect of variable gravity field on thermal instability in a porous medium with inclined temperature gradient and vertical throughflow. J. Porous Media 2002, 5, 137–147. [Google Scholar] [CrossRef]
- Rionero, S.; Straughan, B. Convection in a porous medium with internal heat source and variable gravity effects. Int. J. Eng. Sci. 1990, 28, 497–503. [Google Scholar] [CrossRef]
- Gangadharaiah, Y.H.; Suma, S.P.; Ananda, K. Variable gravity field and throughflow effects on penetrative convection in a porous layer. Int. J. Comput. Technol. 2013, 5, 172–191. [Google Scholar]
- Suma, S.P.; Gangadharaiah, Y.H.; Indira, R. Effect of throughflow and variable gravity field on thermal convection in a porous layer. Int. J. Eng. Sci. Tech. 2011, 3, 7657–7668. [Google Scholar]
- Gangadharaiah, Y.H.; Nagarathnamma, H.; Hanumagowda, B.N. Combined impact of vertical throughflow and gravity variance on Darcy-Brinkman convection in a porous matrix. Int. J. Thermofluid Sci. Technol. 2021, 8, 080303. [Google Scholar]
- Yadav, D. Numerical investigation of the combined impact of the variable gravity field and throughflow on the onset of convective motion in a porous medium layer. Int. Commun. Heat Mass Transf. 2019, 108, 104274. [Google Scholar] [CrossRef]
- Gangadharaiah, Y.H.; Ananda, K.; Aruna, A.S. Effects of throughflow on thermosolutal penetrative convection in a fluid layer with a variable gravity field. Heat Transf. 2022, 51, 7584–7596. [Google Scholar]
- Mahabaleshwar, U.S.; Basavaraja, D.; Wang, S.; Lorenzini, G.; Lorenzini, E. Convection in a porous medium with variable internal heat source and variable gravity. Int. J. Heat Mass Transf. 2017, 111, 651–656. [Google Scholar] [CrossRef]
- Mahajan, A.; Tripathi, V.K. Effects of spatially varying gravity, temperature and concentration fields on the stability of a chemically reacting fluid layer. J. Eng. Math. 2020, 125, 23–45. [Google Scholar] [CrossRef]
- Yadav, D.; Bhargava, R.; Agrawal, G.S. Boundary and internal heat source effects on the onset of Darcy–Brinkman convection in a porous layer saturated by nanofluid. Int. J. Therm. Sci. 2012, 60, 244–254. [Google Scholar] [CrossRef]
- Yadav, D.; Lee, J.; Cho, H.H. Brinkman convection induced by purely internal heating in a rotating porous medium layer saturated by a nanofluid. Powder Technol. 2015, 286, 592–601. [Google Scholar] [CrossRef]
- Yadav, D. The onset of Darcy-Brinkman convection in a porous medium layer with vertical throughflow and variable gravity field effects. Heat Transf. 2020, 49, 3161–3173. [Google Scholar] [CrossRef]
- Bhadauria, B.S. Double-diffusive convection in a saturated anisotropic porous layer with internal heat source. Transp. Porous Med. 2012, 92, 299–320. [Google Scholar] [CrossRef]
- Siddheshwar, P.G.; Bhadauria, B.S.; Srivastava, A. An analytical study of nonlinear double-diffusive convection in a porous medium under temperature/gravity modulation. Transp. Porous Med. 2012, 91, 585–604. [Google Scholar] [CrossRef]
- Deepika, N.; Anjanna Matta; Lakshmi Narayana, P.A. Effect of throughflow on double diffusive convection in a porous medium with concentration based internal heat source. J. Porous Media 2016, 19, 303–312. [Google Scholar] [CrossRef]
- Gaikwad, S.N.; Rangdal, P.B. Effect of gravity and throughflow on double diffusive convection in a couple stress fluid saturated porous media. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 101, 121–136. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Biradar, B.S. The onset of double-diffusive reaction-convection in an anisotropic porous layer. Phys. Fluids 2011, 23, 064102. [Google Scholar] [CrossRef]





| Present Work | Rionero and Straughan [13] | ||||
|---|---|---|---|---|---|
| 0 | 39.477 | 9.871 | 39.478 | 9.870 | |
| 1 | 77.050 | 10.208 | 77.080 | 10.209 | |
| 1.5 1.8 1.9 | 132.020 189.904 212.286 | 12.313 17.197 19.475 | 132.020 189.908 212.281 | 12.314 17.198 19.470 | |
| 0 | 39.478 | 9.872 | 39.478 | 9.870 | |
| 0.2 | 41.832 | 9.873 | 41.832 | 9.874 | |
| 0.4 0.6 0.81 | 44.455 47.389 50.682 54.390 | 9.885 9.916 9.962 10.035 | 44.455 47.389 50.682 54.390 | 9.887 9.915 9.961 10.034 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeliyur Honnappa, G.; Narayanappa, M.; Udhayakumar, R.; Almarri, B.; Elshenhab, A.M.; Honnappa, N. Darcy–Brinkman Double Diffusive Convection in an Anisotropic Porous Layer with Gravity Fluctuation and Throughflow. Mathematics 2023, 11, 1287. https://doi.org/10.3390/math11061287
Yeliyur Honnappa G, Narayanappa M, Udhayakumar R, Almarri B, Elshenhab AM, Honnappa N. Darcy–Brinkman Double Diffusive Convection in an Anisotropic Porous Layer with Gravity Fluctuation and Throughflow. Mathematics. 2023; 11(6):1287. https://doi.org/10.3390/math11061287
Chicago/Turabian StyleYeliyur Honnappa, Gangadharaiah, Manjunatha Narayanappa, Ramalingam Udhayakumar, Barakah Almarri, Ahmed M. Elshenhab, and Nagarathnamma Honnappa. 2023. "Darcy–Brinkman Double Diffusive Convection in an Anisotropic Porous Layer with Gravity Fluctuation and Throughflow" Mathematics 11, no. 6: 1287. https://doi.org/10.3390/math11061287
APA StyleYeliyur Honnappa, G., Narayanappa, M., Udhayakumar, R., Almarri, B., Elshenhab, A. M., & Honnappa, N. (2023). Darcy–Brinkman Double Diffusive Convection in an Anisotropic Porous Layer with Gravity Fluctuation and Throughflow. Mathematics, 11(6), 1287. https://doi.org/10.3390/math11061287








