Delay-Dependent Stability Region for the Distributed Coordination of Delayed Fractional-Order Multi-Agent Systems

Abstract

Delay and especially delay in the transmission of agents’ information, is one of the most important causes of disruption to achieving consensus in a multi-agent system. This paper deals with achieving consensus in delayed fractional-order multi-agent systems (FOMAS). The aim in the present note is to find the exact maximum allowable delay in a FOMAS with non-uniform delay, i.e., the case in which the interactions between agents are subject to non-identical communication time-delays. By proving a stability theorem, the results available for non-delayed networked fractional-order systems are extended for the case in which interaction links have nonequal communication time-delays. In this extension by considering a time-delay coordination algorithm, necessary and sufficient conditions on the time delays and interaction graph are presented to guarantee the coordination. In addition, the delay-dependent stability region is also obtained. Finally, the dependency of the maximum allowable delay on two parameters, the agent fractional-order and the largest eigenvalue of the graph Laplacian matrix, is exactly determined. Numerical simulation results are given to confirm the proposed methodologies.

1. Introduction

The distributed coordination of multiagent systems has attracted great interest in recent years. Some real-world examples of coordination are the formation of birds or fish, the mass movement of animals, and ant colonies. Additionally, it is known that the distributed coordination of networks of agents has a wide range of applications in different fields such as formation control [1], swarm systems [2], or in distributed sensor networks [3]. Until now, different studies have been carried out in order to investigate the properties of distributed coordination systems (for some samples, see [4,5,6,7]). In this regard, consensus is one of the important aims in the distributed control of multi-operating systems.

In these previous studies, the dynamics of agents are considered to be in the format of integer-order differential equations; meanwhile, it has been recently proven that the exact models of a lot of systems are more precisely described by fractional-order equations. Viscoelastic systems, some kind of energy consumption systems, electromagnetic waves, or even underwater vehicles which are moving in the lentic lakes and so on are all in a fractional-order format [2,8,9,10]. As pioneering studies, refs. [11,12] have studied the distributed coordination problem in the networked fractional-order systems. FOMAS with fractional-order dynamics have been also studied in [2,13,14] as fractional-order swarm systems. In nature, some phenomena can be expressed by the coordination of fractional-order dynamic agents, for example, the chemotaxis behavior of microbes and collective movement of bacteria in lubrications that perspired by themselves [15]. The engineering applications of the distributed coordination of networked fractional-order systems include the coordination of submarines operating in lentic lakes that are composed of microbes, bacteria, and viscoelastic materials, flying vehicles when exposed to the particles in air such as rain or snow, and even ground vehicles when moving on top of sand, muddy roads, or grass [2,16,17].

On the other hand, delay is one of the most important causes of disruption and even instability in a MAS and FOMAS. Delay in the transmission of agent information, which takes place in the communication graph, is very important. Consensus control in the presence of delay or finding the necessary and sufficient conditions for consensus in the presence of delay is a hot topic in this field [18,19,20,21,22]. In [18], the containment control of a FOMAS with and without time-delay was studied, and using the frequency domain, a critical amount for delay was obtained for achieving consensus in the presence of delay. Ref. [19] considered double-integrator fractional-order multi-agent systems with undirected graphs, and a sufficient condition of consensus was then derived along with a maximum tolerable delay. In these papers, a specific and exact stable region for delay was not calculated. Additionally, the exact maximum allowable delay was also not obtained. The consensus problem in a FOMAS with input time-delay is also presented in [20]; they showed that by using intermittent sampled-data control, the necessary and sufficient conditions of consensus were obtained depending on some parameters such as order, input delay, and so on. However, the maximum time-delay or a stable region for stability was not calculated. Using iterative learning control (ILC) and fractional PD control, the convergence condition of consensus in a delayed fractional-order multi-agent system is proposed in [21]. The containment control of FOMAS when the dynamics of agents are different along with bounded time-delays was investigated in [22]. In this reference, it is shown that as long as a follower has a path in the topology graph from at least one leader, the followers will finally arrive in a convex hall around stationary leaders [22]. Neural adaptive consensus in a fractional-order nonlinear MAS with both fault and delay was also studied in [23]. They found that in order to deal with the severe faults, an adaptive controller needs to be designed; regarding time-varying delays, two methods are presented based on Lyapunov and Lyapunov Krasovskii functions. Recently, in [24], the leader–follower non-fragile consensus in nonlinear fractional-order MAS in the presence of state time-delay and uncertain parameters was dealt. In this paper, the order-dependent sufficient condition for consensus protocol was obtained.

Most of the necessary and sufficient conditions for consensus in a delayed FOMAS which have appeared in the literature and depend upon some conservative assumptions do not explicitly provide the maximum allowable amount of delay or do not provide a specific stability region.

Notably, in the present study, the aim is to find the exact allowable delay in a FOMAS with non-uniform delay, i.e., the case in which the interactions between agents are subject to non-identical communication time-delays. Like other related works, Ref. [25] obtained the necessary and sufficient conditions on the values of time-delay using a frequency domain approach. However, the point is that the delay-dependent stability region is not obtained, and the maximum allowable delay is not explicitly calculated.

The most important innovations of the present paper compared to the previous studies can be highlighted as follows:

(1)

Obtaining the exact maximum allowable delay at the stability boundary of FOMAS (obtaining the sufficient and necessary condition of consensus in the presence of delay) and comparing with the counterpart integer-order case.

(2)

Providing a new drawing method for calculating the boundary of stability in the presence of delay.

(3)

Drawing the delay-dependent stability region in the FOMAS system.

(4)

Determining the exact dependence of the maximum allowable delay on two parameters: 1—the fractional order of agent models, and 2—the largest eigenvalue of the graph Laplacian matrix among agents.

This paper is organized as follows: The problem formulation is given in Section 2. Section 3 presents the main results of the paper which include the stability analysis of a coordination algorithm for networked fractional-order systems in the presence of time delays. Simulation results in Section 4 are given to confirm the analytical results. Finally, the conclusions in Section 5 close the paper.

2. Problem Formulation

Consider a network of $N$ agents whose dynamics are described by

$$D_t^{\alpha }{x}_i(t)=u_i(t)\hspace{1em}\hspace{1em}\hspace{1em}i=1,2,\dots ,N$$

(1)

where $\alpha \in (0,1]$, $x_i\in R$ is the pseudo state variable [13,16], $u_i\in R$ is the input variable, and $D_t^{\alpha }$ denotes the Caputo fractional derivative operator, defined as follows [26]:

$$D_t^{\alpha }f(t)=\frac{1}{\Gamma (\alpha -\lceil \alpha \rceil )}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{f^{(\lceil \alpha \rceil )}(\tau )}{{(t-\tau )}^{\alpha -\lceil \alpha \rceil +1}}d\tau ,\hspace{1em}\hspace{1em}0}<\alpha \notin n$$

(2)

where $n-1<\alpha <n$ is the order of Caputo fractional derivative, $t$ is time, $\tau$ stands for the Caputo integration variable, $\Gamma \left(x\right)$ denotes the well-known Euler’s Gamma function and notation; $\lceil \alpha \rceil$ maps $\alpha$ to the least integer that is greater than or equal to $\alpha$ [26,27,28].

The communication among agents is expressed by a weighted undirected and simple graph $G$ of order $N$ such that each agent is corresponding to a vertex. Additionally, the value of the arc weight of graph $G$ between ith and jth agents, denoted by $w_{ij}\ge 0$, can be considered as a measure for the strength of the information link. Such a graph can be denoted by its adjacency matrix $W$, i.e.,

$$G:W=\left[\begin{array}{ccc}{w}_{11}& \dots & w_{1N}\\ ⋮& \ddots & ⋮\\ w_{N1}& \cdots & w_{NN}\end{array}\right],$$

which is a symmetric matrix. In this paper, we use the following communication protocol:

$$u_i(t)={\displaystyle \sum _{j\in N_i}{w}_{ij}\left\{[x_j(t-{\tau }_j)-{\delta }_j]-[x_i(t-{\tau }_i)-{\delta }_i]\right\}\hspace{1em}\hspace{1em}{\tau }_{i,j}>0},$$

(3)

which its non-delayed version has been considered in [11]. In Equation (3), $w_{ij}$ is the $(i,j)$th entry of the adjacency matrix $W$, $N_i$ is the neighbor set of agent $i$, ${\tau }_i$ denotes the communication time-delay, and ${\delta }_i$ is a constant. By defining ${\delta }_{ij}={\delta }_i-{\delta }_j$, the objective of the algorithm is to guarantee coordination, i.e., $x_i(t)-x_j(t)\to {\delta }_{ij}$ where $t\to \infty$ for any initial conditions $x_i(0)$ and $x_j(0)$. Using Equation (3), the network dynamics in Equation (1) can be written as

$$D_t^{\alpha }{\tilde{x}}_i(t)={\displaystyle \sum _{j\in N_i}{w}_{ij}\left\{[{\tilde{x}}_j(t-{\tau }_j)]-[{\tilde{x}}_i(t-{\tau }_i)]\right\}}$$

(4)

where $i=1,2,\dots ,N$ and ${\tilde{x}}_i(t)=x_i(t)-{\delta }_i$. If the pseudo state vector of agents is defined as $\tilde{X}(t)={[{\tilde{x}}_1(t),\dots ,{\tilde{x}}_N(t)]}^T$, then the system dynamics in Equation (4) can be expressed as

$$D_t^{\alpha }\tilde{X}(t)=-L\tilde{X}(t-\tau )$$

(5)

where $\tilde{X}(t-\tau )={[{\tilde{x}}_1(t-{\tau }_1),\dots ,{\tilde{x}}_N(t-{\tau }_N)]}^T$ and $L=L(G)$ is the Laplacian matrix of graph $G$ [27]. The following lemma deals with the properties of the Laplacian matrix.

Lemma 1. 

The Laplacian matrix $L$ of the undirected graph $G$ has exactly a single zero eigenvalue with the corresponding eigenvector $\varphi ={[11,\dots ,1]}^T$ if, and only if, $G$ is connected. Moreover, in this case, the other eigenvalues of $L$ are positive real numbers [13,14].

Remark 1. 

As a real application of the fractional-order equation of a multi-agent system similar to Equation (4), we can refer to the formation of aerial vehicles in Figure 1, of which fly in snowy or rainy weather and communicate with each other like graph $G_a$ in Figure 1. The motion of these agents is a real application of the fractional-order swarm system [2]. The aim here is the consensus on the orientation axis of these aerial vehicles in a two-dimensional plane. In this case, the orientation of each vehicle depends on the difference in its orientation with his neighbors. Therefore, the orientation of each agent is described via the following fractional-order model [2]:

$$D_t^{0.8}{x}_i=A_i{x}_i+F_i{\displaystyle \sum _{j=1}^3{w}_{ij}((x_j-{\tau }_j)-(x_i-{\tau }_i)})\hspace{1em}\hspace{1em}\hspace{1em}i=1,2,3$$

where  $x_i=[{\overrightarrow{x}}_i,{\overrightarrow{y}}_i]$ stands for the orientation in  $X-Y$ plane (Figure 1).

Figure 1. Triangular formation of aerial vehicles and graph $G_a$, which indicates the communications among these agents [2].

As other applications of FOMAS, we can refer to the underwater vehicles which are moving in the lentic lakes, mobile robots when they are moving on sandy and muddy ground, or even inverted pendulums that are interconnected by coupling elements and linear springs (Figure 2), in which the equation of the angle of pendulums is written by $D_t^{0.85}{\phi }_i=a_i{\phi }_i+{\displaystyle \sum _{j=1}^4{\sigma }_{ij}({\phi }_j-{\phi }_i)}$ for $i=1,2,\dots ,4$. These are all some real applications of FOMAS, of which are described by Equations (1)–(4).

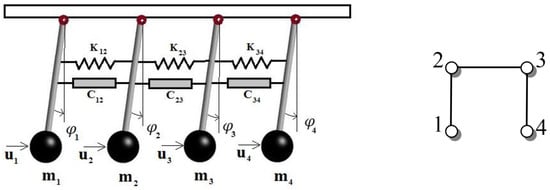
Figure 2. A multi-inverted pendulum system with fractional-order creep elements and the graph that shows the connection among them [2].

3. Stability Analysis of the Coordination Algorithm

Let $J$ denote the Jordan canonical form of the Laplacian matrix $L$ with eigenvalues ${\lambda }_1=0,{\lambda }_2,\dots ,{\lambda }_N\in R^{+}$. This means that the non-singular matrix $T$ is found such that

$$J=T^{-1}LT=\left[\begin{array}{cccc}{\Lambda }_1& 0& \cdots & 0\\ 0& {\Lambda }_2& \cdots & 0\\ \cdots & \cdots & \ddots & ⋮\\ 0& 0& \cdots & {\Lambda }_m\end{array}\right]$$

where ${\Lambda }_1,{\Lambda }_2,\dots ,$ and ${\Lambda }_m$ are standard Jordan blocks. If $Y(t)=T^{-1}\tilde{X}(t)$, Equation (5) is transformed to

$$D_t^{\alpha }Y(t)=-JY(t-\tau )$$

(6)

note that $Y(t-\tau )={[y_1(t-{\tau }_1),\dots ,y_N(t-{\tau }_N)]}^T$ and each Jordan block is in the form $\left[\begin{array}{cccc}{\lambda }_i& 1& \cdots & 0\\ 0& {\lambda }_i& \cdots & 0\\ ⋮& ⋮& \ddots & \\ 0& 0& \cdots & {\lambda }_i\end{array}\right]$ where ${\lambda }_i$ is an eigenvalue of the Laplacian matrix $L$. By considering this point, it is deduced that Equation (6) can be decoupled into $n$ fractional-order differential equations having one of the following forms:

$$D_t^{\alpha }{y}_i(t)=-{\lambda }_i{y}_i(t-{\tau }_i)$$

(7)

or

$$D_t^{\alpha }{y}_i(t)=-{\lambda }_i{y}_i(t-{\tau }_i)-y_{i+1}(t-{\tau }_{i+1}),$$

(8)

where $Y(t)={\left[\begin{array}{ccc}{y}_1(t)& \cdots & y_n(t)\end{array}\right]}^T$. If ${\tau }_{i,i+1}=0$, Equations (7) and (8) are converted to Equations (9) and (10) in [11]. Before deriving the conditions guaranteeing coordination, we need to express and prove a theorem on the stability of the class of fractional-order differential equations described by Equation (7).

Theorem 1. 

The time-delay fractional-order system (7), where $0\le {\lambda }_i\in R$ has the following properties:

(1) 

If ${\lambda }_i>0$ and $\tau \in [0,{\tau }^{*})$ where ${\tau }^{*}=\frac{\pi }{2}(2-\alpha ){\lambda }_i{}^{(-\frac{1}{\alpha })}$, this system is stable and $\underset{t\to \infty }{\lim }{y}_i(t)=0$.

(2) 

If ${\lambda }_i>0$ and $\tau >{\tau }^{*}$ where ${\tau }^{*}=\frac{\pi }{2}(2-\alpha ){\lambda }_i{}^{(-\frac{1}{\alpha })}$, this system is unstable.

(3) 

If ${\lambda }_i=0$, $y_i(t)=y_i(0)$ for all $t\ge 0$.

Proof. 

Proof of Properties 1 and 2: Taking the Laplace transform from both sides of Equation (7) results in

$$L(y_i(t))=\frac{s^{\alpha -1}}{s^{\alpha }+{\lambda }_i{e}^{-{\tau }_{i}s}}{y}_i(0^{-})$$

(9)

where $\alpha \in (0,1]$. According to Equation (9), system in Equation (7) is stable if all roots of the equation $f(s)=0$ where

$$f(s)=s^{\alpha }+{\lambda }_i{e}^{-{\tau }_{i}s}$$

(10)

are in the region $C^{-}=\left\{s\in C|\mathrm{Re}(s)<0\right\}$ where $C$ stands for the complex number set [28]. Define $h_i={\lambda }_i{\tau }_i{}^{\alpha }$ and suppose that $\tau ={\max }_{i=1,\dots ,N}{\tau }_i$. Now, given that function $h(\tau )=\lambda {\tau }^{\alpha }$ is an ascending function relative to $\tau$, by variable changing $\tau s\to s$, equation $f(s)=0$ is converted to equation $g(s)=0$, where

$$g(s)=s^{\alpha }+h_i{e}^{-s}.$$

(11)

□

Clearly, all roots of equation $f(s)=0$ are in the region $C^{-}$ if, and only if, all roots of equation $g(s)=0$ are placed in such a region. All roots of equation $g(s)=0$ are in the region $C^{-}$, if it has no root in the following region:

$$D_R=\left\{s\in C|\left|s\right|\le R\&-\frac{\pi }{2}\le \arg (s)\le \frac{\pi }{2}\right\},$$

(12)

when $R\to \infty$ (Figure 3). The boundary of the semicircle $D_R$, denoted by $C_R$, consists of two parts:

$$C_R^1=\left\{s\in C|\left|s\right|=R\&-\frac{\pi }{2}\le \arg (s)\le \frac{\pi }{2}\right\}$$

(13)

and

$$C_R^2=\left\{s\in C|s=j\omega \&-R\le \omega \le R\right\}.$$

(14)

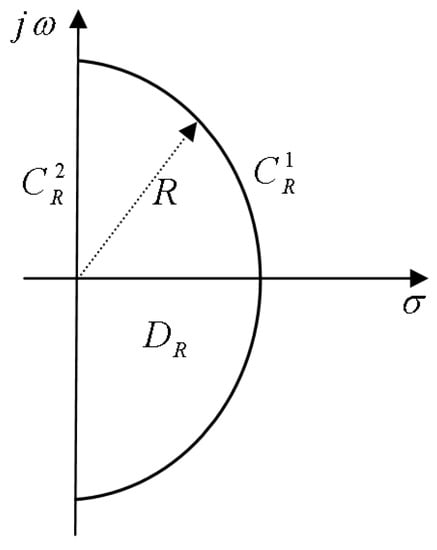
Figure 3. Region $D_R$ and its boundary in the complex plane.

By considering the approach presented in [29] which has been constructed based on the Cauchy’s argument principle, we know that equation $g(s)=0$ does not have any roots in the region $D_R$ if $g(C_R)$ does not encircle the origin. If $R\to \infty$, the image of part $C_R^1$ under mapping $g(s)$ is like an arch that is described by

$$g(C_R^1)=\left\{s\in C|\left|s\right|=R^{\alpha },-\alpha \frac{\pi }{2}<\arg (s)<\alpha \frac{\pi }{2}\right\}.$$

(15)

If system (7) is stable for $\tau <{\tau }^{*}$ and is unstable for $\tau >{\tau }^{*}$, then $g_{h_i^{*}}(C_R^2)$ should pass from the origin where $h_i^{*}={\lambda }_i{\left({\tau }^{*}\right)}^{\alpha }$. In this case, $\omega >0$ is found such that

$${\omega }^{\alpha }\cos \left(\alpha \frac{\pi }{2}\right)+h_i^{*}\cos (\omega )=0$$

(16)

and

$${\omega }^{\alpha }\sin \left(\alpha \frac{\pi }{2}\right)-h_i^{*}\sin (\omega )=0.$$

(17)

By multiplying both sides of Equations (16) and (17) by $\sin (\omega )$ and $\cos (\omega )$, respectively, and then adding the resulting equations together, one can easily obtain $\omega$ as

$$\omega =k\pi -\alpha \frac{\pi }{2},$$

(18)

where $k$ is an integer. Since $\omega >0$ and $0<\alpha \le 1$, $k$ should be a positive integer. By substituting $\omega$ from Equation (17) in Equation (16), it is deduced that

$${\left(k\pi -\alpha \frac{\pi }{2}\right)}^{\alpha }=h_i^{*}{\left(-1\right)}^{k+1}$$

(19)

Equation (19) implies that $k$ should be an odd positive integer. Therefore, some boundaries described by

$${\left(k\pi -\alpha \frac{\pi }{2}\right)}^{\alpha }=h_i^{},k=1,3,5,\cdots$$

(20)

can specify the stability region for system Equation (7) in the $\alpha -h_i$ plane.

From the mentioned discussions, we know that for each pair $(\alpha -h_i)$ settled in the stability region, $g(C_R)$ does not encircle the origin where $R\to \infty$. Hence, selecting a sample point in each region in Figure 4 and checking the encirclements of $g(C_R)$ around the origin lead us to find the stability region. It can be easily verified that for each point settled in the southern region in Figure 4 (the region between the horizontal axis and the curve specified by Equation (20) where $k=1$), $g(C_R)$ does not encircle the origin where $R\to \infty$ (see the sample mapping shown in Figure 5a). Additionally, if the pair $(\alpha -h_i)$ placed on the boundary of this region, $g(C_R)$ passes from the origin (see the sample mapping shown in Figure 5b). Moreover, if the pair $(\alpha -h_i)$ is in the region between boundaries Equation (20) for $k=1$ and $k=3$, $g(C_R)$ encircle the origin twice (see the sample mapping shown in Figure 5c). For the region between boundaries given by $k=3$ and $k=5$, the number of encirclements will be 4 (see the sample mapping shown in Figure 5d), and for the next regions, the number of encirclements will be increased. According to this discussion, the stability boundary can be written as follows (Figure 6):

$${\left(\pi -\alpha \frac{\pi }{2}\right)}^{\alpha }=h_i$$

(21)

since $h_i={\lambda }_i{\tau }^{\alpha }$, system (7) is stable if

$$\tau <\frac{\pi }{2}(2-\alpha ){\lambda }_i{}^{(-\frac{1}{\alpha })}$$

(22)

and is uneatable if

$$\tau >\frac{\pi }{2}(2-\alpha ){\lambda }_i{}^{(-\frac{1}{\alpha })}.$$

(23)

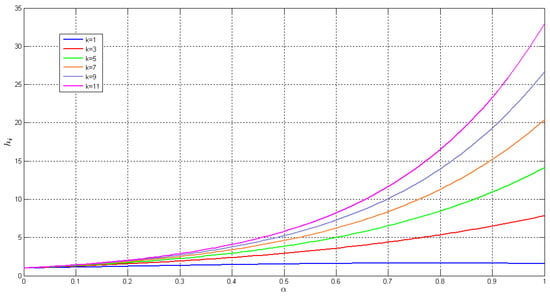
Figure 4. Boundaries specified by Equation (19) for different values of $k$ in the $\alpha -h_i$ plane.

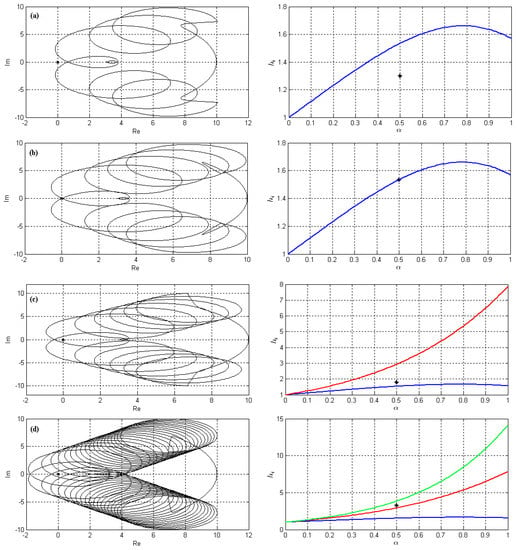
Figure 5. The image of $C_R$ under mapping $g(s)$ (right figures) where $R=100$ for different pairs $(\alpha -h_i)$ (a) $(\alpha -h_i)=(0.5,1.3)$, (b) $(\alpha -h_i)=(0.5,1.535)$, (c) $(\alpha -h_i)=(0.5,1.8)$, (d) $(\alpha -h_i)=(0.5,3)$ (the place of these pairs are shown in the left figures).

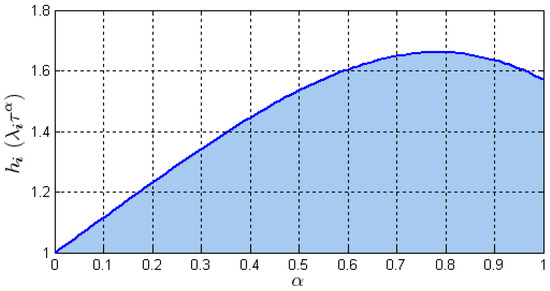
Figure 6. Stability region for system (7).

Proof of Property 3: The proof of Property 3 is the same as the proof of Property 2 in Lemma 2 of [11] and follows from [30].

The following lemma is an extension for Lemma 3 which has been presented in [11] for the case $\tau =0$.

Lemma 2. 

In fractional differential Equation (8), if ${\lambda }_i>0$,$\alpha \in (0,1]$,${\tau }_i\in [0,{\tau }^{*})$ where ${\tau }^{*}=\frac{\pi }{2}(2-\alpha ){\lambda }_i{}^{(-\frac{1}{\alpha })}$, and $y_{i+1}(t)$ is a continuous function with condition $\underset{t\to \infty }{\lim }{y}_{i+1}(t)=0$, then $\underset{t\to \infty }{\lim }{y}_i(t)=0$.

Proof. 

Taking the Laplace transform from both sides of Equation (8) brings about

$$L(y_i(t))=\frac{y_i(0^{-})s^{\alpha -1}-e^{-{\tau }_{i+1}s}L(y_{i+1}(t))}{s^{\alpha }+{\lambda }_i{e}^{-{\tau }_{i}s}},$$

(24)

where $\alpha \in (0,1]$. According to the proof of Property 1 in Theorem 1, we know that the solutions of equation $s^{\alpha }+{\lambda }_i{e}^{-{\tau }_{i}s}=0$ are located in the open left half of the plane if ${\lambda }_i>0$ and $\tau \in [0,{\tau }^{*})$ where ${\tau }^{*}=\frac{\pi }{2}(2-\alpha ){\lambda }_{\max }{}^{\left(-\frac{1}{\alpha }\right)}$. Hence, according to the final value theorem, Equation (24) results in

$$\underset{t\to \infty }{\lim }{y}_i(t)=\underset{s\to 0}{\lim }\frac{y_i(0^{-})s^{\alpha }-e^{-{\tau }_{i+1}s}sL(y_{i+1}(t))}{s^{\alpha }+{\lambda }_i{e}^{-{\tau }_{i}s}}.$$

Since $\underset{t\to \infty }{\lim }{y}_{i+1}(t)=0$, we have $\underset{s\to \infty }{\lim }sL(y_{i+1}(t))=0$. Therefore, from the above equality, it is deduced that $\underset{t\to \infty }{\lim }{y}_i(t)=0$. □

Based on Theorem 1 and Lemma 2, we can find conditions on the time-delay ${\tau }_i$ and the interaction graph, such that coordination is guaranteed. These conditions are presented in the following theorem.

The following Theorem provides the maximum allowable delay to achieve consensus in FOMAS in Equation (1) with protocol in Equation (3).

Theorem 2. 

Consider the networked FOMAS in Equation (1) with communication in Equation (3). In addition, assume that the fixed interaction graph $G$ is undirected and connected. In this case, coordination is achieved if ${\tau }_i\in [0,{\tau }^{*})$ where ${\tau }^{*}=\frac{\pi }{2}(2-\alpha ){\lambda }_{\max }{}^{\left(-\frac{1}{\alpha }\right)}$ and ${\lambda }_{\max }$ denotes the maximum eigenvalue of the Laplacian matrix $L$.

Proof. 

Since the interaction graph is undirected and connected, from Lemma 1, it is deduced that $L$ has a simple zero eigenvalue. Additionally, the other eigenvalues of $L$ are real and positive. Without a loss of generality, assume that ${\lambda }_1=0$, and $0<{\lambda }_2\le \cdots \le {\lambda }_{n-1}\le {\lambda }_n$. For ${\lambda }_1=0$, according to Property 3 in Theorem 1, we have $y_1(t)=y_1(0)$. Moreover, since assumption $0<{\lambda }_2\le \cdots \le {\lambda }_{n-1}\le {\lambda }_n$ results in ${\tau }^{*}=\frac{\pi }{2}(2-\alpha ){\lambda }_n{}^{\left(-\frac{1}{\alpha }\right)}\le \frac{\pi }{2}(2-\alpha ){\lambda }_{n-1}{}^{\left(-\frac{1}{\alpha }\right)}\le \cdots \le \frac{\pi }{2}(2-\alpha ){\lambda }_1{}^{\left(-\frac{1}{\alpha }\right)}$ from Property 1 in Theorem 1 or Lemma 2, it is concluded that $\underset{t\to \infty }{\lim }{y}_i(t)=0$ for $i=2,\dots ,n$. From these results, we have $\underset{t\to \infty }{\lim }Y(t)={[y_1(0),0,\dots ,0]}^T$. The rest of the proof is similar to the proof of Theorem 1 in [11] and is omitted here. □

Remark 2. 

In the case $\alpha =1$ and ${\tau }_1=\dots ={\tau }_N$ (the integer-order case with uniform communication time-delay), Theorem 2 concludes that the consensus is achieved if $\tau \in [0,{\tau }^{*})$ where ${\tau }^{*}=\frac{\pi }{2{\lambda }_{\max }}$. This result is exactly the same as what has been previously presented in Theorem 10 of [31] for the distributed coordination of networks of integer-order agents with uniform time-delay, of which was firstly presented in [31] by Olfati Saber et al.

Consider the maximum time-delay in Theorem 2, i.e., ${\tau }^{*}=\frac{\pi }{2}(2-\alpha ){\lambda }_{\max }{}^{\left(-\frac{1}{\alpha }\right)}$. It can be easily verified that $\frac{\partial {\tau }^{*}}{\partial \alpha }<0$ if $0<{\lambda }_{\max }\le 1$ and $\alpha \in (0,1]$, and $\frac{\partial {\tau }^{*}}{\partial \alpha }>0$ if ${\lambda }_{\max }>e=2.7183$ and $\alpha \in (0,1]$. Additionally, if $1<{\lambda }_{\max }\le e$, then $\frac{\partial {\tau }^{*}}{\partial \alpha }>0$ ($\frac{\partial {\tau }^{*}}{\partial \alpha }<0$) for $\alpha \in (0,{\alpha }_0)$ ($\alpha \in ({\alpha }_0,1]$) where

$${\alpha }_0=\frac{-\ln ({\lambda }_{\max })+\sqrt{\ln {({\lambda }_{\max })}^2+8\ln ({\lambda }_{\max })}}{2}.$$

(25)

Therefore, the following corollary is resulted from Theorem 2.

Corollary 1. 

If ${\lambda }_{\max }$ denotes the maximum eigenvalue of the Laplacian matrix $L$ and $\alpha \in (0,1]$ is the order of the networked fractional-order system considered in Theorem 2, the maximum time-delay resulting in coordination (i.e., ${\tau }^{*}$) has the following properties:

(1) 

If $0<{\lambda }_{\max }\le 1$, the larger values of $\alpha$ results in the smaller allowed maximum time-delay for coordination.

(2) 

If ${\lambda }_{\max }\ge e=2.7183$, the lower values of $\alpha$ results in the smaller allowed maximum time-delay for coordination.

(3) 

If $1<{\lambda }_{\max }<e$, the allowed maximum time-delay for coordination will be maximal if the order of system equals Equation (25).

4. Numerical Simulations

In this section, the previous section results are verified by numerical simulations. To this end, consider the following networked fractional-order system with five agents and constant time-delay.

$$D_t^{0.8}{x}_i(t)={\displaystyle \sum _{j\in N_i}{w}_{ij}\left\{[x_j(t-{\tau }_j)-{\delta }_j]-[x_i(t-{\tau }_i)-{\delta }_i]\right\},i=1,\mathrm{\dots 5}}$$

(26)

Graph $G_a$ expressing the communication among these agents is shown in Figure 7. Additionally, the adjacency matrix of this graph is considered as

$$W=\left[\begin{array}{ccccc}0& 0.5& 0& 0& 0\\ 0.5& 0& 0.4& 0& 0.75\\ 0& 0.4& 0& 0.3& 0.6\\ 0& 0& 0.3& 0& 0.6\\ 0& 0.75& 0.6& 0.6& 0\end{array}\right].$$

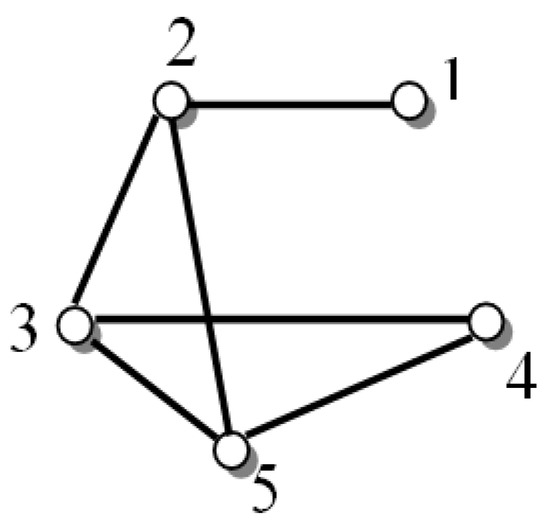
Figure 7. Graph $G_a$ in a numerical example of Section 4.

In this case, the eigenvalues of the Laplacian matrix for the mentioned graph are as follows:

$$\lambda (G_a)=\{0,0.431,1.219,1.903,2.747\}$$

We have used the nid simulation block in the integer matlab toolbox (fractional control toolbox for MatLab) to implement fractional derivatives such as $D^{0.8}$ [32]. Here, for simplicity, we have chosen ${\delta }_i=0,\hspace{1em}i=1,\dots ,5$, i.e., $X(t)=\tilde{X}(t)={[x_1(t),\dots ,x_5(t)]}^T$. According to Theorem 2, coordination is achieved if the time-delay ${\tau }_i$ is less than $0.53$. This point is confirmed by numerical simulation results. Like some samples, Figure 8 shows the state trajectories of the considered fractional-order network for ${\tau }_i=0$, ${\tau }_i=0.4$, ${\tau }_i=0.5$ and ${\tau }_i=0.56$ for $i=1,\dots ,5$.

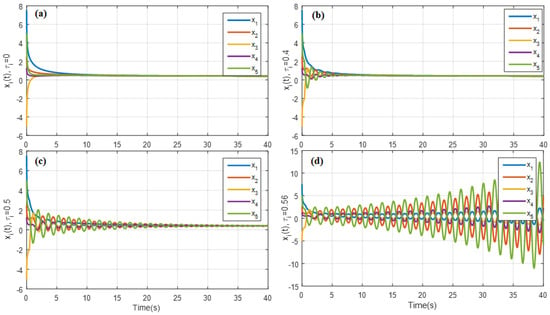
Figure 8. Trajectories of agents in the numerical example of Section 4 for different time delays. (a) ${\tau }_i=0$, (b) ${\tau }_i=0.4$, (c) ${\tau }_i=0.5$, and (d) ${\tau }_i=0.56$.

As we can see, coordination is achieved in Figure 8a–c in which the time-delay τ_i is less than the maximum admissible time-delay in the network that is τ* = 0.53. The time-delay in Figure 8d is more than τ*, and therefore, the system is unstable according to Theorem 2. It can be concluded from Figure 8 that when the amount of communication delay increases and exceeds the permissible limit, the location information of each agent is provided to the neighboring agents with a long delay, causing instability and divergent fluctuations in the agents.

Remark 3. 

It is worth mentioning that the detailed analysis of the behavior and the trajectory of each agent in Figure 8 is not simple due to the different values of communication delays for each agent and the different weights of the communication graph for each agent. However, it can be concluded from Figure 8 that agents 1 and 4, who have less communication with others, are less affected by the communication delay and, as a result, have less fluctuations and oscillations as we can see in all four figures in Figure 8.

5. Conclusions

The distributed coordination of networked fractional-order multi-agent systems in the presence of non-uniform communication time-delays was studied in this paper. In this study, the necessary and sufficient conditions to achieve coordination in the presence of communication time-delays were presented. Based on these conditions, the maximum acceptable delay to guarantee the coordination was found. A delay-dependent stable region was also provided, which is based on the maximum eigenvalue of Laplacian matrix of the graph and fractional order of the system. Extending the paper results to FOMAS with directed graphs, considering the high-order networked fractional-order systems (second-order, third-order, or even systems such as point mass, of which is second-order integer-order dynamics with a fractional-order damping), and finally considering the interaction links with time-varying non-equal communication time-delays can be considered to be interesting topics for future research.