(Iq)–Stability and Uniform Convergence of the Solutions of Singularly Perturbed Boundary Value Problems
Abstract
1. Introduction
2. Boundary Value Problems
- (semilinear problem);
- (quasilinear problem);
- (quadratic problem) [12];
- (k)
- there is a constant such that for
- (kk)
- where A and B are non-negative functions bounded for and (but L need not be an integer). Denotefor
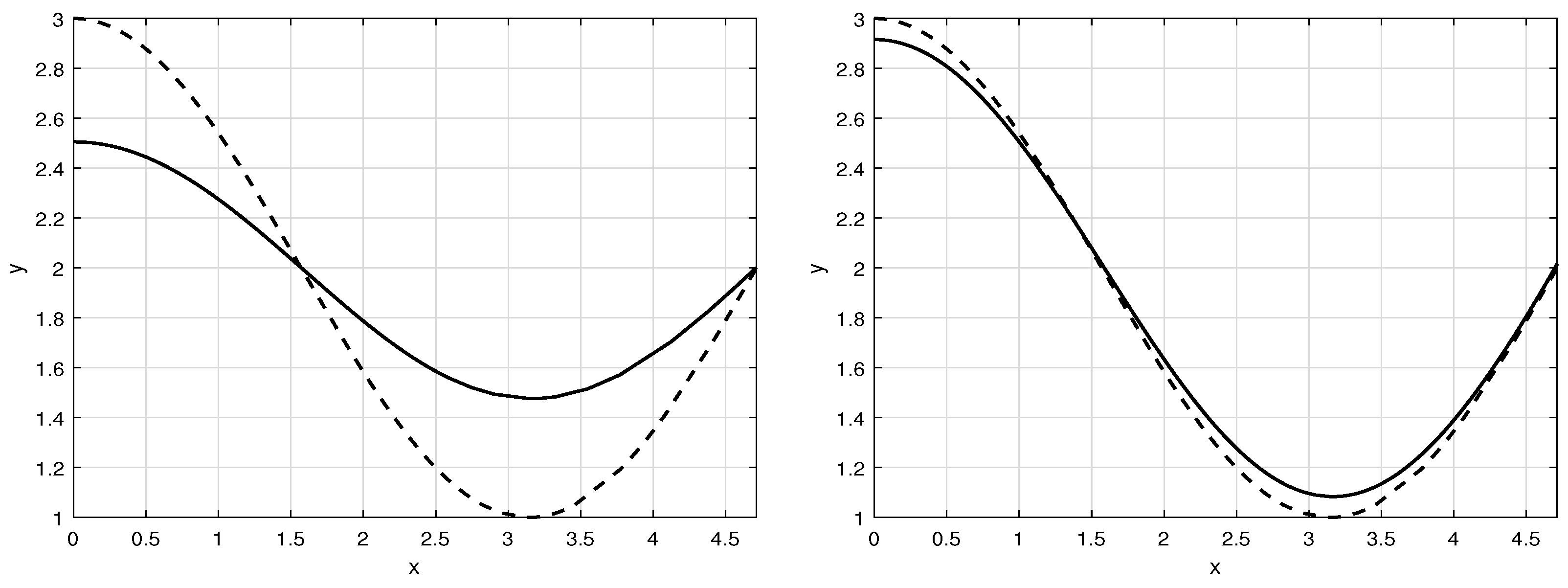
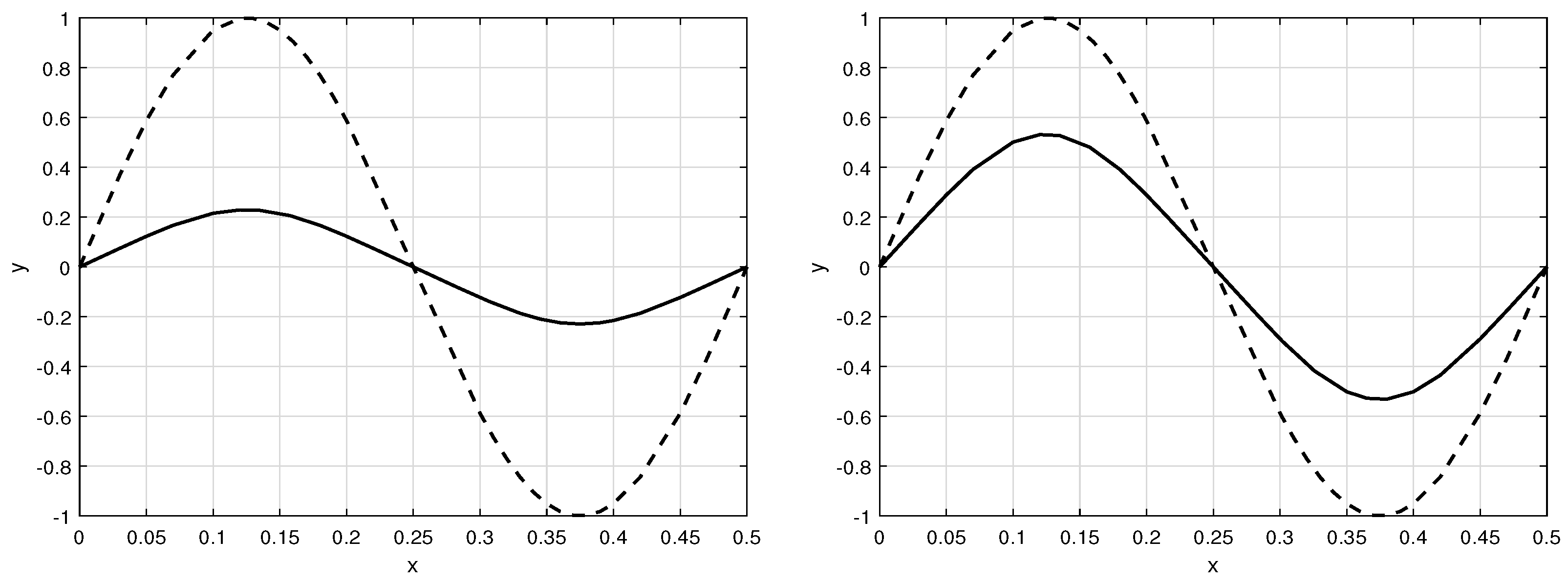
3. Singularly Perturbed Boundary Value Problems
4. Structure of the Solutions Set of the Reduced Problem
- (j)
- is nondecreasing in for each
- (jj)
- for each there is an such thatfor each pair of points
- (a)
- in
- (b)
- if (), then for each () the function is a solution of the SPBVP (1), () ().
- (j’)
- is increasing in for each
- (i)
- ;
- (ii)
- u satisfies the boundary condition () ();
- (iii)
- u is ()–stable in
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 4
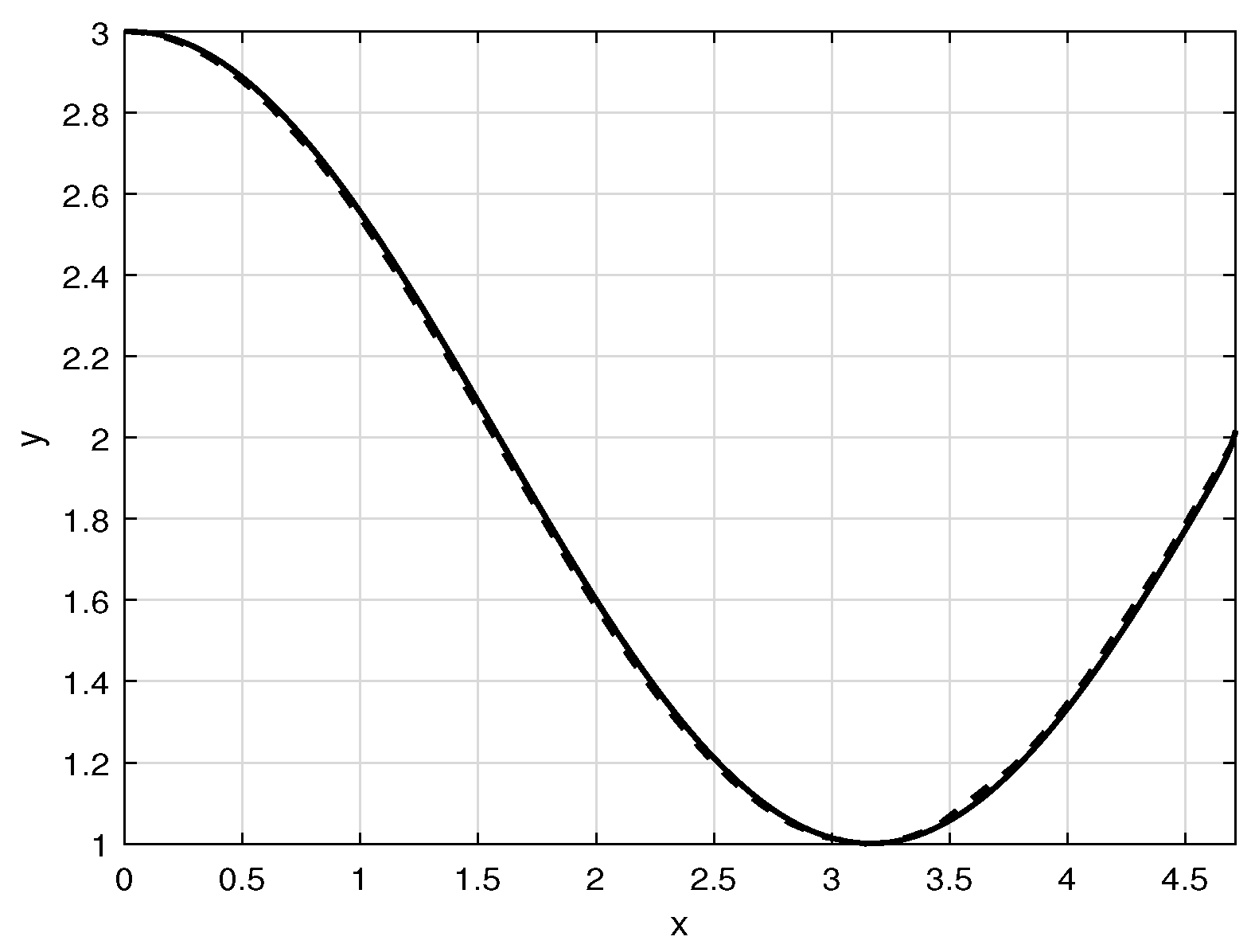
Appendix B. The MATLAB R2022a Code Used for Generating Figure 3
| function Example2_3bvp(solver) |
| % Check for pasting of character " ’ " (<=PDF conversion of code) |
| % Use vertical single quotation mark instead of right single quotation |
| mark ! |
| if nargin < 1 |
| solver = ’bvp4c’; |
| end |
| bvpsolver = fcnchk(solver); |
| % Initial mesh - duplicate the interface point xc |
| xc=0.25; |
| xinit = [0, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, |
| 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.19, 0.20, 0.21, 0.22, |
| 0.23, 0.24, xc, xc, 0.26, 0.27, 0.28, 0.29, 0.30, 0.31, 0.32, 0.33, 0.34, |
| 0.35, 0.36, 0.37, 0.38, 0.39, 0.40, 0.41, 0.42, 0.43, 0.44, 0.45, 0.46, |
| 0.47, 0.48, 0.49, 0.50]; |
| % all points in "xinit" must be in one line !!! |
| yinit = [0.0; -1.0]; |
| sol = bvpinit(xinit,yinit); |
| sol = bvpsolver(@f,@bc,sol); |
| plot(sol.x,sol.y(1,:),’k’,’LineWidth’,1.5) |
| pbaspect([2 1 1]) |
| xlabel(’x’); ylabel(’y’); grid on |
| print(’Figure_3’,’-deps’) % output -> Figure_3.eps |
| function dydx = f(x,y,region) |
| dydx = zeros(2,1); |
| dydx(1)=y(2); % y(1) = y and y(2) = y’ |
| switch region |
| case 1 |
| dydx(2)=0.75*atan(y(1))*(1+sin(y(2)))+(cos(3*pi*x))^3+2*(y(1)); |
| case 2 |
| dydx(2)=0.75*atan(y(1))*(1+sin(y(2)))+(cos(3*pi*x))^3+2*(y(1)); |
| otherwise |
| error(’MATLAB:threebvp3:BadRegionIndex’,’Incorrect region index:%d’, |
| region); |
| end |
| end |
| % ----------------------------------------------------------------------- |
| % Boundary conditions |
| function res=bc(YL,YR) |
| res=[YR(1,1)-YL(1,1) % the first boundary condition y1/4(1)-y0(1)=0 |
| YR(1,1)-YL(1,2) % continuity of y(1) at xc=1/4 |
| YR(2,1)-YL(2,2) % continuity of y(2) at xc=1/4 |
| YR(1,2)-YL(1,2)]; % the second boundary condition y1/2(1)-y1/4(1)=0 |
| end |
| % ----------------------------------------------------------------------- |
| end |
References
- Ingram, S.K. Continuous dependence on parameters and boundary data for nonlinear two-point boundary value problems. Pac. J. Math. 1972, 41, 395–408. [Google Scholar] [CrossRef]
- Vasiliev, N.I.; Klokov, J.A. Foundations of the Theory of Boundary Value Problems for Ordinary Differential Equations; Zinatne: Riga, Latvia, 1978. (In Russian) [Google Scholar]
- Idczak, D. Stability in semilinear problems. J. Differ. Equ. 2000, 162, 64–90. [Google Scholar] [CrossRef]
- Jones, C.K.R.T. Geometric Singular Perturbation Theory. In Dynamical Systems, Part of the Lecture Notes in Mathematics; Springer: Heidelberg, Germany, 2006; Volume 1609, pp. 44–118. [Google Scholar]
- Fenichel, N. Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 1979, 31, 53–98. [Google Scholar] [CrossRef]
- Wiggins, S. Normally Hyperbolic Invariant Manifolds in Dynamical Systems; Springer Science+Business Media: New York, NY, USA, 1994. [Google Scholar]
- Kuehn, C. Multiple Time Scale Dynamics; Springer: Cham, Switzerland; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2015. [Google Scholar]
- Riley, J.W. Fenichel’s Theorems with Applications in Dynamical Systems; University of Louisville: Louisville, KY, USA, 2012. [Google Scholar]
- Vasil’eva, A.B. Asymptotic Behavior of Solutions of Problems for Ordinary Nonlinear Differential Equations with a Small Parameter Multiplying the Highest Derivatives, Russian Math. Surveys 1963, 18, 13–84. [Google Scholar]
- Vasil’eva, A.B.; Butuzov, V.F. Asymptotic Expansions of Solutions of Singularly Perturbed Equations; Nauka: Moscow, Russia, 1973. (In Russian) [Google Scholar]
- De Coster, C.; Habets, P. Two-Point Boundary Value Problems: Lower and Upper Solutions; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Chang, K.W.; Howes, F.A. Nonlinear Singular Perturbation Phenomena: Theory and Applications; Springer: New York, NY, USA, 1984. [Google Scholar]
- Vrabel, R. Upper and lower solutions for singularly perturbed semilinear Neumann’s problem. Math. Bohem. 1997, 122, 175–180. [Google Scholar] [CrossRef]
- Vrabel, R. On the approximation of the boundary layers for the controllability problem of nonlinear singularly perturbed systems. Syst. Control Lett. 2012, 61, 422–426. [Google Scholar] [CrossRef]
- Nagumo, M. Über die Differentialgleichung y″=f(x,y,y′). Proc. Phys. Math. Soc. Jpn. 1937, 19, 861–866. [Google Scholar]
- Jackson, L.K. Subfunctions and Second-Order Ordinary Differential Inequalities. Adv. Math. 1968, 2, 308–363. [Google Scholar] [CrossRef]
- Fabry, C.; Mawhin, J.; Nkashama, M.N. A multiplicity result for periodic solutions of forced nonlinear second order ordinary differential equations. Bull. London Math. Soc. 1986, 18, 173–180. [Google Scholar] [CrossRef]
- Hartman, P. Ordinary Differential Equations; Society for Industrial and Applied Mathematics (Classics in Applied Mathematics): Philadelphia, PA, USA, 2002. [Google Scholar]
- Bernstein, S.N. Sur les équations du calcul des variations. Ann. Sci. Ecole Norm. Sup. 1912, 29, 431–485. [Google Scholar] [CrossRef]
- Granas, A.; Guenther, R.B.; Lee, J.W. Nonlinear boundary value problems for some classes of ordinary differential equations. Rocky Mt. J. Math. 1980, 10, 35–58. [Google Scholar] [CrossRef]
- Granas, A.; Guenther, R.B.; Lee, J.W. On a theorem of S. Bernstein. Pac. J. Math. 1978, 74, 67–82. [Google Scholar] [CrossRef]
- Šeda, V. On some non-linear boundary value problems for ordinary differential equations. Arch. Math. 1989, 25, 207–222. [Google Scholar]
- Schmitt, K. A nonlinear boundary value problem. J. Differ. Equ. 1970, 7, 527–537. [Google Scholar] [CrossRef]
- EMORY, Oxford College. Available online: https://mathcenter.oxford.emory.edu/site/math111/proofs/rollesTheorem/ (accessed on 10 June 2023).




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrabel, R. (Iq)–Stability and Uniform Convergence of the Solutions of Singularly Perturbed Boundary Value Problems. Mathematics 2023, 11, 2717. https://doi.org/10.3390/math11122717
Vrabel R. (Iq)–Stability and Uniform Convergence of the Solutions of Singularly Perturbed Boundary Value Problems. Mathematics. 2023; 11(12):2717. https://doi.org/10.3390/math11122717
Chicago/Turabian StyleVrabel, Robert. 2023. "(Iq)–Stability and Uniform Convergence of the Solutions of Singularly Perturbed Boundary Value Problems" Mathematics 11, no. 12: 2717. https://doi.org/10.3390/math11122717
APA StyleVrabel, R. (2023). (Iq)–Stability and Uniform Convergence of the Solutions of Singularly Perturbed Boundary Value Problems. Mathematics, 11(12), 2717. https://doi.org/10.3390/math11122717