Research Progress of Complex Network Modeling Methods Based on Uncertainty Theory

Abstract

A complex network in reality contains a large amount of information, but some information cannot be obtained accurately or is missing due to various reasons. An uncertain complex network is an effective mathematical model to deal with this problem, but its related research is still in its infancy. In order to facilitate the research into uncertainty theory in complex network modeling, this paper summarizes and analyzes the research hotspots of set pair analysis, rough set theory and fuzzy set theory in complex network modeling. This paper firstly introduces three kinds of uncertainty theories: the basic definition of set pair analysis, rough sets and fuzzy sets, as well as their basic theory of modeling in complex networks. Secondly, we aim at the three uncertainty theories and the establishment of specific models. The latest research progress in complex networks is reviewed, and the main application fields of the three uncertainty theories are discussed, respectively: community discovery, link prediction, influence maximization and decision-making problems. Finally, the prospect of the modeling and development of uncertain complex networks is put forward.

1. Introduction

Networks originally evolved from graph theory in mathematics, and they have been widely used in various fields. Networks in daily life can be briefly summarized into four categories: communication networks, biological networks, technological networks and social networks. The initial research into the network can be traced back to the “seven bridge problem” proposed by the great mathematician Euler in the 18th century. In the natural world, most complex systems can be abstracted into complex networks [1], such as the network formed by the complex relationships of food chains, or the network formed by intertwined railway lines. Complex networks can not only intuitively show the complex relationship between people or things, but they can also be used as a mathematical method to study a whole system.

The research idea of the complex network is to analyze the function of the system from the perspective of structure. The main research areas are briefly summarized as follows: the formation rules of network models, the geometric properties of network models, the mathematical laws of network changes and the dynamic mechanisms of networks. Figure 1 shows a schematic diagram of a complex network.

A complex network in reality contains a large amount of information, but some information cannot be obtained accurately or is missing due to various reasons. For example, in the complex network constructed by the character information stored in Freebase [2], 94% of people lack links to their parents [3]. The transportation network [4] is not a static system, and changes in transportation supply or emergencies will lead to uncertainty in the network. The biochemical reactions and the movement of microorganisms within microorganisms can also constitute a complex network, and the unknown variation process of microorganisms inside the network causes uncertainty in the biological information network [5].

Traditional network modeling only considers the deterministic information in the network, and it is difficult to model uncertain complex networks in reality, which limits their efficient use. Therefore, some scholars have combined uncertainty theory with complex networks to model and represent uncertain complex networks [6,7,8,9,10]. The modeling research into uncertainty theory in complex networks mainly includes set pair analysis (SPA), rough set (RS) theory, fuzzy set (FS) theory and probability theory. Among them, the use of probability theory to model complex network research [11,12] is relatively mature. There are many related achievements, and some scholars have conducted reviews and analyses of the research progress in probability theory [13,14]. According to the statistics of the existing literature, there has been no summary or written prospect of complex network modeling around set pair analysis, rough set theory and fuzzy set theory. The statistical trends of research papers related to set pair analysis, rough sets and fuzzy sets published on Google Scholar in the past forty years are shown in Figure 2 (for statistical convenience, only those papers with theoretical names appearing in the title of the thesis are considered). It can be seen that the development of set pair analysis theory has been relatively slow, and there are still a lot of research gaps. Rough set theory developed rapidly in the ten years after 2000 and then progressed relatively steadily. Fuzzy set theory developed slowly before 2012 and then rapidly after 2012. In 2019, the number of papers published on the subject reached its peak.

The research on applying the above three uncertainty theories to complex networks is also increasing year by year, and the main entry points and research hotspots include the following. The similarity between vertices in complex networks is measured by using the connection degree of set pair analysis. This is mainly used in community discovery [15,16,17,18,19,20,21,22,23,24,25,26], link prediction [16,27,28] and influence maximization [5,14,20], etc. Complex network modeling based on rough set theory involves studying decision-making problems [13,29,30,31,32,33,34,35,36] and community discovery [37,38,39,40,41,42,43,44,45,46,47,48] by constructing upper and lower approximate rough vertices (edges). Most of the research on modeling complex networks using fuzzy set theory focuses on the discovery of overlapping communities [49,50,51,52,53,54,55,56,57,58], by constructing fuzzy membership functions and using methods such as fuzzy clustering algorithms to study them.

In recent years, many scholars have reviewed and predicted the research progress on complex networks. Reference [59] starts with the evolution of complex network models, and on the basis of a brief introduction to the statistical characteristics of complex networks, the author summarizes the research status of complex network theory and its applications in China. Reference [60] divides the main types of complex networks into four categories, reviews the birth and development of complex networks, introduces related concepts and classifications of complex network models and lists some common complex network models with practical significance. Reference [61] introduces the basic concepts of complex networks from the perspective of the definition and statistical properties of complex networks and discusses the advantages and disadvantages of several typical complex network models and their improved models. The current research status of complex networks can be analyzed from two aspects: complex network structure characteristics and network dynamics. With the increasing scale and complex structure of network big data, the uncertain information contained in the network is also increasing. Research on the modeling of uncertain complex networks has attracted more and more attention of scholars. However, there are no comprehensive articles on the research into set pair analysis or fuzzy set and rough set theory in complex network modeling. Therefore, in order to fill this gap, this paper intends to summarize, analyze and discuss the recent literature on complex network modeling and applications based on set pair analysis and rough set and fuzzy set theory, so as to provide references for follow-up research.

The main work of this paper includes:

(1)

The theoretical basis of complex network modeling research around set pair analysis and rough set and fuzzy set fusion includes: using a set pair connection degree to measure the similarity between complex network vertices and modeling complex networks based on set pair similarity; using rough sets with upper and lower approximate sets to construct a complex network of rough vertices (edges); using three-way decision methods (probabilistic rough sets) to model a complex network; and using the fuzzy set membership degree to describe the relationship between vertices and cliques or between cliques and then to model complex networks.

(2)

The modeling methods and applications of set pair analysis, rough set theory and fuzzy set theory in complex networks are summarized and analyzed, including: community discovery, link prediction, influence maximization and decision-making problems. A typical algorithm and an innovative algorithm are analyzed and compared.

(3)

The prospect of uncertainty theory in complex network modeling research and its possible extension in the field of uncertain hypergraphs is put forward.

2. SPA-Based Complex Network Modeling

Set pair analysis [62] (referred to as SPA) was first proposed by Chinese scholar Zhao Keqin in 1989. It is a new mathematical analysis method that uses a connection degree to deal with fuzzy and uncertain information. The research on the integration of set pair analysis and complex networks began in 2011. It was first proposed by Professor Zhang Chunying [17] to construct a set pair social network analysis model and carry out a series of studies.

2.1. Theoretical Basis of Set Pair Modeling for Complex Networks

2.1.1. The Basis of Set Pair Analysis

A set pair is a basic unit composed of two sets with a certain relationship; it is the pair formed by these two sets. The phenomenon of set pairs is ubiquitous, and any two parts in a system, such as a doctor and a patient or an image and an equation, can form a set pair under certain conditions.

Assume that the set pair H composed of set A and set B is analyzed according to the needs of problem W. A total of N features of the set pair H is obtained. Among them, S is common to the two sets in the set pair H, the two sets are opposite in P properties, and they are neither opposed nor identical in the remaining F = N-S-P properties. Then, the set pair connection degree $u$ of the two sets is:

$$u=\frac{S}{N}+\frac{F}{N}i+\frac{P}{N}j.$$

(1)

In the formula, $\frac{S}{N}$, $\frac{F}{N}$ and $\frac{P}{N}$ are abbreviated as $a$, $b$ and $c$. Then, the formula of the connection degree is expressed as:

$$u=a+bi+cj.$$

(2)

Here, $i$ is the difference mark, which takes different values in the interval [−1, 1]. When the value of $i$ is in [0, 1], the different parts tend to be the same, and when it is in [−1, 0], the different parts tend to be opposite. The larger the value of $\left|i\right|$, the greater the conversion probability. $j$ only acts as a marker. The issue the set pair needs to deal with is the difference caused by uncertainty between any two sets, and the degree of connection is used to express the degree of association between the two sets. For example, in the evaluation problem, the measured value of the evaluation index of the sample to be evaluated and the standard of the evaluation index can form a set pair. Then, the same degree a means that the measured value reaches the standard; the degree of difference b represents the difference between the measured value and the index standard by one level; and contradiction c means that the difference between the measured value and the index standard is greater than one level [63,64].

Obviously, under the above definition, $b$ and $c$ satisfy the normalization condition, that is, they satisfy the relational expression:

$$a+b+c=1.$$

2.1.2. Set Pair Similarity Measure between Complex Network Vertices

Node similarity measurement is an important research point for learning complex network structure models. The traditional global similarity measure needs to consider the overall structural relationship of the network. Although it has high accuracy, it is also accompanied by high time and space complexity; the local similarity measure only considers the nearest neighbor vertices, and the time complexity is relatively low, but it underestimates the similarity between directly connected vertices and between vertices connected by paths. The application of set pair analysis theory to the description of the relationship between nodes in a complex network can not only fully take into account the influence of the overall structural information on the nodes, but it can also effectively reduce the time and space complexity.

The similarity measurement method between vertices is an important aspect in the study of complex networks. In 2013, the literature [15,65] proposed a similarity measure between vertices based on set pair theory and common neighbors and applied it to static and dynamic α relation community mining. The source in [15] gives the definition of the connection degree between vertices.

In a complex network, any two nodes $v_k$ and $v_s$ have object attributes and relationship attributes, i.e., $A\left(v_k\right)=\left\{x_{k_1},x_{k_2},\dots ,x_{k_{n1}}\right\}$ and $A\left(v_s\right)=\left\{x_{s_1},x_{s_2},\dots ,x_{s_{n2}}\right\}$, and $\left|A\left(v_k\right)\right|=n_1$, $\left|A\left(v_s\right)\right|=n_2$, respectively. The two nodes’ objects have a total of $N=\left|A\left(v_k\right)\cup A\left(v_s\right)\right|$ attributes. Therefore, the connection degree of the two nodes at a certain time can be expressed as:

$$\mu \left(v_k,v_s\right)\left(t\right)=a_{ks}\left(t\right)+b_{ks}\left(t\right)i+c_{ks}\left(t\right)j.$$

(3)

Here, $a_{ks}\left(t\right)$ is the same degree of nodes $v_k$ and $v_s$ at time t, $b_{ks}\left(t\right)$ is the degree of difference between nodes $v_k$ and $v_s$ at time t, and $c_{ks}\left(t\right)$ is the degree of opposition between nodes $v_k$ and $v_s$ at time t.

Therefore, the set pair connection degree can be used to describe the similarity of two nodes in a complex network.

However, this similarity measurement method only considers the impact of the uncertain number of common neighbor attributes in the network on community formation and network analysis, while ignoring the impact of relationship weights on network analysis. Therefore, the literature [16,17] has defined first-level neighbors, second-level neighbors and common neighbor sets of nodes in complex networks based on set pair analysis theory, and based on this, a new similarity measure between vertices was defined.

Definition 1.

Similarity Measure between Vertices.

The similarity measure between vertices is an important issue in the study of network structure. Zhang Chunying [15,65] once defined the similarity measure between vertices. However, these definitions only consider the influence of the number of common neighbors on the similarity between vertices and not the influence of different network densities and vertex degrees on the similarity between vertices, so they cannot better reflect the network community structure. Therefore, Chen Xiao [16] proposed a new metric, the weighted clustering coefficient connection degree WCCD, and expressed the vertex similarity in a traditional complex network as:

$$S_{ks}^{WCCD}=\frac{{\left(1\right)}_{1\times S}\times {\left(w{\left(v_i\right)}^G\right)}_{S\times 1}}{N}+\frac{{\left(w{\left(v_i\right)}^G\right)}_{1\times F}}{N}\times {\left(i{\left(v_i\right)}^G\right)}_{F\times 1}+\frac{{\left(1\right)}_{1\times P}\times {\left(w{\left(v_i\right)}^G\right)}_{P\times 1}}{N}\times j^G.$$

(4)

Here, ${\left(1\right)}_{1\times S}$ and ${\left(1\right)}_{1\times P}$ represent row vectors of the same attribute and opposite attribute, respectively, and the vector values are both 1. ${\left(\ast \right)}_{1\times F}$ represents the row vector of distinct attributes. $w{\left(v_i\right)}^G$ represents the weight of the corresponding vertex. $i\left(v_i\right)$ represents the difference value of the corresponding vertex.

Chen Xiao applied an index to link the prediction of traditional complex networks and proved the effectiveness of the index through experiments.

2.1.3. Complex Network Set Pair Relationship Matrix

The set pair relationship matrix is composed of the set pair connection degree. The set pair relationship matrix can determine the relationship connection degree of each node in the set pair complex network.

Definition 2.

Set Pair Relationship Matrix.

$R\left(t\right)={\left(\rho \left(v_k,v_s\right)\left(t\right)\right)}_{n\times n}$ represents the set pair relationship matrix between nodes $v_k$ and $v_s$ at time t, which is expressed as:

$$R\left(t\right)=\left[\begin{array}{cccc}\rho \left(v_1,v_1\right)\left(t\right)& \rho \left(v_1,v_2\right)\left(t\right)& \dots & \rho \left(v_1,v_n\right)\left(t\right)\\ \rho \left(v_2,v_1\right)\left(t\right)& \rho \left(v_2,v_2\right)\left(t\right)& \dots & \rho \left(v_2,v_n\right)\left(t\right)\\ ⋮& ⋮& \ddots & ⋮\\ \rho \left(v_n,v_1\right)\left(t\right)& \rho \left(v_n,v_2\right)\left(t\right)& \dots & \rho \left(v_n,v_n\right)\left(t\right)\end{array}\right].$$

(5)

With a constant change in time t, the nodes in the network may change with it, resulting in a constant change in the relationship matrix. When time t is not considered, the matrix is a static relationship matrix. By analyzing the relationship matrix at different times, the changing trend of the complex network can be obtained.

2.1.4. Set Pair Relationship Community Description

A complex network can be regarded as a dataset of individuals and relationships. Its nodes represent individuals to be studied, and edges represent possible relationships between individuals. Based on the theory of set pair analysis, the complex network can be regarded as a complex system of sameness, difference, and antithesis. The source in [17] buildt a SPA-based set pair social network analysis model for the attribute graph of a social network, and the static and dynamic forms of the set pair social network analysis model are discussed [18,19]. Based on this model, the literature proposed a set pair complex network α-relationship community as well as static and dynamic mining algorithms [15,66].

The definition of the α-relationship community is given by the authors of [15]:

According to different practical problems, a threshold $\alpha \in \left[0,1\right]$ is set, and when the identity $a_k$ of the set pair connection degree of nodes in the network is greater than the threshold, the node is divided into the minimum community; when the uncertainty of a node is transformed into the same degree, that is, $a_k+b_k>\alpha$, the node is merged into the largest community. A community pair is thus formed, which is called an α-relational community.

At time t, the community pair composed of the α-minimum relationship community and the α-maximum relationship community is called the α-relationship community at time t, and the formula is expressed as:

$$\mathrm{SN}\mathsf{\alpha }\left(\mathrm{t}\right)=<\mathrm{minSN}\left(\mathrm{t}\right),\mathrm{maxSN}\left(\mathrm{t}\right).$$

(6)

Here, $\mathrm{minSN}\left(\mathrm{t}\right)$ and $\mathrm{maxSN}\left(\mathrm{t}\right)$ represent the α-minimum relational community and the α-maximal relational community, respectively. With the change in time t, the development trend of the community can be predicted.

2.2. SPA-Based Complex Network Modeling and Application

Modeling research on complex networks based on set pair analysis mainly includes research on community discovery, link prediction and influence maximization. Figure 3 lists the main algorithms in the three areas and their proposed time, and the dashed lines with arrows are used to indicate the update and improvement between the algorithms. For example, in the research of “Community discovery”, the algorithm KPCMV is proposed on the basis of the algorithm KPCM, which is an improvement to the algorithm.

2.2.1. Community Discovery

Community structure is a common feature in complex networks. A community consists of a group of similar interconnected nodes. Nodes within the same community are closely connected, whereas connections between different communities are sparse [67]. Community discovery is the process of finding disjoint community structures that exist in the network.

In recent years, aiming at the uncertain information in community discovery, some scholars have used the set pair connection degree to measure the similarity between vertices in the community, and they proposed a series of new models and algorithms, which provide a new direction for complex network research.

Table 1. The current research situation of set pair analysis in social networks.

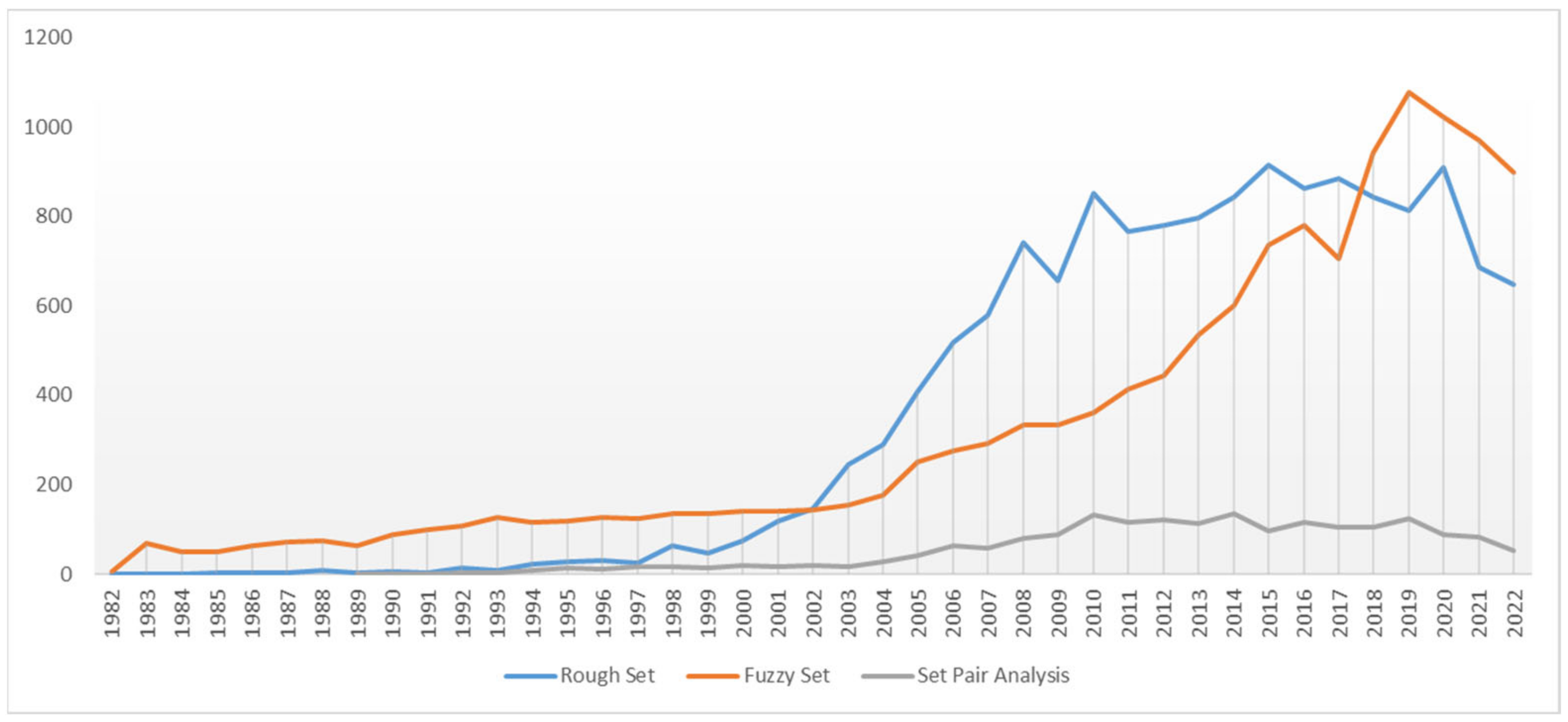
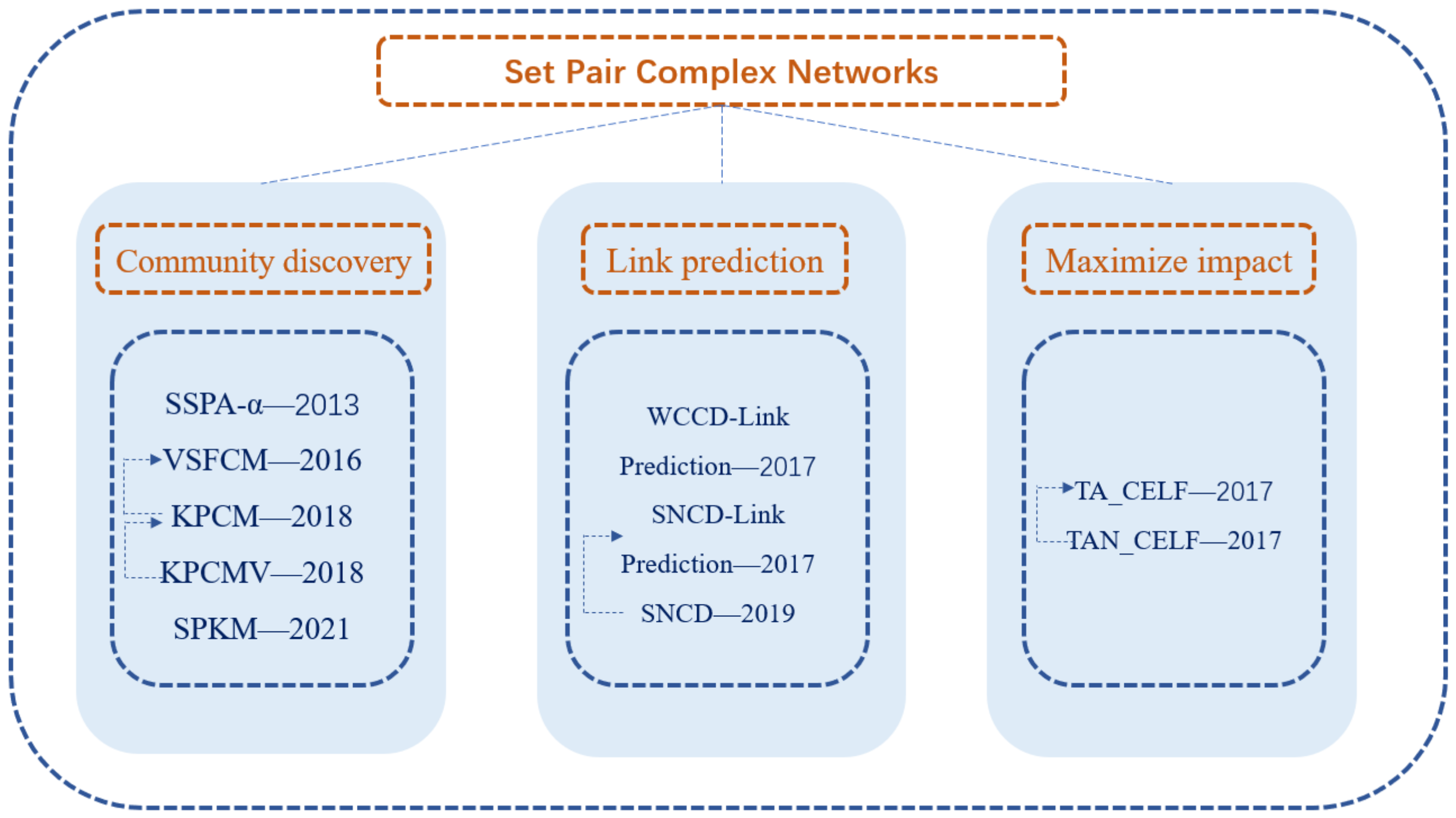
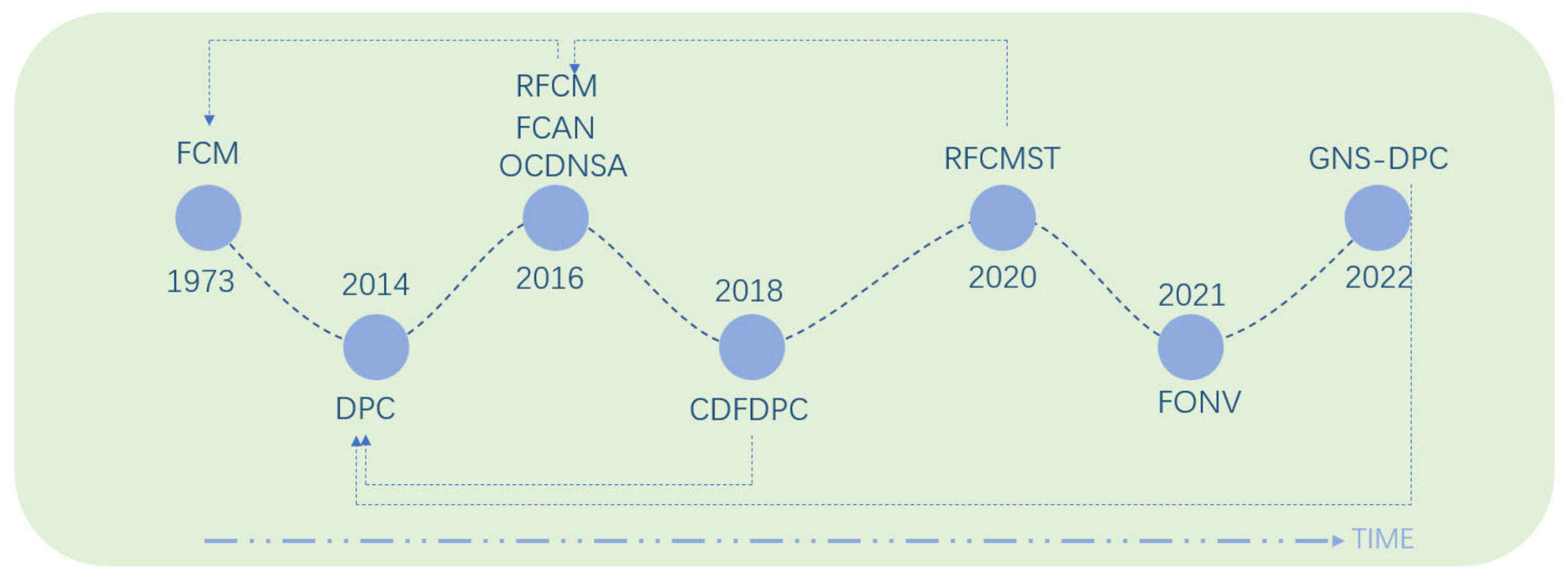
Paper Title	Years	Major Contributions
Set Pair Social Network Analysis Model and Its Application [17]	2011	For the first time, set pair analysis was used in a social network, and a set pair social network analysis model and its related theorems are proposed.
Set Pair Community Mining and Situation Analysis Based on Web Social Network [19]	2011	The set pair connection degree was used in analyzing the sameness, difference and opposites of neighbor nodes, and a set pair community mining algorithm for context analysis is proposed.
The α Relational Communities of Set Pair Social Network and Its Dynamic Mining Algorithms [15]	2013	In the set pair social network, the concept of α-relation community with a given threshold was proposed, and the static and dynamic α-relation community mining algorithms based on set pair analysis theory are given, respectively.
Research on Community Detection Algorithm Based on the Measure of Set Pair Similarity [20]	2016	A similarity measurement method between vertices based on the weighted aggregation coefficient connection degree and a new similarity-based hierarchical clustering algorithm VSFCM were proposed, which are used in the algorithm research of community discovery.
Research on Community Discovery Based on k-shell [21]	2018	Aiming at the problems existing in the VSFCM algorithm, combining the k-shell decomposition method with set pair analysis, the algorithm KPCM and the algorithm KPCMV were proposed and applied to community discovery.
Measuring Similarity Between Vertices and Its Application in Social Network [22]	2017	A new metric, the weighted aggregation coefficient connection degree, was proposed for a traditional social network and applied to social network link prediction and community discovery. The symbolic network is characterized as a system of similarities, differences and antithesis, and a new measure of similarity between vertices was proposed, which is applied to link prediction and dynamic community discovery in a symbolic network. Using the connection degree to describe the similarities, differences and antithesis between vertices of the topic attention network, a new measure of similarity between vertices was proposed and applied to the community discovery and influence maximization research of a topic-attention network.
Study on the Measure Methods of Similarity between Vertices in Network [16]
Research on Network Community Discovery Methods Based on Topic Concern [23]	2017	A topic attention model was constructed, and the similarity between vertices of the model is characterized using the set pair connection degree. With a focus on the characteristics of the topic-attention network, a new measure of similarity between vertices, TANCD, was proposed, and a topic community discovery algorithm based on TANCD was proposed. Combining deep-learning technology with natural language processing, a topic community discovery algorithm based on representation learning was proposed.
A Study on the Influence Propagation Model in Topic Attention Network [24]	2017
Study on the Measure Methods of Similarity between Vertices in Network [16]	2017
Representation Learning of the Topic-Attention Network [25]	2019
Research and Application of Three-way Clustering Based on Set Pair Information Granule [26]	2021	This paper constructs a three-way clustering algorithm SPKM based on set pair information granules and applies the set pair three-way clustering algorithm to community mining in a complex network.

summarizes the main research on set pair analysis in complex networks.

The research on SPA-based complex network community discovery focuses on static community discovery, dynamic community discovery and overlapping community discovery.

(1)

Static community discovery

The source in [19] defines the concept of a set in the complex network model, and the set pair community is then described. This article discovers static communities in complex networks with the help of a set pair relationship matrix, uses thresholds to discover the largest and smallest communities and analyzes the development trend of the communities.

The source in [20] used the similarity, difference and inversion relationship in set pair analysis to propose a similarity measurement method between vertices based on the weighted clustering coefficient connection degree, and based on this method, a new similarity-based hierarchical clustering algorithm VSFCM was proposed. The similarity, difference and inverse relationship between vertices is weighted to achieve the purpose of distinguishing the contribution of paths between different vertices. On the basis of the existing set pair social network research, the unsigned network and the symbolic network were studied, respectively. For the symbolic network, a similarity measurement method between the vertices of the symbolic network based on the set pair connection degree was proposed, which can effectively describe the close relationship between the vertices in the symbolic network. The source in [21] aimed at the problem of the premature merging of vertices in the initial aggregation stage of the independent community in the VSFCM algorithm, introduced the edge aggregation coefficient and similarity together as the community merging criteria and proposed an improved VSFCM algorithm, which effectively improved the accuracy of community merging at this stage. In order to alleviate the problem of excessive time complexity in the original algorithm, the k-shell decomposition method and set pair analysis are combined, the algorithm KPCM and algorithm KPCMV are proposed, and the algorithm is applied to community discovery.

The source in [22] integrated set pair analysis into a complex network with uncertain information, used the set pair connection degree to describe the similarity, difference and reverse relationship between vertices and proposed a similarity measurement method between vertices with a weighted aggregation coefficient connection degree. Then, scholars re-characterized the similarity between network vertices with the set pair connection degree [16] and proposed a new measure of similarity between vertices, WCCD, and weighted it. Aiming at problems such as the high complexity of the global index and the inaccurate estimation of the local index in the index of measuring the similarity between vertices in the symbolic network, a new measurement index SNCD was proposed, which effectively improves the accuracy of measuring the similarity between vertices and lays a good foundation for follow-up research.

The topic-attention model is a new complex network model that has been proposed in recent years. The vertices in the network are composed of entities and topics. Chen Xiao et al. [16,23] considered the social relationship and interest relationship together, constructed a topic-attention model, used the set pair connection degree to describe the similarity between the vertices of the model and set different weights according to different topics and users’ contributions to similarity. The community discovery problem of the topic-attention model is transformed into an agglomerative clustering problem based on the connection degree, and a corresponding algorithm is given. According to the characteristics of the topic-focused network, a new measure of similarity between vertices, TANCD, was proposed, and a topic community discovery algorithm based on TANCD was proposed, so as to achieve the purpose of accurately dividing topic-centered communities. In order to deal with large-scale topic-focused networks, the source in [25] integrated deep-learning technology into natural language processing, used the set pair connection degree to describe the transition probability of vertices in the network and proposed a topic community discovery algorithm based on representation learning. Compared with previous community discovery algorithms, this algorithm takes into account the information of network structure and semantics, which is more comprehensive and has more practical application value.

To solve the problem of the soft clustering of incomplete datasets, the source in [26] introduced set pair information granules into traditional clustering and constructed a three-way clustering algorithm, SPKM, based on set pair information granules. The author proposed a distance calculation method based on the set pair connection degree and then applied it to the CURE algorithm, proposing a set pair three-way hierarchical clustering algorithm, SPGCURE, and the set pair three-way clustering algorithm was then applied to community discovery in a complex network. Compared with other algorithms, this algorithm can handle both complete and incomplete datasets and can maintain good accuracy in both datasets.

(2)

Dynamic community discovery

In [17], in the process of exploring the relationship between individuals in a social network, it was found that the information in this process is uncertain, and the social network is constantly dynamically changing. Aiming at these problems, the author first applies set pair analysis to the social network, proposes a set pair analysis model of the social network and gives the relevant properties of the model.

In [15], aiming at the existence of definite and uncertain relations in a Web social network, the concept of α-relationship community with a given threshold was proposed to be applied to a set pair social network, and a SPA-based dynamic α relationship community mining (DSPA-α) algorithm is given. Experiments prove that the α-relationship community is able to better reflect the dynamic changes of the community. Compared with previous algorithms, this algorithm fully considers the uncertainty of relations. It can figure out the largest relational community and the smallest relational community at the same time and obtain different ranges of communities by adjusting the threshold. The algorithm provides a new idea for further research on community dynamic mining.

(3)

Overlapping community discovery

The modeling research into set pair analysis in complex networks has also been extended to the discovery of overlapping communities. In [68], aiming at the problem of various types of vertices in the social Internet of Things, the author used the idea of set-pair information granule computing and clustering, and the set pair connection degree was used to analyze the similarities, differences and opposites of neighbor vertices. A set pair three-way overlapping Community Discovery Algorithm is proposed. In addition, considering the different connection strengths of vertices and edges and the degree of vertices, the aggregation strength of vertices is defined, and an improved k-means initial value selection algorithm is proposed. Each vertex has different set pair similarities for different communities, and the vertices are assigned into three-way community structures consisting of positive similitude, a border domain and a negative domain.

2.2.2. Link Prediction

Link prediction refers to predicting the possibility of a connection between two nodes that are not connected temporarily in the network by analyzing the known node information in the network and the network structure. This prediction includes predictions for both unknown links and future links [27].

There are few studies on fusion set pair analysis for link prediction in a complex network. Only the source in [16] defines the similarity metrics WCCD and SNCD between vertices for the link prediction problem in a traditional social network and a symbolic network, respectively. In view of the idea of connection degree, a WCCD-Link Prediction algorithm and an SNCD-Link Prediction algorithm were put forward. Experiments showed that the two algorithms can effectively reduce the time complexity and have high accuracy for their corresponding network, which provides a new direction for future research on link prediction problems.

For the deterministic and uncertain information in the symbolic network, considering the local and global characteristics comprehensively, combined with set pair analysis theory, the symbolic network is regarded as a kind of system of sameness, difference and antithesis. For the link prediction problem, a new method is proposed. This method improves the accuracy of predicting positive and negative edges at the same time and has certain stability in networks of different sizes and densities [28].

2.2.3. Maximizing Impact

One of the main tasks of influence maximization research is to think about how to select a set of “seed” vertices with a certain strategy in a complex network and use it as the initial disseminator of information in the network. These “seed” vertices are capable of cascading effects throughout the network to maximize the spread of information [69]. Traditional influence maximization algorithms are mainly based on greedy strategy [70], and heuristic algorithms are based on central strategy [71]. The algorithm based on the greedy strategy has high time complexity, and the effect is not good when dealing with a large-scale complex network. Meanwhile, the heuristic algorithm based on the centrality strategy has its own limitations, resulting in a low solution quality of the algorithm.

The source in [16] used the path relationship and the Markov model to describe the object’s preference for the topic, considering the scope of the topic’s influence. The object’s preference for topic $t_k$ is determined, the topic’s influence within the scope is described, and the influence maximization algorithm is implemented to discover the user group with the greatest influence in a certain topic. In addition, Chen Xiao used the set pair connection degree and random walk model to describe the user’s preference for topics according to the characteristics of a topic-attention network and proposed a topic-based influence maximization algorithm [24]. This is the first attempt toward achieving impact maximization research in the topic-attention network and has achieved good results.

2.2.4. Other Problems

In addition to community discovery, link prediction and influence maximization studies, set pair social networks are also applied in the study of some other problems [72,73].

The source in [72] and others formed a manufacturing service demand network according to the complexity of manufacturing service demand. This article established a manufacturing service value model using set pair analysis theory, and based on this, a dynamic mining algorithm was constructed for manufacturing service value. The model combines set pair analysis theory and a social network, determines the mining object of manufacturing service demand and clarifies the application of a set pair complex network in the manufacturing service industry.

In the literature [73], Zhao Guanghua combined the concept of sameness, difference and antithesis in set pair analysis theory with information entropy, which describes the degree of information confusion. For the uncertainty problem in text sentiment analysis, he proposed the set pair information entropy SP-IE algorithm. Guanghua divided text sentiment into five categories by analyzing the difference coefficient $i$ and calculated the set pair information entropy to judge the polarity and intensity of tendentious texts. The research on this topic can be extended to many fields, such as psychological counseling, public opinion analysis, etc. and has great research potential.

Since the complex network was proposed, it has received extensive attention from scholars. As a new research method proposed in recent years, the complex network has been continuously developed, and its modeling research and application fields need to be further expanded.

3. Complex Network Modeling Based on RS

Using the upper and lower approximations of rough sets to describe the uncertainty of graphs, the source in [74] proposed the concept of rough graphs for the first time, but rough graphs were not extended to an actual complex network. The sources in [65,75] introduced rough set theory into the attribute graph model and analyzed its rough characteristics, concluding that the finer the edge set division degree of the rough attribute graph, the higher the accuracy of the obtained graph. For a complex network with incomplete information, the source in [29] proposed the concept of a rough complex network and offered static geometric characteristics, which provides a theoretical basis for future research on uncertain complex networks.

3.1. Basics of RS Modeling Complex Network

3.1.1. Basic Theory of RS

In the early 1980s, Pawlak [76] proposed the concept of a rough set for G. Frege’s boundary line area thought. Those individuals that cannot be identified belong to the boundary area, and this boundary area is defined as the difference set between the upper approximation set and the lower approximation set. Here, according to the existing knowledge R, the lower approximate set is defined as the set composed of objects that must belong to the set $X$ in the domain of discourse $U$, that is:

$$R_{—}\left(X\right)=\left\{x\in U,{\left[x\right]}_R\subseteq \mathrm{X}\right\}.$$

(7)

The upper approximate set is defined as the set of objects that must belong to and may belong to the set X in the universe U, that is:

$$R^{—}\left(X\right)=\left\{x\in U,{\left[x\right]}_R\cap \mathrm{X}\ne \varnothing \right\}.$$

(8)

Here, ${\left[x\right]}_R$ indicates the equivalence class containing the element $x$ under the equivalence relation $R$.

One of the main advantages of rough set theory is that it does not require any preliminary or additional data information.

3.1.2. RS Complex Network

Rough complex networks [35] are composed of rough vertex complex networks and rough edge complex networks:

Rough vertex complex network RCN_V: In the complex network, for vertex set U_V, there are X_V and R_V, where X_V is a subset of vertex set U_V, and R_V is an equivalence relation of U_V. When X_V is the rough set of R_V, the vertex set of the complex network is said to have rough characteristics, and the complex network is called the rough vertex complex network RCN_V;

Rough edge complex network RCN_E: In the complex network, for edge set U_E, there are X_E and R_E, where X_E is a subset of the edge set U_E, and R_E is an equivalence relationship of the U_E. When X_E is the rough set of R_E, it is said that the edge set of the complex network has rough characteristics, and the complex network is the rough edge complex network RCN_E;

Rough vertex complex network RCN_V and rough edge complex network RCN_E are collectively referred to as rough complex networks.

3.1.3. Rough Complex Network Accuracy Metrics

As in rough sets, the uncertainty and incompleteness of information in complex networks is caused by the existence of boundary domains of vertex sets and edge sets. The larger the boundary domain, the lower the accuracy. In order to express this more accurately, the concepts of precision and roughness of rough complex networks are introduced:

Let the ratio of the measure of the lower approximate complex network ${\underset{¯}{CN}}_V\left(\underset{\_}{R}\left(X_V\right),E\right)$ (or ${\underset{¯}{CN}}_E\left(\underset{\_}{R}\left(X_E\right)\right)$) of the rough complex network RCN_V (or RCN_E) to the measure of the upper approximate complex network ¯) be the precision of the rough vertex (or edge) complex network, denoted as:

$${\alpha }_V\left(RC{N}_V\right)=\frac{card{\underset{¯}{CN}}_V\left(\underset{\_}{R}\left(X_V\right),E\right)}{card{\overline{CN}}_V\left(\overline{R}\left(X_V\right),E\right)},$$

(9)

$${\alpha }_E\left(RC{N}_E\right)=\frac{card{\underset{¯}{CN}}_E\left(\underset{\_}{R}\left(X_E\right)\right)}{card{\overline{CN}}_E\left(\overline{R}\left(X_E\right)\right)}.$$

(10)

The accuracy of the rough complex network RCN is the product of the precision of the rough vertex complex network RCN_V and the rough edge complex network RCN_E precision, namely:

$${\alpha }_{ }\left(RC{N}_{ }\right)={\alpha }_V\left(RC{N}_V\right)\times {\alpha }_E\left(RC{N}_E\right).$$

(11)

That is called:

$$\rho \left(RCN\right)=1-\alpha \left(RCN\right),$$

(12)

This is the roughness of the rough complex network.

3.1.4. Coarse Clustering Coefficients for Rough Complex Network

The clustering coefficient measures the degree of interconnection between a vertex and its neighbors in a network. It can be divided into the overall clustering coefficient and the local clustering coefficient. This paper mainly discusses the local clustering coefficient, which is defined as the ratio of the actual number of connections between all neighbors of the current vertex to the number of possible connections, namely:

$$C_i=\frac{2M_i}{k_i\left(k_i-1\right)}.$$

(13)

Here, $k_i$ is the number of edges connected to the vertex V_i, $\frac{k_i\left(k_i-1\right)}{2}$ is the maximum number of edges that may exist between the $k_i$ vertices, and $M_i$ is the actual number of edges between the $k_i$ vertices.

The source in [35] gives a definition of the coarse clustering coefficient:

In the rough complex network, assuming that the clustering coefficient of the lower approximate complex network is $\underset{\_}{C}$, and the clustering coefficient of the upper approximate complex network is $\overline{C}$, then it is called:

$$RC=\left\{\max \left\{\underset{\_}{C},\overline{C}\times \alpha \left(RCN\right)\right\}\right\}$$

(14)

This is the coarse clustering coefficient of the rough complex network.

3.2. Rough Set Modeling Method for Complex Networks

The research on rough complex networks mainly focuses on the discussion of rough decision-making problems and overlapping community discovery problems. This section will mainly review the literature on these two aspects.

3.2.1. Rough Decision-making Model

As a mathematical research method to characterize incomplete information and uncertainty, rough set theory has applications in many fields.

Table 2. Modeling of rough set theory in decision-making problems.

Paper Title	Years	Major Contributions
Research on Complex Network Attack Modeling and Security Assessment Method [30]	2013	A rough path generation algorithm is proposed. On this basis, the ant colony algorithm is used to further mine k key vulnerable paths to the attack target.
Rough Decision Analysis Model Based on New Feature Dominance Relationship [31]	2015	A decision analysis model based on an extended rough set is constructed, the rough approximation relationship of decision classes is obtained under the new feature of relationship, and the classification decision rules are given.
Decision Methods and Applications of Rough Complex Network Based on Network-Based [34]	2016	Combining rough set theory with complex networks for the first time, the concept of the rough complex network is proposed, and the concepts of positive field, negative field and boundary field of the rough complex network are given. A scale-free benefit risk assessment model is constructed, combined with game theory, to conduct a game analysis of the third-party payment rough network operation risk. A decision method of rough and complex networks is given by defining the network basis of rough and complex networks, and it is used to solve the operation risk decision analysis of third-party payment rough and complex networks.
Research on Risk Analysis and Decision Models of the Third-party Payment Rough Network [35]	2016
A Knowledge Discovery Model for Third-party Payment Network based on Rough Set Theory [33]	2017
Concept Design and Construction Algorithm of Rough Complex Network [32]	2017
Benefit Risk Evaluation of Third-party Payment Network Based on Rough Set [36]	2018
Research on the Statistical Characteristics and Definition of the Complex Network with Uncertainty [29]	2018

shows the main research on rough sets in complex network decision-making problems. In the research in this field, scholars mainly solve practical decision-making problems by constructing rough complex networks [34]. Some scholars have also modeled decision-making problems based on rough paths [30] or feature advantage relations [31].

Decision science is an ancient and emerging discipline, which was born in the 1920s and 1930s and developed rapidly after the 1950s. The source in [31] proposed a decision analysis model based on an extended rough set based on a rough set, obtained the rough approximate relationship of decision-making classes under the new feature relationship, and gave classification decision rules. However, scholars have not used rough sets to solve decision-making problems on complex networks. Since then, some scholars have started research on rough and complex network modeling.

(1)

Rough path and defensive decision making

Cyber defense decisions receive a lot of attention. The source in [30] comprehensively considers network-based remote attacks and host-based local attacks, establishes a construction method that can clearly describe network attack models, defines rough attack paths on the top-level network and then proposes a rough path generation algorithm. On this basis, the ant colony algorithm is used to further mine k key vulnerable paths to the attack target. These vulnerable paths have the highest attack efficiency and are most likely to be taken by the attacker. Finally, by comprehensively considering the rough path and the precise path, an evaluation method for the risk of each vertex and the vulnerability threat is proposed. The construction of this model provides an important basis for network defense decision making.

(2)

Rough and complex network decision-making method

The literature [29,35] combined the rough set and complex network, proposing the concept of a rough complex network, and the positive domain, negative domain and boundary domain of the rough complex network are given. The source in [32] established a rough and complex third-party payment network for practical problems. The research found that the average distance interval of the network is too large, and the rough clustering coefficient is too small, indicating that the network does not have the characteristics of a small-world network, and the network structure is relatively scattered. In addition, scholars have also constructed a scale-free benefit risk assessment model [36] to assess risk levels. Combining this with the thought of game theory, the author conducted a game analysis on the risk of the rough network operation of a third-party payment.

The literature [33,34] has analyzed the risk problems in the network, discussing the various possibilities for the actual situation of third-party payment risk evaluation and management under Internet finance and establishing a relatively complete risk evaluation system. Then, by defining the network basis of the rough and complex network, a decision-making method for the rough and complex network is given, and it is used to solve the operational risk decision analysis of the rough and complex network for third-party payment. By establishing a two-tier risk decision-making model, quantitative decision-making analysis results are given.

3.2.2. Community Discovery

Community discovery is a significant research direction in complex networks. Many scholars have researched and modeled the problem of community discovery from many different angles and applied it to real networks. However, the research in this field still has plenty of deficiencies. For example, the research on the problem of community discovery in uncertain complex networks still needs to be deepened, the accuracy and efficiency of overlapping community discovery algorithms still need to be improved [77], etc. Community discovery includes overlapping community discovery and non-overlapping community discovery, as shown in Figure 4. This section mainly summarizes the modeling research of rough sets in non-overlapping community detection and overlapping community detection. The relevant literature is shown in

Table 3. Modeling of rough sets in community discovery.

Paper Title	Years	Mean Work
Three-way Decision-based Overlapping Community Detection [37]	2017	Using the idea of a three-way decision, a non-overlapping community and overlapping community discovery algorithm based on a three-way decision is proposed [37]. A three-way division [38] is performed for the overlapping communities that appear during the granulation process to obtain non-overlapping communities; aiming at the problem of community merging in the process of hierarchical clustering, a community discovery method based on variable granularity hierarchical clustering is proposed.
Three-way Decision Based on Non-overlapping Community Division [38]	2017
Research on Non-overlapping Community Division Based on Three-way Decision Theory [39]	2018
VGHC: A Variable Granularity Hierarchical Clustering for Community Detection [40]	2020
Application of Rough Set and Ant Colony Algorithm on Community Discovery [41]	2012	A model of network community structure discovery is constructed based on a rough set, and information centrality is used to measure the relationship between vertices.
Research of Community Mining in Social Network Based on Granular Computing [42]	2015	Based on granular computing of a rough set model, a community mining algorithm based on granular computing is constructed.
Research of Community Mining in Social Network Based on Granular Computing [43]	2020	An overlapping community discovery algorithm is proposed based on a rough set and density peaks [43]; an overlapping community discovery algorithm is proposed based on a rough set and distance dynamic models [44].
Overlapping Community Detection Method Based on Rough Set and Distance Dynamic Model [44]	2020
Research on Overlapping Community Detection Algorithm Based on Rough Set [45]	2021
A Rough Connectedness Algorithm for Mining Communities in Complex Network [46]	2016	A new algorithm based on a rough set is proposed to detect disjointed, overlapping and hierarchically nested communities in a network by constructing the granularity of neighborhood vertices and representing them as a rough set [46]; an overlapping community detection algorithm is proposed based on link granularity information and a rough set [47].
An Overlapping Community Detection Algorithm Based on Rough Clustering of Links [47]	2020
Rough Net Approach for Community Detection Analysis in Complex Network [48]	2020	A new rough network model is constructed, and new quality measures are proposed for exploratory analysis of a community structure in a single network and multiple networks.

.

(1)

Non-overlapping community discovery

In the 1990s, Yao proposed a Rough Set–Decision Rough Set based on the probability inclusion relationship [78]. The three-way decision theory connects the positive domain, negative domain and boundary domain in the rough set to the acceptance, rejection and delay decision rules in decision making [79]. Later, some scholars applied three-way decision-making theory to the community discovery problem. The source in [37] divides the affiliation relationship between communities into three types: complete belonging, not completely belonging and incomplete belonging, and then the three-way decision-making idea is used to propose a community discovery algorithm.

The literature [38,39] introduced the three-way decision idea into granular community division. Scholars divide the overlapping communities in the granulation process in three ways to obtain non-overlapping communities. The source in [40] aimed at the problem of community merging in the process of hierarchical clustering and proposed a community discovery method based on variable granularity hierarchical clustering. Aiming at the division of boundary domain vertices, a community discovery method based on random walk boundary domain processing is proposed, which effectively divides overlapping communities into non-overlapping communities.

The source in [41] constructs a network community structure discovery model based on rough set theory for the problem of network community structure discovery. This method uses information centrality to measure the relationship between vertices and uses the concept of upper and lower approximations in a rough set to divide community boundaries. The ideal community structure is then determined by modularity. The number of communities finally obtained by the algorithm does not need to be given manually but is automatically given by the algorithm. The algorithm introduces rough set theory into community division. It has higher accuracy than general algorithms in dealing with boundaries, and the algorithm can realize community structure discovery without knowing the number of communities and the number of vertices in the community.

Since Pawlak put forward the idea of “knowledge is classification” and established a granular computing model based on rough set theory in 1982, rough sets have been widely used in various fields, such as machine learning and data mining. The source in [42] constructed a community mining algorithm based on granular computing of a rough set model. The article defines the granularity in the network structure and discusses the method of granularity conversion. The core of the algorithm is to construct the granularity criterion of the network structure based on the granular computing model based on rough set theory, to generate the network granularity space under the criterion and to convert the problem of community mining into the problem of granularity transformation in different granularity spaces. The algorithm achieves the purpose of community mining through layer-by-layer abstraction with granularity ranging from fine to coarse.

Samrat Gupta [46] proposed a new algorithm based on rough set theory considering the complexity in a real-world network. The algorithm detects disjointed, overlapping and hierarchically nested communities in a network by constructing the granularity of neighborhood vertices and representing them as a rough set. A new metric based on relative connectivity is also introduced, which is used as a measure of merged ensembles. The method has a good competitive advantage for the community detection problem.

The source in [48] combined rough set theory with a complex network, gave a definition of the rough network and proposed a new quality measurement method for exploratory analysis of the community structure in a single network and in multiple networks. The network is able to evaluate detected communities without the need for reference structures. Furthermore, the proposed new method for evolutionary estimation and discovery of interactions among communities enables experts to gain a deep understanding of real systems. Applying rough network theory to community detection analysis shows that the algorithm has huge potential.

(2)

Overlapping community discovery

The source in [43] proposed an overlapping community discovery algorithm, OCDRD, based on rough set theory and density peaks. The algorithm combines the idea of a density peak with a rough set, and it can automatically determine the number of communities, avoiding the subjective influence of humans. This method uses the idea of a rough set to divide the uncertainty area of the community, so as to excavate overlapping vertices in the uncertainty area and obtain a community structure with a better division effect. Later, scholars [44,45] proposed an overlapping community discovery algorithm, OCDRDD, based on rough set theory and distance dynamic models. This method considers that the distance between vertices in the network changes with time. This method takes into account the fact that the distance between vertices in the network is constantly changing over time. According to the network topology, K initial core vertices are determined in combination with the degree centrality, the approximate set and boundary domain of the community are initialized, and the optimal overlapping community structure division is obtained through iterative adjustment of the distance dynamic model.

The source in [47] proposed an overlapping community detection algorithm based on link granularity information and rough set theory [47]. The algorithm uses the neighborhood links around each pair of vertices to form an initial link subset and then iteratively computes the constrained link approximation of the link subset until convergence. The upper approximate subsets after each iteration are constrained and merged using the notion of mutual link reciprocity. Experiments show that the algorithm can effectively detect overlapping communities in a complex network, and the effectiveness of the algorithm is proved by comparing it with advanced algorithms.

3.2.3. Other Problems

The biological transmission network is one of the common complex networks. The source in [80] applied a rough complex network to the problem of malaria parasite transmission. Using a complex network as the underlying model for the spread of Plasmodium parasites in the Phytophthora machine, the vertices in the network are interpreted as the set of origin points for Plasmodium, the set of attractants and the set of repellents. A variable precision rough set model-based measurement method is defined to quantitatively evaluate the cohesion of Plasmodium connections between different regions of interest.

In order to solve the problem that compound faults are difficult to identify in the fault diagnosis of diesel generator sets, scholars [81] proposed a fault diagnosis method based on a neighborhood rough set. The method uses the variational mode decomposition method to decompose the collected acoustic signal and forms an initial feature set, and then the optimized neighborhood rough set is used for feature screening, and the community structure in the complex network is used to establish a fault diagnosis network. The model uses the community distinguishing criterion function to figure out the community structure and achieve the purpose of fault diagnosis and classification.

The source in [82] transformed the multi-granularity rough set attribute reduction problem into a discrete multi-objective optimization problem. The study uses the idea of swarm intelligence as a framework and realizes the precision of attribute reduction by designing a population topology structure with excellent individual information interaction functions and genetic operators that maintain good population diversity. The population topological space has a complex network topology structure, and the spatial structure of the complex network is used to represent the interactional relationship between individuals in the population. The network structure with specific information dissemination performance can improve the transmission efficiency of excellent individuals. The attribute appointment optimization algorithm can obtain more comprehensive and higher-quality reduction results, and it has better feasibility and practical significance.

The source in [83] considers the eye-tracking sequence as a complex network and then uses rough set theory to define a metric for evaluating the cohesion of the saccade connections between object components recognized by visual stimuli in eye movement experiments. The article argues that the viewer’s behavior of viewing a scene is ambiguous. That is, fixation on one object component of a visual stimulus cannot uniquely indicate fixations on other object components in adjacent instants. It is one of the main contributions of this article that scholars use rough sets to construct indicators that can evaluate the cohesion of saccade connections and apply them to the research on eye tracking.

4. Modeling Method Based on Fuzzy Set Theory

4.1. Fuzzy Set Theory Modeling Basis

In 1965, Zadeh published an article [84] that formally proposed the concept of a fuzzy set. In classical set theory, a sample can only belong to a certain set accurately. However, fuzzy set theory supports the idea that all samples can belong to this set, but each sample belongs to the set with different degrees of membership. The degree of membership is characterized by the membership function.

4.1.1. Fuzzy Membership Function

The essence of the fuzzy set is membership functions. Membership functions are also called characteristic functions of a fuzzy set. If there is a number $A\left(x\right)\in \left[0,1\right]$ corresponding to any element x in the universe U, then A is called a fuzzy set on U. $A\left(x\right)$ is called the membership degree of x to A. The membership function is an index used to reflect the membership degree of the element x to the set A. The closer the degree of membership is to 1, the higher the degree of membership x is to A; the closer the degree of membership is to 0, the lower the degree of membership of x to A.

There is no mature and effective method for the establishment of membership functions, and most of the establishment methods of the system are still based on experience and experiments. The membership function must satisfy the following two conditions:

(1)

The membership function must have an upper bound of 1 and a lower bound of 0. That is, the value range of the membership function is [0,1];

(2)

For each sample, its membership must be unique. That is, for a fuzzy set, an element can only correspond to one degree of membership.

4.1.2. Fuzzy Clustering Algorithm

Fuzzy cluster analysis utilizes the language of fuzzy mathematics to classify collections. Its essence is to construct a fuzzy matrix based on individual properties and then cluster according to the relationship of membership.

So far, there have been many algorithms for fuzzy clustering problems, and the question of which algorithm to choose in the research generally depends on the given data type, the purpose of clustering and the actual application object [85]. This section only briefly introduces a classical fuzzy clustering algorithm—a fuzzy C-means clustering algorithm (abbreviation: FCM algorithm).

The FCM algorithm is a clustering algorithm based on the function optimal method. The core idea is: divide the n vectors $x_i$ into C groups and find the cluster center of each group, so that the value function (or objective function) of the dissimilarity (or distance) index can be minimized. The algorithm steps are as follows:

(1)

Initialization: take the fuzzy weighting index m = 2, the number of clusters C (2 ≤ C ≤ n), where n is the number of data sample points, the iteration stop threshold is $\epsilon$, the initial cluster center value is P⁽⁰⁾, and the number of iterations l = 0;

(2)

Calculate the partition matrix U composed of the values of membership degrees U^(l):

For any i, k, $d_{ik}$ represents the distance between the sample point $x_k$ and the i-th class. If $d_{ik}{}^{\left(l\right)}>0$, then the membership degree ${\mu }_{ik}$ of the sample point $x_k$ and the i-th class is:

$${\mu }_{ik}=\frac{1}{{{\displaystyle \sum }}_{j=1}^c{\left(\frac{d_{ik}}{d_{jk}}\right)}^{\frac{2}{m-1}}}.$$

For any i, k, if $d_{ik}{}^{\left(l\right)}=0$, then

$${\mu }_{lr}{}^{\left(l\right)}=1,\mathrm{and}\mathrm{when}j\ne r, {\mu }_{lj}{}^{\left(l\right)}=0.$$

(3)

Update the cluster center value:

$$P_i{}^{\left(l+1\right)}=\frac{{{\displaystyle \sum }}_{k=1}^n{\left({\mu }_{ik}{}^m\right)}^{\left(l+1\right)}{x}_k}{{{\displaystyle \sum }}_{k=1}^n{\left({\mu }_{lk}{}^m\right)}^{\left(l+1\right)}}.$$

(4)

If $||P^{\left(l+1\right)}-P^{\left(l\right)}||<\epsilon$, the algorithm stops; otherwise, go to step (2).

However, the time complexity of the algorithm is relatively high, and the algorithm will directly divide the boundary objects into the cluster where the nearest cluster center is located, which has certain limitations. Therefore, many scholars have made improvements on the basis of this algorithm, and the establishment of the improved algorithm model will be discussed in the next section [55,56,57].

4.1.3. Modularity

Modularity is a measure of network structure or image structure. It is a measure of the quality of the partitioning of network templates (also known as vertex sets or communities). The higher the template degree, the tighter the internal connection of the vertex set, and the sparser the connection between the vertex set and the vertex set.

The concept of modularity was first given in the literature by Newman [86], and then scholars improved the functional expression of modularity [87] and gave the final modularity expression:

$$Q=\frac{1}{2m}{\displaystyle \sum }_{ij}\left(A_{ij}-\frac{k_i{k}_j}{2m}\right){\delta }_{ij}.$$

(15)

Here, m is the number of edges in the network; $k_i$ and $k_j$ are the degrees of vertices, $A_{ij}$ is the element in the network adjacency matrix; ${\delta }_{ij}$ stands for: if $i$ and $j$ are in the same community, the value is 1, otherwise it is 0.

When the entire network data cannot be clearly known, the local modularity of the local community can be used to check the rationality of the community. For a community that has been detected, the vertex set of the community is V, and all adjacent vertices of these vertices are added to the set to form a new set V*, and the adjacency matrix of V* is A*. The quality of a community is measured by the proportion of the elements in the vertex set V* that all belong to the vertex set V:

$$\frac{{{\displaystyle \sum }}_{ij}{L}_{ij}\delta \left(c_i,c_j\right)}{{{\displaystyle \sum }}_{ij}{A}_{ij}}=\frac{1}{2m^{\ast }}{\displaystyle \sum }_{ij} A_{ij}\delta \left(c_i,c_j\right).$$

(16)

Here, $L_{ij}$ is the adjacency matrix of V*. m* represents the number of edges in the adjacency matrix. The value of the function $\delta \left(c_i,c_j\right)$ is defined as: if $i$ and $j$ are in the same community, that is, $c_i=c_j$, then it is 1, otherwise it is 0.

Local modularity indicates that the time complexity is much smaller than the global complexity, but for small- and medium-sized networks, the effect of local modularity may be lower than that of global modularity. Therefore, in actual modeling, it is necessary to select suitable models for networks of different scales.

4.2. Fuzzy Set Theory Modeling Method

4.2.1. Community Discovery

So far, the research on modeling fuzzy sets in complex networks has been mainly applied to the community detection problem, and the relevant literature is shown in

Table 4. Modeling of fuzzy set theory in community discovery.

Paper Title	Years	Mean Work
Fuzzy Overlapping Communities in Network [49]	2011	The concept of a fuzzy overlapping partition is proposed.
Fuzzy Clustering in a Complex Network Based on Content Relevance and Link Structures [50]	2016	Considering the membership degree of the cluster to which the vertex belongs, a clustering algorithm (FCAN) based on fuzzy set theory is proposed.
Overlapping Community Detection with Node Structure and Attribute [51]	2016	Reference [51] proposed a complex network fuzzy overlapping community structure detection method based on vertex topology. However, the average execution time of this algorithm is slightly longer, and it is more suitable for sparse networks. Therefore, the literature [52] proposed a fuzzy overlapping community structure detection model based on two-stage clustering to solve the above problems.
Automatic Detection and Simulation of Complex Network Fuzzy Overlapping Community Structure [52]	2020
Community Discovery of Complex Network Based on Fuzzy Density Peak Clustering Algorithm [53]	2018	In [53], a community discovery algorithm based on the clustering of fuzzy density peaks (CDFDPC) was proposed. The algorithm uses the F_DPC algorithm to determine the core community, and then the fuzzy clustering idea is used to determine the membership degree of each point to complete the distribution of the remaining vertices. Reference [54] proposed a density peak clustering algorithm based on generalized nearest neighbor similarity and designed a multi-step assignment strategy. This strategy effectively avoids the associated errors in the data point allocation process of the traditional DPC algorithm and increases the robustness of the algorithm.
Research on Density Peaks Clustering and Application in Community Detection [54]	2022
Overlapping Community Division Based on Rough Fuzzy Clustering Algorithm [55]	2020	Based on the rough fuzzy clustering algorithm, combined with the concept of signal transmission, an overlapping community structure mining algorithm, RFCMST, based on rough fuzzy clustering and signal transmission is proposed.
Fuzzy Overlapping Community Partitioning Algorithm Based on Vertex Vector Representation [56]	2021	A fuzzy community partition algorithm based on vertex vector representation is proposed.
Research on Design of Fuzzy Clustering Algorithm Based on Q Function Optimization for Weighted Directed Complex Network [57]	2016	On the basis of the traditional algorithm, a new Q function suitable for fuzzy partitioning of a weighted directed complex network is constructed, a fuzzy clustering algorithm for a complex network is designed, and the algorithm is improved for the unstable results of the FCM clustering algorithm.
Fuzzy Analysis and Information Mining on Overlapping Communities in Directed Network Based on Matrix Decomposition [58]	2019	In order to develop a fuzzy community analysis method for a directed network, a new fuzzy metric that can describe the association of directed point groups is introduced, and a new modular index suitable for fuzzy structures of a directed network is constructed.

. Figure 5 lists the main algorithms of fuzzy sets in complex network research and the year they were proposed, and the updates and improvements between the algorithms are indicated by the dotted line with arrows. For example, the algorithm GNS-DPC is proposed on the basis of the algorithm DPC, which is an improvement of the algorithm.

In [88], starting from fuzzy overlapping community detection methods, the authors reviewed the research progress on fuzzy overlapping community detection in complex networks according to different fuzzy membership degree acquisition methods, focusing on the fuzzy modularity optimization method based on an evolutionary algorithm. More than five years after the paper was published, research modeling approaches to this problem have made greater progress. The modeling of complex network community discovery based on fuzzy set theory is mainly researched from the following two perspectives:

(1)

Topological structure

The clique structure is one of the common and important topological properties of complex networks. It has the characteristics of tight intra-cluster connections and sparse inter-cluster connections. For the extraction method of overlapping community structures in complex networks, many scholars have studied the fuzzy points in the network [89,90]. In the source in [91], aiming at the in-depth topology analysis of network overlapping clique structure, a new clique-point similarity fuzzy measurement index is defined. The clique-point similarity fuzzy measurement index can be used to further obtain the connection tightness between cliques, and fuzzy vertices contribute to the connection between the two groups. New indicators are constructed to deeply analyze the network macro-topological connection mode and extract key connection vertices. The post-clustering fuzzy analysis framework given in the above literature can not only perform fuzzy clustering on the network, but it can also support fuzzy analysis on overlapping structures. Then, scholars considered that in the design of the optimization algorithm, excessive constraints would filter out meaningful topological information, so an optimal objective function with fewer constraints was established, and a symmetric matrix decomposition algorithm was used to implement the approximation. The new metric retains more network topology information, so the obtained clustering results are more accurate than the traditional fuzzy membership [92].

The source in [90] proposed a new method to identify group structure in a complex network using fuzzy concepts. The method combines generalized modular functions, spectral mapping and fuzzy clustering techniques to project network vertices into a d-dimensional Euclidean space. Then, the FCM method based on general Euclidean distance is introduced in the d-dimensional space to cluster the data points. The appropriate number of clusters is obtained by maximizing the modularity function for the variable d. Finally, a soft allocation matrix is obtained to determine the membership of the final cluster with a specified threshold. Later, scholars applied this model to the problem of community detection in a complex network [93].

The source in [51] proposed a complex network fuzzy overlapping community structure detection method based on vertex topology. The method uses the cosine similarity to calculate the similarity between the candidate vertices and the fuzzy overlapping community structure, and then a partial modularity incremental algorithm is used to build a partial search model. Combined with the detected communities, the membership matrix is calculated to obtain the fuzzy overlapping community structure. However, the average execution time of this algorithm is slightly longer, and it is more suitable for sparse networks. Aiming at the above problems, the source in [52] proposed a fuzzy overlapping community structure detection model based on two-stage clustering. The model uses a one-pass clustering algorithm to automatically divide the fuzzy overlapping vertices in the model to confirm the number of cluster centers and overlapping community structures in the complex network. Then, the modularity function is used as the objective function, the complex network fuzzy overlapping community structure is output after multiple iterations, and then the automatic detection of the complex network fuzzy overlapping community structure is realized. The algorithm not only shortens the average execution time, but it also reduces the missed detection rate and improves the accuracy rate.

In order to develop the fuzzy community analysis method of a directed network, the source in [58] introduced a new fuzzy measurement index that can describe the relationship between directed point groups, and a new type of module index is constructed that is suitable for the fuzzy structure of the directed network. In addition, the model can also be used for in-depth analysis of the community topology of directed networks, revealing the deep topology information of the network and providing a new research direction for post-clustering analysis of complex networks.

(2)

Fuzzy clustering

The overlapping community structures of complex networks in the real world usually have strong complexity and ambiguity. The complexity is reflected in the fact that some vertices may belong to multiple communities at the same time, and the number of communities to which different overlapping vertices actually belong may be quite different. The ambiguity is mainly reflected in the large difference in the degree of membership of vertices to different communities, and the overlapping degree of boundaries of overlapping communities is fuzzy. Therefore, there is still a large amount of research space for overlapping community detection in complex networks in the real world. The source in [49] proposed the concept of a fuzzy overlapping partition. Fuzzy overlapping community detection is different from traditional discrete overlapping community detection in that it allows for overlapping vertices to have incomplete and inconsistent membership to their communities, and it then uses the fuzzy membership function to quantify the relative membership of overlapping vertices to different communities.

In order to better identify clusters in complex networks, the source in [50] proposed a clustering algorithm (FCAN) based on fuzzy set theory considering the membership degree of the cluster to which the vertex belongs. The algorithm builds a method that can quantify the content correlation between each pair of vertices in the network to process the content information and then uses the connection information in the clustering process to measure the cluster density. This modeling approach identifies fuzzy clusters that are more closely connected and more content related.

The source in [53] improved the density peak clustering (DPC) algorithm based on the data field and information entropy theory and obtained the F_DPC algorithm. This algorithm not only inherits the advantages of a fast clustering speed and the ability to discover different clusters of the DPC algorithm, but it can also automatically determine the threshold and cluster center. Then, the idea of fuzzy clustering is introduced, and a community discovery (CDFDPC) algorithm based on fuzzy density peak clustering is proposed. After using the F_DPC algorithm to determine the core community, the algorithm uses fuzzy clustering to determine the degree of membership of each point, completes the distribution of the remaining vertices and distinguishes overlapping vertices by establishing a threshold for the degree of membership. The clustering performance of the algorithm is good, and the experimental results are close to the real results, which proves the feasibility and effectiveness of the algorithm.

The traditional FCM fuzzy clustering algorithm achieves the purpose of clustering by seeking the optimal cost function, but this algorithm does not consider the distribution of objects. The rough fuzzy clustering algorithm is a generalized form of fuzzy clustering algorithm, which considers the existence of boundary domains, that is, some vertices may vaguely exist in two clusters. The source in [94] applied a rough fuzzy clustering algorithm to image clustering. Based on the rough fuzzy clustering algorithm combined with the concept of signal transmission, the authors of [55] proposed an overlapping community structure mining algorithm, RFCMST, based on rough fuzzy clustering and signal transmission. Experiments were carried out on three classic complex network datasets. The experimental results showed that the algorithm works well and can divide the target network more reasonably.

Aiming at the problems of poor execution efficiency and low accuracy of the existing fuzzy overlapping community partitioning algorithms, the source in [56] proposed a fuzzy community partitioning algorithm based on vertex vector representation. The algorithm regards the vertex sequence as a sentence in the corpus, uses the Skip-gram model to train the vertex vector and introduces the Gaussian mixture model into the fuzzy community partition algorithm FCM. The model achieves multi-peak vertex data fitting and uses the maximum modularity to obtain the optimal number of communities.

There have been a series of studies on the community partitioning problem of undirected complex networks, but there is still a great deal of research space for the fuzzy partitioning problem of weighted directed complex networks. For a weighted directed complex network, the source in [57] constructed a new Q function suitable for fuzzy division of a weighted directed complex network on the basis of traditional algorithms. Scholars have designed a fuzzy clustering algorithm for complex networks and improved the algorithm for the unstable results of the FCM clustering algorithm, making the algorithm more suitable for the real world. The division accuracy of this algorithm is higher, and the result is more stable, which effectively solves the problem of community division in weighted directed networks.

4.2.2. Other Problems

Power system risk assessment is of great significance to the safe operation of a power grid. The source in [95] analyzed the defects of the traditional risk assessment method for power grid systems and proposed a power grid risk assessment method based on a complex network and fuzzy theory. This method comprehensively considers the topological structure and operation mode of the power grid and uses a fuzzy set to describe the fuzziness of the power grid risk assessment model. In addition, using the fuzzy probability theory, considering the risk membership function of line operation and the probability distribution function of line fault occurrence, the risk assessment problem is quantified, so as to realize the risk assessment of the power grid. This paper applies the complex network model to the power grid risk assessment problem for the first time, which provides a new research direction for an in-depth solution to this problem.

The box-covering algorithm is widely used in the calculation of fractal dimensions and plays a major role in complex networks. The source in [96] proposed a complex network fuzzy fractal dimension model with fuzzy properties. This model can not only solve the uncertain polynomial minimum frame problem in the traditional method, but it can also reduce the randomness and time complexity as much as possible.

The key to applying the complex network model to study a real system is to construct a network generation mechanism that conforms to the actual system according to the characteristics of the system itself, and it is particularly important to establish a complex network model corresponding to the actual system. The source in [97] constructed a complex network model based on an improved fuzzy clustering algorithm. The model first performs fuzzy clustering analysis on the original data and clusters the data with the same characteristics into one category. Then, each cluster is regarded as a vertex in the complex network, and the vertices are directly connected to form a network. Finally, by gradually optimizing the complex network topology, the most ideal complex network is constructed. This model-building method can also be applied to the problem of solving the optimal path.

In order to solve the synchronization problem of T-S fuzzy complex networks, the source in [98] designed a fuzzy sampling data control strategy considering the delay effect. This strategy establishes synchronization criteria for a complex network with target vertices by constructing modified time-dependent Lyapunov functions and using mathematical induction.

For complex networks with reaction–diffusion terms, a state feedback controller is described in the literature [99,100,101] to study the synchronization problem of fuzzy complex networks with reaction–diffusion terms. Different from previous studies, the original membership function is approximated by a piecewise linear membership function, and the synchronization conditions related to the membership function to ensure system synchronization are given in the form of linear matrix inequality, which makes the method more effective and convincing.

5. Challenges and Prospects

Uncertainty phenomena appear in large numbers in real complex networks, making the network structure more complex and uncertain. This paper mainly discusses the basic modeling theory of set pair analysis in uncertainty theory, rough set theory and fuzzy set theory in complex network modeling and summarizes the latest research status of the three uncertainty theories in complex network modeling in detail. There are several potential research directions for the modeling of uncertainty theory in complex networks:

(1)

In traditional graph theory, an edge can only connect two vertices, and it is impossible to model and analyze higher-dimensional situations. A hypergraph is a graph model whose edges can connect multiple vertices. Now, some scholars have constructed an uncertain hypergraph model and applied it to the research of practical problems. However, research in this area still has a number of areas for development;

(2)

A three-way decision is an effective rough decision-making model, and the current research on this is far from sufficient. The question of how to reduce time complexity and space complexity as much as possible while ensuring high precision will be a long-term research hotspot;

(3)

Some scholars have combined rough set theory and fuzzy set theory to propose a series of models and algorithms. However, the cross-integration of other uncertainty theories and their modeling in complex networks remains to be studied.