A State-of-the-Art Review of Probabilistic Portfolio Management for Future Stock Markets
Abstract
1. Introduction
2. Time Series Prediction
2.1. Exponential Smoothing Model (ESM)
2.2. Autoregressive Family Models
2.3. Generalized Autoregressive Conditional Heteroscedasticity (GARCH) Family Model
2.4. Other Models
3. Portfolio Management
3.1. Single Objective Models
3.2. Multi Objective Models
3.3. Dynamic Optimization Models
3.4. Downside Risk Measure Models
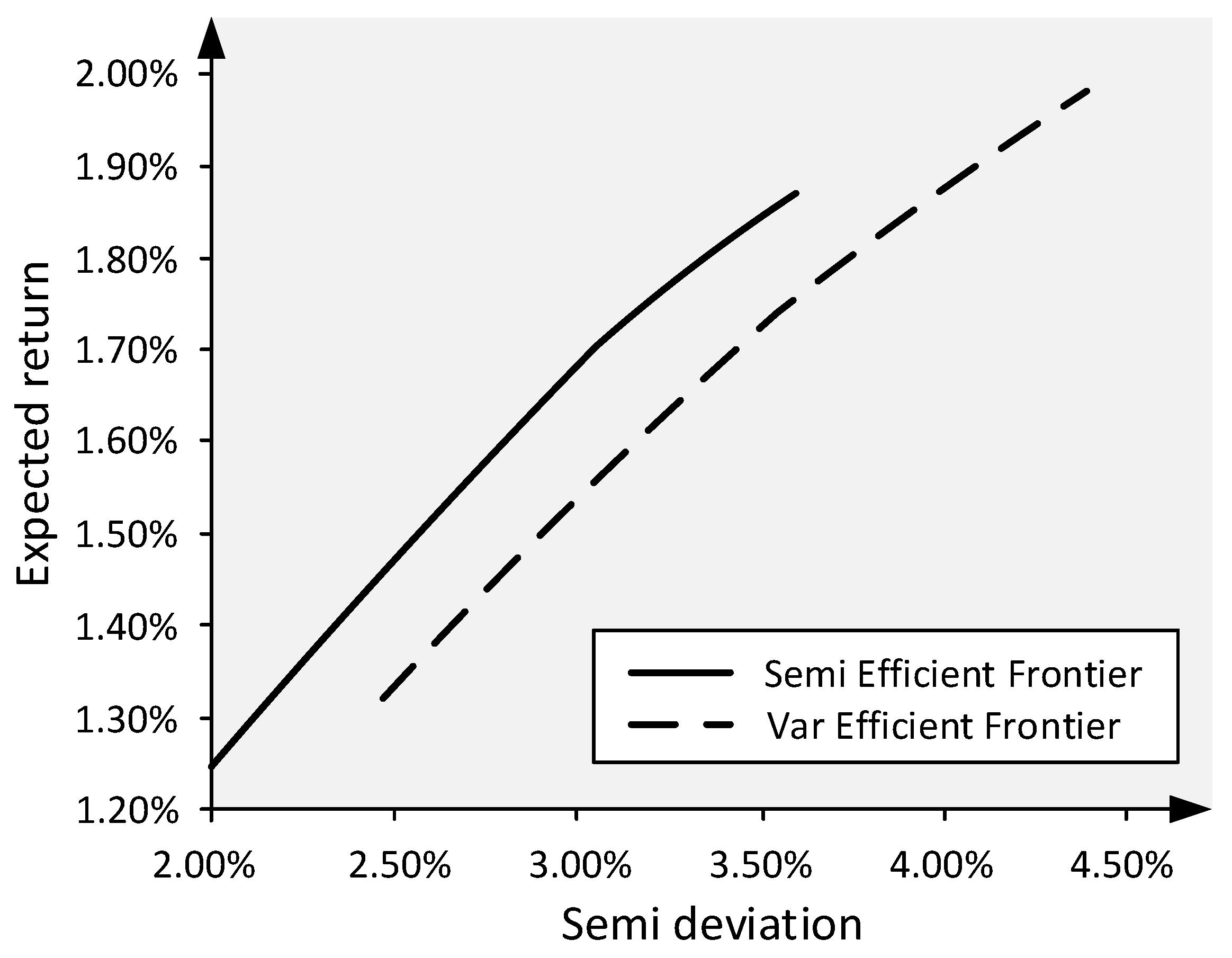
3.4.1. Mean Semi-Variance Model
3.4.2. Mean Absolute Deviation Model
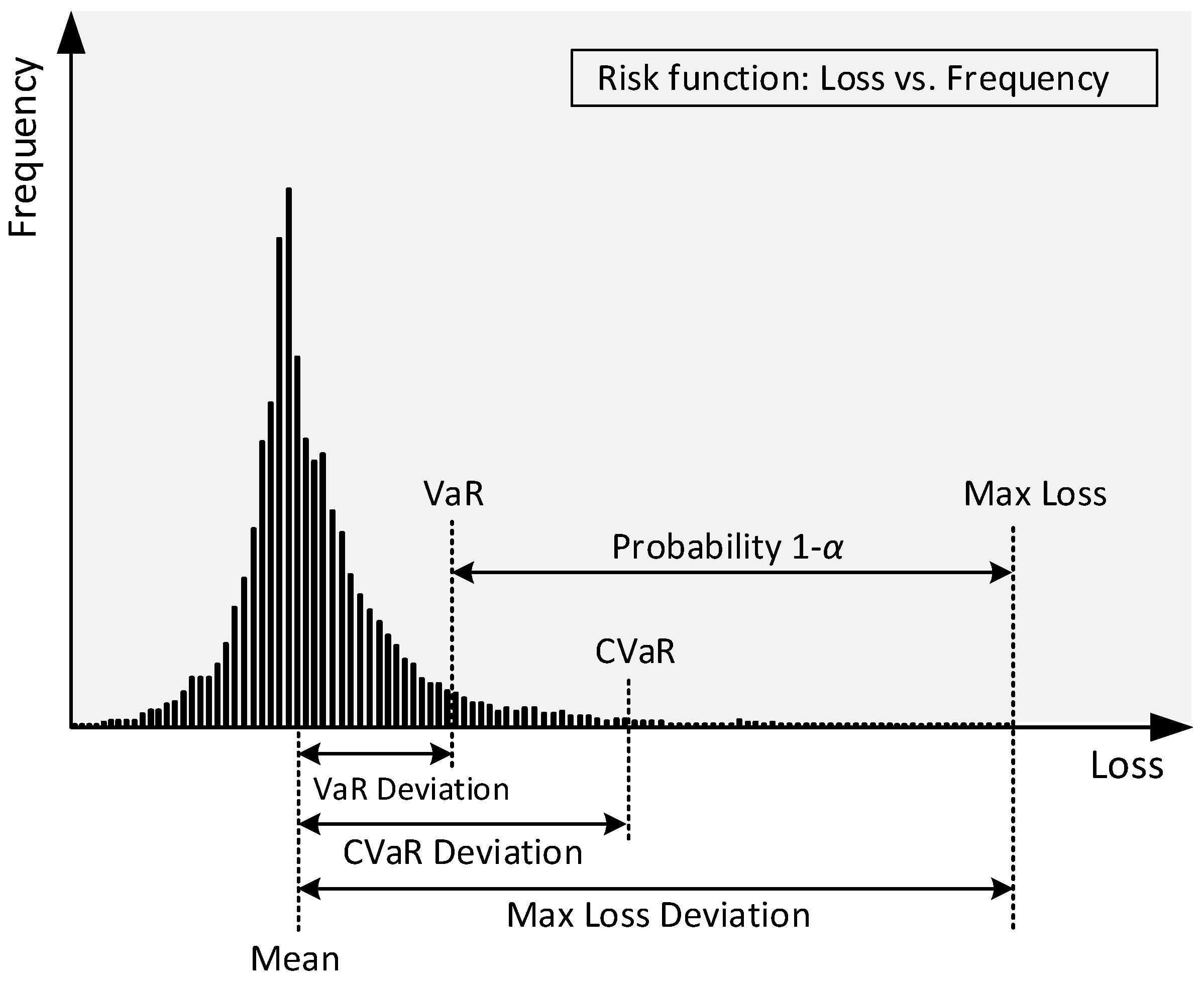
3.4.3. Value at Risk and Conditional Value at Risk Model
3.5. Practical Factors
3.5.1. Transaction Costs
3.5.2. Real World Constraints
3.6. Prediction-Based Models
3.7. Heuristics Methods
4. Monte Carlo Simulation
4.1. Monte Carlo Simulation Definition
4.2. Monte Carlo Simulation in Portfolio Management
Determination of Value at Risk Using Monte Carlo Simulation
4.3. Monte Carlo Simulation in Risk Management
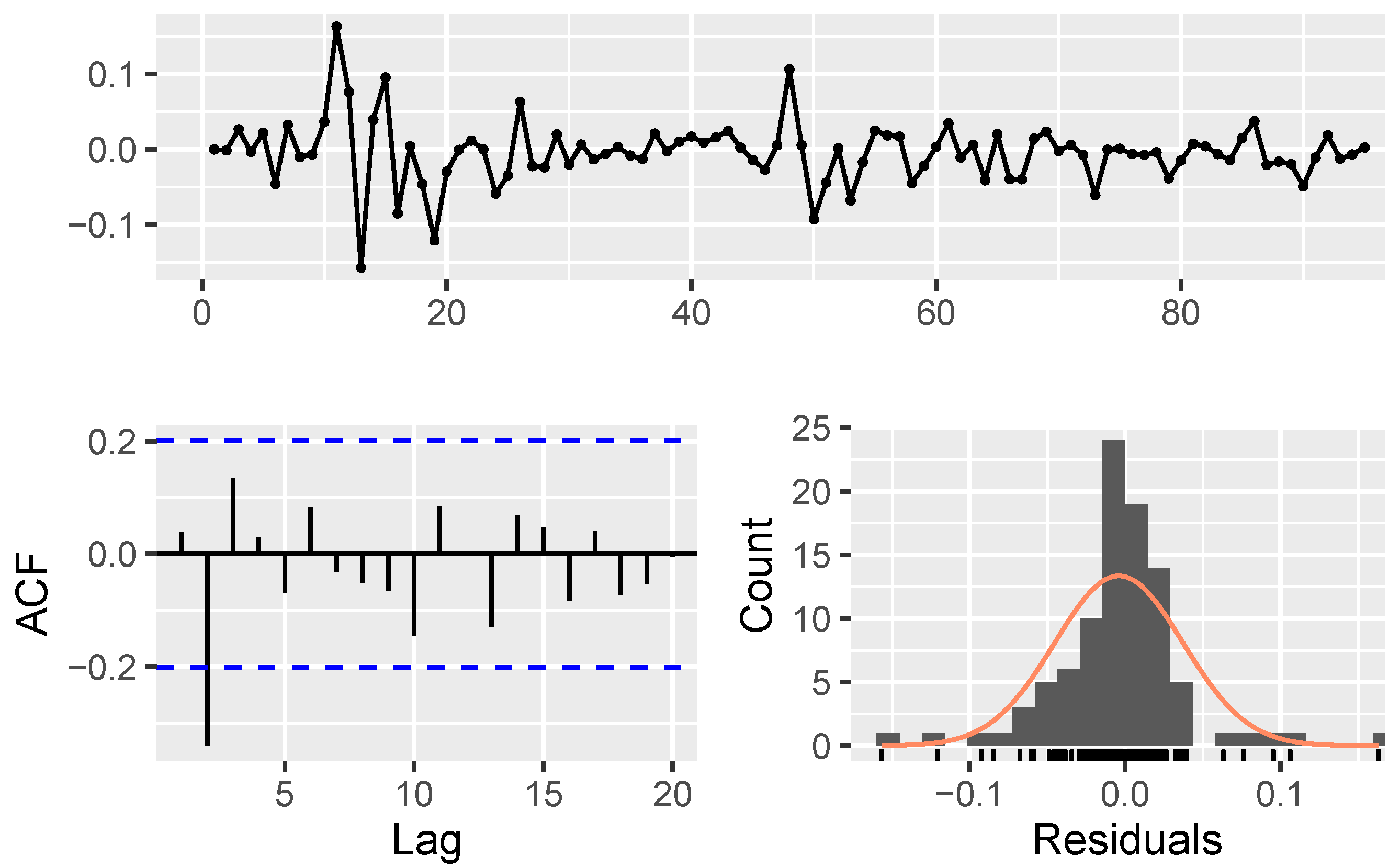
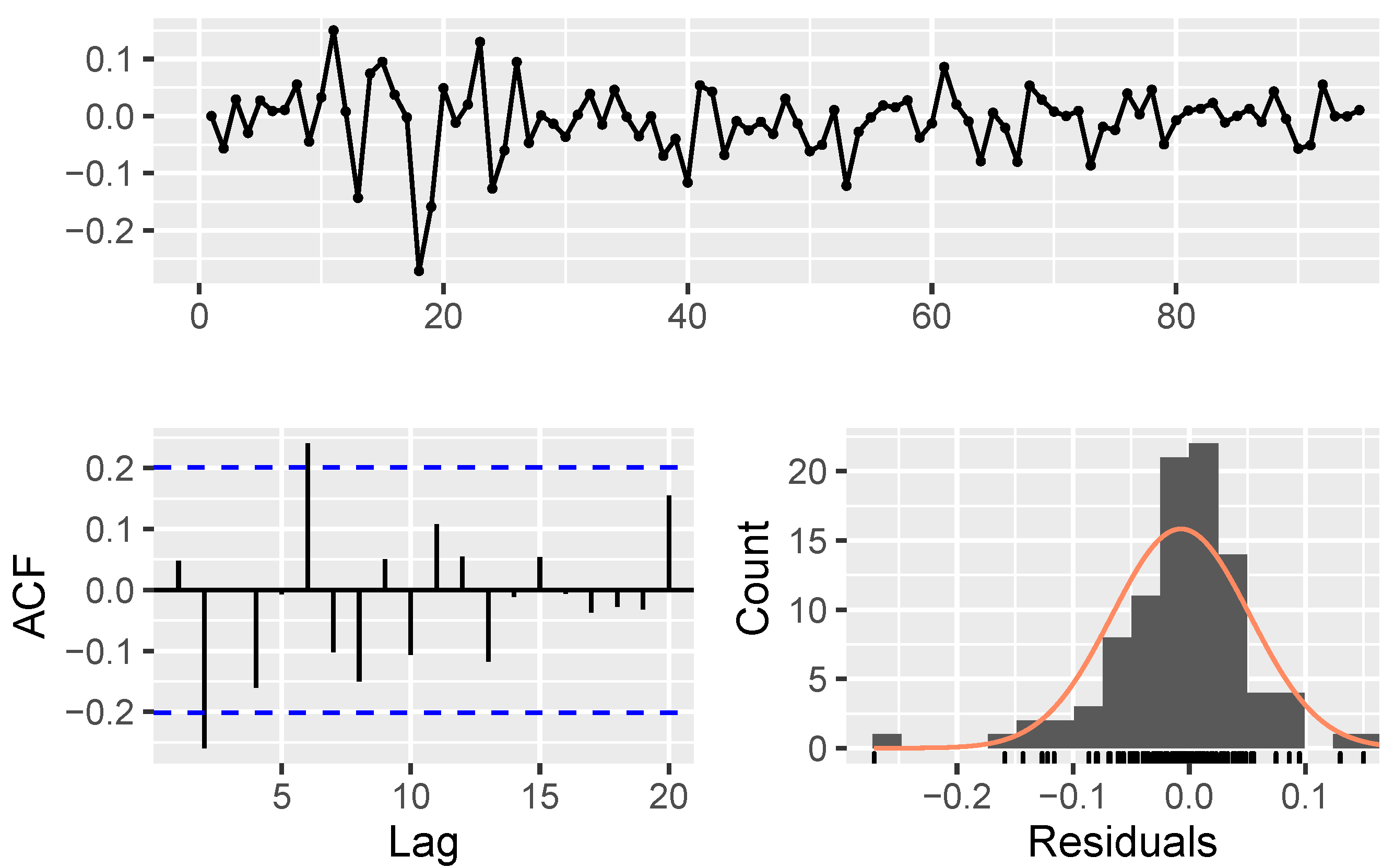
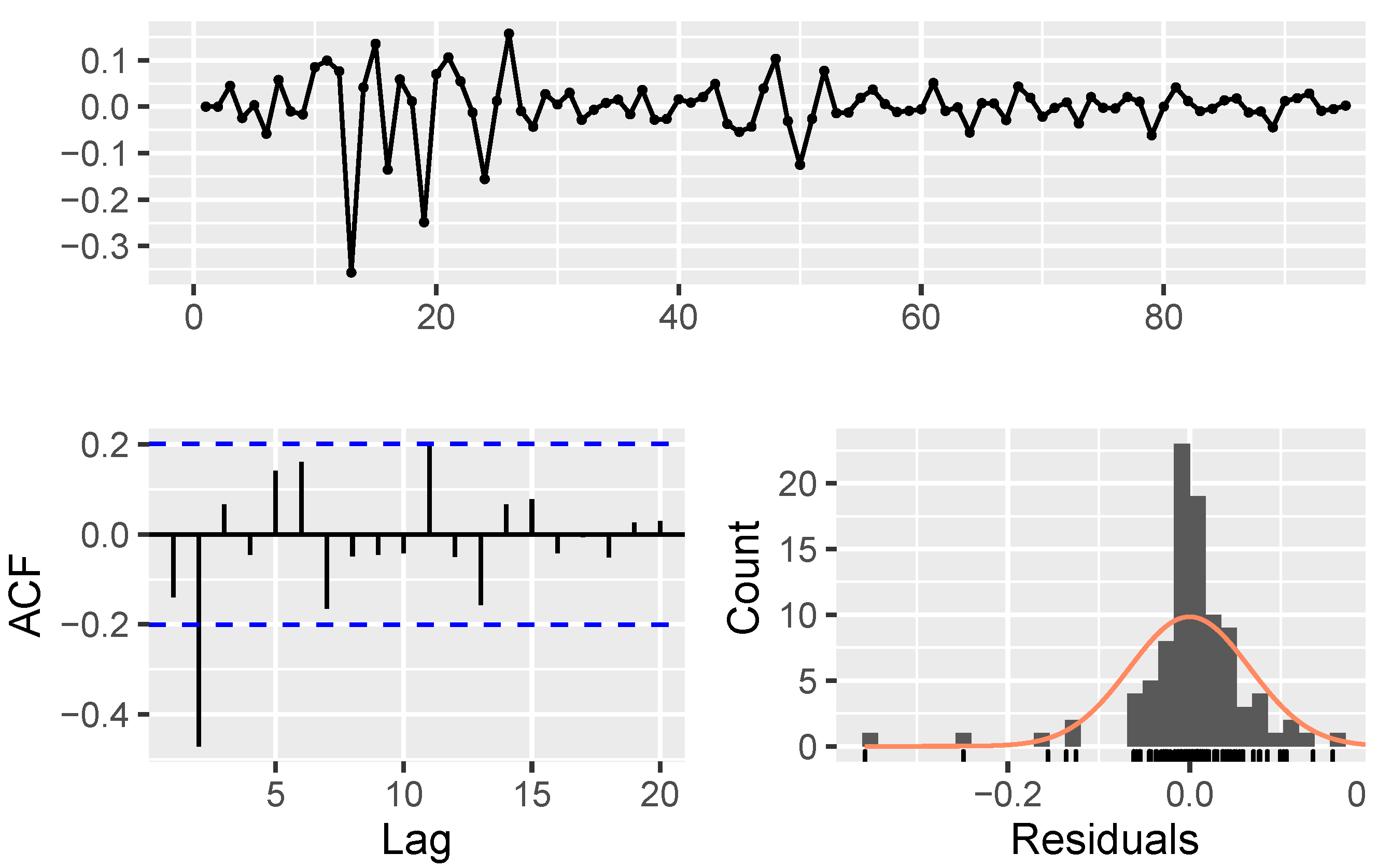
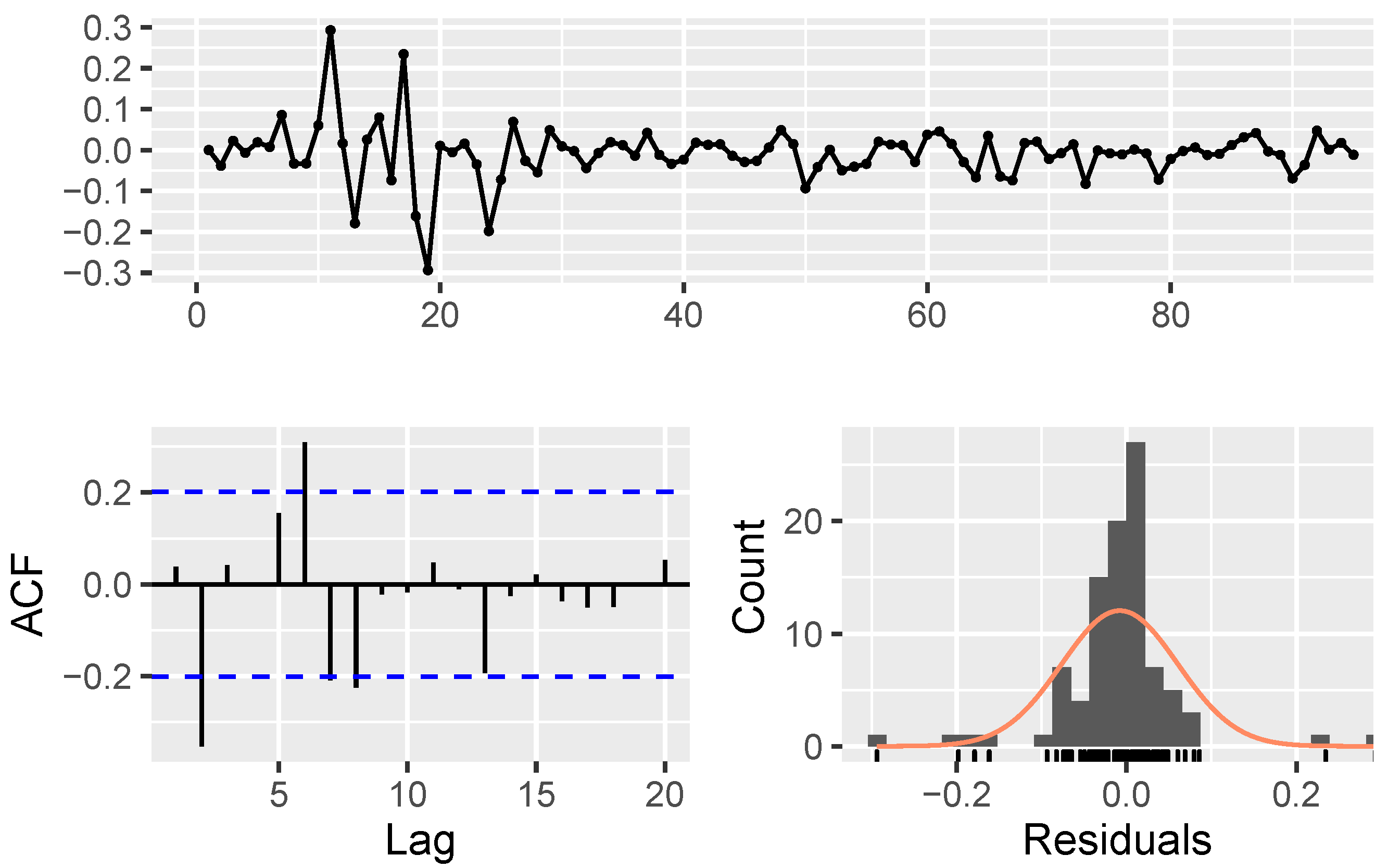
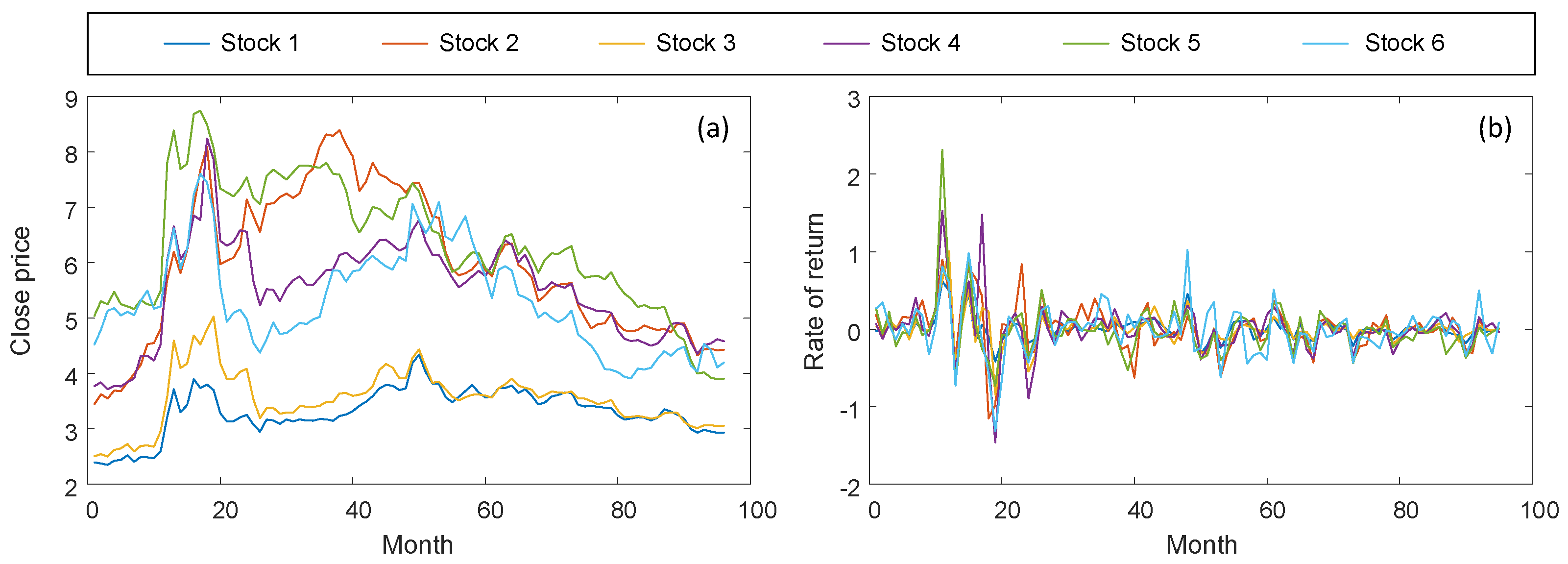
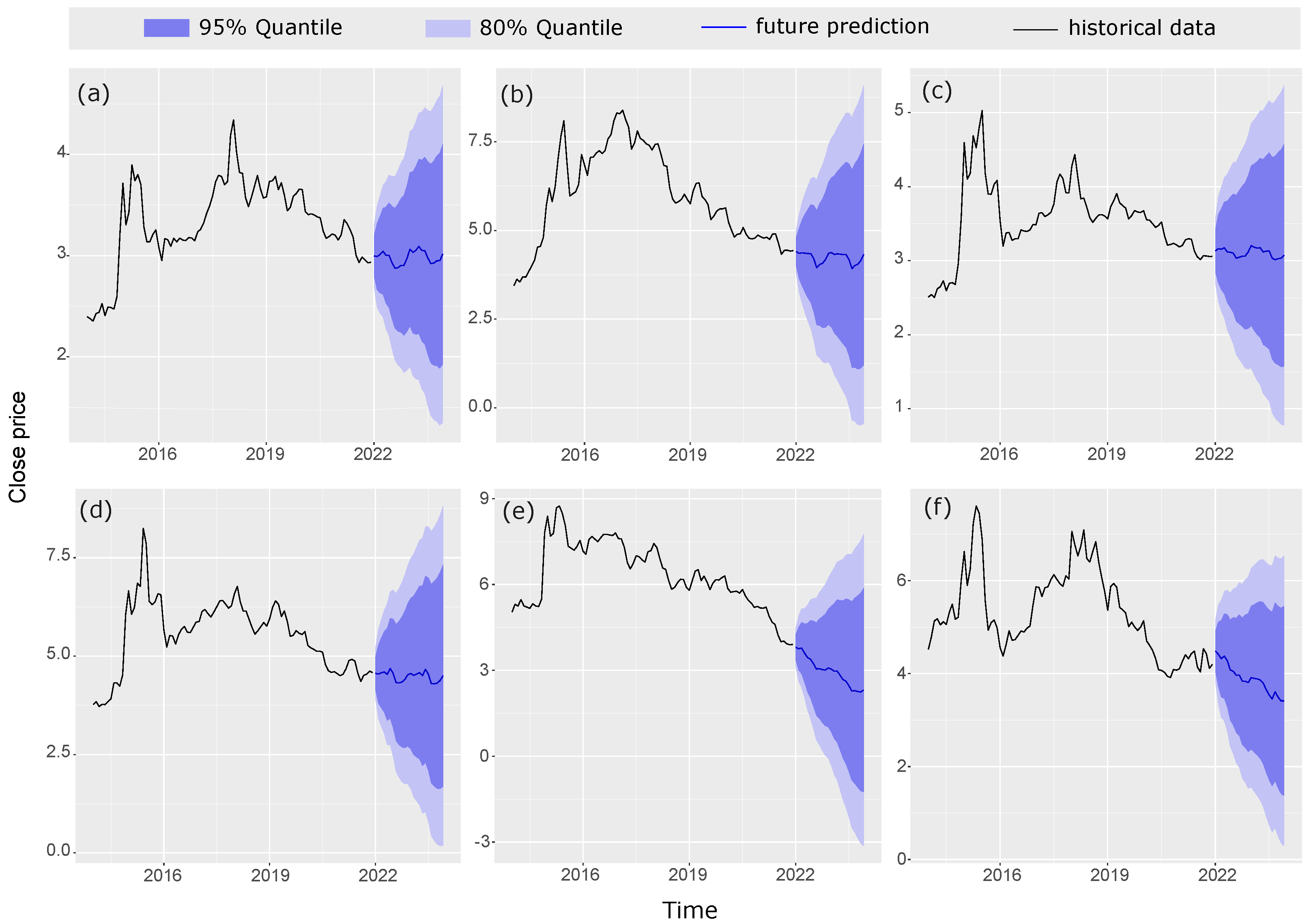
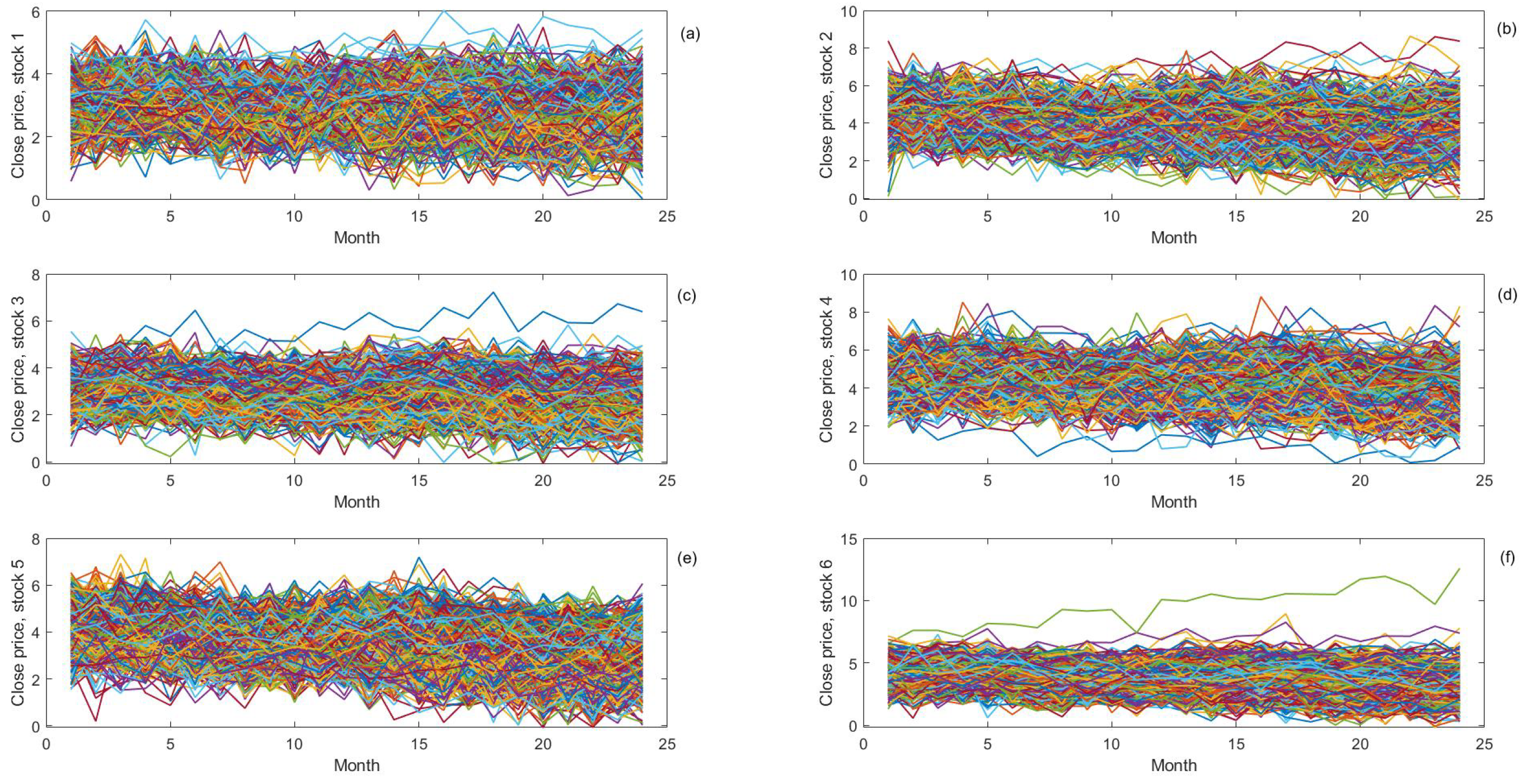
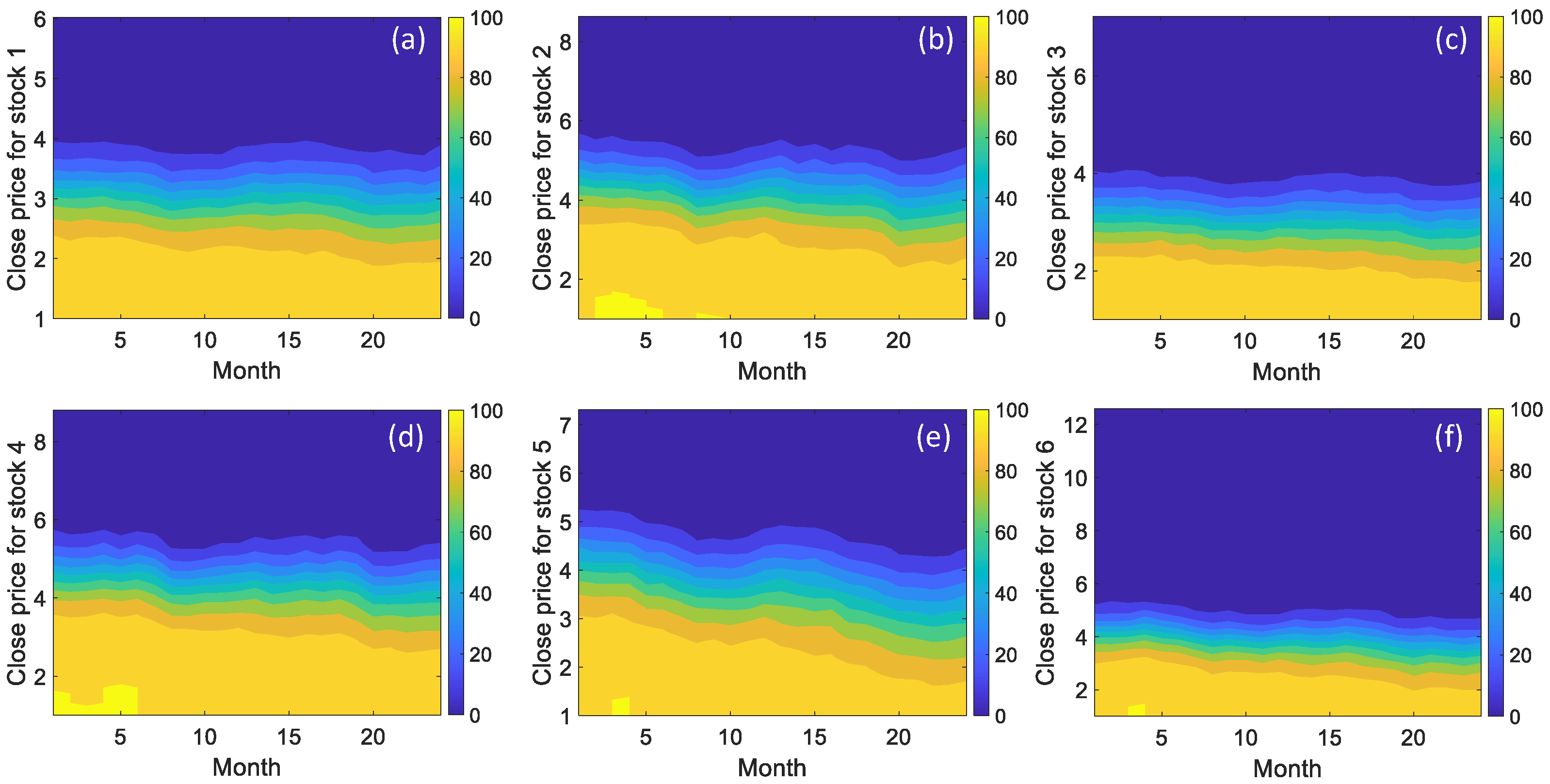
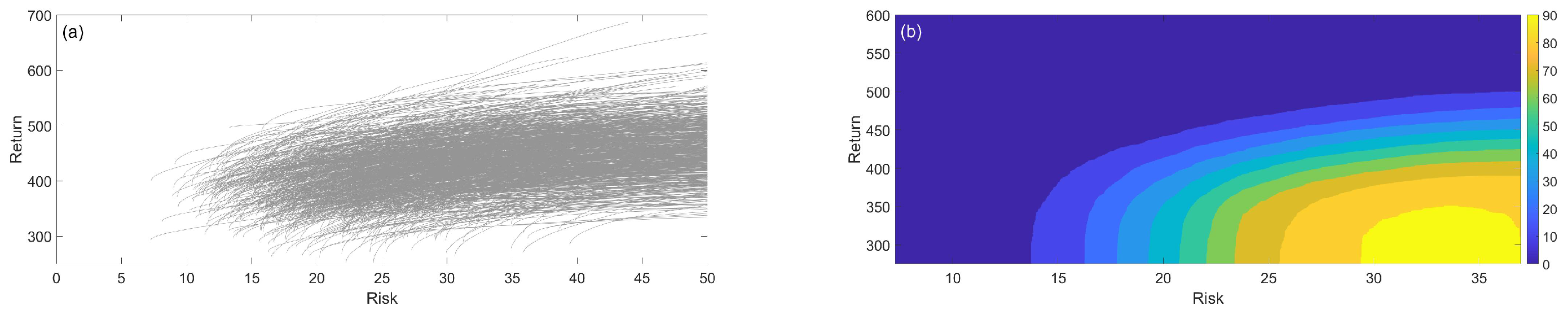
5. Application of the Probabilistic Portfolio Management
- 1.
- All the data were assessed to fill in the missing data.
- 2.
- The trend and seasonality of the time series were also calculated in order to correctly use the NAR model for time series prediction.
- 3.
- The rate of return of the predicted time series was calculated so that the portfolio optimization process can be implemented accurately.
- Importing data into the NAR model and obtaining outputs:
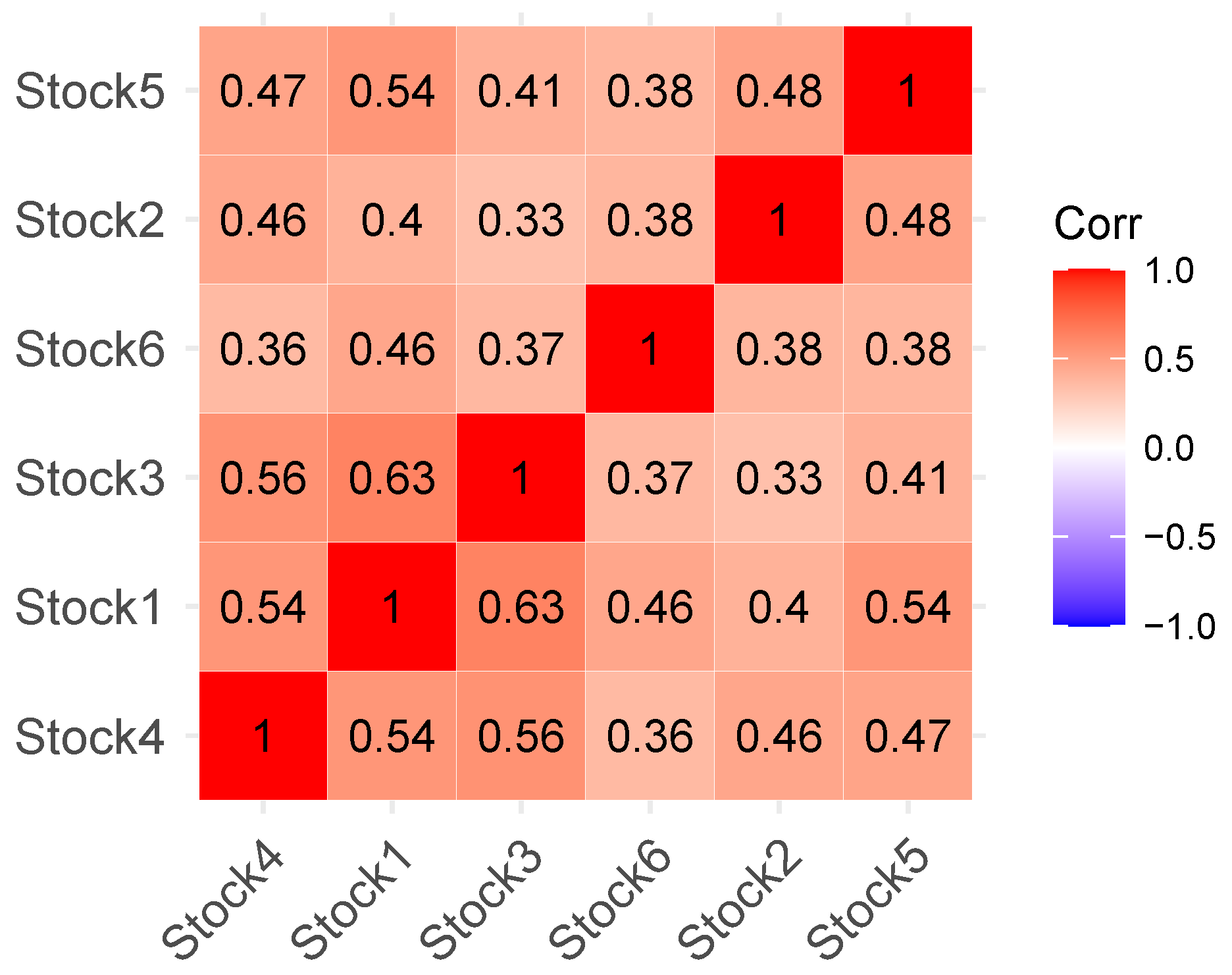
- Correlation matrix:
- Data transformation: Assuming N as the number of companies, the ratio of logs of the closed data, , is defined as follows:
- NAR model formulation:
- where is a hyper-parameter which should be determined by try and error. In cases where , the total sum of adjacency matrix is calculated as . Additionally, , , and follows the normal distribution. A matrix representation of Equation (20) can be provided as follows:
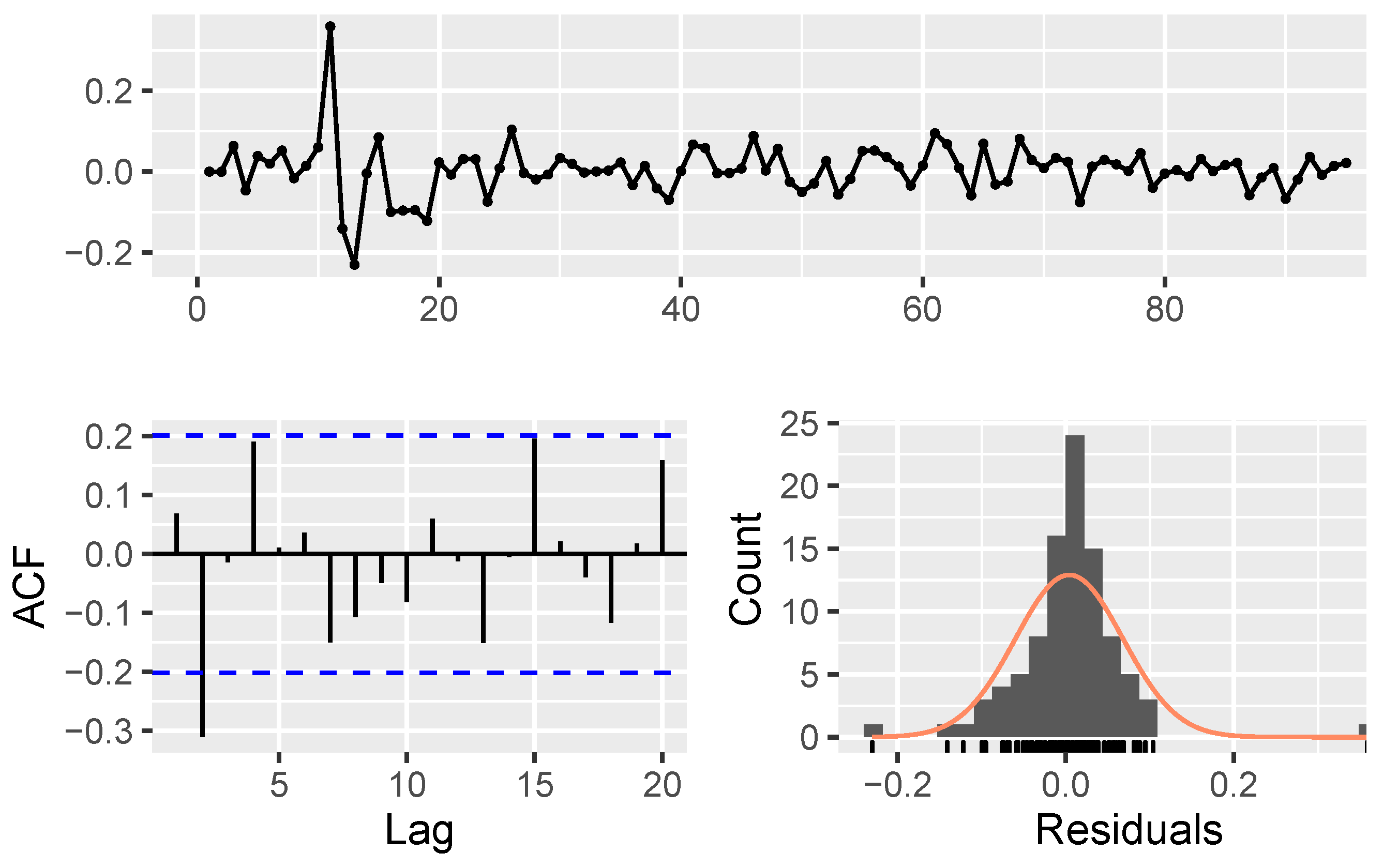
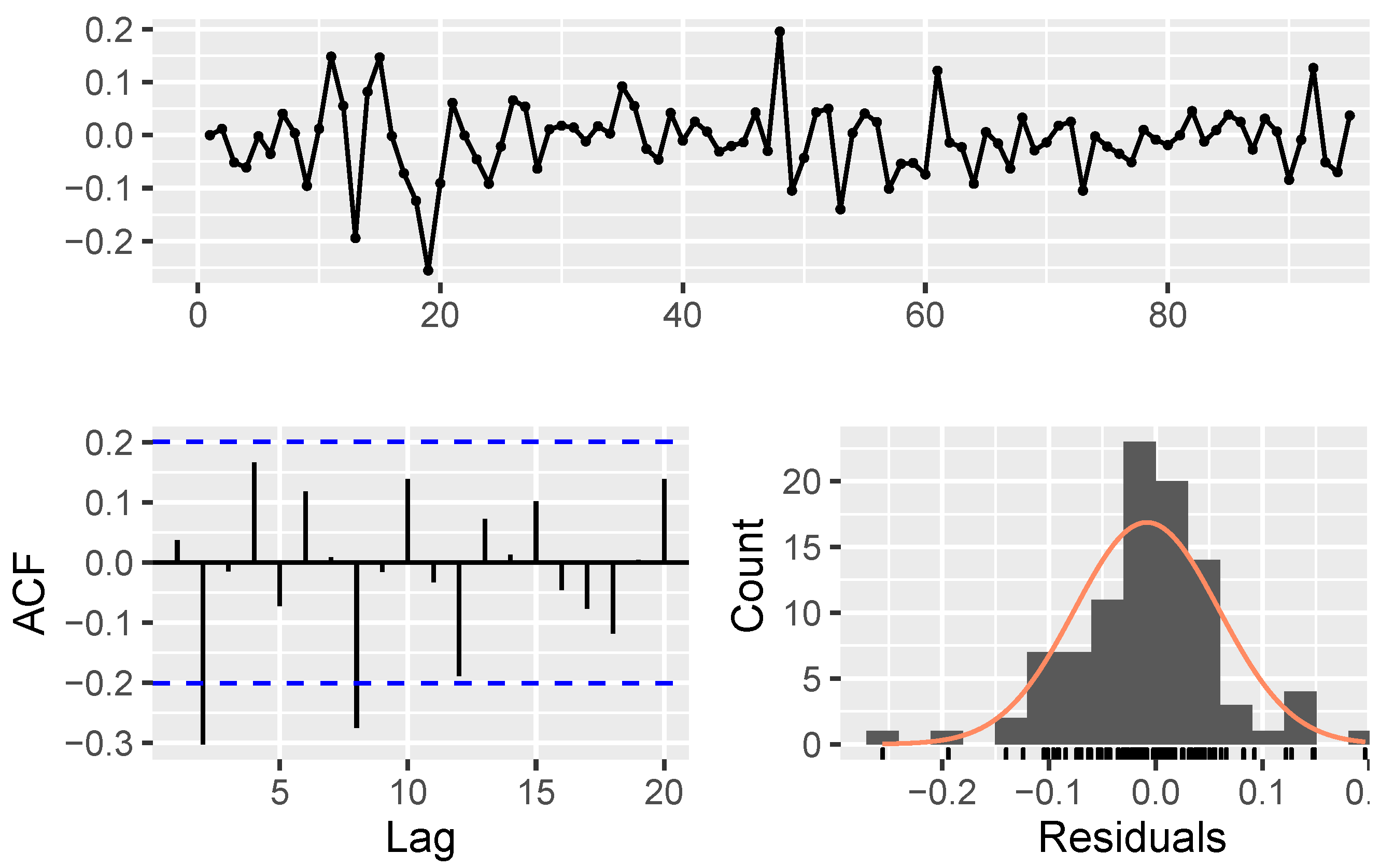
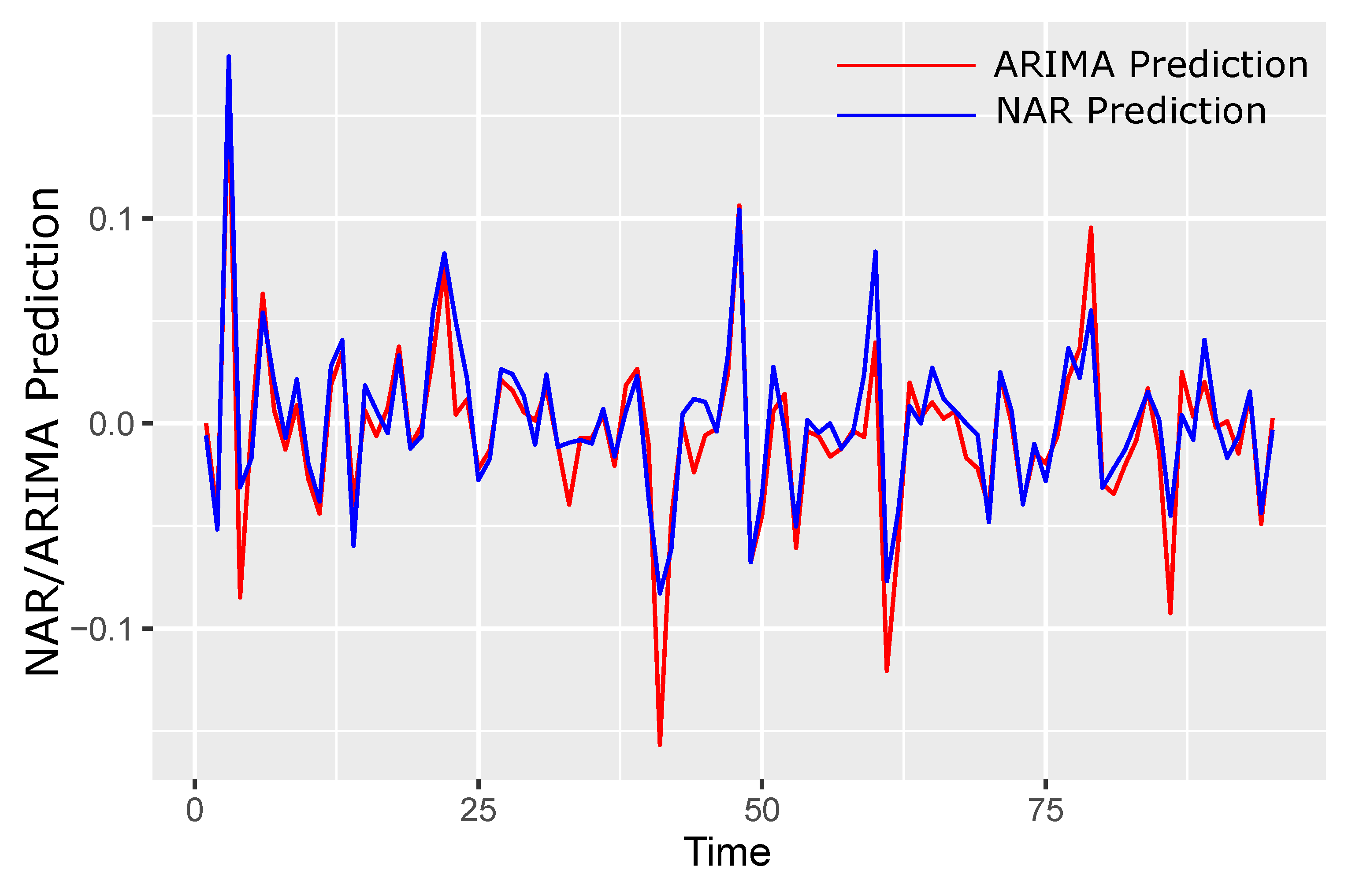
- Model parameters estimation and validation:
| Algorithm 1: The procedure of modeling using NAR |
Data: fetching stock price data Result: estimating . The initialization; Transforming data by Equation 19; Creating correlation matrix, ;  |
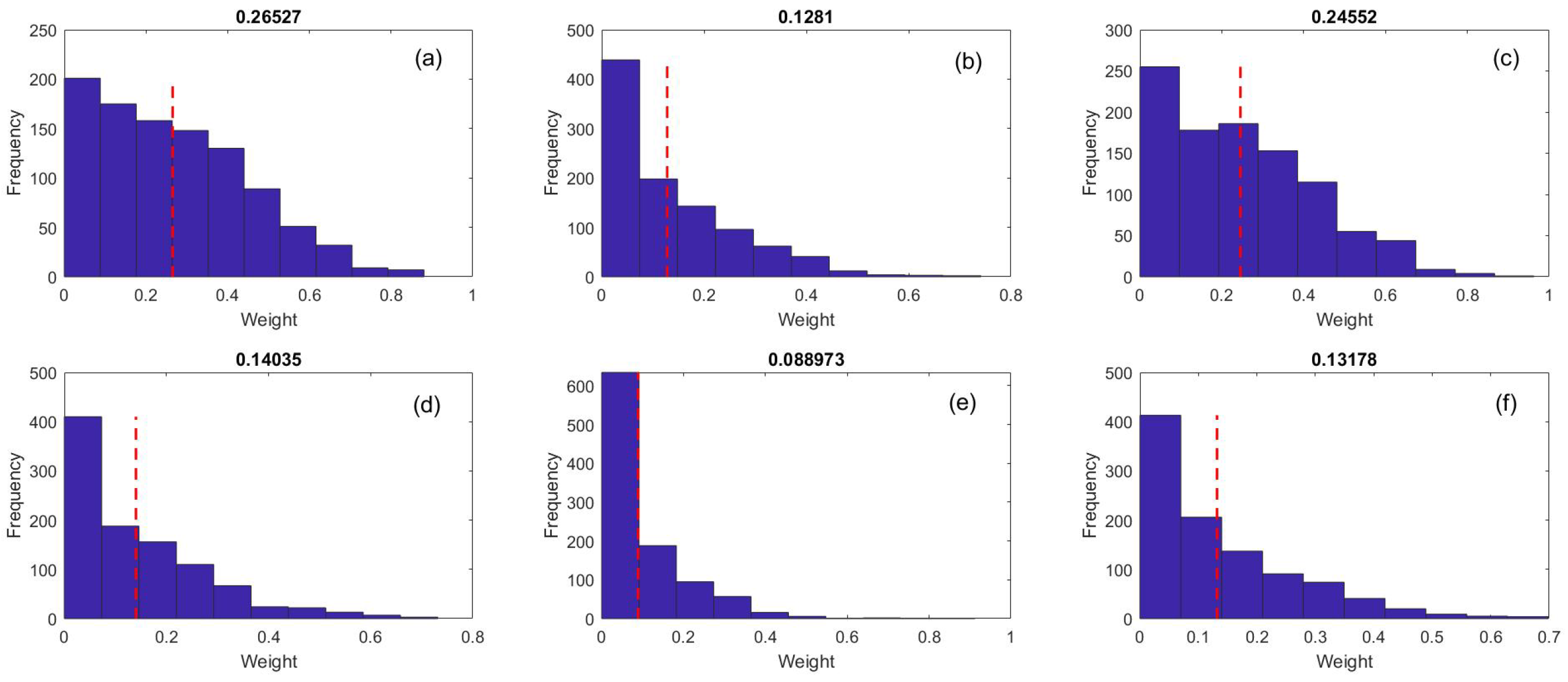
- Given the entire histogram, investors can obtain a more comprehensive view of investment risk, which allows them to set the size of their investment in each company.
- In this investment estimation, uncertainty is taken into account, thereby preventing the output from being confined to one deterministic sample.
- The histogram of investment weight shows what proportion of the generated random realizations corresponds to what amount of investment.
- This expression of investment goes beyond a deterministic expression. That is, in addition to stating the determination of the amount of investment, it also provides its probability distribution.
6. Conclusions
- Using future stock market data instead of historical data provides a more appropriate estimate of stock portfolio risk and return.
- By approximating the time series in the form of a random process by the Monte Carlo sampling method, it can well capture the prevailing uncertainty.
- The portfolio optimization method can be well combined with the random realizations resulting from the Monte Carlo sampling method to provide a probabilistic form of portfolio management.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Billah, B.; King, M.L.; Snyder, R.D.; Koehler, A.B. Exponential smoothing model selection for forecasting. Int. J. Forecast. 2006, 22, 239–247. [Google Scholar] [CrossRef]
- de Faria, E.; Albuquerque, M.P.; Gonzalez, J.; Cavalcante, J.; Albuquerque, M.P. Predicting the Brazilian stock market through neural networks and adaptive exponential smoothing methods. Expert Syst. Appl. 2009, 36, 12506–12509. [Google Scholar] [CrossRef]
- Dutta, A.; Bandopadhyay, G.; Sengupta, S. Prediction of Stock Performance in the Indian Stock Market Using Logistic Regression. Int. J. Bus. Information 2012, 7, 105–136. [Google Scholar]
- Devi, B.U.; Sundar, D.; Alli, P. An Effective Time Series Analysis for Stock Trend Prediction Using ARIMA Model for Nifty Midcap-50. Int. J. Data Min. Knowl. Manag. Process. 2013, 3, 65–78. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, J.Z.; Zhang, Z.G.; Guo, S.P. Stock index forecasting based on a hybrid model. Omega 2012, 40, 758–766. [Google Scholar] [CrossRef]
- Rahman, A.; Hasan, M.M. Modeling and Forecasting of Carbon Dioxide Emissions in Bangladesh Using Autoregressive Integrated Moving Average (ARIMA) Models. Open J. Stat. 2017, 7, 560–566. [Google Scholar] [CrossRef]
- Usha, T.M.; Balamurugan, S.A.A. Seasonal Based Electricity Demand Forecasting Using Time Series Analysis. Circuits Syst. 2016, 7, 3320–3328. [Google Scholar] [CrossRef]
- Nerlove, M.; Diebold, F.X. Time Series Analysis. In Time Series and Statistics; Palgrave Macmillan UK: London, UK, 1990; pp. 294–309. [Google Scholar] [CrossRef]
- Ho, S.; Xie, M. The use of ARIMA models for reliability forecasting and analysis. Comput. Ind. Eng. 1998, 35, 213–216. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series: A Data Analysis Approach Using R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock Price Prediction Using the ARIMA Model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 106–112. [Google Scholar] [CrossRef]
- Bhuriya, D.; Kaushal, G.; Sharma, A.; Singh, U. Stock market predication using a linear regression. In Proceedings of the 2017 International conference of Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 20–22 April 2017; pp. 510–513. [Google Scholar] [CrossRef]
- Liu, W.; Morley, B. Volatility Forecasting in the Hang Seng Index using the GARCH Approach. Asia-Pac. Financ. Mark. 2009, 16, 51–63. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987. [Google Scholar] [CrossRef]
- Mahajan, V.; Thakan, S.; Malik, A. Modeling and Forecasting the Volatility of NIFTY 50 Using GARCH and RNN Models. Economies 2022, 10, 102. [Google Scholar] [CrossRef]
- Haas, M.; Pigorsch, C. Financial Economics, Fat-Tailed Distributions. In Complex Systems in Finance and Econometrics; Springer: New York, NY, USA, 2009; pp. 308–339. [Google Scholar] [CrossRef]
- Shi, F.; Sun, X.Q.; Gao, J.; Wang, Z.; Shen, H.W.; Cheng, X.Q. The prediction of fluctuation in the order-driven financial market. PLoS ONE 2021, 16, e0259598. [Google Scholar] [CrossRef]
- Budiharto, W. Data science approach to stock prices forecasting in Indonesia during Covid-19 using Long Short-Term Memory (LSTM). J. Big Data 2021, 8, 47. [Google Scholar] [CrossRef]
- Cheteni, P. Stock Market Volatility Using GARCH Models: Evidence from South Africa and China Stock Markets. J. Econ. Behav. Stud. 2017, 8, 237–245. [Google Scholar] [CrossRef]
- Nelson, D.B. ARCH models as diffusion approximations. J. Econom. 1990, 45, 7–38. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, Y.; Lei, X.; Zhou, Y. Volatility analysis based on GARCH-type models: Evidence from the Chinese stock market. Econ.-Res.-Ekon. IstražIvanja 2022, 35, 2530–2554. [Google Scholar] [CrossRef]
- Li, W.K.; Mak, T.K. On the Squared Residual Autocorrelations in Non-linear Time Series with Conditional Heteroskedasticity. J. Time Ser. Anal. 1994, 15, 627–636. [Google Scholar] [CrossRef]
- Ma, J.; Liu, L. Multivariate Nonlinear Analysis and Prediction of Shanghai Stock Market. Discret. Dyn. Nat. Soc. 2008, 2008, 1–8. [Google Scholar] [CrossRef]
- Nobi, A.; Maeng, S.E.; Ha, G.G.; Lee, J.W. Effects of global financial crisis on network structure in a local stock market. Phys. Stat. Mech. Its Appl. 2014, 407, 135–143. [Google Scholar] [CrossRef]
- Zhang, W.; Zhuang, X. The stability of Chinese stock network and its mechanism. Phys. Stat. Mech. Its Appl. 2019, 515, 748–761. [Google Scholar] [CrossRef]
- Tabak, B.M.; Serra, T.R.; Cajueiro, D.O. Topological properties of stock market networks: The case of Brazil. Phys. Stat. Mech. Its Appl. 2010, 389, 3240–3249. [Google Scholar] [CrossRef]
- Sioofy, K.A.; Han, D. Network analysis of the Chinese stock market during the turbulence of 2015–2016 using log-returns, volumes and mutual information. Phys. Stat. Mech. Its Appl. 2019, 523, 1091–1109. [Google Scholar] [CrossRef]
- Sioofy, K.A.; Dong, H. Topological Structure of Stock Market Networks during Financial Turbulence: Non-Linear Approach. Univers. J. Account. Financ. 2019, 7, 106–121. [Google Scholar] [CrossRef]
- Sioofy, K.A.; Han, D. Stock price network autoregressive model with application to stock market turbulence. Eur. Phys. J. 2020, 93, 133. [Google Scholar] [CrossRef]
- Sioofy, K.A.; Mahsuli, M.; Shadabfar, M.; Hosseini, V.R.; Kordestani, H. A proposed fractional dynamic system and Monte Carlo-based back analysis for simulating the spreading profile of COVID-19. Eur. Phys. J. Spec. Top. 2022, 231, 3427–3437. [Google Scholar] [CrossRef]
- Ban, G.Y.; El Karoui, N.; Lim, A.E. Machine Learning and Portfolio Optimization. Manag. Sci. 2018, 64, 1136–1154. [Google Scholar] [CrossRef]
- Francesco, C.; Andrea, S.; Tardella, F. Linear vs. quadratic portfolio selection models with hard real-world constraints. Comput. Manag. Sci. 2014, 12, 345–370. [Google Scholar]
- Nasim, D.H.; Abolfazl, K.; Markku, K.; Korhonen, P. Solving cardinality constrained mean-variance portfolio problems via MILP. Ann. Oper. Res. 2017, 254, 47–59. [Google Scholar]
- Strumberger, I.; Bacanin, N.; Tuba, M. Constrained Portfolio Optimization by Hybridized Bat Algorithm. In Proceedings of the 2016 7th International Conference on Intelligent Systems, Modelling and Simulation, Bangkok, Thailand, 25–27 January 2016; pp. 83–88. [Google Scholar] [CrossRef]
- Zaheer, H.; Pant, M. Solving Portfolio Optimization Problem through Differential Evolution. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 3982–3987. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, B.; Wang, S.; Lai, K.K. A model for portfolio selection with order of expected returns. Comput. Oper. Res. 2000, 27, 409–422. [Google Scholar] [CrossRef]
- Liu, Y. An Empirical Portfolio Study Based on Markowitz Theory. In Proceedings of the 7th International Conference on Financial Innovation and Economic Development, Online, 14–16 January 2022; pp. 397–404. [Google Scholar]
- Hadi, A.S.; El Naggar, A.A.; Abdel Bary, M.N. New model and method for portfolios selection. Appl. Math. Sci. 2016, 10, 263–288. [Google Scholar] [CrossRef]
- Qu, B.Y.; Zhou, Q.; Xiao, J.M.; Liang, J.J.; Suganthan, P.N. Large-Scale Portfolio Optimization Using Multiobjective Evolutionary Algorithms and Preselection Methods. Math. Probl. Eng. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Bili, C.; Yangbin, L.; Wenhua, Z.; Hang, X.; Zhang, D. The mean-variance cardinality constrained portfolio optimization problem using a local search-based multi-objective evolutionary algorithm. Appl. Intell. 2017, 47, 505–525. [Google Scholar] [CrossRef]
- Jalota, H.; Thakur, M. Genetic algorithm designed for solving portfolio optimization problems subjected to cardinality constraint. Int. J. Syst. Assur. Eng. Manag. 2017, 9, 294–305. [Google Scholar] [CrossRef]
- Miryekemami, S.A.; Sadeh, E.; Sabegh, Z.A. Using Genetic Algorithm in Solving Stochastic Programming for Multi-Objective Portfolio Selection in Tehran Stock Exchange. Adv. Math. Financ. Appl. 2017, 2, 107–120. [Google Scholar]
- Zhao, P.; Gao, S.; Yang, N. Solving Multi-Objective Portfolio Optimization Problem Based on MOEA/D. In Proceedings of the 12th International Conference on Advanced Computational Intelligence (ICACI), Dali, China, 14–16 August 2020; pp. 30–37. [Google Scholar]
- Samuelson, P.A. Lifetime portfolio selection by dynamic stochastic programming. Rev. Econ. Stat. 1969, 51, 239–246. [Google Scholar] [CrossRef]
- Grauer, R.R.; Hakansson, N.H. On the use of mean-variance and quadratic approximations in implementing dynamic investment strategies: A comparison of returns and investment policies. Manag. Sci. 1993, 39, 856–871. [Google Scholar] [CrossRef]
- Merton, R.C. Lifetime portfolio selection under uncertainty: The continuous-time case. Rev. Econ. Stat. 1969, 51, 247–257. [Google Scholar] [CrossRef]
- Karatzas, I.; Lehoczky, J.P.; Shreve, S.E. Optimal portfolio and consumption decisions for a “small investor” on a finite horizon. Siam J. Control. Optim. 1987, 25, 1557–1586. [Google Scholar] [CrossRef]
- Bajeux-Besnainou, I.; Portait, R. Dynamic Asset Allocation in a Mean-Variance Framework. Manag. Sci. 1998, 44, 79–95. [Google Scholar] [CrossRef]
- Li, D.; Ng, W.L. Optimal Dynamic Portfolio Selection: Multiperiod Mean-Variance Formulation. Math. Financ. 2000, 10, 387–406. [Google Scholar] [CrossRef]
- Yi, L.; Li, Z.F.; Li, D. Multi-period portfolio selection for asset-liability management with uncertain investment horizon. J. Ind. Manag. Optim. 2008, 4, 535–552. [Google Scholar] [CrossRef]
- Sun, Y.; Aw, G.; Teo, K.L.; Yanjian Zhu, X.W. Multi-period Portfolio Optimization Under Probabilistic Risk Measure. Financ. Res. Lett. 2016, 18, 60–66. [Google Scholar] [CrossRef]
- Markowitz, H.; Todd, P.; Xu, G.; Yamane, Y. Computation of mean-semivariance efficient sets by the Critical Line Algorithm. Ann. Oper. Res. 1993, 45, 307–317. [Google Scholar] [CrossRef]
- Henk Grootveld, W.H. Variance vs downside risk: Is there really that much difference? Eur. J. Oper. Res. 1999, 114, 304–319. [Google Scholar] [CrossRef]
- Fama, E.F. Mandelbrot and the Stable Paretian Hypothesis. J. Bus. 1963, 36, 420–429. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Variation of Certain Speculative Prices. J. Bus. 1963, 36, 371–418. [Google Scholar] [CrossRef]
- Quirk, J.P.; Saposnik, R. Admissibility and measurable utility functions. Rev. Econ. Stud. 1962, 29, 140–146. [Google Scholar] [CrossRef]
- Mao, J.C.T. Models of Capital Budgeting, E-V Vs E-S. J. Financ. Quant. Anal. 1970, 4, 657–675. [Google Scholar] [CrossRef]
- Arrow, K.J. Essays in the Theory of Risk-Bearing Paperback; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Bawa, V.S. Optimal rules for ordering uncertain prospects. J. Financ. Econ. 1975, 2, 95–121. [Google Scholar] [CrossRef]
- Foo, T.; Eng, S. Asset allocation in a downside risk framework. J. Real Estate Portf. Manag. 2000, 6, 213–223. [Google Scholar] [CrossRef]
- Estrada, J. Downside Risk in Practice. J. Appl. Corp. Financ. 2006, 18, 117–125. [Google Scholar] [CrossRef]
- Estrada, J. Mean-Semivariance Behaviour: An Alternative Behavioural Model. J. Emerg. Mark. Financ. 2004, 3. [Google Scholar] [CrossRef]
- Boasson, V.; Boasson, E.; Zhou, Z. Portfolio optimization in a mean-semivariance framework. Invest. Manag. Financ. Innov. 2011, 8, 58–68. [Google Scholar]
- Pla-Santamaria, D.; Bravo, M. Portfolio optimization based on downside risk: A mean-semivariance efficient frontier from Dow Jones blue chips. Ann. Oper. Res. 2013, 205, 189–201. [Google Scholar] [CrossRef]
- Liu, Y.J.; Zhang, W.G. A multi-period fuzzy portfolio optimization model with minimum transaction lots. Eur. J. Oper. Res. 2015, 242, 933–941. [Google Scholar] [CrossRef]
- Konno, H.; Yamazaki, H. Mean -Absolute Deviation Portfolio Optimization Model and Its Applications to Tokyo Stock Market. Manag. Sci. 1991, 37, 519–531. [Google Scholar] [CrossRef]
- Chaiyakan, S.; Thipwiwatpotjana, P. Bounds on mean absolute deviation portfolios under interval-valued expected future asset returns. Comput. Manag. Sci. 2021, 18, 195–212. [Google Scholar] [CrossRef]
- Konno, H. Portfolio optimization of small scale fund using mean-absolute deviation model. Int. J. Theor. Appl. Financ. 2003, 6, 403–418. [Google Scholar] [CrossRef]
- Konno, H.; Koshizuka, T. Mean-absolute deviation model. Iie Trans. 2005, 37, 893–900. [Google Scholar] [CrossRef]
- Chang, T.J.; Yang, S.C.; Chang, K.J. Portfolio optimization problems in different risk measures using genetic algorithm. Expert Syst. Appl. 2009, 36, 10529–10537. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–42. [Google Scholar] [CrossRef]
- Jorion, P. How informative are value-at-risk disclosures? Account. Rev. 2002, 77, 911–931. [Google Scholar] [CrossRef]
- Abad, P.; Benito, S.; López, C. A comprehensive review of Value at Risk methodologies. Span. Rev. Financ. Econ. 2014, 12, 15–32. [Google Scholar] [CrossRef]
- Sarykalin, S.; Serraino, G.; Uryasev, S. Value-at-risk vs. conditional value-at-risk in risk management and optimization. In State-of-the-Art Decision-Making Tools in the Information-Intensive Age; Informs: Halethorpe, MD, USA, 2008; pp. 270–294. [Google Scholar]
- Linsmeier, T.J.; Pearson, N.D. Value at Risk. Financ. Anal. J. 2000, 56. [Google Scholar] [CrossRef]
- Alexander, G.; Baptista, A. Economic Implications of Using a Mean-VaR Model for Portfolio Selection: A Comparison with Mean-Variance Analysis. J. Econ. Dybamics Control. 2002, 26, 1159–1193. [Google Scholar] [CrossRef]
- Vo, D.H.; Pham, T.N.; Pham, T.T.V.; Truong, L.M.; Nguyen, T.C. Risk, return and portfolio optimization for various industries in the ASEAN region. Borsa Istanb. Rev. 2019, 19, 132–138. [Google Scholar] [CrossRef]
- Yie, W.L.S.; Chan, K.Y.; Lim, F.P. Estimation of value at risk for stock prices in mobile phone industry. Data Anal. Appl. Math. (DAAM) 2021, 2, 14–26. [Google Scholar]
- Najafi, A.A.; Nopour, K.; Ghatarani, A. Interval optimization of the stock portfolio with the conditional value-at-risk. Financ. Res. 2017, 19, 157–172. [Google Scholar]
- Soleimani, H.; Golmakani, H.R.; Salimi, M.H. Markowitz-based portfolio selection with minimum transaction lots, cardinality constraints and regarding sector capitalization using genetic algorithm. Expert Syst. Appl. 2009, 36, 5058–5063. [Google Scholar] [CrossRef]
- Pogue, G.A. An extension of the Markowitz portfolio selection model to include variable transactions’ costs, short sales, leverage policies and taxes. J. Financ. 1970, 25, 1005–1027. [Google Scholar] [CrossRef]
- Davis, M.H.; Norman, A.R. Portfolio Selection with Transaction Costs. Math. Oper. Res. 1990, 15, 676–713. [Google Scholar] [CrossRef]
- Dumas, B.; Luciano, E. An exact solution to a dynamic portfolio choice problem under transactions costs. J. Financ. 1991, 46, 577–595. [Google Scholar] [CrossRef]
- Morton, A.J.; Pliska, S.R. Optimal portfolio management with fixed transaction costs. Math. Financ. 1995, 5, 337–356. [Google Scholar] [CrossRef]
- Yoshimoto, A. The mean-variance approach to portfolio optimization subject to transaction costs. J. Oper. Res. Soc. Jpn. 1996, 39, 99–117. [Google Scholar] [CrossRef]
- Oksendal, B.; Sulem, A. Optimal consumption and portfolio with both fixed and proportional transaction costs. SIAM J. Control. Optim. 2002, 40, 1765–1790. [Google Scholar] [CrossRef]
- Xue, H.G.; Xu, C.X.; Feng, Z.X. Mean–variance portfolio optimal problem under concave transaction cost. Appl. Math. Comput. 2006, 174, 1–12. [Google Scholar] [CrossRef]
- Lobo, M.S.; Fazel, M.; Boyd, S. Portfolio optimization with linear and fixed transaction costs. Ann. Oper. Res. 2007, 152, 341–365. [Google Scholar] [CrossRef]
- Dai, M.; Zhong, Y. Penalty Methods for Continuous-Time Portfolio Selection with Proportional Transaction Costs. SSRN 2008, 1210105. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S. Multi -period mean-variance portfolio selection with fixed and proportional transaction costs. J. Ind. Manag. Optim. 2013, 9, 643. [Google Scholar] [CrossRef]
- Hui, F.Y.; Ming, N.K.; Boray, H.; Huang, H.C. Portfolio optimization with transaction costs: A two-period mean-variance model. Ann. Oper. Res. 2014, 233, 135–156. [Google Scholar]
- Jianjun, G.; Duan, L.; Xiangyu, C.; Wang, S. Time cardinality constrained mean–variance dynamic portfolio selection and market timing: A stochastic control approach. Automatica 2015, 54, 91–99. [Google Scholar] [CrossRef]
- Andrew, E.B.; Lim, X.Y.Z. Mean-Variance Portfolio Selection with Random Parameters in a Complete Market. Athematics Oper. Res. 2002, 27, 101–120. [Google Scholar]
- Zhu, S.; Li, D.; Wang, S.Y. Risk Control Over Bankruptcy in Dynamic Portfolio Selection: A Generalized Mean-Variance Formulation. IEEE Trans. Autom. Control. 2004, 49, 447–457. [Google Scholar] [CrossRef]
- Xiong, J.; Zhou, X.Y. Mean-variance portfolio selection under partial information. SIAM J. Control. Optim. 2007, 46, 156–175. [Google Scholar] [CrossRef]
- Yuanyuan, Z.; Xiang, L.; Guo, S. Portfolio selection problems with Markowitz’s mean–variance framework: A review of literature. Fuzzy Optim. Decis. Mak. 2017, 17, 125–158. [Google Scholar]
- Enke, D.; Thawornwong, S. The use of data mining and neural networks for forecasting stock market returns. Expert Syst. Appl. 2005, 29, 927–940. [Google Scholar] [CrossRef]
- Azar, A.; Afsar, A. Modeling stock price forecasting with fuzzy neural network approach. Q. J. Bus. Res. 2006, 40, 33–52. [Google Scholar]
- de Freitas, F.D.; De Souza, A.F.; de Almeida, A.R. A Prediction-Based Portfolio Optimization Model. Int. Symp. Robot. Autom. 2006, 520–525. [Google Scholar]
- Centeno, I.R. Georgiev, V.; Mihova, V.P. Price Forecasting and Risk Portfolio Optimization. Aip Conf. Proc. 2019, 2164, 060006. [Google Scholar]
- Chen, Z. Asset Allocation Strategy with Monte-Carlo Simulation for Forecasting Stock Price by ARIMA Model. In Proceedings of the 2022 13th International Conference on E-Education, E-Business, E-Management, and E-Learning (IC4E), Tokyo, Japan, 14–17 January 2022; 2022; pp. 481–485. [Google Scholar]
- Yu, J.R.; Chiou, W.J.P.; Lee, W.Y.; Lin, S.J. Portfolio Models with Return Forecasting and Transaction Costs. Int. Rev. Econ. Financ. 2019, 66, 118–130. [Google Scholar] [CrossRef]
- Ma, Y.; Han, R.; Wang, W. Portfolio optimization with return prediction using deep learning and machine learning. Expert Syst. Appl. 2021, 165, 113973. [Google Scholar] [CrossRef]
- Leung, M.F.; Wang, J. Minimax and biobjective portfolio selection based on collaborative neurodynamic optimization. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2825–2836. [Google Scholar] [CrossRef]
- Min, L.; Dong, J.; Liu, J.; Gong, X. Robust mean-risk portfolio optimization using machine learning-based trade-off parameter. Appl. Soft Comput. 2021, 113, 107948. [Google Scholar] [CrossRef]
- Hai, T.; Min, L. Hybrid Robust Portfolio Selection Model Using Machine Learning-based Preselection. Eng. Lett. 2021, 29, 1626–1635. [Google Scholar]
- Chen, W.; Zhang, H.; Mehlawat, M.K.; Jia, L. Mean–variance portfolio optimization using machine learning-based stock price prediction. Appl. Soft Comput. 2021, 100, 106943. [Google Scholar] [CrossRef]
- Brito, I. A portfolio stock selection model based on expected utility, entropy and variance. Expert Syst. Appl. 2023, 213, 118896. [Google Scholar] [CrossRef]
- Alrabadi, D.W.H.; Aljarayesh, N.I.A. Forecasting Stock Market Returns Via Monte Carlo Simulation: The Case of Amman Stock Exchange. Jordan J. Bus. Adm. 2015, 11, 745–756. [Google Scholar]
- Tan, R. Changes in the Portfolio Management and Construction under the Pandemic Era. In Proceedings of the E3S Web of Conferences, Qingdao, China, 28–30 May 2021. [Google Scholar] [CrossRef]
- Wu, W. Is Evaluation Indicators of Portfolio Performance Reliable? An Empirical Research of Markowitz’s Portfolio Theory Based Monte Carlo Simulation. World Sci. Res. J. 2022, 8, 412–419. [Google Scholar] [CrossRef]
- Koni, W.; Dukalang, H.; Ningsih, S. Estimation of value at risk in Islamic stocks using Monte Carlo simulation in Jakarta Islamic index (JII) period 2017–2020. Eur. J. Res. Dev. Sustain. (EJRDS) 2021, 2, 15–25. [Google Scholar]
- Cakir, H.M. Portfolio Risk Management with Value at Risk: A Monte-Carlo Simulation on ISE-100. Int. Res. J. Financ. Econ. 2013, 118–126. [Google Scholar]
- Pasieczna, A.H. Portfolio Risk Management with Value at Risk: A Monte-Carlo Simulation on ISE-100. Contemp. Trends Challenges Financ. 2021, 109, 75–85. [Google Scholar]
- Sengupta, R.N.; Sahoo, S. Reliability-based portfolio optimization with conditional value at risk (CVaR). Quant. Financ. 2013, 10, 1637–1651. [Google Scholar] [CrossRef]
- Ghodrati, H.; Zahiri, Z. A Monte Carlo simulation technique to determine the optimal portfolio. Manag. Sci. Lett. 2014, 4, 465–474. [Google Scholar] [CrossRef]
- Osei, J.; Sarpong, P.; Amoako, S. Comparing Historical Simulation and Monte Carlo Simulation in Calculating VaR. Quant. Financ. 2018, 3, 22–35. [Google Scholar]
- Amin, F.A.M.; Yahya, S.F.; Ibrahim, S.A.S.; Kamari, M.S.M. Portfolio risk measurement based on value at risk (VaR). AIP Conf. 2018, 1974, 22–35. [Google Scholar]
- Pasieczna, A.H. Monte Carlo simulation approach to calculate value at risk: Application to WIG20 and MWIG40. Financ. Sci. 2019, 24, 61–75. [Google Scholar] [CrossRef]
- Lee, C. Financing method for real estate and infrastructure development using Markowitz’s portfolio selection model and the Monte Carlo simulation. Eng. Constr. 2019, 26, 2008–2022. [Google Scholar] [CrossRef]
- Yu, J. Research on Value at Risk of Lombarda China Medical Health Fund Based on Monte Carlo Simulation. Acad. J. Bus. Manag. 2022, 4, 1–6. [Google Scholar]
- Hosein, N.; Kheyroddin, A.M.S. Risk Assessment in Bridge Construction Projects in Iran Using Monte Carlo Simulation Technique. Pract. Period. Struct. Des. Constr. 2019, 24, 04019026. [Google Scholar]
- Dheskali, E.; Koutinas, A.A.; Kookos, I.K. Risk assessment modeling of bio-based chemicals economics based on Monte-Carlo simulations. Chem. Eng. Res. Des. 2022, 163, 273–280. [Google Scholar] [CrossRef]
- Platon, V.; Constantinescu, A. Monte Carlo Method in Risk Analysis for Investment Projects. Procedia Econ. Financ. 2014, 15, 393–400. [Google Scholar] [CrossRef]
- Albogamy, A.; Dawood, N. Development of a client-based risk management methodology for the early design stage of construction processes. Eng. Constr. Archit. Manag. 2015, 22, 493–515. [Google Scholar] [CrossRef]
- Arnold, U.; Yildiz, Ö. Economic risk analysis of decentralized renewable energy infrastructures – A Monte Carlo Simulation approach. Renew. Energy 2015, 77, 227–239. [Google Scholar] [CrossRef]
- Kumar, L.; Jindal, A.; Velaga, N.R. Financial risk assessment and modelling of PPP based Indian highway infrastructure projects. Transp. Policy 2018, 62, 2–11. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Common risk factors in the returns on stocks and bonds. J. Financ. Econ. 1993, 33, 3–56. [Google Scholar] [CrossRef]
- Brown, R. Smoothing, Forecasting and Prediction; Courier Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Dai, W.; Wu, J.Y.; Lu, C.J. Combining nonlinear independent component analysis and neural network for the prediction of Asian stock market indexes. Expert Syst. Appl. 2012, 39, 4444–4452. [Google Scholar] [CrossRef]
- Sun, X.Q.; Shen, H.W.; Cheng, X.Q. Trading Network Predicts Stock Price. Sci. Rep. 2015, 4, 3711. [Google Scholar] [CrossRef]
- Chang, P.C.; Wang, Y.W.; Yang, W.N. An investigation of the hybrid forecasting models for stock price variation in Taiwan. J. Chin. Inst. Ind. Eng. 2004, 21, 358–368. [Google Scholar] [CrossRef]
- Khashei, M.; Hajirahimi, Z. A comparative study of series arima/mlp hybrid models for stock price forecasting. Commun. Stat. Simul. Comput. 2019, 48, 2625–2640. [Google Scholar] [CrossRef]
- Pan, W. Performing stock price prediction use of hybrid model. Chin. Manag. Stud. 2010, 4, 77–86. [Google Scholar] [CrossRef]
- Rathnayaka, R.K.T.; Seneviratna, D.M.K.N.; Jianguo, W.; Arumawadu, H.I. A hybrid statistical approach for stock market forecasting based on Artificial Neural Network and ARIMA time series models. In Proceedings of the 2015 International Conference on Behavioral, Economic and Socio-cultural Computing (BESC), Nanjing, China, 30 October–1 November 2015; pp. 54–60. [Google Scholar] [CrossRef]
- Kling, J.L.; Bessler, D.A. A comparison of multivariate forecasting procedures for economic time series. Int. J. Forecast. 1985, 1, 5–24. [Google Scholar] [CrossRef]
- Liapis, C.M.; Karanikola, A.; Kotsiantis, S. A Multi-Method Survey on the Use of Sentiment Analysis in Multivariate Financial Time Series Forecasting. Entropy 2021, 23, 1603. [Google Scholar] [CrossRef] [PubMed]
- Markowitz, H. Portfolio Selection: Efficient Diversification of Investments; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Markowitz, H. portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Rubinstein, M. Markowitz’s “Portfolio Selection”: A Fifty-Year Retrospective. J. Financ. 2002, 57, 1041–1045. [Google Scholar] [CrossRef]
- Young, M.R. A Minimax Portfolio Selection Rule with Linear Programming Solution. Manag. Sci. 1998, 44, 673–683. [Google Scholar] [CrossRef]
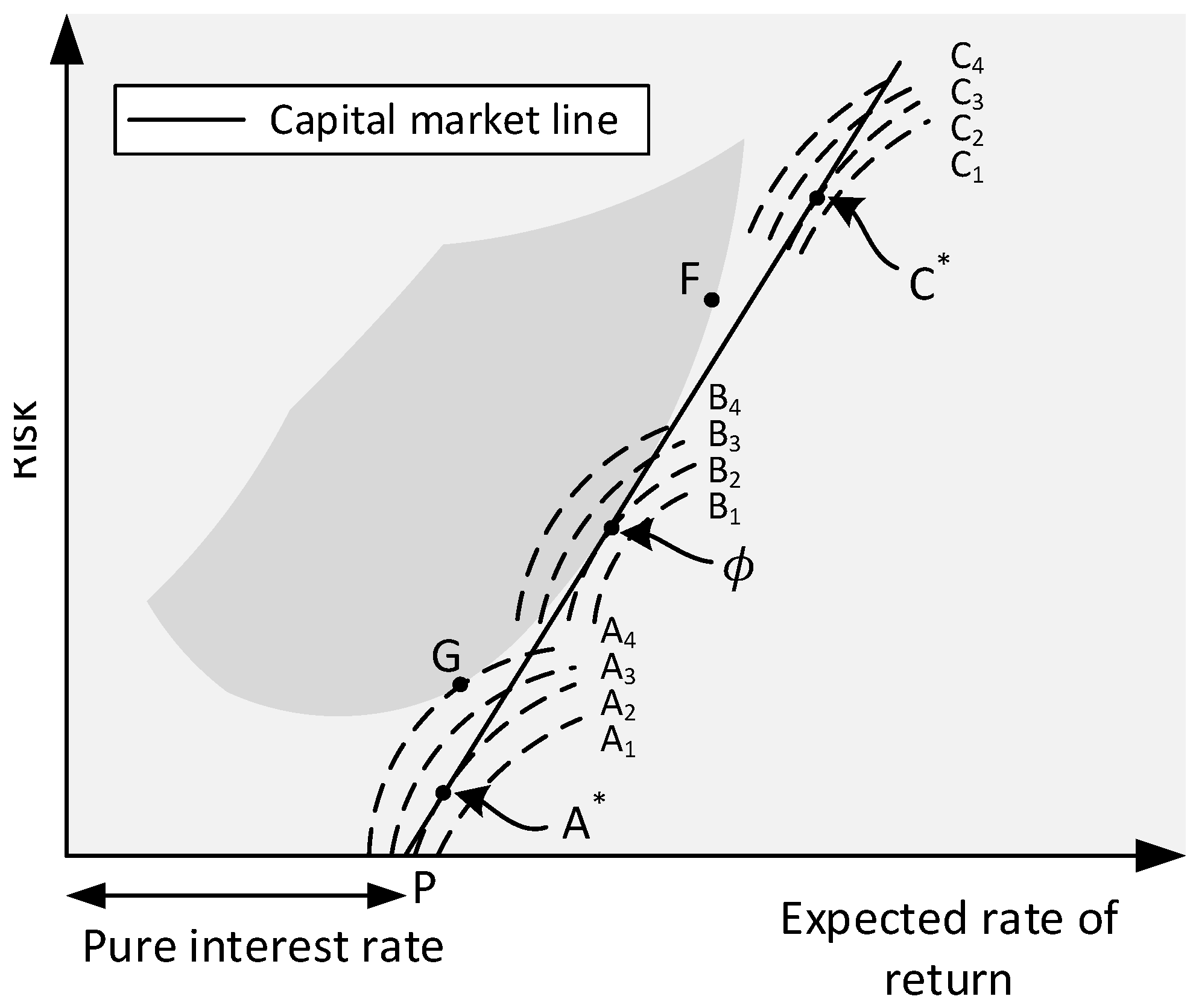
- Tobin, J. Liquidity Preference as Behavior Towards Risk. Rev. Econ. Stud. 1958, 25, 65–86. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Rev. Econ. Stud. 1964, 19, 425–442. [Google Scholar]
- Lintner, J. Security prices, risk, and maximal gains from diversification. J. Financ. 1965, 20, 587–615. [Google Scholar]
- Mossin, J. Equilibrium in a Capital Asset Market. Rev. Econ. Stud. 1966, 34, 768–783. [Google Scholar] [CrossRef]
- Lu, J.; Shazemeen, N.M.; Martinkute-Kauliene, R. Portfolio Decision Using Time Series Prediction and Multi-objective Optimization. Rom. J. Econ. Forecast. 2020, 23, 118–130. [Google Scholar]
- Liu, H.; Loewenstein, M. Optimal portfolio selection with transaction costs and finite horizons. Rev. Financ. Stud. 2002, 15, 805–835. [Google Scholar] [CrossRef]
- Zhang, W.G.; Liu, Y.J.; Xu, W. A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs. Eur. J. Oper. Res. 2012, 222, 341–349. [Google Scholar] [CrossRef]
- Raychaudhuri, S. Introduction to monte carlo simulation. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 91–100. [Google Scholar]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Yahoo! Finance. 2022. Available online: https://finance.yahoo.com/ (accessed on 27 December 2022).
| Main Model | Model | Submodels | References |
|---|---|---|---|
| Timeseries prediction | Exponential smooting method (ESM) | - | [1,2,3,4,5] |
| Autoregressive family models | - | [6,7,8,9,10,11,12] | |
| Generalized auto regressive conditional heterokeasticity (GARCH) family model | - | [13,14,15,16,17,18,19,20,21,22] | |
| Hybrid method | - | [23,24,25,26,27,28,29,30] | |
| Portfolio management | Single objective models | - | [31,32,33,34,35,36,37] |
| Multi objective models | - | [38,39,40,41,42,43] | |
| Dynamic optimization models | - | [44,45,46,47,48,49,50,51] | |
| Downside risk measure models | Mean-semi-variance models | [52,53,54,55,56,57,58,59,60,61,62,63,64,65] | |
| Mean-absolute deviation models | [66,67,68,69,70] | ||
| VaR and CVaR models | [63,71,72,73,74,75,76,77,78,79] | ||
| Practical factors | Transaction cost | [37,80,81,82,83,84,85,86,87,88,89,90,91] | |
| Real world constraints | [92,93,94,95] | ||
| Predicted-based models | - | [96,97,98,99,100,101,102,103] | |
| Heuristics methods | - | [104,105,106,107,108] | |
| Monte Carlo simulation | Monte Carlo simulation in portfolio management | - | [109,110,111] |
| Determination of value at risk | - | [112,113,114,115,116,117,118,119,120,121] | |
| Monte Carlo simulation in risk management | - | [122,123,124,125,126,127] |
| No. | Company | Sectors | Market Capacity (RMB 10,000) s | Stock Ticker |
|---|---|---|---|---|
| 1 | Agricultural Bank of China | Financials–Industry: Diversified Banks | 100,095,147.69 | 601288 |
| 2 | Bank of Beijing | Financials–Industry: Diversified Banks | 8,689,766.54 | 601169 |
| 3 | Bank of Communications | Financials–Industry: Diversified Banks | 34,309,379.71 | 601328 |
| 4 | China Fortune Land Development Co., Ltd. | Real Estate–Industry: Real Estate Investment and Services | 978,430.09 | 600340 |
| 5 | China pacific insurance | Financials–Industry: Insurance | 19,558,154.18 | 601601 |
| 6 | China Petroleum & Chemical Corporation | Energy–Industry: Integrated Oil and Gas | 51,939,548.94 | 600028 |
| No | Company | ARIMA Model’s RMSE | ARIMA Model Parameters (p,d,q) | NAR Model’s RMSE |
|---|---|---|---|---|
| 1 | Agricultural Bank of China | 9.23 | (1,1,1) | 3.45 |
| 2 | Bank of Beijing | 9.32 | (1,1,1) | 3.54 |
| 3 | Bank of Communications | 9.11 | (1,2,1) | 3.32 |
| 4 | China Fortune Land Development Co., Ltd. | 9.03 | (1,1,1) | 3.23 |
| 5 | China pacific insurance | 9.54 | (1,2,2) | 3.67 |
| 6 | China Petroleum & Chemical Corporation | 9.16 | (1,1,1) | 3.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Shadabfar, M.; Sioofy Khoojine, A. A State-of-the-Art Review of Probabilistic Portfolio Management for Future Stock Markets. Mathematics 2023, 11, 1148. https://doi.org/10.3390/math11051148
Cheng L, Shadabfar M, Sioofy Khoojine A. A State-of-the-Art Review of Probabilistic Portfolio Management for Future Stock Markets. Mathematics. 2023; 11(5):1148. https://doi.org/10.3390/math11051148
Chicago/Turabian StyleCheng, Longsheng, Mahboubeh Shadabfar, and Arash Sioofy Khoojine. 2023. "A State-of-the-Art Review of Probabilistic Portfolio Management for Future Stock Markets" Mathematics 11, no. 5: 1148. https://doi.org/10.3390/math11051148
APA StyleCheng, L., Shadabfar, M., & Sioofy Khoojine, A. (2023). A State-of-the-Art Review of Probabilistic Portfolio Management for Future Stock Markets. Mathematics, 11(5), 1148. https://doi.org/10.3390/math11051148







