Abstract
The quality characteristic(s) are assumed to follow the normal distribution in many control chart constructions, although this assumption may not hold in some instances. This study proposes the Bayesian-I and Bayesian-II Shewhart-type control charts for monitoring the Maxwell scale parameter in the phase II study. The posterior and predictive distributions are used to construct the control limits for the proposed Bayesian-I and Bayesian-II Shewhart-type control charts, respectively. Various performance indicators, including average run length, quadratic loss, relative average run length, and performance comparison index, are utilized to evaluate the performance of the proposed control charts. The Bayesian-I and Bayesian-II Shewhart-type control charts are compared to their competitive CUSUMV, EWMAV and V control charts. Sensitivity analysis is also performed to study the effect of hyperparameter values on the performance behavior of the proposed control charts. Finally, real-life data is analyzed for the implementation of the proposed control charts.
Keywords:
hyperparameters; Maxwell distribution; performance measures; posterior predictive distribution; sensitivity analysis MSC:
62P30; 62C10; 62F15; 62F10
1. Introduction
The statistical process control (SPC) kit is a collection of instruments used to monitor the variations in process parameters of the quality characteristic(s). Generally, these variations are categorized into the following two classes: natural (random) causes of variations and special (attributable) causes of variations. The natural causes of variations are harmless and acceptable to any stable process (IC state). On the contrary, the special causes of variations are harmful and create certain problems in the process (OOC state) that can deteriorate the quality of the product. The proper diagnosis and identification of the special causes of variations in the process parameters are essential for achieving high-quality products. Control charts are a statistical tool in the SPC that analyzes and monitor the special causes of variations in the process parameters to ensure the quality of products. The special cause of variations is termed a shift in the process parameters. The most familiar control chart is the classical Shewhart control chart developed by [1], also referred to as the memory-less control chart.
To monitor the shift of the process parameters efficiently, it is necessary to identify the nature of the distribution for the quality characteristic and then monitor the process parameter(s) shift via the control chart. The classical Shewhart-type control chart requires the assumptions of normality and independence of observations for the quality characteristic [2,3]. In literature, numerous authors designed the classical Shewhart-type control charts to detect the shifts in process parameters, assuming that the quality characteristic(s) follows the normal distribution. For instance, Al-Omari and Al-Nasser [4] proposed an efficient control chart based on robust extreme ranked set sampling to detect the shift in the process mean. Similarly, Al-Omari and Haq [5] suggested a double-rank set sampling-based Shewhart-type control chart for monitoring the shift in the process mean. Moreover, Haq and Al-Omari [6] designed an improved Shewhart-type control chart based on partially ordered judgment subset sampling to diagnose changes in the process mean. Equally, Shabbir and Awan [7] suggested the Shewhart-type control chart, which is based on the difference-in-difference estimator and detects a moderate shift in the process mean in the phase-II scenario.
The assumptions of normality for the quality characteristic may not be achieved in practice [8]. Therefore, using the normal distribution for non-normal data may result in a false alarm in process monitoring or may allow for the later detection of changes. In the literature, several researchers suggested control charts for quality characteristic which follows a skewed distribution. For example, Xie et al. [9] discussed the monitoring of shifts in the location parameter of the lognormal process. Likewise, Al-Oraini and Rahim [10] investigated the economic statistical design of control chart when the (Gamma (λ, 2) distribution is considered its failure model. Similarly, Nichols and Padgett [11] offered the bootstrap control chart to monitor the percentiles of the Weibull distribution. Correspondingly, Guo and Wang [12] monitored the shape parameter of the Weibull distribution under type-II censored data. Moreover, Lio et al. [13] designed two parametric bootstrap control charts for monitoring the Burr Type-X percentiles. More comprehensive details about the control charts based on skewed distributions can be seen in the studies of [14,15,16,17,18,19,20].
The Maxwell (or Maxwell–Boltzmann) distribution is a familiar positively skewed distribution. The Maxwell distribution has a smoothly increasing hazard risk; therefore, it is commonly used in life-testing experiments and reliability analysis where the assumption of constant hazard risk, such as in exponential distribution, is not practical. The Maxwell distribution is widely used in statistical machines, physics, chemistry, and life testing experiment, but it is recently has been applied in the SPC techniques. For instance, Hossain et al. [21] suggested a Shewhart-type control chart, called a V control chart when the process variable follows Maxwell distribution. The design structure of the V control chart used the statistic V, which is known as the maximum likelihood estimate for the scale parameter of Maxwell distribution. Similarly, Hossain et al. [22] proposed a V statistic-based cumulative sum (CUSUM) control chart, also denoted as CUSUMV, to detect the changes in the Maxwell process. Likewise, Hossain and Riaz [23] recommended the exponentially weighted moving average (EWMA) control chart based on V denoted by EWMAV for monitoring the Maxwell distribution, and results show that EWMAV control chart outperformed the existing CUSUMV and V control charts. Other control chart schemes based on Maxwell distribution can be seen in the studies, such as [24,25,26].
The Bayesian approach is commonly used in designing control charts to enhance process monitoring. For instance, Menzefricke [27] constructed the Bayesian control limits to monitor the mean of normal distribution. Similarly, Demirhan and Hamurkaroglu [3] suggested the Bayesian control limits for exponentially distributed measurements. Likewise, Saghir [28] proposed the phase-I design scheme for the control chart, which is based on the posterior distribution. Additionally, Raubenheimer and van der Merwe [29] offered the predictive distribution-based Bayesian c-control chart for monitoring nonconformities. Furthermore, Kumar and Chakraborti [30] recommended the Bayesian Shewhart tr-control chart for monitoring the time between events. Moreover, Riaz et al. [31] designed the Bayesian EWMA control chart with three loss functions to monitor the process mean shift. Further related works can be seen in [32,33,34,35,36,37].
As mentioned above, the Bayesian approach can enhance the performance behavior of conventional control charts to monitor the process parameters. Similarly, Hossain et al. [21] implemented a Shewhart-type control chart for monitoring changes in the Maxwell scale parameter. Inspired by the Bayesian approach with control charts, this study introduces the two Bayesian Shewhart-type control charts for monitoring the Maxwell scale parameter, called Bayesian-I and Bayesian-II Shewhart-type control charts in phase II case. The Bayesian approach along the Shewhart-type control charts is expected to further enhance the efficiency of the proposed control charts. The design structures of the Bayesian-I and Bayesian-II Shewhart-type control charts are based on the probability control limits. The Monte Carlo simulations are conducted, and the proposed Bayesian-I and Bayesian-II Shewhart-type control charts are compared to the CUSUMV, EWMAV, and CUSUM control charts. The comparisons indicate that the proposed Bayesian-I and Bayesian-II Shewhart-type control charts outperform the CUSUMV, EWMAV, and V control charts.
The remainder of the paper is organized as follows: Section 2 presents the preliminaries. Besides, Section 3 contains the structures of the proposed control charts for monitoring the shifts in the Maxwell parameter. Furthermore, the simulation study is discussed in Section 4. Moreover, Section 5 illustrates the results and performance comparison of the proposed and existing control charts. Section 6 provides a real-life data analysis for the practical implementation of the proposed and existing control charts. Finally, a summary, conclusions, and recommendations are outlined in Section 7.
2. Preliminaries
This section is organized as follows. Section 2.1 describes the Maxwell distribution. Section 2.2 presents the distribution of the maximum likelihood estimate (V) of for the Maxwell scale parameter. The V control chart to monitor the changes in the Maxwell scale parameter is provided in Section 2.3. Section 2.4 deals with the methodology of the CUSUMV control chart for monitoring the Maxwell process scale shift. Finally, the EWMAV control chart is described in Section 2.5.
2.1. Maxwell Distribution
Suppose that X is a random variable having the Maxwell distribution with scale parameter , then its probability density function (PDF) and cumulative distribution function (CDF) are respectively given as follows:
The π = 3.1429 is constant, , and is an incomplete gamma function, whereas a > 0 and λ > 0 are constants.
2.2. Distribution of Statistic V
Hossain et al. [21] used a sample of size n, which is randomly taken from Equation (1), to derive the maximum likelihood estimate for the scale parameter of the Maxwell distribution, which is given as follows:
and called it statistic V, that is . Hossain et al. [22] showed that the transformations and follow gamma distribution, that is, and , respectively. Similarly, Hossain et al. [23] defined the distribution of statistic V represented by the PDF, and it is given as follows:
The statistic V has the mean and variance, respectively given as follows:
Likewise, the αth quantile function of V is given as; where the inverse CDF of . It is important to note that, here the basic objective is the monitoring of . If δ represents the shift in then for IC and OOC situations, the following hypothesis can be formulated, respectively, as follows:
2.3. V Control Chart
Hossain et al. [21] suggested a V statistic-based Shewhart-type control chart, named as V control chart for monitoring changes in the Maxwell scale parameter. They derived LPLV, CLV, and UPLV for the V control chart in the case of known and unknown . The basic design structure for the probability control limits of V control chart can be presented as follows:
where , , and . The coefficients L1, L2, and L3 are the quantiles of multiplied by some constants.
Practically, the parameter may be known then the probability control limits are defined as follows:
However, if is unknown, then can be estimated using the statistic V. So, in this case, the probability control limits for the V control chart are defined as follows:
where represents the average of the estimated computed at each of the samples over time i.
The ARL is one of the measures that evaluate the performance of the control charts. Mathematically, the ARL can be defined as given below as follows:
where . is the power of the test, that is, the probability of rejecting the null hypothesis (H0) when an alternative hypothesis (H1) is true. For the V control chart, the power of the test is defined as follows:
It further can be expressed as follows:
Finally, the power of the test is given as follows:
In Equation (9) if there is no shift (i.e., δ = 1) in the process, then, in this case, the power is equal to the false alarm rate α.
2.4. CUSUMV Control Chart
Hossain et al. [22] presented the design of the CUSUMV control chart for monitoring the process scale parameter shift. They designed the plotting statistic of the CUSUMV control chart, defined below as follows:
where are starting values and the k is referred to as the slack value that is defined as . For a one-sided upper CUSUMV control chart, the process is considered to be OOC if the charting statistic exceeds then the threshold, h (i.e., control limit), that is, .
2.5. EWMAV Control Chart
Recently, Hossain and Riaz [23] proposed the EWMA control chart that monitors the Maxwell scale parameter shift, which is denoted by the notation by EWMAV. The charting statistic for the EWMAV control chart is represented by , which is based on , and can be given as follows:
where is initial value set as; , and λ is the smoothing constant. The mean of the statistic is , while its variance is . The lower control limit (LCLE), center line (CLE), and the upper control limit (UCLE) for the EWMAV control chart are given as follows:
where and . For a very large value of i, and are reduced to , and , respectively. If is unknown then it can be estimated by , hence Equation (12) can be rewritten, in this case, given as follows:
The EWMAV control chart provides the OOC signal if falls outside the upper or lower control limits.
3. Proposed Bayesian Shewhart-Type Control Charts
This section presents the schemes of the Bayesian-I and Bayesian-II Shewhart-type control charts for monitoring the Maxwell scale parameter shift. The proposed Bayesian-I Shewhart-type control chart is formulated using the posterior distribution, while the Bayesian-II Shewhart-type control chart is designed using the predictive distribution. The details are given in the following subsections.
3.1. Proposed Bayesian-I Shewhart-Type Control Chart
This subsection consists of constructing the posterior distribution for given V using the conjugate prior. This posterior distribution is used to find the probability control limits for the Bayesian-I Shewhart-type control chart. The following theorems may be useful in this regard.
Theorem 1.
Given the prior distribution of is inverted gamma (IG), that is, IG (a, b),
The posterior distribution ofgiven V is IG (3n/2 + a, b +3nV/2), that is,
Proof of Theorem 1.
By definition, the posterior distribution of given V is defined as follows:
From Equations (4), (14), and (15) the posterior distribution of given V that can be specified as follows:
which means that . □
Result 1.
If a = 1 and a = 0 then the prior distribution of becomes an improper prior known as the uniform prior, that is, as follows:
The posterior distribution in this case is as follows:
which implies that .
Result 2.
If a = 0 and b = 0 then the prior distribution becomes an improper prior referred to as Jeffreys prior, that is, as follows:
The posterior distribution in this case is the following:
which suggests that .
Theorem 2.
Given the posterior distribution ofgiven V is IG (3n/2 + a, b + 3nV/2), that is
the transformationgiven V has the PDF of a gamma distribution having shape parameter 3n/2 + a and scale parameter 1, that is,
Proof of Theorem 2.
For the PDF given V in Equation (16), since then the Jacobian of transformation, . Hence using the relation, the PDF of θ given V is written by the following:
which indicates that . □
The probability control limits for the proposed Bayesian-I Shewhart-type control chart can be developed from Equation (16). The lower probability limit , central line , and upper probability limit , at the desired false alarm rate α, based on the posterior distribution, can be given as follows:
where is defined as the median of the posterior distribution. Under the transformation defined by Theorem 2, using the quantiles of the , the probability control limits , , and can be designed as follows:
where , , and the inverse CDF of . Table 1 contains the different values of , , and at various n, α with α = 8.5, 70. Let be the power of the test then in the case of the proposed Bayesian-I Shewhart-type control chart, it can be defined as follows:
which can be solved to the following:

Table 1.
A1, A2, and A3 values for different n and a = 8.5, 70.
Consequently, the OOC ARL, that is ARL1. of the Bayesian-I Shewhart-type control chart is given as follows:
3.2. Proposed Bayesian-II Shewhart-Type Control Chart
Let be the future observation of random sample taken from the Maxwell distribution then the predictive distribution of given V is defined by Equation (24). Assuming that , , and are the probability control limits for the Bayesian-II Shewhart-type control chart to monitor the process scale parameter shift, then the , , and can be defined as follows:
where is regarded as a median of the posterior predictive distribution. To derive the probability control limits, that is, , , and for the proposed Bayesian-II Shewhart-type control chart, the following theorems may help here.
Theorem 3.
Given the posterior distribution ofgiven V is IG (3n/2 + a, b + 3nV/2), that is,
the predictive distribution of a future random variablegiven V is expressed as follows:
Proof of Theorem 3.
The predictive distribution of given V is defined as follows:
From Equation (1), is the PDF of Maxwell distribution, which can be written as follows:
Equations (16) and (22) provide the predictive PDF of given V, which can be written as follows:
where is a Beta function. □
Theorem 4.
Given the posterior predictive distribution given V, that is
the transformationgiven V has the PDF of a Beta (3n/2 + a, 3/2) distribution.
Proof of Theorem 4.
In the PDF of given V in Equation (24), since then the Jacobian of transformation, . Hence, using the expression, the PDF of given V is expressed by the following:
□
Theorem 4 shows that Wf follows the beta distribution with parameters and 3/2. and the probability control limits , and may be expressed in terms of the quantiles of the beta distribution having parameters and 3/2. Thus Equations (22) and (25) provide the solution for Equation (21), which can be presented as given as follows:
where , and and represents the 100p-quantiles of the beta distribution having parameters and . Table 2 contains the different values of , , and for a specified n, α and a. If denotes the power of the test for the Bayesian-II Shewhart-type control chart, then it can be given as follows:
that can be solved to
where is the CDF of the beta distribution having parameters and . Consequently, the for the Bayesian-II Shewhart-type control chart is given by the following:

Table 2.
B1, B2, and B3 values for different n and a = 25.5, 36.9.
4. Proposed Bayesian Shewhart-Type Control Charts
This section discusses the performance evaluation performance measures utilized to investigate the performance behavior of the proposed Bayesian-I and Bayesian-II Shewhart charts. Section 4.1 and Section 4.2 defines the simulation study and average run length. In the same line, Section 4.3 defines the overall performance indicators. Section 4.3 discusses the Monte Carlo simulations. The sensitivity analysis is discussed in Section 4.4.
4.1. Simulation Study
The numerical results are obtained through the Monte Carlo simulation method by using R software. The sample is generated from the specified distribution, and then construct control limits and plotting statistics. The average run length properties are obtained under the assumptions of various parameters and different values of shifts such as 1, 1.25, 1.50, 1.72, 2, 2.25, 2.50, 3, 6. Moreover, different sets of hyperparameters are considered for the sensitivity analysis of the proposed control charts.
4.2. Average Run-Length
The average run length (ARL) is the familiar run-length characteristic that evaluates the performance behavior of the control charts. The ARL can be considered as the average number of sample points plotted on the control chart until the control chart indicates an OOC signal, where sample points are referred to as run-length (RL). The IC ARL () and the OOC ARL () are the two types of ARL It is emphasized that if the operates in the IC state, then the should be larger to prevent frequent false alarms; but, for OOC states, the should be smaller to identify the process change as soon as possible. To enhance the efficiency of the control chart, it is important to attain a smaller for the control chart with predetermined at a desired level.
4.3. Overall Performance Measure
Although the ARL is the best-known measure to assess the performance behavior of the control charts at a single defined shift; however, there are alternative measures that can be used to assess the overall detection ability of a control chart. Extra quadratic loss (EQL), relative average run length (RARL), and performance comparison index (PCI) are among these measures. A control chart with smaller EQL, RARL, and PCI values is regarded to be superior. More detail about these performance measures is provided as follows
4.3.1. Extra Quadratic Loss
The EQL is the weighted ARL over the whole shift domain , where the square of the shift δ is used as a weight. The EQL mathematically can be defined as follows:
where is the minimum shift, is the maximum shift, and is the ARL of a specific control chart at a shift δ.
4.3.2. Relative Average Run Length
The RARL is the ratio of the ARL of a certain control chart (i.e., ARL(δ) to the benchmark control chart (i.e., ). Mathematically the RARL can be defined as follows:
A benchmark control chart is one, which has minimal EQL, or it can be regarded as some of the existing standard control charts.
4.3.3. Performance Comparison Index
The PCI is defined as the ratio between the EQL of the control chart to the EQL of the benchmark control chart. The PCI, mathematically, can be specified as follows:
The PCI = 1 for the benchmark control chart and the remaining control charts have PCI > 1.
4.4. Sensitivity Analysis of Hyperparameters
The Bayesian process monitoring largely depends on the form of the prior distribution. The informative and non-informative prior have a different impact on the control chart performance. In this study, the informative (conjugate) prior is considered for the Maxwell parameter , which is assumed to be inverted gamma with hyperparameters a and b (i.e., ). The sensitivity analysis of hyperparameter values is performed to study the impact of an increase or decrease in hyperparameter values on the performance behavior of the Bayesian-I and Bayesian-II Shewhart-type control charts. Different pairs of hyperparameter values are chosen for this purpose, such as (a, b) = (0, 0), (1, 0), (8.5, 0.005), (25.5, 0.005), (25.5, 1.5), (40.9, 0.005), (70, 0.2), (2.5, 0.005), and (110, 0.005). The impact of various hyperparameter choices on the performance behavior of the proposed control chart is discussed as follows:
- The Bayesian-I and Bayesian-II Shewhart-type control charts are very sensitive to hyperparameter values. A slight change in hyperparameters significantly affects the ARL performance. For example, for n = 2 and δ = 1.5, the ARL for the proposed Bayesian-I Shewhart-type control chart is 211.94, if (a, b) = (0, 0) and when (a, b) = (1, 0) then ARL is 183.01 (see Table 3). Similarly, for the same n = 2, δ = 1.5 the ARL for the proposed Bayesian-II Shewhart-type control chart is 221.54, if (a, b) = (0, 0) and when (a, b) = (1, 0) then ARL is 187.48 (see Table 4);
 Table 3. Run length profile of the Bayesian-I Shewhart-type control chart with different sample sizes and hyperparameter values at α = 0.0027 with ARL ≈ 370.
Table 3. Run length profile of the Bayesian-I Shewhart-type control chart with different sample sizes and hyperparameter values at α = 0.0027 with ARL ≈ 370. Table 4. Run length profile of the Bayesian-II Shewhart-type control chart with different sample sizes and hyperparameter values at α = 0.0027 with ARL ≈ 370.
Table 4. Run length profile of the Bayesian-II Shewhart-type control chart with different sample sizes and hyperparameter values at α = 0.0027 with ARL ≈ 370. - The detection ability of the proposed Bayesian-I and Bayesian-II Shewhart-type control chart improves when a gets larger and b becomes smaller at the same time. For example, for n = 2 and δ = 1.5, the ARL for the proposed Bayesian-I Shewhart-type control chart is 34.00, if (a, b) = (25.5, 1.5), whereas when (a, b) = (40.9, 0.005) then ARL is reduced to 18.35 (see Table 3). Similarly, the ARL for the proposed Bayesian-II Shewhart-type control chart with n = 2, δ = 1.5, is 51.064 when (a, b) = (25.5, 1.5), while for (a, b) = (40.9, 0.005) the ARL for the proposed Bayesian-II Shewhart-type control chart is 1.01 (see Table 4);
- The constants A1, A2 and A3 reduce as a increases. For instance, when n = 2 and α = 0.0027, then A1 = 0.04105, A2 = 0.08955, and A3 = 0.25601 if a = 8.5 and a = 25.2 then A1 = 0.02114, A2 = 0.03539, and A3 = 0.06592 (see Table 1);
- Similarly, the values of B1, B2, and B3 decrease as a gets larger. For example, if n = 2, α = 0.0027, then B1 = 0.00127, B2 = 0.10600, and B3 = 0.94696. Likewise, when a = 8.5 and 25.5 then B1 = 0.00052, B2 = 0.04188, and B3 = 0.31137 (see Table 2).
5. Performance Comparison and Illustration of Results
This section reports the finding and performance comparison of the Bayesian-I and Bayesian-II Shewhart-type control charts against the existing counterparts. Section 5.1 represents the comparison of the Bayesian-I and Bayesian-II Shewhart-type control charts with the CUSUMV control chart. Similarly, the Bayesian-I and Bayesian-II Shewhart-type control charts are compared with the EWMAV control chart in Section 5.2. Likewise, Section 5.1 offers the performance comparison of the Bayesian-I and Bayesian-II Shewhart-type control charts with the V control chart. Finally, Section 5.4 addresses the main outcomes of the study.
5.1. Proposed versus CUSUMV Control Chart
The proposed Bayesian-I and Bayesian-II Shewhart-type control charts are compared against the CUSUMV control chart at , and the results show that the proposed control charts outperformed the CUSUMV control chart. For example, at n = 2 and δ = 1.25, 1.5, the ARL values for the proposed Bayesian-II Shewhart-type control chart (a = 25.5, b = 0.005) are 25.72, 9.74, while for the CUSUMV control chart, the ARL values are; 33.93, 18.71 (see Table 3 vs. Table 5). Along with the ARL values for the proposed Bayesian-I Shewhart-type control chart a = 70, b = 0.2 are 29.36, 23.59 (see Table 4). This indicates that the proposed Bayesian-I and Bayesian-II Shewhart-type control charts perform better against the CUSUMV control chart in monitoring the shift in the Maxwell scale parameter. Correspondingly, in overall performance comparison, the proposed Bayesian-I and Bayesian-II Shewhart-type control charts also demonstrate superior performance than the CUSUMV control chart, as their EQL, PCI, and RARL values are smaller than that of CUSUMV control chart. For instance, for n = 2, the EQL, PCI, and RARL values for the proposed Bayesian-I (a = 110, b = 0.005) and Bayesian-II (a = 25.5, b = 0.005) Shewhart-type control charts are, respectively, given as; 26.79, 1.00, 1.05, and 26.75, 1.00, 1.00, whereas, for the CUSUMV control the EQL, PCI, and RARL values chart are provided as; 57.97, 2.17, 4.10 (see, Table 6).

Table 5.
ARL values of CUSUMV, EWMAV and V control charts.

Table 6.
Overall performance comparison of the Bayesian-I and Bayesian-II Shewhart-type control charts versus the CUSUMV and V control charts.
5.2. Proposed versus EWMAV Control Chart
The proposed Bayesian-I and Bayesian-II Shewhart-type control charts reveal an edge in performance over the EWMAV control chart. In detail, at and , the Bayesian-I () Shewhart-type control chart provides ARL value of 23.78, while the Bayesian-II Shewhart-type control chart bears ARL value of 25.72 and the EWMAV control chart delivers the ARL value of 32.03 (see Table 2 and Table 3 vs. Table 5). Similarly, the proposed Bayesian-I and Bayesian-II Shewhart-type control charts also yield superior overall performance than the EWMAV control chart as the proposed Bayesian-I and Bayesian-II Shewhart-type control charts have minimum EQL, PCI, and RARL values than EWMAV control chart (see Table 6). For example, with , the Bayesian-I (a = 110, b = 0.005) Shewhart-type control chart has EQL, PCI, and RARL values of 26.20, 1.04, and 1.14, the Bayesian-II (a = 25.5, b = 0.005) Shewhart-type control charts address the EQL, PCI, and RARL values of 25.14, 1.00, and 1.00, whereas, for the EWMAV control chart generates the EQL, PCI, and RARL values of 29.53, 1.17, and 1.65 (see Table 6).
5.3. Proposed versus V Control Chart
The proposed Bayesian-I and Bayesian-II Shewhart-type control charts achieve better shift detection ability than the V control chart. For instance, at , , and , the values for the proposed Bayesian-I Shewhart-type control chart are 37.24, 7.01, whereas the ARL values for the V control chart are 69.04 and 17.55 (see Table 4 vs. Table 5). This indicates the superiority of the Bayesian-I Shewhart-type control chart over V control chart. Similarly, when , and , the proposed Bayesian-II Shewhart-type control chart ARL values are 7.94, 1.97, which are smaller than V control chart. Likewise, for , the proposed Bayesian-I (a = 110, b = 0.005) and Bayesian-II (a = 25.5, b = 0.005) Shewhart-type control charts have smaller EQL, PCI, and RARL values (i.e., 25.92, 1.05, 1.49, and 25.57, 1.00, and 1.00) than the EQL, PCI, and RARL values of the V control chart (i.e., 26.53, 1.08, and 1.67); therefore, the proposed Bayesian-I and Bayesian-II Shewhart-type control charts have better overall performance relative to the V control chart (see Table 6).
5.4. Main Finding of the Study
Some important findings about the proposed Bayesian-I and Bayesian-II Shewhart-type control charts are given as follows:
- The Bayesian-I and Bayesian-II Shewhart-type control charts are very sensitive to hyperparameter values. A slight change in hyperparameter values significantly affects the performance of the proposed Bayesian-I and Bayesian-II Shewhart-type control charts in terms of the ARL measure (see, Table 3 and Table 4);
- The proposed Bayesian-I and Bayesian-II Shewhart-type control charts have improved ARL performance than the CUSUMV, EWMAV and V control charts, particularly when hyperparameters a and b increase (see, Table 5);
6. Real Data Analysis
A boring machine is a tool used for making a wide hole in a fixed workpiece. These machines make use of a single steel cutting edge, carbide or diamond, or a small grinding wheel to make the hole cleaner, more accurate, and more specific. Boring machines with multiple spindles are typically used in a manufacturing plant where production is on a large scale. This study uses a real dataset by Hossain et al. [21] that addressed the failure rate of the vertical boring machine. This data set was also considered by Majumdar [38] to review the optimum maintenance approach for the vertical boring machine. Subsequently, Krishna and Malik [39] conducted a detailed statistical investigation to evaluate the distributions, which best fit this data set. They examined models such as exponential, gamma, Maxwell, lognormal, Weibull, and estimated the parameters of these models with the maximum likelihood method. In addition, various information criteria such as Akaike, second-order, Bayesian, and the Kolmogorov–Smirnov test have shown that the Maxwell distribution is the best fitted to this data set. Additionally, Hossain et al. [21] used the Kolmogorov–Smirnov test and showed that the data set followed the Maxwell distribution (p-value 0.4775) with σ = 1777.86. Hossain et al. [21] also verified that no larger change occurs for this data set. The failure time data for a vertical boring machine are specified as follows: 2802, 2937, 2136, 4359, 4020, 1781, 2816, 2655, 3886, 2296, 3158, 3695, 4155, 3811, 2380, 376, 2172, 3705, 2848, 4339, 2076, 2672, 3632, 1976, 1700, 1596, 1701, 3575, 3802, 4351, 4291, and 808.
Hossain et al. [22] first divided this data set into eight groups each of size four, and estimated by using Equation (3), that is, . They specified the various features of the CUSUMV control chart as; n = 4, , h 13,400,000, and k 3,313,881. Using these constants, they simulated 22 OOC samples with an upward change of . So, there are a total of 30 samples, out of which 8 are IC, and the rest of 22 samples are OOC (see Table 7). Following the rationale of Hossain et al. [22], in this study the EWMAV, V, Bayesian-I, and Bayesian-II Shewhart-type control charts are constructed. At , , and , the probability control limits , , and of the V control chart are obtained. Similarly, with and , the EWMAV fixed limits are constructed, i.e., , and . Likewise, the probability control limits , and for the proposed Bayesian-I Shewhart-type control chart using , , , , and are determined. Moreover, the , and present the probability control limits of the proposed Bayesian-II Shewhart-type control chart, which is based on , , , , and . The CUSUMV, EWMAV, V, Bayesian-I, and Bayesian-II Shewhart-type control charts are constructed using the aforementioned information. Figure 1 demonstrates the graphical properties of these control charts.

Table 7.
Charting statistics for various control charts.
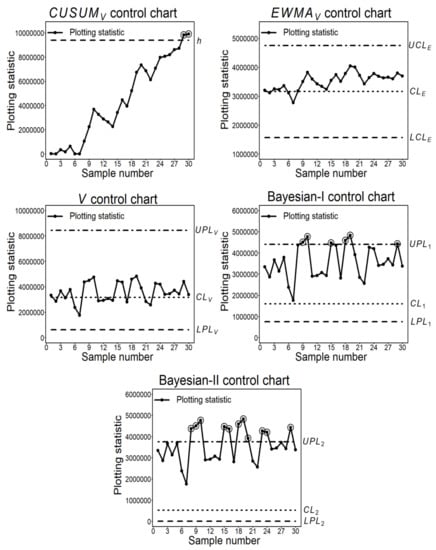
Figure 1.
CUSUMV, EWMAV, V Bayesian-I, and Bayesian-II Shewhart-type control charts with a vertical boring machine failure data.
The proposed Bayesian-I and Bayesian-II Shewhart-type control charts are more sensitive than the CUSUMV, EWMAV, and V control charts, as the comparison reveals that the proposed Bayesian-I and Bayesian-II Shewhart-type control charts detect 6 and 11 OOC signals, respectively, and the CUSUMV control chart identifies 2 OOC points, while the EWMAV and V control charts fail to diagnose the OOC signal. Similarly, the proposed Bayesian-I and Bayesian-II Shewhart-type control charts detect the OOC points at sample numbers 9 and 8, respectively, while the CUSUMV control chart diagnoses the first OOC signal at sample number 29. This indicates that the proposed Bayesian-I and Bayesian-II Shewhart-type control charts are more efficient than the CUSUMV, EWMAV and V control charts.
7. Summary, Conclusions, and Recommendation
This study is performed to propose two Bayesian Shewhart-type control charts, which are based on the probability control limits, to monitor the familiar Maxwell distribution. These control charts are called the Bayesian-I and Bayesian-II Shewhart-type control charts. The design structures for the proposed Bayesian-I and Bayesian-II Shewhart-type control charts are obtained using the posterior and posterior predictive distributions, respectively. These distributions are constructed under the assumption of conjugate prior for the scale parameter of Maxwell distribution, which is assumed to be an inverted gamma distribution with hyperparameters a and b. The performance of the suggested Bayesian-I and Bayesian-II Shewhart-type control charts is evaluated by computing the important performance evaluation measures such as ARL, EQL, RARL, and PCI. A comparative study is carried out among the proposed Bayesian-I and Bayesian-II Shewhart-type control charts, and some existing competitors are more sensitive than the CUSUMV, EWMAV and V control charts. The sensitivity analysis is performed to study the effect of increasing and decreasing hyperparameter values on the performance behavior of the proposed Bayesian-I and Bayesian-II Shewhart-type control charts. The results derived from this study have shown that the proposed Bayesian-I and Bayesian-II Shewhart-type control charts perform well in the monitoring of the Maxwell scale parameter. A real-life data application is also provided for the practical implementation of the proposed Bayesian-I and Bayesian-II Shewhart-type control charts. Finally, it is recommended that the concept of the Bayesian-I and Bayesian-II Shewhart-type control charts can be extended to other distributions, where the manufacturing processes need to diagnose the small and large changes in the process parameters.
Author Contributions
Conceptualization, Z.R.; Methodology, S.M.A.; Software, Z.R.; Formal analysis, S.M.A. and A.N.C.; Investigation, F.A., M.K. and A.N.C.; Resources, M.K.; Data curation, M.K. and Z.R.; Writing—original draft, M.K. and S.M.A.; Writing—review & editing, F.A. and S.M.A.; Supervision, I.M.A.; Project administration, A.N.C.; Funding acquisition, F.A. and I.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R358), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
All the relevant data is already included in the main manuscript.
Acknowledgments
The authors thank the reviewers for their valuable comments which increase the quality of this paper. They also thank and extend their appreciation to Princess Nourah bint Abdulrahman University for funding this work. through Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R358), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shewhart, W.A. Economic Control of Quality of Manufactured Product; D. Van Nostrand Company: New York, NY, USA, 1931. [Google Scholar]
- Montgomery, D.C. Introduction to Statistical Quality Control, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Demirhan, H.; Hamurkaroglu, C. Bayesian X-bar control limits for exponentially distributed measurements. J. Stat. Comput. Simul. 2014, 84, 628–643. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Al-Nasser, A.D. Statistical quality control limits for the sample mean chart using robust extreme ranked set sampling. Econ. Qual. Control 2011, 26, 73–89. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Haq, A. Improved quality control charts for monitoring the process mean using double-ranked set sampling methods. J. Appl. Stat. 2012, 39, 745–763. [Google Scholar] [CrossRef]
- Haq, A.; Al-Omari, A.I. A new Shewhart control chart for monitoring process mean based on partially ordered judgment subset sampling. Qual. Quant. 2015, 49, 1185–1202. [Google Scholar] [CrossRef]
- Shabbir, J.; Awan, W.H. An Efficient Shewhart-Type Control Chart to Monitor Moderate Size Shifts in the Process Mean in Phase II. Qual Reliab Engng Int 2016, 32, 1597–1619. [Google Scholar] [CrossRef]
- Khan, Z.; Gulistan, M.; Kadry, S.; Chu, Y.; Lane-Krebs, K. On Scale Parameter Monitoring of the Rayleigh Distributed Data Using a New Design. IEEE Access 2020, 8, 188390–188400. [Google Scholar] [CrossRef]
- Xie, M.; Goh, T.N.; Kuralmani, V. Statistical Models and Control Charts for High-Quality Processes; Springer Science & Business Media: New York, NY, USA, 2002. [Google Scholar]
- Al-Oraini, H.A.; Rahim, M. Economic statistical design of X control charts for systems with Gamma (λ, 2) in-control times. Comput. Ind. Eng. 2002, 43, 645–654. [Google Scholar] [CrossRef]
- Nichols, M.D.; Padgett, W.J. A Bootstrap Control Chart for Weibull Percentiles. Qual. Reliab. Eng. Int. 2006, 22, 141–151. [Google Scholar] [CrossRef]
- Guo, B.; Wang, B.X. Control Charts For Monitoring The Weibull Shape Parameter Based On Type-II Censored Sample. Qual. Reliab. Eng. Int. 2014, 30, 13–24. [Google Scholar] [CrossRef]
- Lio, Y.L.; Tsai, T.-R.; Aslam, M.; Jiang, N. Control Charts for Monitoring Burr Type-X Percentiles. Commun. Stat.-Simul. Comput. 2014, 43, 761–776. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, M. Process monitoring of exponentially distributed characteristics through an optimal normalizing transformation. J. Appl. Stat. 2000, 27, 1051–1063. [Google Scholar] [CrossRef]
- Chan, L.K.; Cui, H.J. Skewness correction X and R charts for skewed distributions. Nav. Res. Logist. 2003, 50, 555–573. [Google Scholar] [CrossRef]
- Chen, Y.K. Economic design of X-bar control chart for Non-normal data using variable sampling policy. Int. J. Prod. Econ. 2004, 92, 61–74. [Google Scholar] [CrossRef]
- Santiago, E.; Smith, J. Control charts based on the exponential distribution: Adapting runs rules for the t Chart. Qual. Eng. 2013, 25, 85–96. [Google Scholar] [CrossRef]
- Ali, S.; Riaz, M. Cumulative quantity control chart for the mixture of inverse Rayleigh process. Comput. Ind. Eng. 2014, 73, 11–20. [Google Scholar] [CrossRef]
- Sighir, A.; Lin, Z. Designing of Gini-Chart for Exponential, t, Logistic and Laplace Distributions. Commun. Stat.-Simul. Comput. 2015, 44, 2387–2409. [Google Scholar] [CrossRef]
- Haghighi, F.; Castagliola, P. Control chart for monitoring the Weibull shape parameter under two competing risks. Commun. Stat.-Simul. Comput. 2018, 48, 2125–2137. [Google Scholar] [CrossRef]
- Hossain, M.P.; Omar, M.H.; Riaz, M. New V control chart for the Maxwell distribution. J. Stat. Comput. Simul. 2016, 87, 594–606. [Google Scholar] [CrossRef]
- Hossain, M.P.; Sanusi, R.A.; Omar, M.H.; Riaz, M. On designing Maxwell CUSUM control chart: An efficient way to monitor failure rates in boring processes. Int. J. Adv. Manuf. Technol. 2019, 100, 1923–1930. [Google Scholar] [CrossRef]
- Hossain, M.P.; Riaz, M. On designing a new VEWMA control chart for efficient process monitoring. Comput. Ind. Eng. 2021, 162, 107751. [Google Scholar] [CrossRef]
- Hossain, M.P.; Omar, M.H.; Riaz, M. Estimation of mixture Maxwell parameters and its possible industrial application. Comput. Ind. Eng. 2017, 107, 264–275. [Google Scholar] [CrossRef]
- Saghir, A.; Ahmad, L.; Aslam, M. Modified EWMA control chart for transformed gamma data. Commun. Stat.-Simul. Comput. 2021, 50, 3046–3059. [Google Scholar] [CrossRef]
- Godase, D.G.; Mahadik, S.B.; Rakitzis, A.C. The SPRT control charts for the Maxwell distribution. Qual. Reliab. Eng. Int. 2022, 38, 1713–1728. [Google Scholar] [CrossRef]
- Menzefricke, U. On the evaluation of control chart limits based on predictive distributions. Commun. Stat.-Theory Methods 2002, 31, 1423–1440. [Google Scholar] [CrossRef]
- Saghir, A. Phase-I Design Scheme for X-bar chart Based on Posterior Distribution. Commun. Stat.-Theory Methods 2014, 44, 644–655. [Google Scholar] [CrossRef]
- Raubenheimer, L.; van der Merwe, A.J. Bayesian Control Chart for Nonconformities. Qual. Reliab. Eng. Int. 2015, 31, 1359–1366. [Google Scholar] [CrossRef]
- Kumar, N.; Chakraborti, S. Bayesian Monitoring of Times Between Events: The Shewhart tr-Chart. J. Qual. Technol. 2017, 49, 136–154. [Google Scholar] [CrossRef]
- Riaz, S.; Riaz, M.; Hussain, Z.; Abbas, T. Monitoring the performance of Bayesian EWMA control chart using loss functions. Comput. Ind. Eng. 2017, 112, 426–436. [Google Scholar] [CrossRef]
- Menzefricke, U. Combined Exponentially Weighted Moving Average Charts for the Mean and Variance Based on the Predictive Distribution. Commun. Stat.-Theory Methods 2013, 42, 4003–4016. [Google Scholar] [CrossRef]
- Riaz, M.; Ali, S. On process monitoring using location control charts under different loss functions. Trans. Inst. Meas. Control 2016, 38, 1107–1119. [Google Scholar] [CrossRef]
- Raubenheimer, L.; van der Merwe, A.J. Bayesian process control for the Phase II Shewart-type p-chart. Qual. Technol. Quant. Manag. 2016, 13, 453–472. [Google Scholar] [CrossRef]
- Rigdon, S.E.; Woodall, W.H. Using the predictive distribution to determine control limits for the Bayesian MEWMA chart. Commun. Stat.-Simul. Comput. 2017, 46, 7818–7826. [Google Scholar] [CrossRef]
- Aslam, M.; Anwar, S.M. An improved Bayesian Modified-EWMA location chart and its applications in mechanical and sport industry. PLoS ONE 2020, 15, e0229422. [Google Scholar] [CrossRef]
- Noor, S.; Noor-ul-Amin, M.; Mohsin, M.; Ahmed, A. Hybrid exponentially weighted moving average control chart using Bayesian approach. Commun. Stat.-Theory Methods 2022, 51, 3960–3984. [Google Scholar] [CrossRef]
- Majumdar, S.K. An optimum maintenance strategy for a vertical boring machine system. Oper. Res. Soc. India 1993, 30, 344–365. [Google Scholar]
- Krishna, H.; Malik, M. Reliability estimation in Maxwell distribution with progressively Type-II censored data. J. Stat. Comput. Simul. 2012, 82, 623–641. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).