A Flexible Semi-Poisson Distribution with Applications to Insurance Claims and Biological Data
Abstract
1. Introduction
1.1. Characterizations
1.2. The Cumulative Distribution Function
2. Properties
2.1. Natural Exponential Family
2.2. The Generating Functions
2.3. Moments
Incomplete Moments
2.4. Reliability Properties
- i
- Using the relationships between log-concavity and unimodality presented in [16], thedistribution is unimodal.
- ii
- SP is an IFR.
- iii
- Convolution of SP with any other discrete distribution will also result in a log-concave distribution.
- iv
- SP has at most an exponential tail, which implies for some as .
- v
- SP has a monotonically decreasing mean residual life (MRL) time function.
2.5. Entropy
2.6. Infinite Divisibility and Further Properties
3. Estimation
4. Simulations
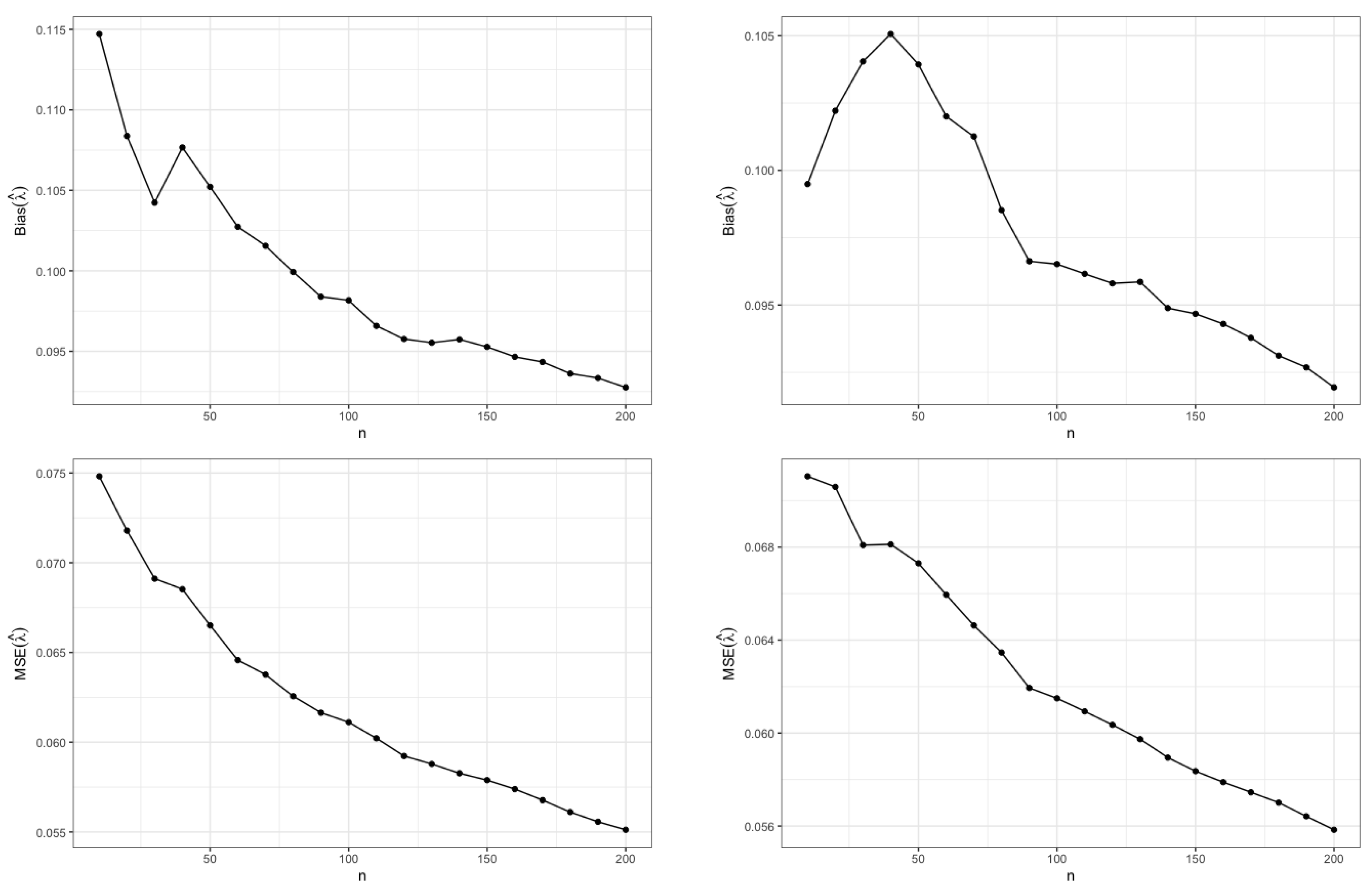
- In order to generate a random sample from the distribution, we make use of the characterization based on the weighted Poisson distribution, as seen in Equation (3). We therefore generate 10,000 samples of size n from the distribution for two specific values of , i.e., and 2.
- The MLEs for a particular are then computed from these 10,000 samples. Let these be denoted by .
- Using the MLEs from step (2), we compute the biases (Biases) and mean squared errors (MSEs) of the estimates using the following forms:
5. Applications to Real Data
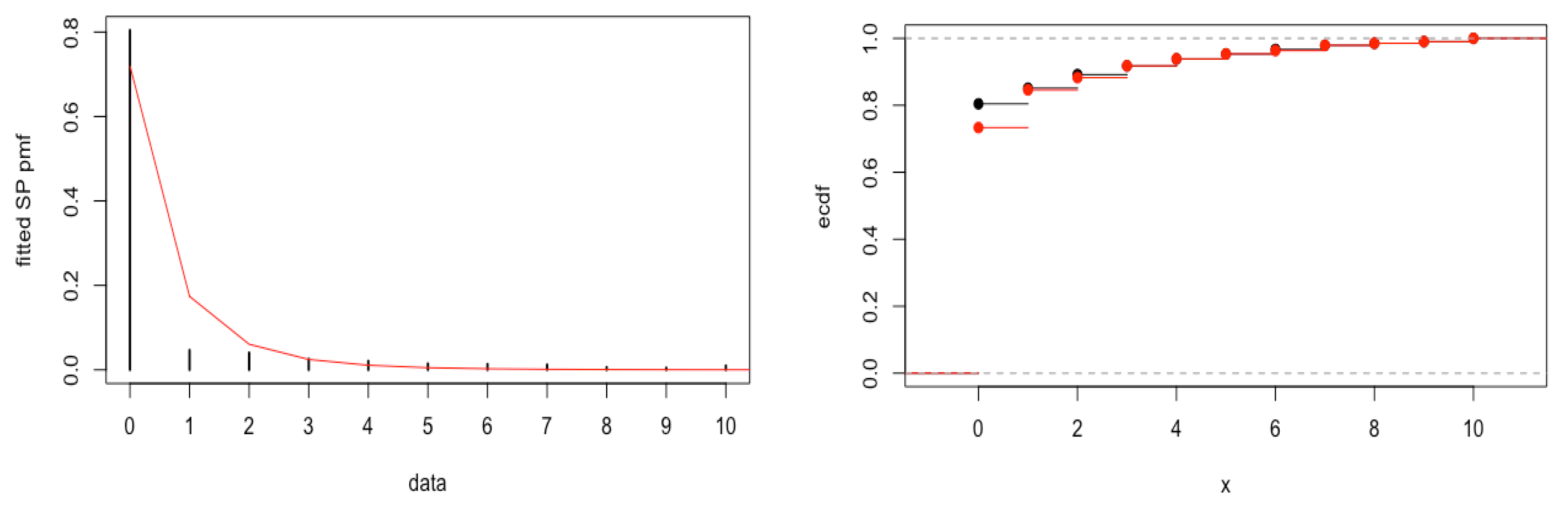
5.1. Dataset 1
- ZIW (zero inflated Waring distribution) given by [25],where and .
- NLD (new logarithmic distribution) given by [26],where .
- NGDP (new geometric discrete Pareto distribution), as proposed by [23],where .
- DGP (discrete generalized Pareto), provided by [27],where .
- PIG (Poisson inverse Gaussian distribution), outlined by [28],where and represent the modified Bessel function of the third kind with .
- NB (negative binomial distribution),where .
- PLD (Poisson Lindley distribution) provided in [29],where .
5.2. Dataset 2
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. R Codes
| x<-c() y<-c() b_l<-c() mse_l<-c() for(n in seq(from=10, to=200, by=10)){ l=0.5 for(i in 1:1000){ nll <- function(lam) { c<-lam^2/(exp(lam) ∗ (lam^2-lam+1)-1) z<-rpois(n,l) -n ∗ log(c)-sum(log((z+1)/(z+2) ∗ /factorial(z))) -sum(z) ∗ log(lam)+n ∗ lam } fit<-optim(l<-c(2),nll,hessian = FALSE) x<-c(x,fit$par[1]) } b_l<-c(b_l,mean(x)-l) mse_l<-c(mse_l,mean((x-l)^2)) } df<-data.frame(b_l,mse_l) n=seq(from=10, to=200, by=10) ggplot(data=df, aes(x=n, y=b_l))+ geom_line()+ geom_point()+ xlab("n")+ ylab(expression(Bias(hat(lambda))))+ theme_bw() |
References
- Lambert, D. Zero-Inflated Poisson regression, with an application to defects in manufacturing. Technometrics 1992, 34, 1–14. [Google Scholar] [CrossRef]
- Böhning, D.; Dietz, E.; Schlattmann, P.; Mendonca, L.; Kirchner, U. The zero-inflated Poisson model and the decayed, missing and filled teeth index in dental epidemiology. J. R. Stat. Soc. Ser. A 1999, 162, 195–209. [Google Scholar] [CrossRef]
- Atkins, D.C.; Gallop, R.C. Rethinking how family researchers model infrequent outcomes: A tutorial on count regression and zero-inflated models. J. Fam. Psychol. 2007, 21, 726–735. [Google Scholar] [CrossRef]
- Fagundes, R.A.A.; Souza, R.M.C.R.; Cysneiros, F.J.A. Zero-inflated prediction model in software-fault data. IET Softw. 2016, 10, 1–9. [Google Scholar] [CrossRef]
- Greene, W.H. Accounting for Excess Zeros and Sample Selection in Poisson and Negative Binomial Regression Models. NYU Working Paper No. EC-94-10. 1994. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1293115 (accessed on 17 January 2023).
- Mullahy, J. Specification and testing of some modified count data models. J. Econom. 1986, 33, 341–365. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; DeSantis, S.M.; Korte, J.E.; Brady, K.T. Some considerations for excess zeroes in substance abuse research. Am. J. Drug Alcohol Abus. 2011, 37, 376–382. [Google Scholar] [CrossRef] [PubMed]
- Coxe, S.; West, S.G.; Aiken, L.S. The analysis of count data: A gentle introduction to Poisson regression and its alternatives. J. Personal. Assess. 2009, 91, 121–136. [Google Scholar] [CrossRef]
- Hu, M.; Pavlicova, M.; Nunes, E.V. Zero-inflated and hurdle models of count data with extra zeros: Examples from an HIV-risk reduction intervention trial. Am. J. Drug Alcohol Abus. 2011, 37, 367–375. [Google Scholar] [CrossRef]
- Usman, M.; Oyejola, B.A. Models for count data in the presence of outliers and/or excess zero. Math. Theory Model. 2013, 3, 94–103. [Google Scholar]
- Tüzen, M.F.; Erbaş, S. A comparison of count data models with an application to daily cigarette consumption of young persons. Commun. Stat.-Theory Methods 2018, 47, 5825–5844. [Google Scholar] [CrossRef]
- Louzayadio, C.G.; Malouata, R.O.; Koukoutikissa, M.D. A weighted Poisson distribution for underdispersed count data. Int. J. Stat. Probab. 2021, 10, 157. [Google Scholar] [CrossRef]
- Rattihalli, R.N.; Bhati, D. Generation of new families of discrete distributions. Calcutta Stat. Assoc. Bull. 2017, 68, 135–146. [Google Scholar] [CrossRef]
- Tripathi, R.C.; Gupta, P.L.; Gupta, R.C. Incomplete moments of modified power series distributions with applications. Commun. Stat.-Theory Methods 1986, 15, 999–1015. [Google Scholar] [CrossRef]
- Gupta, P.L.; Gupta, R.C.; Tripathi, R.C. On the monotonic properties of discrete failure rates. J. Stat. Plan. Inference 1997, 65, 255–268. [Google Scholar] [CrossRef]
- Grandell, J. Mixed Poisson Processes; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Evans, R.J. Ramanujan’s Second Notebook: Asymptotic expansions for hypergeometric series and related functions. In Ramanujan Revisited; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Nekoukhou, V.; Alamatsaz, M.H.; Bidram, H. A discrete analog of the generalized exponential distribution. Commun. Stat.-Theory Methods 2012, 41, 2000–2013. [Google Scholar] [CrossRef]
- Steutel, F.W.; van Harn, K. Infinite Divisibility of Probability Distributions on the Real Line, 1st ed.; CRC Press: Boca Raton, FL, USA, 1979. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 17 January 2023).
- Rohatgi, V.K.; Saleh, A.K. An Introduction to Probability and Statistics, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Zeileis, A.; Kleiber, C. Countreg: Count Data Regression. R Package Version 0.2-0. 2018. Available online: http://R-Forge.Rproject.org/projects/countreg/ (accessed on 17 January 2023).
- Bhati, D.; Bakouch, H.S. A new infinitely divisible discrete distribution with applications to count data modeling. Commun. Stat.-Theory Methods 2019, 48, 1401–1416. [Google Scholar] [CrossRef]
- Shaul, K.B.; Ridder, A. Exponential dispersion models for over-dispersed zero-inflated count data. Commun. Stat.-Simul. Comput. 2021. [Google Scholar] [CrossRef]
- Rivas, L.; Campos, F. Zero inflated Waring distribution. Commun. Stat.-Simul. Comput. 2021. [Google Scholar] [CrossRef]
- Gómez-Déniz, E.; Sarabia, J.M.; Calderín-Ojeda, E. A new discrete distribution with actuarial applications. Insur. Math. Econ. 2011, 48, 406–412. [Google Scholar] [CrossRef]
- Prieto, F.; Gómez-Déniz, E.; Sarabia, J.M. Modelling road accident blackspots data with the discrete generalized Pareto distribution. Accid. Anal. Prev. 2014, 71, 38–49. [Google Scholar] [CrossRef]
- Willmot, G. The Poisson-inverse Gaussian as an alternative to the negative binomial. Scand. Actuar. J. 1987, 3, 113–127. [Google Scholar] [CrossRef]
- Sankaran, M. The Discrete Poisson-Lindley Distribution. Biometrics 1970, 26, 145–149. [Google Scholar] [CrossRef]
- Rose, C.E.; Martin, S.W.; Wannemuehler, K.A.; Plikaytis, B.D. On the use of zero inflated and hurdle models for modeling vaccine adverse events count data. J. Biopharm. Stat. 2006, 16, 463–481. [Google Scholar] [CrossRef] [PubMed]
| Value | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 654 | 38 | 33 | 21 | 17 | 12 | 11 | 10 | 5 | 4 | 8 |
| Model | Fitted Parameters | Log-L | AIC | BIC | K-S | p-Value |
|---|---|---|---|---|---|---|
| SP | −778.18 | 1558.36 | 1563.06 | 0.04 | 0.71 | |
| Poisson | −1332.85 | 2667.71 | 2672.41 | 0.24 | 0.04 | |
| ZIW | −781.56 | 1569.12 | 1583.22 | 0.05 | 0.64 | |
| NLD | −824.19 | 1652.38 | 1661.78 | 0.18 | 0.13 | |
| NGDP | −800.91 | 1605.68 | 1615.08 | 0.11 | 0.36 | |
| DGP | −811.12 | 1626.24 | 1655.64 | 0.15 | 0.26 | |
| PIG | −791.54 | 1587.82 | 1596.48 | 0.21 | 0.42 | |
| NB | −785.41 | 1574.82 | 1584.22 | 0.08 | 0.51 | |
| PLD | −974.37 | 1950.74 | 1955.45 | 0.06 | 0.06 |
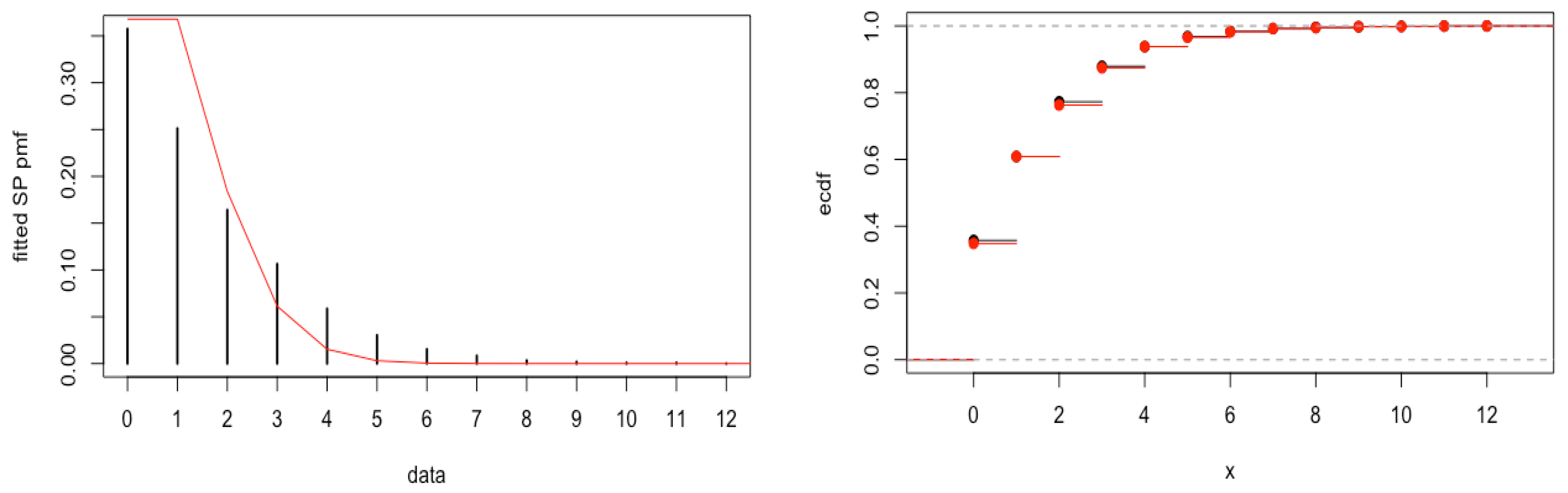
| Value | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 1437 | 1010 | 660 | 428 | 236 | 122 | 62 | 34 | 14 | 8 | 4 | 4 | 1 |
| Model | Fitted Parameters | Log-L | AIC | BIC | K-S | p-Value |
|---|---|---|---|---|---|---|
| SP | −3753.627 | 7149.29 | 7155.54 | 0.04 | 0.58 | |
| Poisson | −7231.13 | 14,464.27 | 14,470.57 | 0.29 | 0.05 | |
| ZIW | −6797.25 | 13,588.51 | 13,619.41 | 0.18 | 0.24 | |
| ZIPD | −6869.55 | 13,741.5 | 13,754.1 | 0.24 | 0.22 | |
| NGDP | −6741.78 | 13,487.57 | 13,500.16 | 0.10 | 0.33 | |
| NB | −6741.6 | 13,485.2 | 13,486.33 | 0.06 | 0.44 | |
| PLD | −6745.99 | 13,493.99 | 13,500.29 | 0.14 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuhayfith, F.E.; Bapat, S.R.; Bakouch, H.S.; Alnaghmosh, A.M. A Flexible Semi-Poisson Distribution with Applications to Insurance Claims and Biological Data. Mathematics 2023, 11, 1122. https://doi.org/10.3390/math11051122
Almuhayfith FE, Bapat SR, Bakouch HS, Alnaghmosh AM. A Flexible Semi-Poisson Distribution with Applications to Insurance Claims and Biological Data. Mathematics. 2023; 11(5):1122. https://doi.org/10.3390/math11051122
Chicago/Turabian StyleAlmuhayfith, Fatimah E., Sudeep R. Bapat, Hassan S. Bakouch, and Aminh M. Alnaghmosh. 2023. "A Flexible Semi-Poisson Distribution with Applications to Insurance Claims and Biological Data" Mathematics 11, no. 5: 1122. https://doi.org/10.3390/math11051122
APA StyleAlmuhayfith, F. E., Bapat, S. R., Bakouch, H. S., & Alnaghmosh, A. M. (2023). A Flexible Semi-Poisson Distribution with Applications to Insurance Claims and Biological Data. Mathematics, 11(5), 1122. https://doi.org/10.3390/math11051122






