Non-Fragile Fuzzy Tracking Control for Nonlinear Networked Systems with Dynamic Quantization and Randomly Occurring Gain Variations
Abstract
1. Introduction
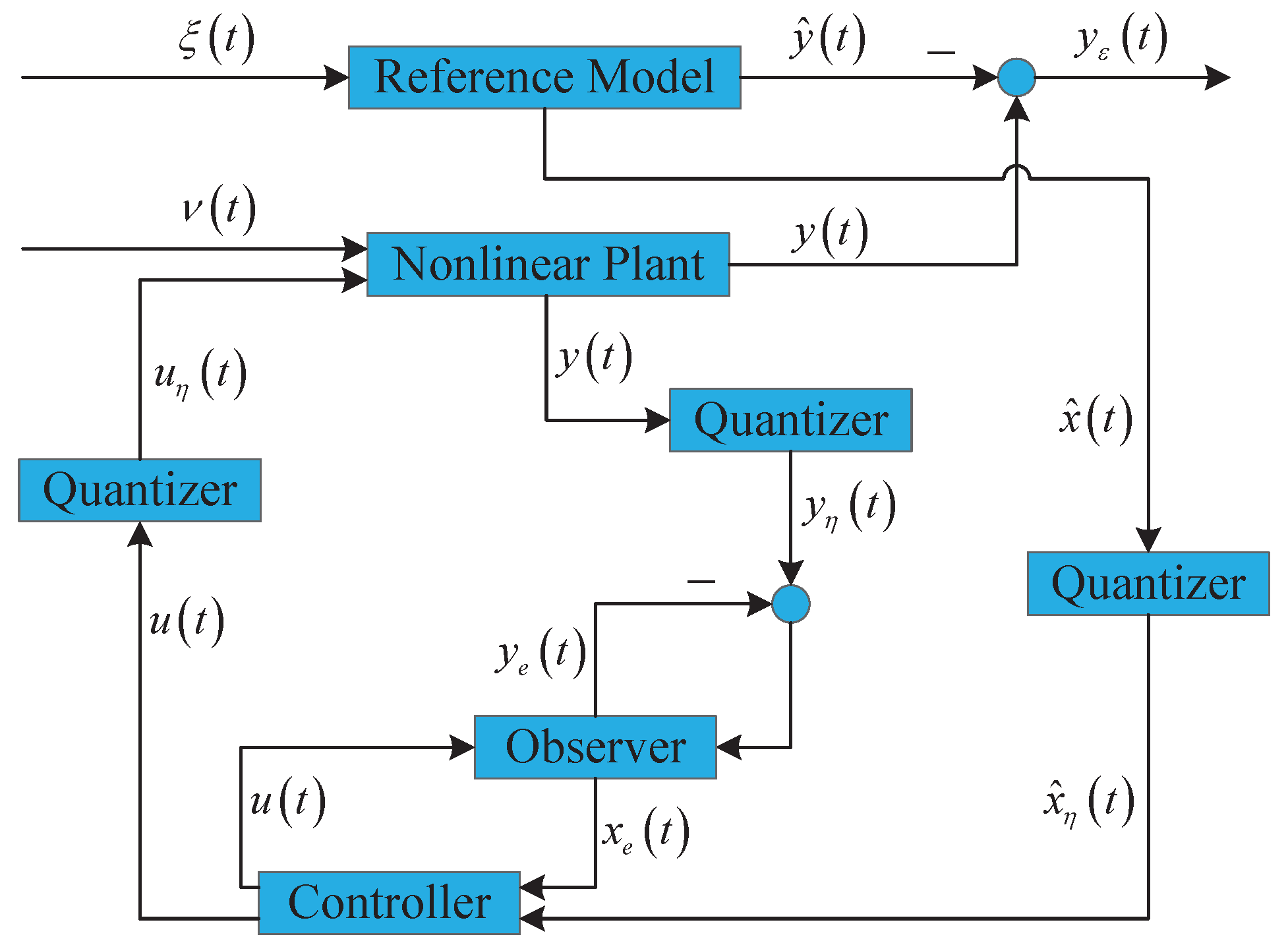
2. Problem Formulation
2.1. T–S Fuzzy Model
2.2. Reference Model
2.3. Observer-Based Output Feedback Tracking Controller
2.4. Dynamic Quantizers
2.5. Resulting System
3. Main Results
3.1. Tracking Performance Analysis
3.2. Non-Fragile Tracking Controller Design
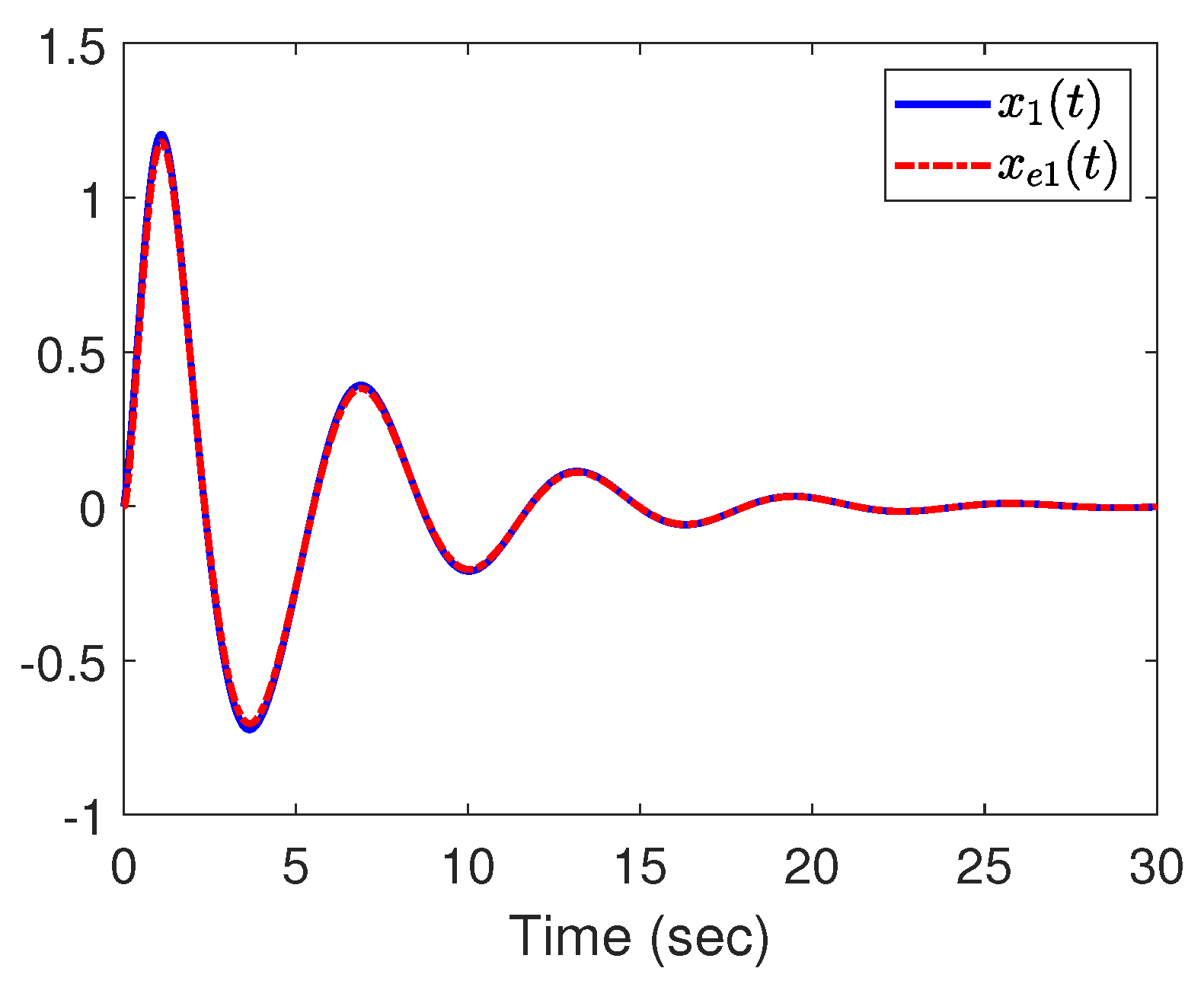
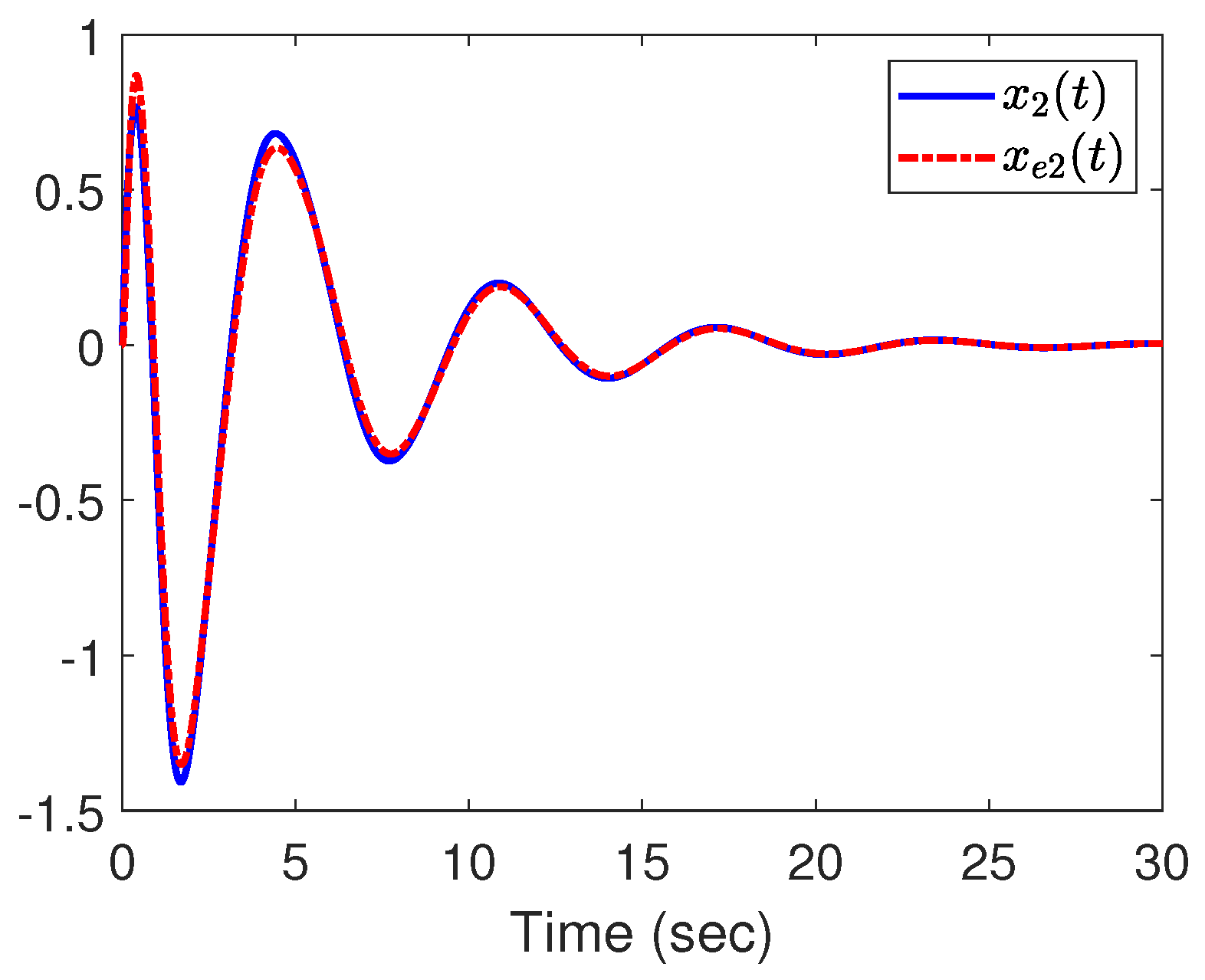
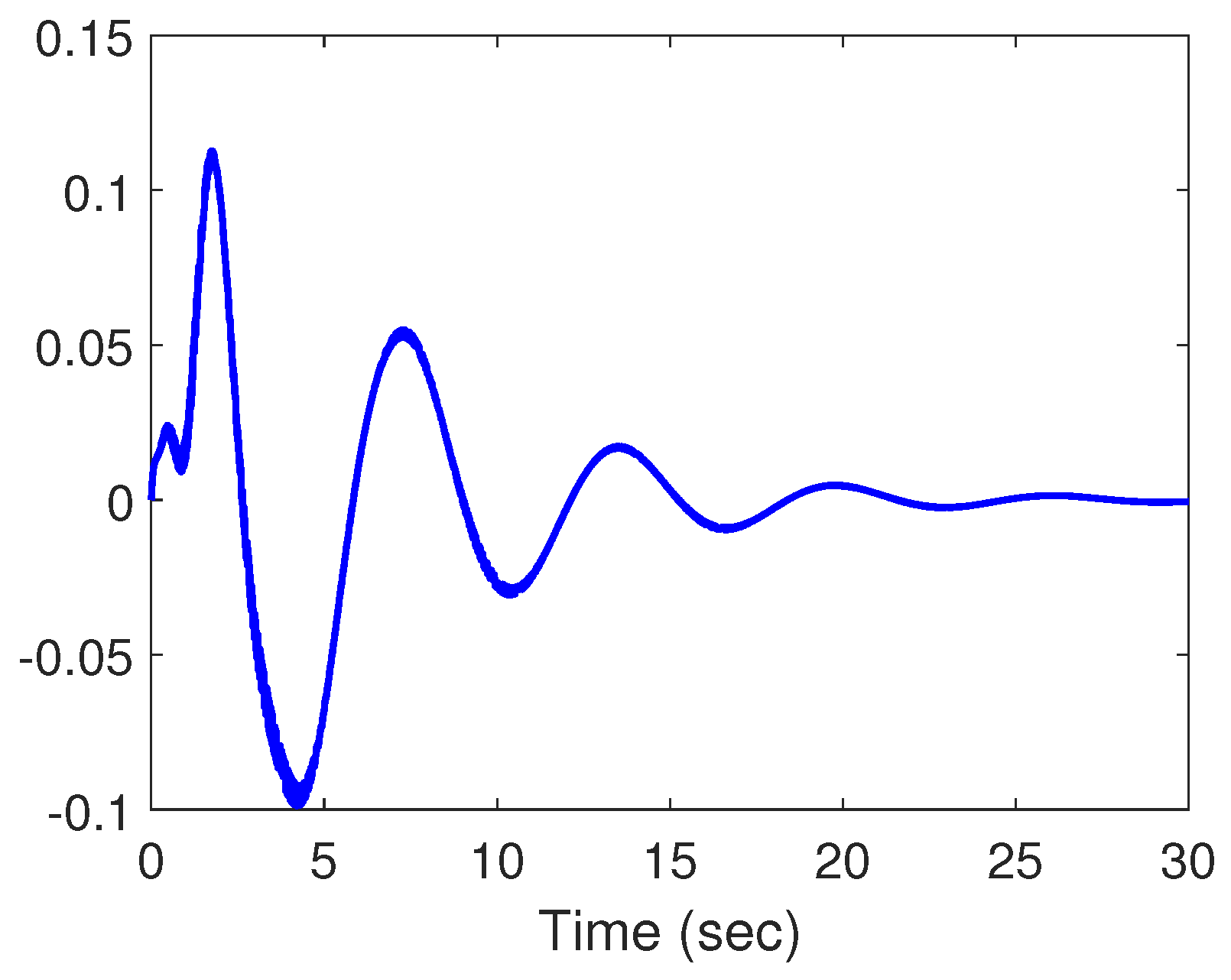
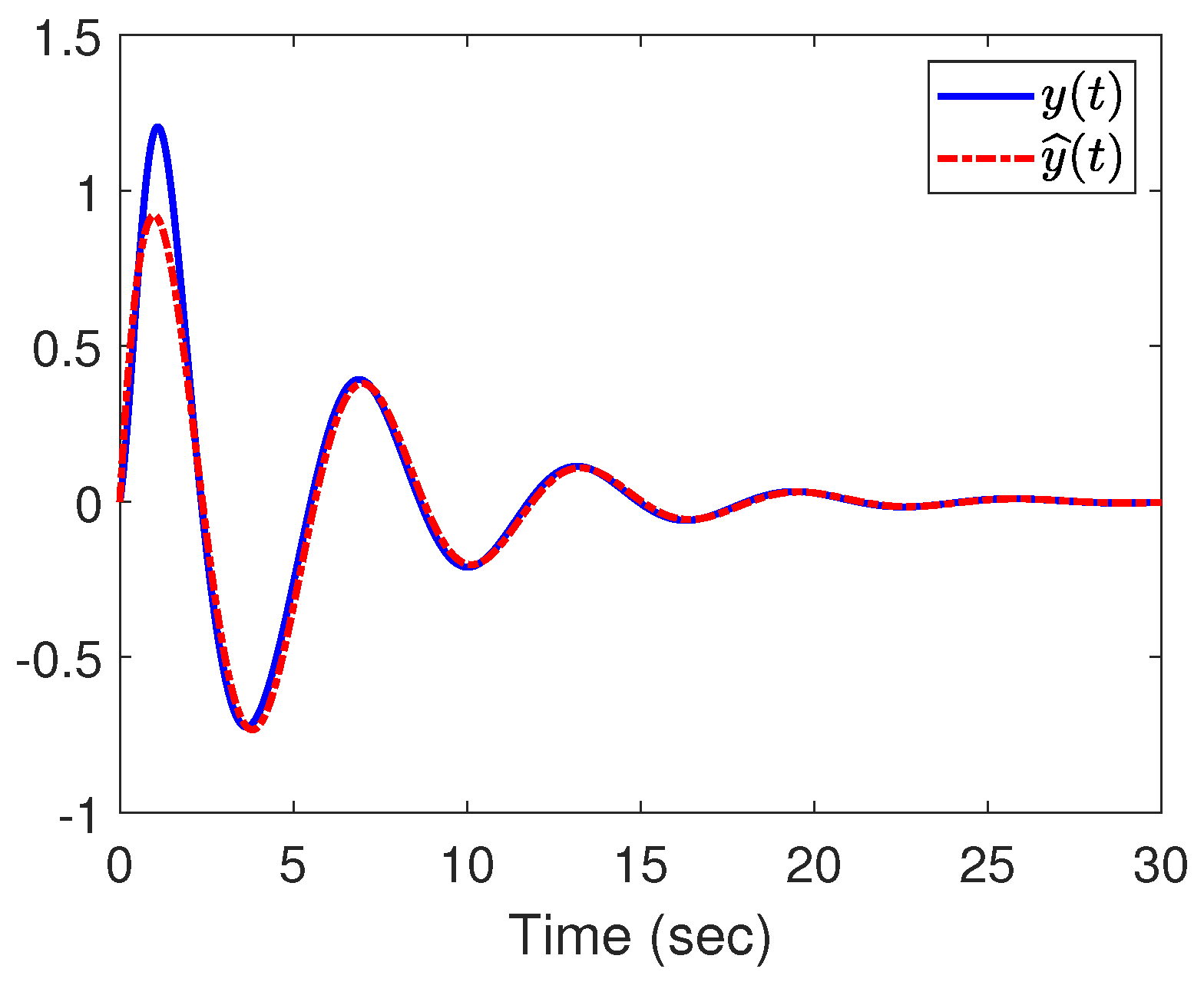
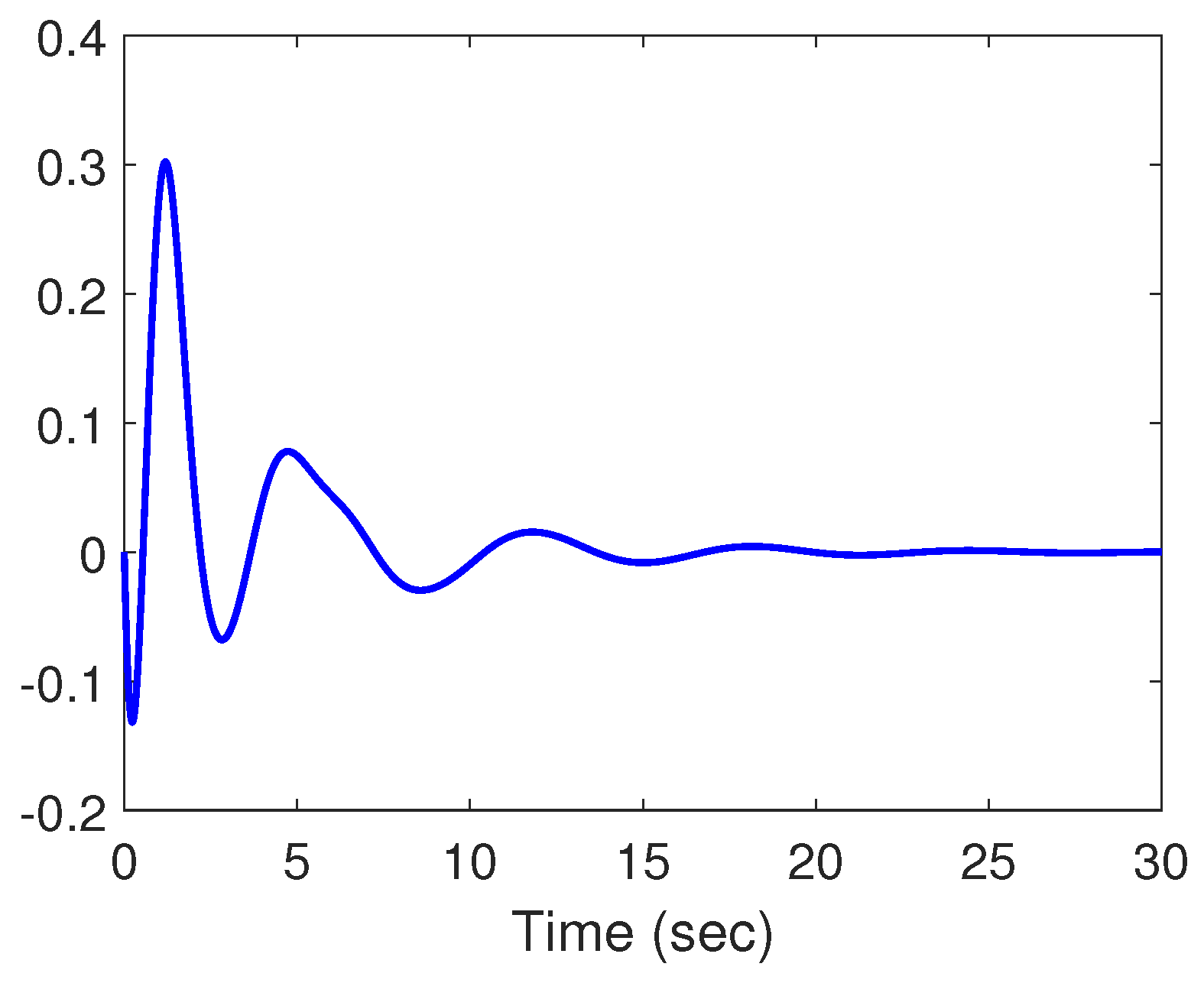
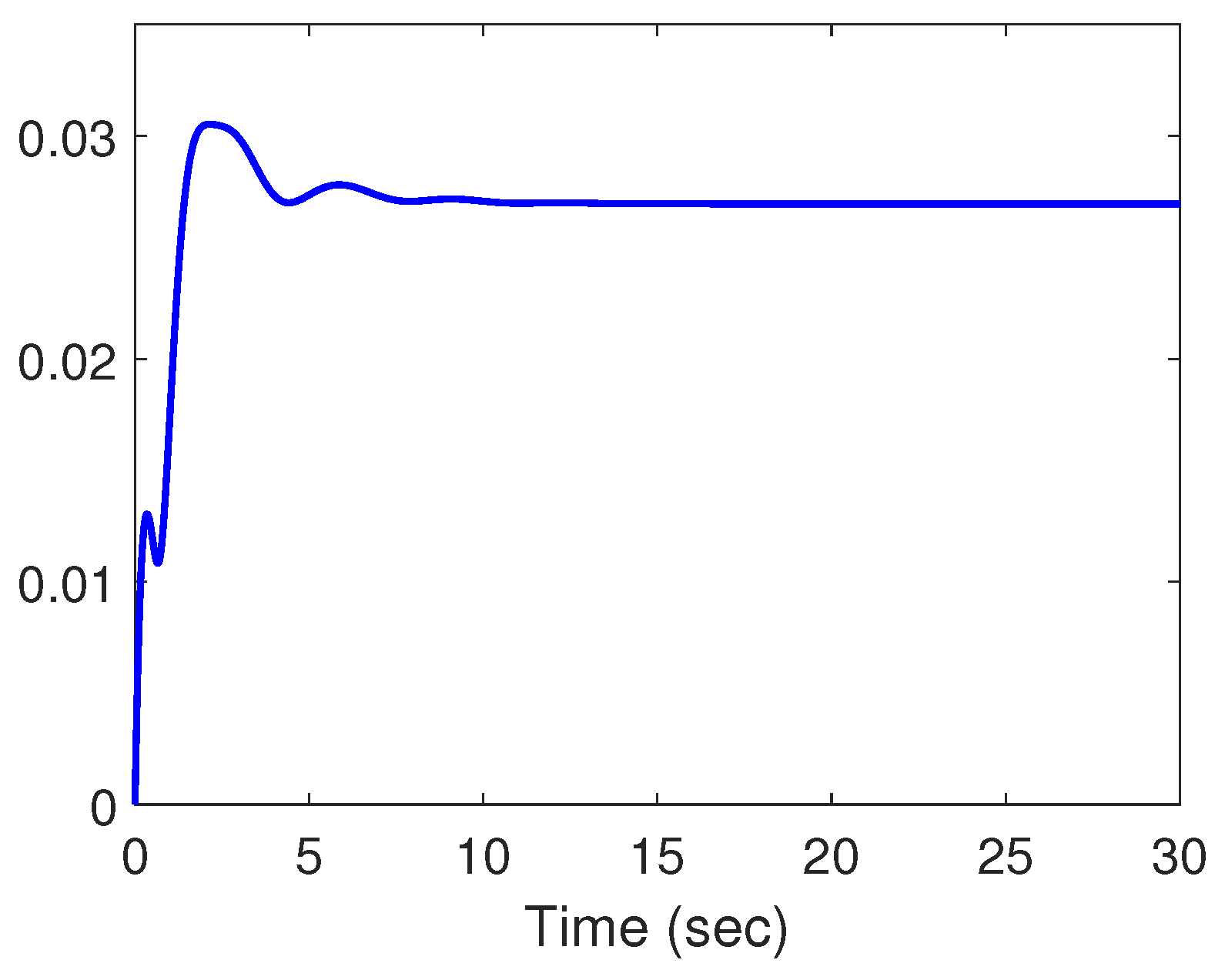
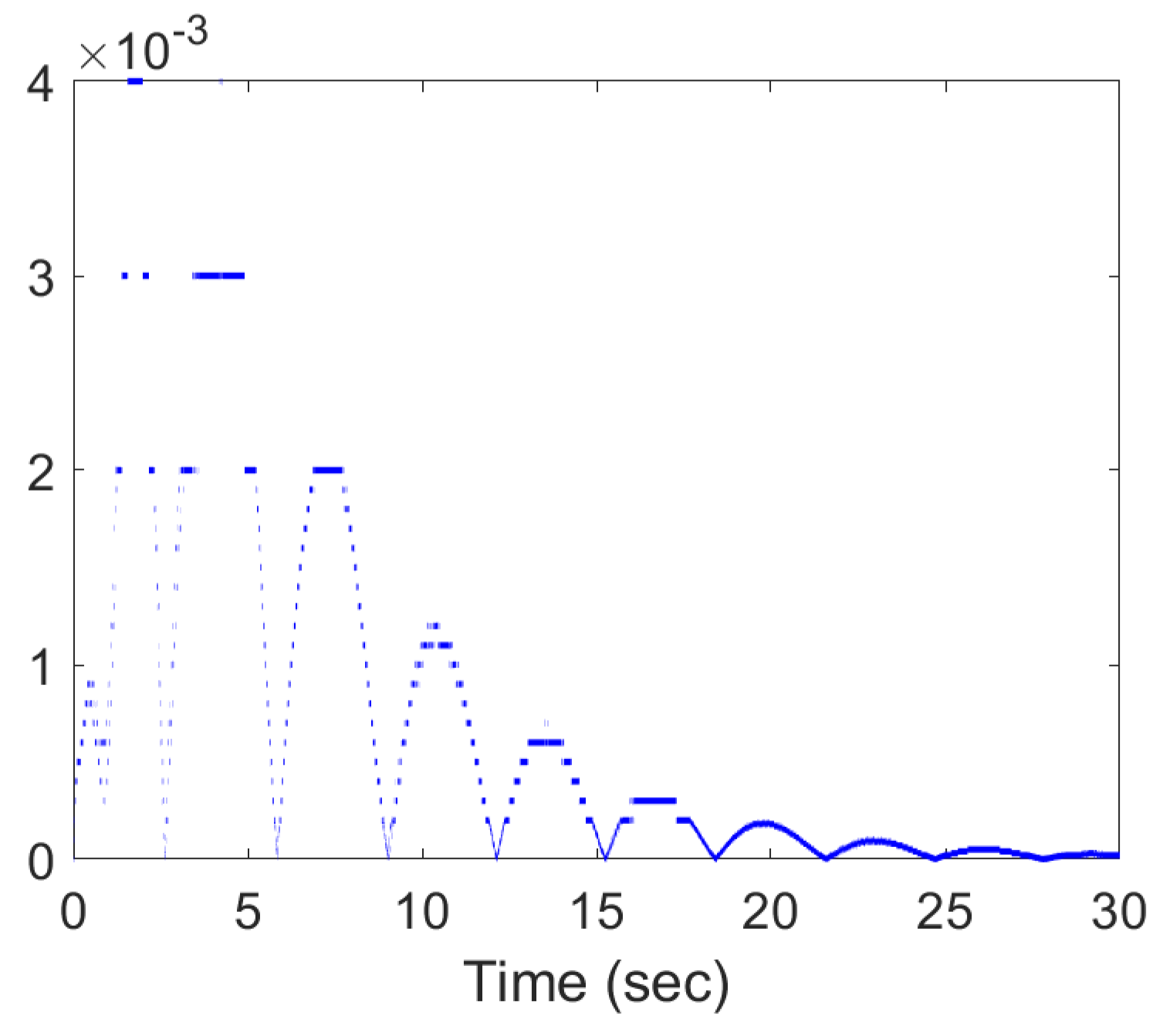
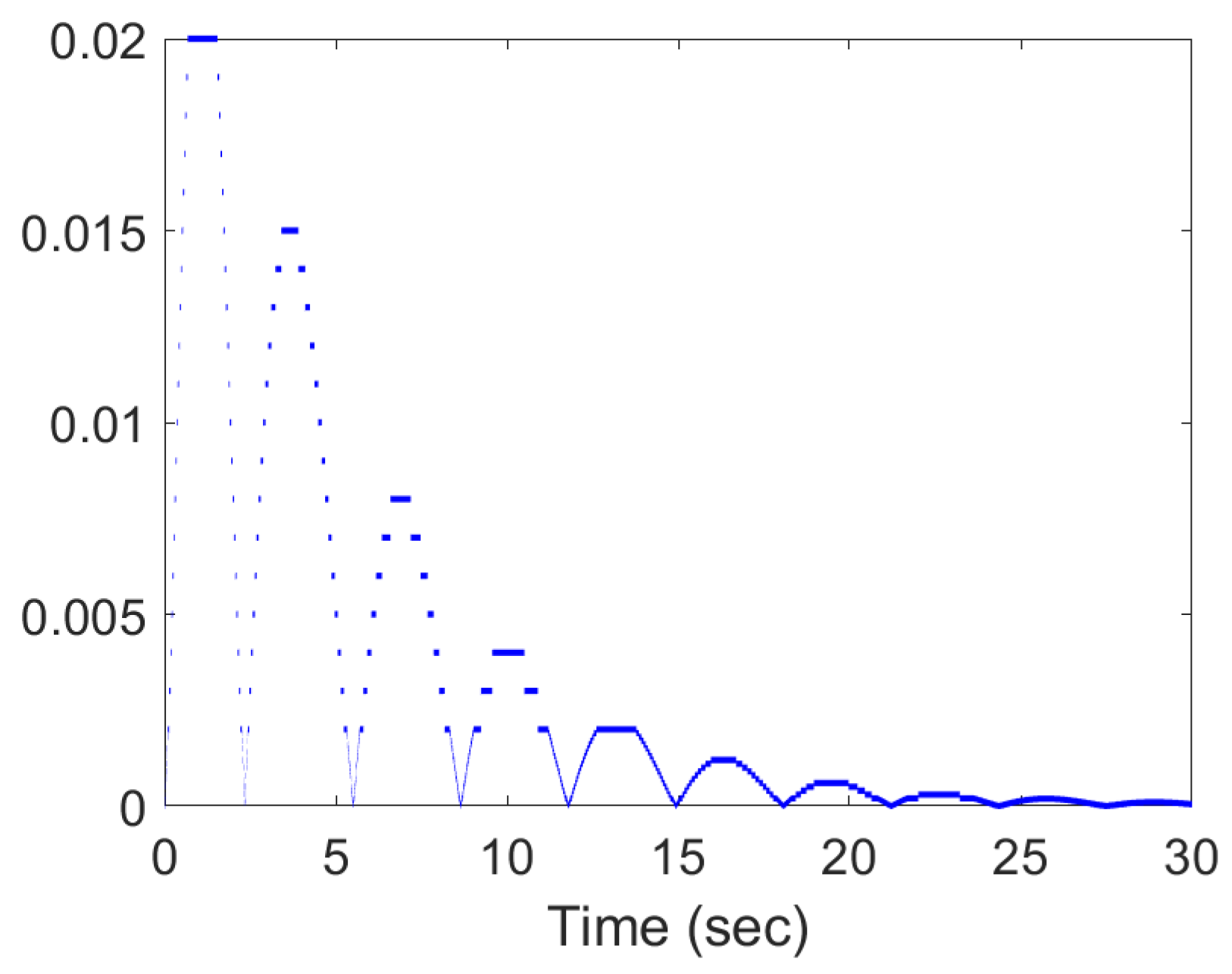
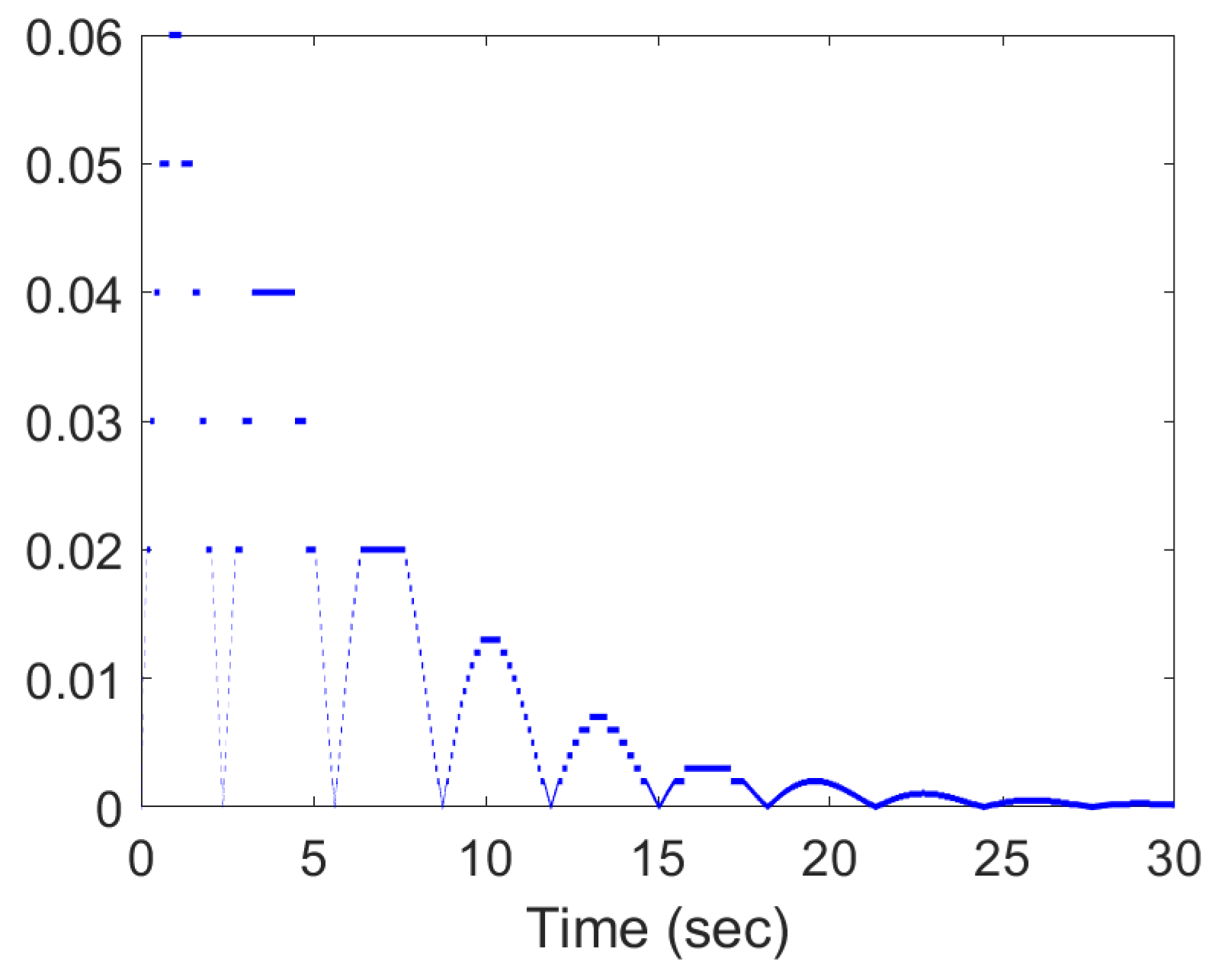
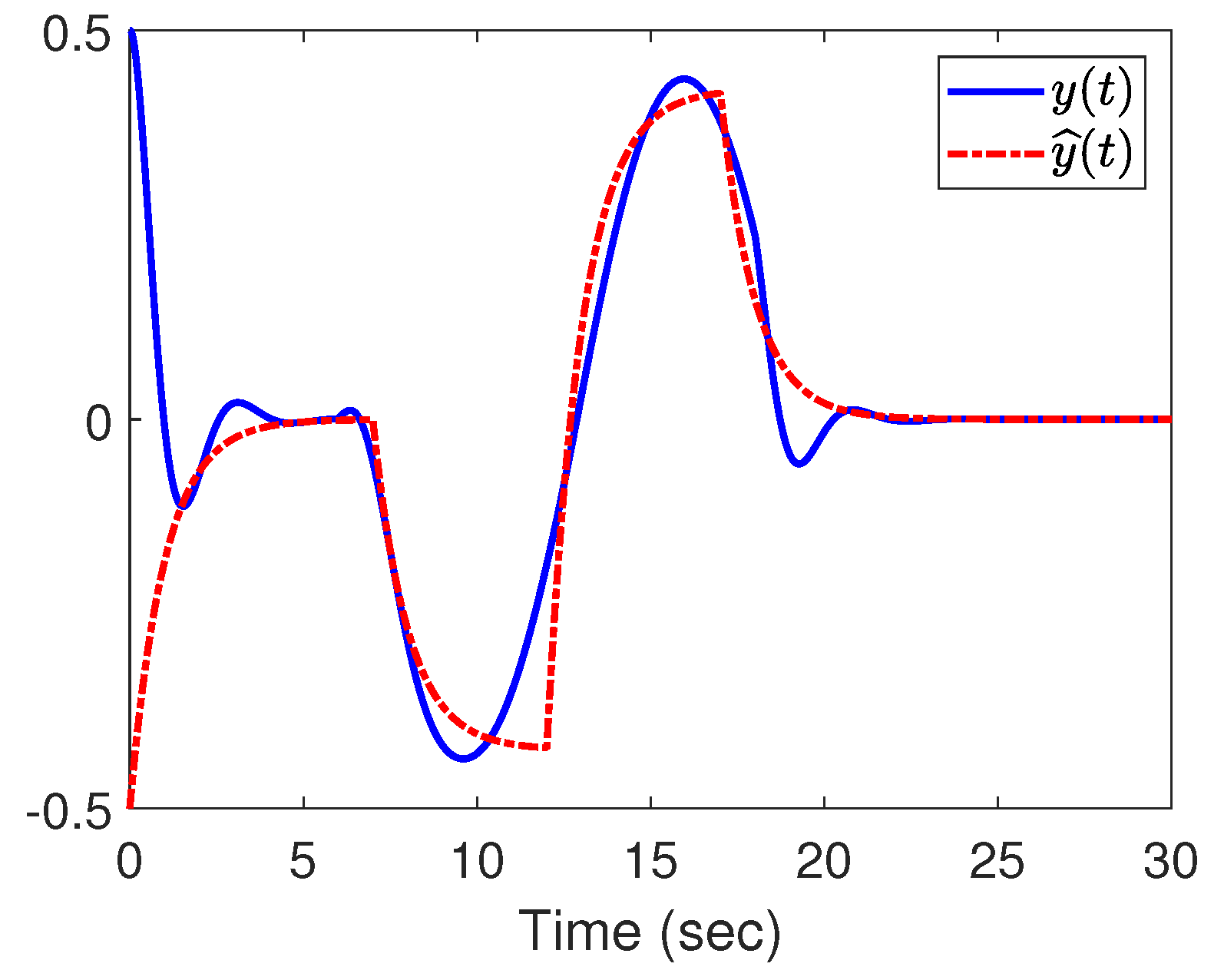
4. Illustrative Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Gao, H.; Kaynak, O. Network-induced constraints in networked control systems—A survey. IEEE Trans. Ind. Inf. 2013, 9, 142–149. [Google Scholar] [CrossRef]
- Su, L.; Chesi, G. Robust stability of uncertain linear systems with input and output quantization and packet loss. Automatica 2018, 87, 267–273. [Google Scholar] [CrossRef]
- Gao, H.; Chen, T. A new approach to quantized feedback control systems. Automatica 2008, 44, 534–542. [Google Scholar] [CrossRef]
- Coutinho, D.F.; Fu, M.; de Souza, C.E. Input and output quantized feedback linear systems. IEEE Trans. Autom. Control 2010, 55, 761–766. [Google Scholar] [CrossRef]
- Liberzon, D. Hybrid feedback stabilization of systems with quantized signals. Automatica 2003, 39, 1543–1554. [Google Scholar] [CrossRef]
- Che, W.W.; Yang, G.H. State feedback H∞ control for quantized discrete-time systems. Asian J. Contr. 2008, 10, 718–723. [Google Scholar] [CrossRef]
- Zheng, B.C.; Yu, X.; Xue, Y. Quantized feedback sliding-mode control: An event-triggered approach. Automatica 2018, 91, 126–135. [Google Scholar] [CrossRef]
- Niu, Y.; Ho, D.W.C. Control strategy with adaptive quantizer’s parameters under digital communication channels. Automatica 2014, 50, 2665–2671. [Google Scholar] [CrossRef]
- Chang, X.H.; Xiong, J.; Li, Z.M.; Park, J.H. Quantized static output feedback control for discrete-time systems. IEEE Trans. Ind. Inf. 2018, 14, 3426–3435. [Google Scholar] [CrossRef]
- Tanaka, K.; Wang, H.O. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, P.; Qiu, J.; Nguang, S.K. A novel observer-based output feedback controller design for discrete-time fuzzy systems. IEEE Trans. Fuzzy Syst. 2015, 23, 223–229. [Google Scholar] [CrossRef]
- Chang, X.H.; Yang, G.H. Nonfragile H∞ filter design for T–S fuzzy systems in standard form. IEEE Trans. Ind. Electron. 2014, 61, 3448–3458. [Google Scholar] [CrossRef]
- Dong, J.; Yang, G.H. Observer-based output feedback control for discrete-time T–S fuzzy systems with partly immeasurable premise variables. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 98–110. [Google Scholar] [CrossRef]
- Chang, X.H.; Yang, G.H. A descriptor representation approach to observer-based H∞ control synthesis for discrete-time fuzzy systems. Fuzzy Sets Syst. 2011, 185, 38–51. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B.Z.; Park, J.H. Non-fragile H∞ filtering for delayed Takagi-Sugeno fuzzy systems with randomly occurring gain variations. Fuzzy Sets Syst. 2017, 316, 99–116. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, D.; Chai, T. Guaranteed cost networked control for T–S fuzzy systems with time delays. IEEE Trans. Syst. Man Cybern. C 2007, 37, 160–172. [Google Scholar] [CrossRef]
- Yao, H.; Gao, F. Design of observer and dynamic output feedback control for fuzzy networked systems. Mathematics 2022, 11, 148. [Google Scholar] [CrossRef]
- Peng, C.; Yang, T.C. Communication-delay-distribution-dependent networked control for a class of T–S fuzzy systems. IEEE Trans. Fuzzy Syst. 2010, 18, 326–335. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, S.; Zhang, Z. Nonfragile H∞ control for uncertain Takagi-Sugeno fuzzy systems under digital communication channels and its application. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3638–3647. [Google Scholar] [CrossRef]
- Shen, H.; Men, Y.; Wu, Z.G.; Cao, J.; Lu, G. Network-based quantized control for fuzzy singularly perturbed semi-Markov jump systems and its application. IEEE Trans. Circuits Syst. I Reg. Papers 2019, 66, 1130–1140. [Google Scholar] [CrossRef]
- Qiu, J.; Feng, G.; Gao, H. Observer-based piecewise affine output feedback controller synthesis of continuous-time T–S fuzzy affine dynamic systems using quantized measurements. IEEE Trans. Fuzzy Syst. 2012, 20, 1046–1062. [Google Scholar]
- Chang, X.H.; Yang, C.; Xiong, J. Quantized fuzzy output feedback H∞ control for nonlinear systems with adjustment of dynamic parameters. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2005–2015. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, S.; Du, B. Quantized guaranteed cost output feedback control for nonlinear networked control systems and its applications. IEEE Trans. Fuzzy Syst. 2022, 30, 2402–2411. [Google Scholar] [CrossRef]
- Pan, T.T.; Chang, X.H.; Liu, Y. Robust fuzzy feedback control for nonlinear systems with input quantization. IEEE Trans. Fuzzy Syst. 2022, 30, 4905–4914. [Google Scholar] [CrossRef]
- Chang, X.H.; Jin, X. Observer-based fuzzy feedback control for nonlinear systems subject to transmission signal quantization. Appl. Math. Comput. 2022, 414, 126657. [Google Scholar] [CrossRef]
- Chang, X.H.; Li, Z.M.; Park, J.H. Fuzzy generalized H2 filtering for nonlinear discrete-time systems with measurement quantization. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 2419–2430. [Google Scholar] [CrossRef]
- Li, Z.M.; Xiong, J. Event-triggered fuzzy filtering for nonlinear networked systems with dynamic quantization and stochastic cyber attacks. ISA Trans. 2022, 121, 53–62. [Google Scholar] [CrossRef]
- Gao, H.; Chen, T. Network-based H∞ output tracking control. IEEE Trans. Autom. Control 2008, 53, 655–667. [Google Scholar] [CrossRef]
- Peng, C.; Song, Y.; Xie, X.P.; Zhao, M.; Fei, M.R. Event-triggered output tracking control for wireless networked control systems with communication delays and data dropouts. IET Control Theory Appl. 2016, 10, 2195–2203. [Google Scholar] [CrossRef]
- Yan, H.; Hu, C.; Zhang, H.; Karimi, H.R.; Jiang, X.; Liu, M. H∞ output tracking control for networked systems with adaptively adjusted event-triggered scheme. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2050–2058. [Google Scholar] [CrossRef]
- Lian, K.Y.; Liou, J.J. Output tracking control for fuzzy systems via output feedback design. IEEE Trans. Fuzzy Syst. 2006, 14, 628–639. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Q.G.; Lee, T.H. H∞ output tracking control for nonlinear systems via T–S fuzzy model approach. IEEE Trans. Syst. Man Cybern. B Cybern. 2006, 36, 450–457. [Google Scholar]
- Tseng, C.S.; Chen, B.S.; Uang, H.J. Fuzzy tracking control design for nonlinear dynamic systems via T–S fuzzy model. IEEE Trans. Fuzzy Syst. 2001, 9, 381–392. [Google Scholar] [CrossRef]
- Li, H.; Wu, C.; Jing, X.; Wu, L. Fuzzy tracking control for nonlinear networked systems. IEEE Trans. Cybern. 2017, 47, 2020–2031. [Google Scholar] [CrossRef]
- Zhang, D.; Han, Q.L.; Jia, X. Network-based output tracking control for a class of T–S fuzzy systems that can not be stabilized by nondelayed output feedback controllers. IEEE Trans. Cybern. 2015, 45, 1511–1524. [Google Scholar] [CrossRef]
- Zhang, D.; Han, Q.L.; Jia, X. Network-based output tracking control for T–S fuzzy systems using an event-triggered communication scheme. Fuzzy Sets Syst. 2015, 273, 26–48. [Google Scholar] [CrossRef]
- Li, Z.M.; Park, J.H. Dissipative fuzzy tracking control for nonlinear networked systems with quantization. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 5130–5141. [Google Scholar] [CrossRef]
- Li, Z.M.; Chang, X.H.; Park, J.H. Quantized static output feedback fuzzy tracking control for discrete-time nonlinear networked systems with asynchronous event-triggered constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3820–3831. [Google Scholar] [CrossRef]
- Li, Z.M.; Chang, X.H.; Xiong, J. Event-based fuzzy tracking control for nonlinear networked systems subject to dynamic quantization. IEEE Trans. Fuzzy Syst. 2022. in press. Available online: https://ieeexplore.ieee.org/abstract/document/9839441 (accessed on 25 July 2022).
- Wu, L.; Yang, X.; Li, F. Nonfragile output tracking control of hypersonic air-breathing vehicles with an LPV model. IEEE/ASME Trans. Mechatron. 2013, 18, 1280–1288. [Google Scholar] [CrossRef]
- Keel, L.H.; Bhattacharyya, S.P. Robust, fragile, or optimal? IEEE Trans. Autom. Control 1997, 42, 1098–1105. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Cao, J.; Chadli, M.; Shen, H. Nonfragile output feedback tracking control for Markov jump fuzzy systems based on integral reinforcement learning scheme. IEEE Trans. Cybern. 2022. in press. Available online: https://ieeexplore.ieee.org/abstract/document/9911218 (accessed on 4 October 2022).
- Han, T.J.; Kim, H.S. Disturbance observer-based nonfragile fuzzy tracking control of a spacecraft. Adv. Space Res. 2022. in press. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0273117722010754 (accessed on 25 November 2022).
- Ghorbel, C.; Benhadj Braiek, N. Nonfragile H∞ tracking control strategies for classes of linear and bilinear uncertain Takagi-Sugeno fuzzy systems. Trans. Inst. Meas. Control 2022, 44, 2166–2176. [Google Scholar] [CrossRef]
- Gao, F.; Wu, Y.; Zhang, Z. Global fixed-time stabilization of switched nonlinear systems: A time-varying scaling transformation approach. IEEE Trans. Circuits Syst. II Exp. Briefs 2019, 66, 1890–1894. [Google Scholar] [CrossRef]
- Gao, F.; Chen, C.C.; Huang, J.; Wu, Y. Prescribed-time stabilization of uncertain planar nonlinear systems with output constraints. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 2887–2891. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lu, C.; Wang, H. Non-Fragile Fuzzy Tracking Control for Nonlinear Networked Systems with Dynamic Quantization and Randomly Occurring Gain Variations. Mathematics 2023, 11, 1116. https://doi.org/10.3390/math11051116
Li Z, Lu C, Wang H. Non-Fragile Fuzzy Tracking Control for Nonlinear Networked Systems with Dynamic Quantization and Randomly Occurring Gain Variations. Mathematics. 2023; 11(5):1116. https://doi.org/10.3390/math11051116
Chicago/Turabian StyleLi, Zhimin, Chengming Lu, and Hongyu Wang. 2023. "Non-Fragile Fuzzy Tracking Control for Nonlinear Networked Systems with Dynamic Quantization and Randomly Occurring Gain Variations" Mathematics 11, no. 5: 1116. https://doi.org/10.3390/math11051116
APA StyleLi, Z., Lu, C., & Wang, H. (2023). Non-Fragile Fuzzy Tracking Control for Nonlinear Networked Systems with Dynamic Quantization and Randomly Occurring Gain Variations. Mathematics, 11(5), 1116. https://doi.org/10.3390/math11051116



