Blockchain-Driven Real-Time Incentive Approach for Energy Management System
Abstract
:1. Introduction
1.1. Research Contributions
- This paper proposes an RI-EMS approach for DR based on Q-learning to prioritize the experience of an agent and for faster convergence of DR using an epsilon greedy policy.
- A novel real-time incentive mechanism is proposed using a smart contract for the end-consumer to motivate them to participate in DR due to the appropriate and optimal incentives obtained for each participant in the EM.
- The proposed RI-EMS approach is evaluated compared to the conventional approaches in terms of consumer participation, energy consumption reduction, transaction efficiency, and data storage cost.
1.2. Organization of the Paper
2. System Model and Problem Formulation
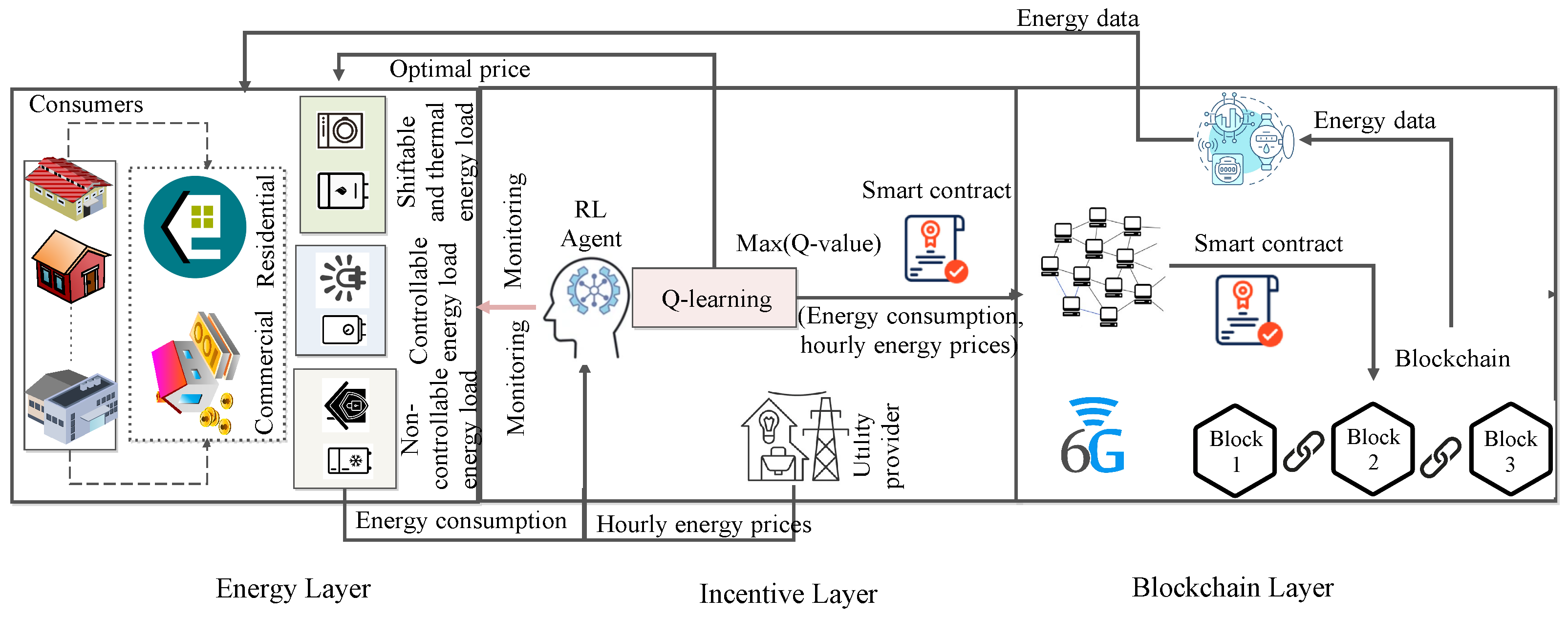
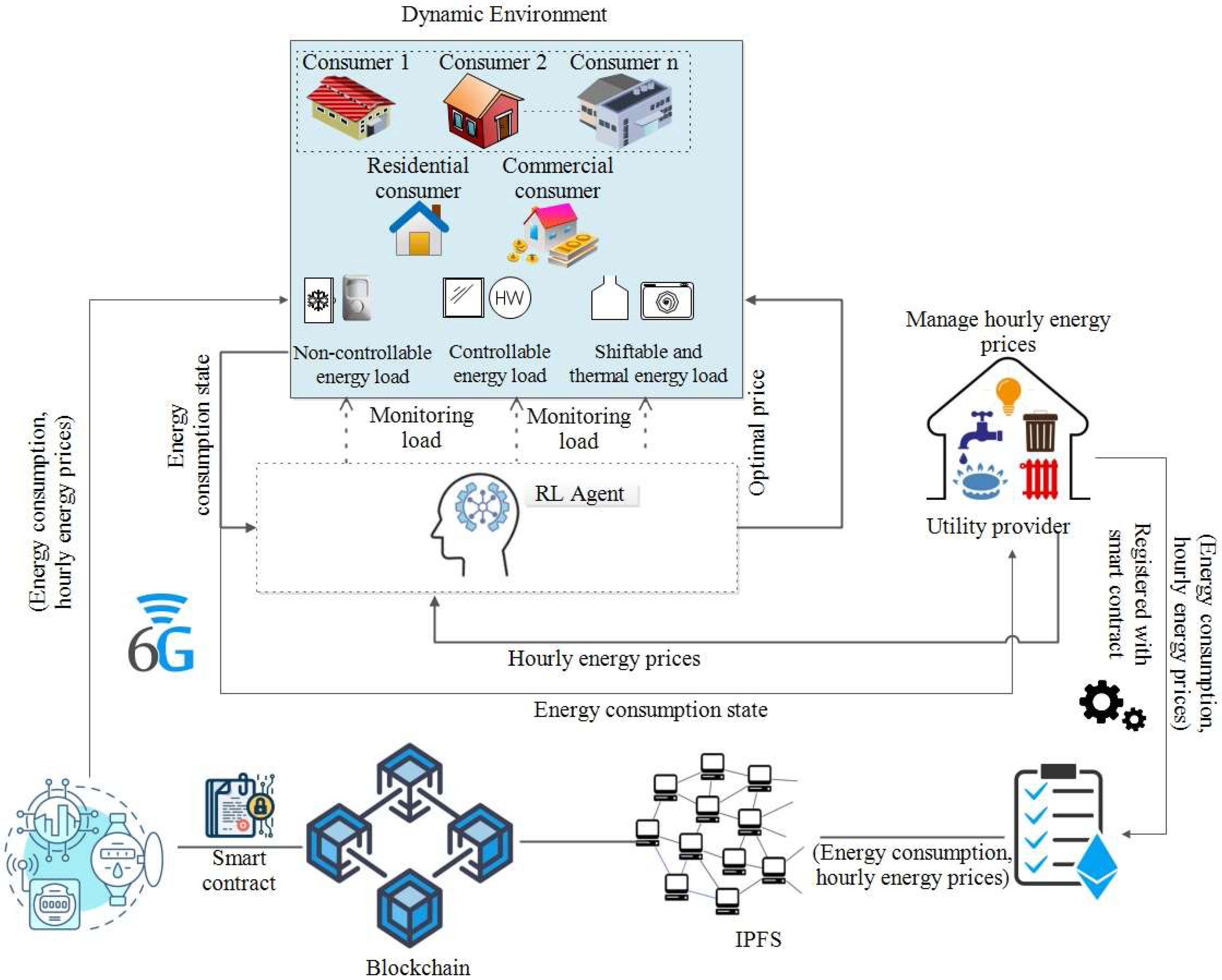
2.1. System Model
2.2. Problem Formulation
3. The Proposed Approach
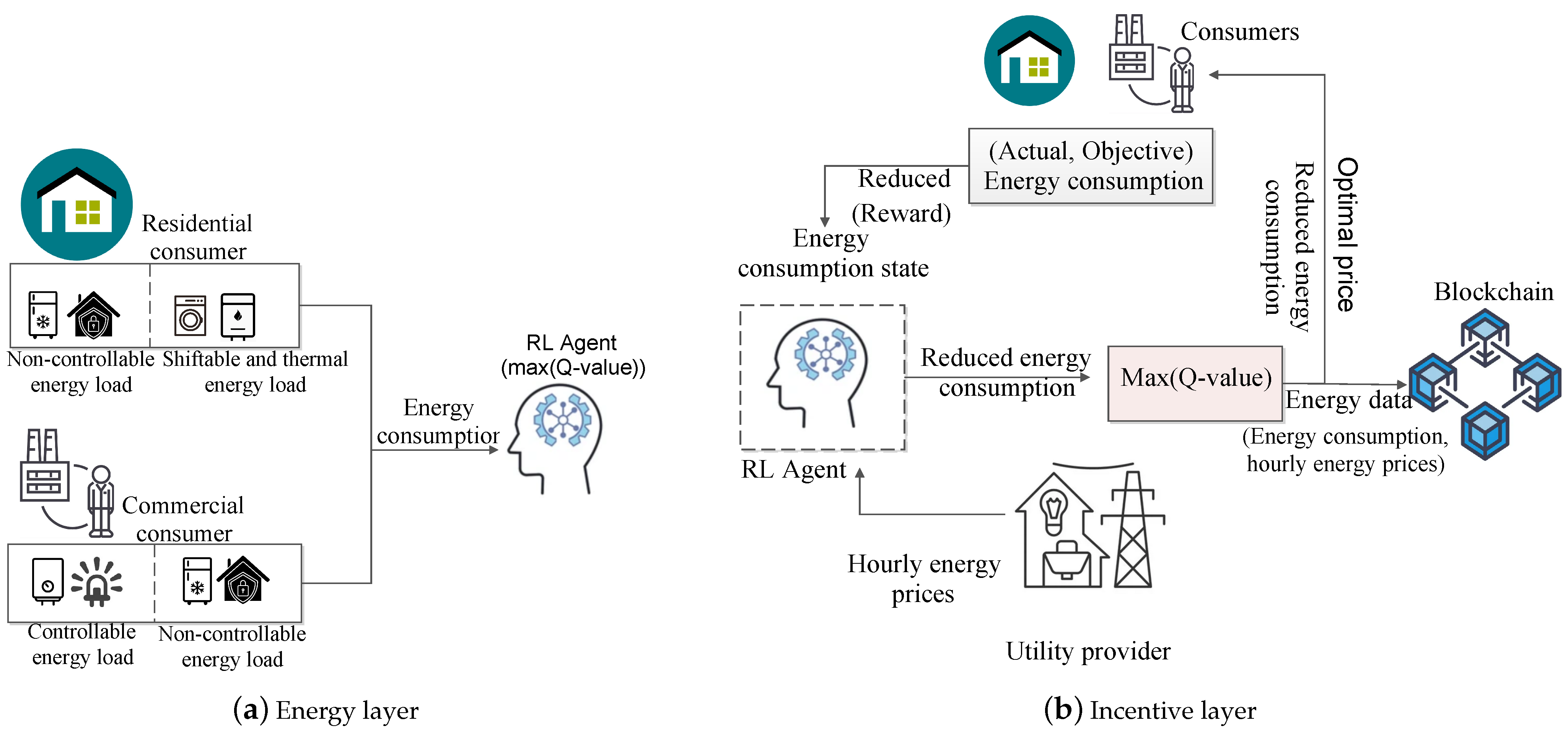
3.1. Energy Layer
3.2. Incentive Layer—Reinforcement Learning Approach
| Algorithm 1 Incentive for Consumers using Q-learning |
Input: Output: Optimized incentive
|
3.3. Blockchain Layer
| Algorithm 2 Blockchain-based algorithm for secure energy data storage |
Input: Output: Add energy data transactions to the blockchain
|
4. Performance Evaluation
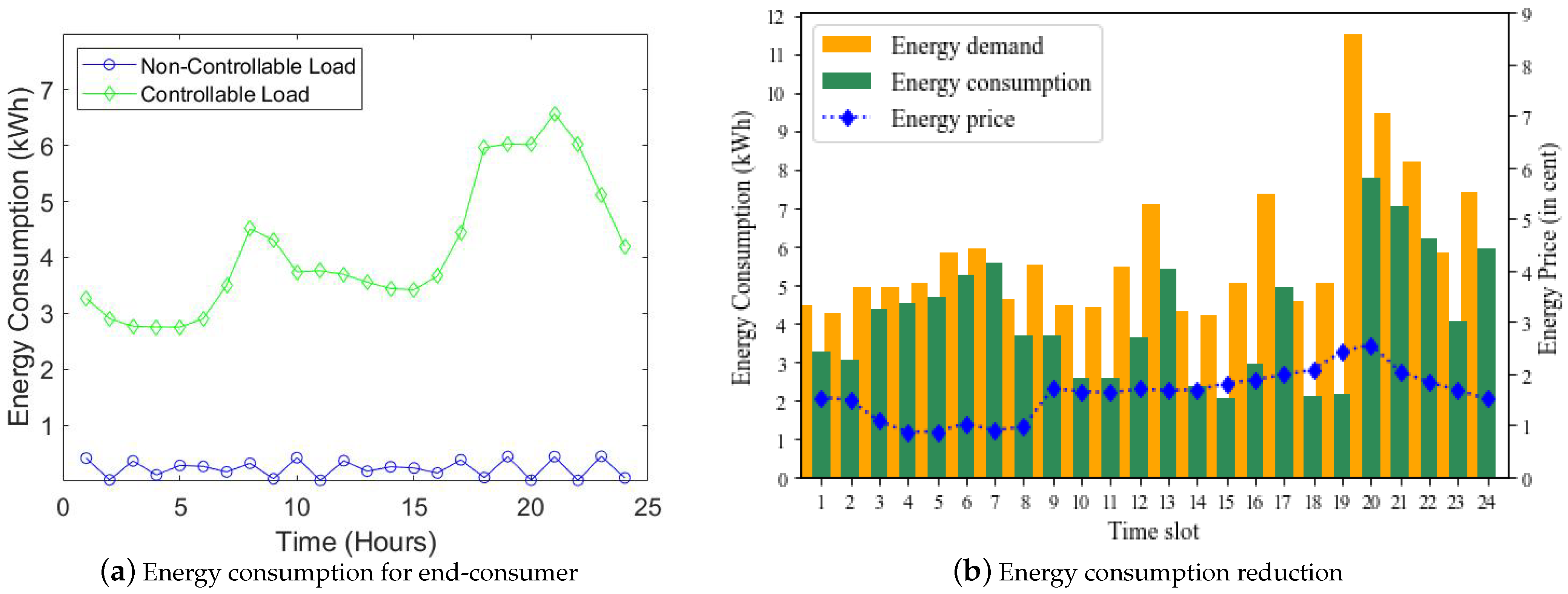
4.1. Dataset Description
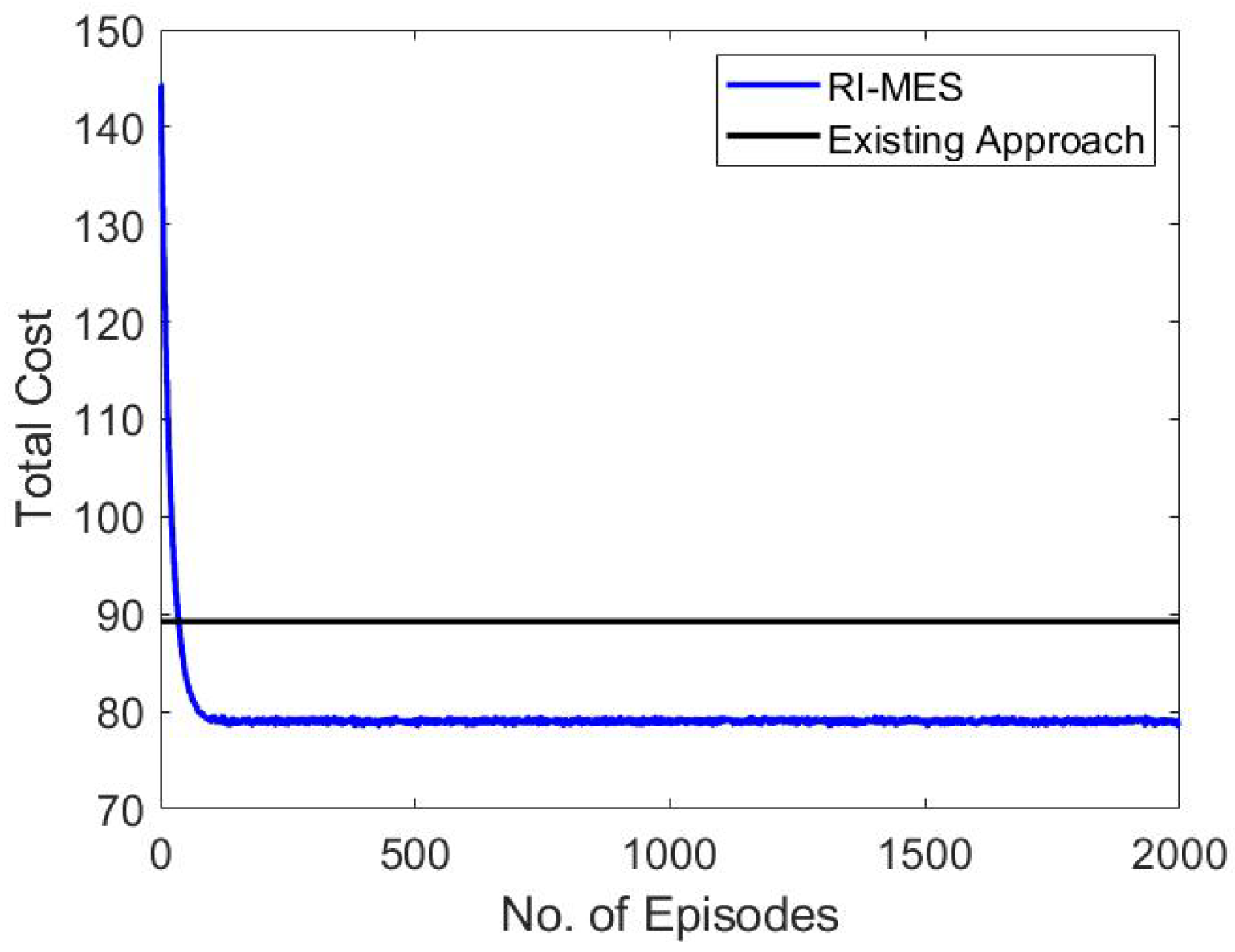
4.2. Energy Consumption Reduction and Comparative Analysis
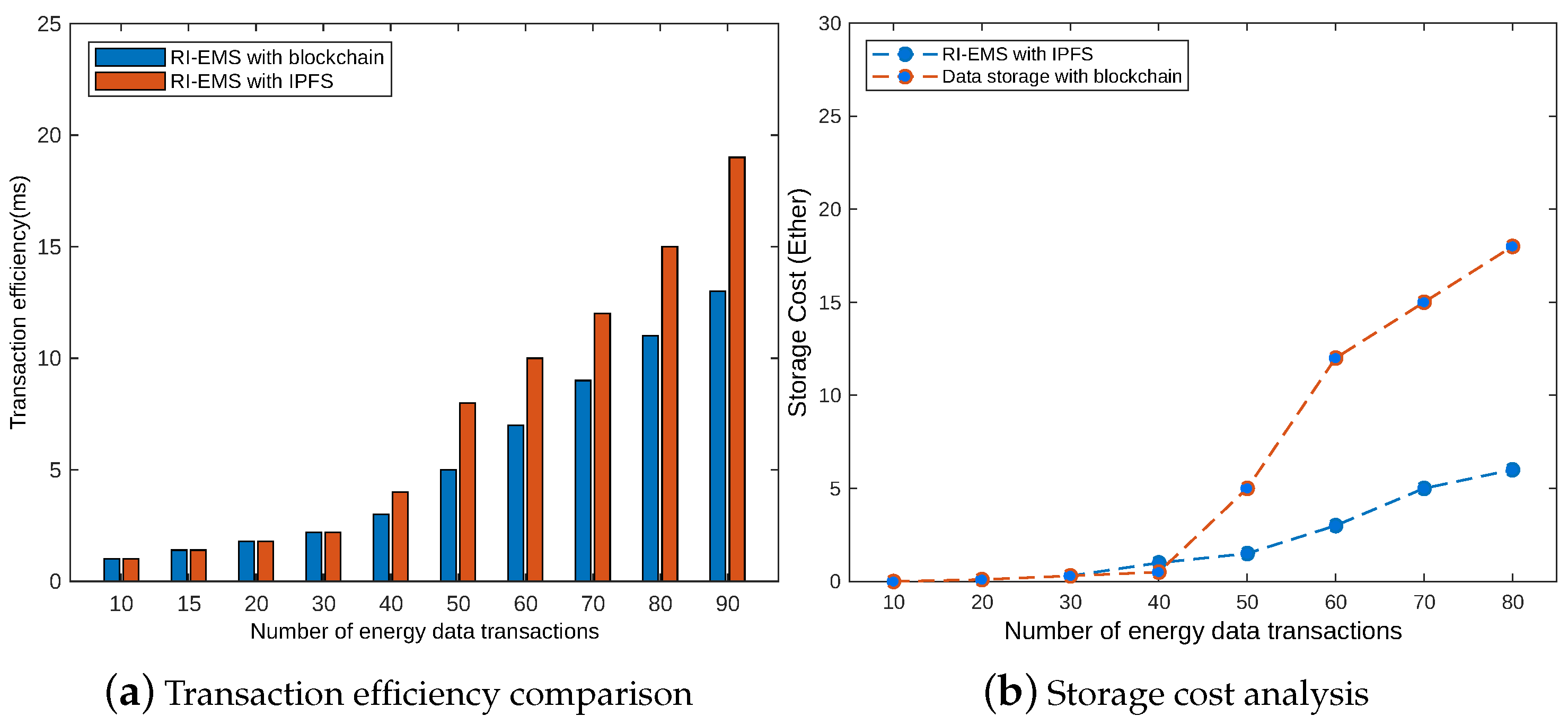
4.3. Transaction Efficiency
4.4. Data Storage Cost
Storage Cost Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| AI | Artificial intelligence |
| CPP | Critical peak pricing |
| DLT | Distributed ledger technique |
| DR | Data rate |
| DL | Deep learning |
| DR | Demand response |
| EMS | Energy management system |
| EUC | Electric utility company |
| EM | Energy management |
| IPFS | Inteplanetary file system |
| IDE | Integrated development environment |
| MDP | Markov decision process |
| NaN | Not-a-number |
| PAR | Peak-to-average ratio |
| RTP | Real-time pricing |
| RL | Reinforcement learning |
| TOU | Time of use |
| VA | Validation authority |
References
- Jindal, A.; Aujla, G.S.S.; Kumar, N.; Villari, M. GUARDIAN: Blockchain-based Secure Demand Response Management in Smart Grid System. IEEE Trans. Serv. Comput. 2019, 13, 613–624. [Google Scholar] [CrossRef]
- Jindal, A.; Singh, M.; Kumar, N. Consumption-Aware Data Analytical Demand Response Scheme for Peak Load Reduction in Smart Grid. IEEE Trans. Ind. Electron. 2018, 65, 8993–9004. [Google Scholar] [CrossRef]
- Asef, P.; Taheri, R.; Shojafar, M.; Mporas, I.; Tafazolli, R. SIEMS: A Secure Intelligent Energy Management System for Industrial IoT Applications. IEEE Trans. Ind. Inform. 2023, 19, 1039–1050. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Erdinç, O.; Catalao, J.P. An overview of Demand Response: Key-elements and international experience. Renew. Sustain. Energy Rev. 2017, 69, 871–891. [Google Scholar] [CrossRef]
- Kumari, A.; Vekaria, D.; Gupta, R.; Tanwar, S. Redills: Deep Learning-Based Secure Data Analytic Framework for Smart Grid Systems. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Miao, H.; Chen, G.; Zhao, Z.; Zhang, F. Evolutionary Aggregation Approach for Multihop Energy Metering in Smart Grid for Residential Energy Management. IEEE Trans. Ind. Inform. 2021, 17, 1058–1068. [Google Scholar] [CrossRef]
- Basnet, S.M.; Aburub, H.; Jewell, W. Residential demand response program: Predictive analytics, virtual storage model and its optimization. J. Energy Storage 2019, 23, 183–194. [Google Scholar] [CrossRef]
- Chen, T.; Bu, S.; Liu, X.; Kang, J.; Yu, F.R.; Han, Z. Peer-to-Peer Energy Trading and Energy Conversion in Interconnected Multi-Energy Microgrids Using Multi-Agent Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 715–727. [Google Scholar] [CrossRef]
- Sun, Y.; Elizondo, M.; Lu, S.; Fuller, J.C. The impact of uncertain physical parameters on HVAC demand response. IEEE Trans. Smart Grid 2014, 5, 916–923. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, W.; Chen, L.; Zheng, B.; Mei, S. Service pricing and load dispatch of residential shared energy storage unit. Energy 2020, 202, 117543. [Google Scholar] [CrossRef]
- Kumari, A.; Tanwar, S. A Reinforcement Learning-based Secure Demand Response Scheme for Smart Grid System. IEEE Internet Things J. 2021, 9, 2180–2191. [Google Scholar] [CrossRef]
- Ruzbahani, H.M.; Karimipour, H. Optimal incentive-based demand response management of smart households. In Proceedings of the 2018 IEEE/IAS 54th Industrial and Commercial Power Systems Technical Conference (I & CPS), Niagara Falls, ON, Canada, 7–10 May 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H. Incentive-based demand response for smart grid with reinforcement learning and deep neural network. Appl. Energy 2019, 236, 937–949. [Google Scholar] [CrossRef]
- Ma, R.; Yi, Z.; Xiang, Y.; Shi, D.; Xu, C.; Wu, H. A Blockchain-Enabled Demand Management and Control Framework Driven by Deep Reinforcement Learning. IEEE Trans. Ind. Electron. 2023, 70, 430–440. [Google Scholar] [CrossRef]
- Lu, R.; Jiang, Z.; Wu, H.; Ding, Y.; Wang, D.; Zhang, H.T. Reward Shaping-Based Actor-Critic Deep Reinforcement Learning for Residential Energy Management. IEEE Trans. Ind. Inform. 2022, 1–12. [Google Scholar] [CrossRef]
- Zheng, S.; Sun, Y.; Li, B.; Qi, B.; Shi, K.; Li, Y.; Tu, X. Incentive-Based Integrated Demand Response for Multiple Energy Carriers Considering Behavioral Coupling Effect of Consumers. IEEE Trans. Smart Grid 2020, 11, 3231–3245. [Google Scholar] [CrossRef]
- Mathew, A.; Jolly, M.J.; Mathew, J. Improved residential energy management system using priority double deep Q-learning. Sustain. Cities Soc. 2021, 69, 102812. [Google Scholar] [CrossRef]
- Kumari, A.; Gupta, R.; Tanwar, S.; Tyagi, S.; Kumar, N. When blockchain meets smart grid: Secure energy trading in demand response management. IEEE Netw. 2020, 34, 299–305. [Google Scholar] [CrossRef]
- Li, Z.; Kang, J.; Yu, R.; Ye, D.; Deng, Q.; Zhang, Y. Consortium Blockchain for Secure Energy Trading in Industrial Internet of Things. IEEE Trans. Ind. Inform. 2018, 14, 3690–3700. [Google Scholar] [CrossRef]
- Kumari, A.; Shukla, A.; Gupta, R.; Tanwar, S.; Tyagi, S.; Kumar, N. ET-DeaL: A P2P Smart Contract-based Secure Energy Trading Scheme for Smart Grid Systems. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1051–1056. [Google Scholar]
- Zhang, L.; Cheng, L.; Alsokhiry, F.; Mohamed, M.A. A Novel Stochastic Blockchain-Based Energy Management in Smart Cities Using V2S and V2G. IEEE Trans. Intell. Transp. Syst. 2022, 20, 915–922. [Google Scholar] [CrossRef]
- AlSkaif, T.; Crespo-Vazquez, J.L.; Sekuloski, M.; van Leeuwen, G.; Catalão, J.P.S. Blockchain-Based Fully Peer-to-Peer Energy Trading Strategies for Residential Energy Systems. IEEE Trans. Ind. Inform. 2022, 18, 231–241. [Google Scholar] [CrossRef]
- Singh, R.; Tanwar, S.; Sharma, T.P. Utilization of blockchain for mitigating the distributed denial of service attacks. Secur. Priv. 2020, 3, e96. [Google Scholar] [CrossRef]
- Hupez, M.; Toubeau, J.F.; Atzeni, I.; Grève, Z.D.; Vallée, F. Pricing Electricity in Residential Communities Using Game-Theoretical Billings. IEEE Trans. Smart Grid, 2022; early access. [Google Scholar] [CrossRef]
- Mota, B.; Faria, P.; Vale, Z. Residential load shifting in demand response events for bill reduction using a genetic algorithm. Energy 2022, 260, 124978. [Google Scholar] [CrossRef]
- Kumari, A.; Tanwar, S. A secure data analytics scheme for multimedia communication in a decentralized smart grid. Multimed. Tools Appl. 2022, 81, 34797–34822. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Li, J.; Wang, S. Modified deep learning and reinforcement learning for an incentive-based demand response model. Energy 2020, 205, 118019. [Google Scholar] [CrossRef]
- Salazar, E.J.; Jurado, M.; Samper, M.E. Reinforcement Learning-Based Pricing and Incentive Strategy for Demand Response in Smart Grids. Energies 2023, 16, 1466. [Google Scholar] [CrossRef]
- Gupta, R.; Reebadiya, D.; Tanwar, S.; Kumar, N.; Guizani, M. When Blockchain Meets Edge Intelligence: Trusted and Security Solutions for Consumers. IEEE Netw. 2021, 35, 272–278. [Google Scholar] [CrossRef]
- OpenEI. Open Energy Information: Smart Meters Data from Houses. Available online: https://openei.org/datasets/files/961/pub (accessed on 29 July 2022).
- Pecan Street Dataport. Available online: https://www.pecanstreet.org/dataport/ (accessed on 18 July 2021).
- pjm Data Miner. Available online: https://www.pjm.com/markets-and-operati\ons/etools/data-miner-2.aspx (accessed on 18 January 2021).
- Gurobi Optimization. Available online: http://www.gurobi.com (accessed on 29 July 2022).
- REMIX: The Native IDE for Web3 Development. Available online: https://remix.ethereum.org/ (accessed on 28 December 2022).

| Author | Year | Objective | Pricing Mechanism | Pros | Cons |
|---|---|---|---|---|---|
| Zhang et al. [10] | 2020 | Presented a load dispatch energy storage method for residential area | Iteration algorithm | Reduced operation cost, convergent | Need to consider energy trading for dynamic energy loads, privacy issues |
| Kumari et al. [11] | 2020 | Implemented the smart contract to ensure secure energy trading for smart grid | No mechanism | High scalability, reduced storage cost, and low latency | Should focus on optimal pricing, efficiency, and energy consumption |
| Zheng et al. [16] | 2020 | Presented a DR model to obtain the incentives for multiple energy carriers | Incentive-based approach | Improved accuracy, reduced dissatisfaction cost | Reduced energy consumption and transaction efficiency is not focused |
| Mathew et al. [17] | 2021 | Proposed a DR learning model for an efficient residential EM | DR-based greedy policy | Optimized peak cost and peak load | Need to implement with larger state space for optimal incentive |
| Li et al. [19] | 2018 | Discussed a secure energy-trading system for the Industrial Internet of Things using consortium blockchain | Stackelberg game | Optimized price, secure against double-spending and adversary attacks | No discussion on energy consumption reduction and cost |
| Hupez et al. [24] | 2022 | Formulated a game-theoretical approach for efficient energy scheduling in residential communities | Non-cooperative game theory | Optimized incentive and fair | No discussion on energy consumption, data storage cost, and transaction efficiency |
| Bruno et al. [25] | 2022 | Presented a residential demand response management for optimal load scheduling | Genetic algorithm | Reduced energy cost and electricity bill | Reliability, data storage cost, and energy consumption need to be considered |
| The proposed approach | 2022 | Proposed a real-time incentive approach for EMS using blockchain | Q-learning | Optimal price, incentive, high efficiency, and reliability | - |
| Particular | Values |
|---|---|
| 1 h | |
| Peak hour | 5 PM to 12 PM |
| Mid-peak | 8 AM to 5 PM |
| Off-peak | 12 AM to 8 AM |
| 0.01 | |
| 0.001 | |
| {0,1} |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumari, A.; Kakkar, R.; Gupta, R.; Agrawal, S.; Tanwar, S.; Alqahtani, F.; Tolba, A.; Raboaca, M.S.; Manea, D.L. Blockchain-Driven Real-Time Incentive Approach for Energy Management System. Mathematics 2023, 11, 928. https://doi.org/10.3390/math11040928
Kumari A, Kakkar R, Gupta R, Agrawal S, Tanwar S, Alqahtani F, Tolba A, Raboaca MS, Manea DL. Blockchain-Driven Real-Time Incentive Approach for Energy Management System. Mathematics. 2023; 11(4):928. https://doi.org/10.3390/math11040928
Chicago/Turabian StyleKumari, Aparna, Riya Kakkar, Rajesh Gupta, Smita Agrawal, Sudeep Tanwar, Fayez Alqahtani, Amr Tolba, Maria Simona Raboaca, and Daniela Lucia Manea. 2023. "Blockchain-Driven Real-Time Incentive Approach for Energy Management System" Mathematics 11, no. 4: 928. https://doi.org/10.3390/math11040928
APA StyleKumari, A., Kakkar, R., Gupta, R., Agrawal, S., Tanwar, S., Alqahtani, F., Tolba, A., Raboaca, M. S., & Manea, D. L. (2023). Blockchain-Driven Real-Time Incentive Approach for Energy Management System. Mathematics, 11(4), 928. https://doi.org/10.3390/math11040928