The Exponentiated Power Alpha Index Generalized Family of Distributions: Properties and Applications
Abstract
:1. Introduction
- i.
- The RF of the EPAIG-G family, using Equation (8), is
- ii.
- The HRF, CHRF, and reversed HRF of the EPAIG-G family are defined below:
2. Useful Expansions of the EPAIG-G Family
3. Structural Properties of the EPAIG-G Family
3.1. Quantile Function (QF)
3.2. Moments
3.3. Moment Generating Function (MGF)
3.4. Mean Deviations (MDs)
3.5. Lorenz and Bonferroni Curves
3.6. Probability Weighted Moments (PWMs)
3.7. Entropies
3.7.1. Rényi Entropy (RE)
3.7.2. Shannon Entropy (SE)
3.8. Order Statistics (OS)
4. Maximum Likelihood Estimation of the EPAIG-G Family
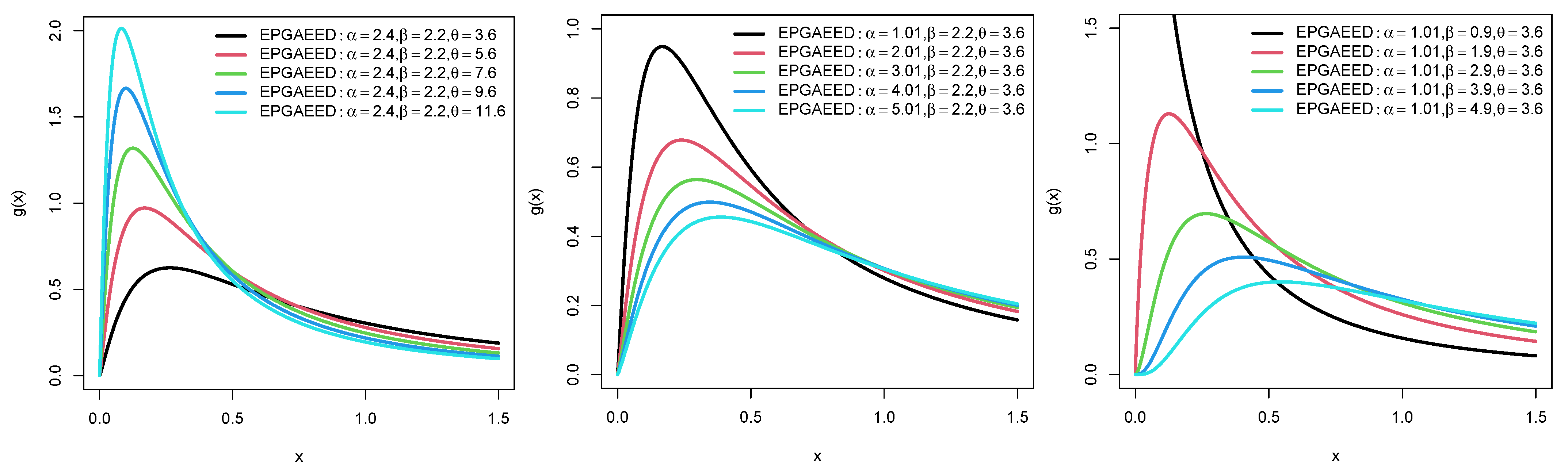
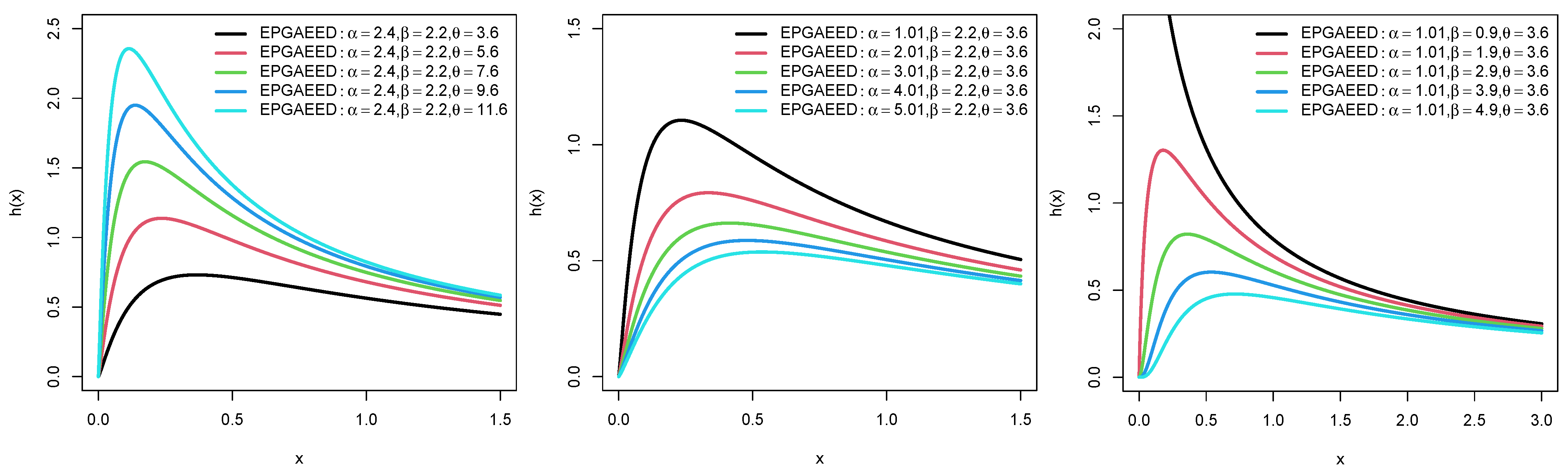
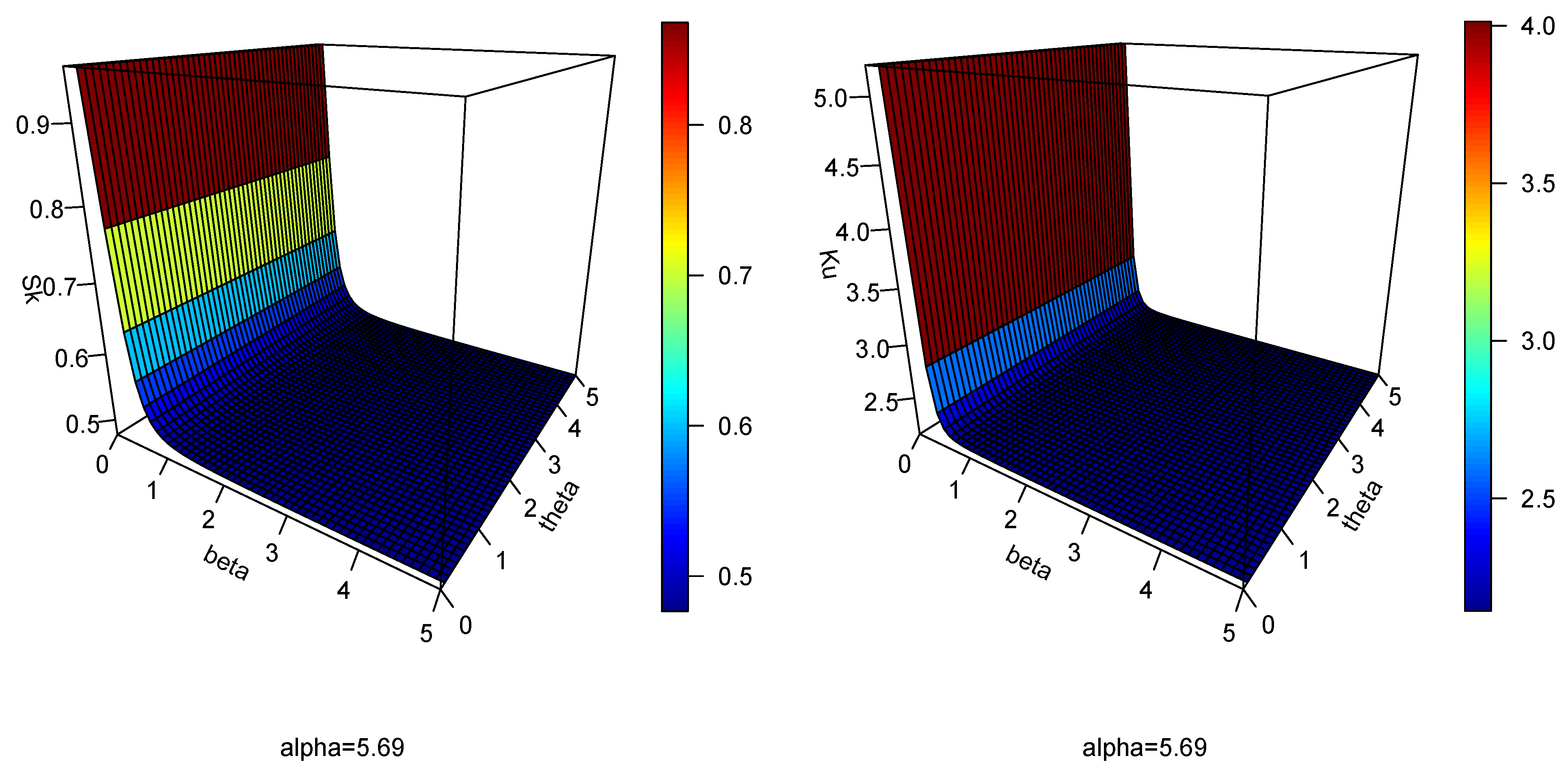
5. The EPAIG-Exponential (EPAIG-E) Distribution
5.1. Quantile Function and Simulation Study of the EPAIG-ED
Simulation
5.2. Estimation of the EPAIG-Exponential Model
5.3. Asymptotic Confidence Bounds of the EPAIG-ED
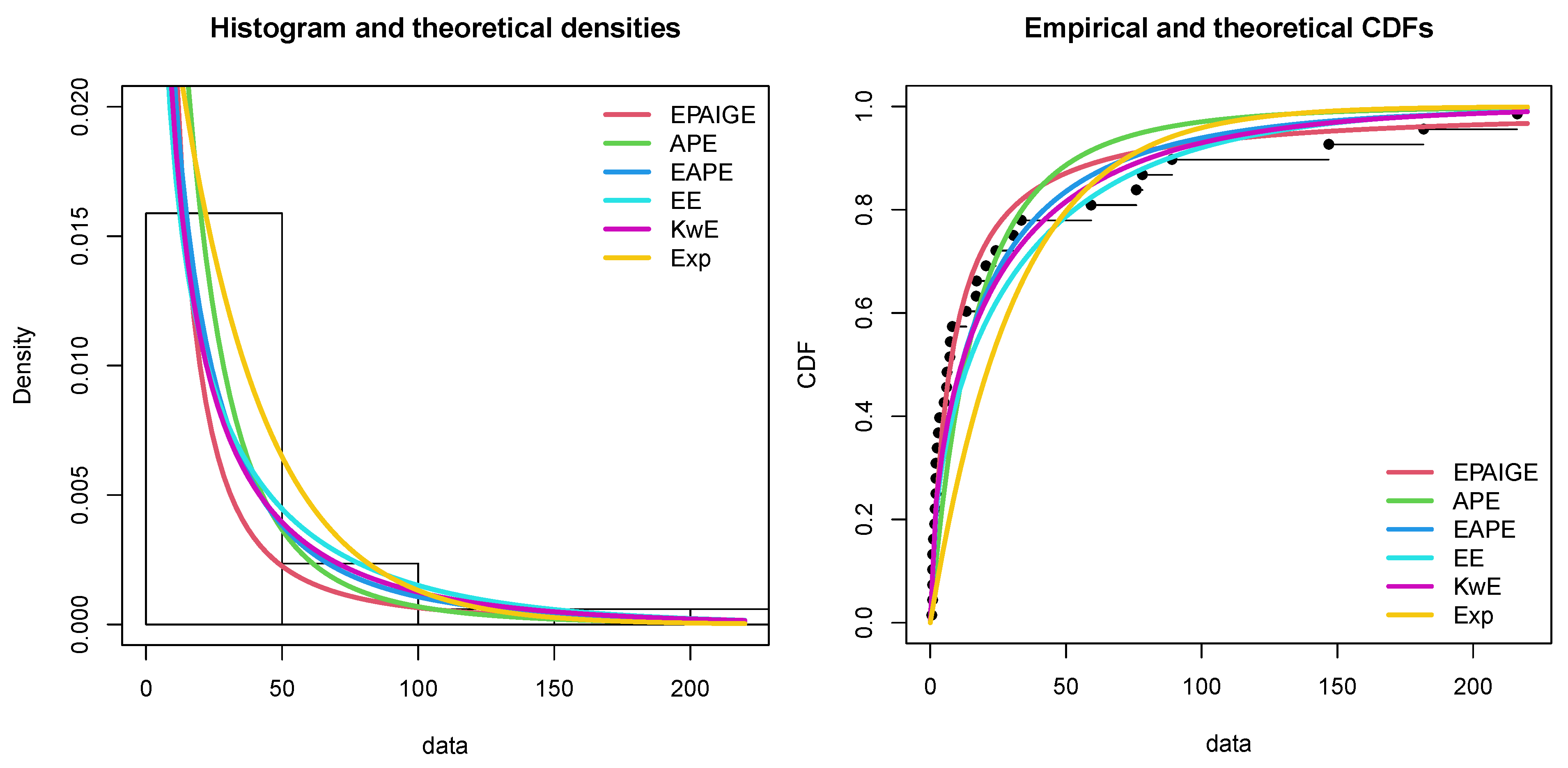
5.4. Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling failure time data by Lehman alternatives. Commun. Stat.-Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Mahdavi, A.; Kundu, D. A new method for generating distributions with an application to exponential distribution. Commun. Statist. Theory Methods 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Exponentiated exponential family: An alternative to gamma and Weibull distributions. Biomed. J. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Tahir, M.H.; Nadarajah, S. Parameter induction in continuous univariate distributions: Well-established G families. Acad. Bras. Cienc. 2015, 87, 539–568. [Google Scholar] [CrossRef] [PubMed]
- ElSherpieny, E.A.; Almetwally, E.M. The Exponentiated Generalized Alpha Power Exponential Distribution: Properties and Applications. Pak. J. Stat. Oper. Res. 2022, 18, 349–367. [Google Scholar] [CrossRef]
- Hussain, S.; Sajid Rashid, M.; Ul Hassan, M.; Ahmed, R. The Generalized Exponential Extended Exponentiated Family of Distributions: Theory, Properties, and Applications. Mathematics 2022, 10, 3419. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distribution. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Flajonet, P.; Odlyzko, A. Singularity analysis of generating function. SIAM J. Discr. Math. 1990, 3, 216–240. [Google Scholar] [CrossRef]
- Flajonet, P.; Sedgewich, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-89806-5. [Google Scholar]
- Rényi, A. On measures of entropy and information. Hung. Acad. Sci. 1961, 1, 547–561. [Google Scholar]
- Shannon, C.E. Prediction and entropy of printed Engish. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Galton, F. Enquiries into Human Faculty and its Development; Macmillan & Company: London, UK, 1883. [Google Scholar]
- Moors, J.J. A quantile alterrnative for kurtosis. Statistician 1988, 37, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S.; Rashid, M.S.; Ul Hassan, M.; Ahmed, R. The Generalized Alpha Exponent Power Family of Distributions: Properties and Applications. Mathematics 2022, 10, 1421. [Google Scholar] [CrossRef]
- Adepoju, K.A.; Chukwu, O.I. Maximum Likelihood Estimation of the Kumaraswamy Exponential Distribution with Applications. J. Mod. Appl. Stat. Methods 2015, 14, 208–214. [Google Scholar] [CrossRef] [Green Version]
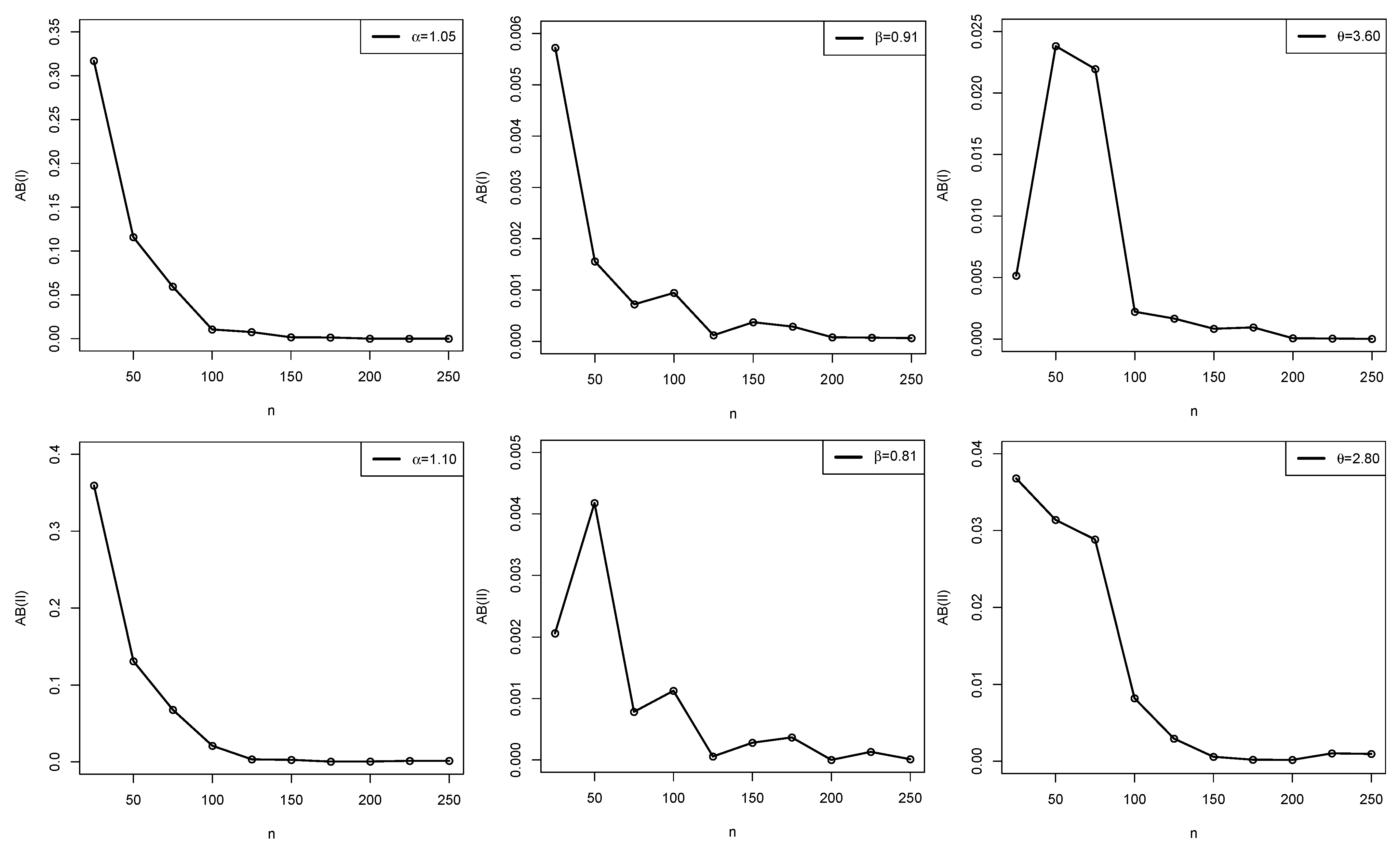
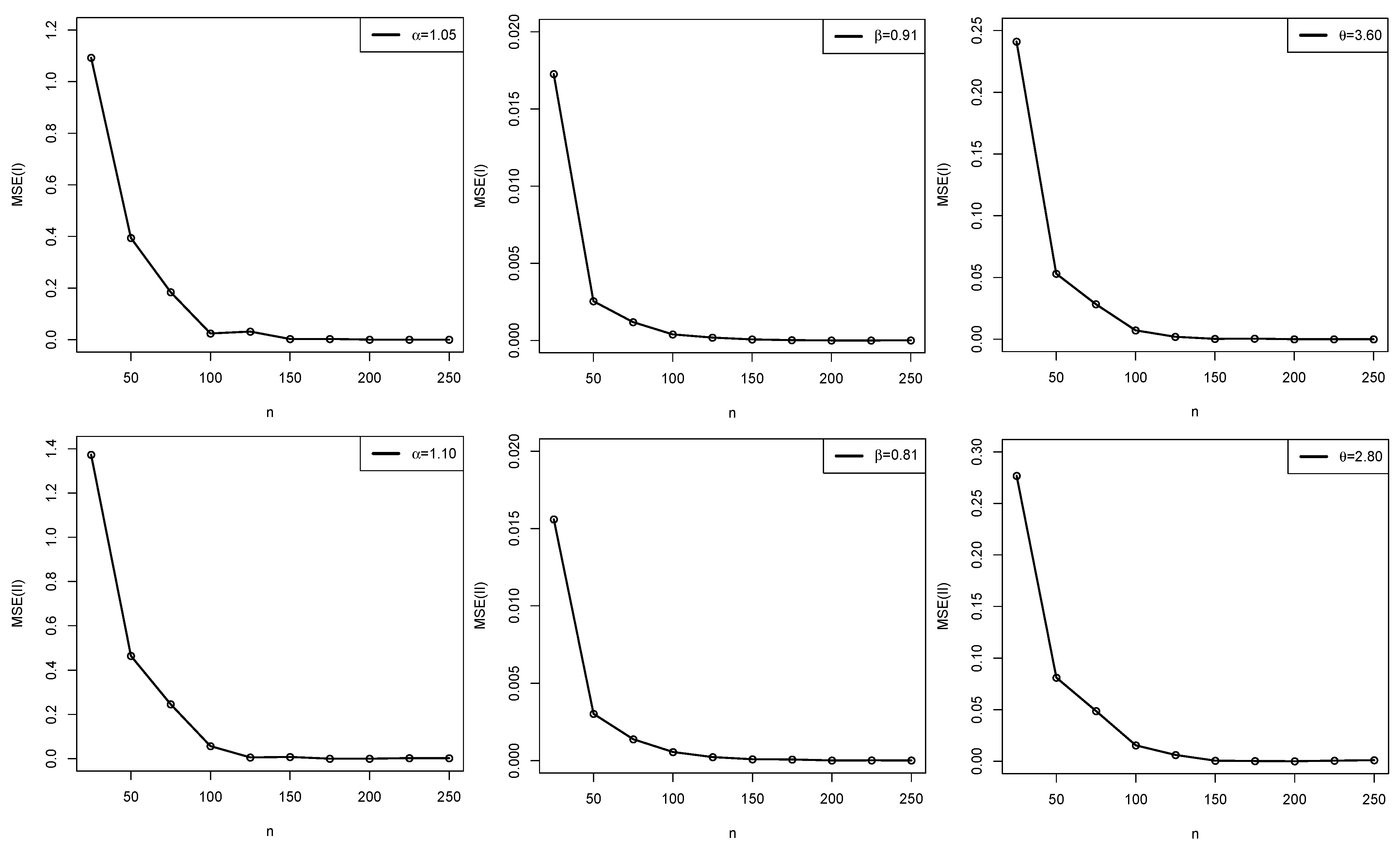
| Set I | Set II | ||||||
|---|---|---|---|---|---|---|---|
| n | Parameter | AEs | ABs | MSEs | AEs | ABs | MSEs |
| 25 | 1.366996 | 0.3169955 | 1.0929629 | 1.459311 | 0.3593107 | 1.3733343 | |
| 0.915721 | 0.0057207 | 0.0172636 | 0.812060 | 0.0020599 | 0.0155931 | ||
| 3.605154 | 0.0051537 | 0.2410440 | 2.836797 | 0.0367966 | 0.2767344 | ||
| 50 | 1.165887 | 0.1158869 | 0.3943543 | 1.231017 | 0.1310174 | 0.4650853 | |
| 0.908440 | 0.0015596 | 0.0025458 | 0.805823 | 0.0041773 | 0.0030314 | ||
| 3.623810 | 0.0238105 | 0.0530842 | 2.831384 | 0.0313836 | 0.0811852 | ||
| 75 | 1.109416 | 0.0594161 | 0.1839869 | 1.167718 | 0.0677182 | 0.2462002 | |
| 0.910724 | 0.0007236 | 0.0011887 | 0.810784 | 0.0007838 | 0.0013861 | ||
| 3.621947 | 0.0219468 | 0.0283753 | 2.828831 | 0.0288310 | 0.0487680 | ||
| 100 | 1.060522 | 0.0105221 | 0.0238978 | 1.120900 | 0.0208998 | 0.0568808 | |
| 0.909054 | 0.0009465 | 0.0003945 | 0.808874 | 0.0011265 | 0.0005601 | ||
| 3.602222 | 0.0022217 | 0.0071837 | 2.808202 | 0.0082021 | 0.0154640 | ||
| 125 | 1.057584 | 0.0075845 | 0.0312413 | 1.103230 | 0.0032299 | 0.0057049 | |
| 0.909879 | 0.0001209 | 0.0001872 | 0.809943 | 0.0000573 | 0.0002313 | ||
| 3.601665 | 0.0016648 | 0.0019889 | 2.802945 | 0.0029449 | 0.0061457 | ||
| 150 | 1.051616 | 0.0016164 | 0.0025074 | 1.102596 | 0.0025959 | 0.0078203 | |
| 0.910375 | 0.0003749 | 0.0000686 | 0.809719 | 0.0002812 | 0.0000922 | ||
| 3.600837 | 0.0008371 | 0.0003068 | 2.800579 | 0.0005788 | 0.0006002 | ||
| 175 | 1.051405 | 0.0014052 | 0.0026240 | 1.099661 | 0.0003391 | 0.0000959 | |
| 0.909711 | 0.0002891 | 0.0000212 | 0.809632 | 0.0003678 | 0.0000766 | ||
| 3.600949 | 0.0009492 | 0.0004894 | 2.800197 | 0.0001968 | 0.0002496 | ||
| 200 | 1.049917 | 0.0000833 | 0.0000029 | 1.099554 | 0.0004462 | 0.0000397 | |
| 0.909919 | 0.0000808 | 0.0000026 | 0.809998 | 0.0000016 | 0.0000143 | ||
| 3.600068 | 0.0000677 | 0.0000039 | 2.800176 | 0.0001765 | 0.0000645 | ||
| 225 | 1.050019 | 0.0000190 | 0.0000029 | 1.101291 | 0.0012907 | 0.0026624 | |
| 0.910074 | 0.0000735 | 0.0000028 | 0.809867 | 0.0001326 | 0.0000191 | ||
| 3.599955 | 0.0000454 | 0.0000020 | 2.801026 | 0.0010258 | 0.0006225 | ||
| 250 | 1.050028 | 0.0000280 | 0.0000008 | 1.101380 | 0.0013803 | 0.0023697 | |
| 0.910065 | 0.0000653 | 0.0000043 | 0.809987 | 0.0000127 | 0.0000164 | ||
| 3.599985 | 0.0000152 | 0.0000002 | 2.800954 | 0.0009540 | 0.0010710 | ||
| Model | ||||||
|---|---|---|---|---|---|---|
| EPAIG-E | 1.694325 | 0.970537 | 0.168391 | – | – | – |
| (2.513402) | (0.400538) | (0.002464) | ||||
| APE | 0.041160 | – | 0.018047 | – | – | – |
| (0.045367) | (0.005782) | |||||
| EAPE | 0.108038 | – | 0.012695 | 0.564599 | – | – |
| (0.176398) | (0.006486) | (0.132784) | ||||
| EE | – | – | 0.018009 | – | – | 0.460035 |
| (0.005133) | (0.092739) | |||||
| KwE | – | – | 0.003560 | 0.543711 | 3.622011 | – |
| (0.002083) | (0.089533) | (1.781159) | ||||
| Exp. | – | – | 0.031892 | – | – | – |
| (0.005464) |
| Model | -L | AIC | BIC | KS | p-Value | CM | AD |
|---|---|---|---|---|---|---|---|
| EPAIG-E | 138.6977 | 283.3954 | 287.9745 | 0.1091 | 0.8129 | 0.084811 | 0.624680 |
| APE | 144.2117 | 292.4233 | 295.4760 | 0.2314 | 0.0524 | 0.530737 | 3.670699 |
| EAPE | 141.0578 | 288.1157 | 292.6948 | 0.1639 | 0.3207 | 0.195203 | 1.180785 |
| EE | 142.2647 | 288.5293 | 291.5821 | 0.1892 | 0.1752 | 0.271831 | 1.485958 |
| KwE | 140.9855 | 287.9711 | 292.5502 | 0.1569 | 0.3724 | 0.175093 | 1.075832 |
| Exp. | 151.1437 | 304.2873 | 305.8137 | 0.3606 | 0.0003 | 1.341393 | 9.032758 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, S.; Ul Hassan, M.; Sajid Rashid, M.; Ahmed, R. The Exponentiated Power Alpha Index Generalized Family of Distributions: Properties and Applications. Mathematics 2023, 11, 900. https://doi.org/10.3390/math11040900
Hussain S, Ul Hassan M, Sajid Rashid M, Ahmed R. The Exponentiated Power Alpha Index Generalized Family of Distributions: Properties and Applications. Mathematics. 2023; 11(4):900. https://doi.org/10.3390/math11040900
Chicago/Turabian StyleHussain, Sajid, Mahmood Ul Hassan, Muhammad Sajid Rashid, and Rashid Ahmed. 2023. "The Exponentiated Power Alpha Index Generalized Family of Distributions: Properties and Applications" Mathematics 11, no. 4: 900. https://doi.org/10.3390/math11040900
APA StyleHussain, S., Ul Hassan, M., Sajid Rashid, M., & Ahmed, R. (2023). The Exponentiated Power Alpha Index Generalized Family of Distributions: Properties and Applications. Mathematics, 11(4), 900. https://doi.org/10.3390/math11040900






