Significance of Tiny Particles of Dust and TiO2 Subject to Lorentz Force: The Case of Non-Newtonian Dusty Rotating Fluid
Abstract
:1. Introduction
2. Mathematical Formulation
3. Results and Discussion
4. Conclusions
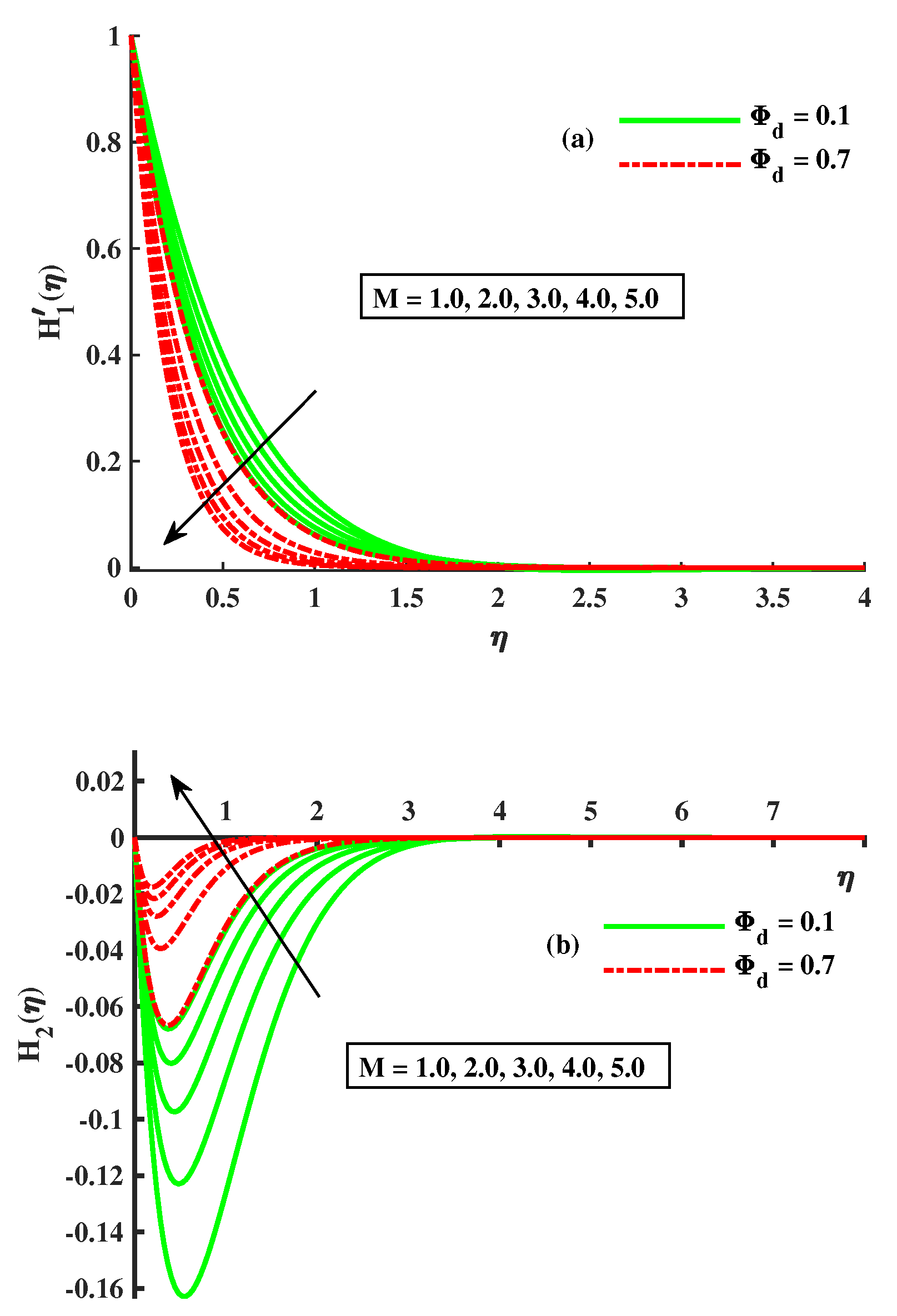
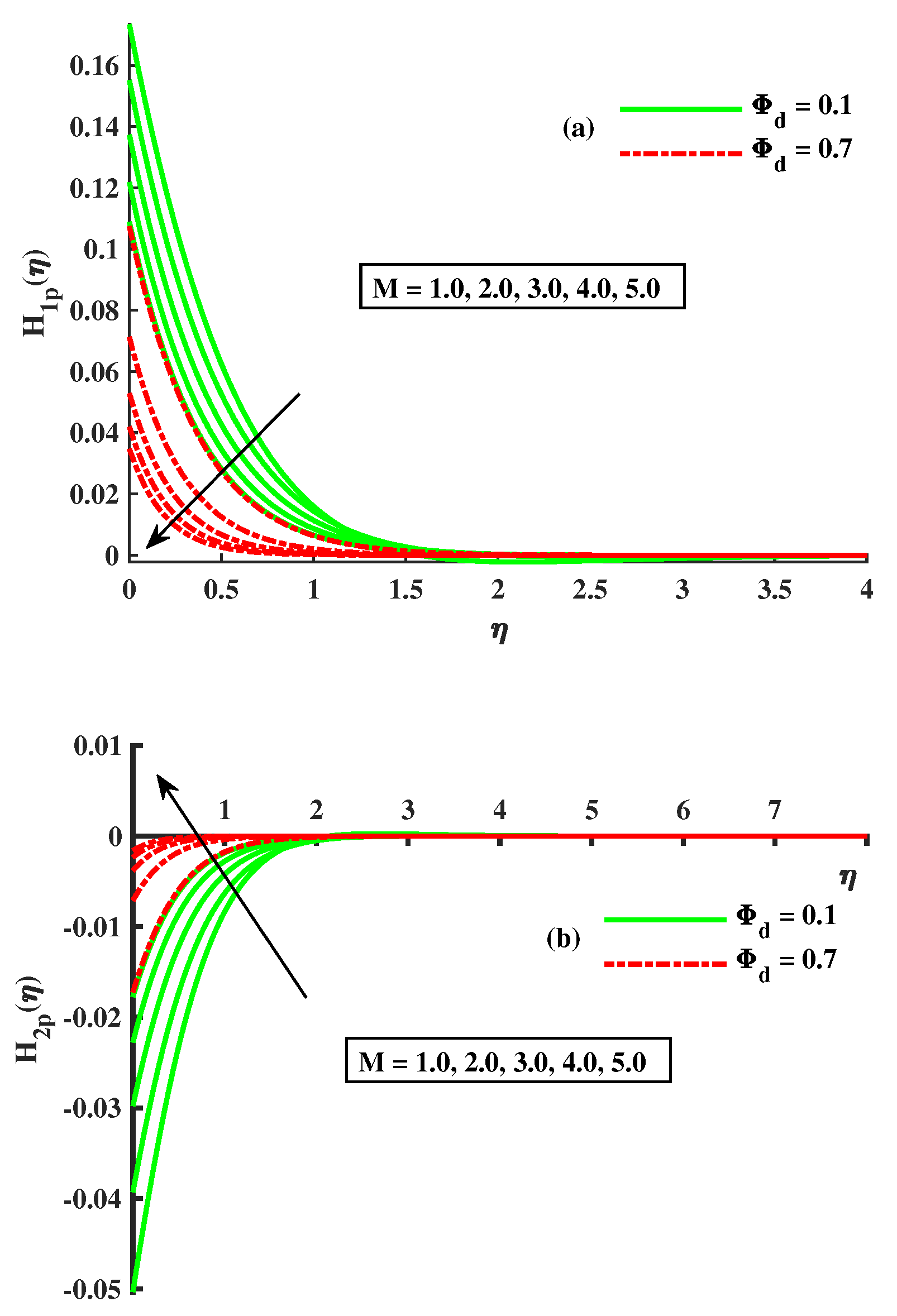
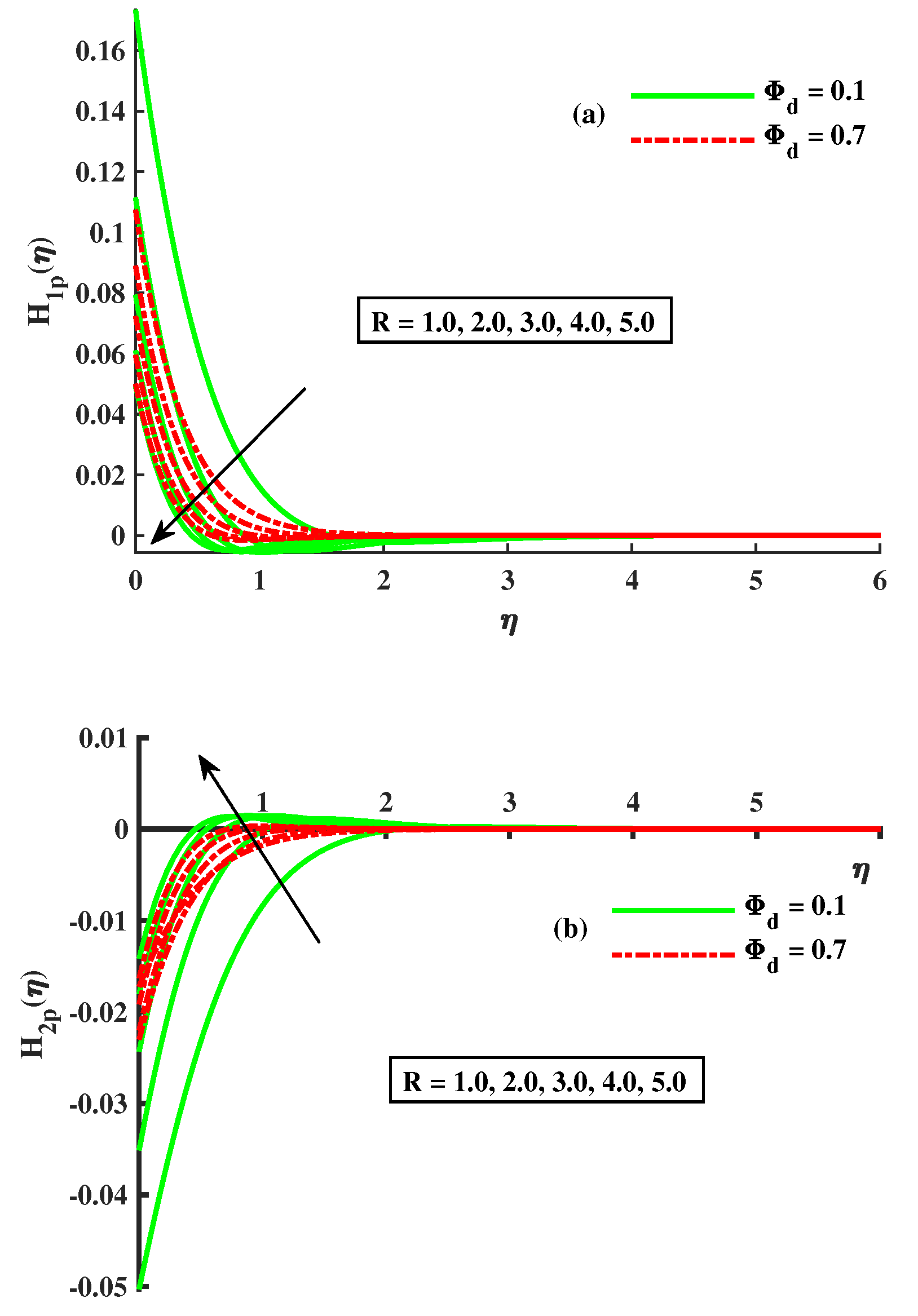
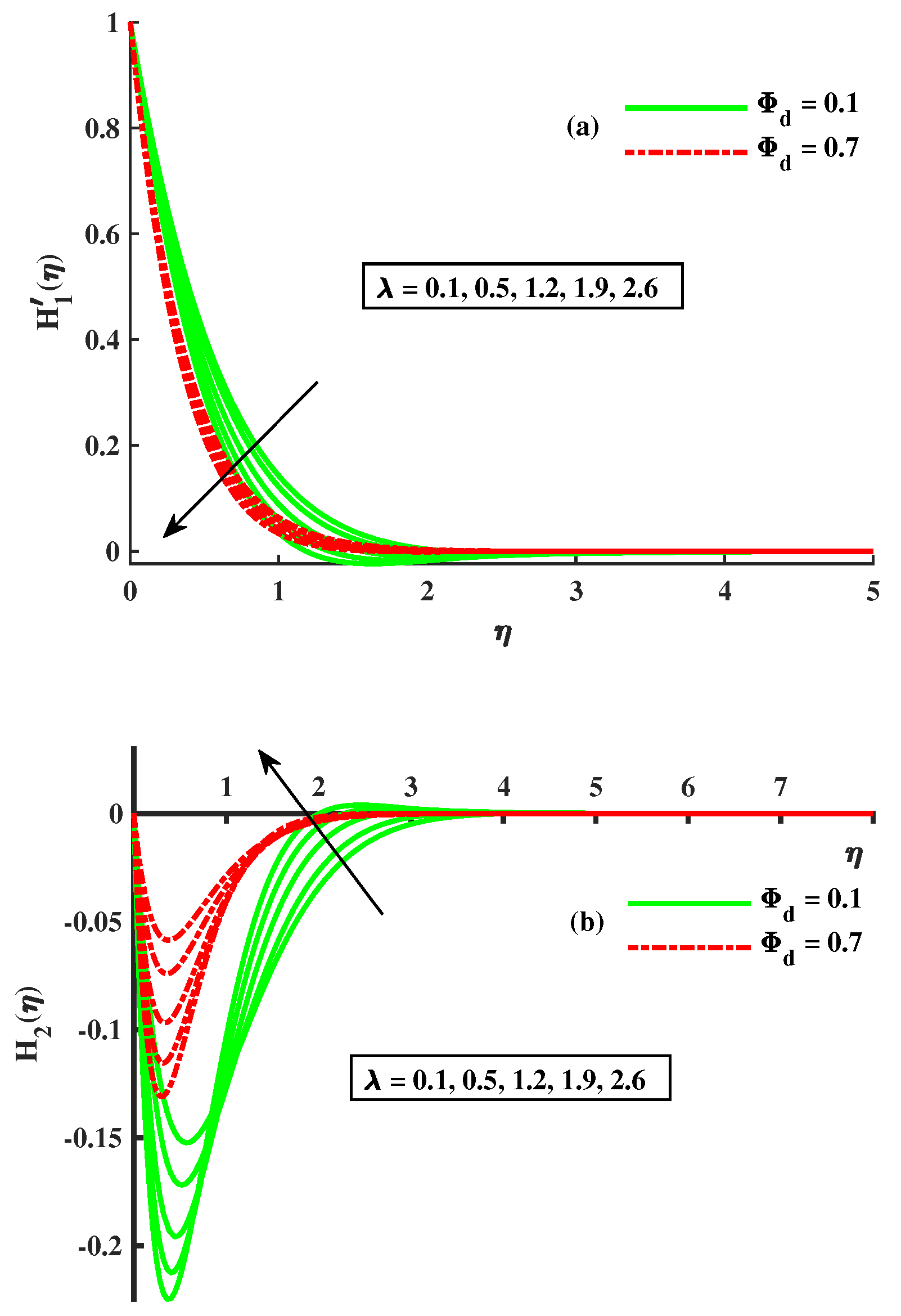
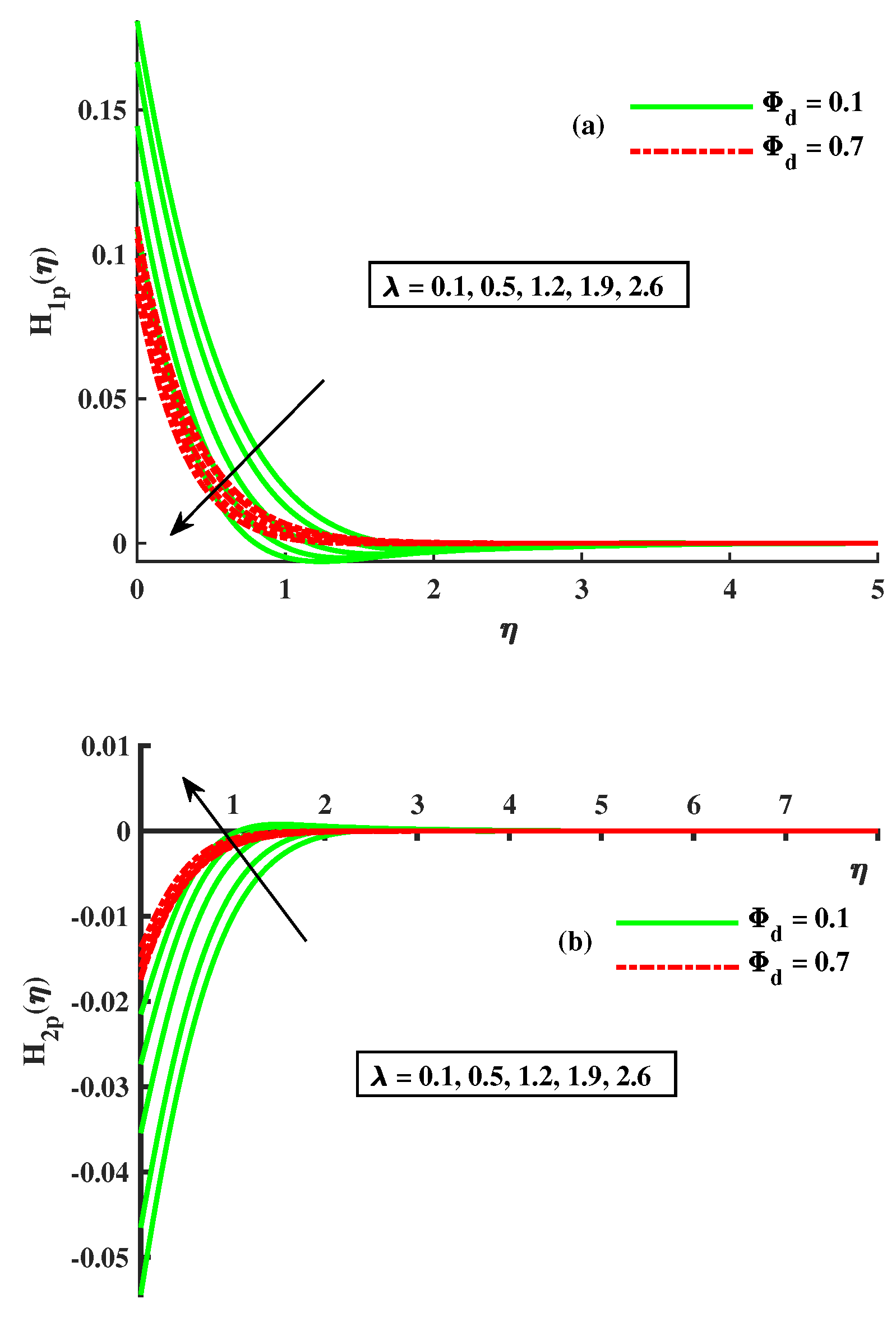
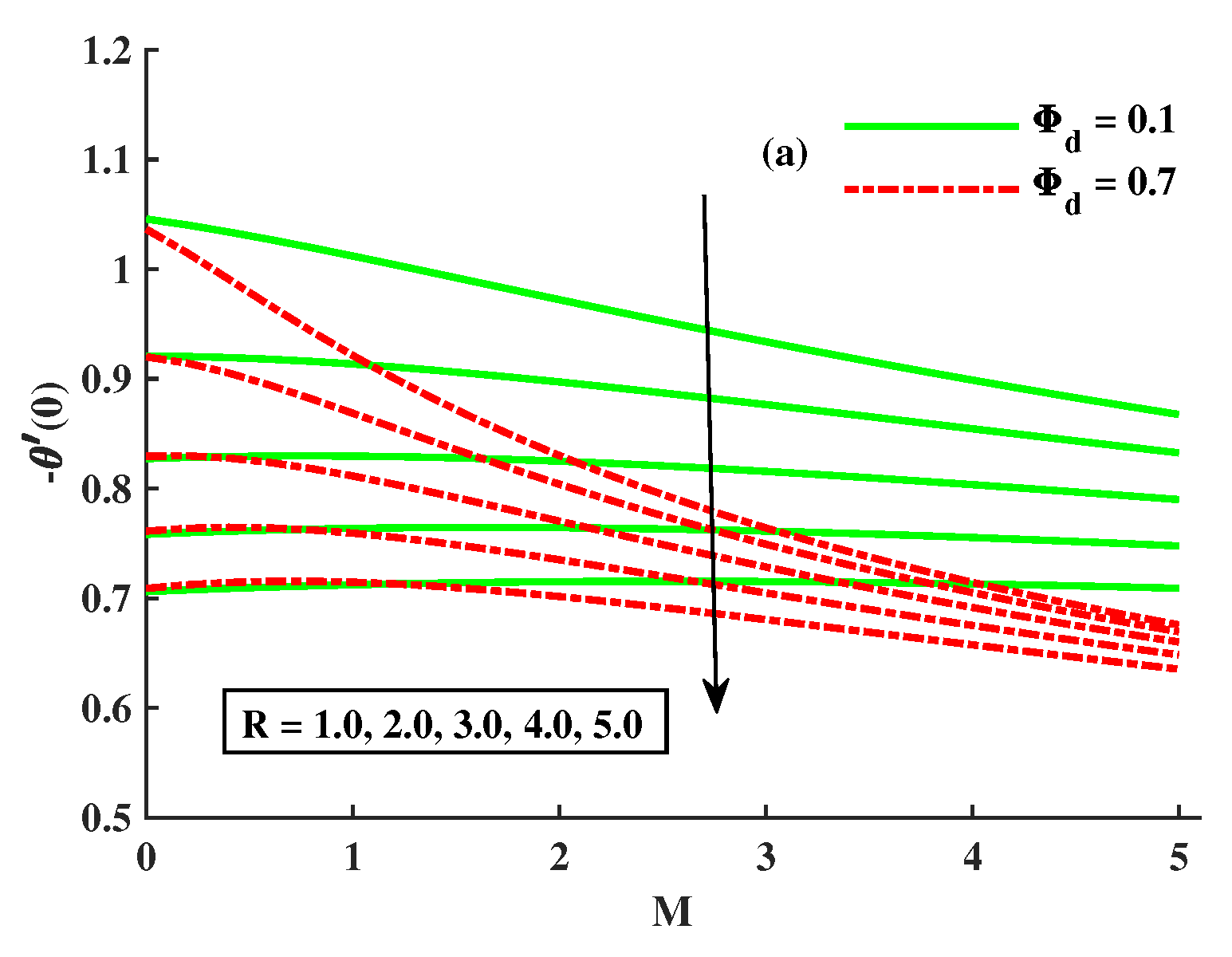
- As the factors M, , R, and increase, and rapidly decrease; however, when the factors and decrease, the reverse phenomenon occurs.
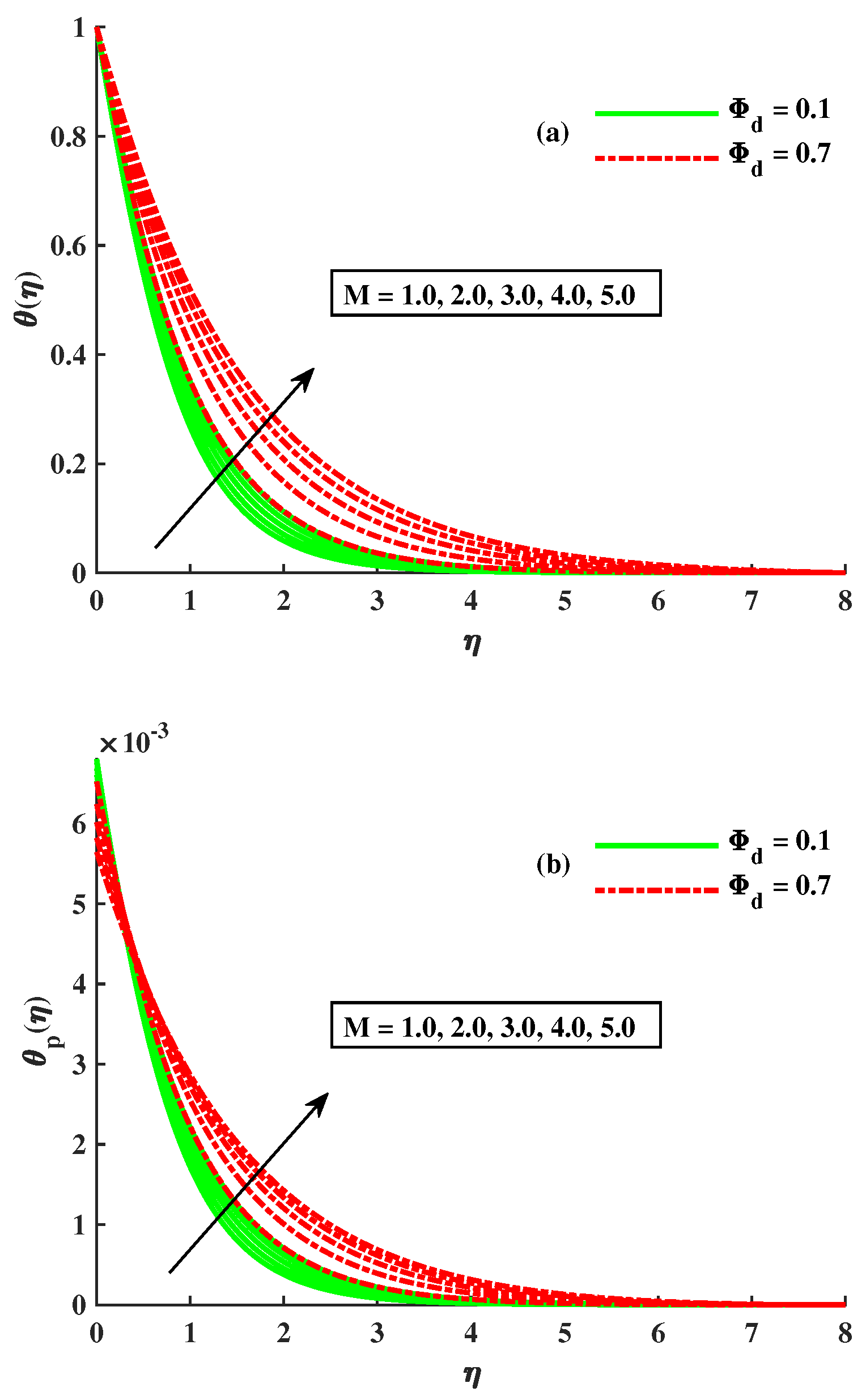
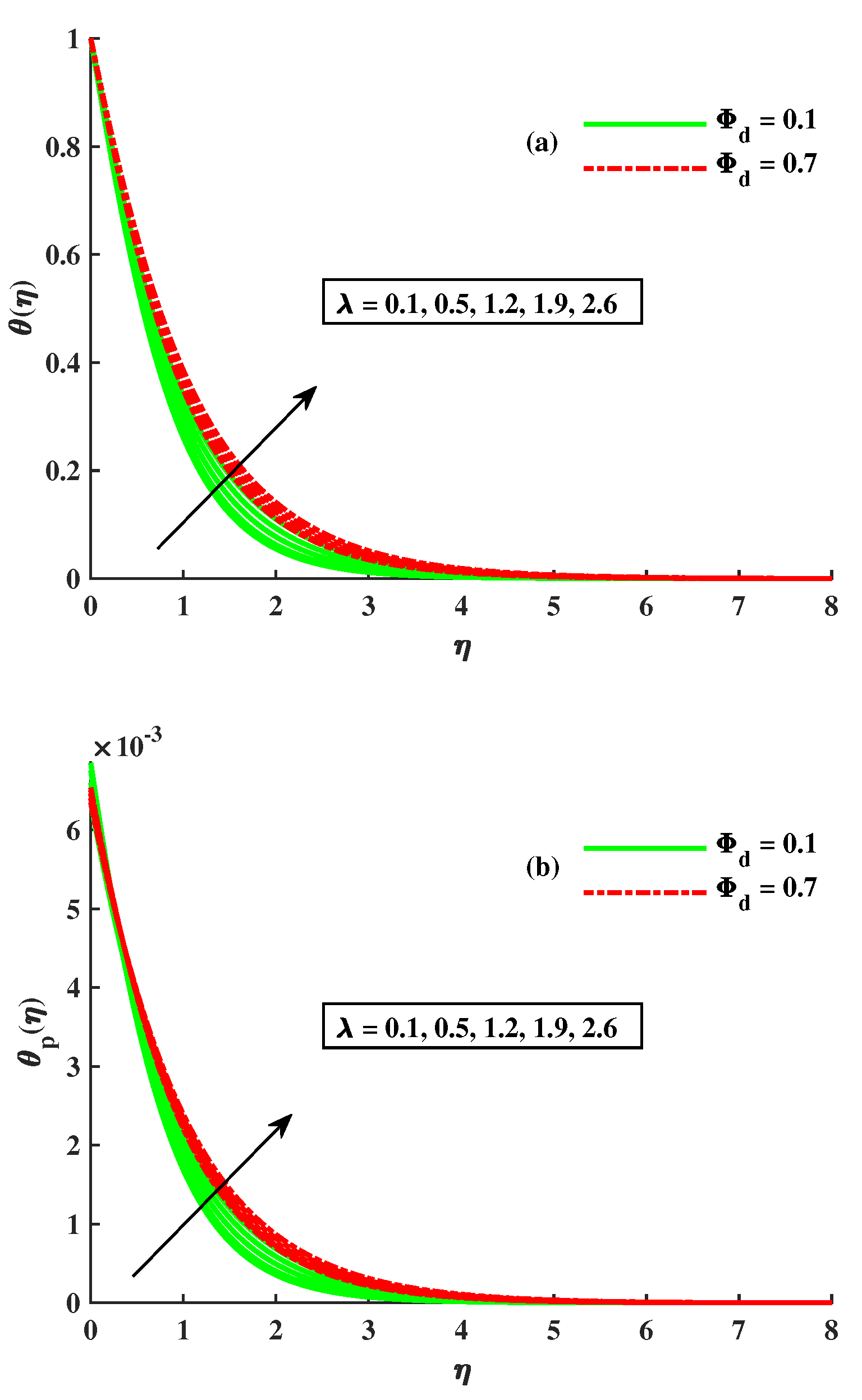
- With more significant magnetic, rotational, and Maxwell inputs and dust-particle density, the temperatures of and increase.
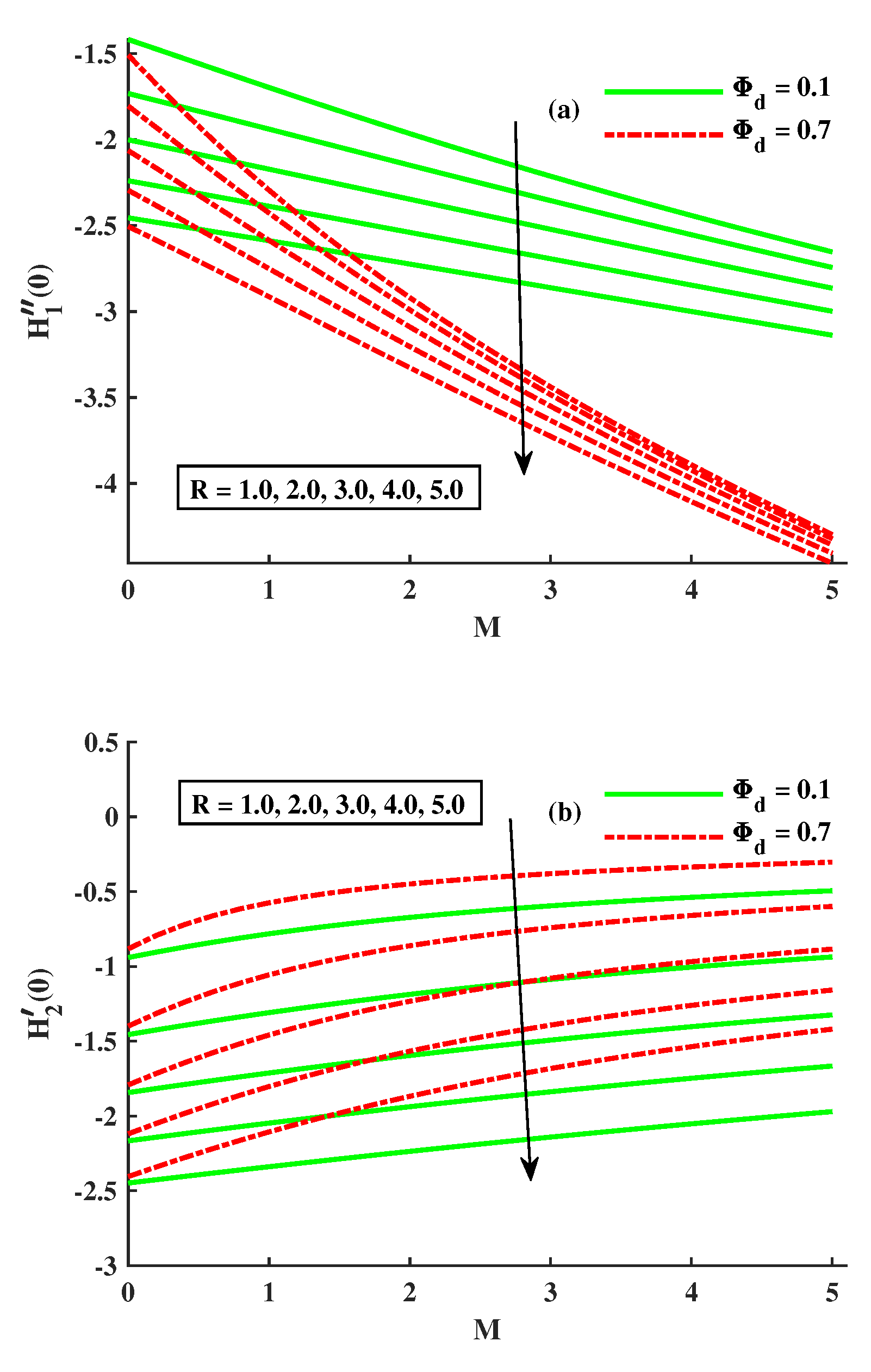
- With the magnified quantities of M, , and R, the skin friction coefficient decreased in the x direction.
- The skin friction coefficient increases along the y axis by increases in M and , but it behaves differently when the rotational parameter increases.
- By increasing M, R, , and contributions, the Nusselt number is reduced.
- The growing strength of tiny particles of dust and TiO2 is responsible for the upshot of temperature in both the dust and nanofluid phases.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Fluid velocity along the -axis | |
| Dusty fluid velocity along the -axis | |
| Density of nanofluid | |
| Density of dust particles | |
| Kinematic viscosity of fluid | |
| Magnetic field strength | |
| Electrical conductivity | |
| Volume fraction of dust particles | |
| N | Dust particle’s number density |
| Heat-flux relaxation time | |
| Dust particle temperature | |
| Thermal equilibrium time | |
| Specific heat of dust particle | |
| T | Non-dimensional temperature |
| Temperature at surface | |
| Specific heat capacity of the fluid | |
| Ambient temperature | |
| Angular velocity | |
| Velocity of stretching sheet | |
| Skin friction along x-direction | |
| Nusselt number | |
| Sherwood number |
References
- Saffman, P. On the stability of laminar flow of a dusty gas. J. Fluid Mech. 1962, 13, 120–128. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Xu, J.; Li, J.; Fan, C.; Hu, Y. Experimental study on effect of dilute coal dust on gas explosion pressure/flame evolution process. Powder Technol. 2022, 404, 117450. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T. MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. Comput. Math. Appl. 2010, 60, 660–669. [Google Scholar] [CrossRef]
- Gnaneswara Reddy, M.; Ferdows, M. Species and thermal radiation on micropolar hydromagnetic dusty fluid flow across a paraboloid revolution. J. Therm. Anal. Calorim. 2021, 143, 3699–3717. [Google Scholar] [CrossRef]
- Wei, Y.; Rehman, S.U.; Fatima, N.; Ali, B.; Ali, L.; Chung, J.D.; Shah, N.A. Significance of Dust Particles, Nanoparticles Radius, Coriolis and Lorentz Forces: The Case of Maxwell Dusty Fluid. Nanomaterials 2022, 12, 1512. [Google Scholar] [CrossRef]
- Attia, H.A. Unsteady MHD Couette flow and heat transfer of dusty fluid with variable physical properties. Appl. Math. Comput. 2006, 177, 308–318. [Google Scholar] [CrossRef]
- Yang, L.; Du, K. A comprehensive review on the natural, forced, and mixed convection of non-Newtonian fluids (nanofluids) inside different cavities. J. Therm. Anal. Calorim. 2020, 140, 2033–2054. [Google Scholar] [CrossRef]
- Zhao, T.H.; Khan, M.I.; Chu, Y.M. Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks. Math. Methods Appl. Sci. 2021, 46, 3012–3030. [Google Scholar] [CrossRef]
- Liu, H.; Lan, L.; Abrigo, J.; Ip, H.L.; Soo, Y.; Zheng, D.; Wong, K.S.; Wang, D.; Shi, L.; Leung, T.W.; et al. Comparison of Newtonian and non-Newtonian fluid models in blood flow simulation in patients with intracranial arterial stenosis. Front. Physiol. 2021, 12, 1464. [Google Scholar] [CrossRef]
- Shende, T.; Niasar, V.J.; Babaei, M. Effective viscosity and Reynolds number of non-Newtonian fluids using Meter model. Rheol. Acta 2021, 60, 11–21. [Google Scholar] [CrossRef]
- Ali, B.; Ali, L.; Abdal, S.; Asjad, M.I. Significance of Brownian motion and thermophoresis influence on dynamics of Reiner–Rivlin fluid over a disk with non-Fourier heat flux theory and gyrotactic microorganisms: A Numerical approach. Phys. Scr. 2021, 96, 094001. [Google Scholar] [CrossRef]
- Qin, Y. Simulation of MHD impact on nanomaterial irreversibility and convective transportation through a chamber. Appl. Nanosci. 2023, 13, 929–942. [Google Scholar] [CrossRef]
- Jang, J.; Lee, S.S. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sens. Actuators Phys. 2000, 80, 84–89. [Google Scholar] [CrossRef]
- Bhatti, M.; Arain, M.; Zeeshan, A.; Ellahi, R.; Doranehgard, M. Swimming of Gyrotactic Microorganism in MHD Williamson nanofluid flow between rotating circular plates embedded in porous medium: Application of thermal energy storage. J. Energy Storage 2022, 45, 103511. [Google Scholar] [CrossRef]
- Li, Y.X.; Alshbool, M.H.; Lv, Y.P.; Khan, I.; Khan, M.R.; Issakhov, A. Heat and mass transfer in MHD Williamson nanofluid flow over an exponentially porous stretching surface. Case Stud. Therm. Eng. 2021, 26, 100975. [Google Scholar] [CrossRef]
- Arulmozhi, S.; Sukkiramathi, K.; Santra, S.; Edwan, R.; Fernandez-Gamiz, U.; Noeiaghdam, S. Heat and mass transfer analysis of radiative and chemical reactive effects on MHD nanofluid over an infinite moving vertical plate. Results Eng. 2022, 14, 100394. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Ur Rehman, S.; Ali, B.; Hussain, S.; Gia, T.N.; Muhammad, T. MHD Williamson Nanofluid Flow over a Slender Elastic Sheet of Irregular Thickness in the Presence of Bioconvection. Nanomaterials 2021, 11, 2297. [Google Scholar] [CrossRef]
- Thumma, T.; Bég, O.A.; Sheri, S.R. Finite element computation of magnetohydrodynamic nanofluid convection from an oscillating inclined plate with radiative flux, heat source and variable temperature effects. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2017, 231, 179–194. [Google Scholar] [CrossRef]
- Thumma, T.; Mishra, S. Effect of nonuniform heat source/sink, and viscous and Joule dissipation on 3D Eyring–Powell nanofluid flow over a stretching sheet. J. Comput. Des. Eng. 2020, 7, 412–426. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Alotaibi, H.; Aljohani, H.M.; Wakif, A.; Khan, I.; Akram, S. Thermally enhanced Darcy-Forchheimer Casson-water/glycerine rotating nanofluid flow with uniform magnetic field. Micromachines 2021, 12, 605. [Google Scholar] [CrossRef]
- Shafiq, A.; Lone, S.; Sindhu, T.N.; Al-Mdallal, Q.; Rasool, G. Statistical modeling for bioconvective tangent hyperbolic nanofluid towards stretching surface with zero mass flux condition. Sci. Rep. 2021, 11, 13869. [Google Scholar] [CrossRef] [PubMed]
- Rout, B.; Mishra, S.; Thumma, T. Effect of viscous dissipation on Cu-water and Cu-kerosene nanofluids of axisymmetric radiative squeezing flow. Heat Transf.—Asian Res. 2019, 48, 3039–3054. [Google Scholar] [CrossRef]
- Ashraf, M.S.; Rehman, U.R.; Farid, S.; Hussein, A.K.; Shah, N.A.; Wajaree, W. Insight into significance of bioconvection on mhd tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics 2022, 15, 2592. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Reham, U.R.; Habib, D.; Abdal, S. Shah, N.A; Dong, J.C. Micropolar dusty fluid: Coriolis force effects on dynamics of MHD rotating fluid when Lorentz force is significant. Mathematics 2022, 15, 2630. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R.; Sait, S.M. Electromagnetic flow of SWCNT/MWCNT suspensions in two immiscible water-and engine-oil-based newtonian fluids through porous media. Symmetry 2022, 14, 406. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys. 2017, 55, 630–651. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Double stratification effects on unsteady electrical MHD mixed convection flow of nanofluid with viscous dissipation and Joule heating. J. Appl. Res. Technol. 2017, 15, 464–476. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Daniel, S.K. Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method. Alex. Eng. J. 2015, 54, 705–712. [Google Scholar] [CrossRef]
- Rashid, S.; Hayat, T.; Qayyum, S.; Ayub, M.; Alsaedi, A. Three-dimensional rotating Darcy–Forchheimer flow with activation energy. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 935–948. [Google Scholar] [CrossRef]
- Tayyab, M.; Siddique, I.; Jarad, F.; Ashraf, M.K.; Ali, B. Numerical solution of 3D rotating nanofluid flow subject to Darcy-Forchheimer law, bio-convection and activation energy. S. Afr. J. Chem. Eng. 2022, 40, 48–56. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Ahmadian, A.; Senu, N.; Ali, L.; Haider, A. Significance of Lorentz and Coriolis forces on dynamics of water based silver tiny particles via finite element simulation. Ain Shams Eng. J. 2022, 13, 101572. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Prasannakumara, B.C.; Khan, U.; Madireddy, S.; Raizah, Z.; Galal, A.M. Time-Dependent Stagnation Point Flow of Water Conveying Titanium Dioxide Nanoparticle Aggregation on Rotating Sphere Object Experiencing Thermophoresis Particle Deposition Effects. Energies 2022, 15, 4424. [Google Scholar] [CrossRef]
- Dinarvand, S.; Mousavi, S.M.; Yousefi, M.; Rostami, M.N. MHD flow of MgO-Ag/water hybrid nanofluid past a moving slim needle considering dual solutions: An applicable model for hot-wire anemometer analysis. Int. J. Numer. Methods Heat Fluid Flow 2021, 32, 488–510. [Google Scholar] [CrossRef]
- Shah, N.A.; Animasaun, I.; Chung, J.D.; Wakif, A.; Alao, F.; Raju, C. Significance of nanoparticle’s radius, heat flux due to concentration gradient, and mass flux due to temperature gradient: The case of Water conveying copper nanoparticles. Sci. Rep. 2021, 11, 1882. [Google Scholar] [CrossRef]
- Rehman, S.U.; Mariam, A.; Ullah, A.; Asjad, M.I.; Bajuri, M.Y.; Pansera, B.A.; Ahmadian, A. Numerical computation of buoyancy and radiation effects on MHD micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 2021, 25, 100867. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Tariq, M. Finite element simulation of multiple slip effects on MHD unsteady maxwell nanofluid flow over a permeable stretching sheet with radiation and thermo-diffusion in the presence of chemical reaction. Processes 2019, 7, 628. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Unsteady boundary layer flow due to a stretching surface in a rotating fluid. Mech. Res. Commun. 2004, 31, 121–128. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Stretching surface in rotating viscoelastic fluid. Appl. Math. Mech. 2013, 34, 945–952. [Google Scholar] [CrossRef]





| Physical Properties | TiO2 | Water/Base Fluid |
|---|---|---|
| density () | 4250 | 997.1 |
| specific heat () | 686.2 | 4179 |
| Thermal conductivity k | 8.9538 | 0.613 |
| Electrical conductivity |
| Properties | Nanofluid |
|---|---|
| Density of nanofluid | , |
| Dynamic viscosity of nanofluid | , |
| Thermal Conductivity of nanofluid | , |
| Electrical Conductivity | , |
| Heat Capacitance |
| M | [35] | [36] | Current Results |
|---|---|---|---|
| 0.5 | 1.2247454 | 1.2247446 | 1.224745 |
| 1.0 | 1.4142180 | 1.4142132 | 1.414218 |
| 1.2 | 1.4832402 | 1.4832393 | 1.483240 |
| 1.5 | 1.5811396 | 1.5811384 | 1.581139 |
| 2.0 | 1.7320516 | 1.7320504 | 1.732051 |
| [35] | [36] | Current Results | |
|---|---|---|---|
| 1.0 | 1.00000 | 1.0000 | 1.0000 |
| 3.0 | 1.92375 | 1.9236 | 1.9238 |
| 10.0 | 3.72061 | 3.7207 | 3.7210 |
| 100.0 | 12.29404 | 12.2940 | 12.2941 |
| Nazar et al. [37] | Zaimi et al. [38] | Current Results | ||||
|---|---|---|---|---|---|---|
| 1 | 1.3250 | 0.8371 | 1.3250 | 0.8371 | 1.3250281 | 0.8371043 |
| 2 | 1.6523 | 1.2873 | 1.6523 | 1.2873 | 1.6523254 | 1.2872538 |
| 3 | 1.6523 | 1.2870 | 1.9289 | 1.6248 | 1.9289404 | 1.6247413 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, B.; Ahammad, N.A.; Windarto; Oke, A.S.; Shah, N.A.; Chung, J.D. Significance of Tiny Particles of Dust and TiO2 Subject to Lorentz Force: The Case of Non-Newtonian Dusty Rotating Fluid. Mathematics 2023, 11, 877. https://doi.org/10.3390/math11040877
Ali B, Ahammad NA, Windarto, Oke AS, Shah NA, Chung JD. Significance of Tiny Particles of Dust and TiO2 Subject to Lorentz Force: The Case of Non-Newtonian Dusty Rotating Fluid. Mathematics. 2023; 11(4):877. https://doi.org/10.3390/math11040877
Chicago/Turabian StyleAli, Bagh, N. Ameer Ahammad, Windarto, Abayomi S. Oke, Nehad Ali Shah, and Jae Dong Chung. 2023. "Significance of Tiny Particles of Dust and TiO2 Subject to Lorentz Force: The Case of Non-Newtonian Dusty Rotating Fluid" Mathematics 11, no. 4: 877. https://doi.org/10.3390/math11040877
APA StyleAli, B., Ahammad, N. A., Windarto, Oke, A. S., Shah, N. A., & Chung, J. D. (2023). Significance of Tiny Particles of Dust and TiO2 Subject to Lorentz Force: The Case of Non-Newtonian Dusty Rotating Fluid. Mathematics, 11(4), 877. https://doi.org/10.3390/math11040877







