Abstract
This work examined the thermodynamics of the MHD rotating dusty Maxwell water-based
nanofluid with suspended dust particles. This study examines the importance of increasing the
volume fraction of tiny particles of TiO2 and dust on fluid dynamics. With appropriate similarity
transformations, the governing PDEs for both fluid and dusty-phase models are transformed into
non-linear linked non-dimensional ODEs. To acquire graphical consequences, the bvp4c technique is
implemented in MATLAB scripts. The primary and secondary velocities’ magnitude in both phases
decreases with an increase in the dust particle volume concentration, Lorentz force, rotating, and
Maxwell fluid parameters. The growing strength of tiny particles of dust and TiO2 is responsible for
the upshot of temperature in both dust and nanofluid phases. A visual representation of the Nusselt
number and skin friction coefficients are is provided.
MSC:
35Q30; 76D05; 76R10
1. Introduction
Investigations appertaining to heat transmission and dusty fluids flow over a stretch surface are extremely good at improving the operation and design of various engineering and industrial devices. They have significant applications in the fields of combustion; the centrifugal separation of matter from fluid; electrostatic precipitation; fluidization; the use of dust in gas-cooling systems; the petroleum industry; polymer technology; the purification of crude oil; and fluid droplet sprays. The investigation of the laminar flux of dusty fluid was begun by Saffman [1]. Wang et al. [2] analyzed the experimental review of dilute coal dust impacts on the explosion pressure of gas. Makinde et al. [3] explored the magneto hydradynamics transient flux, the transmission of the heat of dusty fluid in a channel, and variable physical characteristics. Thermal radiation and species on the flux of micropolar hydromagnetic dusty fluid on paraboloid revolution were examined by Gnaneswara et al. [4]. Wei et al. [5] explained the importance of nanoparticles radius, dust particles, and Lorentz and coriolis force in presence of Maxwell dusty fluid. They solved the elaborated problem via BVP4c and found that the dust particles improved the thermal performance of the base fluid. Time-dependent magneto hydradynamics Couette flux and the heat transmission of dusty fluid with variational physical attributes were reported by Attia et al. [6]. The authors reported that Lorentz force and dust-particle interaction parameters are responsible for enhancing the thermal conductivity of fluid.
Fluids that have continuous viscosity independent of stress and do not obey the Newton law of viscosity are non-Newtonian fluids. Nowadays, non-Newtonian flux of fluid plays a significant role in many industrial applications such as 3D printers, paper manufacturing, the polymer industry, the production of plastics, and in various technological processes. The viscosity of non-Newtonian fluids might be changed by the influence of external forces, resulting in more solids and fluids. Mathematicians all across the world are researching novel research models in order to produce innovative non- Newtonian fluid characteristics. Firstly, non-Newtonian fluids are introduced by Powell and Trying in 1944. Yang et al. [7] analyzed the illustrative review on the forced, mixed, and natural convection of non-Newtonian nano liquids in various cavities. Zhao et al. [8] described the analysis of heat in the flux of non-Newtonian among two rotational disks. Liu et al. [9] studied the comparison of models of Newtonian and non-Newtonian liquids in blood flux simulation in intracranial arterial stenosis. Takshak Shende et al. [10] discussed the Reynolds number and effective viscosity of non-Newtonian liquids by using meter models. Ali et al. [11] examined the significance of Brownian motion and thermophoresis influence on Reiner–Rivlin fluid dynamics on a disk with gyrotactic microorganisms and non-Fourier heat flux theory. They involved gyrotactic microorganisms to avoid the possible sedimentation of nanoparticles to make the fluid stable. They explained the physical behavior of dimensionless parameters on the dynamics of fluid.
Many analysts and investigators have been driven to analyze the MHD flux on the stretching surface due to its efficiency of its heat transfer, its unique attributes, and its crucial implementations in daily life. Mhd flux is significant in a wide range of industrial and technical applications such as the petroleum industry; the cooling of reactors; electrostatic precipitation; the design of heat exchangers; nuclear reactors; and flow meters. Mhd Flux also plays an important role in agriculture, geophysics, metrology, astrophysics, solar physics, and the motion of the earth’s core. Qin [12] considered the simulation of magneto hydradynamics effects on nanomaterial convective and irreversibility transmission through a chamber. Jang et al. [13] illustrated the theoretical and experimental analysis of Mhd micropump. Bhatti et al. [14] deliberated on the Gyrotactic microorganism’s swimming in MHD Williamson nano liquid flux among rotational circular plates in the presence of a porous medium. Li et al. [15] scrutinised the mass and heat transportation in MHD Williamson nano liquid flux on a exponentially permeable stretching surface. Arulmozhi et al. [16] considered the mass and heat transportation analysis of chemical reactive and radiative effects on MHD nano-liquid on a infinite movable vertical plates. Wang et al. [17] analyzed MHD nanofluid across a slender elastic surface, and they reported that the strong magnetic field slows down the fluid velocity and improved fluid temperature.
The nanoscale homogeneous dispersion of particles of metallic oxide and metal results in fluids known as nanofluids [18]. Theoretical and experimental results show that the inclusion of nanomaterials in the base fluid significantly affects the thermophysical characteristics of host fluids [19] with low conductivity properties [20]. Convective nanofluid heat transport flux attracts a huge number of researchers due to its intriguing applications in every field of science and engineering [21]. To mention a few, ceramic nanomaterials are used to enhance the dielectric properties of mineral oil [22], nanomaterial-containing liquid can be used in solar collectors to absorb direct sunlight [23], and titanium oxide materials have antibacterial properties that make them suitable for biomedical applications such as drug delivery and cancer treatment. [24]. Zeeshan et al. [25] studied the magnetic emission of the impact of SWCNT/MWCNT suspensions in two indomitable fluid flow based on motor water and oil. The impact of nanoparticle temperature radiating linked with electromagnetic MHD flow [26], double startification with MHD [27], and buoyancy force with MHD [28] boundary layer flow was investigated by many researchers.
Based on the above, the inspection of the available literature was limited to the investigation of the study of mass and heat transfer of the dusty Newtonian fluid flow model. Motivated due to numerous applications of nanofluid and non-Newtonian fluid subject to Lorentz and Coriolis forces in heat exchangers and many others industries, we investigate the elaborated fluid-flow problem for analysis. To author’s knowledge, there is no such analysis that simultaneously describes the impact of dust particles or of Lorentz and Coriolis forces on the dynamics of the rotating dusty Maxwell nanofluid. To better understand how different parameters and dust particle volume concentrations affect the dynamics of Maxwell dusty fluid over-stretching sheets, the current analysis’ primary objective is to examine these effects. By the utilization of suitable similarity transformation, the related non-linear PDEs are transformed into a couple of ordinary differential equations. The main graphical findings of two-phase fluid temperature; velocity; the Nusselt number; and the skin friction factor are conducted for different physical parameters.
2. Mathematical Formulation
A dusty Maxwell fluid is divined to spin in an incompressible 3D plane on a stretched sheet. Fluid is added as the sheet is extended in the plane. Around the z-axis, fluid rotates at a constant speed ; at first, fluid is stable subject to tiny particles of TiO2 and dust. It is expected that dust particles will be uniformly sized spheres with a consistent density throughout the flow. Further, we considered that the host fluid water and tiny solid particles TiO2 thermo-physical properties of nanofluid are mentioned in Table 1 and Table 2, water and tiny solid particles are in thermal equilibrium, and no slip occurs between these nanoparticles. The solid tiny particle sedimentation is ignored because, under investigation, the base fluid is assumed to be a stable host fluid. Furthermore, are the fluid’s ambient and wall surface temperatures, respectively. Figure 1 shows the coordinate system and the flow properties. For dusty-phase flow, the following governing equations are based on boundary-layer approximations [29,30]:

Table 1.
Thermophysical properties of nanoparticles (TiO2) and base fluid water [32,33].

Table 2.
Thermophysical properties of nanofluids are represented by mathematical relationships [34].
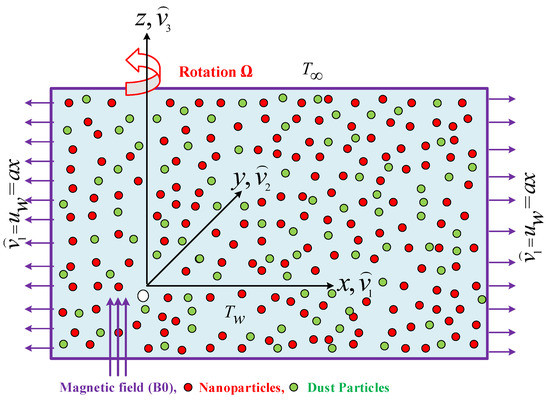
Figure 1.
The physical configuration of non-Newtonian dusty fluid.
For flux of dusty particles
where , , and represnet the components of velocity in direction of the x, y, and z axis, respectively. , and stand for the velocity components of the dust particles. , , and symbolize the angular velocity, heat-flux relaxation time, and electrical conductivity, respectively. denotes the strength of the magnetic field; K signifies the Stoke’s drag constant; N represents the dust particle’s number density; represents the deputize fluid density; denotes the liquid’s specific heat capacity; k denotes the thermal conductivity; T represents the fluid temperature; and signify the density of the dust particles and the dust-particle concentration, respectively; represents the thermal equilibrium time; represents the dust particles temperature; and represents the dust particles’ specific heat.
The boundary conditions are
By introducing the similarity transformation [31]:
Here, represents the similarity variable.
Equation (1) is fulfilled identically in view of above similarity, by substituting the aloft-mentioned transformations; Equations (2)–(8) are converted into following structure:
For the dusty phase
along with the boundary conditions,
where , , , , and . , , and are declared for the Prandtl number, rotational flow, and dusty granules’ mass concentration, respectively, constitutes the fluid particle interaction, represents the fluid interaction for temperature, represents the ratio of specific heat, signifies the Maxwell parameter, and represents the magnetic parameter. The skin friction and Nusselt coefficients are as follows:
with
Finally, we have,
stands for the local Reynolds number.
3. Results and Discussion
The primary objective of present numerical computation is to examine the significance of tiny particles of TiO2 and dust on the flow of Maxwell fluid on a stretched surface. For solving nonlinear equations with constraints, the bvp4c technique, written in MATLAB, and graphical results show the effects of the finite difference behavior of various variables on the momentum and thermal characteristics for both the fluids and dusty phases that are obtained. The applied numerical technique is convergence, and stability is accomplished, to approve the current outcomes with the available literature for limited cases against different parameters recorded in Table 3, Table 4 and Table 5. In these tables, we noticed to an outstanding comparison between the available published studies. The model parameters that we utilized are as follows: , , , , , , , and .

Table 3.
The present skin friction outcomes validation against M when other involved parameters are not considered.

Table 4.
The present Nusselt number outcomes validation against M when other involved parameters are not considered.

Table 5.
The present skin friction coefficient along x-axis and y-axis outcomes validation against when other involved parameters are not considered.
The impact of the dust-particle concentration and magnetic field on the fluid primary and secondary momentum is shown in Figure 2a,b. It reveals that by increasing the strength of , is reduced but has the opposite behavior. Actually, this is due to the fact that the transverse magnetic field to electrical conducting liquid causes the resistive force that is known as Lorentz force, and by this force, in the boundary layer the motion of the fluid slows down. So, the declination of flow is enhanced. The result of on the momentum of the fluid-dust phase is noticed in Figure 3a,b. The dusty-phase-momentum boundary layers in the x-axis and y-axis directions are signified by &. The primary velocity decreased, while the secondary velocity had the opposite behavior to it for the growing strength of both the magnetic field and the dust-particle concentration. To determine the rotation factor and how affects &, Figure 4a,b is shown. With R amplification inputs, there is a slowing in . When , this speed increases to its optimum amount. The Coriolis action causes the fluid flow to slow down; with increasing R levels, the secondary motion behaves in the opposite manner. According to this, when the density of dust particles rises, the fluid thickens and offers resistance to motion; as a result, is decreased, whereas exhibits the inverse tendency. The relationship between R and the volume density of dust is shown in Figure 5a,b for the dusty-phase velocities and . It can be seen that the primary velocity and the magnitude of the secondary velocity decreased with the incremental values of both parameters.
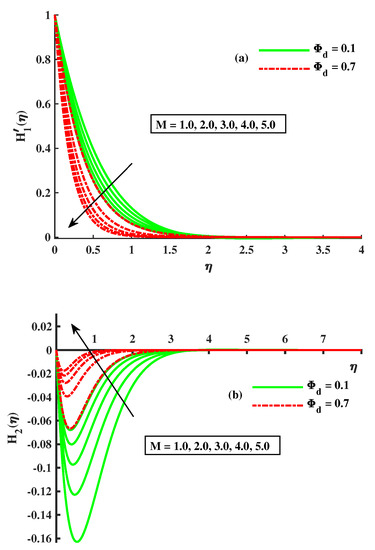
Figure 2.
Influence of M and on (a) (b) .
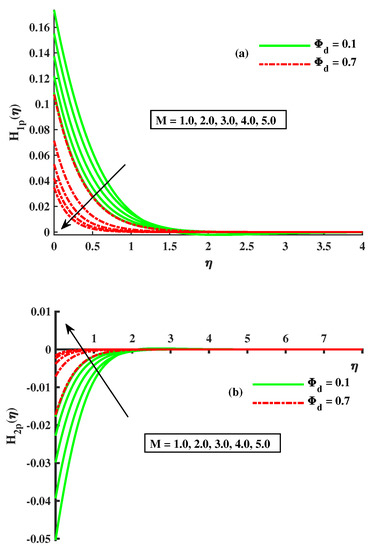
Figure 3.
Influence of on (a) (b) .
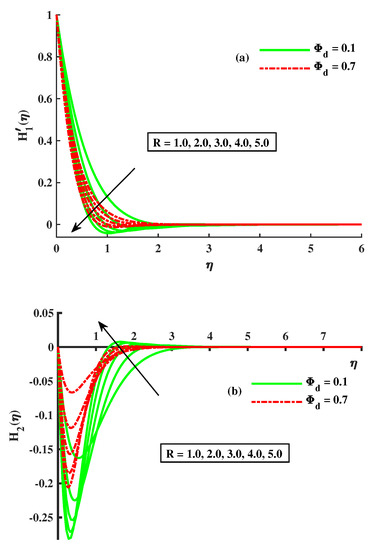
Figure 4.
Influence of on (a) (b) .
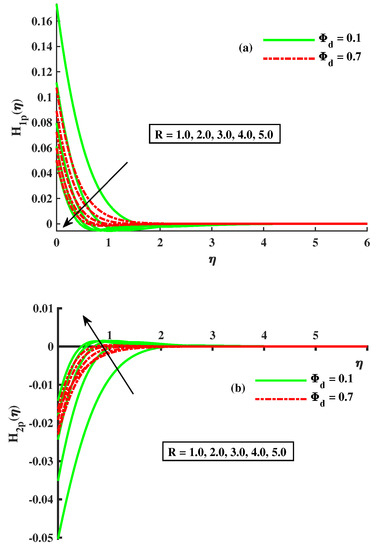
Figure 5.
Influence of on (a) (b) .
Figure 6a,b displays the variation in the temperature distribution of the fluid, and the dust phase of the fluid with varying inputs of rotational and dusty-particle-concentration parameters. The dusty and fluid-phase temperature were enhanced against the higher level of . The heat development was satisfied based on the higher diffusion process and increased rotation. Figure 7a,b shows variation in axial and transverse velocity by various values of and the Maxwell parameters. The axial velocity depreciated, while the behavior of the traverse velocity decreased when the values of and increased. The enhancement in the value of the Maxwell parameter causes the depreciation in axial velocity because its higher inputs offer a strong viscous force, which generates depreciation in flux. Figure 8a,b reveals that and the magnitude of , the velocities of the dusty phase of the fluid, are affected by the enlarging values of the Maxwell parameter and . The velocity declined with the growing inputs of and , but is opposite to it. The variation in the temperature distribution profile for both the fluid and the dusty phase of the fluid by the influence of is sketched by Figure 9a,b. The temperature for both phases is amplified by taking increasing inputs of M and . Actually, by the rising strength of M, the flux of the liquid is stopped and the dissipation appends to the liquid’s thermal heat. So, the temperature increased. The effect of and on and can be visualized in Figure 10a,b. It is noted that the incremented inputs of (the Maxwell fluid parameter) and cause the rise in temperature of the dusty phase of the fluid. The growing level of tiny particles of dust and
TiO2
is responsible for the upshot of temperature in both dust and nanofluid phase (see Figure 11a,b).
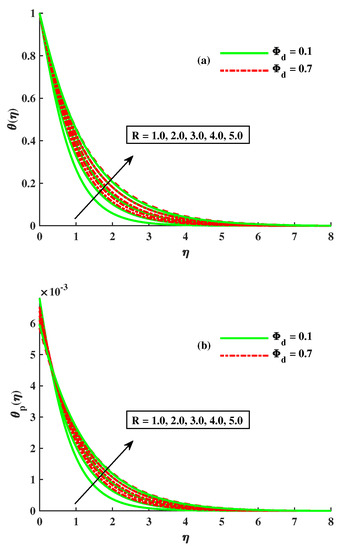
Figure 6.
Influence of on (a) (b) .
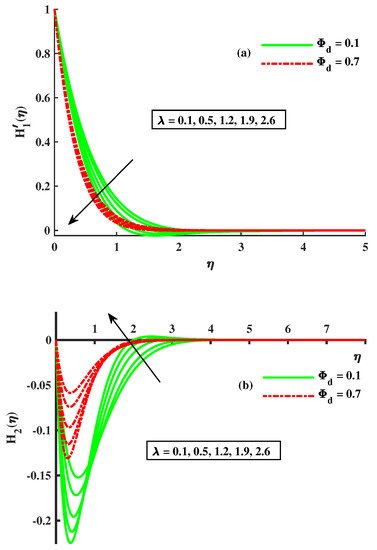
Figure 7.
Influence of on (a) (b) .
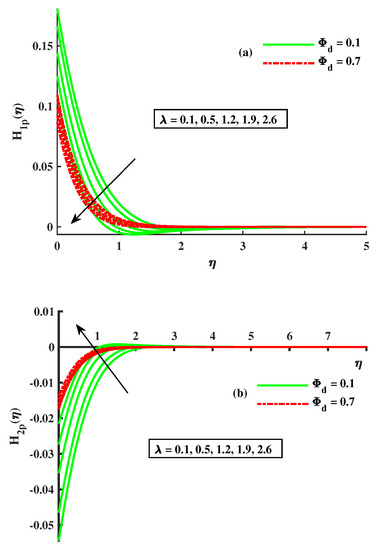
Figure 8.
Influence of and on (a) (b) .
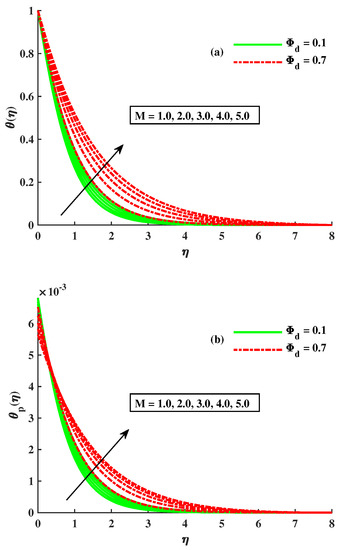
Figure 9.
Influence of on (a) (b) .
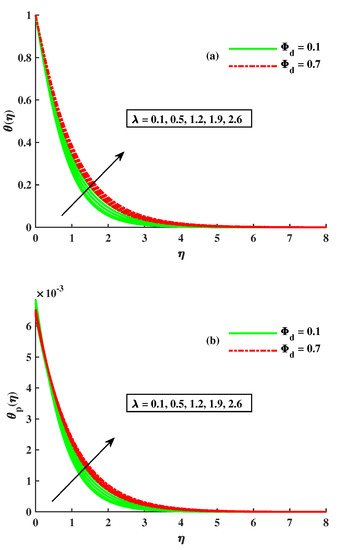
Figure 10.
Influence of on (a) (b) .
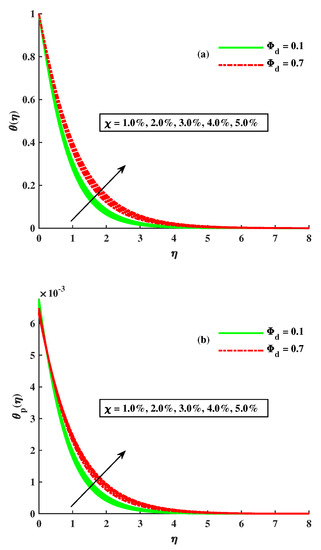
Figure 11.
Influence of on (a) (b) .
For the various entries of the rotational factor, magnetic parameter, and dust-particle-density component, the skin friction factor is shown in Figure 12a,b in the x and y-axes. Figure 12a demonstrates that (skin friction coefficient) is decreased when the values of are increased, while Figure 12b demonstrates that the depreciates when the values of the spinning factor are increased but behaves differently when M and are present. Figure 13a,b indicates how various factors affect the Nusselt number. According to Figure 13a,b, the Nusselt number decreased when rotational, magnetic, Maxwell, and dust particle saturation values increased.
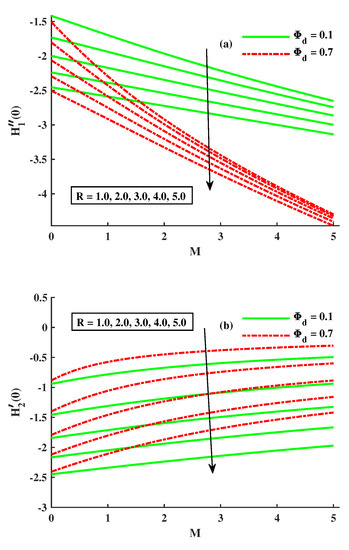
Figure 12.
Influence of on (a) (b) .
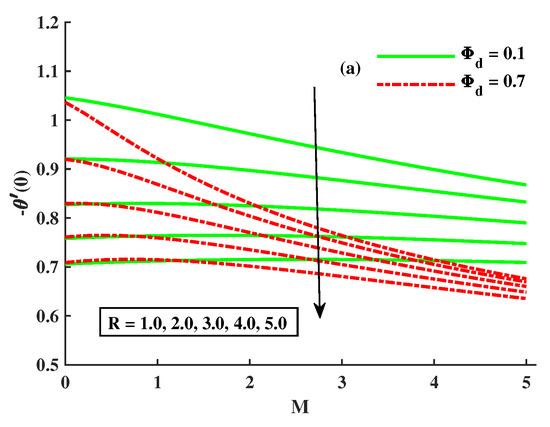
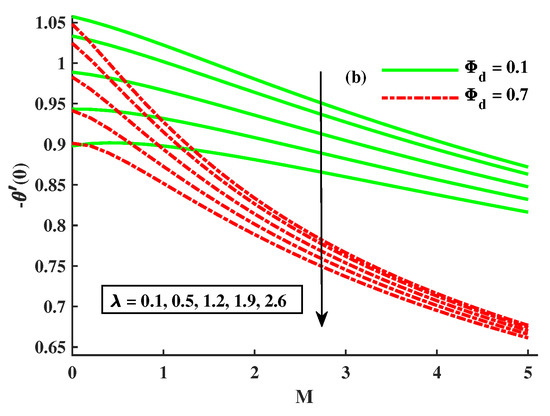
Figure 13.
Influence of R, and on (a,b) .
4. Conclusions
The heat flow over stretched sheets and Maxwell’s dusty fluid’s importance has been explored. The bvp4c approach is utilized in a Mat lab program to resolve non-dimensional problems. The results indicate that
- As the factors M, , R, and increase, and rapidly decrease; however, when the factors and decrease, the reverse phenomenon occurs.
- With more significant magnetic, rotational, and Maxwell inputs and dust-particle density, the temperatures of and increase.
- With the magnified quantities of M, , and R, the skin friction coefficient decreased in the x direction.
- The skin friction coefficient increases along the y axis by increases in M and , but it behaves differently when the rotational parameter increases.
- By increasing M, R, , and contributions, the Nusselt number is reduced.
- The growing strength of tiny particles of dust and TiO2 is responsible for the upshot of temperature in both the dust and nanofluid phases.
Author Contributions
Software, B.A.; validation, N.A.A.; formal analysis, W.; investigation, B.A.; writing original draft, A.S.O.; writing review and editing, N.A.S.; project administration, J.D.C., supervision. All authors have read and agreed to the published version of the manuscript.
Funding
Part of this research has been funded by Airlangga Global Engagement, Universitas Airlangga, Indonesia. This work was supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (No. 20192010107020, Development of hybrid adsorption chiller using unutilized heat source of low temperature).
Data Availability Statement
Not applicable.
Acknowledgments
Part of this research has been funded by Airlangga Global Engagement, Universitas Airlangga, Indonesia.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Fluid velocity along the -axis | |
| Dusty fluid velocity along the -axis | |
| Density of nanofluid | |
| Density of dust particles | |
| Kinematic viscosity of fluid | |
| Magnetic field strength | |
| Electrical conductivity | |
| Volume fraction of dust particles | |
| N | Dust particle’s number density |
| Heat-flux relaxation time | |
| Dust particle temperature | |
| Thermal equilibrium time | |
| Specific heat of dust particle | |
| T | Non-dimensional temperature |
| Temperature at surface | |
| Specific heat capacity of the fluid | |
| Ambient temperature | |
| Angular velocity | |
| Velocity of stretching sheet | |
| Skin friction along x-direction | |
| Nusselt number | |
| Sherwood number |
References
- Saffman, P. On the stability of laminar flow of a dusty gas. J. Fluid Mech. 1962, 13, 120–128. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Xu, J.; Li, J.; Fan, C.; Hu, Y. Experimental study on effect of dilute coal dust on gas explosion pressure/flame evolution process. Powder Technol. 2022, 404, 117450. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T. MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. Comput. Math. Appl. 2010, 60, 660–669. [Google Scholar] [CrossRef]
- Gnaneswara Reddy, M.; Ferdows, M. Species and thermal radiation on micropolar hydromagnetic dusty fluid flow across a paraboloid revolution. J. Therm. Anal. Calorim. 2021, 143, 3699–3717. [Google Scholar] [CrossRef]
- Wei, Y.; Rehman, S.U.; Fatima, N.; Ali, B.; Ali, L.; Chung, J.D.; Shah, N.A. Significance of Dust Particles, Nanoparticles Radius, Coriolis and Lorentz Forces: The Case of Maxwell Dusty Fluid. Nanomaterials 2022, 12, 1512. [Google Scholar] [CrossRef]
- Attia, H.A. Unsteady MHD Couette flow and heat transfer of dusty fluid with variable physical properties. Appl. Math. Comput. 2006, 177, 308–318. [Google Scholar] [CrossRef]
- Yang, L.; Du, K. A comprehensive review on the natural, forced, and mixed convection of non-Newtonian fluids (nanofluids) inside different cavities. J. Therm. Anal. Calorim. 2020, 140, 2033–2054. [Google Scholar] [CrossRef]
- Zhao, T.H.; Khan, M.I.; Chu, Y.M. Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks. Math. Methods Appl. Sci. 2021, 46, 3012–3030. [Google Scholar] [CrossRef]
- Liu, H.; Lan, L.; Abrigo, J.; Ip, H.L.; Soo, Y.; Zheng, D.; Wong, K.S.; Wang, D.; Shi, L.; Leung, T.W.; et al. Comparison of Newtonian and non-Newtonian fluid models in blood flow simulation in patients with intracranial arterial stenosis. Front. Physiol. 2021, 12, 1464. [Google Scholar] [CrossRef]
- Shende, T.; Niasar, V.J.; Babaei, M. Effective viscosity and Reynolds number of non-Newtonian fluids using Meter model. Rheol. Acta 2021, 60, 11–21. [Google Scholar] [CrossRef]
- Ali, B.; Ali, L.; Abdal, S.; Asjad, M.I. Significance of Brownian motion and thermophoresis influence on dynamics of Reiner–Rivlin fluid over a disk with non-Fourier heat flux theory and gyrotactic microorganisms: A Numerical approach. Phys. Scr. 2021, 96, 094001. [Google Scholar] [CrossRef]
- Qin, Y. Simulation of MHD impact on nanomaterial irreversibility and convective transportation through a chamber. Appl. Nanosci. 2023, 13, 929–942. [Google Scholar] [CrossRef]
- Jang, J.; Lee, S.S. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sens. Actuators Phys. 2000, 80, 84–89. [Google Scholar] [CrossRef]
- Bhatti, M.; Arain, M.; Zeeshan, A.; Ellahi, R.; Doranehgard, M. Swimming of Gyrotactic Microorganism in MHD Williamson nanofluid flow between rotating circular plates embedded in porous medium: Application of thermal energy storage. J. Energy Storage 2022, 45, 103511. [Google Scholar] [CrossRef]
- Li, Y.X.; Alshbool, M.H.; Lv, Y.P.; Khan, I.; Khan, M.R.; Issakhov, A. Heat and mass transfer in MHD Williamson nanofluid flow over an exponentially porous stretching surface. Case Stud. Therm. Eng. 2021, 26, 100975. [Google Scholar] [CrossRef]
- Arulmozhi, S.; Sukkiramathi, K.; Santra, S.; Edwan, R.; Fernandez-Gamiz, U.; Noeiaghdam, S. Heat and mass transfer analysis of radiative and chemical reactive effects on MHD nanofluid over an infinite moving vertical plate. Results Eng. 2022, 14, 100394. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Ur Rehman, S.; Ali, B.; Hussain, S.; Gia, T.N.; Muhammad, T. MHD Williamson Nanofluid Flow over a Slender Elastic Sheet of Irregular Thickness in the Presence of Bioconvection. Nanomaterials 2021, 11, 2297. [Google Scholar] [CrossRef]
- Thumma, T.; Bég, O.A.; Sheri, S.R. Finite element computation of magnetohydrodynamic nanofluid convection from an oscillating inclined plate with radiative flux, heat source and variable temperature effects. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2017, 231, 179–194. [Google Scholar] [CrossRef]
- Thumma, T.; Mishra, S. Effect of nonuniform heat source/sink, and viscous and Joule dissipation on 3D Eyring–Powell nanofluid flow over a stretching sheet. J. Comput. Des. Eng. 2020, 7, 412–426. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Alotaibi, H.; Aljohani, H.M.; Wakif, A.; Khan, I.; Akram, S. Thermally enhanced Darcy-Forchheimer Casson-water/glycerine rotating nanofluid flow with uniform magnetic field. Micromachines 2021, 12, 605. [Google Scholar] [CrossRef]
- Shafiq, A.; Lone, S.; Sindhu, T.N.; Al-Mdallal, Q.; Rasool, G. Statistical modeling for bioconvective tangent hyperbolic nanofluid towards stretching surface with zero mass flux condition. Sci. Rep. 2021, 11, 13869. [Google Scholar] [CrossRef] [PubMed]
- Rout, B.; Mishra, S.; Thumma, T. Effect of viscous dissipation on Cu-water and Cu-kerosene nanofluids of axisymmetric radiative squeezing flow. Heat Transf.—Asian Res. 2019, 48, 3039–3054. [Google Scholar] [CrossRef]
- Ashraf, M.S.; Rehman, U.R.; Farid, S.; Hussein, A.K.; Shah, N.A.; Wajaree, W. Insight into significance of bioconvection on mhd tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics 2022, 15, 2592. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Reham, U.R.; Habib, D.; Abdal, S. Shah, N.A; Dong, J.C. Micropolar dusty fluid: Coriolis force effects on dynamics of MHD rotating fluid when Lorentz force is significant. Mathematics 2022, 15, 2630. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R.; Sait, S.M. Electromagnetic flow of SWCNT/MWCNT suspensions in two immiscible water-and engine-oil-based newtonian fluids through porous media. Symmetry 2022, 14, 406. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys. 2017, 55, 630–651. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Double stratification effects on unsteady electrical MHD mixed convection flow of nanofluid with viscous dissipation and Joule heating. J. Appl. Res. Technol. 2017, 15, 464–476. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Daniel, S.K. Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method. Alex. Eng. J. 2015, 54, 705–712. [Google Scholar] [CrossRef]
- Rashid, S.; Hayat, T.; Qayyum, S.; Ayub, M.; Alsaedi, A. Three-dimensional rotating Darcy–Forchheimer flow with activation energy. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 935–948. [Google Scholar] [CrossRef]
- Tayyab, M.; Siddique, I.; Jarad, F.; Ashraf, M.K.; Ali, B. Numerical solution of 3D rotating nanofluid flow subject to Darcy-Forchheimer law, bio-convection and activation energy. S. Afr. J. Chem. Eng. 2022, 40, 48–56. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Ahmadian, A.; Senu, N.; Ali, L.; Haider, A. Significance of Lorentz and Coriolis forces on dynamics of water based silver tiny particles via finite element simulation. Ain Shams Eng. J. 2022, 13, 101572. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Prasannakumara, B.C.; Khan, U.; Madireddy, S.; Raizah, Z.; Galal, A.M. Time-Dependent Stagnation Point Flow of Water Conveying Titanium Dioxide Nanoparticle Aggregation on Rotating Sphere Object Experiencing Thermophoresis Particle Deposition Effects. Energies 2022, 15, 4424. [Google Scholar] [CrossRef]
- Dinarvand, S.; Mousavi, S.M.; Yousefi, M.; Rostami, M.N. MHD flow of MgO-Ag/water hybrid nanofluid past a moving slim needle considering dual solutions: An applicable model for hot-wire anemometer analysis. Int. J. Numer. Methods Heat Fluid Flow 2021, 32, 488–510. [Google Scholar] [CrossRef]
- Shah, N.A.; Animasaun, I.; Chung, J.D.; Wakif, A.; Alao, F.; Raju, C. Significance of nanoparticle’s radius, heat flux due to concentration gradient, and mass flux due to temperature gradient: The case of Water conveying copper nanoparticles. Sci. Rep. 2021, 11, 1882. [Google Scholar] [CrossRef]
- Rehman, S.U.; Mariam, A.; Ullah, A.; Asjad, M.I.; Bajuri, M.Y.; Pansera, B.A.; Ahmadian, A. Numerical computation of buoyancy and radiation effects on MHD micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 2021, 25, 100867. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Tariq, M. Finite element simulation of multiple slip effects on MHD unsteady maxwell nanofluid flow over a permeable stretching sheet with radiation and thermo-diffusion in the presence of chemical reaction. Processes 2019, 7, 628. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Unsteady boundary layer flow due to a stretching surface in a rotating fluid. Mech. Res. Commun. 2004, 31, 121–128. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Stretching surface in rotating viscoelastic fluid. Appl. Math. Mech. 2013, 34, 945–952. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).