Metric Dimensions of Bicyclic Graphs

Abstract

The distance $d(v_a,v_b)$ between two vertices of a simple connected graph G is the length of the shortest path between $v_a$ and $v_b$. Vertices $v_a,v_b$ of G are considered to be resolved by a vertex v if $d(v_a,v)\ne d(v_b,v)$. An ordered set $W=\{v_1,v_2,v_3,\dots ,v_s\}\subseteq V\left(G\right)$ is said to be a resolving set for G, if for any $v_a,v_b\in V\left(G\right),$∃$v_i\in W\ni d(v_a,v_i)\ne d(v_b,v_i)$. The representation of vertex v with respect to W is denoted by $r\left(v\right|W)$ and is an s-vector(s-tuple) $(d(v,v_1),d(v,v_2),d(v,v_3),\dots ,d(v,v_s))$. Using representation $r\left(v\right|W)$, we can say that W is a resolving set if, for any two vertices $v_a,v_b\in V\left(G\right)$, we have $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. A minimal resolving set is termed a metric basis for G. The cardinality of the metric basis set is called the metric dimension of G, represented by $dim\left(G\right)$. In this article, we study the metric dimension of two types of bicyclic graphs. The obtained results prove that they have constant metric dimension.

1. Introduction

While studying the problem of finding out the location of an intruder in a network, Slater in [1], and later in [2], introduced the term “locating set”. He termed the minimum resolving set a “reference set” and referred to the cardinality of a minimum resolving set (reference set) as the “location number”. Harary and Melter [3] also independently discussed these concepts. They used the nomenclature “metric dimension” instead of location number.

In this article, we use the terminology developed by Harary and Melter. Hence, the metric dimension, $dim\left(G\right)$, is the cardinality of the minimum resolving set. Following the convention in [4], we call the minimum resolving set the basis for G. Let $W=\{w_1,w_2,w_3,\cdots ,w_s\}\subset V\left(G\right)$ be a basis for a simple graph G, then the s-tuple $(d(u,w_1),d(u,w_2),d(u,w_3),\dots ,d(u,w_s))$ is termed a distance vector of u corresponding to/with respect to W and is denoted by $r\left(u\right|W)$. It is worthwhile to mention, distinct vertices have a distinct representation with respect to the basis vertices W.

This graph invariant has garnered a lot of attention from researchers. Chartrand et al. [4] characterized graphs with metric dimensions 1, $n-1$, and $n-2$. Klein and Yi [5] compared the metric dimensions of a graph and its line graph. Shao et al. [6] calculated the metric dimensions of generalized Peterson graphs of type $(2k,k)$ and $(3k,k)$ and showed that they have constant metric dimensions. Applications of metric dimensions to various fields, e.g., navigation of robots [7], chemistry [8,9], coin-weighing, and mastermind game [10] have been presented in the literature. Further studies on metric dimension and metric basis were conducted in [11,12,13,14,15,16,17,18,19,20].

Many other variants of metric dimension have been defined to further study the structure of a graph. Okamoto et al. [21] defined local metric dimensions and characterized all nontrivial connected graphs of order n having local metric dimension 1, $n-2$, or $n-1$. Kelenc et al. [22] defined mixed metric dimensions and showed that a graph is a path graph if and only if its mixed metric dimension is 2. They also characterized complete graphs in terms of mixed metric dimensions. Sedlar and Skrekovski [23] determined that for every Theta graph G, the mixed metric dimension equals 3 or 4, with 4 being attained if and only if G is a balanced Theta graph. Moreno et al. [24] defined k-metric dimensions and proved that a graph G is n-metric dimensional if and only if $G\simeq K_2$. They also characterized $(n-1)$-metric dimensional graphs.

Khuller et al. [7] showed that a graph G with metric dimension 2 can not have $K_5$ or $K_{3,3}$ as a subgraph. They also showed that there exist non-planar graphs with metric dimension 2. In light of this information, characterizing all graphs with metric dimension 2 is a daunting task. On the other hand, if we only consider the problem of characterizing planar graphs of metric dimension 2, the problem becomes more manageable.

It is a well known result that $dim\left(C_n\right)=2$. Further studies on metric dimension of unicyclic graphs were conducted in [25,26]. Armed with the knowledge from these articles, we can easily determine unicyclic graphs G, for which, $dim\left(G\right)=2$. We can also easily deduce that, if a planar graph G contains a cycle as a subgraph, then $dim\left(G\right)\ge 2$. This raises a question about metric dimensions of graphs having two or more cycles. In this article, we will discuss the metric dimension of bicyclic graphs. Using these bicyclic graphs as our building blocks, we can then move on to tricyclic and n-cyclic graphs and consider the same problem in that context. The ultimate goal of this line of questioning is to determine all planar graphs with metric dimensions 2.

2. Preliminaries

The order of a graph G is defined to be the cardinality of its vertex set. In what follows, we will use the terms $P_n$ for a path of order n, $C_n$ for cycle, $K_n$ for complete graph, and $\overline{G}$ for the complement of G. Other notations will be defined when they are needed.

Definition 1.

A simple connected graph G with $\left|V\left(G\right)\right|=n$ is said to be bicyclic, if $\left|E\left(G\right)\right|=n+1$.

It is well known that $\left|E\left(G\right)\right|=n-1$ when $G\simeq T_n$. A bicyclic graph can be obtained from this $T_n$ by adding any two new edges.

Let G be a bicyclic graph, then the base bicyclic graph of G, denoted as $\tilde{G}$ is the unique minimal bicyclic subgraph of G. It is easily concluded that $\tilde{G}$ is unique and contains no vertices of degree 1 (a pendant vertex).

There are three types of bicyclic graphs containing no pendant vertices. These are given in the following.

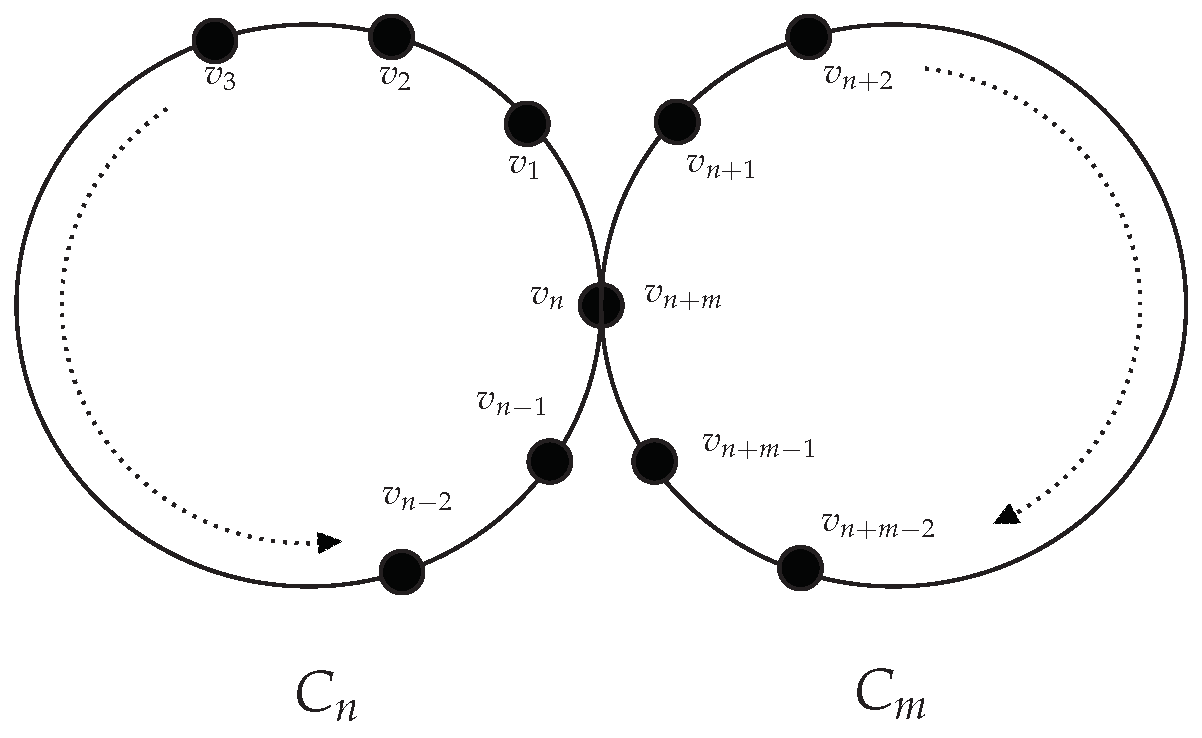
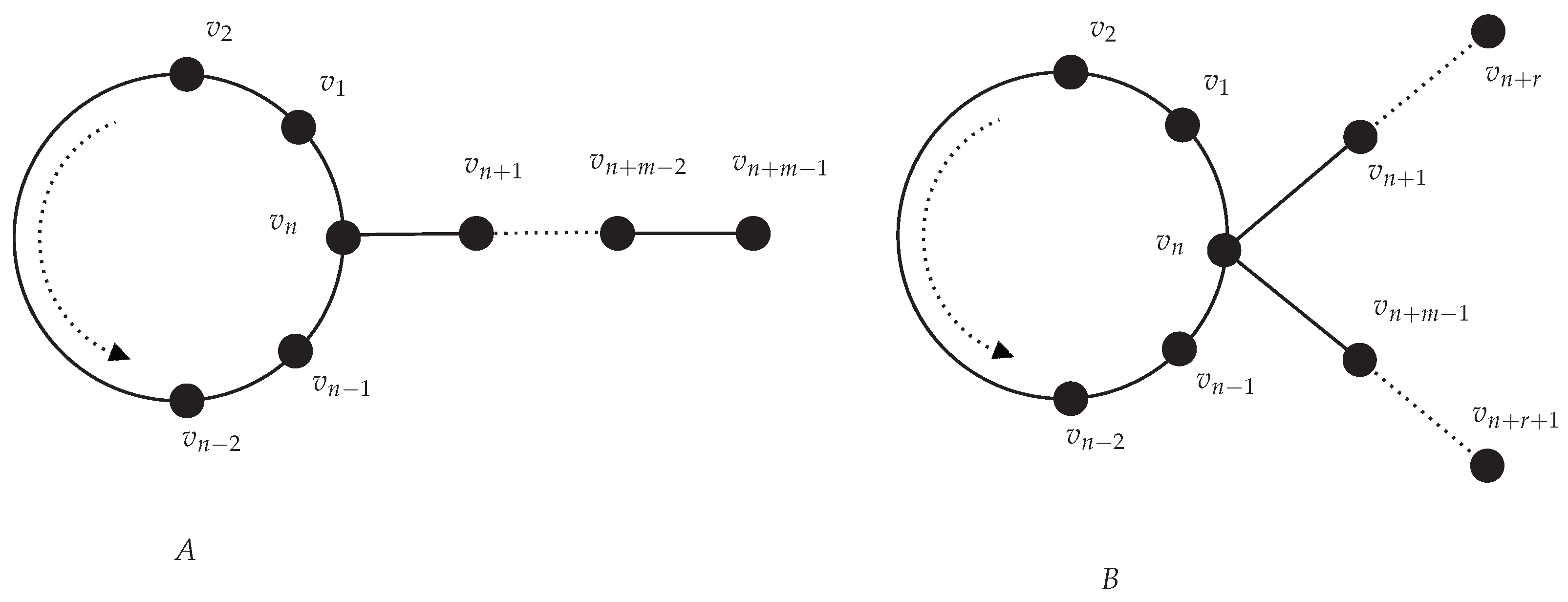
• $C_{n,m}$ obtained from two disjoint cycles $C_n$ and $C_m$, where $C_n$ and $C_m$ share a single vertex. Let us label the vertices as given in Figure 1.
  

  Figure 1. Bicyclic graph of type-I.
  The vertices $v_n$ of $C_n$ and $v_{n+m}$ of $C_m$ are identified together as the common vertex in this labeling. Note that the vertices of $C_n$ are labeled anti-clockwise, while vertices of $C_m$ are labeled clockwise.
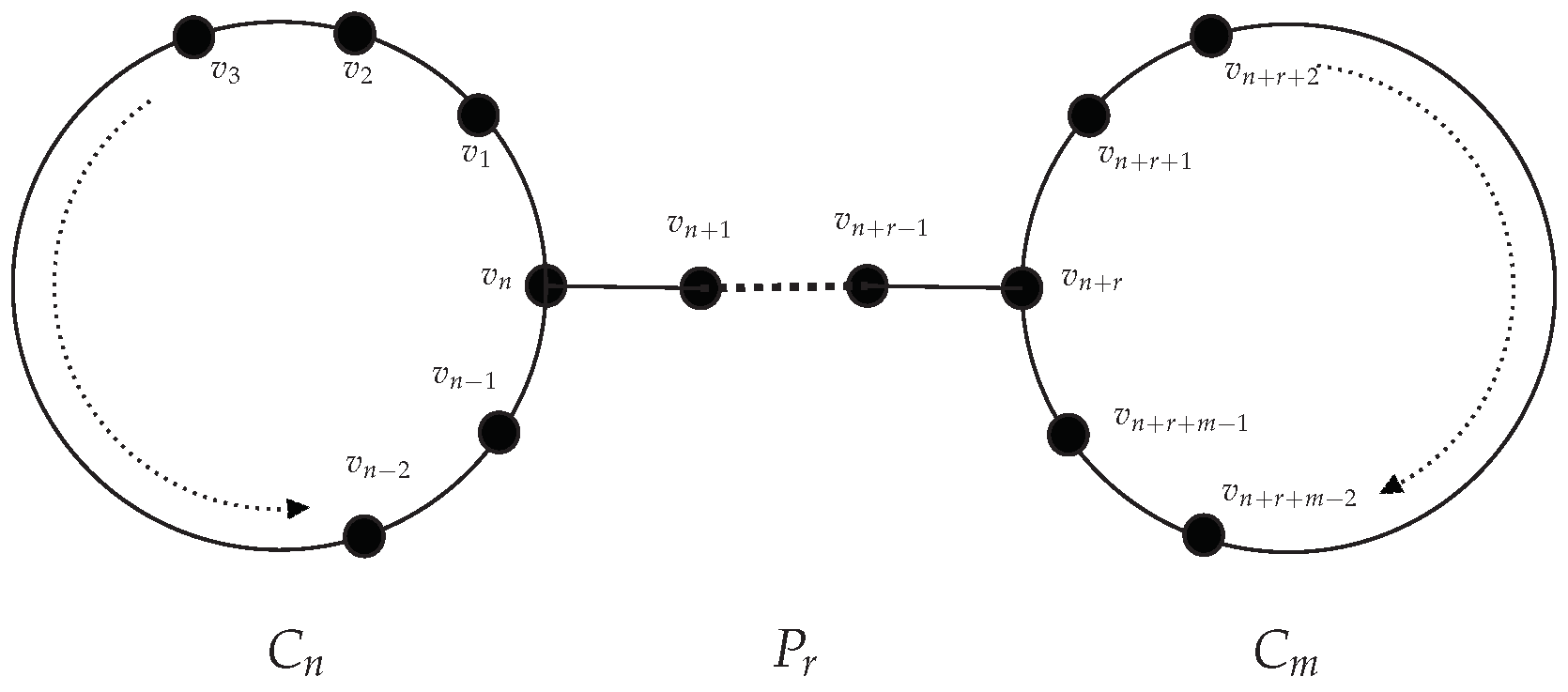
• $C_{n,r,m}$ obtained from two disjoint cycles $C_n$ and $C_m$, by adding a path $P_r(r\ge 1)$, from any vertex of $C_n$ to any vertex of $C_m$. Let us consider the labeling given in Figure 2.
  

  Figure 2. Bicyclic graph of type-II.
  In this labeling, the vertex $v_n$ of $C_n$ is attached to the vertex $v_{n+r}$ of $C_m$, by a path of length r.
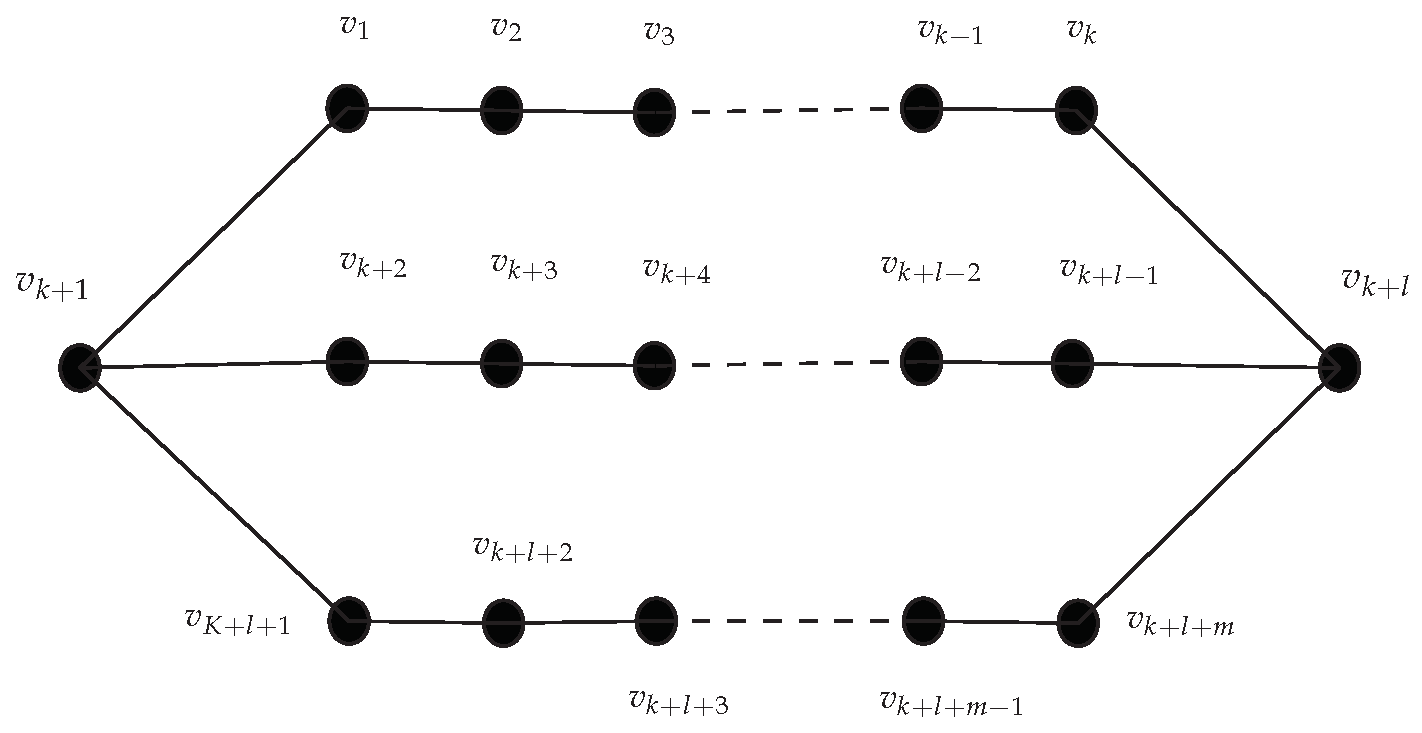
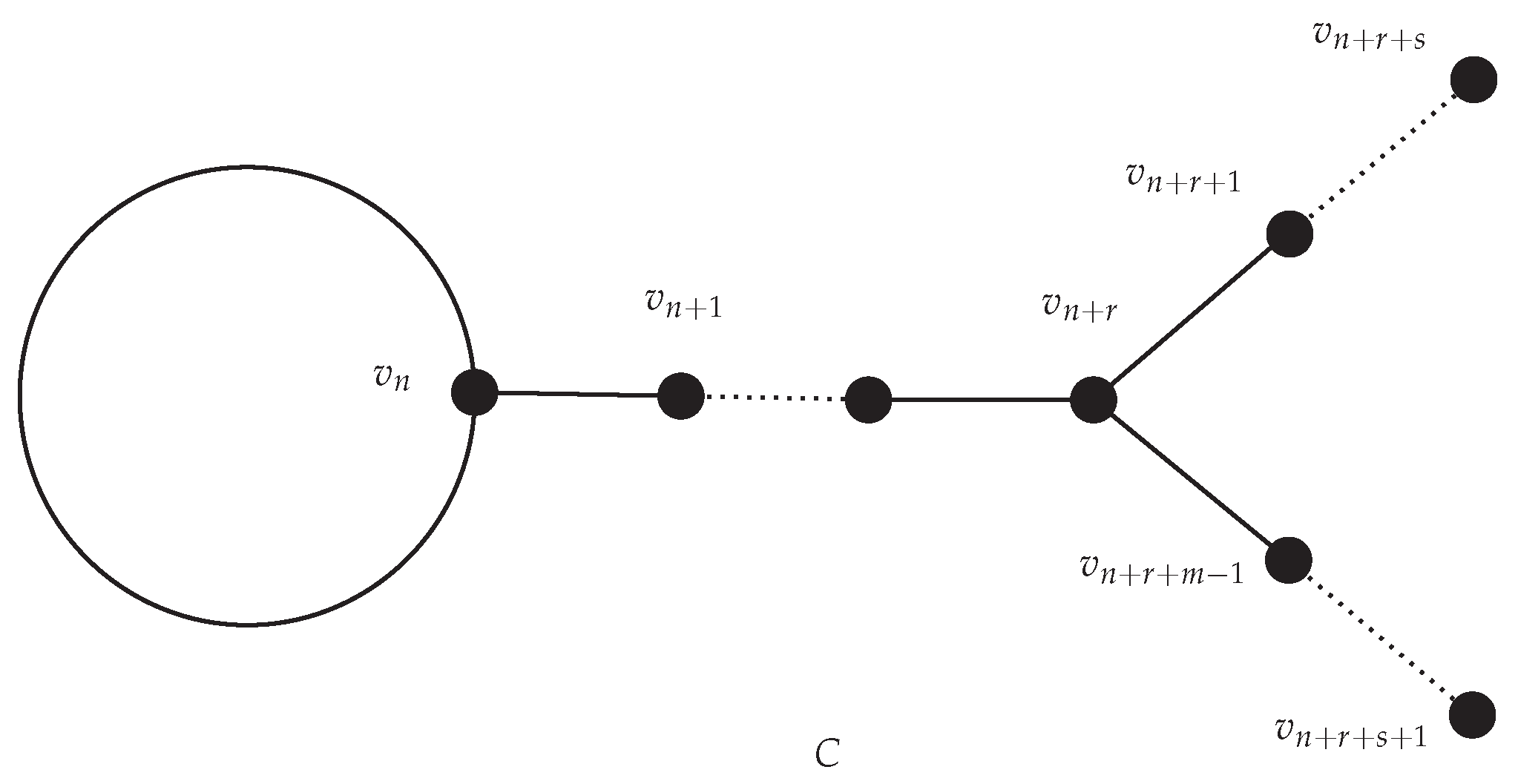
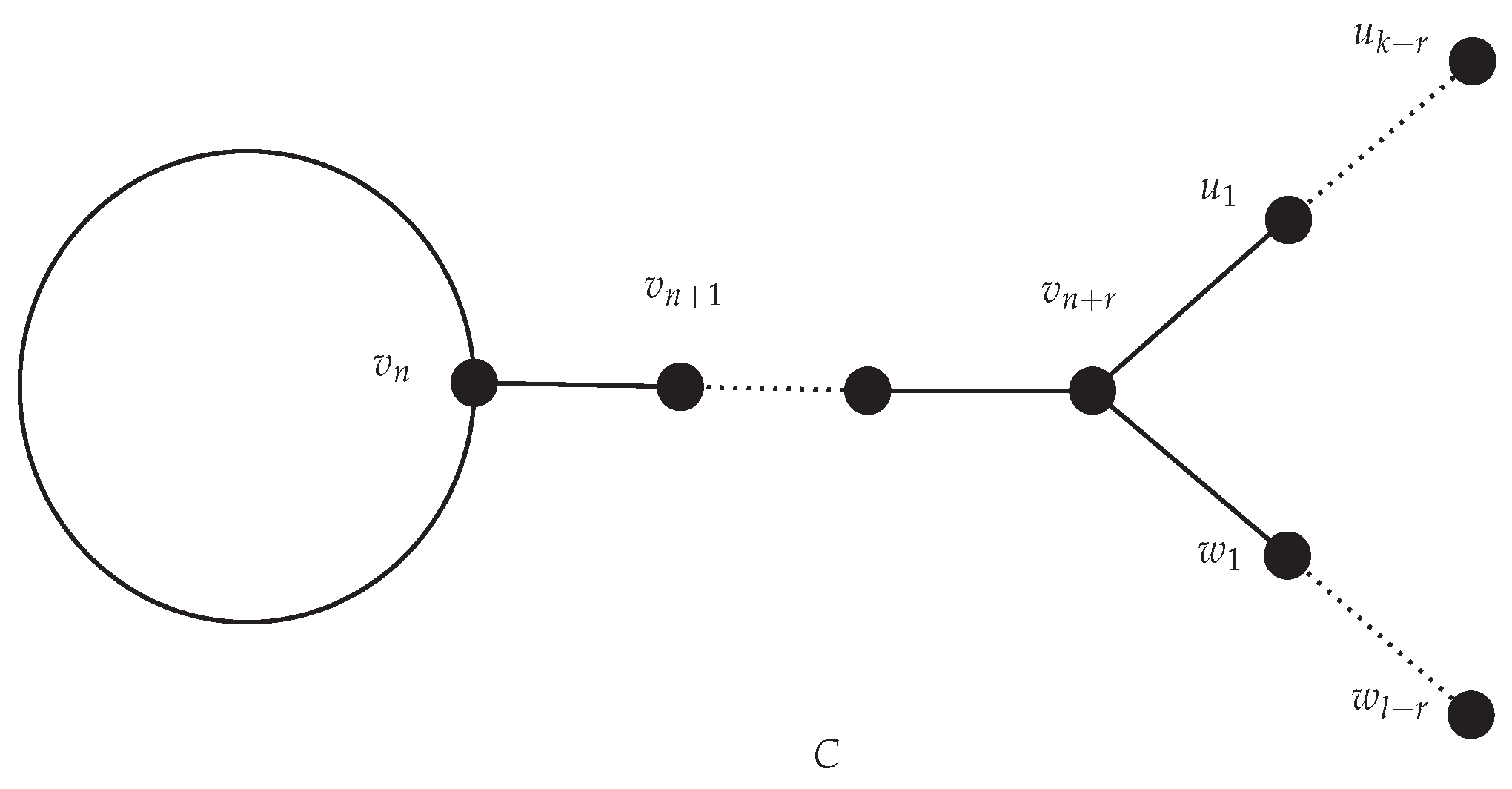
• $C^{k,l,m}$ obtained from three pairwise internal disjoint paths $P_k$, $P_l$, and $P_m$, by joining starting vertices of $P_k$ and $P_m$ to the starting vertex of $P_l$, and ending vertices of $P_k$ and $P_m$, to the ending vertex of $P_l$. Let us denote the vertices of this graph as $v_1,v_2,\cdots ,v_{k+l+m}$, then this type of bicyclic graph is given in Figure 3.
  

  Figure 3. Bicyclic graph of type-III.
  Note that the starting vertices of paths, i.e., $v_1$ of $P_k$, $v_{k+1}$ of $P_l$, and $v_{k+l+1}$ of $P_m$, are joined together. The same is applied to the ending vertices of paths.

Let ${\mathcal{B}}_n$ be the class of all bicyclic graphs of order n. Using the three types of bases given above, bicyclic graphs were divided into three classes, in [27], as follows.

• ${\mathcal{B}}_1\left(n\right)=\left\{G\in {\mathcal{B}}_n|\tilde{G}=C(k,l)\mathrm{for}\mathrm{some}k,l\ge 3\right\}$
• ${\mathcal{B}}_2\left(n\right)=\left\{G\in {\mathcal{B}}_n|\tilde{G}=C(k,r,l)\mathrm{for}\mathrm{some}k,l\ge 3\mathrm{and}r\ge 1\right\}$
• ${\mathcal{B}}_3\left(n\right)=\left\{G\in {\mathcal{B}}_n|\tilde{G}=C(P_k,P_l,P_m)\mathrm{for}\mathrm{some}1\le m\le min\{k,l\}\right\}$

It is obvious that ${\mathcal{B}}_n={\mathcal{B}}_1\left(n\right)\cup {\mathcal{B}}_2\left(n\right)\cup {\mathcal{B}}_3\left(n\right)$. Henceforth, we will use the term base bicyclic graph to refer to the unique minimal bicyclic graph having no pendant vertices.

Let us use the notation $G\cup H$ to denote the disjoint union of graphs G and H, and $G+H$ to denote the graph, obtained from $G\cup H$, by joining every vertex of G with every vertex of H. We also use $K_{r,s}$ to denote a complete bipartite graph with partitions of order r and s. Using these notations, we state the following theorem, which gives the dimensions of some well known graphs.

Theorem 1

([4,7]). Given a connected simple graph G of order $n\ge 2$, we have:

(a) 

$dim\left(G\right)=1$ if and only if $G\simeq P_n$.

(b) 

$dim\left(G\right)=n-1$ if and only if $G\simeq K_n$.

(c) 

For $n\ge 3$, $dim\left(C_n\right)=2$.

(d) 

For $n\ge 4$, $dim\left(G\right)=n-2$ if and only if $G\simeq K_{r,s}(r,s\ge 1,r+s=n),G\simeq K_r+\overline{K_s}(r\ge 1,s\ge 2,r+s=n)$, or $G\simeq K_r+(K_1\cup K_s)(r,s\ge 1,r+s=n-1)$.

3. Results on Bicyclic Graphs of Type I

In what follows, let $C_{n,m}$ be a base bicyclic graph of type I, also known as “∞-graph” [28]. The vertices are labeled as in Figure 1.

Theorem 2.

Let $C_{n,m}$ be a base bicyclic graph of type 1, $n,m\ge 3$. Then,

$$dim\left(C_{n,m}\right)=\left\{\begin{array}{cc}2\hfill & \mathit{when}n,m\mathit{are}\mathit{odd}\hfill \\ 2\hfill & \mathit{when}n\mathit{is}\mathit{even},m\mathit{is}\mathit{odd}\hfill \\ 3\hfill & \mathit{when}n,m\mathit{are}\mathit{even}\hfill \end{array}\right.$$

Proof. 

We will prove all three cases as different parts.

Part 1. Let $C_{n,m}$ be a bicyclic graph of type I where $n,m$ are odd. Let us consider the set

$$W=\left\{v_1,v_{n+⌊\frac{m}{2}⌋}\right\}.$$

Let $V_k$ be as given in the following:

$$V_k=\left\{\begin{array}{cc}\left\{v_1,v_2,\dots ,v_{⌊\frac{n}{2}⌋}\right\},\hfill & \mathrm{for}k=1\hfill \\ \left\{v_{⌊\frac{n}{2}⌋+1}\right\},\hfill & \mathrm{for}k=2\hfill \\ \left\{v_{⌊\frac{n}{2}⌋+1},\dots ,v_n\right\},\hfill & \mathrm{for}k=3\hfill \\ \left\{v_{n+1},\dots ,v_{n+⌊\frac{m}{2}⌋}\right\},\hfill & \mathrm{for}k=4\hfill \\ \left\{v_{n+⌊\frac{m}{2}⌋+1},\dots ,v_{n+m-1}\right\},\hfill & \mathrm{for}k=5.\hfill \end{array}\right.$$

(1)

Then these $V_k$ form a partition for $V\left(C_{n,m}\right)$.

We observe that

$$r\left(v_a\right|W)=\left\{\begin{array}{cc}\left(a-1,⌊\frac{m}{2}⌋+a\right)\hfill & v_a\in V_1\hfill \\ \left(a-1,n+⌊\frac{m}{2}⌋-a\right)\hfill & v_a\in V_2\hfill \\ \left(n+1-a,n+⌊\frac{m}{2}⌋-a\right)\hfill & v_a\in V_3\hfill \\ \left(a+1-n,n+⌊\frac{m}{2}⌋-a\right)\hfill & v_a\in V_4\hfill \\ \left(n+m+1-a,a-n-⌊\frac{m}{2}⌋\right)\hfill & v_a\in V_5.\hfill \end{array}\right.$$

(2)

We will show that any two distinct vertices of $C_{n,m}$ have distinct representation with respect to the set W. Let $v_a,v_b$ be two distinct vertices of $C_{n,m}$. It is straightforward to prove that when both $v_a,v_b$ are in the same partition, then

$$r\left(v_a\right|W)\ne r\left(v_b\right|W).$$

For all other cases, we proceed as follows.

Case 1. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_2.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not the case, then $r\left(v_a\right|W)=r\left(v_b\right|W)$ gives us, $a-1=b-1$ and $⌊\frac{m}{2}⌋+a=n+⌊\frac{m}{2}⌋-b$.

⇒$a=b$ and $a+b=n$.

Solving the above equations for b gives, $b=\frac{n}{2}$, which is a contradiction.

Case 2. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_3.}$

If we take $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get, $a-1=n+1-b$ and $⌊\frac{m}{2}⌋+a=n+⌊\frac{m}{2}⌋-b$. Solving for $a+b$, we get, $a+b=n+2$ and $a+b=n$, which is a contradiction. Hence, $v_a,v_b$ have distinct representations.

Case 3. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_4.}$

If we consider $r\left(v_a\right|W)=r\left(v_b\right|W)$ and use the representation given in Equation sets (2), we get $a+b=n$. This is a contradiction, since $b\in \left\{n+1,\cdots ,n+\lfloor \frac{m}{2}\rfloor \right\}$.

Case 4. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_5.}$

We again claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not the case, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a-1,\lfloor \frac{m}{2}\rfloor +a)=(n+m+1-b,b-n-⌊\frac{m}{2}⌋)$

⇒$a-1=n+m+1-b$ and $\lfloor \frac{m}{2}\rfloor +a=b-n-\lfloor \frac{m}{2}\rfloor$

⇒$a+b=n+m+2$ and $a-b=-(m-1)-n$, since $2\lfloor \frac{m}{2}\rfloor =m-1$.

Solving the above equations for a gives $a=\frac{3}{2}$. Again, this is a contradiction.

Case 5. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_3.}$

Assuming $r\left(v_a\right|W)=r\left(v_b\right|W)$ gives us

$(a-1,n+⌊\frac{m}{2}⌋-a)$=$(n+1-b,n+⌊\frac{m}{2}⌋-b)$

⇒$a-1=n+1-b$ and $n+\lfloor \frac{m}{2}\rfloor -a=n+\lfloor \frac{m}{2}\rfloor -b$

⇒$a+b=n+2$ and $a=b$

⇒$b=\frac{n}{2}+1$,

but $b\in \left\{\lfloor \frac{n}{2}\rfloor +2,\cdots ,n\right\}$. Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 6. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_4.}$

For contradiction, let $r\left(v_a\right|W)=r\left(v_b\right|W)$. This gives,

$(a-1,n+⌊\frac{m}{2}⌋-a)$=$(b+1-n,n+⌊\frac{m}{2}⌋-b)$

⇒$a-1=b+1-n$ and $n+\lfloor \frac{m}{2}\rfloor -a=n+\lfloor \frac{m}{2}\rfloor -b$

⇒$b-a=n-2$ and $a=b$

⇒$n-2=0$.

This is the desired contradiction.

Case 7. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_5.}$

If we take $r\left(v_a\right|W)=r\left(v_b\right|W)$, we obtain

$(a-1,n+⌊\frac{m}{2}⌋-a)$=$(n+m+1-b,b-n-⌊\frac{m}{2}⌋)$

⇒$a-1=n+m+1-b$ and $n+\lfloor \frac{m}{2}\rfloor -a=b-n-\lfloor \frac{m}{2}\rfloor$

⇒$a+b=n+m+2$ and $a+b=2n+2\lfloor \frac{m}{2}\rfloor$, which is a contradiction.

Case 8. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_4.}$

For contradiction, let us suppose that $r\left(v_a\right|W)=r\left(v_b\right|W)$, then

$(n+1-a,n+\lfloor \frac{m}{2}\rfloor -a)=(b+1-n,n+⌊\frac{m}{2}⌋-b)$

⇒$n+1-a=b+1-n$ and $n+\lfloor \frac{m}{2}\rfloor -a=n+\lfloor \frac{m}{2}\rfloor -b$

⇒$a+b=2n$ and $a-b=0$

⇒$b=n$

but $b\in \left\{n+1,\cdots ,n+\lfloor \frac{m}{2}\rfloor \right\}$, hence $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 9. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_5.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not true, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(n+1-a,n+\lfloor \frac{m}{2}\rfloor -a)=(n+m+1-b,b-n-\lfloor \frac{m}{2}\rfloor )$

⇒$n+1-a=n+m+1-b$ and $n+\lfloor \frac{m}{2}\rfloor -a=b-n-\lfloor \frac{m}{2}\rfloor$

⇒$b-a=m$ and $a+b=2n+m-1$.

Solving these, we get $b=n+m-\frac{1}{2}$, which is a contradiction.

Case 10. $\boxed{\mathrm{When} v_a\in V_4 \mathrm{and} v_b\in V_5.}$

To obtain a contradiction, let $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a+1-n,n+\lfloor \frac{m}{2}\rfloor -a)=(n+m+1-b,b-n-\lfloor \frac{m}{2}\rfloor )$

⇒$a+1-n=n+m+1-b$ and $n+\lfloor \frac{m}{2}\rfloor -a=b-n-\lfloor \frac{m}{2}\rfloor$

$\Rightarrow a+b=2n+m$ and $a+b=2n+m-1$, a contradiction.

From the above discussion, we get that $dim\left(C_{n,m}\right)\le 2$. By Theorem 1(c), we have $dim\left(C_{n,m}\right)\ge 2$ and hence, $dim\left(C_{n,m}\right)=2$.

Part 2. Let $C_{n,m}$ be a bicyclic graph of type I, where n is even and m is odd. Let

$$W=\left\{v_1,v_{n+⌊\frac{m}{2}⌋}\right\}.$$

Let $V_k$ be as given in the following:

$$V_k=\left\{\begin{array}{cc}\left\{v_1,v_2,\dots ,v_{⌊\frac{n}{2}⌋}\right\},\hfill & \mathrm{for}k=1\hfill \\ \left\{v_{⌊\frac{n}{2}⌋+1},\dots ,v_n\right\},\hfill & \mathrm{for}k=2\hfill \\ \left\{v_{n+1},\dots ,v_{n+⌊\frac{m}{2}⌋}\right\},\hfill & \mathrm{for}k=3\hfill \\ \left\{v_{n+⌊\frac{m}{2}⌋+1},\dots ,v_{n+m-1}\right\},\hfill & \mathrm{for}k=4.\hfill \end{array}\right.$$

(3)

Then, these $V_k$ form a partition for $V\left(C_{n,m}\right)$. We see that

$$r\left(v_a\right|W)=\left\{\begin{array}{cc}\left(a-1,⌊\frac{m}{2}⌋+a\right)\hfill & v_a\in V_1\hfill \\ \left(n+1-a,n+⌊\frac{m}{2}⌋-a\right)\hfill & v_a\in V_2\hfill \\ \left(a+1-n,n+⌊\frac{m}{2}⌋-a\right)\hfill & v_a\in V_3\hfill \\ \left(n+m+1-a,a-n-⌊\frac{m}{2}⌋\right)\hfill & v_a\in V_4,\hfill \end{array}\right.$$

(4)

for all $v_a\in V\left(C_{n,m}\right)$. We will show that $v_a$ and $v_b$ have distinct representations for all $v_a\ne v_b\in C_{n,m}$. It is obvious that when $v_a,v_b$ are both in the same partition, then

$$r\left(v_a\right|W)\ne r\left(v_b\right|W)$$

When $v_a,v_b$ are in different partitions, the following cases arise.

Case 1. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_2.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not the case, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a-1,\lfloor \frac{m}{2}\rfloor +a)=(n+1-b,n+\lfloor \frac{m}{2}\rfloor -b)$.

This give us $a+b=n+2$ and $a+b=n$, which is a contradiction.

Case 2. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_3.}$

If we assume that $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(a-1,\lfloor \frac{m}{2}\rfloor +a)=(b+1-n,n+\lfloor \frac{m}{2}\rfloor -b)$

⇒$a-1=b+1-n$ and $\lfloor \frac{m}{2}\rfloor +a=n+\lfloor \frac{m}{2}\rfloor -b$

⇒$a-b=2-n$ and $a+b=n$,

but $b\in V_3$$\Rightarrow a+b\ne n$, and hence $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 3. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_4.}$

Assuming $r\left(v_a\right|W)=r\left(v_b\right|W)$, we obtain

$(a-1,\lfloor \frac{m}{2}\rfloor +a)=(n+m+1-b,b-n-\lfloor \frac{m}{2}\rfloor )$

⇒$a-1=n+m+1-b$ and $\lfloor \frac{m}{2}\rfloor +a=b-n-\lfloor \frac{m}{2}\rfloor$

⇒$a+b=n+m+2$ and $a-b=-(m-1)-n$

⇒$a+b=n+m+2$ and $a-b=-m+1-n$.

Solving the above for a gives $a=\frac{3}{2}$, a contradiction. Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 4. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_3.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not true, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(n+1-a,n+\lfloor \frac{m}{2}\rfloor -a)=(b+1-n,n+\lfloor \frac{m}{2}\rfloor -b)$

⇒$n+1-a=b+1-n$ and $n+\lfloor \frac{m}{2}\rfloor -a=n+\lfloor \frac{m}{2}\rfloor -b$

⇒$a+b=2n$ and $a-b=0$ ⇒$b=n$,

but $b\in V_3\Rightarrow b\ne n$, a contradiction again. Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 5. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_4.}$

Proceeding in the same way as before and considering $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get

$(n+1-a,n+\lfloor \frac{m}{2}\rfloor -a)=(n+m+1-b,b-n-\lfloor \frac{m}{2}\rfloor )$

⇒$n+1-a=n+m+1-b$ and $n+\lfloor \frac{m}{2}\rfloor -a=b-n-\lfloor \frac{m}{2}\rfloor$

⇒$b-a=m$ and $a+b=2n+m-1$.

Solving these, we get $b=n+m-\frac{1}{2}$, which is contradiction here, hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 6. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_4.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If not, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a+1-n,n+\lfloor \frac{m}{2}\rfloor -a)=(n+m+1-b,b-n-\lfloor \frac{m}{2}\rfloor )$

⇒$a+1-n=n+m+1-b$ and $n+\lfloor \frac{m}{2}\rfloor -a=b-n-\lfloor \frac{m}{2}\rfloor$

$\Rightarrow a+b=2n+m$ and $a+b=2n+m-1$, a contradiction.

From the above cases, we see that $W=\left\{v_1,v_{n+⌊\frac{m}{2}⌋}\right\}$ is indeed a resolving set of $C_{n,m}$. Hence, $dim\left(C_{n,m}\right)\le 2$. Together with Theorem 1(c), this gives us, $dim\left(C_{n,m}\right)=2$ for n even and m odd.

Part 3. Let n and m be even. Consider the set $W=\left\{v_1,v_{⌊\frac{n}{2}⌋},v_{n+1}\right\}$ and consider the partitions of $V\left(C_{n,m}\right)$ as given in Equation set (3). Noting the representations of all $v_a\in V\left(C_{n,m}\right)$ from the vertices of W, and observing the fact that $⌊\frac{n}{2}⌋=\frac{n}{2}$, we see that

$$r\left(v_a\right|W)=\left\{\begin{array}{cc}\left(a-1,\frac{n}{2}-a,a+1\right)\hfill & v_a\in V_1\hfill \\ \left(n+1-a,a-\frac{n}{2},n+1-a\right)\hfill & v_a\in V_2\hfill \\ \left(a+1-n,a-\frac{n}{2},a-n-1\right)\hfill & v_a\in V_3\hfill \\ \left(n+m+1-a,\frac{3n}{2}+m-a,n+m+1-a\right)\hfill & v_a\in V_4.\hfill \end{array}\right.$$

(5)

To prove that W is a resolving set for $C_{n,m}$, we show that no two distinct vertices of $C_{n,m}$ have same representations with respect to W. It is obvious that when $v_a,v_b$ are either both in $V_1$ or $V_2$, then $r\left(v_a\right|W)\ne r\left(v_{b}W\right)$, since

$$d(v_a,v_1)\ne d(v_b,v_1)\mathrm{or}d(v_a,v_{\frac{n}{2}})\ne d(v_b,v_{\frac{n}{2}}).$$

Similarly, when $v_a,v_b\in V_3$ or $V_4$, it can be easily observed that

$$r\left(v_a\right|W)\ne r\left(v_b\right|W).$$

When $v_a,v_b$ are from different partitions, the following cases arise.

Case 1. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_2.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not the case, then $r\left(v_a\right|W)=r\left(v_b\right|W)$ $\Rightarrow (a-1,\frac{n}{2}-a,a+1)=(n+1-b,b-\frac{n}{2},n+1-b)$

⇒$a-1=n+1-b$, $\frac{n}{2}-a=b-\frac{n}{2}$ and $a+1=n+1-b$

⇒$a+b=n+2$ and $a+b=n$.

This is a contradiction. Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 2. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_3.}$

If we assume that $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get

$(a-1,\frac{n}{2}-a,a+1)=(b+1-n,b-\frac{n}{2},b-n-1)$

⇒$a-1=b+1-n$, $\frac{n}{2}-a=b-\frac{n}{2}$ and $a+1=b-n-1$

⇒$a-b=2-n$ and $a-b=-n-2$.

This is a contradiction. Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 3. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_4.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$, otherwise $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a-1,\frac{n}{2}-a,a+1)=(n+m+1-b,\frac{3n}{2}+m-b,n+m+1-b)$

⇒$a-1=n+m+1-b$, $\frac{n}{2}-a=\frac{3n}{2}+m-b$ and $a+1=n+m+1-b$

⇒$a+b=n+m+2$ and $a+b=n+m$, which is a contradiction.

Case 4. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_3.}$

Considering $r\left(v_a\right|W)=r\left(v_b\right|W)$, we obtain

⇒$(n+1-a,a-\frac{n}{2},n+1-a)=(b+1-n,b-\frac{n}{2},b-n-1)$

⇒$n+1-a=b+1-n$, $a-\frac{n}{2}=b-\frac{n}{2}$ and $n+1-a=b-n-1$

⇒$a+b=2n$ and $a+b=2n+2$, which is again a contradiction.

Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 5. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_4.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$, for if not, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(n+1-a,a-\frac{n}{2},n+1-a)=(n+m+1-b,\frac{3n}{2}+m-b,n+m+1-b)$

⇒$n+1-a=n+m+1-b$, $a-\frac{n}{2}=\frac{3n}{2}+m-b$ and $n+1-a=n+m+1-b$

⇒$b-a=m$ and $b+a=2n+m$.

Solving for b, we get $b=n+m$.

This is a contradiction, since $C_{n,m}$ contains vertices only up to $n+m-1$.

Case 6. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_4.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not the case, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a+1-n,a-\frac{n}{2},a-n-1)=(n+m+1-b,\frac{3n}{2}+m-b,n+m+1-b)$

⇒$a+1-n=n+m+1-b$ and $a-\frac{n}{2}=\frac{3n}{2}+m-b$ and $a-n-1=n+m+1-b$

⇒$a+b=2n+m$ and $a+b=2n+m+2$, again a contradiction.

The above discussion ensures that W is a resolving set for $C_{n,m}$, for even n and m. We now prove that W is indeed a minimal resolving set. For this, consider the set $W_1=W-v_1=\left\{v_{⌊\frac{n}{2}⌋},v_{n+1}\right\}$ and consider the vertices, $v_1,v_{n-1}\notin W_1$. It is easily observable that $W_1$ does not resolve $v_1$ and $v_{n-1}$. Similarly, considering the set $W_2=W-v_{⌊\frac{n}{2}⌋}=\left\{v_1,v_{n+1}\right\}$ and taking the vertices $v_{n-1},v_{n+m-1}$, we see that $W_2$ does not resolve these two. Lastly, considering $W_3=\left\{v_1,v_{⌊\frac{n}{2}⌋}\right\}$, we see that it does not resolve $v_{n+1}$ and $v_{n+m-1}$. This concludes our result for this part. □

4. Results on Bicyclic Graphs of Type II

In this section, we will work with the metric dimensions of base bicyclic graph of type II. Ahmad et al. used the term “Kayak Paddles graph” $KP(l,m,n)$ to represent these graphs and calculated their metric dimension [29]. They showed that whenever $G=KP(l,m,n)$, then $dim\left(G\right)=2$. For completeness, we also provide a proof for these graphs. The combinatorial approach used herein, differs from their proof, and serves as a verification for their result.

Let $C_{n,r,m}$ be a base bicyclic graph of type II. Let the vertices be labeled as in Figure 2.

Theorem 3.

Let $C_{n,r,m}$ be a base bicyclic graph of type II, $n,m\ge 3$ and $r\ge 1$. Then,

$$dim\left(C_{n,r,m}\right)=2.$$

Proof. 

We will discuss the proof for different cases of $n,m$, namely, when both are odd/even or one is odd and the other is even.

Part 1. Let $n,m$ both be even in $C_{n,r,m}$. Let us consider the set $W=\{v_1,v_{n+r+1}\}$.

Let $V_k$ be as given in the following:

$$V_k=\left\{\begin{array}{cc}\left\{v_1,v_2,\dots ,v_{\lfloor \frac{n}{2}\rfloor }\right\}\hfill & \mathrm{for}k=1\hfill \\ \left\{v_{\lfloor \frac{n}{2}\rfloor +1},\dots ,v_n\right\}\hfill & \mathrm{for}k=2\hfill \\ \left\{v_{n+1},\dots ,v_{n+r+\lfloor \frac{m}{2}\rfloor }\right\}\hfill & \mathrm{for}k=3\hfill \\ \left\{v_{n+r+\lfloor \frac{m}{2}\rfloor +1},\dots ,v_{n+m-1}\right\}\hfill & \mathrm{for}k=4\hfill \end{array}\right.$$

(6)

Then these $V_k$ form a partition for the vertices of the given graph.

We observe that

$$r\left(v_a\right|W)=\left\{\begin{array}{cc}(a-1,r+a+1)\hfill & v_a\in V_1\hfill \\ (n+1-a,n+r+1-a)\hfill & v_a\in V_2\hfill \\ (a+1-n,|a-n-r-1\left|\right)\hfill & v_a\in V_3\hfill \\ (n+m+2r+1-a,n+m+r+1-a)\hfill & v_a\in V_4.\hfill \end{array}\right.$$

(7)

Proceeding as before and assuming that $v_a,v_b$ are either both in $V_1$ or $V_2$, we can easily see that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. Similarly, when $v_a,v_b$ are both from $V_3$ or $V_4$, we again see that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

When $v_a,v_b$ are in different partitions $V_k$, we proceed as follows.

Case 1. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_2.}$

Assuming $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get

$(a-1,r+a+1)=(n+1-b,n+r+1-b)$.

This produces a contradiction, whereas, we get $a+b=n+2$ and $a+b=n$.

Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 2. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_3.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If not, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a-1,r+a+1)=(b+1-n,|b-n-r-1\left|\right)$

If $b>n+r+1$, we get,

$a-1=b-n+1$ and $r+a+1=b-n-r-1$

$\Rightarrow a-b=2-n$ and $a-b=-n-2r-2$, a contradiction.

If $b<n+r+1$, we get, $a-b=2-n$ and $a+b=n$. Solving these for b gives the contradiction $b=\frac{n}{2}-1$.

Case 3. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_4.}$

We claim that $v_a$ and $v_b$ have distinct representations with respect to W. If this is not the case, then $r\left(v_a\right|W)=r\left(v_b\right|W)$ gives us the contradiction $a+b=n+m+2r+1$ and $a+b=n+m$.

Case 4. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_3.}$

If we consider $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(n+1-a,n+r+1-a)=(b+1-n,|b-n-r-1\left|\right)$.

If $b>n+r+1$, we get the contradiction $a+b=2n$ and $a+b=2n+2r+2$.

If $b<n+r+1$, we get $a+b=2n$ and $a=b$, but $a\ne b$.

Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 5. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_4.}$

Proceeding as before and considering $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get

$(n+1-a,n+r+1-a)=(n+m+2r+1-b,n+m+r+1-b)$. This again produces a contradiction. Hence, $r\left(v_i\right|W)\ne r\left(v_j\right|W)$.

Case 6. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_4.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If not, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a+1-n,|a-n-r-1\left|\right)=(n+m+2r+1-b,n+m+r+1-b)$.

If $a>n+r+1$, we obtain,

$a+1-n=n+m+2r+1-b$ and $a-n-r-1=n+m+r+1-b$

$\Rightarrow a+b=m+2n+2r$ and $a+b=m+2n+2r+2$, which is a contradiction.

If $a>n+r+1$, we obtain the contradiction $b=n+m+r$.

The above discussion concludes that $dim\left(G\right)\le 2$. Together with Theorem 1(c), we obtain $dim\left(G\right)=2$.

Part 2. Let $G=C_{n,r,m}$ be a bicyclic graph of type II with $n,m$ odd. Considering the set

$$W=\{v_1,v_{n+r+1}\}.$$

Considering $V_k$ as given in the following,

$$V_k=\left\{\begin{array}{cc}\left\{v_1,v_2,\dots ,v_{\lfloor \frac{n}{2}\rfloor }\right\}\hfill & \mathrm{for}k=1\hfill \\ \left\{v_{\lfloor \frac{n}{2}\rfloor +1}\right\}\hfill & \mathrm{for}k=2\hfill \\ \left\{v_{\lfloor \frac{n}{2}\rfloor +2},\dots ,v_n\right\}\hfill & \mathrm{for}k=3\hfill \\ \left\{v_{n+1},\dots ,v_{n+r+\lfloor \frac{m}{2}\rfloor }\right\}\hfill & \mathrm{for}k=4\hfill \\ \left\{v_{n+r+\lfloor \frac{m}{2}\rfloor +1}\right\}\hfill & \mathrm{for}k=5\hfill \\ \left\{v_{n+r+\lfloor \frac{m}{2}\rfloor +2},\dots ,v_{n+r+m-1}\right\}\hfill & \mathrm{for}k=6\hfill \end{array}\right.$$

(8)

we see that these $V_k$ form a partition for $V\left(C_{n,r,m}\right)$.

$$r\left(v_a\right|W)=\left\{\begin{array}{cc}(a-1,r+a+1)\hfill & v_a\in V_1\hfill \\ (a-1,n+r+1-a)\hfill & v_a\in V_2\hfill \\ (n+1-a,n+r+1-a)\hfill & v_a\in V_3\hfill \\ (a+1-n,|a-n-r-1\left|\right)\hfill & v_a\in V_4\hfill \\ (n+m+2r+1-a,a-n-r-1)\hfill & v_a\in V_5\hfill \\ (n+m+2r+1-a,n+m+r+1-a)\hfill & v_a\in V_6.\hfill \end{array}\right.$$

(9)

Case 1. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_2.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If this is not the case then, $r\left(v_a\right|W)=r\left(v_b\right|W)$ gives us, $a-1=b-1$ and $r+a+1=n+r+1-b$⇒$a=b$ and $a+b=n$.

Solving the above equations for b gives $b=\frac{n}{2}$, which is a contradiction.

Case 2. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_3.}$

Assuming $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get $(a-1,r+a+1)=(n+1-b,n+r+1-b)$.

This produces a contradiction, whereas, we get $a+b=n+2$ and $a+b=n$.

Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 3. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_4.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If not, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a-1,r+a+1)=(b+1-n,|b-n-r-1\left|\right)$.

If $b>n+r+1$, we get $a-1=b-n+1$ and $r+a+1=b-n-r-1$

$\Rightarrow a-b=2-n$ and $a-b=-n-2r-2$, a contradiction.

If $b<n+r+1$, we obtain $a-b=2-n$ and $a+b=n$.

This produces the contradiction $b=n-1$.

Case 4. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_5.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If not, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a-1,r+a+1)=(n+m+2r+1-b,b-n-r-1)$

⇒$a-1=n+m+2r+1-b$ and $r+a+1=b-n-r-1$

$\Rightarrow a+b=n+m+2r+2$ and $b-a=n+2r+2$.

Solving the above equations for a gives $b=\frac{m}{2}$, which is a contradiction.

Case 5. $\boxed{\mathrm{When} v_a\in V_1 \mathrm{and} v_b\in V_6.}$

We claim that $v_a$ and $v_b$ have distinct representations with respect to W. If this is not the case, then $r\left(v_a\right|W)=r\left(v_b\right|W)$ gives us the contradiction $a+b=n+m+2r+1$ and $a+b=n+m$.

Case 6. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_3.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$, otherwise $r\left(v_a\right|W)=r\left(v_b\right|W)$ gives us,

$a-1=n+1-b$ and $n+r+1-a=n+r+1-b$.

⇒$a+b=n+2$ and $a=b$.

Solving the above equations for b gives $b=\frac{n}{2}+1$, an obvious contradiction.

Case 7. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_4.}$

If we consider $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(a-1,n+r+1-a)=(b+1-n,|b-n-r-1\left|\right)$.

Two possibilities arise for b. If $b>n+r+1$, we get,

$b-a=n-2$ and $a+b=2n+2r+2$.

Solving the above equations for a gives $a=\frac{n}{2}+r+2$, which is a contradiction.

On the other hand, if $b<n+r+1$, we obtain $b-a=n-2$ and $a=b$. Solving these, we get, $n=2$, which is again a contradiction.

Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 8. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_5.}$

Considering $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(a-1,n+r+1-a)=(n+m+2r+1-b,b-n-r-1)$.

This gives us the contradiction $a+b=n+m+2r+2$ and $a+b=2n+2r+2$.

Case 9. $\boxed{\mathrm{When} v_a\in V_2 \mathrm{and} v_b\in V_6.}$

If we consider $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(a-1,n+r+1-a)=(n+m+2r+1-b,m+n+r+1-b)$

⇒$a+b=n+m+2r+2$ and $b-a=m$.

Solving the above equations for a gives, $a=\frac{n}{2}+r+1$, an obvious contradiction.

Case 10. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_4.}$

Assuming $r\left(v_a\right|W)=r\left(v_b\right|W)$, gives us the contradiction $a+b=2n$ and $a+b=2n+2r+2$, when $b>n+r+1$. On the other hand, if $b<n+r+1$, we obtain $a+b=2n$ and $a=b$. This is the desired contradiction since $v_a$, $v_b$ are distinct vertices.

Case 11. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_5.}$

Proceeding as before and considering $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(n+1-a,n+r+1-a)=(n+m+2r+1-b,b-n-r-1)$

⇒$b-a=m+2r$ and $a+b=2n+2r+2$.

Solving the above equations for b gives $b=n+2r+1+\frac{m}{2}$, which is a contradiction.

Case 12. $\boxed{\mathrm{When} v_a\in V_3 \mathrm{and} v_b\in V_6.}$

If we assume $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(n+1-a,n+r+1-a)=(n+m+2r+1-b,n+m+r+1-b)$. This produces the contradiction $b-a=m+2r$ and $b-a=m$.

Case 13. $\boxed{\mathrm{When} v_a\in V_4 \mathrm{and} v_b\in V_5.}$

We claim that $r\left(v_a\right|W)\ne r\left(v_b\right|W)$. If not, then $r\left(v_a\right|W)=r\left(v_b\right|W)$

⇒$(a+1-n,|a-n-r-1\left|\right)=(n+m+2r+1-b,b-n-r-1)$.

If $a>n+r+1$, we get,

$a+1-n=n+m+2r+1-b$ and $a-n-r-1=b-n-r-1$

$\Rightarrow a+b=m+2n+2r$ and $a=b$.

Solving the above equations for b gives, $b=n+r+\frac{m}{2}$, which is a contradiction.

If $a<n+r+1$, we get, $a+b=m+2n+2r$ and $a+b=2n+2r+2$. This produces the contradiction $m=2$. Hence, $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 14. $\boxed{\mathrm{When} v_a\in V_4 \mathrm{and} v_b\in V_6.}$

If we assume that $r\left(v_a\right|W)=r\left(v_b\right|W)$, we obtain,

$(a+1-n,|a-n-r-1\left|\right)=(n+m+2r+1-b,n+m+r+1-b)$.

If $a>n+r+1$, we get,

$a+1-n=n+m+2r+1-b$ and $a-n-r-1=n+m+r+1-b$

$\Rightarrow a+b=m+2n+2r$ and $a+b=m+2n+2r+2$, an obvious contradiction.

On the other hand, if $a<n+r+1$, we obtain $a+b=m+2n+2r$ and $b-a=m$. Solving for b gives, $b=n+m+r$, a contradiction.

Case 15. $\boxed{\mathrm{When}{v}_a\in V_5 \mathrm{and} v_b\in V_6.}$

If we take $r\left(v_a\right|W)=r\left(v_b\right|W)$, we get,

$(n+m+2r+1-a,a-n-r-1)=(n+m+2r+1-b,n+m+r+1-b)$

⇒$n+m+2r+1-a=n+m+2r+1-b$ and $a-n-r-1=n+m+r+1-b$

$\Rightarrow a=b$ and $a+b=m+2n+2r+2$.

Solving the above equations for b gives $b=n+r+1+\frac{m}{2}$, a contradiction.

All the above cases ensure that $dim\left(C_{n,r,m}\right)\le 2$. This, together with Theorem 1(c), gives $dim\left(C_{n,r,m}\right)=2$ for $n,m$ odd.

Part 3. Let us take $C_{n,r,m}$, n odd, and m even. Let us consider the set $W=\{v_1,v_{n+r+1}\}$. If we take $V_k$ as given in the following,

$$V_k=\left\{\begin{array}{cc}\left\{v_1,v_2,\dots ,v_{\lfloor \frac{n}{2}\rfloor }\right\}\hfill & \mathrm{for}k=1\hfill \\ \left\{v_{\lfloor \frac{n}{2}\rfloor +1}\right\}\hfill & \mathrm{for}k=2\hfill \\ \left\{v_{\lfloor \frac{n}{2}\rfloor +2},\dots ,v_n\right\}\hfill & \mathrm{for}k=3\hfill \\ \left\{v_{n+1},\dots ,v_{n+r+\lfloor \frac{m}{2}\rfloor }\right\}\hfill & \mathrm{for}k=4\hfill \\ \left\{v_{n+r+\lfloor \frac{m}{2}\rfloor +2},\dots ,v_{n+r+m-1}\right\}\hfill & \mathrm{for}k=5,\hfill \end{array}\right.$$

(10)

we see that these $V_k$ form a partition of $V\left(C_{n,r,m}\right)$. Noting the distances of these $V_k$ from W, we get,

$$r\left(v_a\right|W)=\left\{\begin{array}{cc}(a-1,r+a+1)\hfill & v_a\in V_1\hfill \\ (a-1,n+r+1-a)\hfill & v_a\in V_2\hfill \\ (n+1-a,n+r+1-a)\hfill & v_a\in V_3\hfill \\ (a+1-n,a-n-r-1)\hfill & v_a\in V_4\hfill \\ (n+m+2r+1-a,n+m+r+1-a)\hfill & v_a\in V_5.\hfill \end{array}\right.$$

(11)

The rest of the proof pattern is again similar to Part 1 and/or Part 2. □

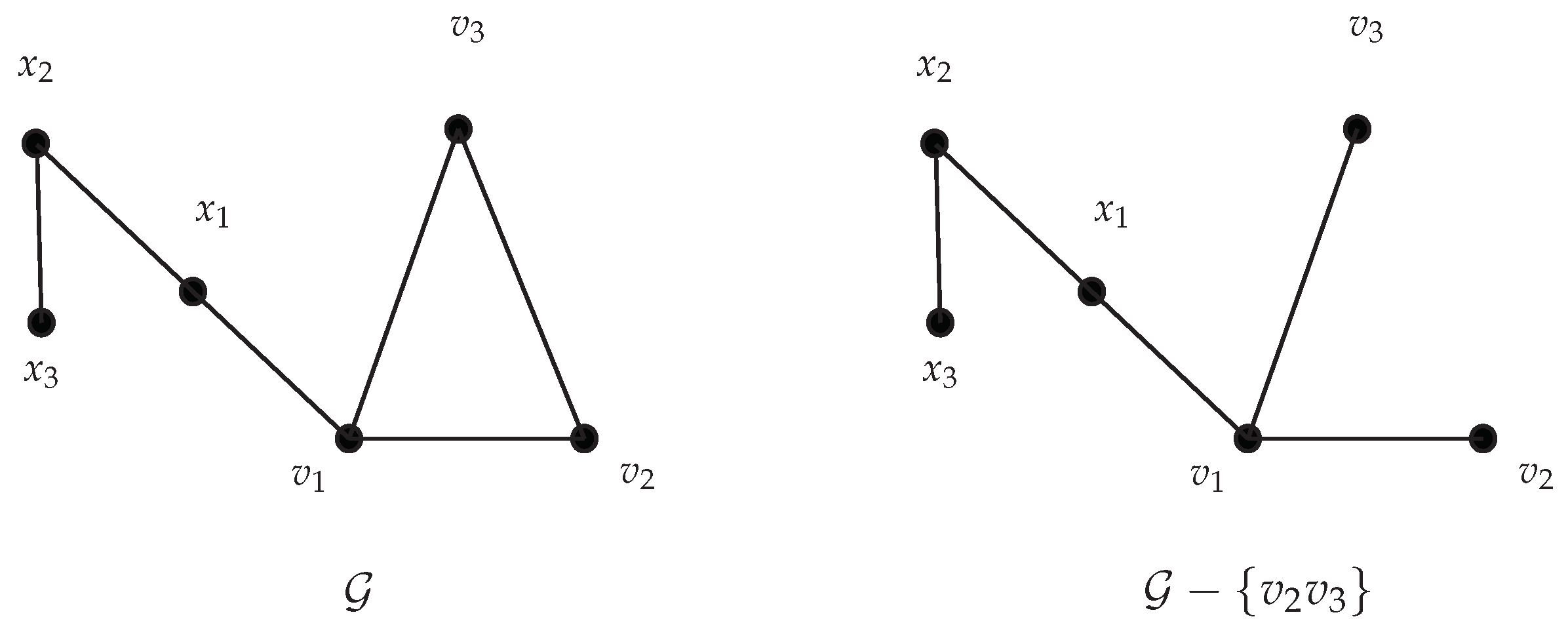
5. Perturbation in Metric Dimension of Bicyclic Graphs after Edge/Vertex Deletion

In this section, we consider the change in the metric dimension of bicyclic graphs type I and II, when an edge is removed. We only consider the cases when such a graph is still connected. Before proceeding further, we introduce some notations and definitions used in this section. The degree of a vertex v of a simple connected graph G, denoted by $d\left(v\right)$, is the number of edges incident at v. By $G-e$, we mean that the edge e has been removed from the graph G. By a “pendant path”, we mean a path $x_1{x}_2\cdots x_k$ such that every $x_i$ is of degree 2 except $x_k$, which is of degree 1, and the vertex $x_1$ is attached to a vertex v of G, where $d\left(v\right)\ge 3$. These ideas are evident in Figure 4.

Figure 4. Graph G with a pendant path $x_1{x}_2{x}_3$ and Graph $G-e$ where $e=\left\{v_2{v}_3\right\}$.

Let G be a bicyclic graph of type I. Let us now consider the graph $G-e$. If e is an edge incident with a vertex of degree 4, $G-e$ is a unicyclic graph with one pendant path. Meanwhile, when e is any other edge, $G-e$ is a unicyclic graph with two pendant paths, we name these configurations A and B, respectively; these are shown in Figure 5.

Figure 5. Configurations A and B of $G-e$ when $G=C_{n,m}$.

Note that the connected graph $G-v(v\in V(G\left)\right)$ gives us the same configurations. We will only discuss the case of $G-e$ here, keeping in mind that the same results are applicable to $G-v$.

We denote the cycle in $G-e$ by $C_n$, even interchanging n and m if necessary. We now introduce the following lemma.

Lemma 1.

For a unicyclic graph G with a pendant path of length $m-1$, $dim\left(G\right)=2$.

Proof. 

Let us denote the cycle in G by $C_n$. Let the vertices be labeled as in Figure 5, Configuration A. Let $W=\left\{v_1,v_{⌊\frac{n}{2}⌋}\right\}$.

When n is even, we have,

$$r\left(v_i\right|W)=\left\{\begin{array}{cc}\left(i+1-n,⌊\frac{n}{2}⌋+i-n\right)\hfill & \forall v_i\in \{v_{n+1},v_{n+2},\cdots ,v_{n+m-1}\}\hfill \\ \left(i-1,⌊\frac{n}{2}⌋-i\right)\hfill & \forall v_i\in \left\{v_1,v_2,\cdots ,v_{⌊\frac{n}{2}⌋}\right\}\hfill \\ \left(n+1-i,i-⌊\frac{n}{2}⌋\right)\hfill & \forall v_i\in \left\{v_{⌊\frac{n}{2}⌋+1},\cdots ,v_n\right\},\hfill \end{array}\right.$$

and when n is odd, we obtain,

$$r\left(v_i\right|W)=\left\{\begin{array}{cc}\left(i+1-n,⌊\frac{n}{2}⌋+i-n\right)\hfill & \forall v_i\in \{v_{n+1},v_{n+2},\cdots ,v_{n+m-1}\}\hfill \\ \left(i-1,⌊\frac{n}{2}⌋-i\right)\hfill & \forall v_i\in \left\{v_1,v_2,\cdots ,v_{⌊\frac{n}{2}⌋}\right\}\hfill \\ \left(i-1,i-⌊\frac{n}{2}⌋\right)\hfill & v_i=v_{⌊\frac{n}{2}⌋+1}\hfill \\ \left(n+1-i,i-⌊\frac{n}{2}⌋\right)\hfill & \forall v_i\in \left\{v_{⌊\frac{n}{2}⌋+2},\cdots ,v_n\right\}.\hfill \end{array}\right.$$

In both cases, it can easily be concluded that no two vertices of G have the same representation with respect to W. This together with Theorem 1(c) gives us, $dim\left(G\right)=2$. □

For configuration B, we see that there are two pendant paths attached at $v_n$. One can see that the vertices on both paths equidistant to $v_n$, e.g., vertices $v_{n+1}$ and $v_{n+m-1}$ can not be distinguished from any vertex of the cycle $C_n$. Similarly, vertices of $C_n$ at equal distance from $v_n$, e.g., $v_1$ and $v_{n-1}$, can not be distinguished from the vertices of attached paths. This brings us to the following lemma.

Lemma 2.

Let G be a unicyclic graph with two pendant paths attached to a vertex of the cycle in G, then $dim\left(G\right)=3$.

Proof. 

Let us denote the vertices of the cycle $C_n$ by $v_1,v_2,\cdots v_n$. Let the two pendant paths attached at $v_n$ be $v_{n+1}{v}_{n+2}\cdots v_{n+r}$ and $v_{n+m-1}{v}_{n+m-2}\cdots v_{n+r+1}$. This representation of vertices is given in Figure 5, Configuration B.

Since the cycle $C_n$ in G has dimension 2, and no vertices of $C_n$ distinguish vertices of both the pendant paths, $dim\left(G\right)>2\Rightarrow dim\left(G\right)\ge 3$. Let $W=\{v_i,v_j\}\subset V\left(C_n\right)$ be the basis for $C_n$ and let $W^{\prime }=W\cup \left\{v_{n+r}\right\}$. Since W resolves $C_n$, and $v_{n+r}$ resolves both pendant paths; $W^{\prime }$ resolves all vertices of G. Hence, $dim\left(G\right)\le 3$ and we obtain our result. □

Combining the results of Lemmas 1 and 2, we obtain the following.

Theorem 4.

Let $G-e$ be a graph obtained by deleting an edge from $G=C_{n,m}$. Then,

$$dim(G-e)=\left\{\begin{array}{cc}2\hfill & \mathit{if}e\mathit{is}\mathit{incident}\mathit{with}a\mathit{vertex}\mathit{of}\mathit{degree}4\hfill \\ 3\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Let us now consider the bicyclic graph of type II, i.e., $G=C_{n,r,m}$. $G-e$ again gives us two configurations depending on whether e is incident with a vertex of degree 2 or 3. One of the configurations we obtain is similar to A, while we name the other one as C, given in Figure 6.

Figure 6. Configuration C when an edge incident at vertices of degree 2 is removed from $G=C_{n,r,m}$.

We again mention here that the connected graph $G-v$ gives us the same configurations, and the results for $G-e$ can easily be applied to $G-v$.

We now present the following lemma for configuration C.

Lemma 3.

Let G be a unicyclic graph with two pendant paths $P_k$ and $P_l$, of lengths k and l, respectively, attached to a vertex of the cycle in G. Let $\left|V\left(P_k\right)\cap V\left(P_l\right)\right|>1$, then $dim\left(G\right)=3$.

Proof. 

Let us label the vertices of the cycle $C_n$ in G by $v_1,v_2,\cdots ,v_n$. Let $\left|V\left(P_k\right)\cap V\left(P_l\right)\right|=r$ and let these vertices be labeled as $v_{n+1},v_{n+2},\cdots ,v_{n+r}$. For an easier proof, we relabel the remaining vertices from Figure 6 as $u_1,u_2,\cdots ,u_{k-r}$ and $w_1,w_2,\cdots ,w_{l-r}$. This representation is given in Figure 7.

Figure 7. Configuration C of $C_{n,r,m}-e$ relabeled.

Let $G_1$ be the induced subgraph of G on the vertices $v_1,v_2,\cdots ,v_{n+r}$, and let $G_2$ be the induced subgraph on the vertices $V\left(G\right)-V\left(G_1\right)\cup \left\{v_{n+r}\right\}$. Since $G_1$ is a unicyclic graph with an attached pendant path, by Lemma 1, $dim\left(G_1\right)=2$. Following a similar argument to Lemma 2, we conclude that $dim\left(G\right)\ge 3$. Let $W=\{v_i,v_j\}\subset V\left(G_1\right)$ be the basis for $G_1$ and let $W^{\prime }=W\cup \left\{u_{k-r}\right\}$. Since W resolves $G_1$, and $u_{k-r}$ resolves $G_2$, $W^{\prime }$ resolves all vertices of G. Hence, $dim\left(G\right)\le 3$ and we obtain our result. □

Lemmas 1 and 3 give us the following theorem.

Theorem 5.

Let $G-e$ be a connected graph, obtained by deleting an edge from $G=C_{n,r,m}$. Then,

$$dim(G-e)=\left\{\begin{array}{cc}2\hfill & \mathit{if}e\mathit{is}\mathit{incident}\mathit{with}\mathrm{a}\mathit{vertex}\mathit{of}\mathit{degree}3\hfill \\ 3\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

If we continue to remove edges from $G-e$ to obtain a connected graph, equivalently, if we remove more than one edge from G in such a way that the final graph is connected (G is bicyclic graph of type I or type II), we either arrive at one of the configurations A, B, or C, or we obtain a tree. In both cases, their metric dimension can easily be concluded by already established results of Lemmas 1–3, or by ([4] Theorem 5).

6. Summary

We studied the resolving set and metric dimension of base bicyclic graphs and showed that they are constant for type I and II base bicyclic graphs. Particularly,

$$dim\left(C_{n,m}\right)=\left\{\begin{array}{cc}2\hfill & \mathrm{when}n,m\mathrm{are}\mathrm{odd}\hfill \\ 2\hfill & \mathrm{when}n\mathrm{is}\mathrm{even}\mathrm{and}m\mathrm{is}\mathrm{odd}\hfill \\ 3\hfill & \mathrm{when}n,m\mathrm{are}\mathrm{even}\hfill \end{array}\right.$$

where $n,m\ge 3$ and

$$dim\left(C_{n,r,m}\right)=2\mathrm{for}\mathrm{all}n\ge 3,m\ge 3,r\ge 1.$$

We also considered the problem of removing an edge/vertex from these graphs and obtained results for $dim(G-e)$.

7. Conclusions

Unicyclic graphs have been studied extensively under varying graph invariants related to metric dimensions. Bicyclic graphs have not enjoyed the same level of interest from researchers till now. In this article, we showed that the base bicyclic graphs of type I and II have constant metric dimensions. This opens up new avenues for researchers to discuss other graph invariants for these types of graphs.

In the future, the following problems are an effective way of extending this research.

Problem 1: Studying the bicyclic graph of type III and providing a generalized proof that they have constant metric dimension.

Problem 2: Studying various other graph invariants, e.g., local metric dimensions, mixed metric dimensions, and k-metric dimensions for bicyclic graphs.

Problem 3: Studying the characterization of a bigger class of graphs with metric dimension 2.

It was observed in [30] that the metric dimension problem is NP-complete for planar graphs. Diaz et al. also proposed an algorithm to calculate the metric dimension of outerplanar graphs in polynomial time. Since bicyclic graphs of type I and type II are also outerplanar graphs, their metric dimension can also be calculated in polynomial time. Following the results from this article, there is no need to apply a generalized algorithm to calculate the metric dimension of bicyclic graphs of type I and II. This effectively reduces the computational time for anyone who wants to use the metric dimension of these graphs in their applications/research.