1. Introduction
Let
S be a commutative, cancellative, reduced and finitely generated monoid. These conditions imply that
S is isomorphic to a quotient of the form
for some positive integer
p and some subgroup
M of
(see (Chapter 3 [
1])). A monoid is called cancellative if for all
such that
and it is called reduced if
Problems involving non-unique factorization in atomic monoids and integral domains have gathered much attention in the mathematical literature (see for instance [
2] and the references therein). Let
S be a monoid, the
-invariant, introduced in [
3], is a well-established invariant in the theory of non-unique factorizations, and appears also in the context of direct-sum decompositions of modules [
4]. This invariant essentially measures how far an element of an integral domain or a monoid is from being prime (see [
3]) and it has been studied for several families of numerical semigroups (see, for instance, [
5,
6]). There are also several algorithms for its computation (see [
7]).
Associated with the
-primality of an element
a of a monoid
S there is its asymptotic version, the asymptotic
-primality or
-primality and denoted by
. This parameter has been object of study in several works, for instance, in [
8], the
-primality is studied for numerical semigroups generated by two elements and it is given a formula for its computation, and, in [
9], it is computed for numerical monoids, but no other studies provide methods to calculate this invariant for other types of monoids. Actually, the main goal of this work is being able to give such procedure to compute it. The asymptotic
-primality of a monoid
S with set of atoms
, denoted by
, is defined as the maximum of the set
. The definition of
is
. Thus, we give a method such that the
-primality of an element is computed using discrete sets of points, but to compute the
-primality it is necessary to use continuous sets of points. Therefore, in this work, we see how to go from discrete to continuous sets and we give a method to compute this invariant in a huge class of finitely generated cancellative monoids. Futhermore, the method uses a partition of
and performs its computations in each of these subsets independently. Thus, this method is suitable of being parallelized.
We would like to thanks to the team of [
10] for its support on doing these computations.
2. Preliminaries and Notations
All monoids appearing in this work are commutative. For this reason, in the sequel we omit this adjective.
Let
S be a commutative, cancellative, reduced (without units) and finitely generated monoid. By [
1], there exists
M a subgroup of
such that
S is isomorphic to
For sake of simplicity, we will identify
S with
. This group is finitely generated and, since
S has no units, it verifies that
. Furthermore, every finitely abelian group
M is isomorphic to a subgroup of
where
and
. Therefore
M is determined by a set of equations of the form:
and, therefore, every monoid
S is determined by the set of equations of
M.
If , then is the element of having all its coordinates equal to zero except the ith which is equal to 1. For every its length is denoted by and, as usual, we denote its maximum norm by . With this norm, we set the distance between two points in as .
The usual cartesian product order ≤ on is defined as follows: verify if and only if . Another map we use is defined as , where is the element of having all its coordinates equal to zero except the ith which is equal to one.
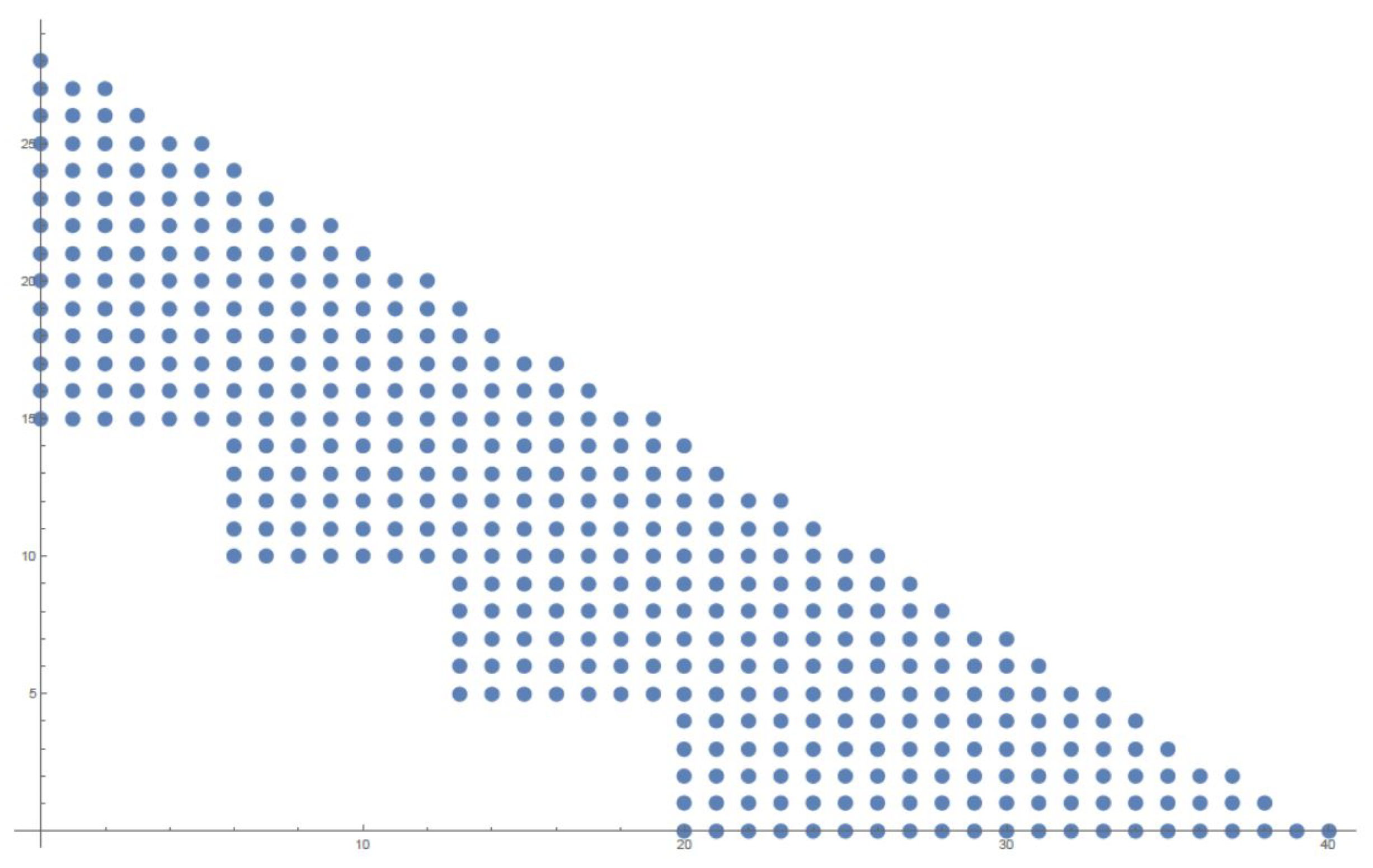
Denote by the projection map. For every denote by the set . Since S is a reduced semigroup, for every , is finite. For all the set is an ideal of , that is, if and , then belongs to . Example 1 shows a graphical representation of the set .
Example 1. Let be a monoid and . Figure 1 represents the ideal . Lemma 1. Let and . The sets , , , and are equal.
Proof. It is straightforward that .
Let . There exists such that ; therefore, , and . Since and , x belongs to .
Assume that . This implies that there exists and such that . Thus , and since , x is also in . □
Given a monoid
S, we define the following binary relation:
Clearly is reflexive and transitive. Moreover, if , then for all . With this notation, .
Factorization-theoretic notions are usually defined for multiplicative monoids, but we use additive notation for our aim. In this way, the notion of “divisibility” is the same as being “less than” with the order . So, if , then a divides b (denoted by ) if and only if .
An element
is called irreducible if there is no
fulfilling
The set of irreducible elements in
S is denoted by
. When
is the minimal generating set of
S, the monoid
S is atomic. In [
11], it is proved that every finitely generated cancelative monoid is atomic. In this way, every concept concerning factorization properties such as the
-primality is well-defined for the monoids appearing in this work.
Definition 1 (See Definition 1.1 [
8]).
Let S be an atomic monoid with set of units and set of irreducibles . For , we define if n is the smallest positive integer with the property that whenever , where each , there is a with such that . If no such n exists, then . For , we define .
The following result appearing (Proposition 3.3 [
12]), and (Algorithm 16 [
13]), give us the key for computing the
-primality in finitely generated monoids.
Lemma 2. Let be a finitely generated atomic monoid and . Then is equal to
We illustrate in an easy example how this lemma works.
Example 2. We continue with Example 1. In this case, we have that . The lengths of these points are 15, 16, 18 and 20, respectively. Therefore, .
The asymptotic version of the -primarity is defined as follows.
Definition 2. Let S be an atomic monoid and, then the asymptotic ω-primality of x is the limit .
By (Lemma 3.3 [
14]), the function
is subadditive, that is,
for all
. Thus, for every
,
. Fekete’s Subadditive Lemma (see [
15]) states that for every subadditive sequence
, the limit
exists and it is equal to
or
. Since
for every
, the limit
always exists for all
Besides, in (Lemma 3.3 [
14]), it is proven that
. Taking
we have that
.
The concept of asymptotic
-primality of an element can be expanded to the semigroup (see [
3]).
Definition 3. Asymptotic ω-primality of S is defined asGiventhe minimal generating set ofis equal to.
Next result proves that the congruence equations from the defining equations of M can be ignored.
Corollary 1. Let M and be two subgroups of
with sets of defining equationsandrespectively. If , and such that then .
Proof. Let k be the least common multiple of . Then □
3. Computing the Asymptotic -Primality
We introduce now some results that will allow us to show that the computation of the asymptotic -primality can be done from some subsets of instead of some subsets of using tools of linear programming. For every , if A is a set, we define .
Assume that
, that is,
is an element in
By Lemma 1,
. Besides, for every
the set
is equal to
, and this implies that
coincides with
and denoting
by
, then
Define
as
. The set
can be expressed as
. Furthermore, if
, there exists
such that
. Thus,
Among the properties of , the following has to be marked:
If
divides
, then
and
. Furthermore, by (Lemma 3.3 [
14]),
, which implies that
.
If
divides
, i.e.,
, applying again (Lemma 3.3 [
14]),
. Thus,
and therefore
.
For every n, and . Besides, and . Since for every , we also have .
The sequence is decreasing.
For every subset
of
define the set
We use the following notation: for every , intersect and and denote by Also define and consider . Next proposition gives us more information about the minimals elements of the set .
Proposition 1. The set is a subset of
,and Proof. If , there exits such that . The difference verifies that all its coordinates are fractions of the form of with ; therefore, .
Let x be an element of . There exists such that . Besides, there exists such that . Since , we have . Take verifying . Then, . Since , , and, thus, .
Now, since
and
we have
□
The computation of gives us the -primality of a when . Since for different values of n we obtain different , we have to study how these sets change when n changes. Moreover, as we are interested in getting the minimal elements of these sets we need to ensure that there exist a bounded region where these elements are found. In the following section, we see how this is solved for many cases using tools of Linear Programming.
4. Computing the Asymptotic -Primality
Let be the vectorial subspace of generated by M. Note that the set is an affine variety (affine subspace) of , and is defined by the set of homogeneous equations of Take into account the following considerations:
For every the set is a cone.
The sets and are polyhedrons, and the projection is also a polyhedron.
For every , and .
In general, is not a subset of .
We illustrate these considerations in a couple of easy examples.
Example 3. Consider the monoidwith M the subgroup ofgenerated by, and. The values of Δ are and:
, and is the segment .
, and is the ray with origin .
, and is the ray with origin .
, and .
Thus,
, and.
, and(the same set of minimals).
, and(they are not equal).
, and.
Previous sets can be computed easily from
Figure 2.
Example 4. Let S be the monoidwhere M is given by the equations, and let γ be the factorization. In this case, we have thatbut.
Note that, in general, Equality (
2) does not hold as Example 4 shows. Moreover, from Example 3, we have that
is not, in general, a subset of
. Since
, it can only be assured that
and that for every
there exists
such that
. Now, we prove that increasing the value of
n these sets of minimal elements get closer.
Theorem 1. For alland for all, there existssuch that ifand, then.
Proof. Let be a subset of and x be a minimal element of . There exists such that . The set is a finitely generated subgroup of and is a submonoid of . Since the monoid is isomorphic to the intersection of a finitely generated group with , it is a finitely generated monoid. Assume that is a system of generators of the monoid so any is the projection of an element belonging to The element x can be expressed as with . If for example , we consider the element . The element z verifies . Since and for any , the element z is equal to , and belongs to . Thus, x is not minimal, which is a contradiction and therefore every minimal element of can be expressed as with . This implies that, for every if , then for every and for every we have .
Since the set is finite, the theorem is satisfied for □
Theorem 2. For every, there existstrictly increasing such that.
Proof. Assume that . The element belongs to . Fixed a generating set of there exist such that . Let d be the least common multiple of the denominators of . The element belongs to for every n. Thus, . Since and , the element y is in with . □
Following corollary gives us the main computational characterization of this work.
Theorem 3. Letand. If the setis equal tothen Proof. Recall that for every , and , and that for every , . Using the triangle inequality, it is not hard to prove that if , then .
The sets
are closed and bounded. The set
is closed subset of
, so it is also closed and bounded. For this reason, there exists
such that
has maximum length, that is
. We also have that there exists
such that
, and by Theorem 2, there exist
and
such that
for every
. By Theorem 1, there exists
such that for every
and every
, there exists
such that
Thus, there exists
such that
for every
n, and for every
there exists
verifying that
.
The sets
are finite; denote by
the element having maximum length and by
an element
verifying that
. Note that
and
for every
. Using the Equality (
1), the sequence
has limit and it is equal to
. Since
, the sequence
also has limit equal to
. Using now that
, the limit
is equal to
. □
From the above results and under certain conditions, we are ready to give a method for computing the asymptotic -primality of a given element of a cancellative monoid.
Algorithm 1 admits a parallel version because each of the needed computations for step 1 can be done as separate procedures. In [
16], a Python implementation of this algorithm can be found.
| Algorithm 1: Computing the asymptotic -primality of an element. |
Input: A system of generators of M and .
Output: The asymptotic -primality of .
For every compute the set minimal vertices . Compute . Return .
|