Decomposition of Linear Operators on Pre-Euclidean Spaces by Means of Graphs

Abstract

In this work, we study a linear operator f on a pre-Euclidean space $\mathcal{V}$ by using properties of a corresponding graph. Given a basis $\mathcal{B}$ of $\mathcal{V}$, we present a decomposition of $\mathcal{V}$ as an orthogonal direct sum of certain linear subspaces ${\left\{U_i\right\}}_{i\in I}$, each one admitting a basis inherited from $\mathcal{B}$, in such way that $f={\sum }_{i\in I}{f}_i$. Each $f_i$ is a linear operator satisfying certain conditions with respect to $U_i$. Considering this new hypothesis, we assure the existence of an isomorphism between the graphs of f relative to two different bases. We also study the minimality of $\mathcal{V}$ by using the graph of f relative to $\mathcal{B}$.

1. Introduction

This paper is motivated by the following problem: If we consider a family ${\{f_i:{\mathcal{V}}_i\to {\mathcal{V}}_i\}}_{i\in I}$ of linear operators, where any ${\mathcal{V}}_i$ is a pre-Euclidean space, then we can construct a new linear operator in a natural way

$$f:\underset{i\in I}{⟂}{\mathcal{V}}_i\to \underset{i\in I}{⟂}{\mathcal{V}}_i$$

as $f={\sum }_{i\in I}{f}_i$, where $\mathcal{V}:={⟂}_{i\in I}{\mathcal{V}}_i$ is the pre-Euclidean space defined by componentwise operations. However, what about the converse? That is, if

$$f:\mathcal{V}\to \mathcal{V}$$

is a linear operator in a pre-Euclidean space, could we find a family ${\left\{{\mathcal{V}}_i\right\}}_{i\in I}$ of pre-Euclidean spaces and a family of linear operators ${\{f_i:{\mathcal{V}}_i\to {\mathcal{V}}_i\}}_{i\in I}$ in such a way that the following equations are true?

$$\mathcal{V}=\underset{i\in I}{⟂}{\mathcal{V}}_i\mathrm{and}f=\sum _{i\in I}{f}_i$$

(1)

The aim of the present work is to study this problem by giving a positive answer. A pre-Euclidean space is simply a linear space provided with a bilinear form, hence our work covers a wide range of structures. As a tool for our study, we use the techniques of graphs. This allows us to determine the decomposition (1) in an easy way, by looking at a graph of f (and a fixed basis). This result gives us the opportunity to recover a (possible) large linear operator $f:\mathcal{V}\to \mathcal{V}$ from a family of easier linear operators $f_i:{\mathcal{V}}_i\to {\mathcal{V}}_i$ in a visual and computable way, which we hope will be useful in dealing with linear operators in a vector space endowed with a bilinear map. In recent years, the use of graphs has increased in order to apply them to other areas [1,2,3,4,5]. The application of graphs has been used for the study of linear operators and algebras [6,7,8,9,10,11,12]. As some recently published articles show, this topic is currently very active [13,14,15,16,17,18,19,20,21,22].

For a linear operator $f:\mathcal{V}\to \mathcal{V}$ in a pre-Euclidean space $\mathcal{V}$ with a fixed basis $\mathcal{B}$, we obtain its decomposition as the orthogonal direct sum of certain linear subspaces ${\left\{U_i\right\}}_{i\in I}$, with each one admitting a basis inherited from $\mathcal{B}$. This way, f is decomposed as $f={\sum }_{i\in I}{f}_i$, with each $f_i$ being a linear operator satisfying certain conditions relative to $U_i$. In addition, for the linear operator f, we present conditions in order to guarantee the existence of an isomorphism between the graphs of f relative to two different bases of $\mathcal{V}$. Finally, we analyze the minimality property for $\mathcal{V}$ by using the graph of f relative to $\mathcal{B}$.

The paper is organized as follows. Section 2 contains basic notions needed for the following sections. In Section 3, we associate a graph $\Gamma (f,\mathcal{B})$ to any linear operator f, defined in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with a fixed basis $\mathcal{B}$. In addition, we introduce the notion of f-indecomposable, in order to characterize it using the connectivity of $\Gamma (f,\mathcal{B})$. In Section 4, we give a definition of f-equivalence, under which the graphs $\Gamma (f,\mathcal{B})$ and $\Gamma (f,{\mathcal{B}}^{\prime })$ are isomorphic for two different bases, $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ of $\mathcal{V}$. Moreover, we relate these properties with a definition of equivalent decomposition for f. In Section 5, we analyze the minimality property for $\mathcal{V}$ by using $\Gamma (f,\mathcal{B})$, the graph of f relative to $\mathcal{B}$. Finally, we present our conclusions, where we critically highlight our contributions, and identify strengths and weaknesses to propose paths for future research.

2. Basic Definitions

Throughout this paper, $\mathbb{F}$ denotes an arbitrary field and all vector spaces are assumed to be arbitrary dimensional and over base field $\mathbb{F}$.

Definition 1. 

A pre-Euclidean space is a pair $(\mathcal{V},\langle ·,·\rangle )$, where $\mathcal{V}$ is an $\mathbb{F}$-vector space and $\langle ·,·\rangle :\mathcal{V}\times \mathcal{V}\to \mathbb{F}$ is a bilinear form.

Example 1. 

$\mathbb{R}$ endowed with the bilinear form $\langle ·,·\rangle :\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ given as $\langle x,y\rangle :=\lambda xy$, for $x,y\in \mathbb{R}$ and fixed $\lambda \in \mathbb{R}$ is a pre-Euclidean space.

A pre-Euclidean space over the field $\mathbb{R}$ endowed with an scalar product is a pre-Hilbert space. Therefore, the results in this paper apply to pre-Hilbert spaces. A pre-Euclidean subspace of $(\mathcal{V},\langle ·,·\rangle )$ is a linear subspace U of $\mathcal{V}$ endowed with the bilinear form ${\langle ·,·\rangle |}_{U\times U}$. Additionally, given two pre-Euclidean spaces $(\mathcal{V},{\langle ·,·\rangle }_{\mathcal{V}})$ and $(\mathcal{W},{\langle ·,·\rangle }_{\mathcal{W}})$, a morphism from $\mathcal{V}$ to $\mathcal{W}$ is a linear map $\varphi :\mathcal{V}\to \mathcal{W}$, satisfying ${\langle x,y\rangle }_{\mathcal{V}}={\langle \varphi \left(x\right),\varphi \left(y\right)\rangle }_{\mathcal{W}}$ for $x,y\in \mathcal{V}$. An isomorphism is a bijective morphism from $\mathcal{V}$ to $\mathcal{W}$. Moreover, an automorphism is an isomorphism from $\mathcal{V}$ to itself.

Definition 2. 

Let $(\mathcal{V},\langle ·,·\rangle )$ be a pre-Euclidean space.

i.

We say that two elements, $x,y\in \mathcal{V}$, are orthogonal if $\langle x,y\rangle =0$.

ii.

The vector subspaces U and W of $\mathcal{V}$ are orthogonal if $\langle u,w\rangle =0$ for $u\in U,w\in W$. In this case, we denote it as $\langle U,W\rangle =\left\{0\right\}$.

iii.

$\mathcal{V}$ is an orthogonal direct sum of linear subspaces $U_i$ of $\mathcal{V}$, with $i\in I$, denoted as

$$\mathcal{V}=\underset{i\in I}{⟂}{U}_i,$$

if $\mathcal{V}$ decomposes as a direct sum $\mathcal{V}={⨁}_{i\in I}{U}_i$ of linear subspaces $U_i$, such that $\langle U_i,U_j\rangle =\left\{0\right\}$ whenever $i\ne j$.

3. Linear Operator in a Pre-Euclidean Space and Graphs: Decomposition Theorem

We recall that a (directed) graph is a pair $(V,E)$, where V is a set of vertices and $E\subset V\times V$ is a set of (directed) edges connecting the vertices.

Definition 3. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with a fixed basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$. The directed graph of f relative to $\mathcal{B}$ is $\Gamma (f,\mathcal{B}):=(V,E)$, where $V:=\mathcal{B}$ and

$$E:=\left\{(e_i,e_j)\in V\times V:\{\langle e_i,e_j\rangle ,\langle e_j,e_i\rangle \}\ne \left\{0\right\} or f\left(e_i\right)=\sum _j{\lambda }_j{e}_j for some 0\ne {\lambda }_j\in \mathbb{F}\right\}.$$

We say that $\Gamma (f,\mathcal{B})$ is the (directed) graph associated to f relative to basis $\mathcal{B}$.

Example 2. 

Let $(\mathcal{V},\langle ·,·\rangle )$ be the pre-Euclidean space over $\mathbb{R}$ with a fixed basis $\mathcal{B}=\{e_1,e_2,\dots ,e_5\}$, such that $\langle e_2,e_5\rangle =7$ and the rest zero. Let $f:\mathcal{V}\to \mathcal{V}$ be the linear operator, defined as

$$f\left(e_1\right)=f\left(e_3\right)=f\left(e_5\right):=e_1+2e_3+e_5,f\left(e_2\right)=f\left(e_4\right):=-e_4.$$

Then, the associated graph $\Ga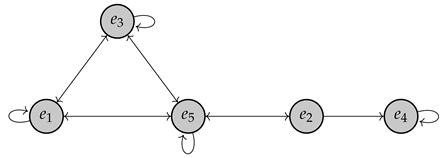mma (f,\mathcal{B})$ is:

Example 3.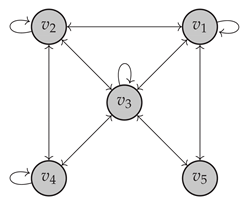 

Let $(\mathcal{V},\langle ·,·\rangle )$ be the pre-Euclidean space over $\mathbb{R}$ with basis $\mathcal{B}:=\{v_1,v_2,v_3,v_4,v_5\}$ and the bilinear form defined as

$$\langle v_4,v_3\rangle =\langle v_1,v_5\rangle :=1,\langle v_4,v_2\rangle =\langle v_3,v_5\rangle :=3.$$

Let $f:\mathcal{V}\to \mathcal{V}$ be the linear operator, given as

$$f\left(v_1\right)=f\left(v_3\right)=f\left(v_2\right):=2v_1+2v_2+v_3,f\left(v_4\right)=v_4.$$

Thus, the graph $\Gamma (f,\mathcal{B})$ is:

Given two vertices $v_i,v_j\in V$, an undirected path from $v_i$ to $v_j$ is a sequence of vertices $(v_{i_1},\dots ,v_{i_n})$ with $v_{i_1}=v_i$, $v_{i_n}=v_j$, such that either $(v_{i_r},v_{i_{r+1}})\in E$ or $(v_{i_{r+1}},v_{i_r})\in E$, for $1\le r\le n-1$. We may introduce an equivalence relation in V: we say that $v_i$ is related to $v_j$ in V, and denote $v_i\sim v_j$ if either $v_i=v_j$ or there exists an undirected path from $v_i$ to $v_j$. In this case, we assert that $v_i$ and $v_j$ are connected and the equivalence class of $v_i$, denoted by $\left[v_i\right]\in V/\sim$, corresponds to a connected component ${\mathcal{C}}_{\left[v_i\right]}$ of the graph $\Gamma (f,\mathcal{B})$. Therefore,

$$\Gamma (f,\mathcal{B})=\bigcup _{\left[v_i\right]\in V/\sim }^{\dot{}}{\mathcal{C}}_{\left[v_i\right]}.$$

(2)

To any ${\mathcal{C}}_{\left[v_i\right]}$, we can associate the linear subspace

$${\mathcal{V}}_{{\mathcal{C}}_{\left[v_i\right]}}:=\underset{v_j\in \left[v_i\right]}{⟂}\mathbb{F}{v}_j.$$

(3)

Definition 4. 

Let $(\mathcal{V},\langle ·,·\rangle )$ be a pre-Euclidean space with basis $\mathcal{B}$. A linear subspace U of $\mathcal{V}$ admits a basis ${\mathcal{B}}^{\prime }$ inherited from $\mathcal{B}$, if ${\mathcal{B}}^{\prime }$ is a basis of U satisfying ${\mathcal{B}}^{\prime }\subset \mathcal{B}$.

Definition 5. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator on a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$. The space $\mathcal{V}$ is f-decomposable with respect to $\mathcal{B}$ if $\mathcal{V}=U_1\perp U_2$, being $U_1,U_2$ non-zero linear subspaces admitting a basis inherited from $\mathcal{B}$ and $f\left(U_1\right)\subset U_1$, $f\left(U_2\right)\subset U_2$. Otherwise, $\mathcal{V}$ is said to be f-indecomposable with respect to $\mathcal{B}$.

Example 4. 

The pre-Euclidean space over $\mathbb{R}$ of Example 2 is f-indecomposable with respect to $\mathcal{B}$.

Example 5. 

Let $\mathcal{V}$ be the pre-Euclidean space defined by the 5-dimensional $\mathbb{C}$-vector space with basis $\mathcal{B}:=\{e_1,e_2,e_3,e_4,e_5\}$, and the bilinear form defined as

$$\langle e_1,e_3\rangle :=4i,\langle e_4,e_5\rangle :=2-11i,$$

and the rest zero. We consider the linear operator $f:\mathcal{V}\to \mathcal{V}$ given as

$$f\left(e_1\right):=2e_1-e_2,f\left(e_2\right):=e_3,$$

and zero on the rest. Then, by denoting $U_1,U_2$ as the $\mathbb{C}$-linear subspaces of $\mathcal{V}$ with bases $\{e_1,e_2,e_3\}$, $\{e_4,e_5\}$, respectively, we easily see that

$$\mathcal{V}=U_1\perp U_2$$

and $\mathcal{V}$ is f-decomposable with respect to $\mathcal{B}$. The associated graph $\Ga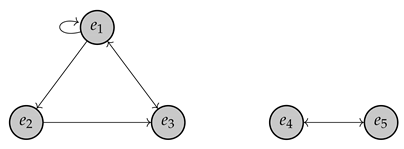mma (f,\mathcal{B})$ is:

A graph $(V,E)$ is connected if any two vertices are connected. Equivalently, a graph is connected if and only if for every partition of its vertices into two non-empty sets, there is an edge with an endpoint in each set.

Theorem 1. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator on a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$. Then, the following statements are equivalent.

i.

The graph $\Gamma (f,\mathcal{B})$ is connected.

ii.

$\mathcal{V}$ is f-indecomposable with respect to $\mathcal{B}$.

Proof. 

First, we suppose that the graph $\Gamma (f,\mathcal{B})$ is connected. Let us assume that $\mathcal{V}$ is f-decomposable with respect to $\mathcal{B}$. Thus, $\mathcal{V}$ is the orthogonal direct sum

$$\mathcal{V}=U_1\perp U_2$$

of two linear subspaces $U_1$ and $U_2$, admitting each one a basis ${\mathcal{B}}_1:=\{e_j:j\in J\}$ and ${\mathcal{B}}_2:=\{e_k:k\in K\}$, respectively, inherited from $\mathcal{B}$ such that $f\left(U_1\right)\subset U_1$ and $f\left(U_2\right)\subset U_2$. Hence, $\mathcal{B}={\mathcal{B}}_1\dot{\cup }{\mathcal{B}}_2.$ Fix some $e_j\in {\mathcal{B}}_1$ and $e_k\in {\mathcal{B}}_2$. As the graph $\Gamma (f,\mathcal{B})$ is connected, it follows that $e_j$ is connected to $e_k$. Thus, there exists an undirected path

$$(e_j,v_{i_2},\dots ,v_{i_{n-1}},e_k)$$

from $e_j$ to $e_k$. From here, there are $e^{\prime }=v_{i_s}\in {\mathcal{B}}_1$ and $e^{″}=v_{i_{s+1}}\in {\mathcal{B}}_2$, such that either $(e^{\prime },e^{″})\in E$ or $(e^{″},e^{\prime })\in E$. As $\langle e^{\prime },e^{″}\rangle =\langle e^{″},e^{\prime }\rangle =0$, we have either $P_{\mathbb{F}{e}^{″}}\left(f\left(e^{\prime }\right)\right)\ne 0$ or $P_{\mathbb{F}{e}^{\prime }}\left(f\left(e^{″}\right)\right)\ne 0$, where $P_U:\mathcal{V}\to U$ is the projection of $\mathcal{V}$ onto the linear subspace U. Hence, we have either $f\left(U_1\right)\not\subset U_1$ or $f\left(U_2\right)\not\subset U_2$, where in both cases, it is a contradiction. Therefore, $\mathcal{V}$ is f-indecomposable with respect to $\mathcal{B}$.

Conversely, let us suppose that $\mathcal{V}$ is f-indecomposable with respect to $\mathcal{B}$ and $\Gamma (f,\mathcal{B})$ is not connected. Then, there exists a partition $\mathcal{B}={\mathcal{B}}_1\dot{\cup }{\mathcal{B}}_2$, such that both $(x,y)$ and $(y,x)$ are not in E, for any $x\in {\mathcal{B}}_1$ or $y\in {\mathcal{B}}_2$. Set $U_1:={⨁}_{x\in {\mathcal{B}}_1}\mathbb{F}x$ and $U_2:={⨁}_{y\in {\mathcal{B}}_2}\mathbb{F}y$. Then, we have $\langle x,y\rangle =\langle y,x\rangle =0$ for any $x\in {\mathcal{B}}_1$ and $y\in {\mathcal{B}}_2$. Moreover, $f\left(U_1\right)\subset U_1$ and $f\left(U_2\right)\subset U_2$. Thus, $\mathcal{V}$ is the orthogonal direct sum

$$\mathcal{V}=U_1\perp U_2,$$

of two linear subspaces $U_1$ and $U_2$, admitting each one a basis ${\mathcal{B}}_1$ and ${\mathcal{B}}_2$, respectively, inherited from $\mathcal{B}$. Thus, $\mathcal{V}$ is f-decomposable with respect to $\mathcal{B}$, which is a contradiction. □

Corollary 1. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with the basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$. Then, for each $\left[v_i\right]\in V/\sim$, the linear subspace ${\mathcal{V}}_{{\mathcal{C}}_{\left[v_i\right]}}:={⟂}_{v_j\in \left[v_i\right]}\mathbb{F}{v}_j$ of $\mathcal{V}$ is f-indecomposable with respect to $\left[v_i\right]$.

We illustrate our results with a simple example.

Example 6. 

Let $(\mathcal{V},\langle ·,·\rangle )$ be the pre-Euclidean space over $\mathbb{R}$ with a fixed basis $\mathcal{B}=\{e_1,e_2,e_3,e_4\}$, such that $\langle e_1,e_3\rangle =-5$, $\langle e_2,e_4\rangle =1$, and zero on the rest. Let $f:\mathcal{V}\to \mathcal{V}$ be the linear operator, defined as

$$f\left(e_1\right)=f\left(e_3\right):=-2e_3,f\left(e_2\right)=f\left(e_4\right):=5e_2+e_4.$$

Then, the associated graph $\Gamma (f,\mathcal{B})$ is:

We have $\mathcal{V}=U_1\perp U_2$, where $U_1,U_2$ are the subspaces with bases $\{e_1,e_3\}$ and $\{e_2,e_4\}$, respectively. As the graph $\Gamma (f,\mathcal{B})$ is not connected, we conclude that $\mathcal{V}$ is f-decomposable with respect to $\mathcal{B}$. However, $U_1$ and $U_2$ are f-indecomposable with respect to $\{e_1,e_3\}$ and $\{e_2,e_4\}$, respectively.

Theorem 2. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$. Then, for a fixed basis $\mathcal{B}:={\left\{e_j\right\}}_{j\in J}$ of $\mathcal{V}$, it holds that

$$\mathcal{V}=\underset{i\in I}{⟂}{U}_i,$$

with each $U_i$ being a linear subspace of $\mathcal{V}$ admitting ${\mathcal{B}}_{\left[i\right]}:=\{e_j:e_j\in \left[e_i\right]\}$ as a basis inherited from $\mathcal{B}$. In addition, we have

$$f=\sum _{i\in I}{f}_i,$$

with each $f_i$ being a linear operator in the pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$, for $i\in I$, such that

$$f_i{{|}_{U_i}=f|}_{U_i},f_i\left(U_i\right)\subset U_i,f_i\left({\perp }_{i\ne j}{U}_j\right)=0.$$

Further, for each $i\in I$, $U_i$ is $f_i$-indecomposable with respect to ${\mathcal{B}}_{\left[i\right]}$.

Proof. 

Let $V/\sim ={\left\{\left[e_i\right]\right\}}_{i\in I}$. Then, from Equations (2) and (3), we can assert that $\mathcal{V}:={⨁}_{i\in I}{U}_i$ is the direct sum of the family of linear subspaces $U_i:={\mathcal{V}}_{{\mathcal{C}}_{\left[e_i\right]}}$, and ${\mathcal{B}}_{\left[i\right]}=\{e_j:e_j\in \left[e_i\right]\}$ is the basis for $U_i$, with $i\in I$. Thus, if $U_i\ne U_j$ then $\left[e_i\right]\ne \left[e_j\right]$, and hence, $\{\langle x,y\rangle ,\langle y,x\rangle \}=\left\{0\right\}$ for any $x\in \left[e_i\right]$, $y\in \left[e_j\right]$. From here, it follows that $\langle U_i,U_j\rangle =\langle U_j,U_i\rangle =0$ for any $i\ne j$. That is, $\mathcal{V}={⟂}_{i\in I}{U}_i$.

Assuming now that $P_{U_j}\left(f\left(U_i\right)\right)\ne \left\{0\right\}$ for $i\ne j$, where $P_{U_j}:\mathcal{V}\to U_j$ is the projection of $\mathcal{V}$ onto $U_j$. Then, there exist $e^{\prime }\in \left[e_i\right]$ and $e^{″}\in \left[v_j\right]$, such that $P_{U_j}\left(f\left(e^{\prime }\right)\right)=\lambda e^{″}+u$ with $\lambda \in \mathbb{F}\setminus \left\{0\right\}$ and $u\in {⨁}_{e\ne e^{″}\in \left[e_j\right]}\mathbb{F}e\subset U_j$. As $\lambda \ne 0$, we have $(e^{\prime },e^{″})\in E$, and therefore, $e^{\prime }\sim e^{″}$, i.e. $\left[e^{\prime }\right]=\left[e^{″}\right]$. As $\left[e_i\right]=\left[e^{\prime }\right]$ and $\left[e_j\right]=\left[e^{″}\right]$, we have $\left[e_i\right]=\left[e_j\right]$, and so, $U_i=U_j$, which is a contradiction. Thus, $P_{{\perp }_{i\ne j}{U}_j}\left(f\left(U_i\right)\right)=0$, and we conclude that $f\left(U_i\right)\subset U_i$. Consequently, each linear subspace $U_i$ of $\mathcal{V}$ admits a basis ${\mathcal{B}}_{\left[i\right]}$ inherited from $\mathcal{B}$.

As $\mathcal{V}={\perp }_{i\in I}{U}_i$, for each $i\in I$ we define the linear operator $f_i:\mathcal{V}\to \mathcal{V}$ as $f_i\left(U_i\right):=f\left(U_i\right)$ and $f_i({⟂}_{i\ne j}{U}_j):=\left\{0\right\}$, so $f={\sum }_{i\in I}{f}_i$.

Now, let us show that each $U_i$ is $f_i$-indecomposable with respect to ${\mathcal{B}}_{\left[i\right]}$. We assume that

$$U_i=U_1^{\prime }\perp U_2^{\prime },$$

where $U_1^{\prime }$ and $U_2^{\prime }$ are non-zero linear subspaces of $U_i$ admitting the $f_i$-basis ${\mathcal{B}}_1:=\{e_j:j\in J\}$ and ${\mathcal{B}}_2:=\{e_k:k\in K\}$, inherited from ${\mathcal{B}}_{\left[i\right]}$, respectively. That is,

$${\mathcal{B}}_{\left[i\right]}={\mathcal{B}}_1\dot{\cup }{\mathcal{B}}_2.$$

Fix some $e_j\in {\mathcal{B}}_1$ and $e_k\in {\mathcal{B}}_2$. As $e_j$ is connected to $e_k$, there exists an undirected path

$$(e_j,v_{i_2},\dots ,v_{i_{n-1}},e_k)$$

from $e_j$ to $e_k$. From here, there are $e^{\prime }=v_{i_s}\in {\mathcal{B}}_1$ and $e^{″}=v_{i_{s+1}}\in {\mathcal{B}}_2$, such that either $(e^{\prime },e^{″})\in E$ or $(e^{″},e^{\prime })\in E$. As $\langle e^{\prime },e^{″}\rangle =\langle e^{″},e^{\prime }\rangle =0$, we have either $P_{\mathbb{F}{e}^{″}}\left(f_i\left(e^{\prime }\right)\right)\ne 0$ or $P_{\mathbb{F}{e}^{\prime }}\left(f_i\left(e^{″}\right)\right)\ne 0$. Therefore, we have either $f_i\left(U_1^{\prime }\right)\not\subset U_1^{\prime }$ or $f_i\left(U_2^{\prime }\right)\not\subset U_2^{\prime }$. In both cases, it is a contradiction and the proof is completed. □

Example 7. 

Let $\mathcal{V}$, the 6-dimensional $\mathbb{F}$-vector space with basis $\mathcal{B}:=\{e_1,e_2,\dots ,e_6\}$, and bilinear form be defined as

$$\langle e_1,e_2\rangle :=\alpha ,\langle e_5,e_6\rangle :=\beta ,$$

and the rest zero, with $\alpha ,\beta \in \mathbb{F}\setminus \left\{0\right\}$. We consider the linear operator $f:\mathcal{V}\to \mathcal{V}$, given as

$$f\left(e_1\right):=\alpha e_1,f\left(e_3\right):=\beta e_2,f\left(e_4\right):=-\beta e_4,f\left(e_5\right):=-\alpha e_5+\alpha e_6,$$

and zero on the rest, with $\alpha ,\beta$ being the same previous scalars. By denoting $U_1,U_2$, and $U_3$ as the linear subspaces of $\mathcal{V}$ with bases ${\mathcal{B}}_{\left[1\right]}:=\{e_1,e_2,e_3\}$, ${\mathcal{B}}_{\left[2\right]}:=\left\{e_4\right\}$, ${\mathcal{B}}_{\left[3\right]}:=\{e_5,e_6\}$, respectively, we have $\mathcal{V}$ being f-decomposable with respect to $\mathcal{B}$, as

$$\mathcal{V}=U_1\perp U_2\perp U_3.$$

The associated graph $\Gamma (f,\mathcal{B})$ is:

Moreover, for $i\in \{1,2,3\}$, we define $f_i:\mathcal{V}\to \mathcal{V}$ as $f_1\left(e_1\right):=\alpha e_1$, $f_1\left(e_3\right):=\beta e_2$, $f_2\left(e_4\right):=-\beta e_4$, $f_3\left(e_5\right):=-\alpha e_5+\alpha e_6$, and zero on the rest ($\alpha ,\beta$ being the same previous non-zero scalars). We show that

$$f=f_1+f_2+f_3$$

satisfies the condition of Theorem 2, and then $U_i$ is $f_i$-indecomposable with respect to ${\mathcal{B}}_{\left[i\right]}$, for $i\in \{1,2,3\}$. Clearly, $\mathcal{V}$ is f-decomposable with respect to $\mathcal{B}$.

To identify the components of the decomposition given in Theorem 2, we only need to focus on the connected components of the associated graph.

4. Relating the Graphs Given by Different Choices of Bases

In general, for a linear operator $f:\mathcal{V}\to \mathcal{V}$ in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$, two different bases of $\mathcal{V}$ determine associated graphs to be not isomorphic, which can give rise to a different decomposition of f, as in Theorem 2. We recall that two graphs, $(V,E)$ and $(V^{\prime },E^{\prime })$, are isomorphic if there exists a bijection $\varphi :V\to V^{\prime }$, such that $(v_i,v_j)\in E$ if and only if $(\varphi \left(v_i\right),\varphi \left(v_j\right))\in E^{\prime }$. This is shown in the next example.

Example 8. 

For the linear operator and pre-Euclidean space of Example 3, if we consider $w_1:=v_1+v_2$, $w_2:=v_1-v_2$, $w_3:=v_4+v_5$, $w_4:=v_4-v_5$, and $w_5:=v_3$ for the basis ${\mathcal{B}}^{\prime }:=\{w_1,w_2,w_3,w_4,w_5\}$, we get

$$\langle w_1,w_3\rangle =-\langle w_1,w_4\rangle =\langle w_2,w_3\rangle =-\langle w_2,w_4\rangle =\langle w_3,w_5\rangle =\langle w_4,w_5\rangle =1,$$

$$\langle w_3,w_1\rangle =-\langle w_3,w_2\rangle =\langle w_4,w_1\rangle =-\langle w_4,w_2\rangle =\langle w_5,w_3\rangle =-\langle w_5,w_4\rangle =3,$$

and also,

$$f\left(w_1\right)=4w_1+2w_5,f\left(w_3\right)=f\left(w_4\right)=\frac{1}{2}{w}_3+\frac{1}{2}{w}_4,f\left(w_5\right)=2w_1+w_5.$$

Thus, we obtain the associated graph 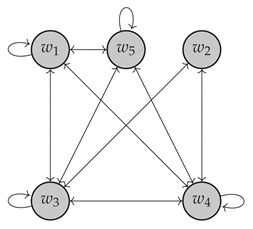$\Gamma (f,{\mathcal{B}}^{\prime })$:

Clearly, $\Gamma (f,{\mathcal{B}}^{\prime })$ is not isomorphic to the associated graph $\Gamma (f,\mathcal{B})$, as stated in Example 3.

Next, we give a condition under which the graphs associated to a linear operator $f:\mathcal{V}\to \mathcal{V}$ in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$, performed by two different bases, are isomorphic. As a consequence, we establish a sufficient condition under which two decompositions of f, induced by two different bases, are equivalent.

Definition 6. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$. Two bases, $\mathcal{B}={\left\{v_i\right\}}_{i\in I}$ and ${\mathcal{B}}^{\prime }={\left\{w_i\right\}}_{i\in I}$ of $\mathcal{V}$, are f-equivalent if there exists an automorphism $\varphi :\mathcal{V}\to \mathcal{V}$ satisfying $\varphi \left(\mathcal{B}\right)={\mathcal{B}}^{\prime }$ and $\varphi \circ f=f\circ \varphi$.

Lemma 1. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with the basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$. Consider the two bases $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ of $\mathcal{V}$. If $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ are f-equivalent bases, then the associated graphs $\Gamma (f,\mathcal{B})$ and $\Gamma (f,{\mathcal{B}}^{\prime })$ are isomorphic.

Proof. 

Let us suppose that $\mathcal{B}={\left\{v_i\right\}}_{i\in I}$ and ${\mathcal{B}}^{\prime }={\left\{w_i\right\}}_{i\in I}$ are two f-equivalent bases of $\mathcal{V}$. Then, there exists an automorphism $\varphi :\mathcal{V}\to \mathcal{V}$ satisfying $f\circ \varphi =\varphi \circ f$ and

$$\langle x,y\rangle =\langle \varphi \left(x\right),\varphi \left(y\right)\rangle$$

(4)

for $x,y\in \mathcal{V}$, in such a way that for every $v_i\in \mathcal{B}$, there exists a unique $w_{j_i}\in {\mathcal{B}}^{\prime }$ verifying $\varphi \left(v_i\right)=w_{j_i}$.

Let us denote by $(V,E)$ and $(V^{\prime },E^{\prime })$ the set of vertices and edges of $\Gamma (f,\mathcal{B})$ and $\Gamma (f,{\mathcal{B}}^{\prime })$, respectively. Taking into account that $V=\mathcal{B}$ and $V^{\prime }={\mathcal{B}}^{\prime }$, and the fact $\varphi \left(\mathcal{B}\right)={\mathcal{B}}^{\prime }$, we have that $\varphi$ defines a bijection from V to $V^{\prime }$. Given $v_i,v_k\in V$, we want to show that $(v_i,v_k)\in E$ if and only if $(\varphi \left(v_i\right),\varphi \left(v_k\right))=(w_{j_i},w_{j_k})\in E^{\prime }$. Supposing that $(v_i,v_k)\in E$, either $\{\langle v_i,v_k\rangle ,\langle v_k,v_i\rangle \}\ne \left\{0\right\}$ or $f\left(v_i\right)={\sum }_k{\lambda }_k{v}_k \mathrm{for} \mathrm{some} 0\ne {\lambda }_k\in \mathbb{F}$. If $\{\langle v_i,v_k\rangle ,\langle v_k,v_i\rangle \}\ne \left\{0\right\}$, then by Equation (4), we have $\{\langle w_{j_i},w_{j_k}\rangle ,\langle w_{j_k},w_{j_i}\rangle \}\ne \left\{0\right\}$. If $f\left(v_i\right)={\sum }_k{\lambda }_k{v}_k \mathrm{for} \mathrm{some} 0\ne {\lambda }_k\in \mathbb{F}$, applying $\varphi$ to this relation, we would find that $f\left(w_{j_i}\right)=f\left(\varphi \left(v_i\right)\right)=\varphi \left(f\left(v_i\right)\right)=\varphi \left({\sum }_k{\lambda }_k{v}_k\right)={\sum }_k{\lambda }_k\varphi \left(v_k\right)={\sum }_k{\lambda }_k{w}_{j_k} \mathrm{for} \mathrm{some} 0\ne {\lambda }_k\in \mathbb{F}$. Thus, $(w_{j_i},w_{j_k})\in E^{\prime }$. The same argument using ${\varphi }^{-1}$ shows that if $(w_{j_i},w_{j_k})\in E^{\prime }$, then $(v_i,v_k)\in E$, because ${\varphi }^{-1}\circ f=f\circ {\varphi }^{-1}$. This fact concludes the proof that $\Gamma (f,\mathcal{B})$ and $\Gamma (f,{\mathcal{B}}^{\prime })$ are isomorphic via $\varphi$. □

The following concept is borrowed from the theory of graded algebras (see [23] for examples).

Definition 7. 

Let $(\mathcal{V},\langle ·,·\rangle )$ be a pre-Euclidean space and let

$$\mathsf{{\rm Y}}:=\mathcal{V}=\underset{i\in I}{⟂}{\mathcal{V}}_i\mathrm{and}{\mathsf{{\rm Y}}}^{\prime }:=\mathcal{V}=\underset{j\in J}{⟂}{\mathcal{V}}_j^{\prime }$$

be two decompositions of $\mathcal{V}$ as the orthogonal direct sums of linear subspaces. It is said that Υ and ${\mathrm{{\rm Y}}}^{\prime }$ are equivalent if there exists an automorphism $\varphi :\mathcal{V}\to \mathcal{V}$, and a bijection $\sigma :I\to J$, such that $\varphi \left({\mathcal{V}}_i\right)={\mathcal{V}}_{\sigma \left(i\right)}^{\prime }$ for all $i\in I$.

Theorem 3. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$. Then, for the two bases $\mathcal{B}:={\left\{v_i\right\}}_{i\in I}$ and ${\mathcal{B}}^{\prime }:={\{v_j^{\prime }\}}_{j\in J}$ of $\mathcal{V}$, consider the following assertions:

i.

The bases $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ are f-equivalent.

ii.

The graphs $\Gamma (f,\mathcal{B})$ and $\Gamma (f,{\mathcal{B}}^{\prime })$ are isomorphic.

iii.

The decomposition of the linear operator $f:\mathcal{V}\to \mathcal{V}$ with respect to $\mathcal{B}$ is

$$\mathsf{{\rm Y}}:=\mathcal{V}=\underset{\left[v_i\right]\in V/\sim }{⟂}{\mathcal{V}}_{{\mathcal{C}}_{\left[v_i\right]}},$$

given by

$$f=\sum _{i\in I}{f}_i,$$

with $f_i{{|}_{{\mathcal{V}}_{{\mathcal{C}}_{\left[v_i\right]}}}=f|}_{{\mathcal{V}}_{{\mathcal{C}}_{\left[v_i\right]}}}$, $f_i({\mathcal{V}}_{{\mathcal{C}}_{\left[v_i\right]}})\subset {\mathcal{V}}_{{\mathcal{C}}_{\left[v_i\right]}}$, $f_i({\perp }_{i\ne k}{\mathcal{V}}_{{\mathcal{C}}_{\left[v_k\right]}})=0,$ and the decomposition of f with respect to ${\mathcal{B}}^{\prime }$ being

$${\mathsf{{\rm Y}}}^{\prime }:=\mathcal{V}=\underset{\left[v_j^{\prime }\right]\in V^{\prime }/\sim }{⟂}{\mathcal{V}}_{{\mathcal{C}}_{\left[v_j^{\prime }\right]}^{\prime }},$$

performed by

$$f=\sum _{j\in J}{f}_j^{\prime }$$

with $f_j^{\prime }{|}_{{\mathcal{V}}_{{\mathcal{C}}_{\left[v_j^{\prime }\right]}^{\prime }}}=f{|}_{{\mathcal{V}}_{{\mathcal{C}}_{\left[v_j^{\prime }\right]}^{\prime }}}$, $f_j^{\prime }({\mathcal{V}}_{{\mathcal{C}}_{\left[v_j^{\prime }\right]}^{\prime }})\subset {\mathcal{V}}_{{\mathcal{C}}_{\left[v_j^{\prime }\right]}^{\prime }}$, $f_j^{\prime }({\perp }_{i\ne k}{\mathcal{V}}_{{\mathcal{C}}_{\left[v_k^{\prime }\right]}^{\prime }})=0,$ are equivalent.

Then, i. implies ii. and iii.

Proof. 

The implication from i. to ii. was shown in Lemma 1. Let us prove the implication from i. to iii. Suppose that $\varphi :\mathcal{V}\to \mathcal{V}$ is an automorphism satisfying $\varphi \left(\mathcal{B}\right)={\mathcal{B}}^{\prime }$ and $\varphi \circ f=f\circ \varphi$. By the implication from i. to ii., we know that $\Gamma (f,\mathcal{B})$ and $\Gamma (f,{\mathcal{B}}^{\prime })$ are isomorphic via $\varphi$, and thus $\varphi \left(\right[v\left]\right)=\left[\varphi \right(v\left)\right]$ for all $v\in V=\mathcal{B}$. It follows that $\varphi ({\mathcal{V}}_{{\mathcal{C}}_{\left[v\right]}})={\mathcal{V}}_{{\mathcal{C}}_{\left[\varphi \right(v\left)\right]}}$ for all $\left[v\right]\in V/\sim$, which proves that the decomposition of $\mathcal{V}$ corresponding to $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ are equivalent. □

Remark 1.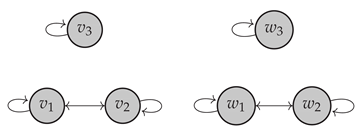 

In general, the implication of ii. to i. of Theorem 3 (as well the converse of Lemma 1) is not valid. That is, the fact that the graphs associated with the two bases are isomorphic does not imply that these two bases are f-equivalent. Let $\mathcal{V}$ be a pre-Euclidean space with the basis $\mathcal{B}:=\{v_1,v_2,v_3\}$, endowed with a bilinear form defined as

$$\langle v_1,v_1\rangle =\langle v_2,v_2\rangle =\langle v_3,v_3\rangle =\langle v_1,v_2\rangle :=1$$

and zero on the rest. By denoting $w_1:=v_1+v_2$, $w_2:=v_1-v_2$, and $w_3:=v_3$, we consider the basis ${\mathcal{B}}^{\prime }:=\{w_1,w_2,w_3\}$; thus, we obtain

$$\langle w_1,w_1\rangle =3,\langle w_2,w_2\rangle =\langle w_3,w_3\rangle =\langle w_2,w_1\rangle =1,\langle w_1,w_2\rangle =-1.$$

Therefore, for a zero linear operator f, the associated graphs $\Gamma (f,\mathcal{B})$ and $\Gamma (f,{\mathcal{B}}^{\prime })$ are isomorphic:

However, $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ are not f-equivalent. Indeed, if there exists an isomorphism $\varphi :\mathcal{V}\to \mathcal{V}$, such that $\varphi \left(\mathcal{B}\right)={\mathcal{B}}^{\prime }$, we get, for instance,

$$\varphi \left(v_1\right):=w_1,\varphi \left(v_2\right):=w_3,\varphi \left(v_3\right):=w_2,$$

but $0=\langle v_1,v_3\rangle \ne \langle \varphi \left(v_1\right),\varphi \left(v_3\right)\rangle =\langle w_1,w_2\rangle =-1.$

5. Characterization of the Minimality and Weak Symmetry

Let $(V,E)$ be a graph. Given $v_i,v_j\in V$, we say that a directed path from $v_i$ to $v_j$ is a sequence of vertices $(v_{i_1},\dots ,v_{i_n})$ satisfying $v_{i_1}=v_i$ and $v_{i_n}=v_j$, such that $(v_{i_r},v_{i_{r+1}})\in E$, for $1\le r\le n-1$. We also say that $(V,E)$ is symmetric if $(v_i,v_j)\in E$ for all $(v_j,v_i)\in E$. Thus, we present the next (weaker) concept in the following section.

Definition 8. 

A graph $(V,E)$ is weakly symmetric if, for any $(e_j,e_i)\in E$, there exists a directed path from $e_i$ to $e_j$.

Of course, every symmetric graph is weakly symmetric.

Example 9. 

The following graphs are weakly symmetric: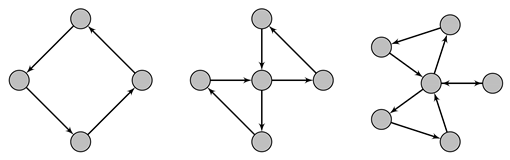

Definition 9. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with a basis $\mathcal{B}$. We say that $\mathcal{V}$ is minimal if the unique pre-Euclidean subspaces U admit an inherited basis from $\mathcal{B}$, such that $f\left(U\right)\subset U$ are $\left\{0\right\},\mathcal{V}$.

Theorem 4. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with the basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$. If $\mathcal{V}$ is minimal, then the associated graph $\Gamma (f,\mathcal{B})$ of f relative to $\mathcal{B}$ is weakly symmetric.

Proof.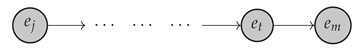 

If $\mathcal{V}$ is minimal, we know that $\mathcal{V}$ is the unique non-zero pre-Euclidean subspace that satisfies $f\left(\mathcal{V}\right)\subset \mathcal{V}$. Let $\Gamma (f,\mathcal{B}):=(V,E)$ be the associated graph and take some $(e_i,e_j)\in E$. Therefore, either $\langle e_i,e_j\rangle \ne 0$ or $\langle e_j,e_i\rangle \ne 0$ or $f\left(e_i\right)={\sum }_j{\lambda }_j{e}_j$ for some $0\ne {\lambda }_j\in \mathbb{F}$. The first two cases imply $(e_j,e_i)\in E$. In the last case, we have $f\ne 0$. Let us now define

$${\mathcal{B}}_j:=\{e_k\in \mathcal{B}:e_k=e_j \mathrm{or} \mathrm{there} \mathrm{exists} \mathrm{a} \mathrm{directed} \mathrm{path} \mathrm{from} e_j \mathrm{to} e_k\}.$$

As $e_j\in {\mathcal{B}}_j$, we have ${\mathcal{B}}_j\ne \varnothing$. Thus, let U be the space spanned by ${\mathcal{B}}_j$. Let $e_t\in {\mathcal{B}}_j$ and $f\left(e_t\right)={\sum }_m{\lambda }_m{e}_m$. If ${\lambda }_m\ne 0$, we get $(e_t,e_m)\in E$, and hence, there exists a directed path from $e_j$ to $e_m$:

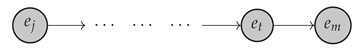
Thus, it implies $e_m\in {\mathcal{B}}_j$, and therefore, $f\left(U\right)\subset U$. As ${\mathcal{B}}_j\ne \varnothing$ and $\mathcal{V}$ is minimal, we have $U=\mathcal{V}$, so we conclude ${\mathcal{B}}_j=\mathcal{B}$ and $e_i\in {\mathcal{B}}_j$. Thus, there exists a directed path from $e_j$ to $e_i$, as required. □

Corollary 2. 

Let $f:\mathcal{V}\to \mathcal{V}$ be a linear operator in a pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ with the basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$. If $\mathcal{V}$ is minimal, then the associated graph $\Gamma (f,\mathcal{B})$ of f relative to $\mathcal{B}$ is connected.

Proof. 

This is an immediate consequence of Corollary 1 and Theorems 1 and 2. □

Remark 2. 

In general, the converse of the previous results are not valid. As a counterexample, let $(\mathcal{V},\langle ·,·\rangle )$ be the pre-Euclidean space over $\mathbb{R}$, with the basis $\mathcal{B}:=\{e_1,e_2,e_3,e_4\}$ and a bilinear form, given as

$$\langle e_1,e_2\rangle =\langle e_2,e_3\rangle =\langle e_3,e_4\rangle =\langle e_4,e_1\rangle :=1.$$

Let $f:\mathcal{V}\to \mathcal{V}$ be the linear operator, defined as $f\left(e_i\right):=e_i$ for $i\in \{1,2,3,4\}$. Then, $\mathcal{V}$ is not minimal, as, for instance, the pre-Euclidean subspace U with inherited basis $\left\{e_1\right\}$ from $\mathcal{B}$ satisfies $f\left(U\right)\subset U$. However, the associated graph $\Gamma (f,\mathcal{B})$ is clearly connected and weakly symmetric: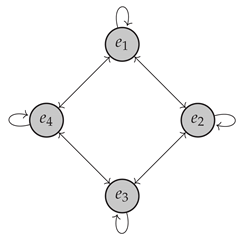

6. Conclusions

We were motivated by the following situation: If we consider a family of linear operators

$${\{f_i:{\mathcal{V}}_i\to {\mathcal{V}}_i\}}_{i\in I},$$

where any $V_i$ is a pre-Euclidean space, we can then naturally construct a new linear operator

$$f:\underset{i\in I}{⨁}{\mathcal{V}}_i\to \underset{i\in I}{⨁}{\mathcal{V}}_i$$

as $f={\sum }_{i\in I}{f}_i$, where $\mathcal{V}:={⨁}_{i\in I}{\mathcal{V}}_i$ is the pre-Euclidean space defined by componentwise operations.

In this paper, our purpose was to study the converse problem, and we gave a positive answer by proving in Theorem 2 that, given a linear operator $f:\mathcal{V}\to \mathcal{V}$ in a pre-Euclidean space, it is possible to find a family of pre-Euclidean spaces ${\left\{{\mathcal{V}}_i\right\}}_{i\in I}$, and a family of linear operators ${\{f_i:{\mathcal{V}}_i\to {\mathcal{V}}_i\}}_{i\in I}$ in such a way that $\mathcal{V}={\perp }_{i\in I}{\mathcal{V}}_i$ and $f={\sum }_{i\in I}{f}_i$. In order to approach our question, we used the technique of graphs. This allowed us to obtain the above decomposition of the pre-Euclidean space $\mathcal{V}$ and linear operator f in a very practical way, by simply looking at the graph $\Gamma (F,\mathcal{B})$ associated to f (and a fixed basis $\mathcal{B}$). In addition, the minimality of our structure was characterized in Theorem 4, which states that, for a linear operator $f:\mathcal{V}\to \mathcal{V}$ in a minimal pre-Euclidean space $(\mathcal{V},\langle ·,·\rangle )$ (with the basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$), then the associated graph $\Gamma (f,\mathcal{B})$ to f relative to $\mathcal{B}$ is weakly symmetric.

Finally, we would like to note that future research on this topic should work to generalize this result for different classes of operators (not necessarily linear operators) and consider operators on structures different from pre-Euclidean spaces (for instance, Banach spaces).