A Differential Flatness-Based Model Predictive Control Strategy for a Nonlinear Quarter-Car Active Suspension System
Abstract
1. Introduction
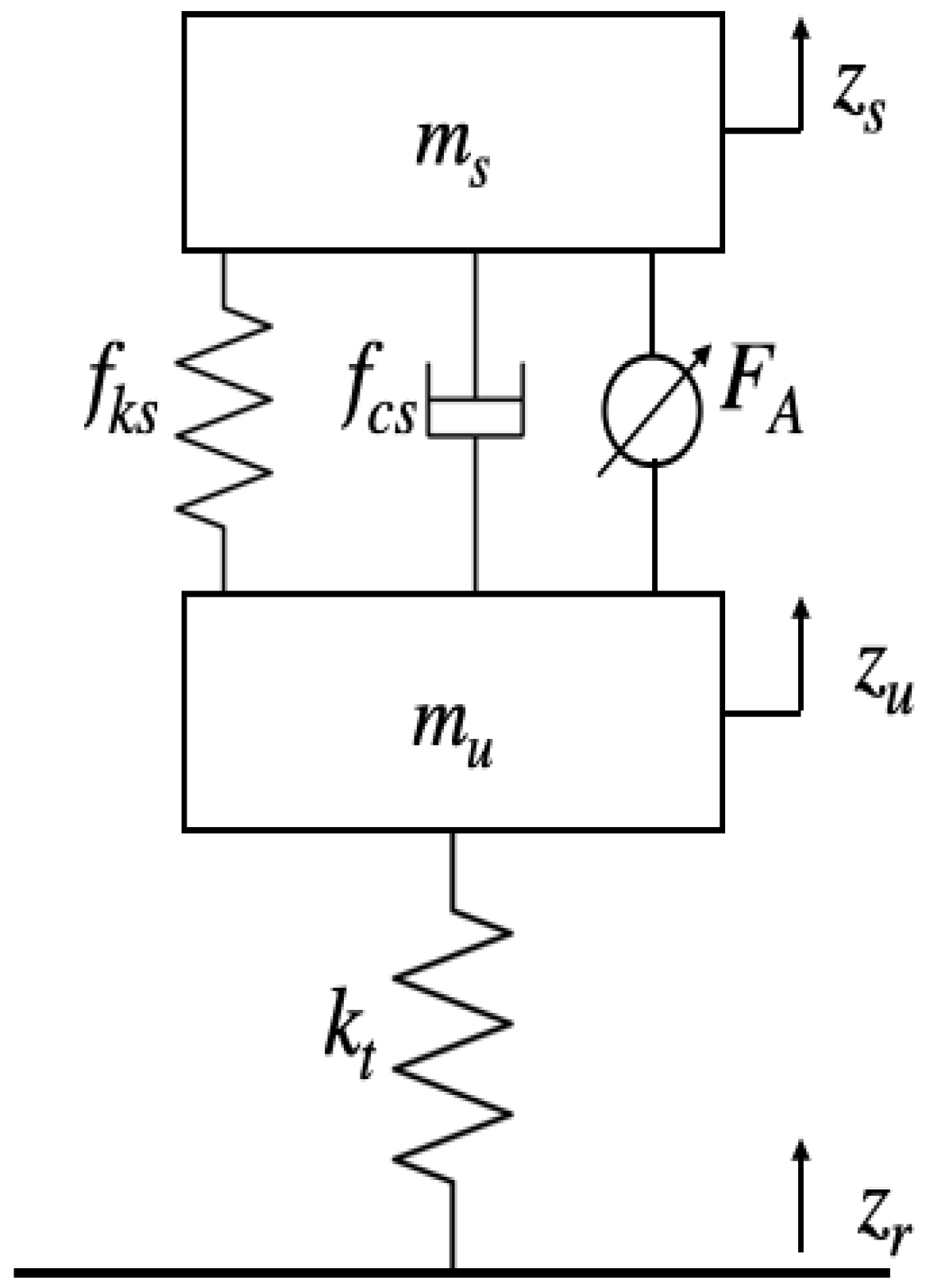
2. Nonlinear Quarter-Car Active Suspension System
3. Differential Flatness Representation
4. Model Predictive Control Based on Differential Flatness
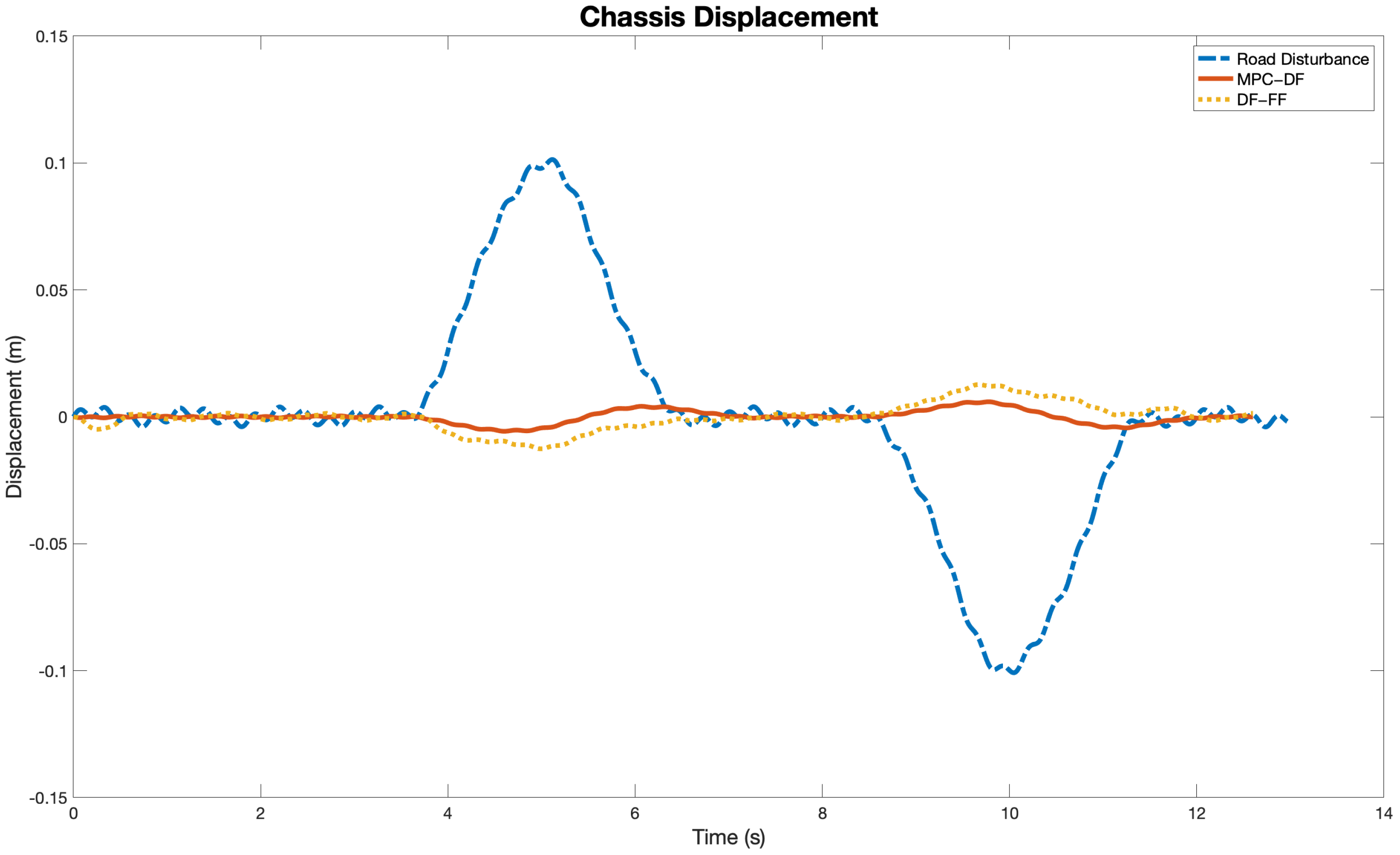
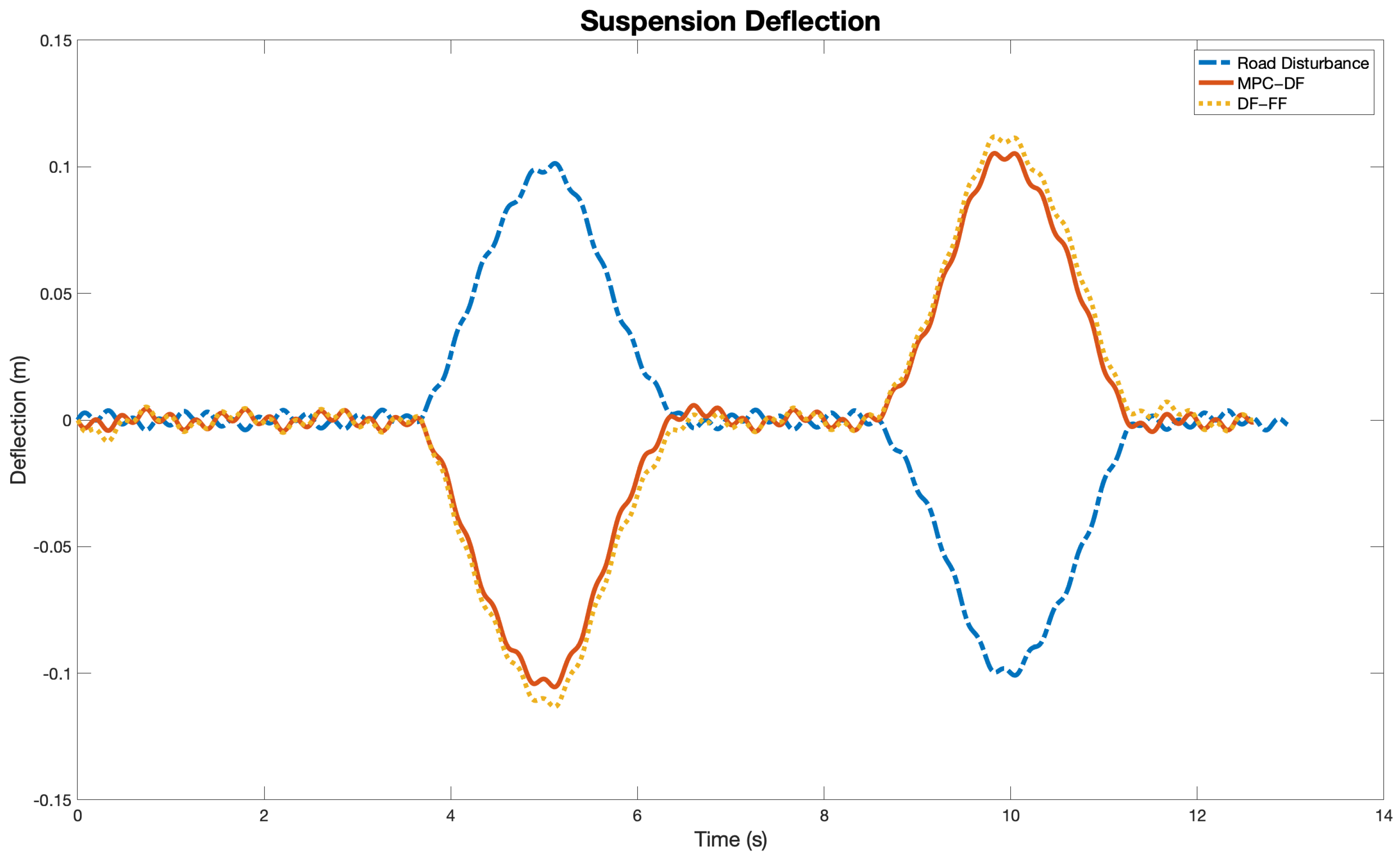
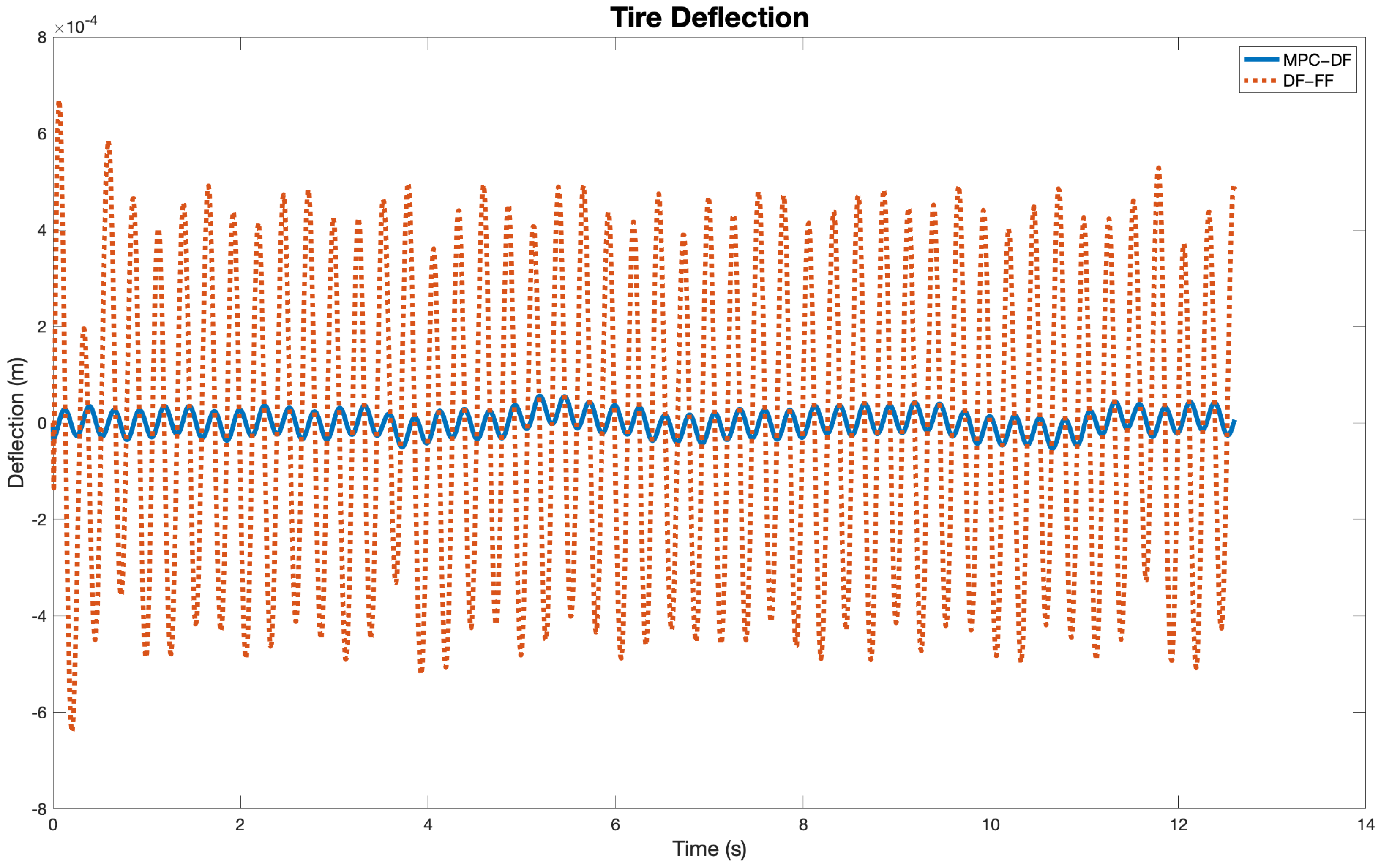
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phu, D.X.; An, J.-H.; Choi, S.-B. A Novel Adaptive PID Controller with Application to Vibration Control of a Semi-Active Vehicle Seat Suspension. Appl. Sci. 2017, 7, 1055. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Abidou, D.; Maged, S.A. LQR and PID Controllers Performance on a Half Car Active Suspension System. In Proceedings of the 2021 International Mobile, Intelligent, and Ubiquitous Computing Conference (MIUCC), El Cairo, Egypt, 26 May 2021; pp. 48–53. [Google Scholar]
- Zhao, L.; Zeng, Z.; Wang, Z.; Ji, C. PID control of vehicle active suspension based on particle Swarm optimization. J. Phys. Conf. Ser. 2020, 1748, 032028. [Google Scholar] [CrossRef]
- Shafiei, B. A Review on PID Control System Simulation of the Active Suspension System of a Quarter Car Model While Hitting Road Bumps. J. Inst. Eng. India Ser. C 2022, 103, 1001–1011. [Google Scholar] [CrossRef]
- Luo, J.; Pang, H.; Wang, M.; Yao, R. PI Observer-Based Fault-Tolerant Tracking Controller for Automobile Active Suspensions. IEEE Access 2022, 10, 47203–47218. [Google Scholar] [CrossRef]
- Afshar, K.K.; Javadi, A.; Jahed-Motlagh, M.R. Robust H∞ control of an active suspension system with actuator time delay by predictor feedback. IET Control. Theory Appl. 2018, 12, 1012–1023. [Google Scholar] [CrossRef]
- Kaleemullah, M.; Faris, W.; Ghazaly, N.M. Analysis of active suspension control policies for vehicle using robust controllers. Int. J. Adv. Sci. Technol. 2019, 28, 836–855. [Google Scholar]
- Pham, T.P.; Tran, G.Q.B.; Sename, O.; Van Phan, T.T.; Hoang, D.; Nguyen, Q.D. Real-time Damper Force Estimation for Automotive Suspension: A Generalized H2/LPV Approach. Period. Polytech. Transp. Eng. 2022, 50, 309–317. [Google Scholar] [CrossRef]
- Ma, X.; Wong, P.K.; Li, W.; Zhao, J.; Ghadikolaei, M.A.; Xie, Z. Multi-objective H 2/H∞ control of uncertain active suspension systems with interval time-varying delay. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2022. [Google Scholar] [CrossRef]
- Alfadhli, A.; Darling, J.; Hillis, A.J. The Control of an Active Seat Suspension Using an Optimised Fuzzy Logic Controller, Based on Preview Information from a Full Vehicle Model. Vibration 2018, 1, 20–40. [Google Scholar] [CrossRef]
- Avesh, M.; Srivastava, R.; Sharma, R.C.; Sharma, N. Effective design of active suspension system using fuzzy logic control approach. Int. J. Veh. Struct. Syst. 2019, 11, 536–539. [Google Scholar] [CrossRef]
- Yatak, M.Ö.; Şahin, F. Ride comfort-road holding trade-off improvement of full vehicle active suspension system by interval type-2 fuzzy control. Eng. Sci. Technol. Int. J. 2021, 24, 259–270. [Google Scholar] [CrossRef]
- Anh, N.T. Control an active suspension system by using PID and LQR controller. Int. J. Mech. Prod. Eng. Res. Dev. 2021, 10, 7003–7012. [Google Scholar]
- Yu, W.; Li, J.; Yuan, J.; Ji, X. LQR controller design of active suspension based on genetic algorithm. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 15 October 2021; Volume 5, pp. 1056–1060. [Google Scholar]
- Thi Thu Huong, T.; Tuan Anh, N.; Thang Binh, H.; Duc Ngoc, N.; Ngoc Duyen, D. Optimizing the Parameter of the LQR Controller for Active Suspension System. In Proceedings of the The AUN/SEED-Net Joint Regional Conference in Transportation, Energy, and Mechanical Manufacturing Engineering, RCTEMME 2021, Singapore, 1 June 2022. [Google Scholar]
- Taghavifar, H.; Mardani, A.; Hu, C.; Qin, Y. Adaptive robust nonlinear active suspension control using an observer-based modified sliding mode interval type-2 fuzzy neural network. IEEE Trans. Intell. Veh. 2019, 5, 53–62. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Fayaz, M. Hybrid Modelling and Sliding Mode Control of Semi-Active Suspension Systems for Both Ride Comfort and Road-Holding. Symmetry 2020, 12, 1286. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Fayaz, M.; Qureshi, M.S.; Boujoudar, Y. Hybrid sliding mode control of full-car semi-active suspension systems. Symmetry 2021, 13, 2442. [Google Scholar] [CrossRef]
- Theunissen, J.; Sorniotti, A.; Gruber, P.; Fallah, S.; Ricco, M.; Kvasnica, M.; Dhaens, M. Regionless explicit model predictive control of active suspension systems with preview. IEEE Trans. Ind. Electron. 2019, 67, 4877–4888. [Google Scholar] [CrossRef]
- Narayan, J.; Gorji, S.A.; Ektesabi, M.M. Power reduction for an active suspension system in a quarter car model using MPC. In Proceedings of the IEEE International Conference on Energy Internet (ICEI), Sydney, Australia, 24–28 August 2020; pp. 140–146. [Google Scholar]
- Piñón, A.; Favela-Contreras, A.; Félix-Herrán, L.C.; Beltran-Carbajal, F.; Lozoya, C. An ARX Model-Based Predictive Control of a Semi-Active Vehicle Suspension to Improve Passenger Comfort and Road-Holding. Actuators 2021, 10, 47. [Google Scholar] [CrossRef]
- Yao, J.; Wang, M.; Li, Z.; Jia, Y. Research on model predictive control for automobile active tilt based on active suspension. Energies 2021, 14, 671. [Google Scholar] [CrossRef]
- Enders, E.; Burkhard, G.; Munzinger, N. Analysis of the Influence of Suspension Actuator Limitations on Ride Comfort in Passenger Cars Using Model Predictive Control. Actuators 2020, 9, 77. [Google Scholar] [CrossRef]
- Göhrle, C.; Schindler, A.; Wagner, A.; Sawodny, O. Model predictive control of semi-active and active suspension systems with available road preview. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 1499–1504. [Google Scholar]
- Rathai, K.M.M.; Alamir, M.; Sename, O.; Tang, R. A parameterized NMPC scheme for embedded control of semi-active suspension system. IFAC-PapersOnLine 2018, 51, 301–306. [Google Scholar] [CrossRef]
- Dalboni, M.; Tavernini, D.; Montanaro, U.; Soldati, A.; Concari, C.; Dhaens, M.; Sorniotti, A. Nonlinear model predictive control for integrated energy-efficient torque-vectoring and anti-roll moment distribution. IEEE/ASME Trans. Mechatronics 2021, 26, 1212–1224. [Google Scholar] [CrossRef]
- Pedro, J.O.; Nhlapo, S.M.; Mpanza, L.J. Model predictive control of half-car active suspension systems using particle swarm optimisation. IFAC-PapersOnLine 2020, 53, 14438–14443. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, D.; Gong, M.; Yang, B. Research on robust model predictive control for electro-hydraulic servo active suspension systems. IEEE Access 2017, 6, 3231–3240. [Google Scholar] [CrossRef]
- Rodriguez-Guevara, D.; Favela-Contreras, A.; Beltran-Carbajal, F.; Sotelo, D.; Sotelo, C. Active Suspension Control Using an MPC-LQR-LPV Controller with Attraction Sets and Quadratic Stability Conditions. Mathematics 2021, 9, 2533. [Google Scholar] [CrossRef]
- Rodriguez-Guevara, D.; Favela-Contreras, A.; Beltran-Carbajal, F.; Sotelo, C.; Sotelo, D. An MPC-LQR-LPV Controller with Quadratic Stability Conditions for a Nonlinear Half-Car Active Suspension System with Electro-Hydraulic Actuators. Machines 2022, 10, 137. [Google Scholar] [CrossRef]
- Morato, M.M.; Normey-Rico, J.E.; Sename, O. Novel qLPV MPC design with least-squares scheduling prediction. IFAC-PapersOnLine 2019, 52, 158–163. [Google Scholar] [CrossRef]
- Morato, M.M.; Normey-Rico, J.E.; Sename, O. Short-sighted robust lpv model predictive control: Application to semi-active suspension systems. In Proceedings of the 2021 European Control Conference (ECC), Delft, The Netherlands, 29 June 2021; pp. 1525–1530. [Google Scholar]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Chavez-Conde, E.; Favela-Contreras, A.; Chavez-Bracamontes, R. Active nonlinear vehicle suspension control based on real-time estimation of perturbation signals. In Proceedings of the 2011 IEEE International Conference on Industrial Technology, Auburn, AL, USA, 14 March 2011; pp. 437–442. [Google Scholar]
- Diwakar, A.D.; Manivannan, P.V. Differential flatness based LQR control of a magnetorheological damper in a quarter-car semi-active suspension system. Int. J. Mech. Eng. Robot Res. 2020, 9. [Google Scholar] [CrossRef]
- Darus, R.B. Modeling and Control of Active Suspension for a Full Car Model; Faculty of Electrical Engineering, University of Technology Malaysia: Skudai, Malaysia, 2008. [Google Scholar]
- Chávez Conde, E.; Beltrán Carbaja, F.; Valderrábano González, A.; Favela Contreras, A. Active vibration control of vehicle suspension systems using sliding modes, differential flatness and generalized proportional-integral control. Rev. Fac. Ing. Univ. Antioq. 2011, 61, 104–113. [Google Scholar]
- Velagić, J.; Hrusto, A. Design of coupled disturbance observers for nonlinear half-car active suspension system. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3 July 2017; pp. 547–552. [Google Scholar]
- Mauledoux, M.M.; Caldas, O.I.; Avilés, O.F.; Mejía-Ruda, E.; Jiménez, S. A hybrid differential flatness and sliding modes controller for dynamical structural testing on lower limp prostheses. Appl. Mech. Mater. 2015, 713, 777–780. [Google Scholar]
- Conde, E.C.; Carbajal, F.B.; González, A.V.; Bracamontes, R.C. Robust control of active vehicle suspension systems using sliding modes and differential flatness with MATLAB. In MATLAB for Engineers-Applications in Control; Electrical Engineering, IT and Robotics; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar]
- Lin, B.; Su, X.; Li, X. Fuzzy sliding mode control for active suspension system with proportional differential sliding mode observer. Asian J. Control 2019, 21, 264–276. [Google Scholar] [CrossRef]
- Xia, Y.; Lin, M.; Zhang, J.; Fu, M.; Li, C.; Li, S.; Yang, Y. Trajectory planning and tracking for four-wheel steering vehicle based on differential flatness and active disturbance rejection controller. Int. J. Adapt. Control Signal Process. 2021, 35, 2214–2244. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Valderrabano-Gonzalez, A.; Favela-Contreras, A.R.; Rosas-Caro, J.C. Active disturbance rejection control of a magnetic suspension system. Asian J. Control 2015, 17, 842–854. [Google Scholar] [CrossRef]
- Rigatos, G.G. Nonlinear Control and Filtering Using Differential Flatness Approaches: Applications to Electromechanical Systems; Springer: Berlin/Heidelberg, Germany, 2015; Volume 25. [Google Scholar]
- Tahboub, K.A. Active nonlinear vehicle-suspension variable-gain control. In Proceedings of the 2005 IEEE International Symposium on, Mediterranean Conference on Control and Automation Intelligent Control, Limassol, Cyprus, 27 June 2005; pp. 569–574. [Google Scholar]
- Chen, P.C.; Huang, A.C. Adaptive sliding control of non-autonomous active suspension systems with time-varying loadings. J. Sound Vib. 2005, 282, 1119–1135. [Google Scholar] [CrossRef]




| Symbol | Value | Units |
|---|---|---|
| 216.75 | kg | |
| 28.85 | kg | |
| 21,700 | N/m | |
| 1200 | N·s/m | |
| 2170 | N/m | |
| 120 | N·s/m | |
| 184,000 | N/m |
| Controller | Chassis Displacement (m) | Suspension Deflection (m) | Chassis Acceleration (m/s) | Tire Deflection (cm) |
|---|---|---|---|---|
| MPC-DF | 0.0050 | 0.1054 | 1.3896 | 0.0056 |
| DF-FF | 0.0126 | 0.1129 | 1.3872 | 0.0549 |
| Controller | Chassis Displacement (m) | Suspension Deflection (m) | Chassis Acceleration (m/s) | Tire Deflection (cm) |
|---|---|---|---|---|
| MPC-DF | 0.0021 | 0.0436 | 0.7935 | 0.0024 |
| DF-FF | 0.0053 | 0.0471 | 0.7903 | 0.0269 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Guevara, D.; Favela-Contreras, A.; Beltran-Carbajal, F.; Sotelo, C.; Sotelo, D. A Differential Flatness-Based Model Predictive Control Strategy for a Nonlinear Quarter-Car Active Suspension System. Mathematics 2023, 11, 1067. https://doi.org/10.3390/math11041067
Rodriguez-Guevara D, Favela-Contreras A, Beltran-Carbajal F, Sotelo C, Sotelo D. A Differential Flatness-Based Model Predictive Control Strategy for a Nonlinear Quarter-Car Active Suspension System. Mathematics. 2023; 11(4):1067. https://doi.org/10.3390/math11041067
Chicago/Turabian StyleRodriguez-Guevara, Daniel, Antonio Favela-Contreras, Francisco Beltran-Carbajal, Carlos Sotelo, and David Sotelo. 2023. "A Differential Flatness-Based Model Predictive Control Strategy for a Nonlinear Quarter-Car Active Suspension System" Mathematics 11, no. 4: 1067. https://doi.org/10.3390/math11041067
APA StyleRodriguez-Guevara, D., Favela-Contreras, A., Beltran-Carbajal, F., Sotelo, C., & Sotelo, D. (2023). A Differential Flatness-Based Model Predictive Control Strategy for a Nonlinear Quarter-Car Active Suspension System. Mathematics, 11(4), 1067. https://doi.org/10.3390/math11041067







