Abstract
We consider a discrete-time single server queueing system, where arrivals stem from a multi-type Galton–Watson branching process with migration. This branching-type arrival process exhibits intricate correlation, and the performance of the corresponding queueing process can be assessed analytically. We find closed-form expressions for various moments of both the queue content and packet delay. Close inspection of the arrival process at hand, however, reveals that sample paths consist of large independent bursts of arrivals followed by geometrically distributed periods without arrivals. Allowing for non-geometric periods without arrivals, and correlated bursts, we apply -thinning on the arrival process. As no closed-form expressions can be obtained for the performance of the corresponding queueing system, we focus on approximations of the main performance measures in the light and heavy traffic regimes.
MSC:
60K25
1. Introduction
Input traffic at intermediate routers in packet-switched communication networks typically exhibits considerable time correlation. Similar arrival correlation is also observed for arrival processes of goods or customers at queues in manufacturing and logistic systems. Correlated arrivals lead to increased variability in the arrival rate, which can make it more difficult to predict and manage the flow of goods and customers through the system. This results in longer queues, increased waiting times, and reduced system capacity. Moreover, correlated arrivals can also lead to increased variability in the utilization of resources, which in turn leads to increased maintenance costs and decreased efficiency.
Arrival correlation significantly affects queueing performance [1], and there is a continuing interest in analytically tractable queueing models with arrival correlation. Models of interest include, in particular, Markovian arrival models. Such models may have a finite state space, such as the discrete-time batch-Markovian arrival model [2,3,4], or a structured infinite state space, such as the discrete autoregressive arrival models [5,6] and the train and session arrival models [7,8]. For queues with an unstructured finite state space arrival model, the performance measures of interest are typically not available in closed form. Instead, numerically efficient algorithms are devised that yield the numerical values of the various performance measures once all model parameters are specified. In contrast, for some models with infinite state spaces, structural properties of the state space allow for expressions of the performance measures of interest in closed form.
In this paper, a Markovian arrival process is proposed with an infinite state space that is both structured and multi-dimensional: the Galton–Watson arrival process. More precisely, we assess the performance of a discrete-time queueing system, where the arrivals during the time slots are modeled as the size of the consecutive generations in multi-type Galton–Watson branching processes with migration [9,10,11,12]. Galton–Watson branching processes were originally investigated to study the extinction of family names, and constitute a convenient abstraction for modeling the evolution of populations over time. Some recent applications of branching processes include pandemic spread [13], in vitro bactericidal potency [14], antibody affinity maturation [15], the dismantling of terrorist networks [16] and earthquake occurrence [17].
The main motivation for studying queues with Galton–Watson arrival processes stems from a combination of the analytical tractability of the queue content and packet delay and the observation that this arrival process exhibits intricate arrival correlation. The arrival process at hand generalizes train arrival models [7,8] with phase-type distributed train lengths. Moreover, there is a connection between branching processes and Hawkes processes, which can serve as arrival processes in infinite server queues [18,19]. Not unlike train and session arrival models, the Galton–Watson model is in a fixed state when there are no arrivals. It is, in fact, this property which enables closed-form expressions for the moments of the queue content and delay [20]. This also implies that periods without arrivals are geometrically distributed, and that the single-server queue is overloaded whenever there are arrivals. To overcome these rather stringent assumptions, we also investigate the queueing system with branching arrivals after applying -thinning on the arrival process. With -thinning, each packet arrival is discarded with a fixed probability so that the state of the arrival process is no longer fixed in the absence of arrivals. Unfortunately, no closed-form expressions can be obtained for the performance of the corresponding queueing system. Therefore, we focus on the light traffic and heavy traffic regimes. Our approach extends the results of [21], which investigated -thinning of a queue with geometric train arrivals.
While Galton–Watson arrival processes are new, various queueing processes can be modeled as multi-type branching processes. First, the time till extinction in a branching process relates to busy periods in queues [22,23]. The branching property here follows from the observation that during a customer’s service, new customers arrive that bring additional work. Secondly, many polling systems can be modeled as multi-type branching processes [24,25,26], the branching property of polling disciplines being a key facilitator of the analysis [27]. Finally, multi-type branching processes can also model the dynamics of infinite server queues [28].
The remainder of the paper is organized as follows. In the next section, the assumptions and notation of the arrival process are introduced, as well as the queueing model at hand. Following a probability generating the functions approach in Section 3, we find expressions for performance measures of interest, such as the moments of the queue content and the waiting times. Our results are then illustrated by some numerical examples in Section 4, where we also discuss a simple arrival correlation fitting procedure. We then consider the branching arrival model subject to -thinning in the light traffic regime and heavy traffic regime in Section 5 and Section 6, respectively. Finally, conclusions are drawn in Section 7.
2. Queueing Model
We consider a discrete-time queueing system; time is divided into fixed-length intervals or slots. Incoming packets are stored in an unlimited buffer and serviced in the order they arrived, with fixed service times equal to the slot length. Service is synchronized with respect to slot boundaries, so packets cannot be serviced during their arrival slot.
Packet arrivals stem from a sub-critical multi-type Galton–Watson process with migration; the number of (arriving packet) types of this process is denoted by K, and the number of arriving packets of type k during slot n is denoted by . We can then express the number of arriving packets of type k during slot n in terms of the number of arrivals of the different types at the previous slot as follows:
Here, is the type k off-spring of the jth type i packet at slot , and denotes the number of new type k packets at slot n. The total number of packet arrivals during slot n is then simply the sum of the arrivals of the different types:
In (1), the vectors constitute a doubly indexed sequence of independent and identically distributed (iid) random vectors for all . To characterize this sequence, we need to specify the joint distribution or the joint probability generating function of the offspring of the different types for an arrival of type . Hence, the random vectors are completely characterized by the vector-valued joint probability generating function:
with . Similarly, the vectors constitute a sequence of iid random vectors, characterized by the common joint probability generating function:
Finally, we introduce notation for the mean offspring and migration of the different types. Let denote the mean type k offspring of a type i packet. Similarly, denotes the mean number of new type k arrivals in a slot. For notational convenience, we collect these averages in a matrix and in a column vector , respectively. With this notation, the mean number of arrivals in a slot equals
Here, denotes a row vector of ones and is the identity matrix. As we assume that the multi-type branching process is sub-critical, the spectral radius of is smaller than one. Hence, exists, and the mean arrival load is finite. This assumption will be retained in the following sections.
3. Queueing Analysis
With the notation of the arrival process established, we now focus on the queueing analysis. Let denote the queue content at the beginning of slot n. The queue contents at the beginning of consecutive slots are then related as follows:
Here, is the usual shorthand notation for .
The state of the queueing system at slot boundary n is completely described in the Markovian sense by the vector of state variables ; see Equations (1), (2) and (6). Following a standard Loynes-type argument [29], the Markov process exhibits a unique stationary (and limiting) distribution for . Recall that (5) expresses in terms of the parameters of the branching process with migration. Therefore, let denote the joint probability generating function of this vector in steady state:
In view of Equations (1), (2) and (6) and by standard z-transform techniques, it is found that satisfies the following functional equation:
Noting that implies and therefore also for , we have , with a row vector of zeros. The functional equation therefore simplifies to
The remaining unknown constant follows from the normalization condition . More precisely, multiplying both sides of Equation (8) by z and evaluating the first-order derivatives of the resulting expression in yields a system of linear equations for and for the derivatives . For , this system of equations has a unique solution. In particular, equals
This is not entirely unexpected, as represents the probability that the server is idle.
By recursive substitution, we can also obtain an explicit expression for the joint generating function . To this end, recursively define the row vector as follows:
for . Successive application of the functional Equation (8) then yields
Clearly, the probability generating function of the queue content equals . Additionally, the probability generating function for the queue content relates to the probability generating function for the packet delay. We can easily obtain the probability generating function for the packet delay (i.e., the number of slots between the arrival and departure of a packet) using the distributional form of Little’s result for discrete-time queues with single-slot service times [30]:
Finally, exploiting the moment-generating property of probability generating functions immediately yields expressions for the various moments of the queue content and packet delay. Note that expressions of the derivatives of in and can also be directly obtained by evaluating the derivatives of the functional Equation (8) in and . Compared to evaluating the derivatives of (10), such an approach is more convenient, as there is no need to evaluate the derivatives of the infinite sum.
4. Numerical Results
With the formulas at hand, we now investigate the mean delay of the queueing system with multi-type Galton–Watson arrivals. We focus on a simplified arrival model, where the arrivals stem from a two-type Galton–Watson model with neither migration between the types () nor correlation between the new arrivals of the different types. For this arrival process, we introduce a convenient parameter estimation procedure.
The load and the autocorrelation function of this arrival process are equal to
Here, is the variance of the number of type-i arrivals in a slot, and is the variance of the number of arrivals in a slot. Further, and denote the variances of and , respectively. To limit the number of parameters, assume that (i) is Bernoulli distributed such that and that (ii) and have the same index of dispersion (or variance-to-mean ratio), . Figure 1 displays the autocorrelation function of the arrival process for various parameter settings. The tangent in 0 and the asymptote are depicted as well in the logarithmic plot. These are given by
with . Here, we assumed , without loss of generality.
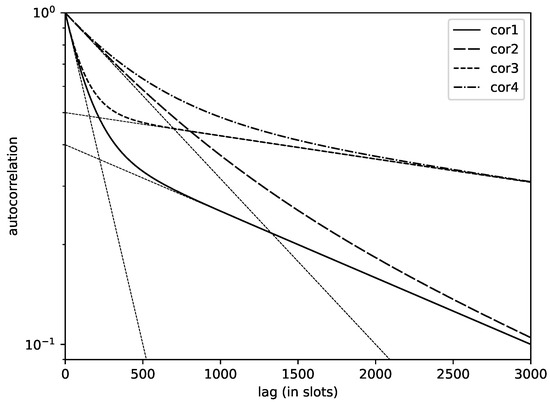
Figure 1.
Autocorrelation function of the arrival process for different parameter settings: = (0.4, 0.999538, 0.992660) for cor1, (0.4, 0.999538, 0.998391) for cor2, for (0.5, 0.999839, 0.990991) cor3 and (0.5, 0.999839, 0.997861) for cor4.
The selection of the tangent and asymptote can be used to find suitable parameters for the arrival process. Modifying the decay rate of the tangent and the asymptote changes the long- and short-time correlation in the arrival process. The selection of the tangent and asymptote uniquely determines the parameters , and , which, in turn, uniquely determine the autocorrelation function; see Equations (12) and (13). It now suffices to additionally fix the total arrival load and the variance of the number of arrivals in a slot . We can then express the remaining parameters , and in terms of , , , and :
where r is the unique root in of the quadratic equation:
The solution is a valid parameter set for the process at hand, provided that . This is possible provided that is sufficiently large, and a simple sufficient condition for that is .
Summarizing, the procedure above can be used to match the characteristics of the multi-type branching arrival process with the corresponding characteristics of a traffic trace. That is, parameter estimation for a given traffic trace reduces to (i) the estimation of the mean and variance of the number of arrivals in a slot and to (ii) estimating and for the empirical autocorrelation function of the trace.
Figure 2 displays the mean delay as a function of the arrival load , for an index of dispersion , and for the various autocorrelation curves from Figure 1. Recall that by using the estimation procedure described above, all arrival process parameters can be determined given the load, index of dispersion, and autocorrelation curve. Figure 2 illustrates the impact of the arrival correlation on the performance measures, highlighting the significant negative impact of a slow decay of the long-term correlation (cor3 and cor4) on system performance. Short-term correlation (cor2 and cor4) also results in performance degradation, although to a lesser extent than long-term correlation.
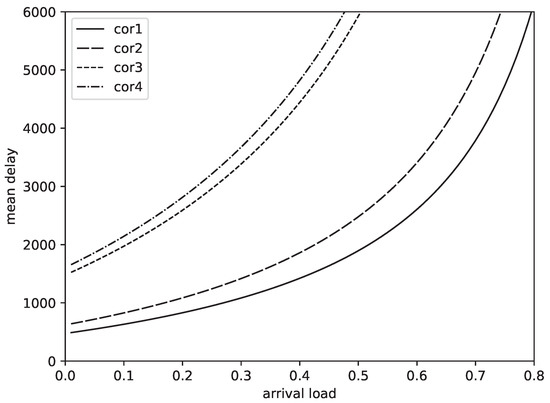
Figure 2.
Mean packet delay vs. the arrival rate for the parameter settings of Figure 1 and for an index of dispersion .
5. Light-Traffic Analysis
In the analysis of Section 3, it is key that implies for . More precisely, as the queue can only become empty when there are no new arrivals, the arrival process is always in state , when the queue becomes empty. Hence, we have , and one only needs to determine a constant instead of the unknown partial joint probability generating function .
While the modeling assumptions above allow for intricate correlation, the direct mapping of the population size on the number of arrivals does impose some limitations: whenever the total population size is larger than 1, the queue is overloaded, such that the arrival process will be in state most of the time for (which is needed for stability). Therefore, the present section considers the case where -thinning is applied to the arrival process. That is, each individual of the population in a slot will contribute a packet to the arrival process with probability q, and does not contribute to the arrival process with probability . The number of arrivals during slot n can therefore be expressed as
where is defined as before, see Equations (1) and (2), and where is a double-indexed sequence of independent Bernoulli-distributed random variables with success probability q. As in Section 3, let denote the queue content at the nth slot boundary, where the superscript makes the thinning probability q explicit. As a single packet departs in a slot, we again have
As for the queueing model without thinning, the process constitutes a Markov process. Let denote the probability generating function of the stationary distribution of the Markov process:
Using standard z-transform techniques, we find the following functional equation for this generating function:
In contrast to the model of Section 3, there is no straightforward solution for this functional equation. Therefore, we focus on the system’s performance in the light-traffic regime. More precisely, we determine the terms in the series expansion of around . To this end, we consider the following series expansion of :
Note that there are no terms in for . This follows from the so-called n-events rule. The nth term in the series expansion of the stationary probability of a state is zero if this state cannot be reached by at most nq-events from a state which is reachable for the case . In our case, q-events are arrivals, and the queue content cannot grow beyond n with at most n arrivals.
As is a probability function for each q, the normalization condition leads to the following normalization conditions for the terms :
We now show that we can recursively retrieve all derivatives of the terms in . Substituting the series expansion (18) in the functional Equation (17) yields
In order to compare terms in equal powers of q at both sides of the equation, we need to introduce the Maclaurin series expansion of the terms and . For the latter, the expansion reads
with,
In the expression above, the sum runs over all nth-order derivatives of N, and , , and are shorthands for,
for . The expansion of is somewhat more involved. First note, that
with,
Moreover, let be the vector with entries , . We can then use the multivariate extension of Faa di Bruno’s formula [31] to calculate the nth derivative of q in :
with,
and,
Finally, the Maclaurin series expansion reads
Substituting the expansions of and in (20) yields
The former expression now allows for identifying the coefficients of the terms , yielding
for and,
with
for and . Close inspection of the expression above shows that only depends on for . Moreover, as , we can retrieve all derivatives of in from the system of functional Equation (22) and the normalization condition (19) in terms of the derivatives of for . Summarizing, we can recursively determine all derivatives .
Once these terms have been found, it is now trivial to calculate the light-traffic approximation of the mean queue content. From the series expansion (18), we immediately find the following expression for the Kth-order expansion of the nth moment of the queue content:
Finally, note that, as for the system without -thinning, the distributional form of Little’s result applies. Hence, we can express moments of the delay in terms of moments of the queue content, and our approximation of the moments of the queue content can be used to approximate the moments of the delay.
To illustrate the light-traffic analysis, we reconsider the numerical example of Section 4, albeit with different parameters to ensure that the system is in overload, prior to -thinning. More specifically, we set , and . It then suffices to specify the variance of the number of arrivals in a slot and the thinning probability q to fully specify the arrival model. Figure 3 depicts the 7th-order light-traffic approximation of the mean delay as a function of the traffic load. The load is varied by varying the thinning probability q for fixed . To verify the accuracy of the light-traffic approximation, we also simulate the queueing system. The markers on the plot show the values of the mean delay as obtained by simulation. We rely on the deletion–replication approach (p. 241, [32]) with 100 replications of slots to assess the accuracy of the simulation results but omit the confidence intervals from the plot, as the upper and lower boundaries of the confidence intervals are visually indistinguishable. The first 1000 slots of each run are deleted to reduce bias, in line with the method of Welch (p. 238, [32]).
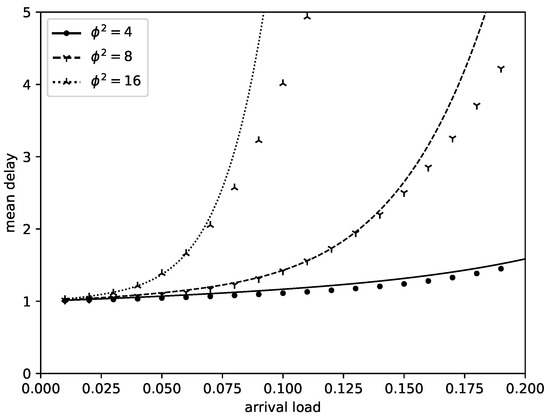
Figure 3.
Light-traffic approximation of the mean delay as a function of the load for different values of the arrival variance as indicated. The load is varied by varying the thinning probability.
Clearly, the light traffic approach is accurate for low loads, while the approximation deviates from the simulation results for higher loads. Additionally, more accurate results are obtained if the arrival variance is smaller. Additional experimentation with higher-order approximations shows that the approximation for low load further improves by increasing the order of the approximation, but this is not necessarily the case for higher load.
6. Heavy Traffic Approximation
In line of the arguments of the preceding section, we again apply -thinning on the Galton–Watson arrival process. As before, let q denote the probability that an individual in the population contributes a packet. While the preceding section considered the light-traffic regime, we now consider the heavy-traffic regime as pioneered by Kingman in the seminal paper [33]. To this end, we assume that the arrival rate prior to thinning exceeds 1, . In this case, the queue is not stable for , and we study the limit .
Following the exposition in chapter 9 of [34], the heavy traffic performance measures are given in terms of the load and the asymptotic variance V:
where is the stationary arrival process with -thinning with parameter . By the stationarity of the arrival process, the former expression simplifies to
We now express the variance V in terms of the process without -thinning. In view of the definition of , see Equation (14), we have
where is an independent Bernoulli random variable with success probability for each index n and ℓ. By conditioning on the unthinned arrival process and by noting that constitutes a doubly indexed sequence of independent and identically distributed random variables, the variance and covariances in the former expression simplify to
As is a Bernoulli random variable with success probability for each index n and ℓ, we have and such that
By conditioning on the number of arrivals of the different types in the consecutive slots, we have
where is the matrix of the mean offspring of the different types as introduced in Section 2 and where is a column vector of ones. Moreover, is the covariance matrix of the branching arrival process. We can easily express the covariance in terms of the joint probability generating function :
Having determined the asymptotic variance, we can now have the following expressions for the first two moments of the buffer content under heavy traffic:
To evaluate the accuracy of the heavy-traffic limit, we reconsider the numerical example of the light-traffic approximation: we set , and . Table 1 lists the values of the scaled queue content for different values of the load up to , as well as the corresponding heavy traffic limit value . The pre-limit values are obtained by simulation, using a replication–deletion approach with 100 replications, each replication simulating slots, where the first 1000 slots of each run are discarded to reduce the bias. Table 1 also lists the confidence interval. The results show that the scaled mean queue content indeed converges to the heavy traffic limit.

Table 1.
The scaled queue content for different values of the load , and the corresponding heavy traffic limit value .
7. Conclusions
This paper presented closed-form expressions for the probability generating functions of the queue content and packet delay in a discrete-time queueing system, where arrivals stem from a multi-type Galton–Watson branching process. The model is useful for analyzing buffers with significant arrival correlation, which was demonstrated by a parameter estimation procedure for a simplified Galton–Watson-type arrival process. We showed that the parameters of this simplified Galton–Watson-type arrival process for a given empirical auto-correlation function are easily estimated. Moreover, once these parameters are known, evaluating the relevant performance measures is straightforward. We then applied -thinning on the Galton–Watson arrival process. In contrast to the unthinned process, closed-form expressions for the various performance measures of interest are no longer available. We therefore studied the corresponding thinned queueing system in both the light-traffic and heavy-traffic regimes. Finally, to verify the accuracy of the approximations in these regimes, we simulated the queueing process with thinning.
Author Contributions
Conceptualization, D.F. and K.D.T.; methodology, D.F. and K.D.T.; software, D.F.; validation, D.F. and K.D.T.; formal analysis, D.F. and K.D.T.; writing—original draft preparation, D.F. and K.D.T.; writing—review and editing, D.F. and K.D.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schwefel, H.P.; Antonios, I.; Lipsky, L. Understanding the relationship between network traffic correlation and queueing behavior: A review based on the N-Burst ON/OFF model. Perform. Eval. 2017, 115, 68–91. [Google Scholar] [CrossRef]
- Blondia, C.; Casals, O. Statistical multiplexing of VBR sources: A matrix-analytic approach. Perform. Eval. 1992, 16, 5–20. [Google Scholar] [CrossRef]
- Herrmann, C. The complete analysis of the discrete time finite DBMAP/G/1/N queue. Perform. Eval. 2001, 43, 95–121. [Google Scholar] [CrossRef]
- Pradhan, S.; Gupta, U. Analysis of an infinite-buffer batch-size-dependent service queue with Markovian arrival process. Ann. Oper. Res. 2019, 277, 161–196. [Google Scholar] [CrossRef]
- Hwang, G.U.; Sohraby, K. On the exact analysis of a discrete-time queueing system with autoregressive inputs. Queueing Syst. 2003, 43, 29–41. [Google Scholar] [CrossRef]
- Kamoun, F. The discrete-time queue with autoregressive inputs revisited. Queueing Syst. 2006, 54, 185–192. [Google Scholar] [CrossRef]
- Wittevrongel, S. Discrete-time buffers with variable-length train arrivals. Electron. Lett. 1998, 34, 1719–1721. [Google Scholar] [CrossRef]
- Hoflack, L.; De Vuyst, S.; Wittevrongel, S.; Bruneel, H. Analytic traffic model of web server. Electron. Lett. 2008, 44, 61–62. [Google Scholar] [CrossRef]
- Athreya, K.; Ney, P. Branching Processes; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Kevei, P.; Wiandt, P. Moments of the stationary distribution of subcritical multitype Galton-Watson processes with immigration. Stat. Probab. Lett. 2021, 173, 109067. [Google Scholar] [CrossRef]
- Barczy, M.; Nedenyi, F.; Pap, G. On aggregation of multitype Galton-Watson branching processes with immigration. Mod. Stoch. Theory Appl. 2018, 5, 53–79. [Google Scholar] [CrossRef]
- Dyakonova, E.E. Multitype Galton-Watson branching processes in Markovian random environment. Theory Probab. Its Appl. 2012, 56, 508–517. [Google Scholar] [CrossRef]
- Minzer, D.; Oz, Y.; Safra, M.; Wainstain, L. Pandemic spread in communities via random graphs. J. Stat.-Mech.-Theory Exp. 2021, 2021, 113501. [Google Scholar] [CrossRef]
- Bogdanov, A.; Kevei, P.; Szalai, M.; Virok, D. Stochastic Modeling of In Vitro Bactericidal Potency. Bull. Math. Biol. 2022, 84, 6. [Google Scholar] [CrossRef] [PubMed]
- Balelli, I.; Milisic, V.; Wainrib, G. Multi-type Galton-Watson Processes with Affinity-Dependent Selection Applied to Antibody Affinity Maturation. Bull. Math. Biol. 2019, 81, 830–868. [Google Scholar] [CrossRef]
- Collins, B.; Hoang, D.T.; Nguyen, N.T.; Hwang, D. A New Model for Predicting and Dismantling a Complex Terrorist Network. IEEE Access 2022, 10, 126466–126478. [Google Scholar] [CrossRef]
- Kovchegov, Y.; Zaliapin, I.; Ben-Zion, Y. Invariant Galton-Watson branching process for earthquake occurrence. Geophys. J. Int. 2022, 231, 567–583. [Google Scholar] [CrossRef]
- Koops, D.T.; Saxena, M.; Boxma, O.J.; Mandjes, M. Infinite-server queues with Hawkes input. J. Appl. Probab. 2018, 55, 920–943. [Google Scholar] [CrossRef]
- Selvamuthu, D.; Tardelli, P. Infinite-server systems with Hawkes arrivals and Hawkes services. Queueing Syst. 2022, 101, 329–351. [Google Scholar] [CrossRef]
- Fiems, D.; De Turck, K. The Mean Queue Content of Discrete-time Queues with Zero-regenerative Arrivals. Oper. Res. Lett. 2012, 40, 235–238. [Google Scholar] [CrossRef]
- Fiems, D.; De Turck, K. Taylor-series approximations for queues with arrival correlation. Appl. Math. Model. 2019, 69, 113–126. [Google Scholar] [CrossRef]
- Nakayama, M.K.; Shahabuddin, P.; Sigman, K. On finite exponential moments for branching processes and busy periods for queues. J. Appl. Probab. 2004, 41A, 273–280. [Google Scholar] [CrossRef]
- Ernst, P.A.; Asmussen, S.; Hasenbein, J.J. Stability and busy periods in a multiclass queue with state-dependent arrival rates. Queueing Syst. 2018, 90, 207–224. [Google Scholar] [CrossRef]
- Altman, E.; Fiems, D. Expected waiting time in symmetric polling systems with correlated walking times. Queueing Syst. 2007, 56, 241–253. [Google Scholar] [CrossRef]
- Vatutin, V.A. Polling systems and multitype branching processes in random environment with final product. Theory Probab. Its Appl. 2011, 55, 631–660. [Google Scholar] [CrossRef]
- Fiems, D.; Altman, E. Gated polling with stationary ergodic walking times, Markovian routing and random feedback. Ann. Oper. Res. 2012, 198, 145–164. [Google Scholar] [CrossRef]
- Resing, J. Polling systems and multi-type branching processes. Queueing Syst. 1993, 13, 409–426. [Google Scholar] [CrossRef]
- Altman, E. On stochastic recursive equations and infinite server queues. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005. [Google Scholar]
- Baccelli, F.; Bremaud, P. Elements of Queueing Theory; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Vinck, B.; Bruneel, H. Delay analysis for single server queues. Electron. Lett. 1996, 32, 802–803. [Google Scholar] [CrossRef]
- Constantine, G.; Savits, T. A multivariate Faa di Bruno formula with applications. Trans. Am. Math. Soc. 1996, 348, 503–520. [Google Scholar] [CrossRef]
- Banks, J. (Ed.) Handbook of Simulation: Principles, Methodology, Advances, Applications, and Practice; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Kingman, J. On queues in heavy traffic. J. R. Stat. Soc. Ser. B (Methodol.) 1962, 24, 383–392. [Google Scholar] [CrossRef]
- Whitt, W. Stochastic-Process Limits: An Introduction to Stochastic-Process Limits and Their Application to Queues; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).