A Novel Double-Layered Central Pattern Generator-Based Motion Controller for the Hexapod Robot

Abstract

To implement the various movement control of the hexapod robot, a motion controller based on the double-layered central pattern generator (CPG) is proposed in this paper. The novel CPG network is composed of a rhythm layer and a pattern layer. The CPG neurons are constructed based on Kuramoto nonlinear oscillator. The parameters including the frequency, coupling strength, and phase difference matrix of the CPG network for four typical gaits are planned. The mapping relationship between the signals of the CPG network and the joint trajectories of the hexapod robot is designed. The co-simulations and experiments have been conducted to verify the feasibility of the proposed CPG-based controller. The actual average velocities of the wave gait, the tetrapod gait, the tripod gait, and the self-turning gait are 10.8 mm/s, 25.5 mm/s, 37.8 mm/s and 26°/s, respectively. The results verify that the hexapod robot with the proposed double-layered CPG-based controller can perform stable and various movements.

1. Introduction

Bio-inspired robots perform well in terms of their mechanism and mobility, and are widely applied in various unstructured environments [1]. Equipped with multiple degree-of-freedom legs, the legged bio-inspired robots can freely cross the complex terrains [2]. In recent years, bio-inspired legged robots have become one of the hot topics in robotics research.

Compared with biped and quadruped robots, hexapod robots have better environmental adaptability. Hexapod robots are developed for post-disaster searches, planet exploration, and other dangerous tasks [3,4]. Otherwise, the redundant limbs of hexapod robots are helpful to deal with problems of limb damage. Numerous typical hexapod robots have been developed [5,6,7]. The research on these hexapod robots provides valuable experience for the following studies.

The control methods for hexapod robots include the compliant control, the model-based control, and the CPG-based control. The compliant control method proposed in [8] could improve the environmental adaptability. The model-based control method is the most widely used in the motion control of legged robots. The virtual model controller was proposed to control the hexapod robot, and the joint torque was calculated based on the dynamic model [9]. Several advanced control methods such as sliding mode control [10,11,12] and PID controller [13] can be used for robot control based on the model. CPGs are common neural elements for locomotion control in insects. They are crucial for the generation of rhythmic movement in the behaviors, i.e., flight, walking, and crawling [14]. The CPG-based control has been proven to be effective in various robots, i.e., crawling robots, swimming robots, flying robots, climbing robots, and other robots with rhythmic locomotion [15]. The motion control mechanism of multi-legged insects is always used to design the control system of hexapod robots. A CPG-based control strategy was proposed to adjust the motion speed according to visual information. The proposed control strategy can ensure the smooth gait transition of the hexapod robot [16]. Compared with the other methods, the model of the CPG-based method owns fewer control parameters. Meanwhile, the CPG-based method can control various forms of locomotion, perform smooth transition, and easily integrate abundant sensing signals [17,18]. Fractional calculus and the investigation of fractional-order systems have been extensively studied in the last decades [19,20,21]. Fractional central pattern generator (CPG) models for locomotion systems have been researched in the reference [22,23]. This paper focuses on the research of integer order CPG.

According to the model of CPG neurons, the CPG network can be classified into two types, i.e., the CPG network based on the biological neuron models and the CPG network based on the nonlinear oscillators [24]. The former CPG models simulate the dynamic behavior of action potential in the biological neurons. The Matsuoka model is widely used to model the CPG neuron [25]. A CPG neuron composed of two modified Matsuoka models was proposed to control the motion of flexor and extensor [26]. However, the tuning parameters of biological neuron models were too many. The representative CPG network models based on nonlinear oscillators are Kuramoto model, Hopfield model, and Van der Pol model. The Kuramoto model is widely used to model the neural oscillations [27,28]. Several extensions have been proposed to increase its neuro-biological plausibility. An adaptive CPG based on the Hopfield model was constructed to control the walking motion of biped robot HOAP-2 [29]. Van der Pol et al. proposed the Van der Pol vibrator model based on the study of a tube oscillation circuit. This model can generate different rhythmic oscillation signals by tuning the oscillation parameters. It is widely used for modeling the CPG neurons [30]. The CPG neurons based on the Hopfield model and Van der Pol model both generate the trajectory and phase of the joints. The Kuramoto oscillator-based CPG neurons only generate the phase of each joint. It is conducive to discretionarily design the trajectory. This can improve the motion flexibility of the hexapod robot.

The biological CPG network is proved to be a multi-layered structure. The layered structure allows the biological CPG network to hierarchically process sensory information to control different body parts, which can improve the environmental adaptability. A two-layered CPG network with a self-learning function was established for the walking motion control of legged robots on unstructured terrain [31]. In the two-layered CPG controller, the high-level network was used for gait control, and the low-level network was used for motor control [32,33]. A two-level controller including a CPG and RBF network was proposed, and the RBF network was used to model the joint trajectories [34].

Gait planning is vital for improving stability and flexibility. It also optimizes energy consumption. According to the number of supporting legs, the gaits of the hexapod can be divided into the wave gait, the tetrapod gait, and the tripod gait. An adaptive tripod static gait was designed for the hexapod robot to overcome obstacles by using spatial parallel mechanism legs [35]. The locomotion transition of the hexapod robot from flat to slope was studied in [36]. A modular algorithm was proposed to reduce the computation consumption. The hexapod robot can move forward and backward [37]. The current research on gait planning based on the CPG method is only for some of the typical gaits.

This paper presents a novel double-layered CPG-based motion controller for the hexapod robot, which can achieve the control of four different gaits. The overview of the hexapod robot platform is presented in Section 2. A motion controller based on the double-layered CPG is designed in Section 3. Four different gaits of the hexapod robot are introduced and planned in Section 4. The co-simulations of the four gaits and the stability margin analysis of each gait are carried out in Section 5. The experiments are carried out to verify the effectiveness of the proposed double-layered CPG-based motion controller in Section 6. A discussion and a conclusion are summarized in Section 7.

2. Overview of the Hexapod Robot Platform

The hexapod robot platform used in this paper is shown in Figure 1. Each leg has three joints: hip joint, knee joint, and ankle joint. The rotation range of the hip joints is ±45°. The rotation ranges of the knee and ankle joints are both ±90°. The joints are driven by the AX-12A servo motors. The maximum torque of the servo motor is 1.5 Nm. The rotation speed of the servo motor is 59 rpm. The communication among the servo motors is half-duplex serial communication bus. The joint commands of the servo motors are sent from an embedded controller CM-530, of which the central control unit is STM32. The power supply of the hexapod robot is a lithium battery, of which the capacity is 1000 mAh.

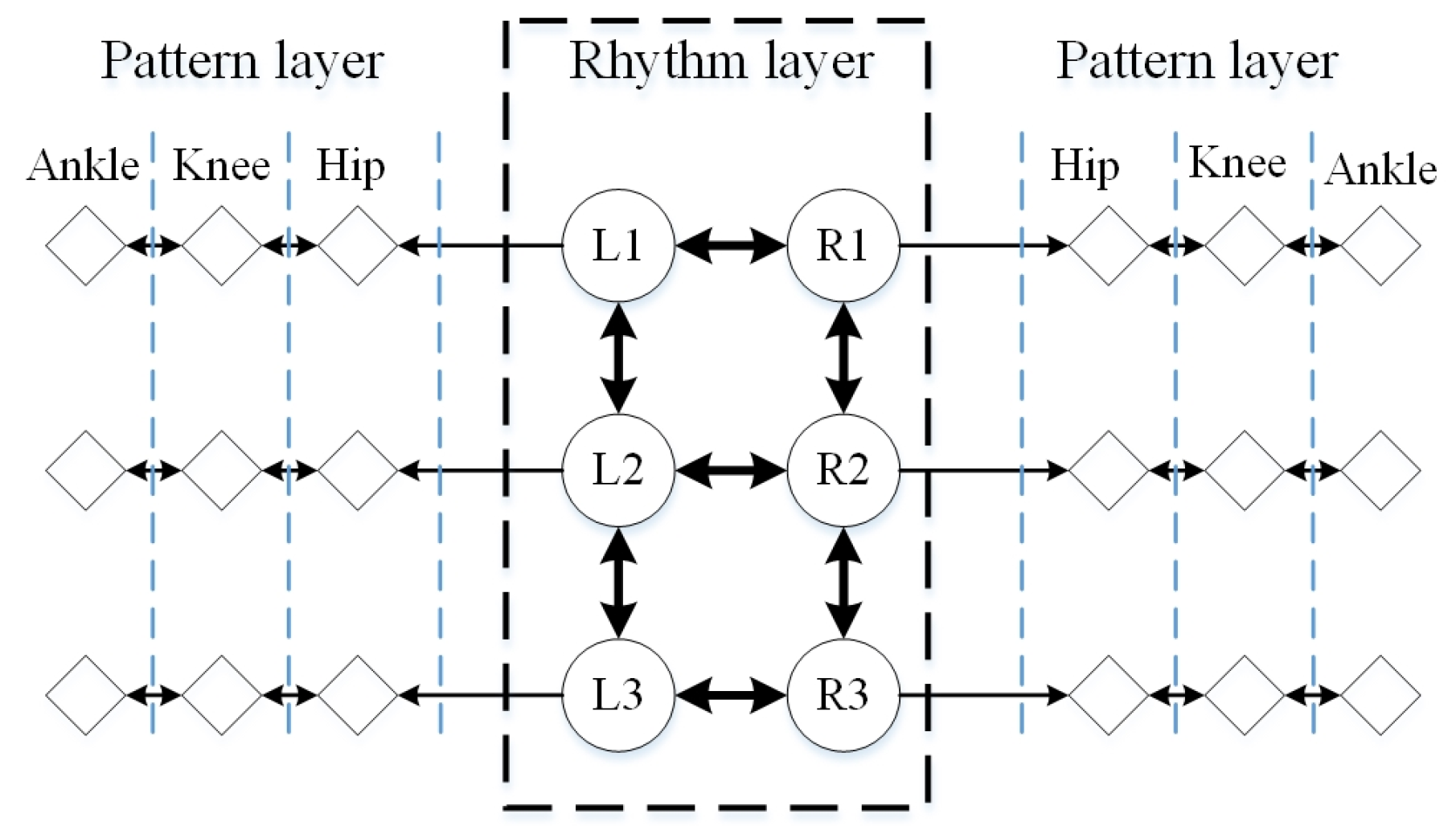
3. Motion Controller Based on the Double-Layered CPG

The plasticity of CPG neuron coupling connection makes its output diverse, which can realize the control of multiple locomotion modes of the hexapod robot. A double-layered CPG network is proposed to control the hexapod robot. The proposed CPG network is divided into a rhythm layer and a pattern layer. The pattern layer is controlled by the rhythm layer. The functions of each layer should meet the following requirements:

(1) CPG neurons in the rhythm layer establish the phase relationship between each functional unit (legs and trunk).

(2) CPG neurons in the pattern layer correspond to the joints inside each functional unit (such as hip joint, knee joint, and ankle joint), and control the joint phase relationship and joint trajectory.

(3) The output signal of pattern layer is based on the output signal of the rhythm layer, and the rhythm layer signal is not affected by the pattern layer signal.

Based on the structural characteristics of the hexapod robot, the rhythm layer of the CPG network contains six CPG neurons, which determine the motion phase of each leg, respectively. The pattern layer contains 18 CPG neurons, which are divided into six groups corresponding to the six legs. Each group contains three CPG neurons, which respectively determines the motion phase and trajectory of the hip, knee, and ankle joints. The coupling relationship between CPG neurons in the rhythm layer and CPG neurons in the pattern layer is unidirectional. The CPG neurons in different neuron groups have no coupling relationship. To improve the synchronization speed of the proposed CPG network, the coupling relation of CPG neurons in each level or group is bidirectional. The hierarchical scheme of the proposed double-layered CPG network is shown in Figure 2. The CPG neurons in the rhythm layer are not used to control the joint trajectories. It can integrate the sensory information to coordinate the leg motion sequence. The foot trajectory is determined by the pattern layer.

The Kuramoto model is used as the mathematical model of CPG neurons in this paper. The neurons in the rhythm layer only determine the phase relations of legs. The mathematical model of CPG neurons in the rhythm layer is as follows [38]:

$${\theta }_{Ri}=2\mathsf{\pi }\omega +{\displaystyle {\sum }_{j=1}^{N}w\sin \left({\theta }_{Rj}-{\theta }_{Ri}-{\phi }_{Rij}\right)}$$

(1)

where θ_Ri is the phase signal of CPG neuron, ω is the frequency, N is the number of the neurons in the rhythm layer, w is the coupling factor of the neighboring neurons, and φ_Rij is the phase difference between the CPG neuron i and the CPG neuron j.

The neurons in the pattern layer can both determine the phase difference and trajectory of each joint. The mathematical model of CPG neurons in the pattern layer is as follows:

$$\left\{\begin{array}{l}{\theta }_{Pi}=2\mathsf{\pi }\omega +{\displaystyle {\sum }_{j=1}^{M-1}w\sin \left({\theta }_{Pj}-{\theta }_{Pi}-{\phi }_{Pij}\right)}\\ \hspace{1em} +w\sin \left({\theta }_{Pj}-{\theta }_{Ri}-{\phi }_{PRij}\right)\\ {\varphi }_i=f\left({\theta }_{Pi}\right)\end{array}\right.$$

(2)

where M is the number of coupling neurons, θ_Pi is the phase signal of CPG neurons in the pattern layer. φ_Pij is the phase difference between the CPG neurons in the pattern layer. φ_PRij is the phase difference between the CPG neurons in the pattern layer and the CPG neurons in the rhythm layer. f is the mapping function from phase θ_Pi to the joint trajectory ${\varphi }_i$.

The simulation outputs of the proposed double-layered CPG network are shown in Figure 3. The rhythm layer of the proposed CPG network controls the phase of each leg. The pattern layer determines the phase of each joint, i.e., hip joint, knee joint, and ankle joint. As shown in Figure 3a,b, the initial phases of the rhythm layer and the pattern layer are disordered. To avoid the effect of randomness on the joint trajectories, the output of the pattern layer is rewritten as (3). It can be seen from Figure 3c that the joint output is smooth and continuous.

$$\left\{\begin{array}{l}{\theta }_{Pi}=2\mathsf{\pi }\omega +{\displaystyle {\sum }_{j=1}^{M-1}w\sin \left({\theta }_{Pj}-{\theta }_{Pi}-{\phi }_{Pij}\right)}\\ \hspace{1em} +w\sin \left({\theta }_{Pj}-{\theta }_{Ri}-{\phi }_{PRij}\right)\\ {\varphi }_i=\left(1-e^{-bt}\right)f\left({\theta }_{Pi}\right)\end{array}\right.$$

(3)

where b is used to control the transition time of the proposed double-layered CPG network.

4. Gait Planning of the Hexapod Robot

Gait planning is composed of movement phase planning and joint trajectory planning. In the movement process of hexapod robots, the state of each leg is divided into the stance phase and the swing phase. As shown in Figure 4, in the swing phase, the leg moves from the posterior extreme position (PEP) to the anterior extreme position (AEP). In the stance phase, the leg moves from AEP to PEP. Each leg of the hexapod robot alternates between the swing phase and the stance phase.

A gait occurs when each leg performs the swing phase and the stance phase. The gait period T is defined as the time required for the robot to complete a gait. The duty factor β is a crucial parameter to evaluate the gait. The definition is given as:

$$\beta =\frac{T_{st}}{T}=1-\frac{T_{sw}}{T}$$

(4)

where T_st is the time of the stance phase, T_sw is the time of the swing phase.

The moving distance of a single step is defined as s, and the velocity of the hexapod robot is as follows:

$$v=\frac{s}{T_{st}}=\frac{s}{T_{sw}}\times \left(\frac{1}{ \beta }-1\right)$$

(5)

when s and T are constants, the minor β will lead to faster velocity and vice versa. The larger β means that the longer time each leg is in the stance phase, the more legs that are used to bear the body load.

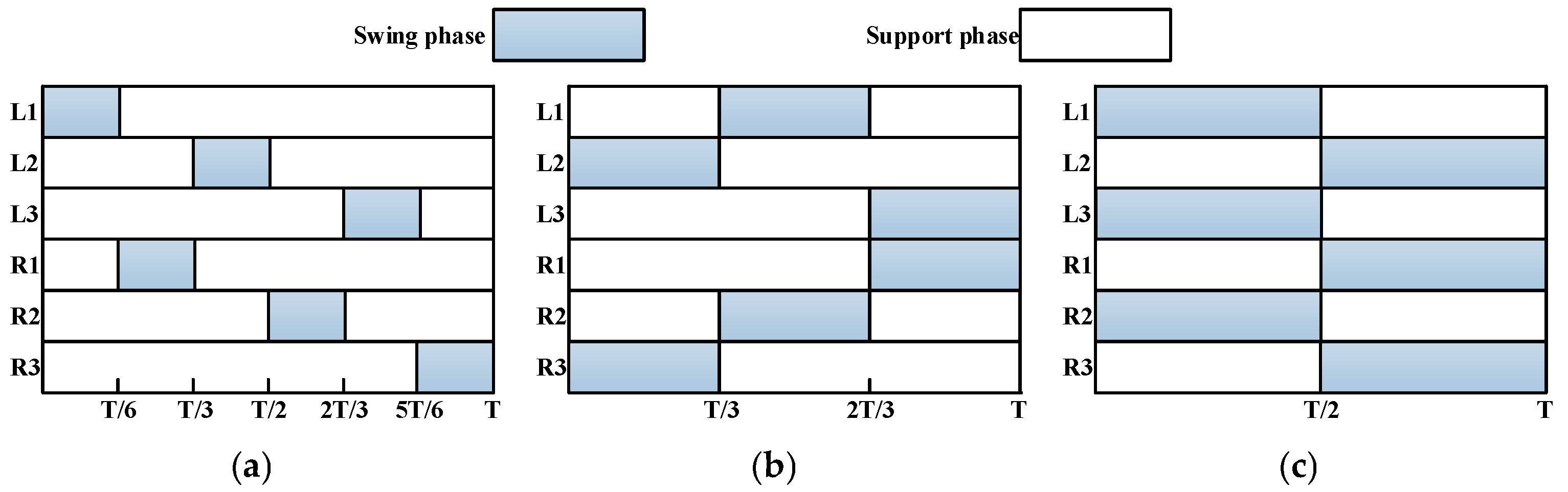
4.1. Phase Analysis of Each Gait

The hexapod robot can perform four kinds of gaits, which are wave gait, tetrapod gait, tripod gait, and self-turning gait. The phase relationships of the CPG neurons in the rhythm layer are different.

When the hexapod robot performs the wave gait, only one leg stays in the swing phase at any time. The duty factor β of the wave gait is 5/6. As shown in Figure 5a, the swing sequence of each leg is L1, R1, L2, R2, L3, R3. The phase difference of the neighboring legs is π/3. Because the five legs stay in the stance phase, the carrying capacity and the stability are better than that of the other gaits. The phase difference matrix is as follows:

$${\phi }_{ij}=\left[\begin{array}{cccccc}0& -2\mathsf{\pi }/3& -4\mathsf{\pi }/3& -5\mathsf{\pi }/3& -\mathsf{\pi }& -\mathsf{\pi }/3\\ 2\mathsf{\pi }/3& 0& -2\mathsf{\pi }/3& -\mathsf{\pi }& -\mathsf{\pi }/3& \mathsf{\pi }/3\\ 4\mathsf{\pi }/3& 2\mathsf{\pi }/3& 0& -\mathsf{\pi }/3& \mathsf{\pi }/3& \mathsf{\pi }\\ 5\mathsf{\pi }/3& \mathsf{\pi }& \mathsf{\pi }/3& 0& 2\mathsf{\pi }/3& 4\mathsf{\pi }/3\\ \mathsf{\pi }& \mathsf{\pi }/3& -\mathsf{\pi }/3& -2\mathsf{\pi }/3& 0& 2\mathsf{\pi }/3\\ \mathsf{\pi }/3& -\mathsf{\pi }/3& -\mathsf{\pi }& -4\mathsf{\pi }/3& -2\mathsf{\pi }/3& 0\end{array}\right]$$

(6)

In the tetrapod gait, the legs of the hexapod robot are divided into three groups. As shown in Figure 5b, the swing sequence of each leg is L1/R2, L2/R3, L3/R1. There are also other group combinations of the legs. When the hexapod robot performs the tetrapod gait, two legs stay in the swing phase at any time. The duty factor β of tetrapod gait is 2/3. The phase difference of the legs in different groups is 2π/3. The phase difference matrix is as follows:

$${\phi }_{ij}=\left[\begin{array}{cccccc}0& 2\mathsf{\pi }/3& -2\mathsf{\pi }/3& 2\mathsf{\pi }/3& 0& -2\mathsf{\pi }/3\\ -2\mathsf{\pi }/3& 0& -4\mathsf{\pi }/3& 0& -2\mathsf{\pi }/3& -4\mathsf{\pi }/3\\ 2\mathsf{\pi }/3& 4\mathsf{\pi }/3& 0& 4\mathsf{\pi }/3& 2\mathsf{\pi }/3& 0\\ -2\mathsf{\pi }/3& 0& -4\mathsf{\pi }/3& 0& -2\mathsf{\pi }/3& -4\mathsf{\pi }/3\\ 0& 2\mathsf{\pi }/3& -2\mathsf{\pi }/3& 2\mathsf{\pi }/3& 0& -2\mathsf{\pi }/3\\ -2\mathsf{\pi }/3& 4\mathsf{\pi }/3& 0& 4\mathsf{\pi }/3& 2\mathsf{\pi }/3& 0\end{array}\right]$$

(7)

In the tripod gait, the legs of the hexapod robot are divided into two groups. As shown in Figure 5c, the swing sequence of the legs is L1/L3/R2, L2/R1/R3. There are also other group combinations of the legs. When the hexapod robot performs the tripod gait, there are three legs stay in the swing phase at any time. The duty factor β of tripod gait is 1/2. The phase difference of the legs in different groups is set as π. The phase difference matrix is as follows:

$${\phi }_{ij}=\left[\begin{array}{cccccc}0& -\mathsf{\pi }& 0& -\mathsf{\pi }& 0& -\mathsf{\pi }\\ \mathsf{\pi }& 0& \mathsf{\pi }& 0& \mathsf{\pi }& 0\\ 0& -\mathsf{\pi }& 0& -\mathsf{\pi }& 0& -\mathsf{\pi }\\ \mathsf{\pi }& 0& \mathsf{\pi }& 0& \mathsf{\pi }& 0\\ 0& -\mathsf{\pi }& 0& -\mathsf{\pi }& 0& -\mathsf{\pi }\\ \mathsf{\pi }& 0& \mathsf{\pi }& 0& \mathsf{\pi }& 0\end{array}\right]$$

(8)

The planned wave gait, tetrapod gait, and tripod gait are used to control the hexapod robot moves straightly. To implement the navigation, a self-turning motion based on the tripod gait is designed. The self-turning directions of all the legs are the same. The hexapod robot will turn left when all the legs swing counterclockwise and vice versa.

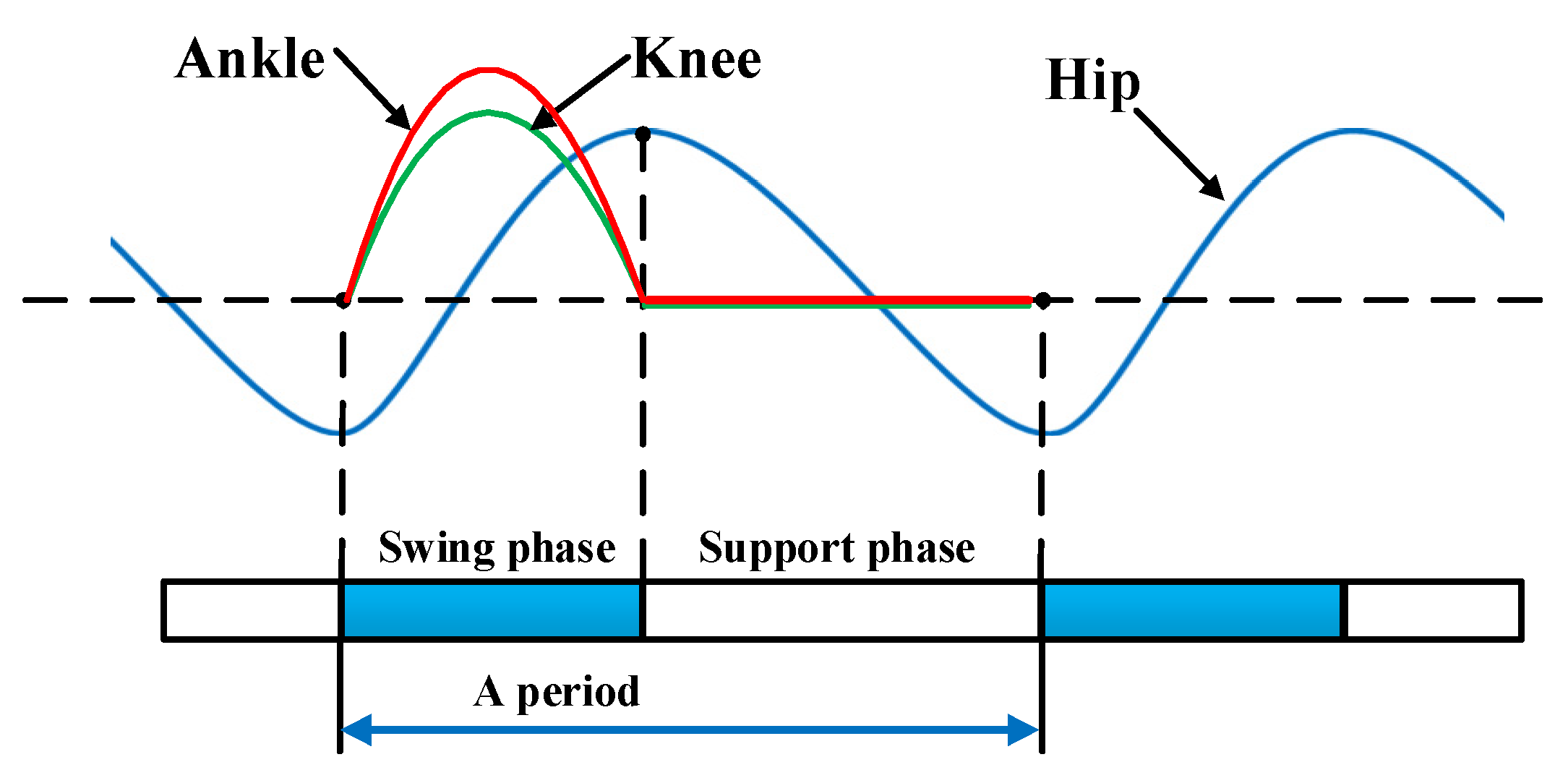
4.2. Joint Trajectory of Each Gait

By observing the leg movement of animals, there is a fixed phase relationship among the hip joint, the knee joint, and the ankle joint in one gait. As shown in Figure 6, the rising edge of the hip joint trajectory corresponds to the swing phase. On the contrary, the descending edge of the hip joint trajectory corresponds to the stance phase. The phase difference between the knee joint and the hip joint is π/2. The phase difference between the ankle joint and the knee joint is 0. When the joint trajectories are invariant, the phase difference among the three joints can be used to slightly adjust the foot trajectory to overcome the obstacle.

The outputs of CPG neurons in the pattern layer are processed by the mapping function. As shown in Figure 6, the joint trajectory of the hip joint is a signal similar to sine wave. In the swing phase, the joint trajectory shapes of the ankle joint and the knee joint are both half sine waves. The ankle and knee joints keep still in the stance phase. The control functions of the knee and ankle joints are shown as Equations (9) and (10). The control function of the hip joint is given in the next section.

$${\varphi }_k=\left\{\begin{array}{cc}{A}_k\left(1+\frac{\left|{\varphi }_h\right|}{A_h}\right)\left(A_h-\left|{\varphi }_h\right|\right)& {\varphi }_h\ge 0\\ 0& {\varphi }_h\le 0\end{array}\right.$$

(9)

$${\varphi }_a=\left\{\begin{array}{cc}{A}_a\left(1+\frac{\left|{\varphi }_h\right|}{A_h}\right)\left(A_h-\left|{\varphi }_h\right|\right)& {\varphi }_h\ge 0\\ 0& {\varphi }_h\le 0\end{array}\right.$$

(10)

where ${\varphi }_h$ and ${\varphi }_k$ are the angle control signals of the hip joint and the knee joint, respectively, and A_h and A_k are the altitudes of the hip joint and the knee joint, respectively.

5. Locomotion Simulation of the Hexapod Robot

The co-simulations of the four gaits have been carried out, and the stability margin of each gait has been analyzed. The dynamic model of the hexapod robot is built in MSC.Adams. The double-layered CPG-based motion controller is built in Simulink. The simulation time is set as 10 s. The single gait period is set as 2 s, so the frequency factor v is 0.5, and the coupling strength factor w is set as 20. The amplitudes of the knee joint and the ankle joint are A_k = 40° and A_a = 45°, respectively.

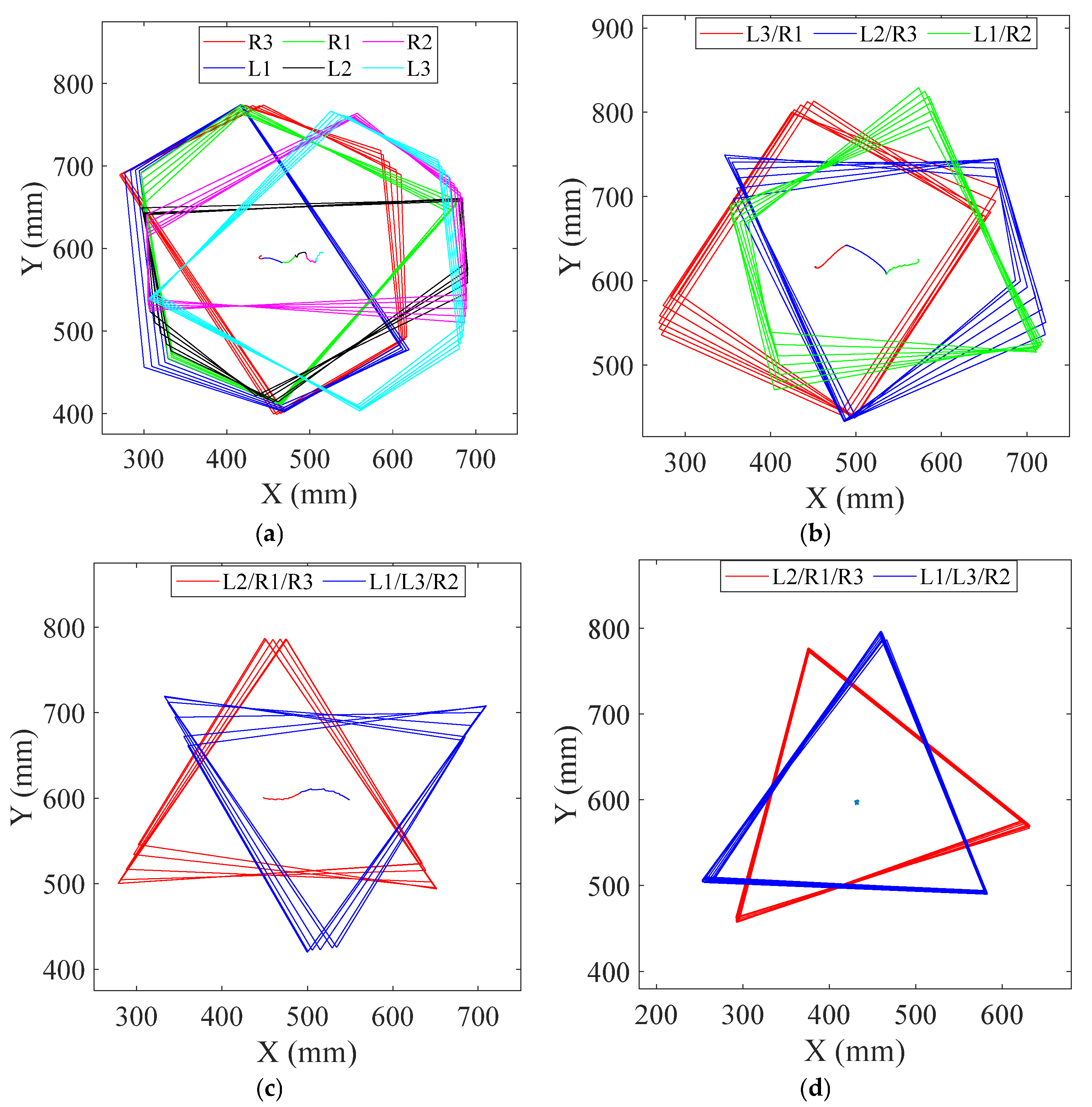
5.1. Simulation of the Wave Gait

In the wave gait of the hexapod robot, the phase difference of the neighboring legs is π/3. The duty factor β is 5/6. During a period, each leg in the swing phase is 1/3 s, and the time in the stance phase is 5/3 s. The monocyclic trajectory of the hip joint is given as Equation (11).

$${\varphi }_h=f\left({\theta }_i\right)=\left\{\begin{array}{cc}\frac{\mathsf{\pi }}{6}\sin \left(3{\theta }_i-\frac{\mathsf{\pi }}{2}\right)& 0\le {\theta }_i\le \frac{\mathsf{\pi }}{3}\\ \frac{\mathsf{\pi }}{6}\sin \left(\frac{3}{5}{\theta }_i+\frac{3\mathsf{\pi }}{10}\right)& \frac{\mathsf{\pi }}{3}<{\theta }_i\le 2\mathsf{\pi }\end{array}\right.$$

(11)

The trajectories of the knee joint and the ankle joint are calculated by (9) and (10). The control functions of the trajectories are both piecewise functions. To avoid the discontinuities of the trajectories, the following equation is applied for fitting the trajectories.

$$f\left({\theta }_i\right)={\displaystyle \sum _{i=1}^8{a}_i\sin (b_i{\theta }_i+c_i)}$$

(12)

The simulation screenshots of the wave gait are shown in Figure 7. In the moving process with the wave gait, the average velocity of the hexapod robot is 39 mm/s.

5.2. Simulation of the Tetrapod Gait

The hexapod robot can perform the tetrapod gait with different modes. In this paper, the phases of legs L2 and R3 are set as 0, and the phases of legs L1 and R2 are set as 2π/3, and the phases of legs L3 and R1 are set as 4π/3. The time of the swing phase is 2/3 s, and the time of the stance phase is 4/3 s. The monocyclic trajectory of the hip joint is given as follows:

$${\varphi }_h=f\left({\theta }_i\right)=\left\{\begin{array}{cc}\frac{\mathsf{\pi }}{6}\sin \left(\frac{3}{2}{\theta }_i-\frac{\mathsf{\pi }}{2}\right)& 0\le {\theta }_i\le \frac{2}{3}\mathsf{\pi }\\ \frac{\mathsf{\pi }}{6}\sin \frac{3}{4}{\theta }_i& \frac{2}{3}\mathsf{\pi }<{\theta }_i\le 2\mathsf{\pi }\end{array}\right.$$

(13)

The trajectory function of each joint is fitted by Equation (12). The simulation screenshots of the tetrapod gait are shown in Figure 8. At the beginning of the movement, amplitude modulation is introduced into the robot, which results in the first period being incomplete and the movement direction exists as offset. The distance in the z-axis is 170 mm, and the distance in the x-axis is 570 mm. The average velocity of the hexapod robot is 59.5 mm/s.

5.3. Simulation of the Tripod Gait

In the tripod gait of the hexapod robot, the phases of legs L1, L3, and R2 are set as 0, and the phases of legs L2, R1, and R3 are set as π. In addition, the hexapod robot can perform two other configurations. In the tripod gait, the duty factor β is 1/2. The times of the swing phase and stance phase are both 1/2 s. The monocyclic trajectory of the hip joint is given as follows:

$${\varphi }_h=f\left({\theta }_i\right)=\frac{\mathsf{\pi }}{6}\sin {\theta }_i$$

(14)

The simulation screenshots of the tripod gait are shown in Figure 9. The distances in the y-axis and the z-axis are about 0, which means there is no bouncing and offset movement. The distance in the x-axis is 800 mm. The average velocity of the robot is 80 mm/s.

5.4. Simulation of the Self-Turning Gait

The turning motion of the hexapod robot is designed based on the tripod gait. Therefore, the phase difference matrix of the self-turning gait is the same as the tripod gait. The hip joint trajectories of the legs L1, L2 and L3 are contrary to the others of the tripod gait. The simulation screenshots of the self-turning gait are shown in Figure 10. The times of the swing phase and stance phase are both set as 1 s. The distances in the three axes are all about 0. It means that the hexapod robot can perform self-turning. The hexapod robot rotates 60 degrees around the y-axis in a gait period.

5.5. The Stability Analysis of Each Gait

The stability margin is applied to analyze the static gait stability of legged robots quantitatively. The stability margin is defined as the shortest distance among the distances from the projection point of the CoM (center of mass) to the sides of the supporting polygon. The stability margin of the wave gait is shown in Figure 11. The leg L1 stays in the swing phase, and all the other legs are in the stance phase. Point O is the CoM projection point on the supporting polygon, and d_i (i = 1,2,…,5) is the distance between point O and the line of the neighboring support legs. The stability margin of the robot is as follows:

$$S=\min \left\{d_1,d_2,d_3,d_4,d_5\right\}$$

(15)

Based on the definition of a stability margin, the CoM trajectory and the supporting polygon in a single period are shown in Figure 12. In the figure, the lines enveloped by polygons are the CoM trajectories, and the legends indicate the legs in swing phase. It can be seen that the stability margin of the four gaits are always positive in the moving processes. It means that the stability of the hexapod robot is good, and the hexapod robot is suitable for complex environments.

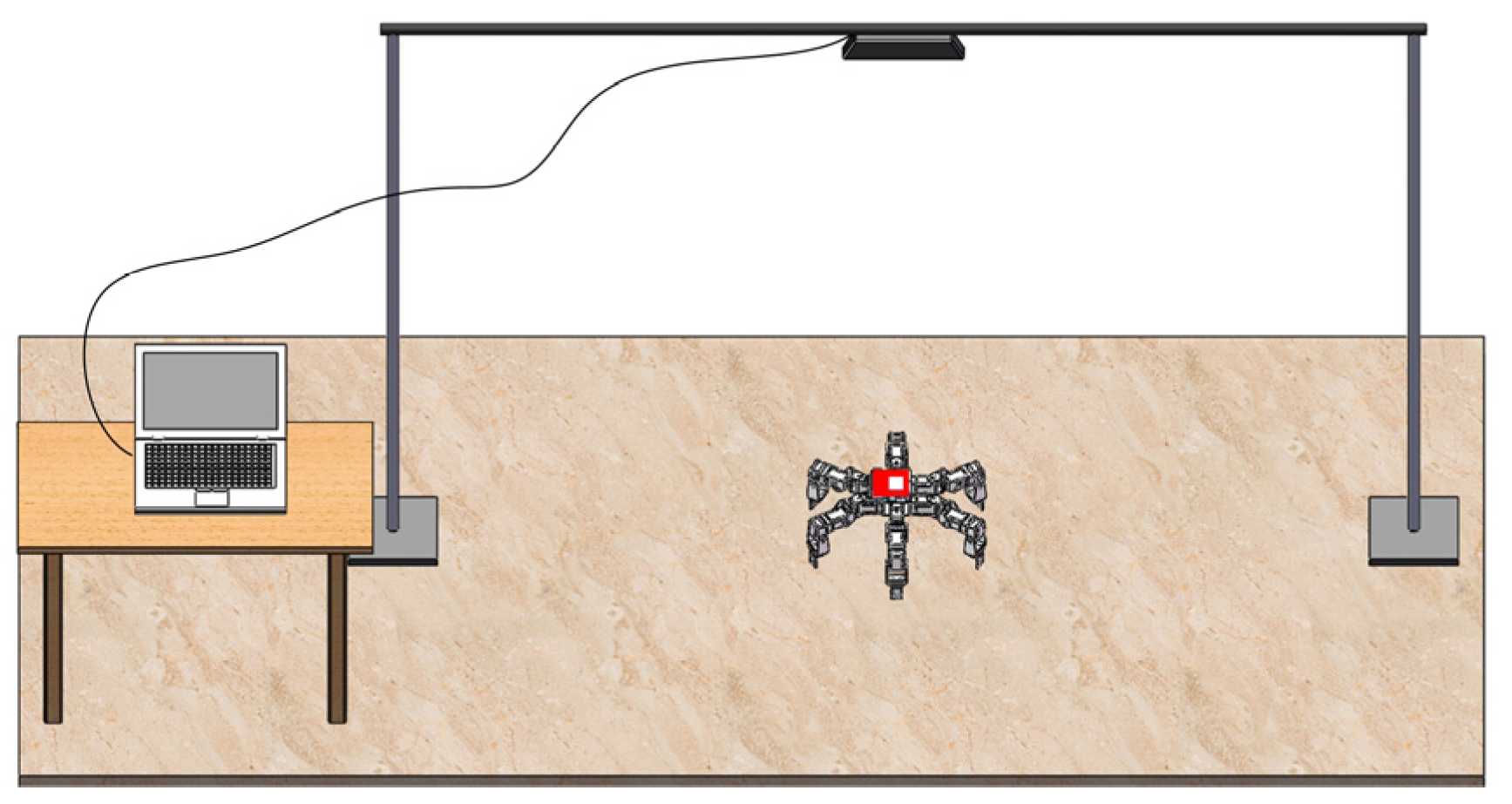
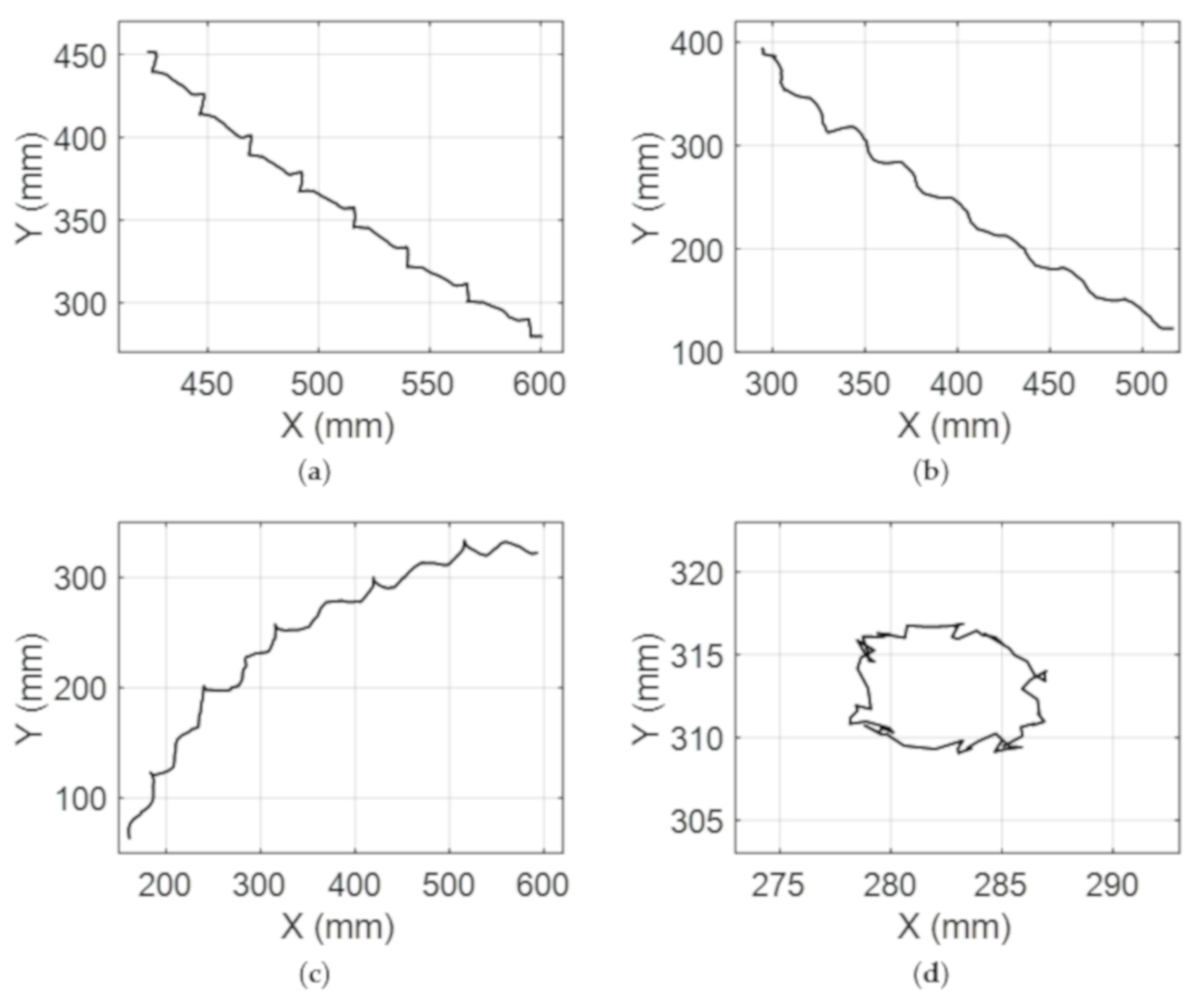
6. Experimental Results of the Hexapod Robot

To evaluate the performance of the proposed double-layered CPG-based controller and the gait planning, an experimental platform is built. As shown in Figure 13, an overhead camera is used to record the position of the hexapod robot, and the robot is on the wood floor. Two rectangular markers with different sizes and colors are pasted on the hexapod robot to measure the position of the robot.

The motion videos are recorded when the hexapod robot performs the wave gait, the tetrapod gait, the tripod gait, and the self-turning gait. The key frames of the motion video are respectively shown in Figure 14, Figure 15, Figure 16 and Figure 17. The gait period of the wave gait, the tetrapod gait, the tripod gait, and the self-turning gait are 4.8 s, 2.4 s, 2 s, and 2 s, respectively. The hexapod robot can perform the four gaits effectively based on the proposed double-layered CPG motion controller.

During the experiments, the trajectories of the hexapod robot are measured and presented in Figure 18. As shown in Figure 18a, the hexapod robot performs the wave gait. The hexapod robot moves about 108 mm within 10 s. The average velocity is 10.8 mm/s. Figure 18b presents the trajectory of the hexapod robot when it performs the tetrapod gait. The hexapod robot moves about 255 mm within 10 s. The average velocity is 25.5 mm/s. The trajectory of the hexapod robot performing the tripod gait is shown in Figure 18c. The hexapod robot moves about 378 mm within 10 s. The average velocity is 37.8 mm/s. There is a deviation in the moving direction when the hexapod robot performs the above three gaits. As shown in Figure 18d, the trajectory of the self-turning gait is recorded. The hexapod robot rotates around the z-axis counterclockwise. The hexapod robot rotates about 260° within 10 s. The average rotational speed is 26°/s. The experimental results show that the controller based on the double-layered CPG has excellent effects on controlling the four different gaits of the hexapod robot.

7. Discussion and Conclusions

Hexapod robots have significant advantages of various locomotion and mechanical redundancy. To implement the control of the hexapod robot, a double-layered CPG-based motion controller is presented in this paper. The proposed CPG model includes a rhythm layer and a pattern layer. The rhythm layer is used to control the motion sequence of legs. The pattern layer is used to control the foot trajectory of each leg with three joints. The proposed CPG-based motion controller can coordinate the 18 joints synchronously. When the foot trajectory is planned, the trajectory will be changed by tuning the phases of the hip, knee, and ankle joints. Four different gaits are designed for the hexapod robots, i.e., wave gait, tetrapod gait, tripod gait, and self-turning gait. Each proposed gait is evaluated through the co-simulation platform established based on Simulink and MSC.Adams. Moreover, the stability of the hexapod robot is analyzed based on the stability margin. The results show that the stability of the hexapod robot fluctuates slightly when the hexapod robot performs four different gaits. Finally, several experiments have been carried out to verify the effectiveness of the proposed double-layered central pattern generator-based motion controller and the four different gaits. The experimental results show that the proposed motion controller can control the movement of the hexapod robot flexibly with the four different gaits. The comparisons of the proposed CPG with other CPG-based biomimetic hexapod robots are shown in

Table 1. The comparisons of the proposed CPG with other CPG-based biomimetic hexapod robots.

Prototype	Leg Joint	CPG Model	Layered Configuration	Number of Oscillators	Coupling Relationship	Gait Types	Implementation
Proposed hexapod	3	Kuramoto oscillator	Two layers	24	Mesh/Chain type	Wave gait Tetrapod gait Tripod gait Self-turing gait	Software Simple
Hexapod [16]	3	Van der Pol oscillator	Single layer	6	Mesh type	Walk (Speed control)	Software Simple
Hexapod [17]	2	Tegotae-based control	Single layer	6	Mesh type	Wave gait Tetrapod gait Tripod gait	Software Simple
Hexapod [39]	3	Spiking neuron model	Single layer	12	Mesh type	Walk (Speed control)	Hardware Complex
Hexapod [40]	3	Hopfield oscillator	Single layer	6	Mesh type	Wave gait Tetrapod gait Tripod gait	Software Medium
Hexapod [41]	3	Hopfield oscillator	Two layers	18	Mesh type	Tripod gait Tetrapod gait	Software Medium
Hexapod [42]	3	Non-linear oscillator	Two layers	18	Mesh type	Wave gait Tripod gait Tetrapod gait	Hardware Complex

. It can be seen that the coupling structure of the proposed CPG-based controller can realize the control of four different gaits simply.

In this paper, the proposed double-layered CPG based motion controller for the hexapod robot is not integrated with sensor signals. The hexapod robot cannot adapt to complex environments. The sensor signals’ integration to improve the performance of the proposed double-layered CPG will be the main work in the future.