Bounds and Maxima for the Workload in a Multiclass Orbit Queue

Abstract

In this research, a single-server M-class retrial queueing system (orbit queue) with constant retrial rates and Poisson inputs is considered. The main purpose is to construct the upper and lower bounds of the stationary workload in this system expressed via the stationary workloads in the classical $M/G/1$ systems where the service time has M-component mixture distributions. This analysis is applied to establish the extreme behaviour of stationary workload in the retrial system with Pareto service-time distributions for all classes.

1. Introduction

In this paper, we study the extreme values of the stationary workload in a multiclass constant-retrial-rates system with a mixture-type service-time distribution. The retrial queueing models with constant retrial rates are used to model the dynamics of the wireless communication systems. The fundamental works [1,2] can serve as the main sources on the applications and mathematical methods of analysis of the retrial systems, including retrial systems with constant retrial rates. Below we mention in brief some specific important applications of the retrial systems with constant retrial rates. For instance, a telephone exchange system has been modelled in [3] by means of such a system, and a similar system was used in the works [4,5] to describe a wide class of multiple access protocols, including an unslotted carrier sense multiple access with collision detection protocol and some versions of the ALOHA protocol. In particular, the constant retrial rate appears to reduce the rate of attempts (in the unslotted multiple access) inversely proportionally to the number of backlogged packets; see [6]. As a result, the total retrial rate becomes insensitive to the virtual "orbit size" (the number of backlogged packets). Moreover, the systems with constant retrial rates have been used to describe TCP traffic with short HTTP connections [7,8] and a optical-electrical hybrid contention resolution scheme [9,10].

In this research, we consider a single-server, multiclass retrial system with constant retrial rates with Poisson inputs and class-dependent exponential retrial times. The distribution of the stationary workload, W, in this system is not analytically available, and we construct the corresponding minorant and majorant single-class classic queueing systems to obtain the lower and upper bounds for the unknown distribution of W. The main feature of these associated systems is that the service time is represented as a mixture of the service times of different classes of customers from the original system. It is worth mentioning that these new associated systems give an important motivation to study queueing systems in which service-time distribution is a mixture.

The analysis of the workload process in this research is not limited to constructing the bounds for the (unknown) stationary distribution. The approach we apply in this work allows one also to consider a closely related problem, the asymptotic behaviour of the workload maxima which in turn is directly related to the problem of the overload of the system. It is known that extreme values of workload or queue can lead to system overload. In order to provide a required quality of service, it is necessary to evaluate the risk that the accumulated backlog exceeds a buffer capacity. From an engineering point of view, exceeding this (high) threshold can lead to various types of failure in servers, natural disasters, data loss during transmission, etc. Moreover, observations show that the exceedances often do not occur one at a time, but are grouped over time, forming so-called clusters [11]. Such clustering in the theory of extreme values is characterised via the so-called extremal index [12], which determines the limiting distribution of the extreme values of a stationary random sequences [13,14,15]. One of the most practically important interpretations of the extremal index $\theta$ is that $1/\theta$ approximately equals to the average cluster size. This allows us to estimate the extremal index using nonparametric methods [12,16,17].

When the service times are subexponential, for example, they are mixtures of the Pareto distributions, then the tail asymptotics of the stationary workload obtained in [18] can be applied. We use this approximation to obtain the limiting distribution of the workload maxima in the minorant and majorant single-class queueing systems corresponding to the given retrial system with Pareto service times. Moreover, based on the monotonicity of the workload in all three systems, we made an assumption about the bounds for the workload extremal index in the retrial system.

The topic of extreme values of the performance indexes in the queuing setting is studied in [19,20,21,22,23,24,25], to mention a few. We also mention some works in this field of the authors of this research [26,27,28,29,30]. The extreme behaviour of the stationary waiting time in classical $GI/G/1$ systems has been studied in the works [26,27]. Moreover, it has been proved in [30] that, if service times are stochastically ordered in two systems, then the extremal indexes of stationary waiting times are ordered in the opposite way. The extreme behaviour of the waiting time in a steady-state $GI/G/1$ system with exponential-Pareto service time is studied in [28]. It has been established in [28] that the limiting distribution of the waiting-time maxima in the systems with exponential-Pareto service times is Frechet-type. In the paper [29], the authors use failure-rate ordering and stochastic ordering to construct the upper and lower bounds for the stationary workload in a multiserver queueing system with multicomponent exponential-Pareto service time.

Summarising, the main contributions of this research are as follows. The lower and upper bounds for the stationary workload in a multiclass retrial system with constant retrial rates are constructed. The corresponding monotonicity property is established. While applying the known tail asymptotic in the case of subexponential service times, the limiting distribution of the workload maxima is discussed.

The structure of the paper is as follows. Section 2 contains a detailed description of the original retrial system denoted by $\Sigma$ (Section 2.1). Then, in Section 2.2, we construct single-class minorant and majorant classic systems for the original system. More exactly, we prove (Theorem 1) that the stationary workloads in these systems are, respectively, lower and upper (stochastic) bounds for the stationary workload W in the system $\Sigma$. Finally, in Section 2.3, a useful representation of the Polaczek–Khintchine formula for the Laplace–Stieltjes transform of the mean stationary waiting time in the system with mixture service time is derived. The retrial system with mixture Pareto service times is considered in Section 3. In this regard, the stationary workload distribution in the corresponding the minorant system is given in Theorem 2. In Section 4, the extremal properties of stationary workload are discussed.

2. Workload in a Multiclass Retrial System

In this section, we establish upper and lower bounds for the workload distribution in a multiclass single-server retrial system by means of stochastic comparisons with classical M/G/1 systems with mixed service-time distributions. These results are applied then to establish explicit results for the upper and lower bounds using Pareto service-time distributions. These results are further used to establish limiting results and extremal indices for the systems under study.

2.1. Description of the Model

We consider a retrial single-server system $\Sigma$ with M classes of customers and M class-dependent orbits with constant retrial rates. Class-k customers follow a Poisson input with rate ${\lambda }_k,k=1,\dots ,M$. If a class-k customer meets an idle server, he starts receiving service immediately; otherwise, if server is busy, then the customer joins the ‘end’ of the k-orbit, $k=1,\dots ,M$. The customers at the head of orbits make independent attempts to enter service, and the per-orbit retrial rate does not depend on the orbit size (but may depend on the orbit class, k), which is known as constant-retrial-rate property. Thus, the orbits are dependent due to a common service facility. Denote by $t_n$ the arrival instant of the nth customer in the superposed Poisson input process ($t_1=0$) and by $S_n\left(k\right)$ the service time of the n-th class-k customer $k=1,\dots ,M;n⩾1$. The sequence of the independent and identically distributed (iid) interarrival times $\{T_n:=t_{n+1}-t_n,n⩾1\}$ and the sequence of the iid service times $\{S_n\left(k\right),n⩾1\}$ are assumed to be independent for each k. The inter-retrial times from the (non-empty) k-orbit follow an exponential distribution with rate ${\eta }_k$ and are independent of the orbit size (number of customers in orbit k). The class-k generic service time $S\left(k\right)$ has general distribution function (d.f.) $F_{S\left(k\right)},k=1,\cdots ,M.$ (In what follows, we will omit the serial index to denote the generic element of an iid sequence.) Then,

$$\lambda =\sum _{k=1}^M{\lambda }_k,{\rho }_k={\lambda }_k\mathrm{E}S\left(k\right),\rho =\sum _{k=1}^M{\rho }_k.$$

(1)

Let $W\left(t\right)$ be the remaining work (workload) at instant $t^{-}$, and assume an initially empty system, $W\left(0\right)=0$. Then, $W_n=W\left(t_n\right),n⩾1$. It has been established in [31] that the inequality

$$\rho +\underset{k=1,\cdots ,M}{max}\frac{\lambda }{\lambda +{\eta }_k}<1,$$

(2)

is a sufficient stability condition of the system under consideration. In other words, under this condition, there exist the following weak limits:

$$W_n\Rightarrow W,n\to \infty .$$

(Hereafter, ⇒ denotes convergence in distribution.) The d.f. $F_W$ of the stationary workload W is in general unknown. On the other hand, W is a critically important QoS parameter of the system. For this reason, as we mention above, the main idea of this research is to construct suitable upper and lower bounds for $F_W$ using the classic M/G/1 systems with mixture service-time distributions.

2.2. Minorant and Majorant Queueing Systems

In this section, we construct two new classic (buffered) FIFO M/G/1 queues, a minorant system denoted by ${\Sigma }^{\left(1\right)}$, and a majorant system denoted by ${\Sigma }^{\left(2\right)}$. (Hereafter, the superscript $\left(i\right)$ relates to system i.) These systems have the same (superposed) input Poisson process with rate $\lambda$, as in the original retrial system $\Sigma$.

In the minorant system ${\Sigma }^{\left(1\right)}$, the generic service time S has the following finite-mixture representation:

$$S=\sum _{k=1}^{M}I\left(k\right)S\left(k\right),n⩾1,$$

(3)

where $I\left(k\right)$ is an indicator function such that $\mathrm{E}I\left(k\right)=p_k={\lambda }_k/\lambda$, and $S\left(k\right)$ is the service time for k-class customers. We stress that ${\Sigma }^{\left(1\right)}$ is a single-class $M/G/1$ system in which service time (3) is a mixture of the service times corresponding to all classes of customers in the original system.

The majorant system ${\Sigma }^{\left(2\right)}$ is the following single-class classic (buffered) $M/G/1$ system: each customer occupies the server for the service time S satisfying (3), and additionally, for the time ${\xi }_0$ having an exponential distribution with rate

$${\mu }_0=\underset{1⩽k⩽M}{min}(\lambda +{\eta }_k),$$

that is,

$$S^{\left(2\right)}=S+{\xi }_0.$$

(4)

Thus, the (exponential) r.v. ${\xi }_0$ corresponds to orbit with the ‘largest’ inter-retrial time. It should be noted that the majorant system ${\Sigma }^{\left(2\right)}$ has a different load:

$${\rho }^{\left(2\right)}=\lambda \mathrm{E}S+\frac{\lambda }{{\mu }_0}=\rho +\frac{\lambda }{{\mu }_0},$$

(5)

and thus the stability condition (2) is indeed

$${\rho }^{\left(2\right)}<1.$$

Remark 1. 

The equality in (4) and similar (in)equalities below can be treated as stochastic if we deal with the original variables, or as an equality with probability one (w.p.1) if we use a coupling, that is, equivalent r. v.’s defined on a common probability space [19]. The stochastic relations are sufficient for the analysis below to be correct, and for this reason we mainly do not specify the type of the relations between the corresponding r.v.s.

The next theorem gives the upper and lower bounds for the stationary workload W in the original retrial system $\Sigma$.

Theorem 1. 

Consider the zero initial state systems ${\Sigma }^{\left(1\right)},{\Sigma }^{\left(2\right)}$, and Σ; that is,

$$W_1^{\left(1\right)}=W_1=W_1^{\left(2\right)}=0.$$

(6)

Then, under stability condition (2),

$$W^{\left(1\right)}⩽W⩽W^{\left(2\right)}.$$

(7)

Proof. 

As shown in [31], condition (2) indeed implies stability of the system ${\Sigma }^{\left(2\right)}$, which in turn leads to stability of the original system. Additionally, note that $\rho <1$ is a well-known stability criterion of the system ${\Sigma }^{\left(1\right)}$, and thus, this system is stable under condition (2) as well. Moreover, it has been proved in [31] (Theorem 3) that the workload $W^{\left(2\right)}$ (stochastically) dominates the workload W, and it then follows that the upper bound in (7) is established.

Now, we establish the lower bound in (7). This bound seems intuitive, and indeed, the proof is based on a direct application of the following version of the Lindley recursion defining the workload sequence in the original system $\Sigma$ at the arrival instants $t_n$:

$$\begin{array}{c}\hfill W_{n+1}=max(0,W_n+S_n-Z_n),n⩾1,\end{array}$$

(8)

where $S_n$ is the service time of the nth arrived customer and $Z_n$ is the busy time of the server within interval $\left[t_n{t}_{n+1}\right]$, which in turn equals the amount of work leaving the system in this interval. Now we use a coupling allowing to take the arrival instants $\left\{t_n^{\left(1\right)}\right\}$ and the iid service times $\left\{S_n^{\left(1\right)}\right\}$ in the system ${\Sigma }^{\left(1\right)}$ in such a way that the interarrival times $T_n=T_n^{\left(1\right)}$ and service times $S_n=S_n^{\left(1\right)}$ are w.p.1 for $n⩾1$. Thus, we will not distinguish the corresponding variables in both systems. The workload sequence in the system ${\Sigma }^{\left(1\right)}$ satisfies the classic Lindley recursion:

$$\begin{array}{c}\hfill W_{n+1}^{\left(1\right)}=max(0,W_n^{\left(1\right)}+S_n-T_n),n⩾1.\end{array}$$

(9)

It is evident that $Z_n⩽T_n$, and it then immediately follows by induction on n that

$$\begin{array}{c}\hfill W_n^{\left(1\right)}⩽W_n,n⩾1.\end{array}$$

(10)

By the stationarity, the latter inequality holds for the stationary versions of the workloads, that is, for W and $W^{\left(1\right)}$, and the proof is completed. □

2.3. Waiting-Time Distribution for Systems with Finite Mixtures

In this section, we consider the waiting time distribution in the $M/G/1$ systems ${\Sigma }^{\left(1\right)}$ and ${\Sigma }^{\left(2\right)}$ with Poisson input with rate $\lambda$ using the celebrated Pollaczek–Khinchine formula given below.

Consider the system ${\Sigma }^{\left(1\right)}$ with service times ${\left\{S_n\right\}}_{n⩾1}$ having finite-mixture representation (3). It then follows from (3) that the (generic) service time S has density

$$f_S\left(x\right)=\sum _{k=1}^M{p}_k{f}_{S\left(k\right)}\left(x\right),$$

(11)

and denoting the tail distribution by $\overline{F}=1-F$,

$${\overline{F}}_S\left(x\right)=\sum _{k=1}^M{p}_k{\overline{F}}_{S\left(k\right)}\left(x\right).$$

(12)

It follows from (3) that the average service time $\mathrm{E}S$ satisfies

$$\mathrm{E}S=\sum _{k=1}^M{p}_k\mathrm{E}S\left(k\right).$$

Denoting by $\mu =1/\mathrm{E}S$ the service rate of the mixture (3) and by ${\mu }_k=1/\mathrm{E}S\left(k\right)$ the service rates of the kth component, we obtain easily from (12) that the service rate is

$$\mu ={\left[\sum _{k=1}^M\frac{p_k}{{\mu }_k}\right]}^{-1}.$$

(13)

In the remaining part of this section, we study the Pollaczek–Khinchine formula for the M/G/1 system with a finite-mixture service-time distribution. To do so, we introduce the Laplace–Stieltjes transform (LST)

$${\psi }_{S_e}\left(z\right)={\int }_0^{\infty }{e}^{-zt}d{F}_{S_e}\left(t\right),$$

(14)

where $F_{S_e}$ is the so-called integrated tail distribution having density

$$f_{S_e}\left(x\right)=\mu {\overline{F}}_S\left(x\right),x⩾0.$$

(15)

The distribution $F_{S_e}$ corresponds to the stationary overshoot in the renewal process generated by the iid sequence of service times $\left\{S_n\right\}$; see, for instance, [19].

Now we express the target LST ${\psi }_{S_e}\left(z\right)$ through the LST ${\psi }_{S_e\left(k\right)}\left(z\right)$ corresponding (in obvious notation) to the integrated tail distributions of the mixture components. It follows from (12)–(15) that

$${\psi }_{S_e}\left(z\right)=\mu {\int }_0^{\infty }{e}^{-zt}{\overline{F}}_S\left(t\right)dt=\mu \sum _{k=1}^M{p}_k{\int }_0^{\infty }{e}^{-zt}{\overline{F}}_{S\left(k\right)}\left(t\right)dt=\sum _{k=1}^M\frac{{\rho }_k}{\rho }{\psi }_{S_e\left(k\right)}\left(z\right).$$

(16)

Note that the LST (16) is a linear combination of the LST of the mixture components; however, the coefficients differ from the original mixing coefficients $p_1,\cdots ,p_M$.

Now, we plug (16) into the celebrated Pollaczek–Khinchine formula for the LST ${\psi }_{W^{\left(1\right)}}\left(z\right)$ of the d.f. of the stationary workload $W^{\left(1\right)}$ in the system ${\Sigma }^{\left(1\right)}$:

$${\psi }_{W^{\left(1\right)}}\left(z\right)=\frac{1-\rho }{z(1-\rho {\psi }_{S_e}\left(z\right))}.$$

(17)

It gives the following expression in the terms of the mixture components.

$${\psi }_{W^{\left(1\right)}}\left(z\right)=\frac{1-\rho }{z\left(1-\rho {\sum }_{k=1}^M\frac{{\rho }_k}{\rho }{\psi }_{S_e\left(k\right)}\left(z\right)\right)}=\frac{1-\rho }{z\left(1-{\sum }_{k=1}^M{\rho }_k{\psi }_{S_e\left(k\right)}\left(z\right)\right)}.$$

(18)

We formulate the obtained result as the following statement that we use in Section 3.

Lemma 1. 

In an $M/G/1$ system ${\Sigma }^{\left(1\right)}$ with the generic service time as a finite mixture (3), the LST of the stationary workload W is given by expression (18).

To establish a similar result for ${\Sigma }^{\left(2\right)}$, we need to obtain the corresponding expression for the LST of the generic service time $S_e^{\left(2\right)}$ defined in (4) and the corresponding LST of the integrated tail distribution $S_e^{\left(2\right)}$. By the properties of the LST (see, e.g., [32]), it follows from (4) that

$${\psi }_{S^{\left(2\right)}}\left(z\right)={\psi }_S\left(z\right)\frac{{\mu }_0}{{\mu }_0+z}.$$

(19)

Consider now $S_e^{\left(2\right)}$, and note that by properties of the LST of the integrated tail distribution (see, e.g., [33]),

$${\psi }_{S_e^{\left(2\right)}}\left(z\right)=\frac{1-{\psi }_{S^{\left(2\right)}}\left(z\right)}{z\mathrm{E}(S+{\xi }_0)}=\frac{1-{\psi }_S\left(z\right)\frac{{\mu }_0}{{\mu }_0+z}}{z\mathrm{E}(S+{\xi }_0)}=\frac{{\mu }_0}{{\mu }_0+z}\left(\frac{1-{\psi }_S\left(z\right)}{z\mathrm{E}(S+{\xi }_0)}+\frac{\mathrm{E}{\xi }_0}{\mathrm{E}(S+{\xi }_0)}\right).$$

(20)

It follows from (20), using (16), that

$${\psi }_{S_e^{\left(2\right)}}\left(z\right)=\frac{\mathrm{E}S}{\mathrm{E}(S+{\xi }_0)}\sum _{k=1}^M\frac{{\rho }_k}{\rho }{\psi }_{S_e\left(k\right)}\left(z\right)\frac{{\mu }_0}{{\mu }_0+z}+\frac{\mathrm{E}{\xi }_0}{\mathrm{E}(S+{\xi }_0)}\frac{{\mu }_0}{{\mu }_0+z}.$$

(21)

It can be seen in (21) that $S_e^{\left(2\right)}$ is indeed a finite mixture of the exponential component ${\xi }_0$ and the sums $S\left(k\right)+{\xi }_0$ for $k=1,\cdots ,M$. This result has a clear intuitive interpretation in terms of a renewal process, with $S+{\xi }_0$ being generic renewal interval and $S_e^{\left(2\right)}$ being the stationary residual renewal time. Now, plugging (21) into (17) (and replacing $S_e$ with $S_e^{\left(2\right)}$ and $\rho$ with ${\rho }^{\left(2\right)}$) and denoting

$$p_0=\frac{\mathrm{E}S}{\mathrm{E}S+\mathrm{E}{\xi }_0},$$

(22)

we arrive at the following expression:

$${\psi }_{W^{\left(2\right)}}=\frac{1-{\rho }^{\left(2\right)}}{z\left(1-{\rho }^{\left(2\right)}\left(p_0{\sum }_{k=1}^M\frac{{\rho }_k}{\rho }{\psi }_{S_e\left(k\right)}\left(z\right)+1-p_0\right)\frac{{\mu }_0}{{\mu }_0+z}\right)}.$$

Some straightforward manipulations lead to the following statement.

Lemma 2. 

In an $M/G/1$ system ${\Sigma }^{\left(2\right)}$ with the generic service time given in (4), the LST of the stationary workload $W^{\left(2\right)}$ is given by

$${\psi }_{W^{\left(2\right)}}=\frac{1-\rho -\frac{\lambda }{{\mu }_0}}{z\left(1-\frac{{\mu }_0}{{\mu }_0+z}\left({\sum }_{k=1}^M{\rho }_k{\psi }_{S_e\left(k\right)}\left(z\right)+\frac{\lambda }{{\mu }_0}\right)\right)}.$$

(23)

3. Retrial System with Pareto Service-Time Distribution

In this section, we assume that class-k customers in the original retrial system $\Sigma$ have Pareto service-time distribution (denoted by $Pareto({\alpha }_k,{\beta }_k)$) with d.f.

$$F_{S\left(k\right)}\left(x\right)=1-{\left(\frac{{\beta }_k}{{\beta }_k+x}\right)}^{{\alpha }_k},x⩾0,{\alpha }_k,{\beta }_k>0,k=1,\cdots ,M.$$

(24)

Hereafter, to avoid unnecessary technical details, we assume ${\alpha }_k$ is not an integer; $k=1,\cdots ,M$. It can be obtained from (24) (see [34]) that

$$\begin{array}{cc}\hfill {\psi }_{S\left(k\right)}& =1-{\left({\beta }_{k}z\right)}^{{\alpha }_k}{e}^{{\beta }_{k}z}\mathsf{\Gamma }(1-{\alpha }_k,{\beta }_{k}z),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\psi }_{S_e\left(k\right)}& =({\alpha }_k-1){\left({\beta }_{k}z\right)}^{{\alpha }_k-1}{e}^{{\beta }_{k}z}\mathsf{\Gamma }(1-{\alpha }_k,{\beta }_{k}z),\hfill \end{array}$$

(26)

where $\mathsf{\Gamma }(a,z)={\int }_z^{\infty }{t}^{a-1}{e}^{-t}dt$ is the upper incomplete gamma function.

To study the stationary workload in the system $\Sigma$, we explicitly obtain the workload distribution in the minorant system ${\Sigma }^{\left(1\right)}$ and construct the LST of the stationary workload in the system ${\Sigma }^{\left(2\right)}$. We start with the minorant system.

To obtain an explicit expression for the steady-state workload distribution $F_{W^{\left(1\right)}}$ in the system ${\Sigma }^{\left(1\right)}$, we recall that, by construction, ${\Sigma }^{\left(1\right)}$ has finite mixture distribution (12) of the service times and the same Poisson input as the original system $\Sigma$.

The result below elaborates on the representation obtained in Lemma 1 and relies on [34], which, in turn, uses [35,36] for explicit expressions of the LST of Pareto service-time distribution. Since our result is essentially a proof of [34] extended to the finite-mixture case, we repeat the proof only briefly and refer to [34] for necessary details.

Theorem 2. 

The steady-state workload $W^{\left(1\right)}$ in an M/G/1 system with a finite mixture (12), where $S\left(k\right)$ are $Pareto({\alpha }_k,{\beta }_k)$, $k=1,\cdots ,M$, which have the following distribution:

$$F_{W^{\left(1\right)}}\left(x\right)=1-\rho (1-\rho ){\int }_0^{\infty }\frac{e^{-xu}}{u}\frac{\tilde{I}\left(u\right)}{{(1-\rho \tilde{R}\left(u\right))}^2+{\left(\pi \rho \tilde{I}\left(u\right)\right)}^2}du,$$

(27)

where ρ is given in (1),;

$$\tilde{R}\left(u\right)=\sum _{k=1}^M\frac{{\rho }_k}{\rho }R({\beta }_{k}u,{\alpha }_k-1)and\tilde{I}\left(u\right)=\sum _{k=1}^M\frac{{\rho }_k}{\rho }I({\beta }_{k}u,{\alpha }_k-1),$$

with ${\rho }_k$ defined in (1), $k=1,\cdots ,M$; and

$$I(x,a)=\frac{x^a{e}^{-x}}{\mathsf{\Gamma }\left(a\right)},R(x,a)={}_1{F}_1(1,1-a,-x)-\pi I(x,a)cot\left(\pi a\right),$$

(28)

where ${}_1{F}_1(a,b,z)$ is confluent hypergeometric function of the first kind (also known as the Kummer function $M(a,b,z)$ [37]),

$${}_1{F}_1(a,b,z)=\sum _{i=1}^{\infty }\frac{{\left(a\right)}_i}{{\left(b\right)}_{i}i!}{z}^i,$$

(29)

and ${\left(a\right)}_i={\prod }_{j=0}^{i-1}(a+j)$, ${\left(a\right)}_0=1$—is the Pochhammer symbol (rising factorial) [37].

Before proving Theorem 2, we note that (27) is an extension of the result (26) in [34] to the finite-mixture case. Since the original result of [34] is required for the proof, we discuss it in brief hereafter. In [34], the stationary workload distribution $F_{\tilde{W}}$ in an $M/G/1$ system with a Poisson input with rate $\lambda$, $Pareto(\alpha ,\beta )$ service-time distribution (for non-integer $\alpha >1$), and the load coefficient

$$\tilde{\rho }=\lambda \beta /(\alpha -1),$$

is given in the following explicit form:

$$F_{\tilde{W}}\left(x\right)=1-{\int }_0^{\infty }\frac{\tilde{\rho }(1-\tilde{\rho })u^{\alpha -2}}{\mathsf{\Gamma }(\alpha -1)H_1(u,\alpha ,\tilde{\rho })}{e}^{-(1+x/\beta )u}du,$$

(30)

where function $H_1$ is defined as

$$H_1(x,\alpha ,\rho )={\left[1-\rho R(x,\alpha -1)\right]}^2+{\left[\pi \rho I(x,\alpha -1)\right]}^2,$$

$I(x,a)$ satisfies (28), and function $R(x,a)$ is defined as

$$R(x,a)=1+\sum _{r=1}^{\infty }\frac{x^r}{(a-1)\cdots (a-r)}-I(x,a)cot\left(\pi a\right).$$

(31)

It is clear from (29) that the definition of $R(x,a)$ in (31) is exactly the same as in (28) (it is also noted implicitly in [34]).

Proof of Theorem 2. 

We start with expression (18). Inversion of the LST can be performed by the so-called Bromwich complex integral [34]:

$$F_{W^{\left(1\right)}}\left(x\right)=\frac{1}{2\pi i}{\int }_{s-i\infty }^{s+i\infty }{e}^{-xz}{\psi }_{W^{\left(1\right)}}\left(z\right)dz,$$

(32)

where $s>0$ is large enough. It was shown in [34] that (32) can be evaluated as

$$F_{W^{\left(1\right)}}\left(x\right)=1-\frac{1}{2\pi i}{\int }_0^{\infty }{e}^{-xu}\left({\psi }_{W^{\left(1\right)}}\left(u{e}^{i\pi }\right)-{\psi }_{W^{\left(1\right)}}\left(u{e}^{-i\pi }\right)\right)du.$$

(33)

Expression (33) has been obtained in [34] for a system with Pareto service time; however, the arguments can be extended to a finite mixture (12), as we show below. Note that, if needed, we repeat the statements given in [34] for distributions $Pareto({\alpha }_k,{\beta }_k)$, $k=1,\cdots ,M$.

The key argument in [34] is the result that $1-\tilde{\rho }{\psi }_{{\tilde{S}}_e}\left(z\right)=0$ has no zeros in the complex plane, where r.v. ${\tilde{S}}_e$ is $Pareto(\alpha ,\beta )$ with $\alpha >1$ and $\tilde{\rho }\in [0,1)$ is a constant. We repeat this key argument for the real analytic function $1-\tilde{\rho }{\psi }_{S_e}\left(z\right)$, where ${\psi }_{S_e}\left(z\right)$ is represented as in (16). Let $z_1=x_1+i{y}_1$ be a zero of the equation $1-\tilde{\rho }{\psi }_{S_e}\left(z\right)$; then ${\overline{z}}_1=x_1-i{y}_1$ is also a zero, which gives

$$\tilde{\rho }({\psi }_{S_e}\left(z_1\right)-{\psi }_{S_e}\left({\overline{z}}_1\right))=0.$$

(34)

Using (16), Equation (34) can be rewritten as

$$\tilde{\rho }\sum _{k=1}^M\frac{{\rho }_k}{\rho }({\psi }_{S_e\left(k\right)}\left(z_1\right)-{\psi }_{S_e\left(k\right)}\left({\overline{z}}_1\right))=0.$$

(35)

It is shown in [34] that for all $k=1,\cdots ,M$, transform (26), on $\mathbb{D}=\mathbb{C}\setminus (-\infty ,0]$ (complex plane with negative axis removed), is equivalent to

$${\psi }_{S_e\left(k\right)}\left(z\right)=\frac{{\alpha }_k-1}{\mathsf{\Gamma }\left({\alpha }_k\right)}{\int }_0^{\infty }\frac{t^{{\alpha }_k-1}{e}^{-t}}{(t+{\beta }_{k}z)}dt,z\in \mathbb{D}.$$

(36)

Using (36), Equation (35) can be written, after some algebra, as

$$2i{y}_1\frac{\tilde{\rho }}{\rho }\sum _{k=1}^M\frac{{\lambda }_k{\beta }_k^2}{\mathsf{\Gamma }\left({\alpha }_k\right)}{\int }_0^{\infty }\frac{t^{{\alpha }_k-1}{e}^{-t}}{{(t+{\beta }_k{x}_1)}^2+{\left({\beta }_k{y}_1\right)}^2}dt=0.$$

(37)

The remaining arguments follow [34]. Namely, if $y_1=0$, then $z_1$ is real; however, since for any $k=1,\cdots ,M$, ${\psi }_{S_e\left(k\right)}\left(x\right)\le 1$ as discussed in [34], then it follows from (16) that ${\psi }_{S_e}\left(x\right)\le 1$, and hence $1-\tilde{\rho }{\psi }_{S_e}\left(z_1\right)>0$ for $\tilde{\rho }\in [0,1)$. Otherwise, if $y_1\ne 0$ and $z_i\in \mathbb{D}$, then l.h.s. of (37), being a linear combination of real non-negative integrals, is non-zero. Finally, on the negative axis $z_1=x{e}^{\pm i\pi }$ (for $x>0$), it is shown in [34] that, for $k=1,\cdots ,M$,

$${\psi }_{S_e\left(k\right)}\left(x{e}^{\pm i\pi }\right)=R({\beta }_{k}x,{\alpha }_k-1)\mp i\pi I({\beta }_{k}x,{\alpha }_k-1),$$

(38)

where the functions I and R are given in (28). Thus, for $x>0$, it follows from (16) and (28) that ${\psi }_{S_e\left(k\right)}\left(x{e}^{\pm i\pi }\right)$ has the non-zero imaginary part

$$\mp i\pi \sum _{k=1}^M\frac{{\rho }_k}{\rho }\frac{{\left({\beta }_{k}x\right)}^{{\alpha }_k-1}{e}^{-{\beta }_{k}x}}{\mathsf{\Gamma }({\alpha }_k-1)}.$$

The integral (32) is evaluated in [34] using the so-called Hankel-type contour, where the following fact is used. As the equation $1-\tilde{\rho }{\psi }_{{\widehat{S}}_e}\left(z\right)=0$ has no zeros in the complex plane, it follows that the complex integral along the path equals zero. This allows one to express (32) using parts of the aforementioned contour. Along the same arguments as in [34] (with small modifications related to the representation (16)), expression (33) can be established. Finally, from (33), using (18) and (38), after some straightforward algebraic manipulations, the statement of the theorem follows. □

Although the d.f. of $W^{\left(1\right)}$ is obtained in an explicit form, obtaining the d.f. of $W^{\left(2\right)}$ seems to be not straightforward. Instead, we suggest to apply numerical LST inversion after using explicit expressions (26) for the LST of the steady-state workload $W^{\left(2\right)}$ of the form (23) given in Lemma 2.

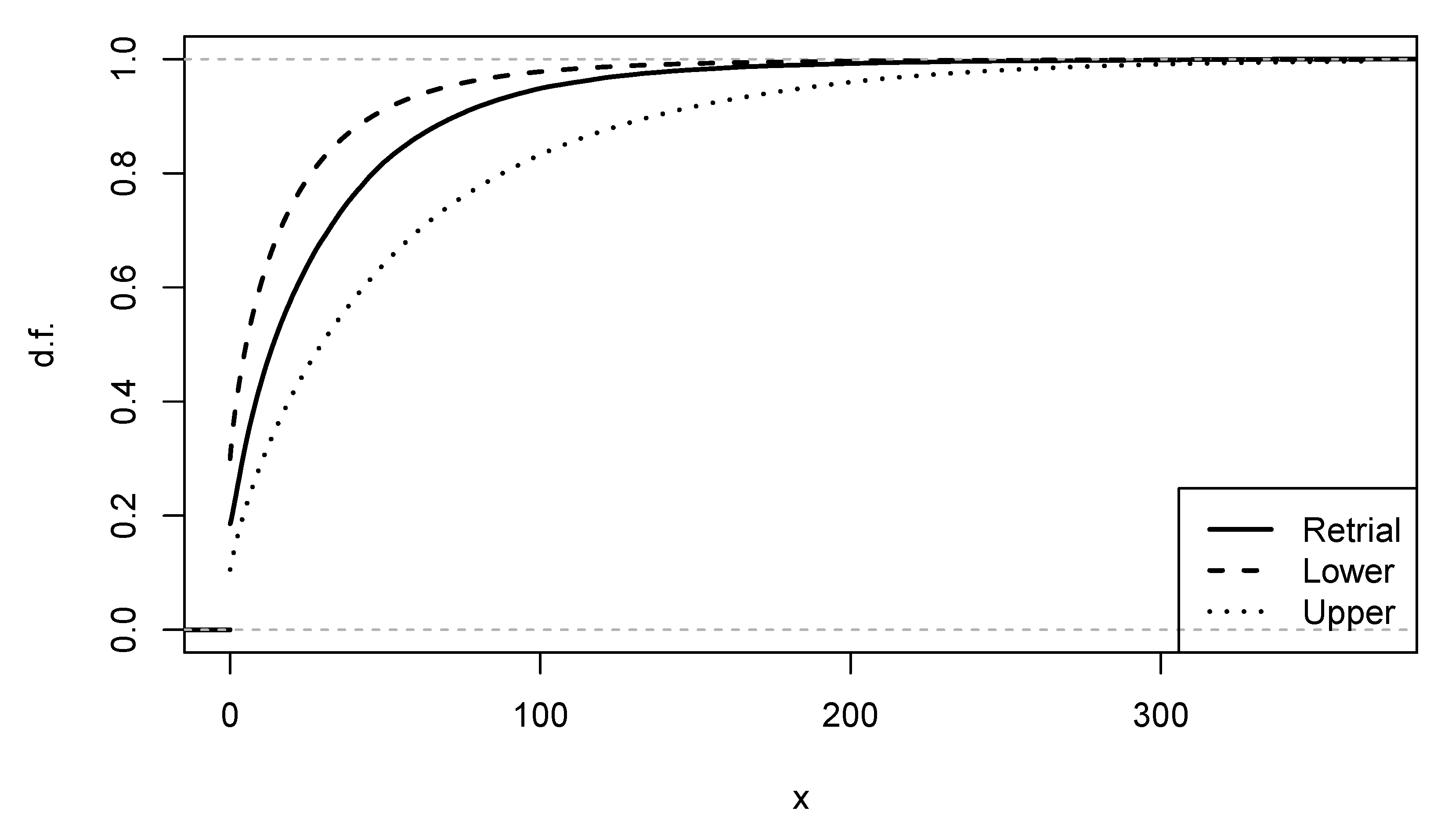
Theorem 3. 

It is worth mentioning that there exist explicit expressions for the density of mixture of Pareto and exponential distribution as in (4); see [38].

To illustrate the results obtained in Theorems 1 and 2, we performed a numerical experiment. Namely, we considered two-class system with the following parameters:

$${\alpha }_1=3.3,{\beta }_1=10,{\alpha }_2=4.3,{\beta }_2=2,p_1=0.6,{\eta }_1=1,{\eta }_2=2,\rho =0.7.$$

(39)

Further, in the system ${\Sigma }^{\left(1\right)}$, we take the load to be $\rho$, implying $\lambda \approx 0.246$ (to guarantee such a load). In the system ${\Sigma }^{\left(2\right)}$, we found that ${\mu }_0\approx 1.246$. Hence, ${\rho }_2\approx 0.897$ and all systems are stable. Further, we used an explicit expression (30) to obtain the distribution of the steady-state workload in the system ${\Sigma }^{\left(1\right)}$ and used discrete-event simulation to calculate the empirical distributions of the steady-state workloads in systems $\Sigma$ and ${\Sigma }^{\left(2\right)}$. Note that we use recursion (8) and ${10}^6$ events to obtain the estimates for the steady-state workload d.f. in the system ${\Sigma }^{\left(2\right)}$. The results of this experiment depicted on Figure 1 demonstrate the theoretical results nicely.

4. Asymptotic Analysis of the Workload

In this section, we establish the tail asymptotics for the stationary workload distribution in the retrial system $\Sigma$ in the case of a heavy-tailed (Pareto) service time distribution. To do this, we used the properties of the bounds established in Section 2 and Section 3. We obtained the limiting distribution of the workload maxima observed upon customer arrivals, and we elaborate on the extremal index of the workload sequence. As me mentioned above, the extremal index is an important QoS characteristic of the system.

4.1. Maxima and Extremal Index

First, we give in brief some necessary background. It is said that the maximum $M_n=max(X_1,\cdots ,X_n)$ of an iid sequence ${\left\{X_n\right\}}_{n⩾1}$ belongs to the domain of attraction for maxima (MDA) of a distribution G, if G is the limit of $F_{M_n}$ under appropriate linear normalisation [15], i.e., for every x:

$$F_X^n\left(u_n\left(x\right)\right)\to G\left(x\right),n\to \infty ,$$

(40)

where $F_X$ is the distribution of the (generic) element X, and

$$u_n\left(x\right)=a_{n}x+b_n,$$

(41)

is the (linear) normalizing sequence. The key result is the so-called extremal-types theorem [15] ([Theorem 1.4.2]), which states that the limiting distribution G, if it exists, may be only of the following extreme-value types: Gumbel distribution, Frechet distribution, or reversed Weibull distribution. The result (40) is a particular case of a more general result that relates the properties of maxima $M_n$ to asymptotic properties of the tail distribution ${\overline{F}}_X$ of X. More exactly, if $\tau \in [0,\infty ]$ and ${\left\{u_n\right\}}_{n⩾1}$ is such a sequence of real numbers that

$$\underset{n\to \infty }{lim}n{\overline{F}}_X\left(u_n\right)=\tau ,$$

(42)

then

$$\underset{n\to \infty }{lim}{F}_{M_n}\left(u_n\right)=e^{-\tau },$$

(43)

and conversely, (43) implies (42) (see [15] ([Theorem 1.5.1])). Using the linear sequence (41), the value $\tau$ may be obtained explicitly (as a function of x) for all three extreme value types. In particular, $\tau =x^{-a}$ for the Frechet (type II) MDA. Thus, by constructing coefficients $a_n,b_n(n⩾1)$ in (41) such that (42) holds, it is then straightforward to establish the limiting distribution of maxima in (43).

While the limit in (43) is established for an iid sequence ${\left\{X_n\right\}}_{n⩾1}$, a similar result may be obtained for a stationary sequences (possibly with dependent r.v.s), which are commonly studied by queueing theory under mild mixing conditions that guarantee an appropriate decay rate for the dependence (for more details, see [15]). In such a case, an appropriate modification of (43) is

$$\underset{n\to \infty }{lim}{F}_{M_n}\left(u_n\right)=e^{-\theta \tau },$$

(44)

where the parameter $\theta \in [0,1]$ is the so-called extremal index [13]. Note that $\theta =1$ for the iid sequence. The limits (42) and (44) imply the following basic relation for the extremal index:

$$\theta =\underset{n\to \infty }{lim}\frac{log{F}_{M_n}\left(u_n\right)}{nlogF\left(u_n\right)}.$$

(45)

4.2. Extremes in Queues with Subexponential Mixed Service Times

One of the important (dependent) sequences is the sequence ${\left\{W_n\right\}}_{n⩾1}$ of the stationary workloads at the arrival epochs. To study the limiting distribution of the maximum or the extremal index of such a sequence, the asymptotics of the type (42) for $F_W$ should be established, where W is a stochastic copy of any $W_n$. We note that while the d.f. $F_{W^{\left(1\right)}}$ of the stationary workload in the system ${\Sigma }^{\left(1\right)}$ (being an $M/G/1$ system) is obtained in explicit form in (27), the corresponding d.f. for a stationary workload in the system ${\Sigma }^{\left(2\right)}$ is available only in the form of the LST.

The Pareto distribution belongs to the family of the so-called subexponential distributions: their tails decay slower than any exponential; see, e.g., [18]. The known result for the classical $GI/G/1$ system (and in particular, for an $M/G/1$ system) is the so-called tail equivalence of the stationary workload, denoted by $\tilde{W}$, and the subexponential residual service time ${\tilde{S}}_e$ having integrated tail distribution [18,19]

$$\mathrm{P}(\tilde{W}>x)\sim \frac{\tilde{\rho }}{1-\tilde{\rho }}\mathrm{P}({\tilde{S}}_e>x),x\to \infty ,$$

(46)

where $\tilde{\rho }$ is the load coefficient and $a\sim b$ means $a/b\to 1$. It is straightforward to apply this result to the system ${\Sigma }^{\left(1\right)}$, where service time S is a finite mixture with the tail distribution given in (12). In such a case, recall from (16) that $S_e$ is a similar mixture with coefficients ${\rho }_1/\rho ,\cdots ,{\rho }_M/\rho$, and provided $S_e\left(k\right)$ are all subexponential, (46) turns into

$$\mathrm{P}(W^{\left(1\right)}>x)\sim \frac{\rho }{1-\rho }\sum _{k=1}^M\frac{{\rho }_k}{\rho }{\overline{F}}_{S_e\left(k\right)}\left(x\right)=\sum _{k=1}^M\frac{{\rho }_k}{1-\rho }{\overline{F}}_{S_e\left(k\right)}\left(x\right),x\to \infty .$$

(47)

We formulate the obtained result as the following statement.

Lemma 3. 

If $\rho <1$, service time S with tail d.f. (12) has a finite mean, and moreover, if $S\left(k\right)$ and $S_e\left(k\right)$ are subexponential, $k=1,\cdots ,M$, then the tail distribution of the stationary waiting time $W^{\left(1\right)}$ in the system ${\Sigma }^{\left(1\right)}$ satisfies

$$\mathrm{P}(W^{\left(1\right)}>x)\sim \sum _{k=1}^M\frac{{\rho }_k}{1-\rho }{\overline{F}}_{S_e\left(k\right)}\left(x\right),x\to \infty .$$

(48)

While Lemma 3 is directly applicable to ${\Sigma }^{\left(1\right)}$, it is rather straightforward to use it for the system ${\Sigma }^{\left(2\right)}$ as well, with a small modification. Indeed, it is seen in (21) that the value $S_e^{\left(2\right)}$ in the system ${\Sigma }^{\left(2\right)}$ is a mixture of the exponential r.v. ${\xi }_0$ and the sum of the type $S_e\left(k\right)+{\xi }_0$. In turn, it follows by the convolution closure of the subexponential class [39] ([Theorem 5.1]) that each summand $S_e\left(k\right)+{\xi }_0$ is tail-equivalent to the (subexponential) variable $S_e\left(k\right)$. It remains to note that the exponential component ${\xi }_0$ presented in the mixture (21) can be omitted in the current asymptotic analysis, since the tail of subexponential distribution is ‘heavier’ than the any exponential tail; see, e.g., property (1.4) in [39]. Moreover, since the ‘upper’ system ${\Sigma }^{\left(2\right)}$ has different loads ${\rho }^{\left(2\right)}$ given in (5), one should use ${\rho }^{\left(2\right)}$ instead of $\rho$ in (46). Thus, Lemma 3 remains valid for the system ${\Sigma }^{\left(2\right)}$ with subexponential components $S_e\left(k\right)$ as well. However, since the mixing coefficients in (21) slightly differ from the ones obtained in (16), the corresponding asymptotics becomes

$$\mathrm{P}(W^{\left(2\right)}>x)\sim \sum _{k=1}^M\frac{{\rho }_k}{1-{\rho }^{\left(2\right)}}{\overline{F}}_{S_e\left(k\right)}\left(x\right),x\to \infty .$$

(49)

It is straightforward to see that, since ${\rho }^{\left(2\right)}>\rho$, the mixing coefficients in asymptotic relations (49) and (48) coincide with the ordering (7) obtained in Theorem 1.

4.3. Extremes in Retrial Systems with Pareto Service Times

We are now ready to formulate the limiting results for workload maxima in the original retrial system $\Sigma$ where class-k service times $S\left(k\right)$ are $Pareto({\alpha }_k,{\beta }_k)$ with d.f. given in (24). W.o.l.o.g. assume that

$${\alpha }_1⩾\cdots ⩾{\alpha }_M⩾1.$$

It is easy to check then that $S_e\left(k\right)$ have d.f.:

$$F_{S_e\left(k\right)}\left(x\right)=\frac{{\alpha }_k-1}{{\beta }_k}\underset{0}{\overset{x}{\int }}{\left(\frac{{\beta }_k}{{\beta }_k+y}\right)}^{{\alpha }_k}dy=1-{\left(\frac{{\beta }_k}{{\beta }_k+x}\right)}^{{\alpha }_k-1},x⩾0.$$

(50)

By substituting (50) in the asymptotics (48), we obtain

$${\overline{F}}_{W^{\left(1\right)}}\left(x\right)\sim \sum _{k=1}^M\frac{{\rho }_k}{1-\rho }{\left(\frac{{\beta }_k}{{\beta }_k+x}\right)}^{{\alpha }_k-1}\sim \frac{{\rho }_M}{1-\rho }{\left(\frac{{\beta }_M}{{\beta }_M+x}\right)}^{{\alpha }_M-1},x\to \infty .$$

(51)

Similarly, it follows from (49) that

$${\overline{F}}_{W^{\left(2\right)}}\left(x\right)\sim \sum _{k=1}^M\frac{{\rho }_k}{1-{\rho }^{\left(2\right)}}{\left(\frac{{\beta }_k}{{\beta }_k+x}\right)}^{{\alpha }_k-1}\sim \frac{{\rho }_M}{1-{\rho }^{\left(2\right)}}{\left(\frac{{\beta }_M}{{\beta }_M+x}\right)}^{{\alpha }_M-1}.$$

(52)

In the next theorem, we obtain the MDA for the workload in the stationary systems ${\Sigma }^{\left(1\right)}$ and ${\Sigma }^{\left(2\right)}$.

Theorem 4. 

Assume stability condition (2) holds and the (per-class) service times have distribution (24). Then, the limiting distribution of the maximal workload in the systems ${\Sigma }^{\left(i\right)},i=1,2,$ belongs to the Frechet-type distribution: $F_{W_{n_{max}}^{\left(i\right)}}\in MDA\left({\mathsf{\Phi }}_{{\alpha }_M-1}\right)$.

Proof. 

First we find the limiting distribution of $W_{n_{max}}^{\left(1\right)}=max(W_1^{\left(1\right)},\cdots ,W_n^{\left(1\right)})$ in the system ${\Sigma }^{\left(1\right)}$. By (51), the tail ${\overline{F}}_{W^{\left(1\right)}}$ is asymptotically equivalent to the tail ${\overline{F}}_{S_e\left(M\right)}$. Then, by closure properties of $MDA\left(\mathsf{\Phi }\right)$ (see [13] ([Proposition 3.3.9])), it follows that the maxima of the iid sequence sampled from ${\overline{F}}_{W^{\left(1\right)}}$ belongs to the domain $MDA\left({\mathsf{\Phi }}_{{\alpha }_M-1}\right)$, which is the MDA of $S_e\left(M\right)$ by [13] ([Theorem 3.3.7]). Then, by [15] ([Corollary 3.7.3]), the original (dependent) stationary sequence ${\left\{W_n^{\left(1\right)}\right\}}_{n\ge 1}$ belongs to the same domain $MDA\left({\mathsf{\Phi }}_{{\alpha }_M-1}\right)$. We can also demonstrate the result for $S_e\left(M\right)$ explicitly by using (42) and constructing the sequence $u_n\left(x\right)={\beta }_{M}x{n}^{1/({\alpha }_M-1)}-{\beta }_M,n⩾1$. Using $u_n\left(x\right)$ in (42), we have

$$\begin{array}{ccc}\hfill n{\overline{F}}_{S_e\left(M\right)}\left(u_n\left(x\right)\right)& =& n{\left(\frac{{\beta }_M}{{\beta }_M+u_n\left(x\right)}\right)}^{{\alpha }_M-1}=\hfill \\ & =& n{\left(\frac{{\beta }_M}{{\beta }_{M}x{n}^{1/({\alpha }_M-1)}}\right)}^{{\alpha }_M-1}\to \hfill \\ & \to & x^{-{\alpha }_M+1},asn\to \infty .\hfill \end{array}$$

(53)

The maximal workload in the system ${\Sigma }^{\left(2\right)}$ is considered similarly, since, by (52), $W^{\left(2\right)}$ is tail-equivalent to the same component $S_e\left(M\right)$. Thus, it remains to replace index ${}^{\left(1\right)}$ with ${}^{\left(2\right)}$ in the proof. □

The following discussion is not completely rigorously justified, and thus is given as a conjecture. Since the inequalities $W^{\left(1\right)}⩽W⩽W^{\left(2\right)}$ are satisfied (see Theorem 1) and both $W_{n_{max}}^{\left(1\right)}$ and $W_{n_{max}}^{\left(2\right)}$ have the same type of distribution ${\mathsf{\Phi }}_{{\alpha }_M-1}$, it seems natural to assume that $W_{n_{max}}$ has the same MDA of ${\mathsf{\Phi }}_{{\alpha }_M-1}$. However, the convergence (42) needs to be demonstrated for the (unknown) function $F_W$, and the upper/lower bounds seem insufficient for this purpose due to a non-negligible gap between those d.f.s. Moreover, the monotonicity of the workload in all three systems and relation (45) allows one to assume that the following inequality holds good:

$$\begin{array}{c}\hfill {\theta }_{W^{\left(1\right)}}⩾{\theta }_W⩾{\theta }_{W^{\left(2\right)}}.\end{array}$$

(54)

The inequalities (54) allow one to obtain the appropriate bounds for the extremal index ${\theta }_W$, since the indices for the ‘upper’ and ‘lower’ system can be explicitly computed, as is stated in [23]. With a slight abuse of the notation, we state the desired result (which goes back to [40] ([Section III.7.4])) and refer the reader to [23] ([Section 4]) for more details. The extremal index ${\theta }_{W^{\left(i\right)}}$ of system ${\Sigma }^{\left(i\right)},i=1,2,$ is obtained as

$${\theta }_{W^{\left(i\right)}}=\frac{{\gamma }_i(1-{\rho }^{\left(i\right)})}{{\gamma }_i+\lambda },$$

(55)

where ${\rho }^{\left(1\right)}=\rho$ and ${\gamma }_i>0$ is the unique real solution of the nonlinear equation

$${\psi }_{S^{\left(i\right)}}(-\gamma )=1+\frac{\gamma }{\lambda },$$

(56)

where $S^{\left(1\right)}=S$ is used for notation convenience, and the corresponding LST are given explicitly in (25) and (19), respectively.

In this regard, it is interesting to note that the lower bound, ${\Sigma }^{\left(1\right)}$, may be treated as the limiting case of the system ${\Sigma }^{\left(2\right)}$ as ${\mu }_0\to \infty$, which opens the way of studying the parametric sensitivity of the systems to the retrial rates. This topic, however, goes far beyond the present paper, and we leave it for future research.

5. Discussion and Conclusions

The lower and upper (stochastic) bounds for the stationary workload W in the multiclass orbit-queue via stationary workloads of minorant and majorant classic $M/G/1$ systems were derived. These results were applied via known asymptotic of integrated tail distribution for subexponential service times to establish the extreme behaviour of stationary workload in the original retrial system.