1. Introduction
According to projections, the percentage of Thai nationals aged 65 years or older will surpass 28% in less than 30 years. This threshold is significant as it marks a country as a ‘super-aged country’ [
1]. Projections by the Office of the National Economic and Social Development Board under the Office of the Prime Minister in Bangkok anticipate a rise in the population of elderly individuals living independently and experiencing health issues [
2]. Home healthcare (HHC) is a crucial component of a proactive healthcare system, particularly for population segments who suffer from chronic illnesses or are bedridden and need long-term care [
3]. Providing care for these individuals may involve treatments by psychiatrists, delivery of injections or wound care by nurses, and delivery of rehabilitation programs by physical therapists, as well as arrangement of health-related guidance. From the perspective of sustainability and quality-of-life enhancement, visiting the elderly at home to deliver care represents a more effective utilization of human resources compared to having them visit the hospital individually.
Chiang Mai is Thailand’s second largest city after Bangkok, in both population density and economic significance. Additionally, it is the primary medical hub of the country’s northern region. According to a recent study [
4], Chiang Mai’s elderly population is currently estimated to be 20% of its total population. Approximately 38%, or 675,440 individuals out of a total population of 1,779,254, reside within the city center, a similar percentage to contemporary trends in other major urban areas around the world. The urban area of the city of Chiang Mai has 310,771 households, and approximately 20% of the population have medical requirements and have duly enrolled themselves at one of the 15 healthcare facilities dispersed across the city. Assuming that 10% of the households registered for healthcare services require regular visits from healthcare personnel, it follows that each health center will be required to schedule appointments for approximately 400 clients, and this number is increasing over time. Trying to reduce the cost while managing the scheduling and routing of this care service requires specific strategies and techniques. According to a report by Glinskaya et al. [
5], most elderly individuals in Thailand experience the aging process within their own households and receive care from their families. However, the conventional familial care structure faces growing challenges from the rise in the elderly population in relation to the working-age population. According to projections, the number of Thais aged 80 and above will increase more than six-fold, to approximately 2.5 million, over the next two decades. This group will require assistance.
The growing need for aged care services offers potential for business investment and employment opportunities. It is essential to have the ability to address problems in the provision of affordable and adequate care for elderly individuals with long-term care requirements, covering care delivered at home, within communities, and in institutional settings. From a financial perspective, the total cost must be minimized, but home healthcare is a people-centered business and focusing on cost reduction alone can result in unsatisfied staff and retention problems. One approach to solving this dilemma is to consider multiple objectives simultaneously. The contributions of this paper are to better capture the nature of the home visits, improve caretakers’ workflow efficiency, and suggest a better solution to routing and scheduling. We consider models that cover all four major aspects of these undertakings: (1) compatibility matching of patients and healthcare staff (compatibility), (2) routing for healthcare staff to visit their clients (routing), (3) meeting applicable service conditions, such as the time availability of patients and staff (time windows), and (4) the total costs of the whole system (costs). We focus on routing and scheduling and incorporate all four major aspects of home healthcare. The objective function is set to only minimize the total completion time exclusively rather than minimizing total distance to the exclusion of all else. Moreover, we provide single objective model formulation based on vehicle routing problems with time windows and a solution approach that focuses primarily on total completion time followed by total distance. Our model still minimizes the single objective function, but the proposed solution method primarily minimizes total completion time, while also trying to minimize total distance if possible. The reason is to prevent the possibility that there exists a solution that has the same total completion time but a different total distance. The solution approach contains routing operators modified to suit the objective function as well as a proof to ensure feasibility, which will reduce the overall computational time.
A VRPTW problem in any of its variations falls in the NP-hard category, requiring the use of customized heuristics in its resolution. A home healthcare system presents a highly complicated problem with numerous factors to be considered. As much of the existing literature on the vehicle routing problem with time windows (VRPTW) is focused on minimizing the distance travelled, we decided to develop a model that prioritizes the minimization of total completion time. This alternative would enhance the model’s suitability for real-world applications, as waiting-time minimization and a balanced allocation of jobs per vehicle are significant in the context of VRPTW. The process of assigning a healthcare worker to a client requires that such factors as arrival time, finishing time, and processing time be taken into consideration. The objective function can include various components such as travel cost, penalty cost, fixed cost, and staff overtime cost. Among the various objective functions considered, Wirnitzer et al. [
6] employed Gurobi optimization version 5.6 to minimize the number of nurses assigned to each tour and per patient, as well as the number of nurse switches per patient. Nasir and Kuo [
7] employed a genetic algorithm to minimize the combined costs of travel and staff assignment. In contrast, Kandakoglu et al. [
8] aimed to minimize a weighted sum of various factors, including the total distance travelled by nurses, overall travel expense, and overtime expense, as well as the maximum workload and number of working staff, in order to achieve a balanced distribution of workload. The problem is solved using the Gurobi optimization software version 8.0. In their research, Braekers et al. [
9] studied the minimization of two objectives; the first objective applies to minimizing the total travel costs accrued by nurses and the associated overtime costs, while the second involves minimizing the combined penalty cost resulting from assigning an undesirable nurse to a patient and the inconvenience scores associated with nurses’ job assignments. The problem is solved using a large neighborhood search algorithm. The authors Cissé et al. [
10] and Mascolo et al. [
11] provided comprehensive analyses on state-of-the-art HHC routing and scheduling problems by studying the literature on home visits in HHC systems. Goodarzian et al. [
12] provided state-of-the-art operations research including models and applications in home healthcare systems.
The VRPTW has garnered significant attention in the research community due to its practical relevance and applicability to real-world scenarios. Numerous heuristic approaches have been extensively investigated, and researchers remain captivated by them. Of the recently suggested techniques for addressing the VRPTW, which are above the complexity of the NP-hard VRP, the majority fall under the category of metaheuristics. The benchmark instances provided in reference [
13], commonly referred to as Solomon’s instances, can be utilized for evaluating constructed heuristics. The dataset consists of a total of 100 customers and one depot node. Additionally, a distance matrix is provided, representing the distances between each pair of nodes. Every individual customer node is assigned a specific time window, demand, and service time. The primary goal is to minimize the total distance travelled. There are three categories of Solomon’s instances. After plotting these instances, the customers in Group C instances are dispersed in groups or clusters. These instances are similar to real-world problems where customers live in geographically scattered villages. Group R instances have relatively random placement, corresponding to customers living in a large city. The customers in Group RC are randomly clustered, i.e., they appear in groups but their placement within these groups is more or less random.
The aforementioned properties can be seen in a conventional system in the real world. The application and utility of VRPTW in addressing practical problems have led to significant research efforts in developing heuristics for its solution, and a substantial number of researchers remain engaged in investigating and advancing the field of VRPTW heuristics. A model was proposed by Ahn and Shin [
14] for the purpose of minimizing the total distance in the vehicle routing problem with time windows (VRPTW). This model is based on the utilization of insertion and saving heuristics. Rochat and Taillard [
15] introduced an algorithm that relied on a probabilistic tabu search and used probabilistic techniques to enhance the effectiveness of the tabu search. Additionally, they presented the solutions obtained with their algorithm. Li and Lim [
16] implemented a metaheuristic approach using the simulated annealing algorithm and incorporated K-restart strategies as a means of enhancing the local search process. The performance of their algorithm, evaluated in the Solomon benchmark instances, shows that it has the potential to enhance existing solutions reported in the literature. Following this, Pisinger and Popke [
17] introduced the concept of an adaptive large neighborhood search (ALNS) and applied it to evaluate Solomon instances, as well as Gehring and Homberger benchmark instances [
18], specifically focusing on scenarios involving over 100 customers. Low et al. [
19] employed a genetic algorithm and conducted tests on the modified Solomon instances. The problem was adapted to align with the specific context of production and scheduling. After that, Khoo and Mohammad [
20] proposed the parallelization of ruin and recreated strategies and the use of a genetic algorithm as a means to address the vehicle routing problem with time windows (VRPTW). Addressing a variant of multiple depots vehicle routing problem, Bi et al. [
21] applied the ant lion optimizer to solve two types of logistic modes in meal delivery routing with two objectives, customer satisfaction and cost.
Table 1 presents the minimum values of the objective function obtained from the most recent literature. Note that only works that consider hard time windows, i.e., the service providers need to wait for customers to become available, are presented. The problem type is denoted by the letters C, R, or RC in the first column, representing instances with nodes in clusters, randomly placed nodes, and clusters with randomly placed nodes inside each cluster, respectively. The objective function values obtained from the most recent literature are shown in
Table 1. The first value in the table represents the total distance, followed by the required number of vehicles (in brackets). Note that some corresponding solutions are unavailable or inaccessible. We have underlined the works that provide solutions based on objective function values. The optimal results, according to the authors, are marked with “*” next to the objective value. For each instance, the minimum objective value (total distance) across all publications, regardless of the associated solutions, is shown in boldface. It is notable that all works with corresponding solutions have objective function values that are relatively higher. Note also that some of the work may truncate the distance between a node to one digit, resulting in a lower objective value than others.
The remaining sections of this paper are structured as follows:
Section 2 presents model construction, with the model being modified from the vehicle routing problem with time windows.
Section 3 describes the solution approach. The results and simulation analysis are presented in
Section 4. The case study is shown
Section 5.
Section 6 presents the conclusions.
2. Model Construction
The routing and scheduling in a home healthcare system (HHC) is based on the vehicle routing problem, where the vehicles visit all customer nodes. Each node can be visited by only one vehicle within the time frame. This particular problem involves a collection of vehicles (caretakers), denoted as , and a set of time intervals associated with each caretaker. The main goal is to determine the optimal routes for each caretaker, starting and ending at the depot location, in order to minimize the total completion time required to complete all tasks. Each patient is set to receive a single visit within a designated time frame, and each caretaker is obligated to start and finish their duties within the specified window.
The concept in a HHC system can be represented mathematically as a complete graph denoted as . In this graph, represents the set of clients or patients, ranging from 0 to , written as . The value corresponds to the starting location of the route (depot node), which is the health center. represents the set of edges in the graph, indicating the connections between different clients or patients. The provided data include the distances (duration of travel between each pair of points), as well as the amount of time required to deliver service at the respective point. The compatibility for visiting between the nodes and vehicles is given, which takes the value 1 if the caretaker is allowed to visit the patient, and otherwise, 0. The mathematical programming problem is formulated as a vehicle routing problem with time windows (VRPTW) including strict limitations on time, inspired by situations where patients have time-sensitive medical requirements and caretakers who arrive before the designated time windows will be required to wait.
The parameters used in the HHC system are as follows:
Indices:
- 0
The starting point of the route, which can be the health center
- i,j
The patients
- k
The caretaker
Parameters:
The travel time from patient to patient
The service time for patient
The start time (or available time) of patient
The finish time of patient
The requirement of patient
The capacity of all vehicles
A sufficiently large number
A compatibility matching matrix whose element means patient can be served by caretaker ; otherwise,
Variables:
1 if caretaker travels from the origin to patient ; otherwise, 0
1 if caretaker travels from node to patient ; otherwise, 0
1 if patient is the last patient visited by caretaker ; otherwise, 0
Starting (available) time of patient
Completion time of patient
Variables for subtour elimination
The problem, which can be formulated as a mixed integer linear program, is given below. The problem aims to minimize total completion time, with each caretaker following restrictions, including routing and time constraints.
The subtour elimination constraint combined with capacity constraints:
The compatibility constraints:
The starting time and time windows constraints:
The calculation of completion time:
The variable constraints:
A detailed description of the constraints is as follows: routing constraints (2)–(8) relate to the organization of caretaker routes. Constraints (2) and (3) guarantee that each caretaker starts and ends their route at the designated starting point. Constraints (4) and (5) ensure that each patient is visited and departed by only one caretaker. Constraint (6) ensures that a caretaker departs from a patient after completing their service and proceeds to the next patient. Constraints (7) and (8) are designed to eliminate subtours. Constraints (9) are compatibility-matching constraints limiting the caretaker’s ability to travel only to particular patients. The activation of constraints (10) occurs when caretaker switches from going to patient to going to patient (). In other words, the sum of the duration of patient i’s completion time (or the expected start time and service duration at patient ) and the travel time from patient to patient must be shorter than the starting time window for patient . Constraints (11) make sure that the start time of patient falls within his/her specific time window. Constraints (12) apply to the calculation of the completion times for all patients. Lastly, constraints (13) guarantee the requirements of integrality and positivity.
3. Solution Approach
As mentioned earlier, VRPTW is an extension of the vehicle routing problem which lies in the NP-hard problem category; as such, VRPTW is also an NP-hard problem. Given the NP-hard nature of the proposed problem, the exact approach cannot solve or even provide a solution when the number of nodes increases.
Our proposed algorithm begins with Phase 1, where the jobs are partitioned into clusters using a K-means algorithm. The number of clusters is predefined. Subsequently, within each cluster, the insertion procedure is employed to organize jobs in a manner that ensures there are no cases of tardiness or lateness among the assigned jobs. Positions that are unable to take on any job candidates will be considered tardy. Starting with two clusters and increasing when the inserting procedure cannot find a feasible solution, Phase 1 is iterated until all remaining tasks have been allocated; otherwise, the problem is infeasible. Phase 2 is subsequently implemented to enhance the solution by reassigning tasks (moving and swapping) either within or between clusters to achieve a more optimal outcome. When the process of swapping and moving does not lead to an improvement in the solution, it is referred to as a local optimal state for the current solution. Phase 3 involves implementing a shooting procedure, which aims to enhance the solution by randomly repositioning jobs before the next use of Phase 2. The implementation of Phase 3 is conditional upon obtaining the designated number of iterations. The procedures are summarized in
Section 3 and described in detail in the following section.
As presented in
Section 2, our model is a single objective function, which aims to exclusively minimize the total completion time. Since total completion time is the combination of the starting time, service time, and distance between nodes, minimizing the total completion time can result in a reduction in the total distance. In contrast, minimizing the total distance does not take the service time into account. Minimizing the total completion time will therefore result in simultaneous reduction of both operation time and distance. Moreover, minimizing only the total completion time obviously increases the total distance (minimizing one objective leads to an increase in another objective), which in turn will increase the overall cost of the system. For this reason, we modify the algorithm to consider more than one aspect rather than turn it into a problem with multiple objective functions. Note that this approach can be reversed, i.e., using total distance as the primary objective function and total completion time as the secondary objective function.
The remainder of this section is organized as follows: the solution representation is given in
Section 3.1. The modified K-means clustering is described in
Section 3.2.
Section 3.3 explains the inserting procedure. The local search procedures (swapping and moving procedures) are given in
Section 3.4 and
Section 3.5. Finally, the algorithm, including Phases 1, 2, and 3, is summarized.
3.1. Solution Representation
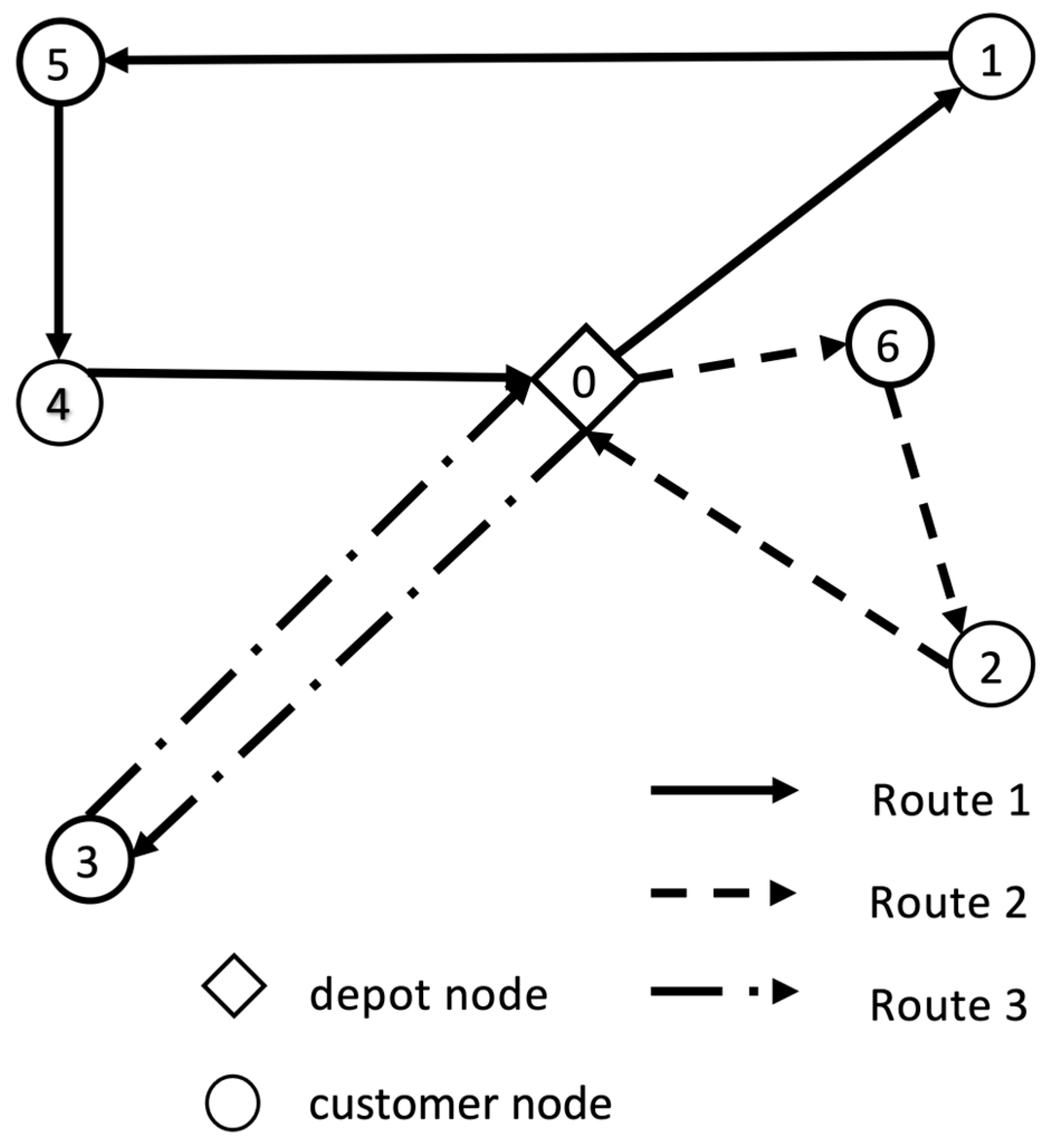
For convenience’s sake, the solution in this problem is defined as a single vector which starts and ends at node “0”. Next to node 0 is the subsequent node that the vehicle travels to in the sequence. The representation contains all routes where each vehicle is separated by “0”. For example, suppose the solution has the first vehicle start from the depot node and travel to node 1, 5, and 4, respectively, before returning to the depot node; the second route starts from the depot and travels to node 6 and 2; and the third route starts from the depot, goes to node 3, and then returns to the depot node. The solution which has two vehicles can be written as [0, 1, 5, 4, 0, 6, 2, 0, 6, 0], as shown in
Figure 1.
Definition 1. The routing sequence with
vehicles can be written as
, where each route
is represented by
, and
represents the number of visiting nodes, excluding depot, in route
.
Definition 2. The starting time of the job,
, is the minimum between the combination of the starting time of the immediately processed job with the service time and the travel distance, i.e.,
, and the lower time window of the jobs.
Definition 3. The completion time of a job
, written as
, is the combination of its starting time and its service time, i.e.,
.
Example 1. The routing sequence is as shown in Figure 1, with 3 routes and 6 nodes. The first vehicle starts from the depot and travels to nodes 1, 5, and 4, and then returns to depot. Vehicle 2 starts from the depot and travels to node 6 and node 2. Vehicle 3 travels from the depot node, goes to node 3, and then returns to the depot. The routes can be written as follows: . The routing sequence can be written as . Note that the duplicate zero in the routing sequence is deleted. From the definition, the three routes can be described as:
Route , , and .
Route , , and .
Route , and .
3.2. Modified K-Means Clustering
K-means clustering is a classification method for classifying data by identifying the features. Classification methods can be divided into hierarchical clustering and partitioned clustering. In hierarchical clustering, data are clustered using a dendrogram of an agglomerative method and a divisive method. The partitioned clustering method clusters data based on the heuristic approach using a single criteria function (feature function) to all data objects [
29]. In this study, the K-means algorithm, a partitioned clustering method, is selected for clustering the nodes based on the distance function. The K-means algorithm is selected because it is one of the most common methods for clustering, and because of its simple calculation, ease of implementation, and efficiency.
The procedure of K-means proceeds as follows: the number of clusters, called , must be predefined before the start of algorithm. The centroids are then generated, each one representing a cluster. After that, each remaining node is added to the nearest compatible cluster. The process will iterate by changing the centroids and recalculating the distance again until there is no change in the centroids. Due to the objective function to minimize total completion time and the time window constraints, we present a modified K-means clustering which changes the feature function from distance to the average upper time windows, indicated as (1) and (2), respectively, in the pseudocode. The first version is the original version of K-means, while the second version is the modified version. The pseudocode is given below (Algorithm 1).
| Algorithm 1: Modified K-means clustering |
| 1. | Input. |
| 2. | nodes within the space, set as centroids . |
| 3. | While the set centroid is changed do |
| 4. | | Define the set of clusters as where for . |
| 5. | | For in the set of all nodes do |
6.
7. | | | - (1)
Add node to the compatible cluster () that has the shortest distance between centroid and node . - (2)
Add node to the compatible cluster () that has the lowest of the average of upper time windows between all nodes in that cluster and node .
|
| 8. | | End For |
9.
10. | | - (1)
Find new set of centroid nodes by the average of each position of node in the cluster. - (2)
Find new set of centroid nodes by the average of position of three nodes in the cluster: the previous center, the node that has maximum upper bound, and the node that has minimum upper bound.
|
| 11. | End While |
| 12. | Return: Set of clustered nodes. |
3.3. Inserting Procedure
The inserting procedure aims to create an initial solution by inserting the incoming jobs in the best position until there are no jobs left. The algorithm aims to create a route from the solution obtained from the K-means clustering. Due to the restriction of the hard time windows, both lower and upper, some of the inserts may not be feasible to apply. We provide some conditions that ensure a node will be inserted into the routing position.
For each cluster, the first step is to sort and reorder all jobs’ upper time windows in ascending order in the cluster. Each job (customer node) will then be inserted one by one until there are no jobs left. In each iteration, there is more than one possible position to insert. As the aim is to minimize total completion time, the best insertion must therefore be in the position that increases it the least. One way to obtain the best solution is to insert jobs into all possible positions and then check for feasibility and objective value; after that, the best inserting position will be obtained. Since the possible inserting position increases at each iteration, in factorial, considering all jobs will cause the execution time to increase. It is better to check inserting conditions before fully checking feasibility and calculate objective value after insertion. In this study, two conditions are provided, each requiring only small calculation steps.
Suppose that the current cluster has number of jobs (nodes) to be scheduled. In the middle of the procedure, let the current partial routing sequence at cluster be and the remaining jobs waiting to be inserted be . The next candidate to be inserted is the job . To check the feasibility, each constraint in the proposed model must be satisfied. However, while the procedure has not completely inserted all remaining jobs, some of the constraints are not satisfied. The steps in the inserting procedure will ensure the feasibility of the routing constraints, and the feasibility of compatibility constraints is ensured by the clustering. The feasibility of the solution can therefore be obtained by checking only time windows constraints, i.e., Constraints (10) and (11).
Lemma 1. Consider a routing sequence . A job can feasibly insert in a position between job and , i.e., the inserted routing sequence , if two of the following conditions are satisfied: the lower time window of job does not exceed the completion time of job , i.e., and the upper time window of job is after the lower time window of job , i.e., , and the completion time of job together with the distance from job to job , to , and the service time of job does not exceed the lower time window of . That is, .
Proof. Suppose job is inserted in the position between job and .
Since , job can start immediately after arriving at node .
Moreover, the starting time of job
is equal to the combination between the completion time of job
, i.e.,
The possible starting time of job
, defined as
, is thus the completion time of job
together with the service time and the travel distance, i.e.,
From Equations (14) and (15), and Condition 2,
thus,
From the definition of the problem, if the vehicle arrives before the lower time window, it must wait and cannot provide service until the time is reached. That is, the vehicle must start at time
or,
Next, we ascertain the feasibility of the inserted routing sequence by checking only Constraints (10) and (11), i.e., for all . Since the starting time of each of the jobs processed before job , i.e., for , has not been changed, Constraints (10) and (11) are satisfied for job for . For job , from Equation (14), , and Condition 1, , we have . From and Equation (16), we have . Constraints (10) and (11) are therefore satisfied for job .
From (16), the new starting time of job is the lower time window, which must be less than the starting time before inserting job . The starting time, after inserting job , of each job processed after job therefore remains the same. Thus, Constraints (10) and (11) are satisfied for all job .
Constraints (10) and (11) are satisfied for route , and therefore the routing sequence is feasible.
Lemma 2.
A job cannot be inserted into any position in a routing sequence if the starting time (starting time together with service time) of each of the jobs in the routing sequence and its service time combined with the double minimum distance from the job to each node exceeds its upper time windows. That is, for each , .
Proof. Similar to Lemma 1, the feasibility can be checked only on Constraints (10) and (11).
Suppose the inserting of job is feasible.
The routing, when inserting job into some position, will always have at least one job processed after job . Let and be jobs in routing sequence that are processed before and after job , respectively.
The starting time of job
is:
and the starting time of job
is:
Then, from the assumption,
,
which contradicts the feasibility of the problem; therefore, the insertion is infeasible.
The pseudocode for the inserting procedure is given below (Algorithm 2).
| Algorithm 2: Inserting Procedure |
| 1. | Input. |
| 2. | Set
|
| 3. | . |
| 4. | and repeat the process in line 3. |
| 5. | For do |
| 6. | | Define empty route . |
| 7. | | For in the cluster do |
| 8. | | | in the position that satisfies conditions in Lemma 1.
If there is more than one candidate, prioritize the one having lowest total completion time first, followed by the one with minimum distance.
Elseif there is no position that satisfies Lemma 1, insert job into the best feasible position in the current route giving the lowest total completion time.
Else generate a new cluster and increase the number of clusters by 1.
End If |
| 9. | | | from cluster . |
| 10. | | End For |
| 11. | End For |
| 12. | Return: . |
3.4. Local Search Algorithms
After applying the inserting procedure, we now obtain an initial solution, and this is the end of Phase 1. After this, the local search, or neighborhood search, seeks to find an improved solution by searching around their neighborhoods. In this study, moving and swapping procedures are selected as the local search algorithm.
3.4.1. Moving Procedure
The moving procedure will be applied to find the best new solution by moving some jobs to other positions in a routing sequence. The move can occur on the same route or to another route. That is, the move is equivalent to deleting followed by inserting. The conditions from Lemmas 1 and 2 can therefore also be applied to check the feasibility. In each iteration, the job with the lowest upper time window that has never been moved is selected to move. The selected job will be checked for feasibility by Lemma 1 and 2 before calculating the objective value. The pseudocode is given below (Algorithm 3).
| Algorithm 3: Moving Procedure |
| 1. | Input. |
| 2. | that is the sorted upper time window of all nodes. |
| 3. | For do |
| 4. | | Remove job from its original position in . |
| 5. | | For in the routing sequence do |
| 6. | | | into the position that satisfies conditions in Lemma 1.
If there is more than one candidate, prioritize the one having lowest total completion time first, followed by the one with minimum distance.
Elseif there is no position that satisfies Lemma 1, insert job into the best feasible position in the current route giving the lowest total completion time.
Else generate a new cluster and increase the number of clusters by 1.
End If |
| 7. | | | . |
| 8. | | End For |
| 9. | | ; if there is more than one candidate, choose the one with the lowest . |
| 10. | End For |
| 11. | Return: . |
3.4.2. Swapping Procedure
The swapping procedure aims to switch the positions of two jobs when switching results in a feasible routing sequence with total completion time reduction. If the upper time windows are close to each other, the swapping processes will likely return a feasible routing sequence. The candidate list is modified to be the list of two jobs sorted by the differences of their upper time windows, i.e.,
where:
The pseudocode is given below (Algorithm 4).
| Algorithm 4: Swapping Procedure |
| 1. | Input. |
| 2. | that is the sorted upper time window of all nodes. |
| 3. | For do |
| 4. | | Remove jobs from their original positions in . |
| | | Switch the positions of job and job . |
| 5. | | If the solution after switching the jobs is not feasible or the new total completion time is increased do |
| 6. | | | Switch the positions of job and job back to their original positions. |
| | | End If |
| 7. | End For |
| 8. | Return: . |
3.5. Shooting Procedure
The procedure contains two main search mechanisms, indicated as (1) and (2), which are the random search and the tabu search. The tabu search, a metaheuristic search introduced by Glover [
30], explores solutions that are in its neighborhoods, that have not been visited before. The search can therefore avoid the cycling of the visits and also reduce the search space, which means it can avoid sticking in the local optimum.
If the local search (Phase 2) cannot improve the solution further, we consider the solution to be stuck in a local optimum. To get away from the local optimum, we constructed the shooting procedure to find a new local optimum. The idea of the procedure is to randomly swap or move some jobs to another position in the routing sequence without considering the objective value or feasibility of routing. The infeasible jobs will then be removed from the routing and inserted into a feasible position using the inserting procedure and then local search procedure will be applied. To obtain the best performance, the tabu search will be applied once the random search can no longer find an improved solution, rather than at the start of the procedure. Additionally, if the procedure fails to find an improved solution after several attempts, it will deploy the tabu search strategy (2), which will then reject the swapping and moving that have been tried before to widen the exploration. The tabu list is updated each iteration by adding nodes that immediately process before and after the moving and swapping nodes. These processes will continue until either the maximum iteration number is reached, or the total completion time does not change for iterations. The pseudocode is given below (Algorithm 5).
| Algorithm 5: Shooting Procedure |
| 1. | Input. |
| 2. | (1) times.
(2) times if it is not in the TabuList. |
| 3. | Add the nodes that immediately visit before and after the moving nodes to the TabuList. |
| 4. | , add to the remaining list, . |
| 5. | For do |
| 6. | | Apply inserting procedure to job to the compatible routing. |
| | | If the inserting procedure cannot find a feasible position for job , stop the procedure and return to the original solution. |
| | End For |
| 7. | Apply swapping procedure and moving procedure |
| 8. | Return: . |
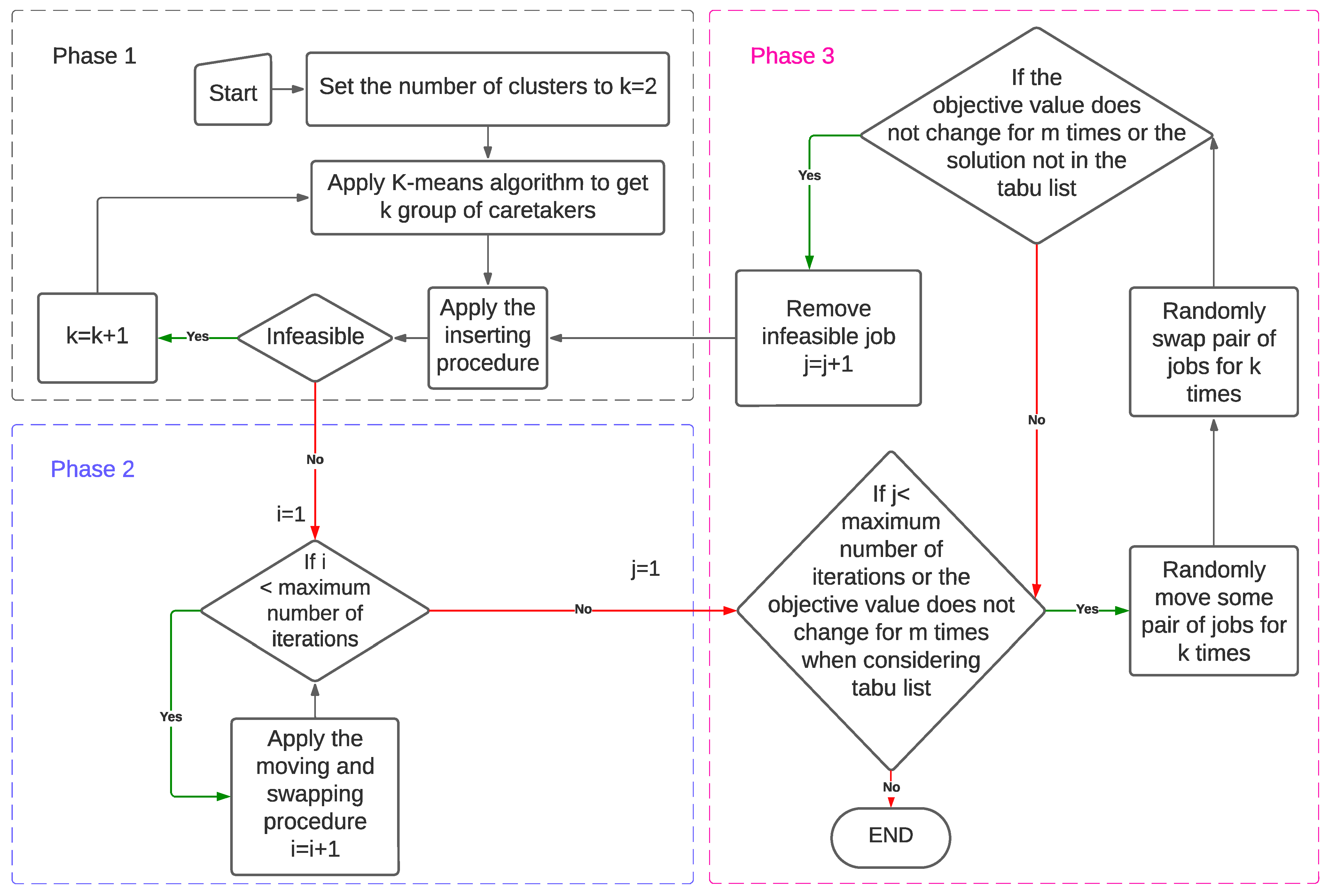
To summarize, the heuristic is divided into three phases: the initializing phase, the improvement phase, and the randomization phase. The summary flowchart is given in
Figure 2. Phase 1 includes K-means clustering followed by the inserting procedure. K-means clustering will apply a strategy to select the centroids based on distance. If the inserting procedure cannot find a feasible solution, the K-means clustering will apply a strategy to select centroids based on the average upper bound. Phase 2 improves the solution obtained from Phase 1 using the swapping and moving procedures until there is no change in the total completion time. Phase 3 seeks to improve the solution by randomly modifying the solution, or randomly modifying only if the solution is not in the tabu list, without considering the feasibility or total completion time, then applying the inserting procedure to fix the feasibility and reapplying Phase 2 again. Phase 3 will be attempted until the maximum number of iterations is reached, or the objective value does not change for a certain number of iterations.
4. Experimental Results
To demonstrate its performance, the heuristic is implemented using the Julia programming language [
31,
32] and executed on AMD Ryzen 9 12-Core processors with a CPU clock speed of 3.8 GHz and RAM of 64 GB. The problem is solved several times to obtain the parameter settings. The settings are as follows: the number of vehicles will start as two and continue to increase by one when the algorithm cannot find any feasible solution; the maximum number of iterations is set to 500; the number of iterations to attempt when the objective value (total completion time) does not change is set to five (used in Phase 3); and the number of random swaps and moves is set to 10 (used for Phase 3).
Solomon instances are used to measure the algorithm efficiency. The benchmark instances are classified into three groups: clustered (C-type), random (R-type), and random clustered (RC-type). The numbers that follow the distribution of nodes are “1” and “2”, indicating narrow time windows and wide time windows, respectively. Each instance includes 100 customers, time windows for each customer, the demand for each customer, and the distance between each pair of customer nodes. Note that in the benchmark, one unit of distance is equal to one unit of traveled time.
The simulation results are divided into two settings: the results using the total distance as the primary objective function and the results using the total completion time as the primary objective function. The first simulation setting seeks to test the efficiency of using our proposed objective function (total completion time) instead of comparing total distance. Since there is no benchmark instance using the total completion time as the objective function to demonstrate our algorithm’s efficiency, the second aims to test the efficiency of the proposed algorithm by using the total distance as the objective function to solve the problem. Therefore, the results can be directly compared to Solomon’s instances.
Table 2 presents the results for total distance minimization as the objective function. Each problem is solved using the proposed algorithm, while the objective function is changed from the total completion time to the total distance. Columns 3 to 5 show the calculated total completion times from the results associated with the distances shown in column 6 to 8, respectively. The results show that the algorithm can find the solution that is, on average, within 9.04% of the best known total distance from the literature and can, moreover, find the optimal solution in all clustered cases. Note that in most cases, reducing the total distance results in reduced total completion time as well. Moreover, Phase 2 can reduce the total distance from Phase 1 by 29.1% on average, while Phase 3 achieves a reduction of only 3% from Phase 2.
To demonstrate the efficacy of the methodologies employed and the importance of using the total completion time as the objective function (the primary objective, with total distance as a second objective), a comparative analysis is conducted on our proposed solution and the best solution from Solomon’s benchmark instances, as shown in
Table 1. Note that some of the best known solutions are not available, preventing us from calculating the total completion time associated with the best distance solutions. To obtain that information, we apply our algorithm to optimize the total distance and obtain the corresponding travel time.
Table 3 presents the most widely recognized solutions for total distance, along with the corresponding total completion time of the caretaker. Note that the number of vehicles is the same as that shown in
Table 2. Column 7 shows the solution of our algorithm by minimizing the total distance, and the corresponding calculated total completion time is shown in column 8. Columns 2–4 show the results from our algorithm for the total completion time minimization objective function, while columns 5–7 show the total distance calculated from the corresponding solution from columns 2–4. This value is consistently smaller in all cases when compared to the solutions provided by Solomon’s instances. However, it is important to note that the total distance traveled is expected to increase. Moreover, when the algorithm minimizes the total completion time for instance C101, Phase 1 (the initial solution) obtains the best solution for total distance, and then the algorithm obtains the best new solution in which the total distance increases by 14.13% and total completion time decreases by 0.05%. In this case, we found that some caretakers travel more distance to cover a node that is currently available.
The execution time for Phase 1 is approximately 0.28 s for R-type instances, 0.06 s for C-type instances, and 0.17 s for RC-type instances. Phase 2 requires a comparable amount of time to Phase 1, whereas Phase 3 accounts for approximately 99.68% of the time spent. It should be noted that the duration of execution in Phase 3 is based on the maximum number of iterations, set at 500 for this particular instance. The average reduction in the objective function value was 19.40% from Phase 1 to Phase 2 and 3.55% from Phase 2 to Phase 3.
When determining the percentage difference between the total completion times solved using Solomon’s instances and the completion times obtained from each phase of our algorithm, we observed that in all instances, the total completion times achieved with our algorithm were, on average, 25.86% lower. Additionally, the average total distance traveled increased by 90.00%. Note that there is a small improvement in the total completion time from Phase 2 to Phase 3, while the algorithm spends the most time in this phase. In most cases, the total completion time improvement from Phase 2 to Phase 3 may result in an increase in the total distance. In contrast, several instances in
Table 3, C202, C203, R101, RC105, RC106, and RC204, show a reduction in the total completion time and total distance simultaneously. This demonstrates that the total distance may decrease simultaneously with the total completion time when the distribution of nodes is more random than clustered. The algorithm can find the solution that minimizes the total completion time and try to reduce the total distance at the same time.
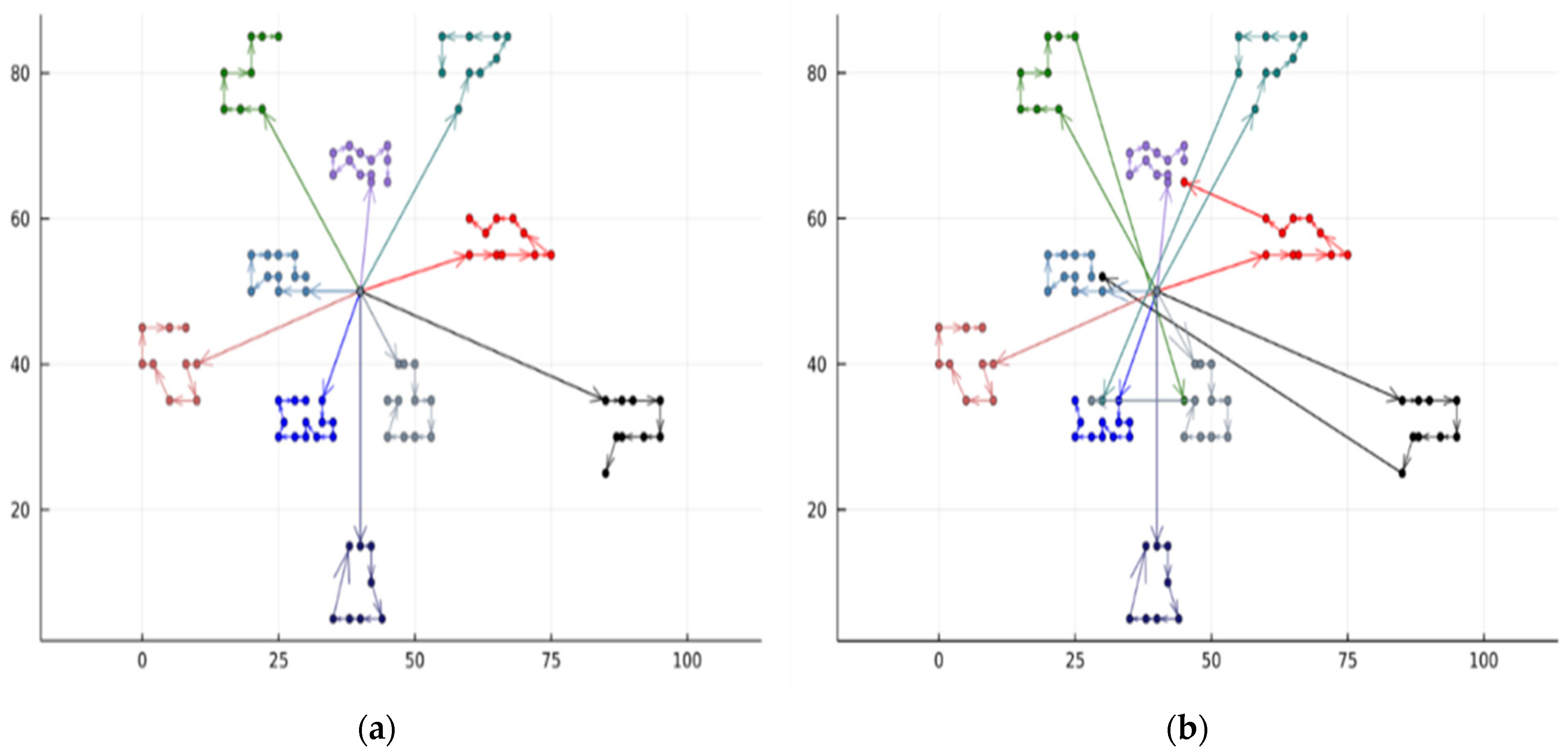
Figure 3 illustrates a representative path within the solutions of the “C101” instance.
Figure 3a displays the routings obtained from the optimal benchmark solution resulting from minimizing the total distance traveled.
Figure 3b shows the solution obtained with our procedure, where the objective was to minimize the total completion time. Note that, to prevent confusion when several lines cross each other, the lines from the last node to the depot node are not shown. The final customer in the purple route of the optimal solution in
Figure 3a transitions to being a customer in the red route illustrated in
Figure 3b. The result leads to an increase in total distance covered, while simultaneously decreasing the total completion time of the entire system.
5. Case Study
To examine the advantages of the total completion time objective function, our study focuses on minimizing the total completion time in a case study simulating the HHC system in Chiang Mai, Thailand. The proposed heuristic uses the same parameter settings as when solving Solomon’s instances.
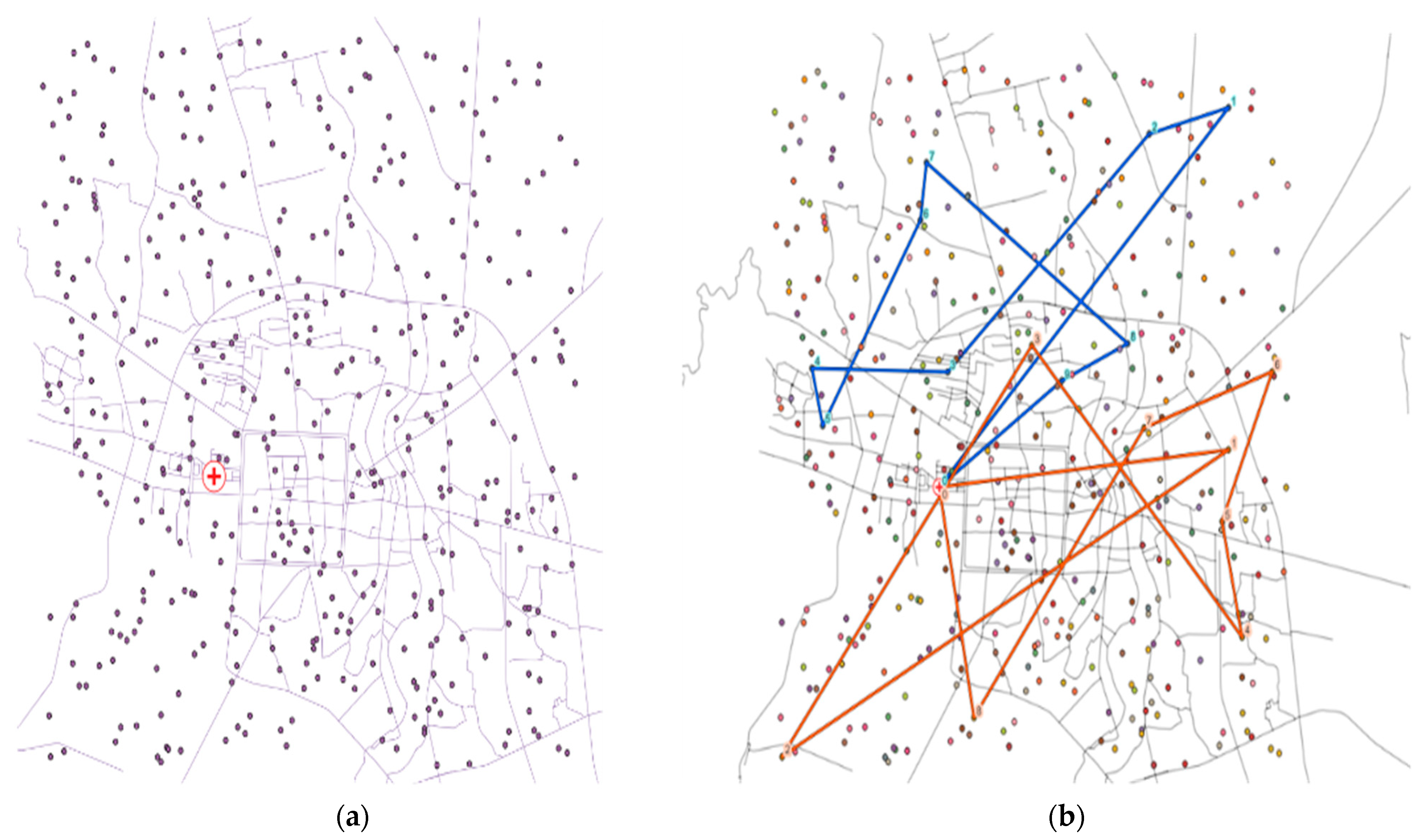
We assume that 400 households currently registered with the largest health center in central Chiang Mai, an area with over a half a million people and over 300,000 households, require regular home visits. These prospective customers are dispersed at random across the map of the city center, where the location of the designated health center is denoted by a red cross (
Figure 4a). It is expected that caretakers will serve all customers in a single workday. A caretaker will not accept a job that is beyond his or her capabilities, and there are enough caretakers to attend to all the customers. The times listed for travel between each pair of nodes come directly from Google Maps. The time windows for each client are randomly generated, anywhere from zero to eight hours (28,800 s). The amount of time spent serving each customer is randomly determined, ranging from 5 to 20 min.
Table 4 presents a summary of the results obtained from both objective functions. The second column, labelled “NC”, shows the number of caretakers needed. The columns labelled as “Min”, “Max”, and “Avg” correspond to the minimum, maximum, and average number of patients attended to by a caretaker, respectively. The lower and upper bounds for the number of patients in relation to the total distance objective function are three and forty-two, respectively. This implies that in the process of minimizing the total distance, certain caretakers are required to attend to significantly more patients, up to 14 times more, than their coworkers. This number drops by a factor of seven when the objective of minimizing the overall completion time is achieved. Additionally, in seeking to minimize the completion time, the required number of caretakers will increase to effectively distribute the workload among them. In the context of caretaker management, we propose that the total completion time is a more suitable objective function compared to the total distance, as it leads to a decrease in both the average number and maximum number of patients that a caretaker serves.
The two routes depicted in
Figure 4b illustrate the routing obtained by implementing our heuristic algorithm. The numerical values assigned to the routes correspond to the sequential order in which a caretaker performs his/her visits. Both routes show chaos as a result of the time constraints imposed by patients’ availability (time windows). Upon completion of service to patient 2 along the blue route, the care staff makes the decision to attend to patient 3 due to their earlier time window, despite the fact that visiting patient 7 first would result in a shorter travel distance overall.
6. Conclusions and Discussions
In this paper, we study home healthcare routing and scheduling involving the need for staff members to visit designated patients within predefined time windows and with compatibility requirements. In this scenario, it is crucial for healthcare staff to start and finish their service to patients strictly within the designated timeframe, and they are only able to visit compatible patients. In the event that staff arrives at the patient node before the designated time, they are required to wait until the scheduled time to deliver care. The given problem can be reformulated as a vehicle routing problem with time windows (VRPTW) and compatibility constraints, a problem that originally seeks to minimize the total distance travelled. To ensure suitability for practical applications, we choose to set minimizing the completion time as our objective function rather than focus on minimizing the total distance alone.
The vehicle routing problem is an NP-hard problem. Adding constraints or changing the objective function makes the problem even more complex. Our problem on its own is an NP-hard problem; addressing situations where optimal solutions cannot be obtained in a reasonable time with an exact algorithm requires that heuristics be developed. The heuristic employed in our study comprises three distinct phases. The primary phase (Phase 1) aims to generate a solution from the ground up, with patients systematically clustered and inserted one by one into positions that minimize the total completion time. The second phase (Phase 2) focuses on enhancing the solution by implementing swap and move operators. Phase 3 seeks to prevent the problem of local optimum by randomly exchanging or moving a pair of patients that do not violate the tabu list within the solution. Moreover, the heuristic simultaneously seeks to minimize the total distance as a secondary objective.
To demonstrate the performance of the algorithm, comparisons are made between the results from our model and an existing benchmark instance which includes 100 customer nodes. When the total completion time is minimized, the total distance traveled increases. However, our total completion time tends to be lower generally. We modified our algorithm to simultaneously reduce the total distance as a second priority. After the initial phase, the algorithm can, in some instances, find a solution with a reduction in both the total completion time and total distance. Further, the algorithm is compared to the best known solutions with total distance minimization as the primary objective. The optimal solution is found by the algorithm in all clustered cases, and the overall percentage gap is within 10%. From these results, we can see that switching from minimizing the total distance to minimizing the total completion time will increase the total distance by around 90.00%, while the total completion time drops by 25.86%. In practice, both objective functions should be minimized separately, and the decision made by the administrator which of the solutions will minimize operation costs. Note that the reduction in the total distance may cause some staff to work longer, a scenario that can be more costly than increasing the total distance traveled.
Our case study pertains to the home healthcare system in Chiang Mai, Thailand’s second most populous city. The system consists of 15 health centers serving over 300,000 households. Based on the results from our simulation, we recommend that minimizing the total completion time, rather than the total distance, should be prioritized in order to ensure staff satisfaction, which is vital in a people-centered business with ever-increasing demand for qualified staff. When total completion time minimization is prioritized, each caretaker is assigned a roughly equal number of patients, which is not the case when minimizing the total distance is the primary objective function.