An Extended Gradient Method for Smooth and Strongly Convex Functions
Abstract
:1. Introduction
2. Analysis of the Extended Gradient Method
3. Analysis of the Decentralized Extended Gradient Method
3.1. Decentralized Extended Gradient Method
3.2. Convergence Result
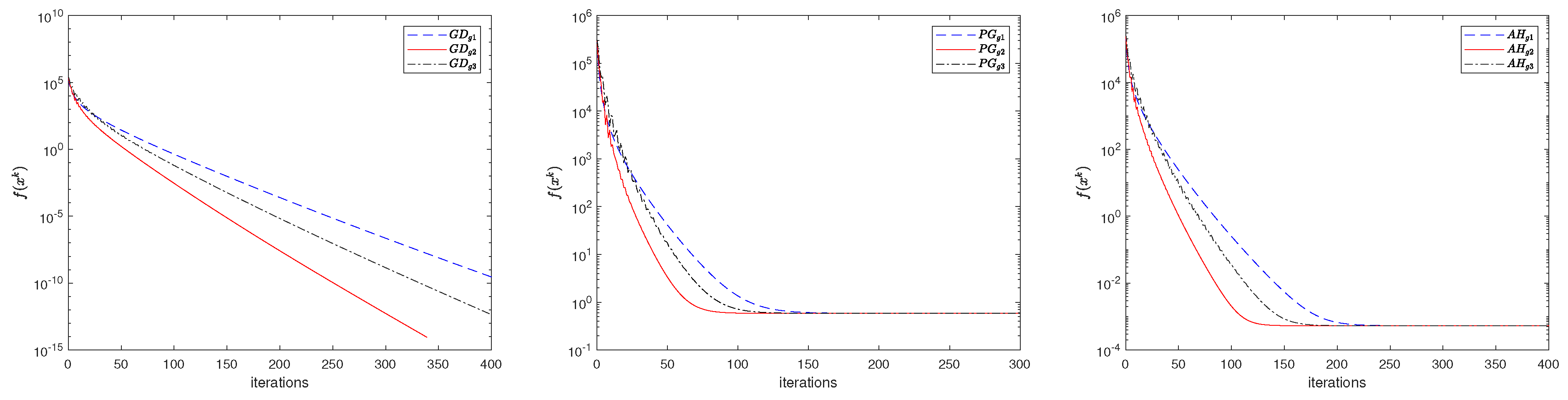
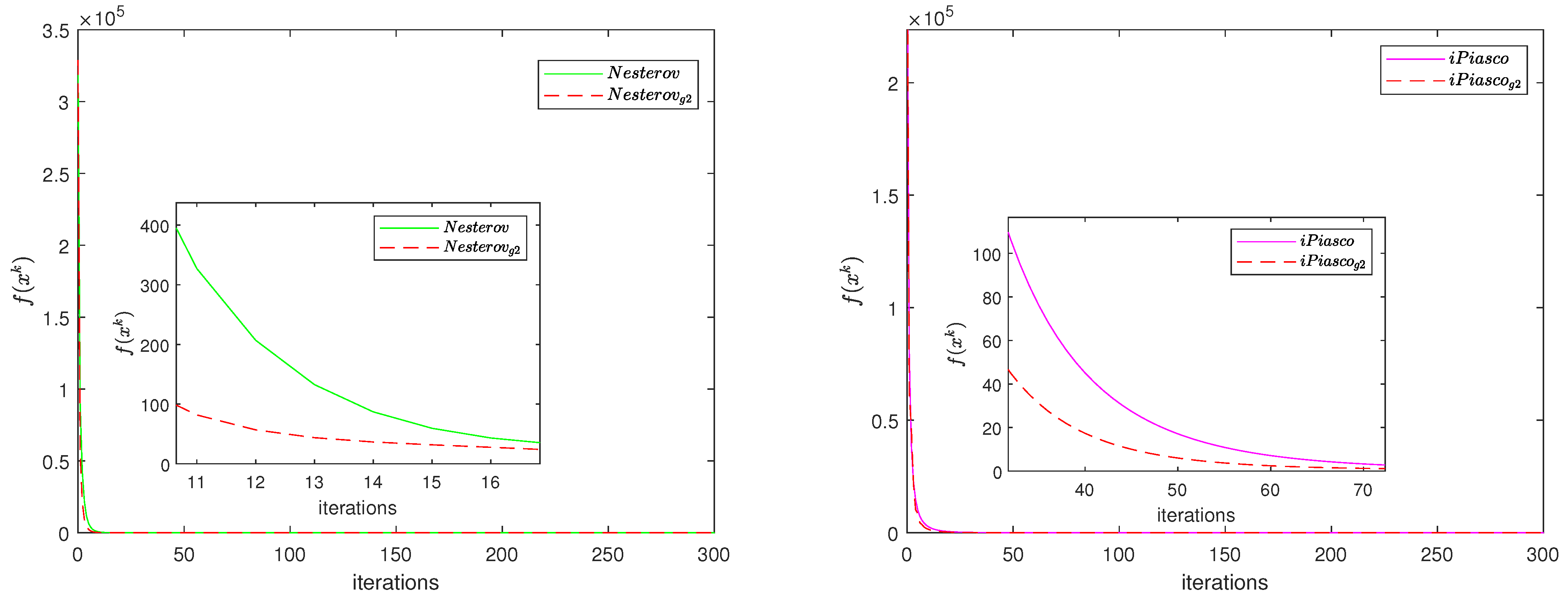
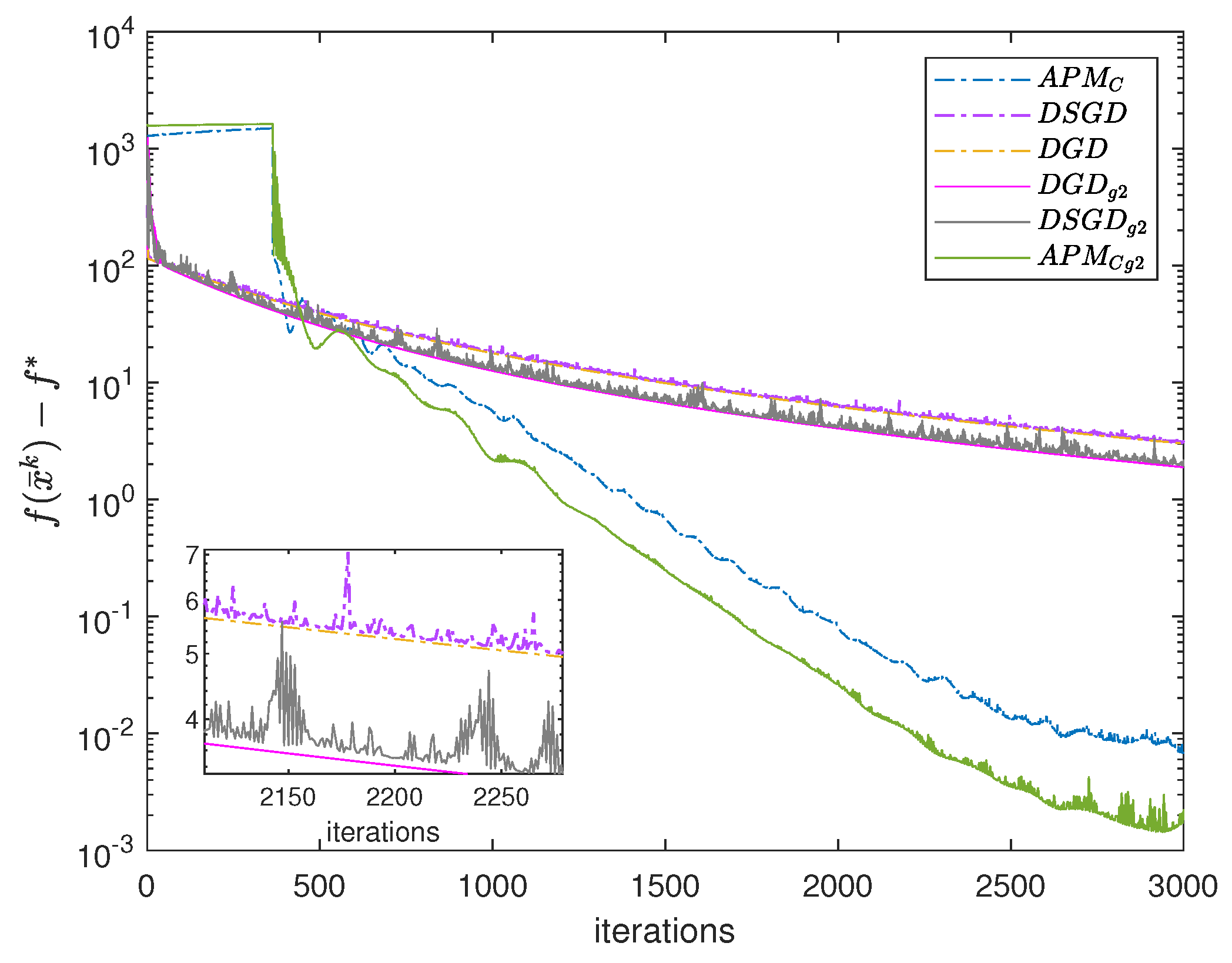
4. Numerical Experiments
4.1. Centralized Problem
4.2. Decentralized Problem
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Ochs, P.; Brox, T.; Pock, T. iPiasco: Inertial Proximal Algorithm for Strongly Convex Optimization. J. Math. Imaging Vis. 2015, 53, 171–181. [Google Scholar] [CrossRef]
- Lessard, L.; Recht, B.; Packard, A. Analysis and design of optimization algorithms via integral quadratic constraints. SIAM J. Optim. 2016, 26, 57–95. [Google Scholar] [CrossRef]
- Hagedorn, M.; Jarre, F. Iteration Complexity of Fixed-Step-Momentum Methods for Convex Quadratic Functions. arXiv 2022, arXiv:2211.10234. [Google Scholar]
- Nesterov, Y. Introductory Lectures on Convex Optimization: A Basic Course; Springer: New York, NY, USA, 2003; Volume 87. [Google Scholar]
- Bertsekas, D. Convex Optimization Algorithms; Athena Scientific: Nashua, NH, USA, 2015. [Google Scholar]
- Popov, L.D. A modification of the Arrow-Hurwicz method for search of saddle points. Math. Notes Acad. Sci. USSR 1980, 28, 845–848. [Google Scholar] [CrossRef]
- Attouch, H.; Chbani, Z.; Fadili, J.; Riahi, H. First-order optimization algorithms via inertial systems with Hessian driven damping. Math. Program. 2022, 193, 113–155. [Google Scholar] [CrossRef]
- Ahmadi, M.J.; Arablouei, R.; Abdolee, R. Efficient estimation of graph signals with adaptive sampling. IEEE Trans. Signal Process. 2020, 68, 3808–3823. [Google Scholar] [CrossRef]
- Torkamani, R.; Zayyani, H.; Korki, M. Proportionate Adaptive Graph Signal Recovery. IEEE Trans. Signal Inf. Process. Netw. 2023, 9, 386–396. [Google Scholar] [CrossRef]
- Mai, V.; Johansson, M. Anderson acceleration of proximal gradient methods. International Conference on Machine Learning. PMLR 2020, 119, 6620–6629. [Google Scholar]
- Devolder, O.; Glineur, F.; Nesterov, Y. First-order methods of smooth convex optimization with inexact oracle. Math. Program. 2014, 146, 37–75. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Poljak, B.T. Introduction to Optimization; Optimization Software, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Khanh, P.D.; Mordukhovich, B.S.; Tran, D.B. Inexact reduced gradient methods in nonconvex optimization. J. Optim. Theory Appl. 2023. [Google Scholar] [CrossRef]
- Khanh, P.D.; Mordukhovich, B.S.; Tran, D.B. A New Inexact Gradient Descent Method with Applications to Nonsmooth Convex Optimization. arXiv 2023, arXiv:2303.08785. [Google Scholar]
- Schmidt, M.; Le Roux, N.; Bach, F. Minimizing finite sums with the stochastic average gradient. Math. Program. 2017, 162, 83–112. [Google Scholar] [CrossRef]
- Lee, J.D.; Lin, Q.; Ma, T.; Yang, T. Distributed stochastic variance reduced gradient methods by sampling extra data with replacement. J. Mach. Learn. Res. 2017, 18, 4404–4446. [Google Scholar]
- Jakovetić, D.; Xavier, J.; Moura, J.M.F. Fast distributed gradient methods. IEEE Trans. Autom. Control 2014, 59, 1131–1146. [Google Scholar] [CrossRef]
- Yuan, K.; Ling, Q.; Yin, W. On the convergence of decentralized gradient descent. SIAM J. Optim. 2016, 26, 1835–1854. [Google Scholar] [CrossRef]
- Nedic, A.; Ozdaglar, A. Distributed Subgradient Methods for Multi-Agent Optimization. IEEE Trans. Autom. Control 2009, 54, 48–61. [Google Scholar] [CrossRef]
- Berahas, A.S.; Bollapragada, R.; Keskar, N.S.; Wei, E. Balancing communication and computation in distributed optimization. IEEE Trans. Autom. Control 2018, 64, 3141–3155. [Google Scholar] [CrossRef]
- Shi, W.; Ling, Q.; Wu, G.; Yin, W. Extra: An exact first-order algorithm for decentralized consensus optimization. SIAM J. Optim. 2015, 25, 944–966. [Google Scholar] [CrossRef]
- Nedic, A.; Olshevsky, A.; Shi, W. Achieving geometric convergence for distributed optimization over time-varying graphs. SIAM J. Optim. 2017, 27, 2597–2633. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–60. [Google Scholar]
- Boyd, S.; Diaconis, P.; Xiao, L. Fastest mixing Markov chain on a graph. SIAM Rev. 2004, 46, 667–689. [Google Scholar] [CrossRef]
- Li, H.; Fang, C.; Yin, W.; Lin, Z. Decentralized Accelerated Gradient Methods With Increasing Penalty Parameters. IEEE Trans. Signal Process. 2020, 68, 4855–4870. [Google Scholar] [CrossRef]
- Chen, J.S.; Sayed, A.H. Diffusion Adaptation Strategies for Distributed Optimization and Learning Over Networks. IEEE Trans. Signal Process. 2012, 60, 4289–4305. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liu, S.; Zhao, N. An Extended Gradient Method for Smooth and Strongly Convex Functions. Mathematics 2023, 11, 4771. https://doi.org/10.3390/math11234771
Zhang X, Liu S, Zhao N. An Extended Gradient Method for Smooth and Strongly Convex Functions. Mathematics. 2023; 11(23):4771. https://doi.org/10.3390/math11234771
Chicago/Turabian StyleZhang, Xuexue, Sanyang Liu, and Nannan Zhao. 2023. "An Extended Gradient Method for Smooth and Strongly Convex Functions" Mathematics 11, no. 23: 4771. https://doi.org/10.3390/math11234771
APA StyleZhang, X., Liu, S., & Zhao, N. (2023). An Extended Gradient Method for Smooth and Strongly Convex Functions. Mathematics, 11(23), 4771. https://doi.org/10.3390/math11234771





