Stability of Stochastic Networks with Proportional Delays and the Unsupervised Hebbian-Type Learning Algorithm
Abstract
:1. Introduction
- (1)
- There exist few results for stochastic networks with proportional delays and unsupervised Hebbian-type learning algorithms. Our research has enriched the research content and developed the research methods for the considered system.
- (2)
- (3)
- In contrast to the existing research methods, we introduce some new research methods (including inequality techniques, stochastic analysis techniques and the It formula) to deal with the proportional delays and the unsupervised Hebbian-type learning algorithm. Particularly, we construct a new function and obtain the stochastic stability results of system (3) using the stability theory of stochastic differential systems and some inequality techniques. Furthermore, using the stochastic analysis technique and the It formula, we obtained the estimation of the second moment.
2. Preliminaries
3. Stability of Equilibrium
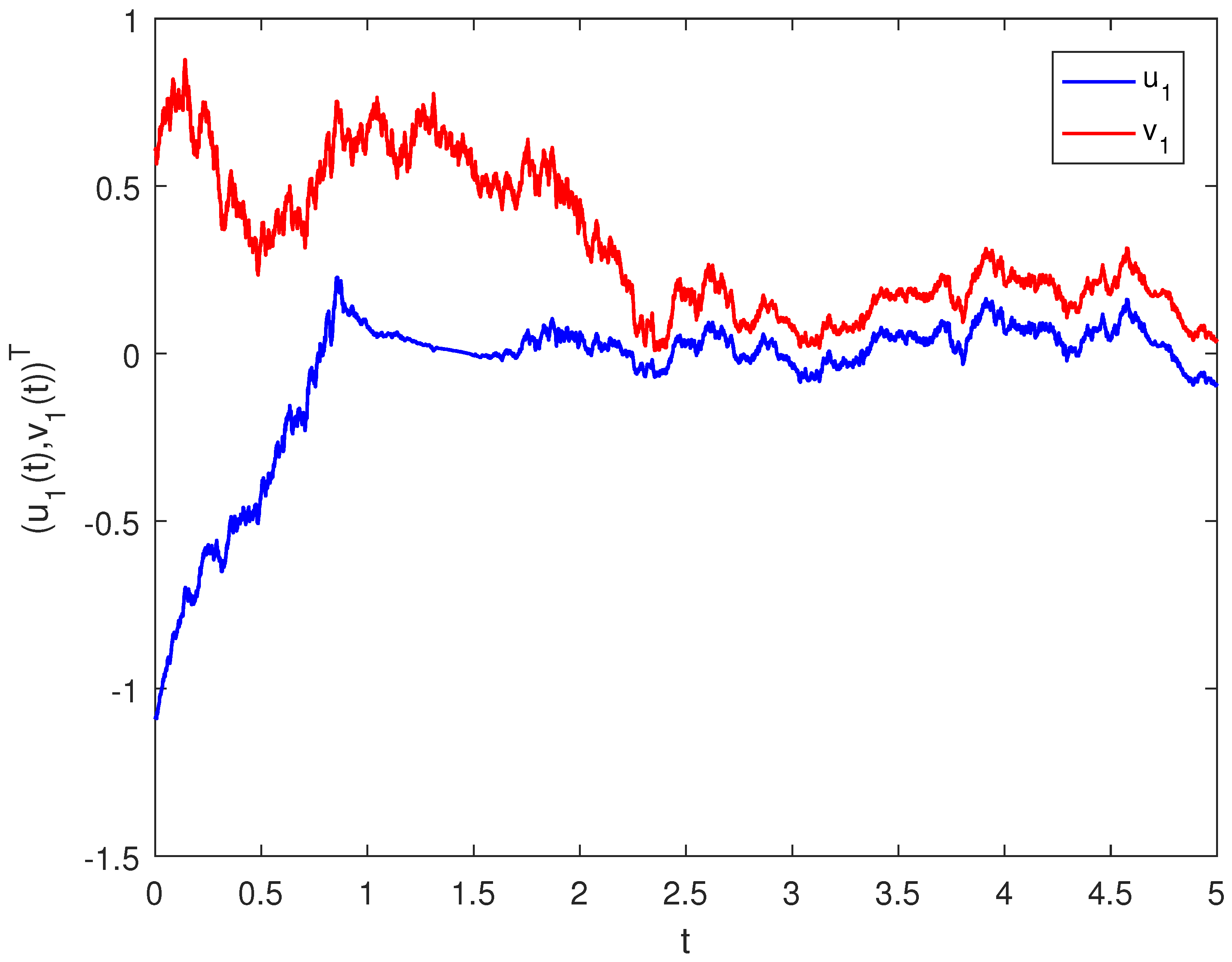
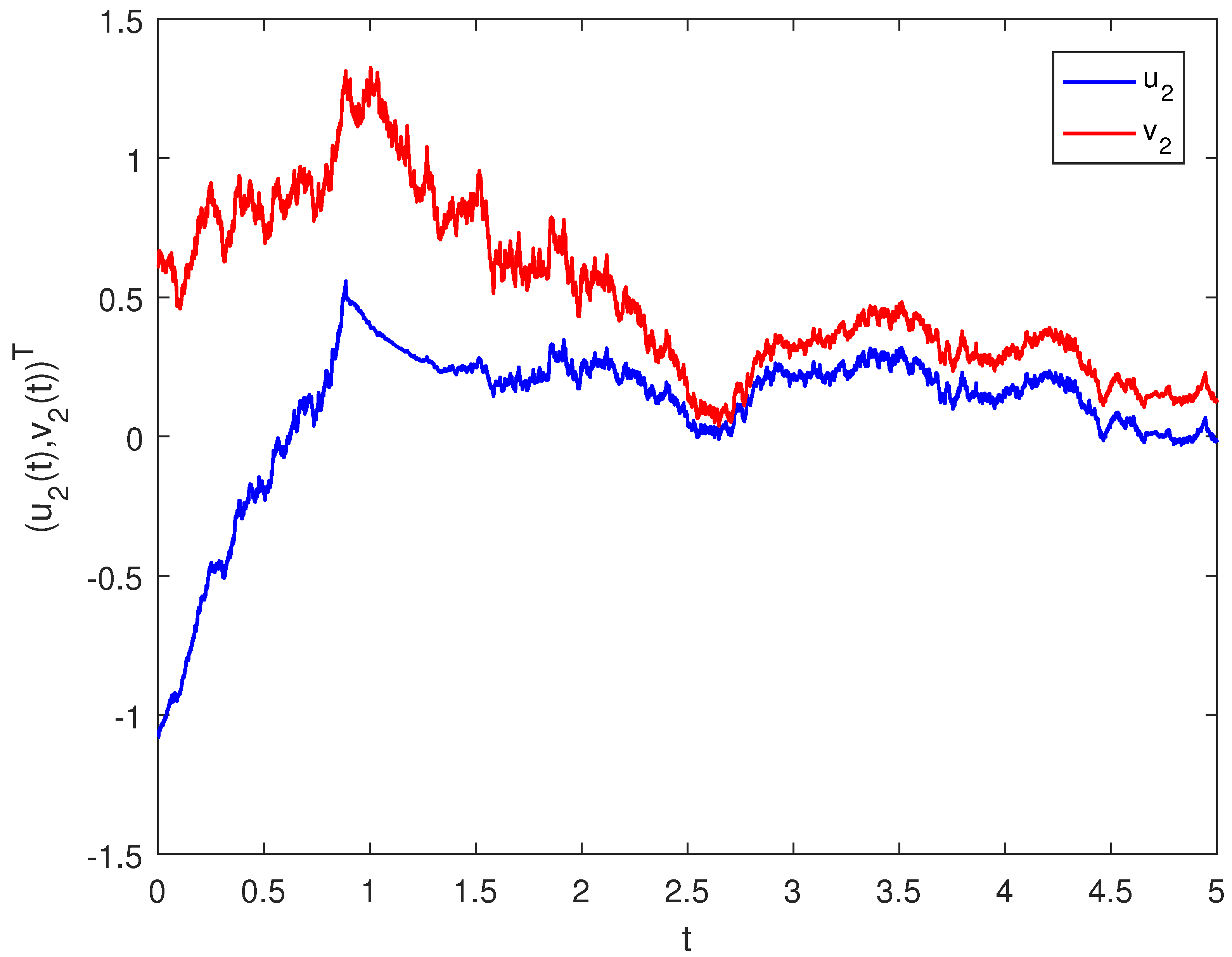
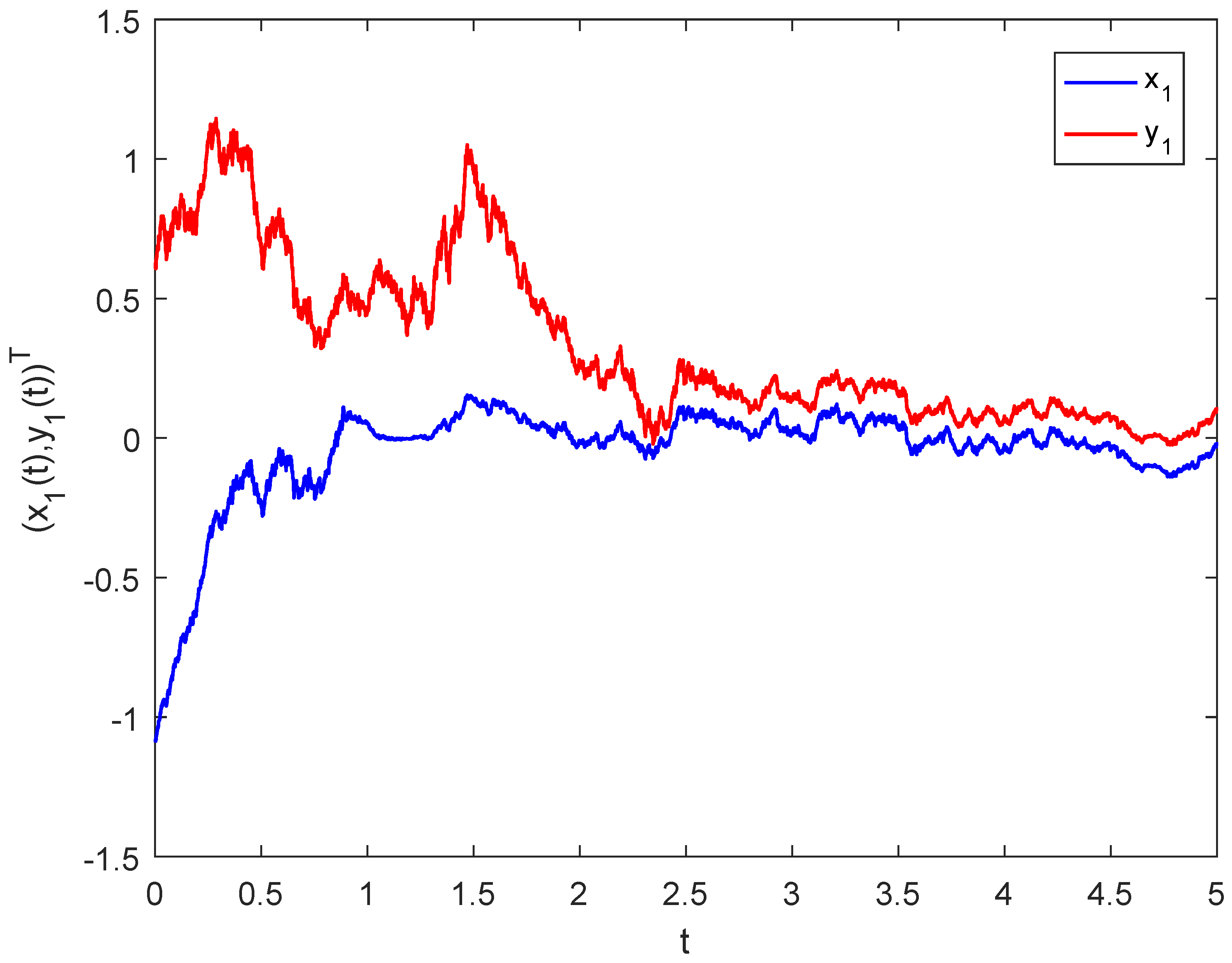
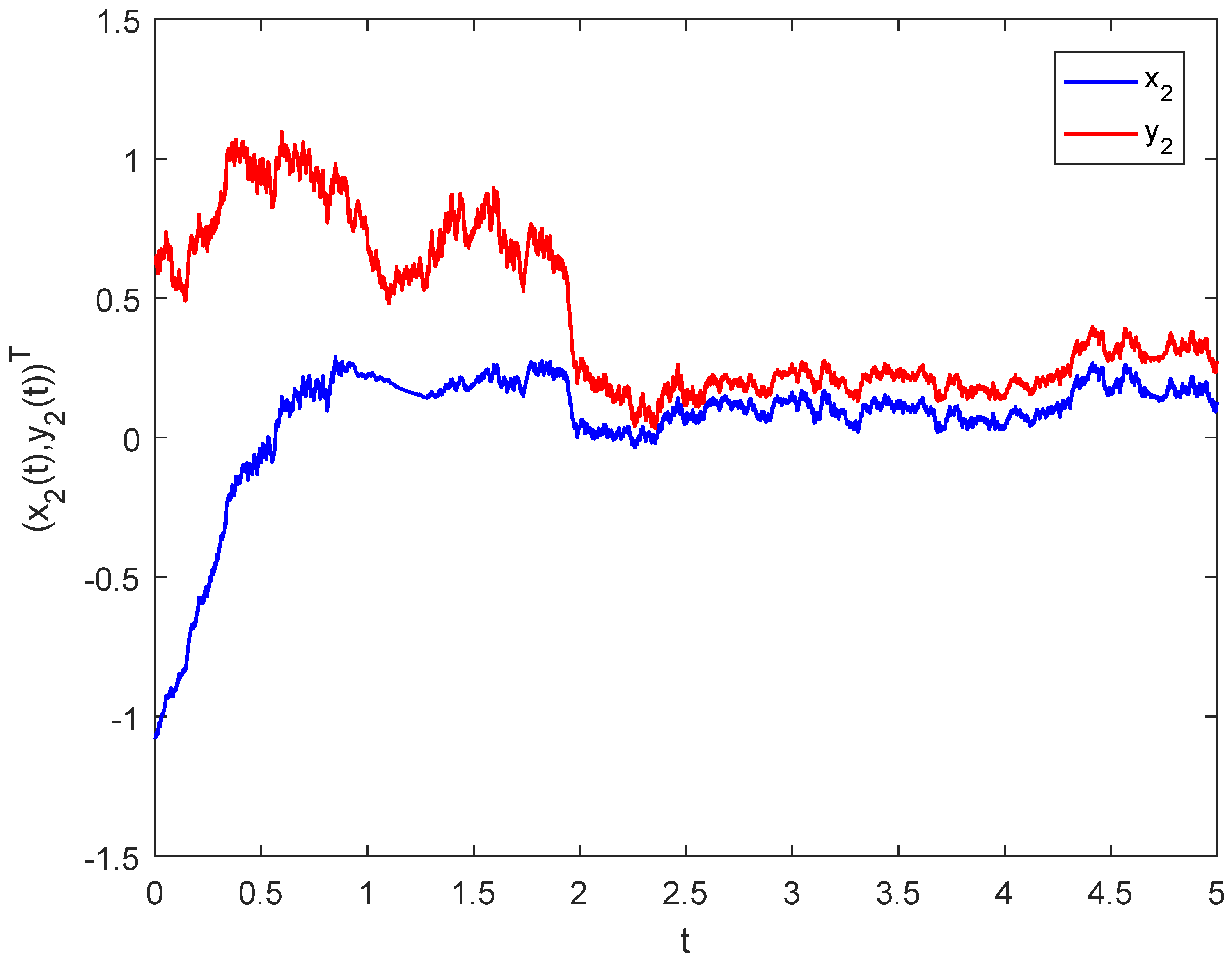
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gopalsamy, K. Learning dynamics in second order networks. Nonlinear Anal. Real World Appl. 2007, 8, 688–698. [Google Scholar] [CrossRef]
- Huang, Z.; Feng, C.; Mohamad, S.; Ye, J. Multistable learning dynamics in second-order neural networks with time-varying delays. Int. J. Comput. Math. 2011, 88, 1327–1346. [Google Scholar] [CrossRef]
- Gopalsamy, K. Learning dynamics and stability in networks with fuzzy syapses. Dyn. Syst. Appl. 2006, 15, 657–671. [Google Scholar]
- Chu, D.; Nguyen, H. Constraints on Hebbian and STDP learned weights of a spiking neuron. Neural Netw. 2021, 135, 192–200. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Z.; Cai, J. Global Exponential Stability of Learning-Based Fuzzy Networks on Time Scales. Abstr. Appl. Anal. 2015, 2015, 83519. [Google Scholar] [CrossRef]
- Huang, Z.; Raffoul, Y.; Cheng, C. Scale-limited activating sets and multiperiodicity for threshold-linear networks on time scales. IEEE Trans. Cybern. 2014, 44, 488–499. [Google Scholar] [CrossRef]
- Cao, J.; Liang, J.; Lam, J. Exponential stability of high order bidirectional associative memory neural networks with time delays. Phys. D 2004, 199, 425–436. [Google Scholar] [CrossRef]
- Kosmatopoulos, E.; Polycarpou, M.; Christodoulou, M.; Ioannou, P. High order neural network structures for identification of dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 422–431. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, K. Existence and global exponential stability of a periodic solution to interval general bidirectional associative memory (BAM) neural networks with multiple delays on time scales. Neural Netw. 2011, 24, 427–439. [Google Scholar] [CrossRef]
- Kamp, Y.; Hasler, M. Recursive Neural Networks for Associative Memory; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Liu, Y.; Wang, Z.; Liu, X. An LMI approach to stability analysis of stochastic high-order Markovian jumping neural networks with mixed time delays. Nonlinear Anal. Hybrid Syst. 2008, 2, 110–120. [Google Scholar] [CrossRef]
- Xing, J.; Peng, C.; Cao, Z. Event-triggered adaptive fuzzy tracking control for high-order stochastic nonlinear systems. J. Frankl. Inst. 2022, 359, 6893–6914. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Chen, C.; Zhang, Y. Event-triggered fuzzy adaptive compensation control for uncertain stochastic nonlinear systems with given transient specification and actuator failures. Fuzzy Sets Syst. 2019, 365, 1–21. [Google Scholar] [CrossRef]
- Yang, G.; Li, X.; Ding, X. Numerical investigation of stochastic canonical Hamiltonian systems by high order stochastic partitioned Runge–Kutta methods. Commun. Nonlinear Sci. Numer. Simul. 2021, 94, 105538. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Q. Output-feedback stabilization of a class of stochastic high-order nonlinear systems with stochastic inverse dynamics and multidelay. Int. J. Robust Nonlinear Control. 2021, 13, 5580–5601. [Google Scholar] [CrossRef]
- Xie, X.; Duan, N.; Yu, X. State-Feedback Control of High-Order Stochastic Nonlinear Systems with SiISS Inverse Dynamics. IEEE Trans. Autom. Control. 2011, 56, 1921–1936. [Google Scholar]
- Fei, F.; Jenny, P. A high-order unified stochastic particle method based on the Bhatnagar-Gross-Krook model for multi-scale gas flows. Comput. Phys. Commun. 2022, 274, 108303. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Horwood: Buckinghamshire, UK, 1997. [Google Scholar]
- Forti, M.; Tesi, A. New conditions for global stability of neural networks with application to linear and quadratic programming problems. IEEE Trans. Circuits Syst. 1995, 42, 354–366. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, F.; Wang, X.; Cheng, X. Stability of Stochastic Networks with Proportional Delays and the Unsupervised Hebbian-Type Learning Algorithm. Mathematics 2023, 11, 4755. https://doi.org/10.3390/math11234755
Zheng F, Wang X, Cheng X. Stability of Stochastic Networks with Proportional Delays and the Unsupervised Hebbian-Type Learning Algorithm. Mathematics. 2023; 11(23):4755. https://doi.org/10.3390/math11234755
Chicago/Turabian StyleZheng, Famei, Xiaojing Wang, and Xiwang Cheng. 2023. "Stability of Stochastic Networks with Proportional Delays and the Unsupervised Hebbian-Type Learning Algorithm" Mathematics 11, no. 23: 4755. https://doi.org/10.3390/math11234755
APA StyleZheng, F., Wang, X., & Cheng, X. (2023). Stability of Stochastic Networks with Proportional Delays and the Unsupervised Hebbian-Type Learning Algorithm. Mathematics, 11(23), 4755. https://doi.org/10.3390/math11234755



