Output Feedback Control Design for Switched Systems with Unmatched Uncertainties Based on the Switched Robust Integral Sliding Mode
Abstract
:1. Introduction
2. Problem Formulation
3. Switched Robust Integral Sliding-Mode Surface Design via the State Observer
3.1. Sliding Surface with Multiple Sliding Modes
3.2. Sliding Mode Design of Subsystems
3.3. SRISM Sliding-Mode Surface and Its Stability
- (1)
- When , the system state will be exponentially stable.
- (2)
- When , the system state trajectory will exponentially converge to
- (1)
- In the case where :
- (2)
- In the case where :
- (1)
- When , the system state will be asymptotically stable, i.e., .
- (2)
- When , the following inequality
- (1)
- In the case where :
- (2)
- In the case where :
- (1)
- When , the system state will be exponentially stable.
- (2)
- When , the system state trajectory will exponentially converge to
4. SMC Controller
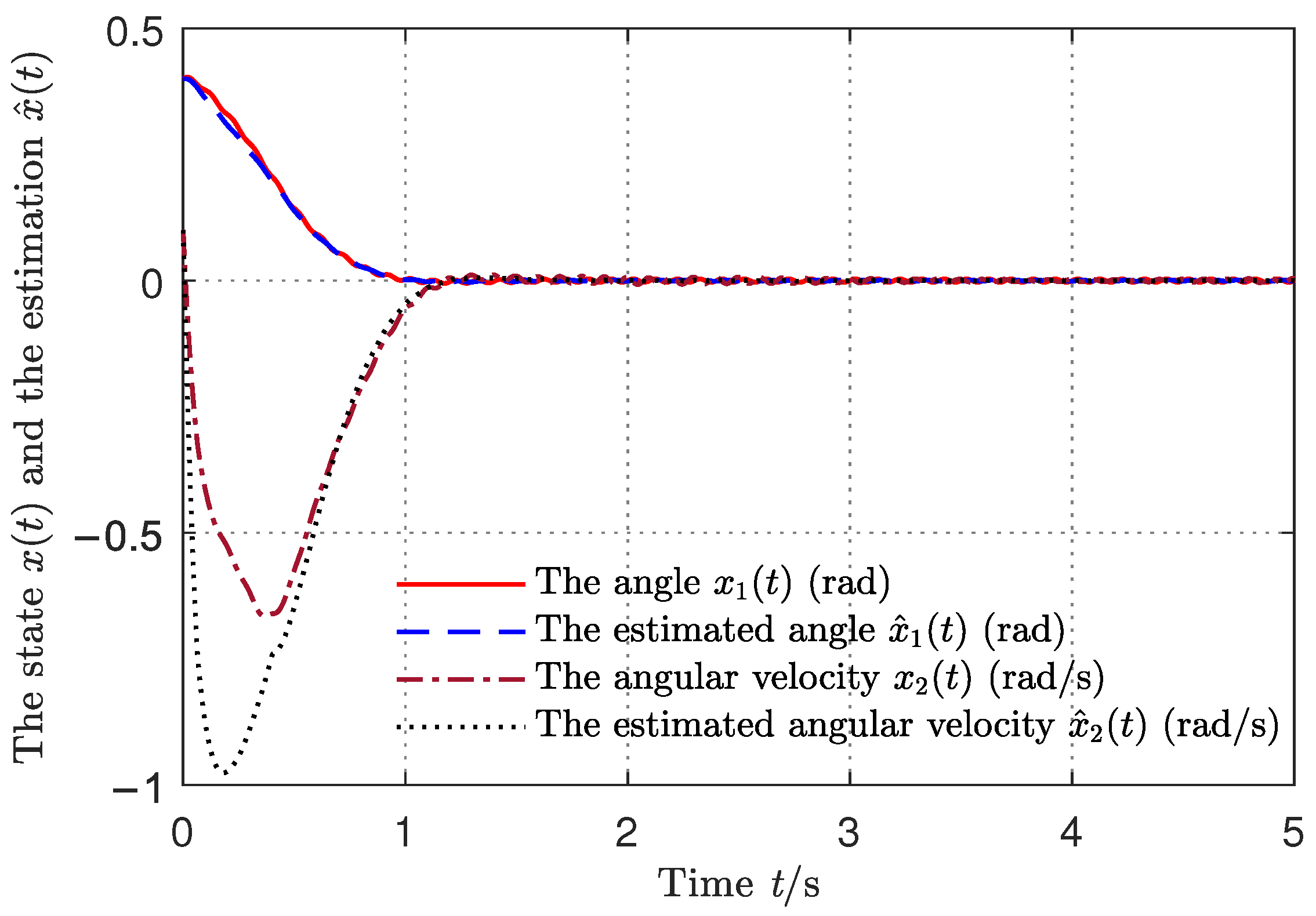
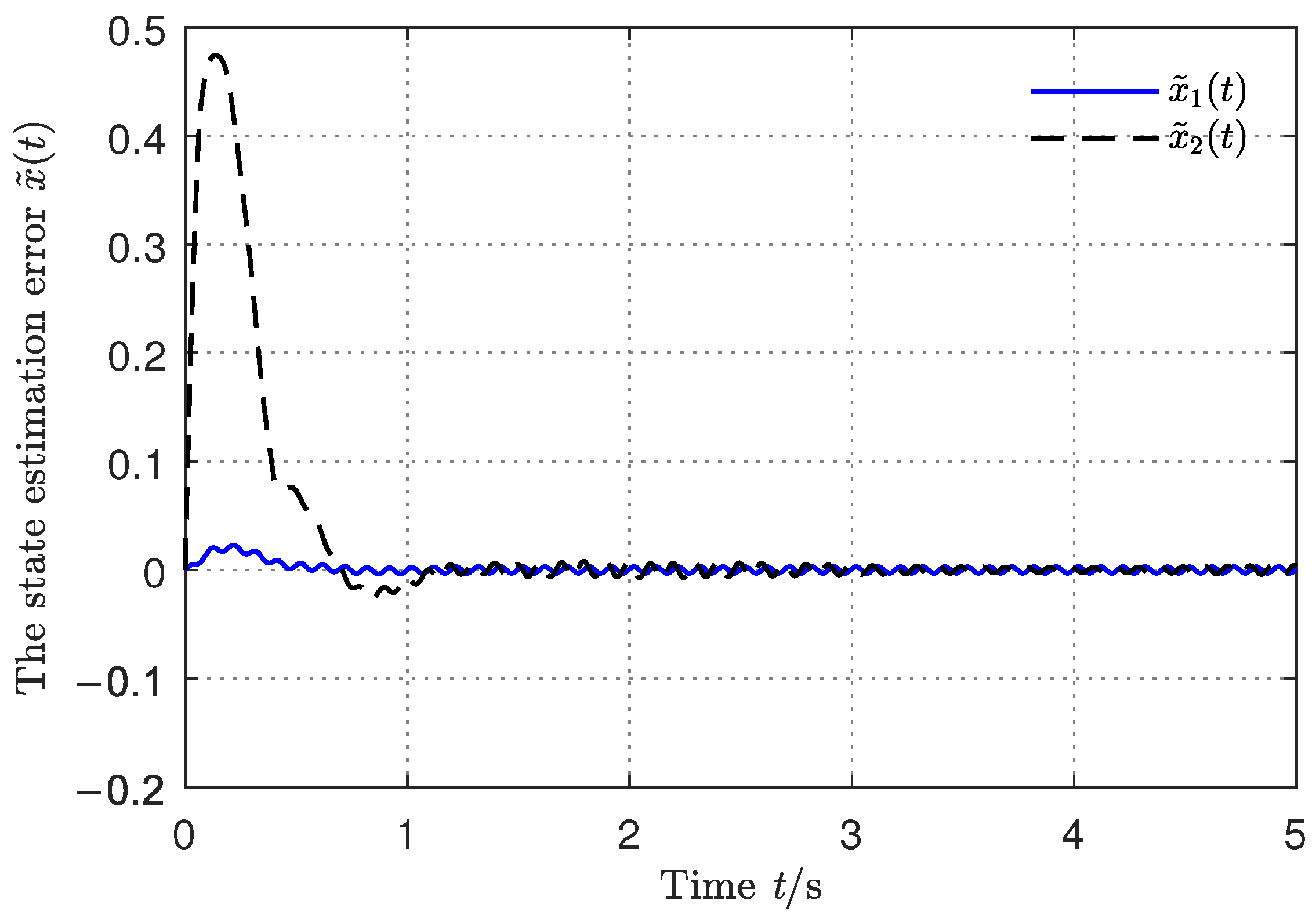
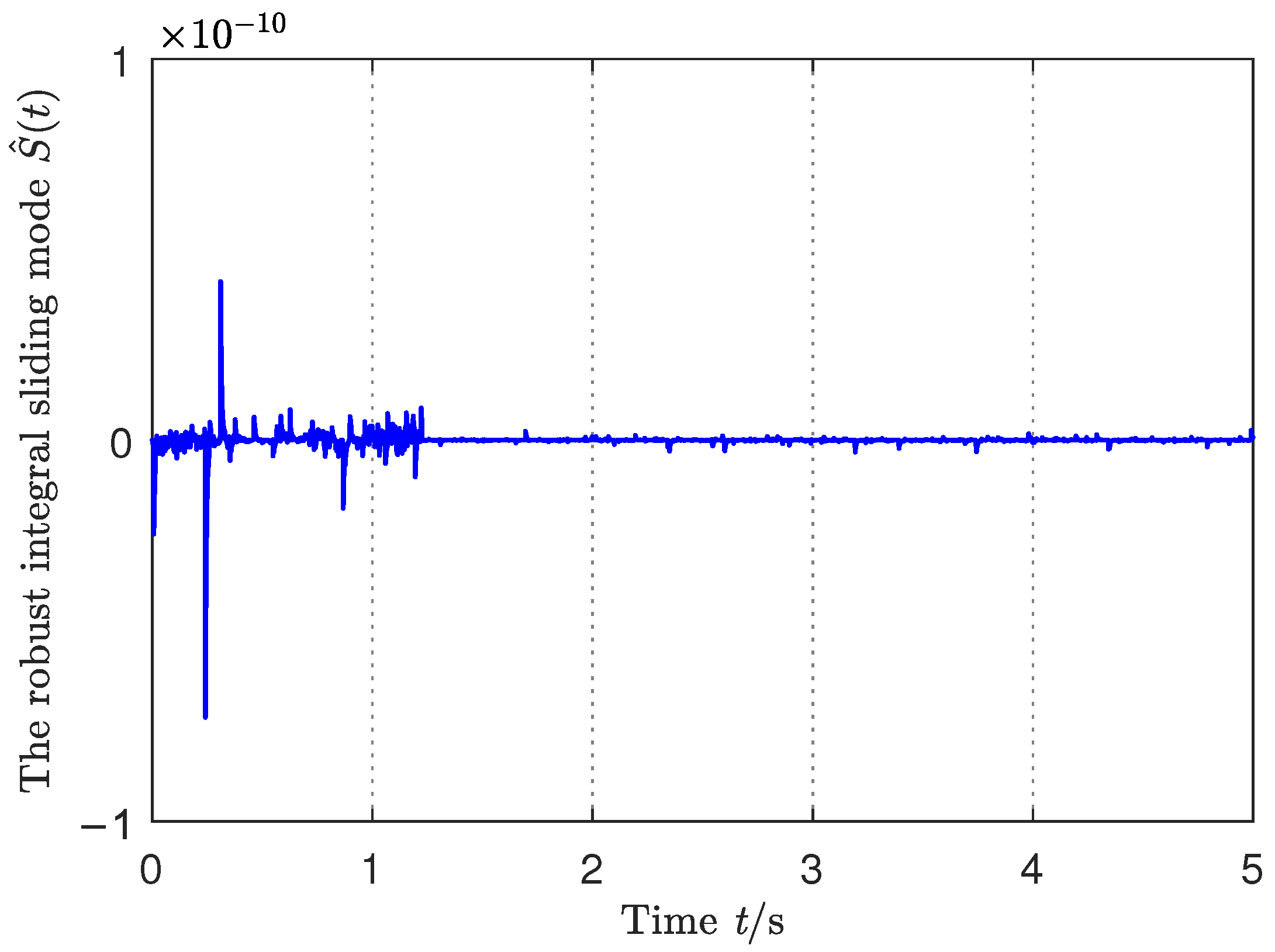
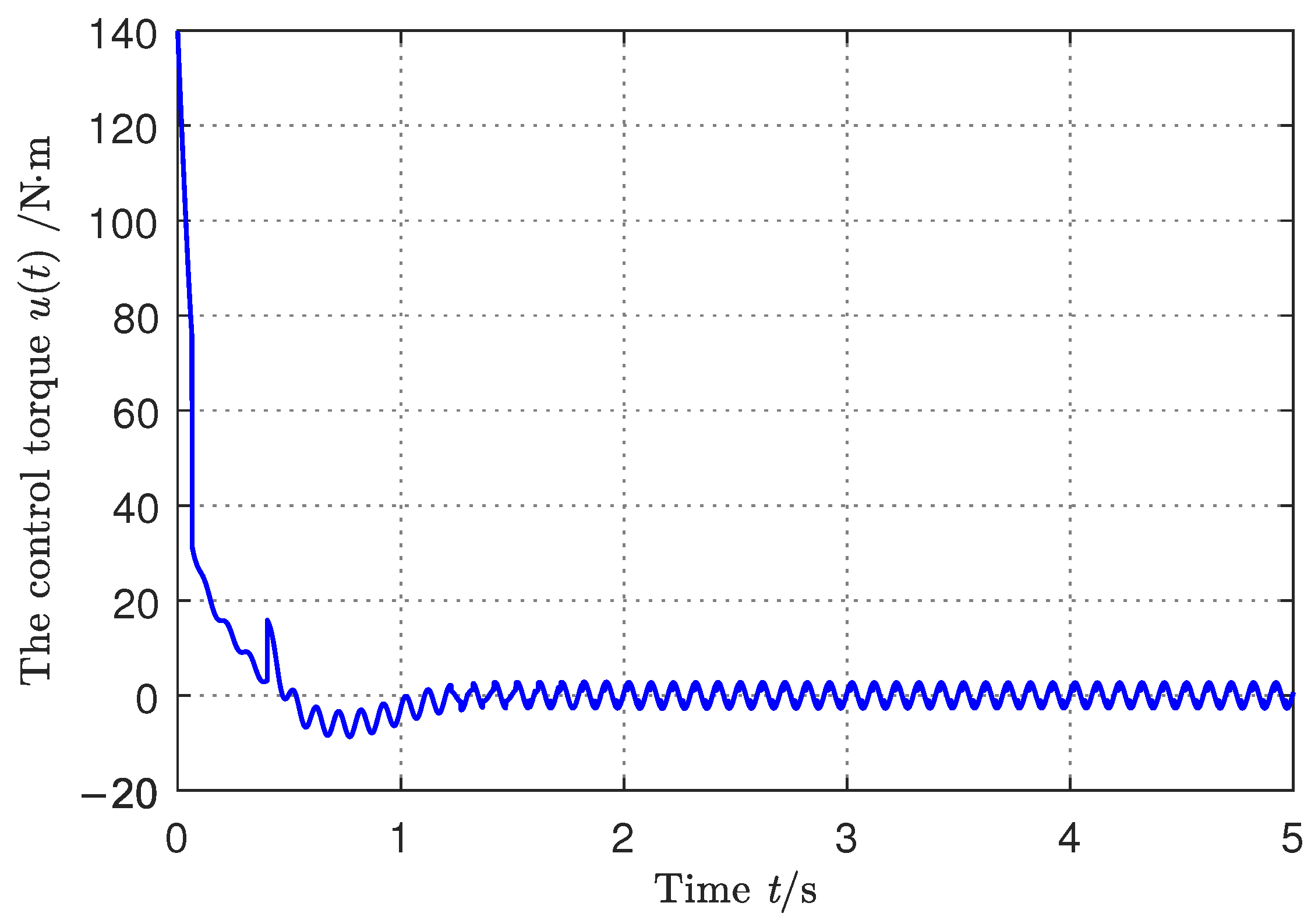
5. Illustrative Example
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liberzon, D. Switching in Systems and Control; Birkhauser: Boston, MA, USA, 2003. [Google Scholar]
- Margaliot, M. Stability analysis of switched systems using variational principles: An introduction. Automatica 2006, 42, 2059–2077. [Google Scholar] [CrossRef]
- Wu, L.; Shi, P.; Su, X. Sliding Mode Control of Uncertain Parameter-Switching Hybrid Systems; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Tóth, R.; Felici, F.; Heuberger, P.; Van den Hof, P. Crucial aspects of zero-order hold LPV state-space system discretization. IFAC Proc. Vol. 2008, 41, 4952–4957. [Google Scholar] [CrossRef]
- Krasnova, S.A.; Utkin, V.A.; Utkin, A.V. Block approach to analysis and design of the invariant nonlinear tracking systems. Autom. Remote Control 2017, 78, 2120–2140. [Google Scholar] [CrossRef]
- Andrievsky, B.R.; Furtat, I.B. Disturbance observers: Methods and applications. I. Methods. Autom. Remote Control 2020, 81, 1563–1610. [Google Scholar] [CrossRef]
- Andrievsky, B.R.; Furtat, I.B. Disturbance observers: Methods and applications. II. Applications. Autom. Remote Control 2020, 81, 1775–1818. [Google Scholar] [CrossRef]
- Wang, J.; Huo, S.; Xia, J.; Park, J.H.; Huang, X.; Shen, H. Generalised dissipative asynchronous output feedback control for Markov jump repeated scalar nonlinear systems with time-varying delay. IET Control Theory Appl. 2019, 13, 2114–2121. [Google Scholar] [CrossRef]
- Geromel, J.C.; Colaneri, P.; Bolzern, P. Dynamic Output Feedback Control of Switched Linear Systems. IEEE Trans. Autom. Control 2008, 53, 720–733. [Google Scholar] [CrossRef]
- Li, L.; Zhao, J.; Dimirovski, G.M. Observer-based reliable exponential stabilization and control for switched systems with faulty actuators: An average dwell time approach. Nonlinear Anal. Hybrid Syst. 2011, 5, 479–491. [Google Scholar] [CrossRef]
- Deaecto, G.S.; Geromel, J.C.; Daafouz, J. Dynamic output feedback control of switched systems. Automatica 2011, 47, 1713–1720. [Google Scholar] [CrossRef]
- Li, Z.G.; Wen, C.Y.; Soh, Y.C. Observer-based stabilization of switching linear systems. Automatica 2005, 41, 181–195. [Google Scholar] [CrossRef]
- El-Farra, N.H.; Mhaskar, P.; Christofides, P.D. Output feedback control of switched nonlinear systems using multiple Lyapunov functions. Syst. Control Lett. 2005, 54, 1163–1182. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Sun, C. Fixed-time sliding mode output tracking control for second-order switched systems with power integrators. Comput. Electr. Eng. 2021, 96, 107503. [Google Scholar] [CrossRef]
- Qi, S.; Zhao, J.; Tang, L. Adaptive Output Feedback Control for Constrained Switched Systems with Input Quantization. Mathematics 2023, 11, 788. [Google Scholar] [CrossRef]
- Qi, Y.; Hu, J. Observer-based bumpless switching control for switched linear systems with sensor faults. Trans. Inst. Meas. Control 2018, 40, 1490–1498. [Google Scholar] [CrossRef]
- Zhao, H.; Niu, Y.; Song, J. Finite-time output feedback control of uncertain switched systems via sliding mode design. Int. J. Syst. Sci. 2018, 49, 984–996. [Google Scholar] [CrossRef]
- Yin, S.; Gao, H.; Qiu, J.; Kaynak, O. Descriptor reduced-order sliding mode observers design for switched systems with sensor and actuator faults. Automatica 2017, 76, 282–292. [Google Scholar] [CrossRef]
- Wu, L.; Lam, J. Sliding mode control of switched hybrid systems with time-varying delay. Int. J. Adapt. Control Signal Process. 2008, 22, 909–931. [Google Scholar] [CrossRef]
- Wu, L.; Ho, D.W.C.; Li, C.W. Sliding mode control of switched hybrid systems with stochastic perturbation. Syst. Control Lett. 2011, 60, 531–539. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhauser, Springer: New York, NY, USA, 2014. [Google Scholar]
- Gao, R.; Zhai, D.; Xie, X. On the design of output information-based sliding mode controllers for switched descriptor systems: Linear sliding variable approach. Appl. Math. Comput. 2020, 364, 124680. [Google Scholar] [CrossRef]
- Kchaou, M.; Regaieg, M.A.; Al-Hajjaji, A. Quantized asynchronous extended dissipative observer-based sliding mode control for Markovian jump TS fuzzy systems. J. Frankl. Inst. 2022, 359, 9636–9665. [Google Scholar] [CrossRef]
- Qi, W.; Zong, G.; Karimi, H.R. Finite-time observer-based sliding mode control for quantized semi-Markov switching systems with application. IEEE Trans. Ind. Inform. 2020, 16, 1259–1271. [Google Scholar] [CrossRef]
- Zhang, P.; Kao, Y.; Hu, J.; Niu, B.; Xia, H.; Wang, C. Finite-time observer-based sliding-mode control for Markovian jump systems with switching chain: Average dwell-time method. IEEE Trans. Cybern. 2023, 53, 248–261. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Qi, W.; Pang, G.; Cheng, J.; Shi, K. Observer-based sliding mode control for fuzzy stochastic switching systems with deception attacks. Appl. Math. Comput. 2022, 427, 127153. [Google Scholar] [CrossRef]
- Li, J.; Guo, X.; Chen, C.; Su, Q. Robust fault diagnosis for switched systems based on sliding mode observer. Appl. Math. Comput. 2019, 341, 193–203. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Li, S.; Yan, H.; Fan, Q.Y. Sliding mode switching observer-based actuator fault detection and isolation for a class of uncertain systems. Nonlinear Anal. Hybrid Syst. 2019, 33, 322–335. [Google Scholar] [CrossRef]
- Meng, X.; Jiang, B.; Karimi, H.R.; Gao, C. An event-triggered mechanism to observer-based sliding mode control of fractional-order uncertain switched systems. ISA Trans. 2023, 135, 115–129. [Google Scholar] [CrossRef]
- Utkin, V.I.; Shi, J. Integral sliding mode in systems operating under uncertainty conditions. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; pp. 4591–4596. [Google Scholar]
- Cao, W.J.; Xu, J.X. Nonlinear integral-type sliding surface for both matched and unmatched uncertain systems. IEEE Trans. Autom. Control 2004, 49, 1355–1360. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, C.; Pan, L.; Yu, H. Integral sliding mode control: Performance, modification, and improvement. IEEE Trans. Ind. Inform. 2018, 14, 3087–3096. [Google Scholar] [CrossRef]
- Kchaou, M.; Al Ahmadi, S. Robust H∞ control for nonlinear uncertain switched descriptor systems with time delay and nonlinear input: A sliding mode approach. Complexity 2017, 2017, 1027909. [Google Scholar] [CrossRef]
- Chen, H.; Lim, C.C.; Shi, P. Robust H∞-based control for uncertain stochastic fuzzy switched time-delay systems via integral sliding mode strategy. IEEE Trans. Fuzzy Syst. 2022, 30, 382–396. [Google Scholar] [CrossRef]
- Qi, W.; Gao, X.; Ahn, C.K.; Cao, J.; Cheng, J. Fuzzy integral sliding-mode control for nonlinear semi-Markovian switching systems with application. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1674–1683. [Google Scholar] [CrossRef]
- Zhang, X. Robust integral sliding mode control for uncertain switched systems under arbitrary switching rules. Nonlinear Anal. Hybrid Syst. 2020, 37, 100900. [Google Scholar] [CrossRef]
- Kao, Y.; Liu, X.; Song, M.; Zhao, L.; Zhang, Q. Nonfragile-observer-based integral sliding mode control for a class of uncertain switched hyperbolic systems. IEEE Trans. Autom. Control 2023, 68, 5059–5066. [Google Scholar] [CrossRef]
- Wang, C.; Li, R.; Su, X.; Shi, P. Output feedback sliding mode control of Markovian jump systems and its application to switched boost converter. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 5134–5144. [Google Scholar] [CrossRef]
- Lian, J.; Ge, Y. Robust H∞ output tracking control for switched systems under asynchronous switching. Nonlinear Anal. Hybrid Syst. 2013, 8, 57–68. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, L.; Souza, C.E.D. Robust control of a class of uncertain nonlinear systems. Syst. Control Lett. 1992, 19, 139–149. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, L.; Li, H. Robust control for switched systems with unmatched uncertainties based on switched robust integral sliding mode. IEEE Access 2020, 8, 138396–138405. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xiong, S. Output Feedback Control Design for Switched Systems with Unmatched Uncertainties Based on the Switched Robust Integral Sliding Mode. Mathematics 2023, 11, 4674. https://doi.org/10.3390/math11224674
Zhang X, Xiong S. Output Feedback Control Design for Switched Systems with Unmatched Uncertainties Based on the Switched Robust Integral Sliding Mode. Mathematics. 2023; 11(22):4674. https://doi.org/10.3390/math11224674
Chicago/Turabian StyleZhang, Xiaoyu, and Shuiping Xiong. 2023. "Output Feedback Control Design for Switched Systems with Unmatched Uncertainties Based on the Switched Robust Integral Sliding Mode" Mathematics 11, no. 22: 4674. https://doi.org/10.3390/math11224674
APA StyleZhang, X., & Xiong, S. (2023). Output Feedback Control Design for Switched Systems with Unmatched Uncertainties Based on the Switched Robust Integral Sliding Mode. Mathematics, 11(22), 4674. https://doi.org/10.3390/math11224674






