Abstract
This research delves into the intricacies of a two-dimensional, steady flow of a ferrofluid within a porous medium, where the thermal conductivity is subject to temperature variations. The study encompasses the influence of magnetic dipoles, radiation, Brownian motion, and thermophoresis phenomena as they interact with a stretching sheet. A novel aspect of this investigation is the detailed analysis of Brownian and thermophoresis effects on nanoparticles while considering Nield’s boundary conditions. The study involves the transformation of flow equations into ordinary differential equations through standard similarity transformations, unraveling the governing equations using the BVP4C method. The outcomes are presented graphically, providing a comprehensive assessment of the factors impacting the fluid properties, including velocity, temperature, and concentration. Notably, this study reveals that an increase in the ferrofluid parameter leads to elevated temperature profiles while causing a decrease in velocity. Furthermore, an increase in the viscosity parameter is associated with a reduction in velocity. Some technological applications of the problem include magnetically controlled actuation and drug targeting.
MSC:
80M10; 80M15; 80M20; 80M30
1. Introduction
Magnetic dipoles have been found to have a significant impact on the temperature and momentum boundary layers when combined with a fluid, which serves as a heat transporter. The presence of magnetic dipoles in the flow field gradually reduces turbulent effects. The effect of a magnetic dipole is characterized by the constraint on one of two forms—the closed loop of electric current or a couple of poles—as the bulk of the source diminishes to zero profile in the case of a constant magnetic moment. As the distance from the source increases, the magnetic field around the source begins to resemble that of a magnetic dipole. As fluids have common utilization for the phenomenon of heat dissipation as heat transporters, the combined effects of the magnetic dipole with fluids have proven influential in constraining the temperature and momentum boundary layers. Engineering, physics, and environmental sciences all heavily depend on heat transfer, a fundamental phenomenon that occurs in various systems. Due to its numerous applications, such as heat exchange, pharmaceuticals, and biotechnology, the study of heat transfer in fluids is of utmost importance.
Ferrofluids are highly suitable for applications involving rotary seals, hard drives with rotating shafts, and vibration-damping systems in speakers. Due to their paramagnetic properties, these fluids have garnered significant attention from scientists. Their utility extends across various technical disciplines, such as electronics, materials science, thermal engineering, biomechanical engineering, and aerospace. Additionally, they find applications in medical magnetic resonance imaging as a contrast agent. Researchers have explored the convection of a magnetite–water nanofluid under gravity and radiative heat transfer on a swinging vertical surface in a magnetic field. They have also investigated ferrofluids’ entropy generation and convection in partially filled chambers with porous materials. They have also studied natural convection and entropy production in open chambers containing ferrofluid-infused permeable blocks. Convection of a magnetite–water nanofluid, driven by gravity and assisted by radiating heat transfer via a swinging vertical surface in a magnetic region, was suggested by Seth and Mandal []. Naturally, the entropy formation and convection of ferrofluids were described by Astanina et al. [], using an open trapezoidal chamber partly crammed with porous material. Gibanov et al. [] executed natural convection and entropy production in an open chamber across a variety of horizontal permeable blocks imbued with ferrofluid. The heat transfer of a ferrofluid with a non-uniform magnetic region through a channel via sinusoidal walls was explored by Asadi et al. []. The impact of a magnetic region on the convection and heat radiation of an Fe3O4–water ferrofluid was experimentally and numerically studied by Sheikholeslami and Abelman [].
Furthermore, there have been studies on heat transfer in ferrofluids under non-uniform magnetic fields in channels with sinusoidal walls. The impact of magnetic fields on convection and heat radiation in an Fe3O4–water ferrofluid has been examined experimentally and numerically. With a non-uniform transverse magnetic field, Aminfar et al. [] conducted heat transfer and flow analyses of a ferrofluid via a rectangular duct. In the realm of porous media, researchers have made significant progress in understanding heat transport, a critical area of investigation given the diverse applications of porous media. Natural convection, which occurs when a hot surface heats a fluid, has been explored in the solid and porous domains, considering various factors, such as radiation and Hall current. The effects of chemical reactions and radiation on the flow of Casson magnetohydrodynamic fluids across a heat source/sink have been documented. There are a number of technical applications that make use of flow and heat transmission via porous media. These include chemical reactors, thermal insulation, and groundwater hydrology. Vafai and Tien [] found that the flow was affected by both boundary conditions and inertia. Modather and Chamkha [] reviewed the oscillatory flow of a micropolar fluid across a vertical permeable plate in a porous medium. Elbashbeshy et al. [] studied the flow and heat transfer in a Maxwell fluid and porous medium with radiation across a stretched surface with a changeable thickness.
The exchange of energy between bodies at different temperatures occurs through various means, including thermal radiation, which involves the emission of electromagnetic waves from a substance, leading to its warming up. Researchers have investigated the influence of metallic nanoparticles on the motion of a moving magnetohydrodynamic radiation beam and radiative non-Darcy nanofluid flow with convective Neild conditions and energy activation. The effects of heat production and radiation on natural convection in magnetohydrodynamic flow have also been studied. Bidin and Nazar [] explored the boundary layer flow owing to the exponential stretching of a sheet with thermal radiation. This work was further examined and extended by Mukhopadhyay and Gorla [] with a partial slip effect. Chaudhary et al. [] analyzed the effects of radiation on MHD past an exponentially stretched sheet. In their work, the temperature became higher with each increase in the radiation parameter.
Nanofluids, characterized by particles on the nanoscale, have been explored for their potential to enhance heat transfer in various applications due to their stability, minimal clogging, and high thermal conductivity. Research has demonstrated that Brownian-motion-induced convection and propagation through nanoparticle pathways are common mechanisms for improved heat transfer in nanofluids. Many scholars have delved into the consequences of Brownian motion and thermophoresis in different technical setups. They have examined the impacts of various parameters on heat transfer, entropy generation, and other relevant factors. Numerous scholars [,,] have thoroughly examined the consequences of Brownian motion and thermophoresis. With heat augmentation as their ultimate aim, their research has examined various technical setups. Waqas et al. [] used a Cu–water nanofluid with MHD to investigate the effects of varying nanofluid densities in a sinusoidal cavity with wavelength variations along two sides. Their research showed that, in most situations, the kinetic energy, heat transfer rate, and entropy formation all increase as the concentrations fall in volume. Nano/micropolar fluids over a 3D rotating surface were the subject of a recent numerical investigation, as described by Waqas et al. []. Brownian motion improves heat transmission, and a rise in the volumetric concentration field is seen, increasing the activation energy parameter. Waqas et al. [] studied the free convection heat transfer effects of Cu–water nanofluid flow using an annulus with inserted fins in the inner cylinder. These researchers found that solid nanoparticles significantly increased the heat transfer, and that this effect was augmented by increasing the solid particle content. Waqas et al. [] set out to analyze the impact of magnetic flow within a stenotic artery on silver–gold nanoparticles submerged in human blood. With increasing Biot number and radiation parameter differences, they observed a rising behavior in the thermal distribution profile. Using the Cattaneo–Christov heat flux model and the Powell–Eyring hybrid nanofluid with slip boundary conditions, Waqas et al. [] wanted to learn more about these phenomena and their application to a moving surface. The thickness of the temperature layer was found to grow when the thermal radiation parameter, the volumetric proportion of nanoparticles parameter, the Biot number, and the thermal relaxation parameter all rose. Numerous articles [,,,,] detail the results of such investigations.
However, a significant research gap existed in studying 2D nanoparticle motion in steady flow over a ferromagnetic stretched surface with Nield’s conditions. In this study, we use a novel boundary condition recently given by Nield and Kuznetsov [,,,,,] for the nanofluid model first developed by Buongiorno. Nield and Kuznetsov’s [] model has the drawback of requiring active management of the nanoparticle volume fraction at the border, as detailed in []. A revised model has been presented to account for the scenario in which the proportion of nanofluid particles at the border is passively rather than actively regulated [,,,]. This study addresses this gap by utilizing Nield and Kuznetsov’s boundary condition for nanofluid modeling. The study extends previous work by Saeed et al. [] by investigating the influence of magnetic dipoles, nonlinear thermal ferromagnetic radiation, and Nield’s conditions on a stretching surface through numerical analysis.
The main objectives of this study are as follows:
- Present a model for the flow of a viscous, incompressible, radiating, electrically conductive nanofluid over a stretching sheet.
- Employ appropriate similarity transformations to convert the main equations into a system of nonlinear ordinary differential equations, which are numerically solved using the BVP4C method.
- Examine and interpret how various parameters affect the fluid and boundary characteristics.
- Report on the impact of ferromagnetic properties on nanofluid velocity.
- Analyze the influences of Brownian motion and thermophoresis effects.
The findings of this research have potential applications in improving heat transfer and mass flow in boundary layers, especially in scenarios involving stretched surfaces and the presence of thermophoresis and Brownian motion.
2. Mathematical Formulation
The scenario under consideration involves an impermeable stretching sheet that drives a continuous two-dimensional flow of an incompressible and viscous magnetite ferrofluid. Several key assumptions characterize this situation:
- Flow direction: The x-axis represents the direction of the flow, driven by the interplay of two opposing forces.
- Flow normality: The y-axis is perpendicular to the direction of flow.
- Velocity profile: The velocity of the fluid varies along the x-axis inversely with distance from the origin, indicating that it stretches the sheet as it moves.
- Magnetic dipole: Positioned beneath the sheet, there exists a magnetic dipole. This dipole is responsible for creating a magnetic field.
- Magnetic saturation: The magnetic field created by the dipole is strong enough to saturate the points of the ferrofluid in the positive x-direction. This implies that the ferrofluid in this region becomes magnetized.
- Temperature control: To prevent the stretched sheet from becoming magnetized, it is maintained at a constant temperature, Tw, which is kept below the Curie temperature (TC). The Curie temperature is when a ferromagnetic material loses its permanent magnetization.
- Uniform temperature: Fluid components located at a given distance from the sheet are considered to have a uniform temperature equal to the Curie temperature (T = TC).
This setup forms the basis for the model’s physical flow, where the interplay of magnetic forces, temperature control, and the stretching sheet influences the behavior of the magnetite ferrofluid (Figure 1).
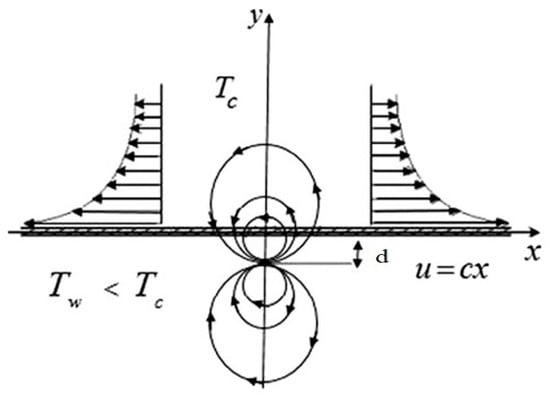
Figure 1.
A symbolic depiction of the model’s physical flow.
The components of magnetic potential and strength of H are as follows [,]:
From Equations (3) and (4), we have
The ferrofluid boundary layer equations follow [,]:
The boundary conditions of the problem are as follows []:
The boundary condition, as indicated by the mass flux of nanoparticles at y = 0 in Equation (11), becomes irrelevant when considering thermophoresis, as described by Nield and Kuznetsov [].
The heat flux and T4 [] are adopted:
Temperature gives rise to an exponential relationship with viscosity, which can be precisely expressed as follows:
The similarity transformations are as follows:
All of the parameters and their definitions can be found in the Nomenclature section. The dimensionless equations are as follows:
The boundary conditions that are related or relevant in this context are as follows:
Physically significant numbers include Sk, Nu, and Sh, which may be stated as follows:
where is the Reynolds number.
3. Solution Methodology
Numerical methods are employed to handle the boundary constraints, represented by Equations (19) and (20), within the dimensionless flow system described by Equations (16)–(18). Due to the inherent nonlinear nature of the equations, exact solutions are extremely challenging to obtain. Therefore, we have opted to utilize a well-established numerical approach, the BVP4C method, within the MATLAB 2020b computational environment. To apply the BVP4C method, the higher-order boundary value problem must be transformed into a 1st-order initial value problem. The numerical process is outlined in Figure 2, and a high degree of accuracy, up to six decimal places, is achieved by configuring the convergence criteria with a relative error tolerance of 10−6. Various initial estimates for the values of f″(0), θ′(0), and ϕ′(0) are utilized to obtain solutions that ensure that the velocity, temperature, and concentration profiles asymptotically satisfy the far-field boundary conditions. Adjusting the boundary layer thickness, which is influenced by the parameter values, is crucial for this purpose. To ensure the validity of the numerical calculations, it is imperative that all profiles asymptotically satisfy the infinite boundary conditions. Additionally, the obtained results are compared with the findings of other researchers whose work has been previously published.
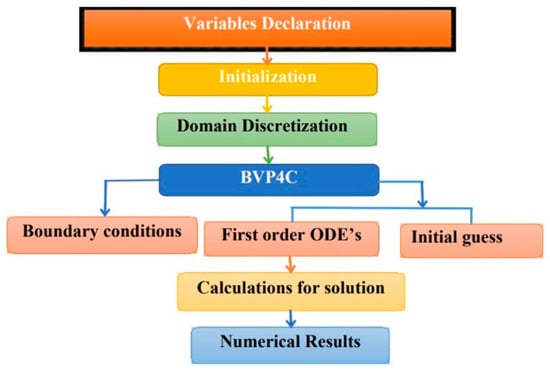
Figure 2.
Flowchart of the solution method (ODE: ordinary differential equation).
The boundary value problem is effectively transformed into an initial value problem through the BVP4C technique. This transformation involves maintaining a fixed condition throughout the analysis. The calculation of the given end condition relies on estimations for the missing initial condition. As long as the governing differential equation remains linear, the equation system can be treated as linear. The BVP4C method facilitates this transformation, enabling a more manageable and effective numerical solution process.
The boundary conditions that correspond to this situation are as follows:
Advantages:
Higher precision: Compared to more basic numerical approaches, BVP4C typically provides more precise and accurate results, especially for BVPs with higher-order forms. This accuracy is valuable when exact solutions are difficult or impossible to obtain.
Continuity: BVP4C solutions on the interval [a, b] have continuous first derivatives. This characteristic ensures the quality and smoothness of the solution throughout the specified range, making it suitable for various applications.
Ease of use: BVP4C is often relatively user-friendly and does not require extensive mathematical or programming expertise to implement effectively.
Efficiency: BVP4C can quickly generate results, essential when dealing with complex boundary value problems or time-sensitive applications.
Broad applicability: BVP4C can solve a wide range of boundary value problems, including finding an analytic solution that is challenging or not feasible.
Disadvantages:
Lack of elegance: BVP4C solutions are not as elegant as analytic solutions. They involve numerical approximations and may not provide the same level of insight into the underlying mathematical structure of the problem.
Limited generalization: While BVP4C can effectively solve specific boundary value problems, it may not easily extend to more generalized cases or different problems. Each problem typically requires a tailored approach.
Lack of exactness: BVP4C solutions are numerical approximations, and the exact solution is often not immediately clear. Users must rely on the method’s accuracy and perform convergence checks to assess the reliability of the results.
In summary, the BVP4C method is a valuable tool for solving boundary value problems, offering high precision and practicality in many cases. However, it lacks analytical solutions’ elegance and generalization capabilities, and users should remain mindful of its numerical nature and perform validation checks for reliability.
4. Results and Discussion
A 2D steady flow of a ferrofluid in a porous medium whose thermal conductivity varies with temperature was explored. Furthermore, magnetic dipole, radiation, Brownian motion, and thermosphere effects across a stretching sheet were considered. Here, we present the physical meanings of the findings from the relevant numerical calculations. As a result, we extended the work of Saeed et al. [] using the above sources to experience these kinds of consequences. The assumed values in this work are as follows: β = 0.5; α = 0.5; Γ = 0.4; λ1 = 0.5; γ1 = 0.5; Tr = 3; δ = 0.2; Le = 0.5; Nt = 0.1; Nb = 0.1.
The velocity and concentration profiles are shown in Figure 3. As β increases, the ferrohydrodynamic interaction makes the fluid more viscous, with higher adhesive forces, resulting in increased velocity. The concentration profiles exhibit the opposite trend. Physically, this occurs when the ferromagnetic parameter in fluid motion increases due to the rise of the momentum boundary layer.
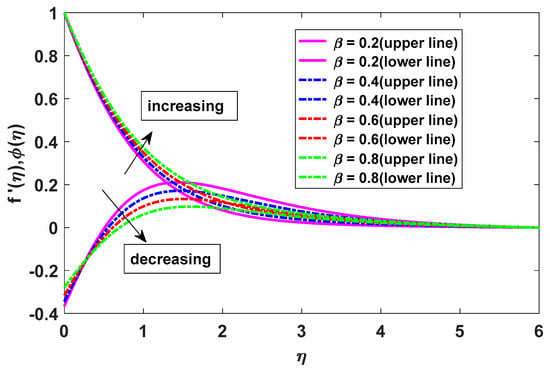
Figure 3.
Effects of β on velocity and concentration.
Figure 4 illustrates the effects of α on the velocity and concentration profiles. Higher α values reduce the velocity, while the concentration profiles show the opposite behavior. Viscous forces diminish as the fluid moves away from the magnetic dipole. Figure 5 shows the impact of λ1 on the velocity profiles. Increasing λ1 results in velocity profiles in opposite directions. The growth of the mixed convection parameter leads to faster velocity as the buoyancy effects become more pronounced. A scatterplot in Figure 6 demonstrates how Ec affects the temperature distribution. As Ec increases, the temperature increases. This is due to the action of viscous heating.
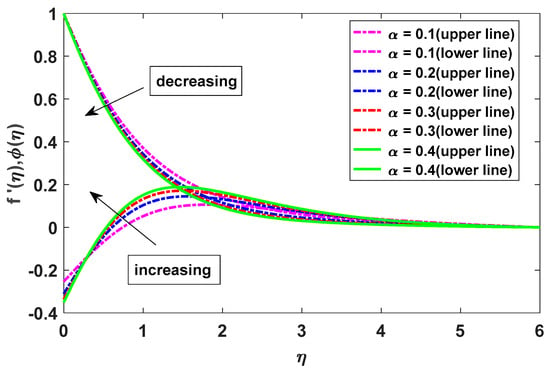
Figure 4.
Effects of α on velocity and concentration.
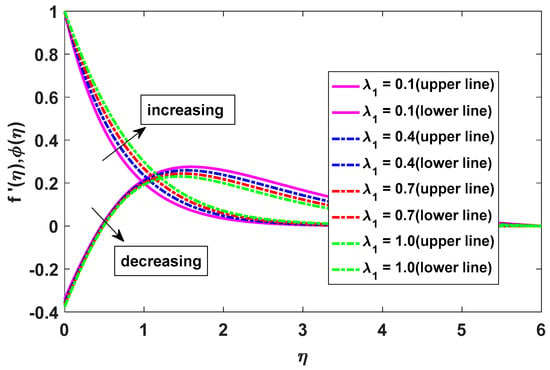
Figure 5.
Effects of λ1 on velocity and concentration.
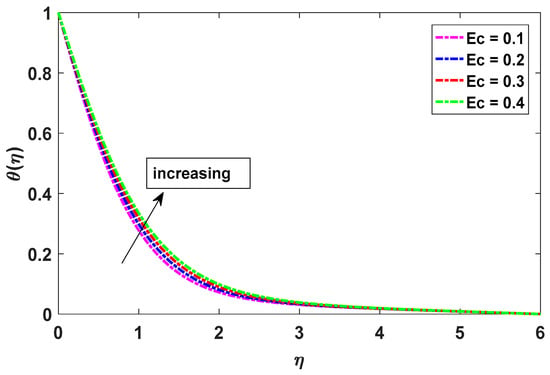
Figure 6.
Effect of Ec on temperature.
The influence of Tr on temperature is discussed using a scatterplot in Figure 7. When Tr increases, so does the temperature. When the boundary layer is thickened, the radiative forcing causes the temperature profiles to climb. Since all non-absolute-zero-temperature matter emits electromagnetic radiation in the form of thermal radiation, its purpose is to increase the medium’s thermal diffusivity, leading to more noticeable heat production in the boundary layer.
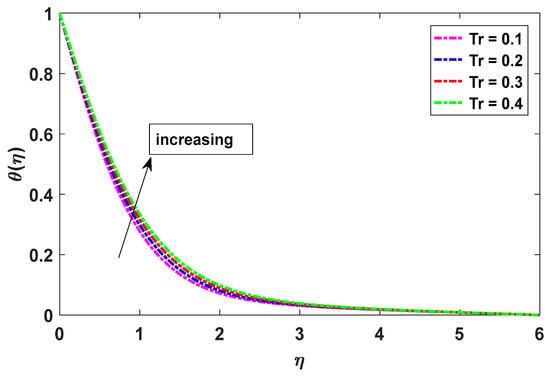
Figure 7.
Effect of Tr on temperature.
The consequences of the thermophoresis parameter Nt on the distribution of concentrations are shown in Figure 8. The concentration fields increase as Nt grows. Also, as Nt grows, the thermophoresis force rises, moving the nanoparticles from a warm region to a cold one; this, in turn, causes the concentration distributions to grow. Physically, thermophoretic force is to the result of a temperature differential that induces fast flow away from the wall, and it is well known that an elevation in the intensity of Brownian motion augments the thermal conductivity of the base fluid. As a result, the thermal boundary layer thickens as the hot fluid is channeled away from the wall.
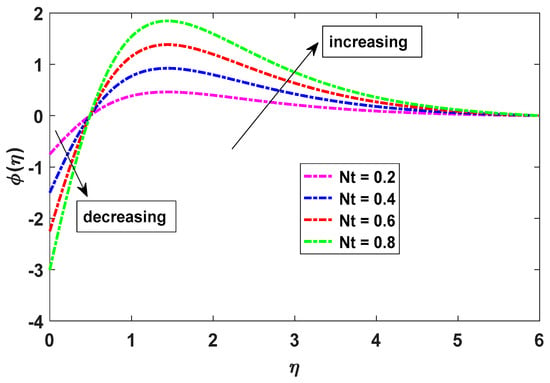
Figure 8.
Effect of Nt on concentration.
Figure 9 shows how the limit layer viscosity and concentration distribution grow with increasing Nb concentrations. As Nb increases, the liquid’s macroscopic particles become more likely to move randomly and collide with one another. As a result, there will be a higher concentration of liquid. By increasing Nb, the fluid velocity may be arbitrarily increased.
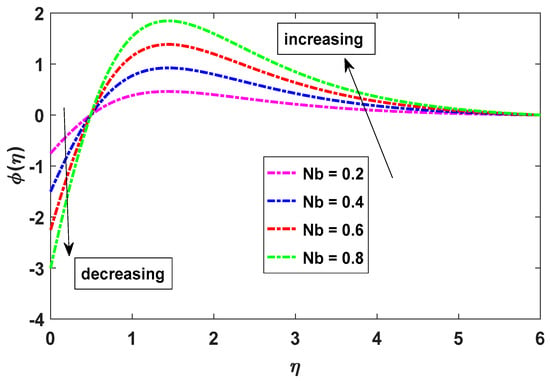
Figure 9.
Effect of Nb on concentration.
A plot of the Cf viscosity parameter vs. the Lewis number is illustrated in Figure 10. The Cf rises when the viscosity parameter is increased. It can be seen that an increase in skin friction occurs for the viscosity parameter. This helps enrich the momentum boundary layer, while the inverse occurs on the stretching surface.
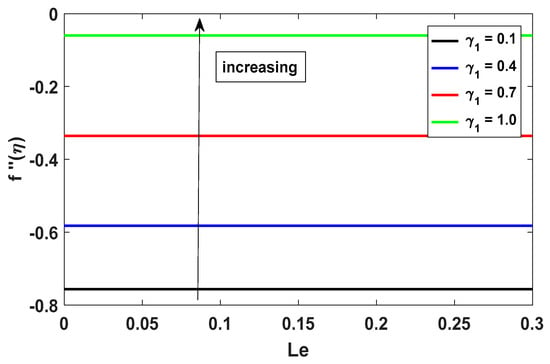
Figure 10.
Effect of γ1 on Cf against Le.
The effects of the ferromagnetic parameter on the local Nusselt number are depicted in Figure 11a. When the ferromagnetic parameter increases, the heat transfer rate declines, decreasing the heat transfer rate from the surface. Figure 11b demonstrates the variations in the local Sherwood numbers with varying thermophoresis parameters. And since the Sherwood number is indirectly proportional to the thermophoresis parameter, alternatively, it decreases, as verified by Figure 11, which depicts the flow pattern as streamlines for β.
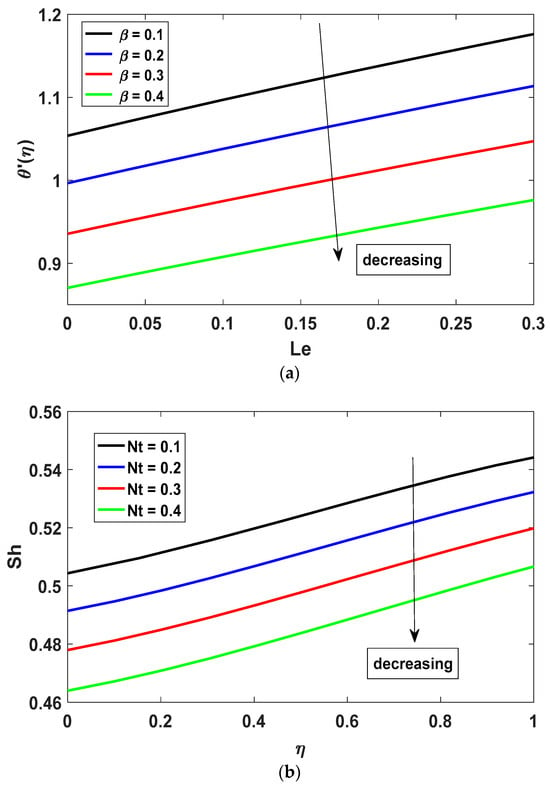
Figure 11.
(a) Effect of β on Nu against Tr; (b) effect of Nt on Sh against η.
Compared to previously published studies, our research findings align very well with the results presented in reference []. The consistency between our findings and those in Table 1 from reference [] indicates that our study is in agreement with prior research in this field. This agreement adds credibility to our research and suggests that our numerical calculations and simulations produce results that are consistent with established knowledge and research in the same area.

Table 1.
Results from prior applications of the Nusselt distribution [] compared with the present distribution.
5. Conclusions
This study delved into the theoretical investigation of a two-dimensional ferromagnetic nanofluid flow that incorporates a dipole past a stretching surface. We formulated mathematical equations and converted them into ODEs, utilizing the Runge–Kutta-based shooting technique, and solved them numerically with the MATLAB package. Our findings could contribute significantly to the development of new insights and approaches towards the study of ferromagnetic nanofluids and their applications. The originality of our investigation is that we studied the motion of a ferromagnetic nanofluid in a Nield’s field created by a magnetic dipole as it moved over a stretching zone. This highly nonlinear system was solved numerically. The most significant result of our model is that it provides valuable insights into the following:
- The velocity profile possesses reverse behavior for the ferromagnetic interaction parameter and the mixed convective parameter.
- The temperature distribution enhances for more significant Reynolds numbers and thermal radiation.
- The occurrence of thermophores and Brownian motion parameters is a source of diminution in the thickness of the opposite concentration boundary layer near the wall.
- Skin friction is improved with a more significant viscosity parameter.
- The ferromagnetic interaction parameter diminishes both the local Nusselt number and the Sherwood numbers.
- Shear-thinning fluids possess a more significant temperature than shear-thickening fluids.
Future work:
Further research is required to gain a better understanding of magnetic dipole processes under varying geometries. Future studies should consider the integration of activation energy and ohmic heating models, potentially incorporating hybrid nanofluids with minor adjustments. Enhanced mathematical models are essential to advance the realm of engineering simulation.
Author Contributions
Methodology, G.D., J.L.R.P., C.B.R., D.G., A.W., Y.B. and N.E.; software, D.G. and A.W.; validation, G.D., A.W., K.V. and N.E.; formal analysis, J.L.R.P. and N.E.; investigation, C.B.R. and A.W.; resources, J.L.R.P. and D.G.; data curation, C.B.R.; writing—original draft, G.D., Y.B., K.V. and J.L.R.P.; writing—review and editing, G.D., D.G. and N.E.; visualization, D.G.; supervision, N.E.; project administration, N.E.; funding acquisition, N.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| x | Horizontal coordinate (m) |
| u | Horizontal velocity (m/s) |
| T | Fluid temperature inside the boundary layer (K) |
| T∞ | Fluid temperature far away from the sheet (K) |
| H | Magnetic field intensity (A/m) |
| y | Vertical coordinate (m) |
| Nu | Local Nusselt number |
| Cp | Specific heat at constant pressure (J/(kg·K)) |
| v | Vertical velocity (m/s) |
| Cf | Skin friction coefficient |
| Tw | Temperature of the sheet (K) |
| Dm | Mass diffusivity (cm2/s) |
| Mean absorption coefficient (m2kg−1) | |
| d | Distance between the origin and center of the magnetic dipole/distance parameter (Am−2) |
| Tr | Radiation parameter (Jm−2s−1) |
| Pr | Prandtl number (m2s−1) |
| Le | Lewis number |
| δ | First-order velocity slip parameter |
| Sh | Local Sherwood number |
| M | Magnetization () |
| Cw | Concentration of the fluid near the surface |
| θ(η) | Dimensionless temperature |
| f′(η) | Dimensionless velocity |
| Nt | Thermophoresis parameter |
| Nb | Brownian motion parameter |
| Greek symbols: | |
| η | Similarity variable |
| ψ | Stream function (m2/s) |
| ρ | Density of the fluid (kg/m3) |
| μ | Dynamic viscosity (kg/m·s) |
| τw | Wall shear stress (Pa) |
| σ | Electrical conductivity (s·m−1) |
| Stefan–Boltzmann constant | |
| γ | Strength of the magnetic field |
| β | Ferromagnetic interaction parameter |
| Γ | Magnetic permeability (m−2·s2) |
| α | Distance parameter |
| γ1 | Viscosity parameter |
| λ1 | Mixed convective parameter |
| ε | Dimensionless Curie temperature |
References
- Seth, G.S.; Mandal, P.K. Gravity-driven convective flow of magnetite water nanofluid and radiative heat transfer past an oscillating vertical plate in the presence of magnetic field. Latin Am. Appl. Res. 2018, 48, 7–13. [Google Scholar] [CrossRef]
- Astanina, M.; Sheremet, M.; Oztop, H.; Abu-Hamdeh, N. MHD natural convection and entropy generation of ferrofluid in an open trapezoidal cavity partially filled with a porous medium. Int. J. Mech. Sci. 2018, 136, 493–502. [Google Scholar] [CrossRef]
- Gibanov, N.; Sheremet, M.; Oztop, H. MHD natural convection and entropy generation in an open cavity having different horizontal porous blocks saturated with a ferrofluid. J. Magn. Magn. Mater. 2018, 452, 193–204. [Google Scholar] [CrossRef]
- Asadi, A.; Hossein Nezhad, A.; Sarhaddi, F.; Keykha, T. Laminar ferrofluid heat transfer in presence of non-uniform magnetic field in a channel with sinusoidal wall: A numerical study. J. Magn. Magn. Mater. 2019, 471, 56–63. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Abelman, S. Numerical study of the consequences of magnetic field on Fe3O4-water ferrofluid convection with thermal radiation. Eng. Comput. 2018, 35, 1855–1872. [Google Scholar] [CrossRef]
- Aminfar, H.; Pourfard, M.; Ahangar Zonouzi, S. Numerical study of the ferrofluid flow and heat transfer through a rectangular duct in the presence of a non-uniform transverse magnetic field. J. Magn. Magn. Mater. 2013, 327, 31–42. [Google Scholar] [CrossRef]
- Vafai, K.; Tien, C.L. Boundary and inertia effects on flow and heat transfer in porous media. Int. J. Heat Mass Transf. 1981, 24, 195–203. [Google Scholar] [CrossRef]
- Modather, M.; Chamkha, A. An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Turkish J. Eng. Environ. Sci. 2010, 33, 245–258. [Google Scholar]
- Elbashbeshy, E.M.A.; Asker, H.G.; Abdelgaber, K.M. Flow and heat transfer over a stretching surface with variable thickness in a Maxwell fluid and porous medium with radiation. Therm. Sci. 2019, 23, 3105–3116. [Google Scholar] [CrossRef]
- Bidin, B.; Nazar, R. Numerical solution of boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur. J. Sci. Res. 2009, 33, 710–717. [Google Scholar]
- Mukhopadhyay, S.; Gorla, R.S.R. Effects of partial slip on boundary layer flow past a permeable exponential stretching sheet in presence of thermal radiation. Heat Mass Transf. 2012, 48, 1773–1781. [Google Scholar] [CrossRef]
- Chaudhary, S.; Singh, S.; Chaudhary, S. Thermal radiation effects on MHD boundary layer flow over an exponentially stretching surface. Appl. Math. 2015, 6, 295–303. [Google Scholar]
- Durgaprasad, P.; Varma, S.V.K.; Hoque, M.M.; Raju, C.S.K. Combined consequencess of Brownian motion and thermophoresis parameters on three-dimensional (3D) Casson nanofluid flow across the porous layers slendering sheet in a suspension of graphene nanoparticles. Neural Comput. Appl. 2018, 31, 6275–6286. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Nisar, K.S. Brownian Motion and Thermophoretic Diffusion Consequencess on Micropolar Type Nanofluid Flow with Soret and Dufour Impacts over an Inclined Sheet: Keller-Box Simulations. Energies 2019, 12, 4191. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, Y. Consequencess of Brownian motion and thermophoresis on nanofluids in a rotating circular groove: A numerical simulation. Int. J. Heat Mass Transf. 2018, 123, 569–582. [Google Scholar] [CrossRef]
- Waqas, H.; Hasan, M.J.; Majeed, A.H.; Liu, D.; Muhammad, T. Hydrothermal characteristics, entropy and kinetic energy investigation in a sinusoidal cavity for variable wavelengths and solid volume fraction using Cu-water nanofluid. J. Mol. Liq. 2023, 389, 122911. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.A.; Ali, B.; Liu, D.; Muhammad, T.; Hou, E. Numerical computation of Brownian motion and thermophoresis effects on rotational micropolar nanomaterials with activation energy. Propuls. Power Res. 2023, 12, 397–409. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.A.; Yasmin, S.; Liu, D.; Imran, M.; Muhammad, T.; Alhushaybari, A.; Farooq, U. Galerkin finite element analysis for buoyancy driven copper-water nanofluid flow and heat transfer through fins enclosed inside a horizontal annulus: Applications to thermal engineering. Case Stud. Therm. Eng. 2022, 40, 102540. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Liu, D.; Alghamdi, M.; Noreen, S.; Muhammad, T. Numerical investigation of nanofluid flow with gold and silver nanoparticles injected inside a stenotic artery. Mater. Des. 2022, 223, 111130. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Liu, D.; Imran, M.; Muhammad, T.; Alshomrani, A.S.; Umar, M. Comparative analysis of hybrid nanofluids with Cattaneo-Christov heat flux model: A thermal case study. Case Stud. Therm. Eng. 2022, 36, 102212. [Google Scholar] [CrossRef]
- Thiyagarajan, P.; Sathiamoorthy, S.; Balasundaram, H.; Makinde, O.D.; Fernandez-Gamiz, U.; Noeiaghdam, S.; Santra, S.S.; Altanji, M. Mass transfer effects on mucus fluid in the presence of chemical reaction. Alex. Eng. J. 2023, 62, 193–210. [Google Scholar] [CrossRef]
- Hameed, N.; Noeiaghdam, S.; Khan, W.; Pimpunchat, B.; Fernandez-Gamiz, U.; Khan, M.S.; Rehman, A. Analytical analysis of the magnetic field, heat generation and absorption, viscous dissipation on couple stress Casson hybrid Nano fluid over a nonlinear stretching surface. Results Eng. 2022, 16, 100601. [Google Scholar] [CrossRef]
- Manvi, B.; Tawade, J.; Biradar, M.; Noeiaghdam, S.; Fernandez-Gamiz, U.; Govindan, V. The effects of MHD radiating and non-uniform heat source/sink with heating on the momentum and heat transfer of Eyring-Powell fluid over a stretching. Results Eng. 2022, 14, 100435. [Google Scholar] [CrossRef]
- Tawade, J.V.; Guled, C.N.; Noeiaghdam, S.; Fernandez-Gamiz, U.; Govindan, V.; Balamuralitharan, S. Effects of thermophoresis and Brownian motion for thermal and chemically reacting Casson nanofluid flow over a linearly stretching sheet. Results Eng. 2022, 15, 100448. [Google Scholar] [CrossRef]
- Arulmozhi, S.; Sukkiramathi, K.; Santra, S.S.; Edwan, R.; Fernandez-Gamiz, U.; Noeiaghdam, S. Heat and Mass transfer analysis of Radiative and Chemical reactive effects on MHD Nanofluid over an infinite moving vertical plate. Results Eng. 2022, 14, 100394. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng-Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. The Cheng-Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: A revised model. Int. J. Heat Mass Transf. 2013, 65, 682–685. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. Int. J. Therm. Sci. 2014, 77, 126–129. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. Thermal instability in a porous medium layer saturated by a nanofluid: A revised model. Int. J. Heat Mass Transf. 2014, 68, 211–214. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of convection in a horizontal nanofluid layer of finite depth: A revised model. Int. J. Heat Mass Transf. 2014, 77, 915–918. [Google Scholar] [CrossRef]
- Saeed, M.; Ahmad, B.; ul Hassan, Q.M. Variable thermal consequencess of viscosity and radiation of ferrofluid submerged in porous medium. Ain Shams Eng. J. 2022, 13, 101653. [Google Scholar] [CrossRef]
- Andersson, H.I.; Valnes, O.A. Flow of a heated ferrofluid over a stretching sheet in the presence of a magnetic dipole. Acta Mech. 1998, 128, 39–47. [Google Scholar] [CrossRef]
- Hayat, T.; Ijaz Khan, M.; Imtiaz, M.; Alsaedi, A.; Waqas, M. Similarity transformation approach for ferromagnetic mixed convection flow in the presence of chemically reactive magnetic dipole. Phys. Fluids 2016, 28, 102003. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).