Numerical Computation of Distributions in Finite-State Inhomogeneous Continuous Time Markov Chains, Based on Ergodicity Bounds and Piecewise Constant Approximation
Abstract
:1. Introduction
2. Preliminaries
3. Estimation through Piecewise Constant Approximation
4. Estimation of the State Probabilities
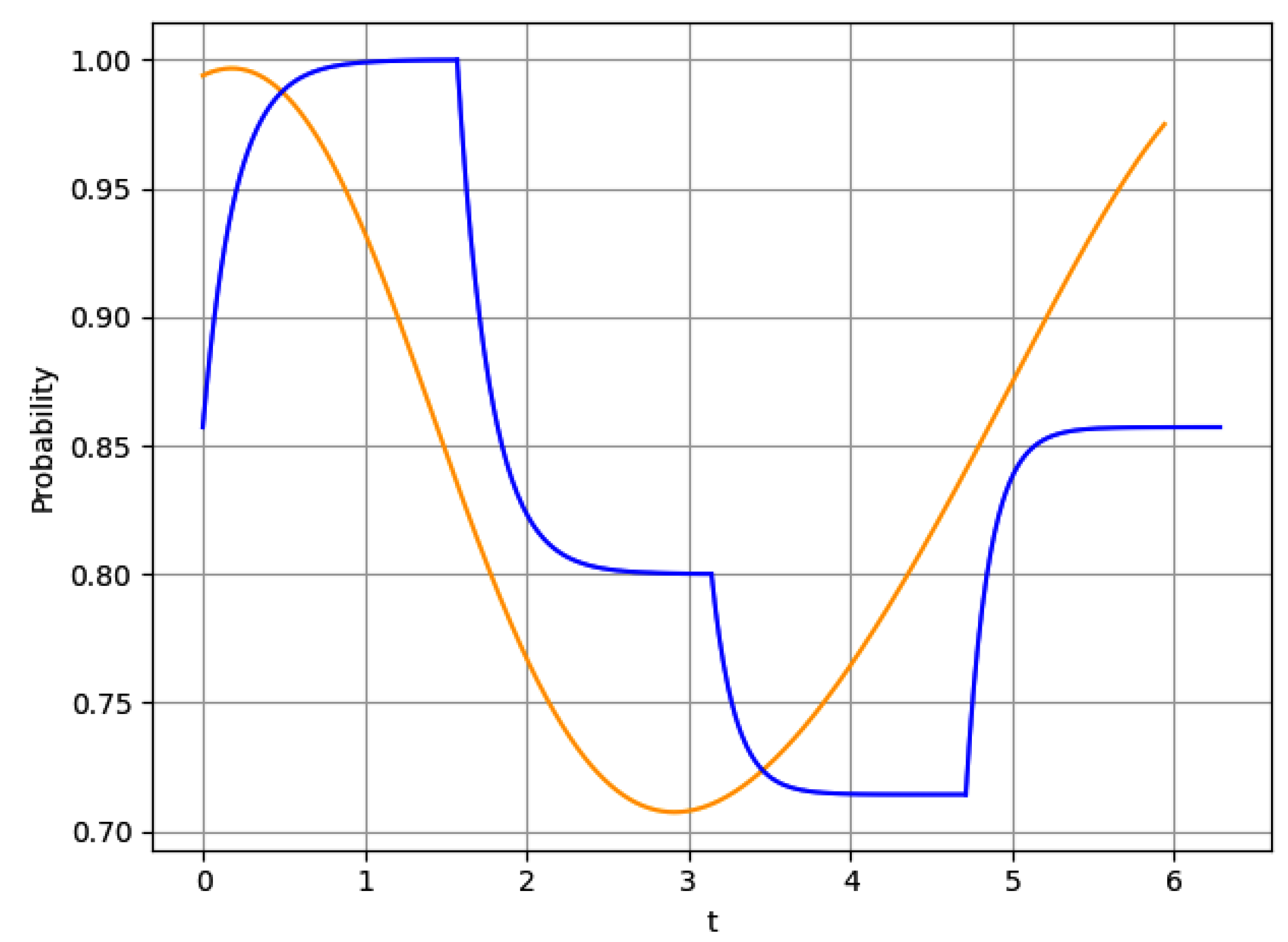
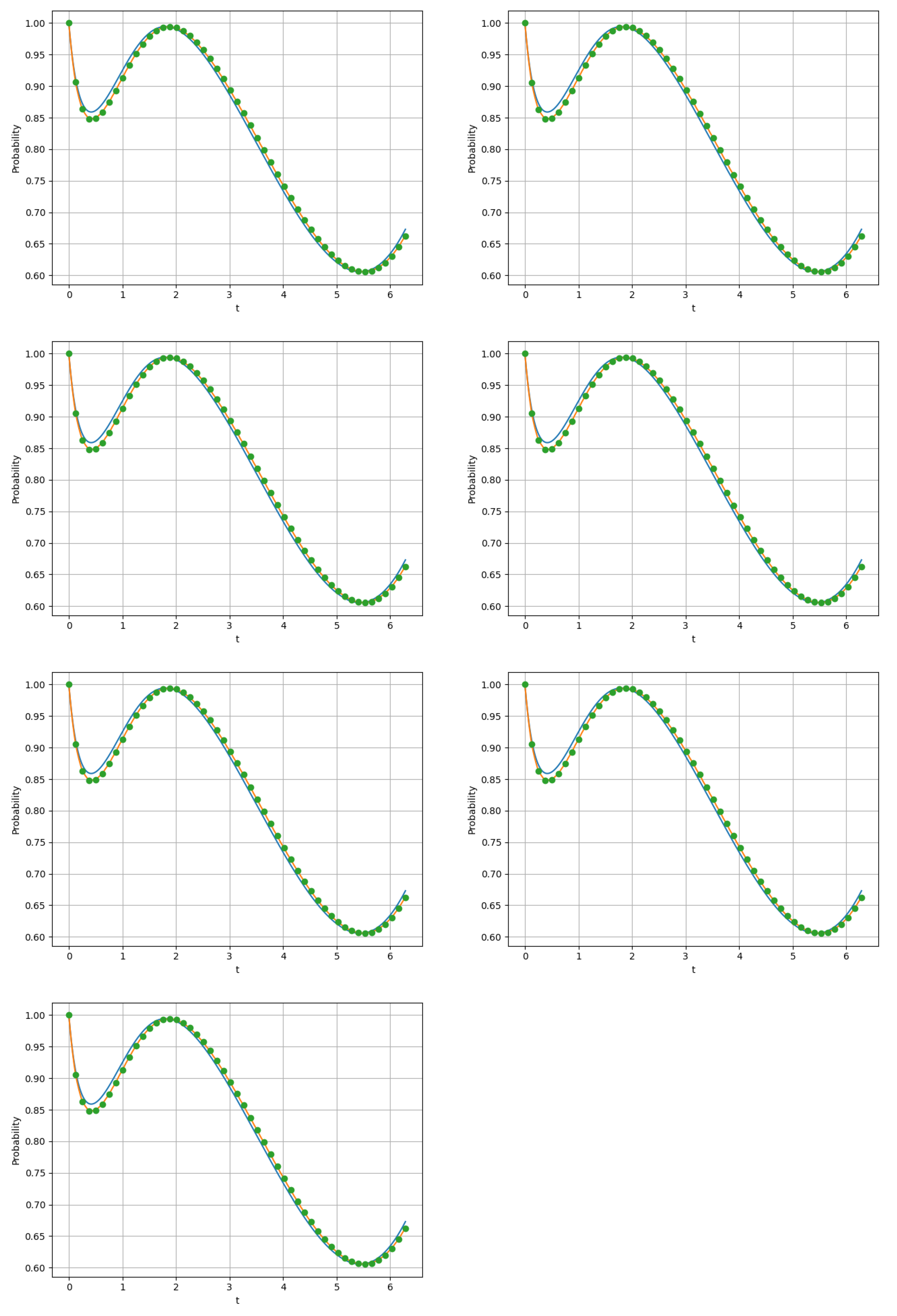
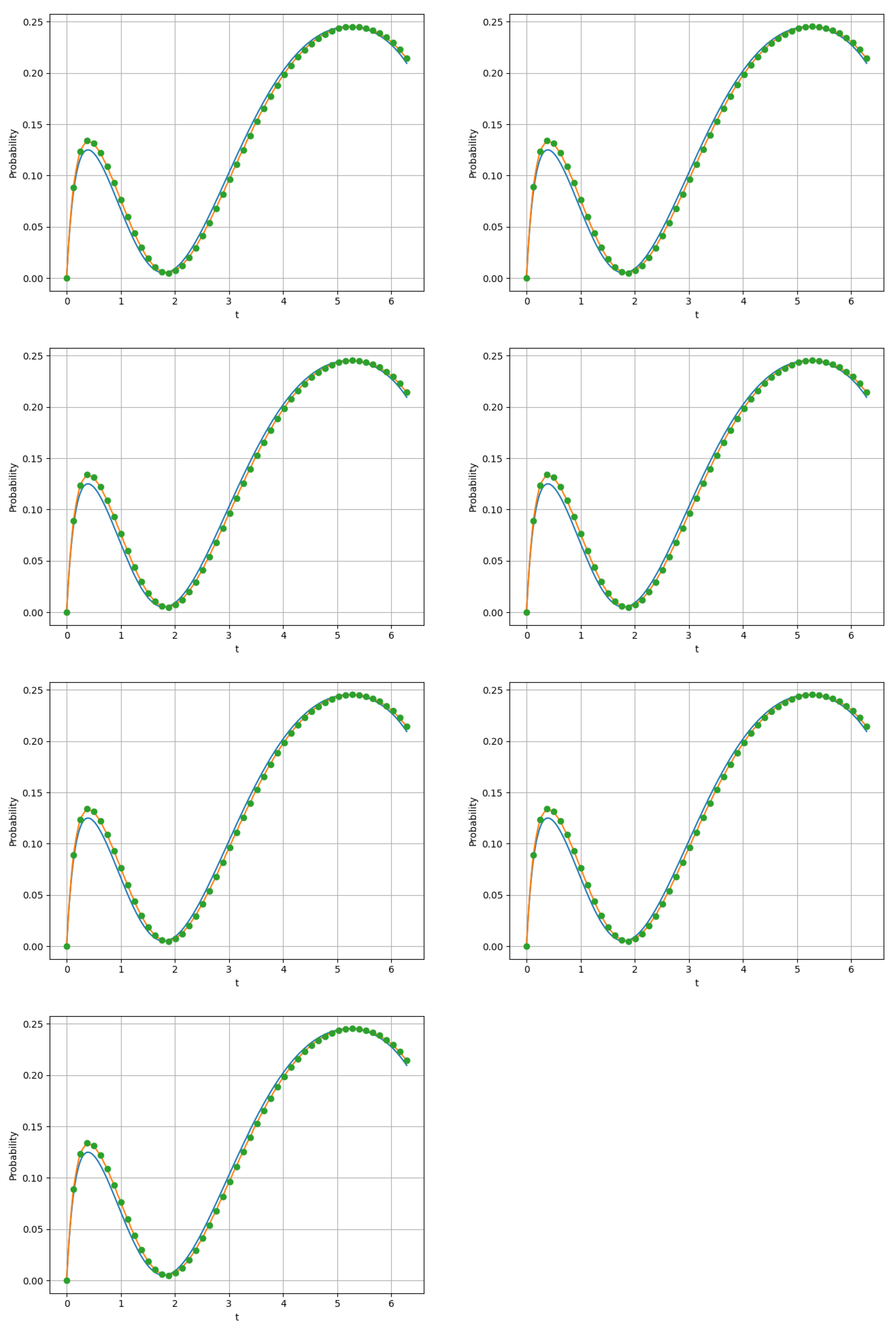
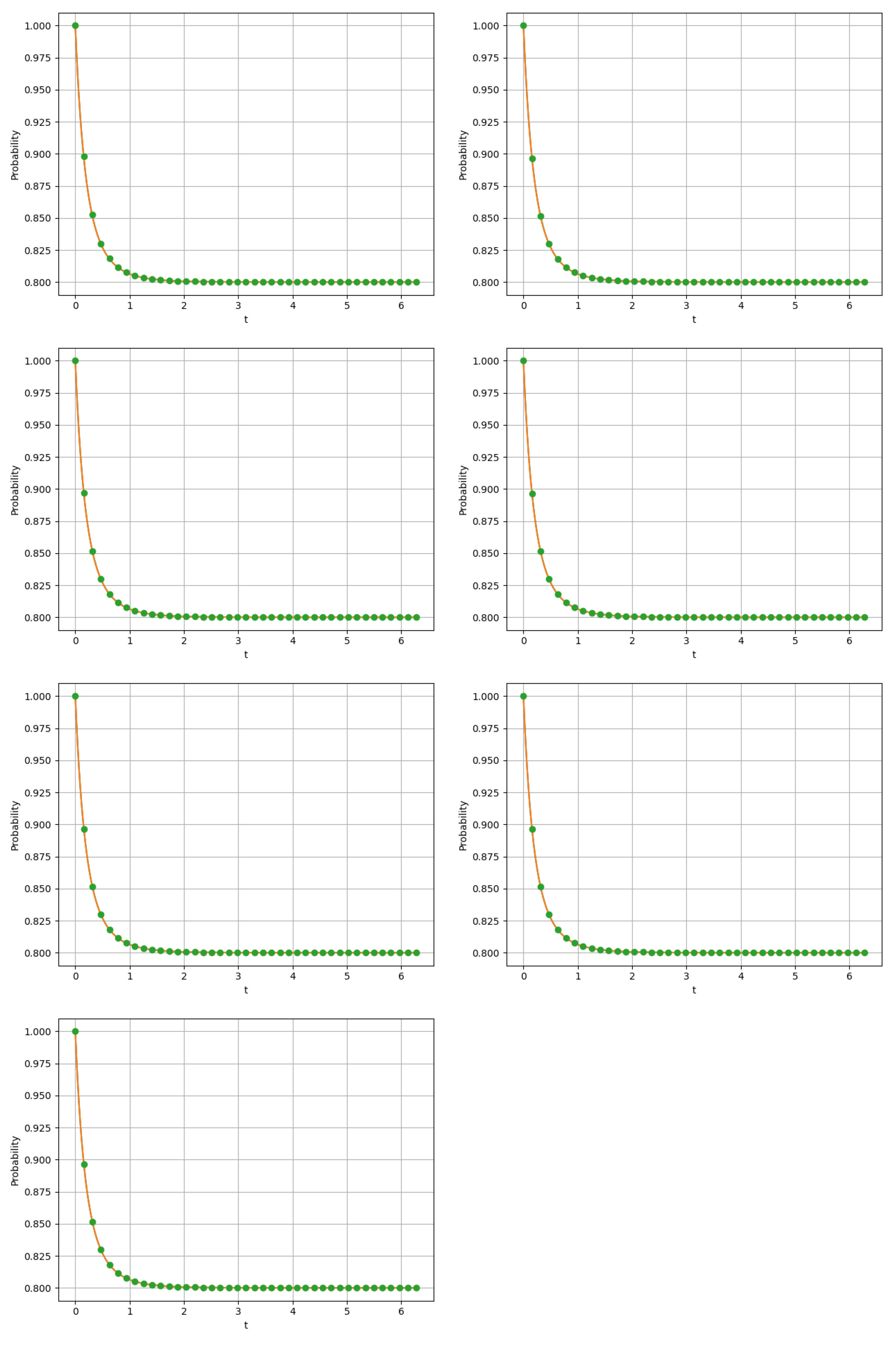
5. Numerical Examples
5.1. Example 1
5.2. Example 2
5.3. Example 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schwarz, J.A.; Selinka, G.; Stolletz, R. Performance analysis of time-dependent queueing systems: Survey and classification. Omega 2016, 63, 170–189. [Google Scholar] [CrossRef]
- Kwon, S.; Gautam, N. Guaranteeing performance based on time-stability for energy-efficient data centers. IIE Trans. 2016, 48, 812–825. [Google Scholar] [CrossRef]
- Whitt, W.; You, W. Time-Varying Robust Queueing. Oper. Res. 2019, 67, 1766–1782. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin, Y.; Kovalev, I.; Razumchik, R.; Korolev, V. Facilitating Numerical Solutions of Inhomogeneous Continuous Time Markov Chains Using Ergodicity Bounds Obtained with Logarithmic Norm Method. Mathematics 2021, 9, 42. [Google Scholar] [CrossRef]
- Vishnevsky, V.; Vytovtov, K.; Barabanova, E.; Semenova, O. Analysis of a MAP/M/1/N queue with periodic and non-periodic piecewise constant input rate. Mathematics 2022, 10, 1684. [Google Scholar] [CrossRef]
- Barabanova, E.A.; Vishnevsky, V.M.; Vytovtov, K.A.; Semenova, O.V. Methods of analysis of information-measuring system performance under fault conditions. Phys. Bases Instrum. 2022, 11, 49–59. [Google Scholar]
- Green, L.; Kolesar, P. The pointwise stationary approximation for queues with nonstationary arrivals. Manag. Sci. 1991, 37, 84–97. [Google Scholar] [CrossRef]
- Reibman, A.; Trivedi, K. Numerical transient analysis of markov models. Comput. Oper. Res. 1988, 15, 19–36. [Google Scholar] [CrossRef]
- Van Dijk, N.M.; van Brummelen, S.P.J.; Boucherie, R.J. Uniformization: Basics, extensions and applications. Perform. Eval. 2018, 118, 8–32. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Nobile, A.G. Diffusion approximation to a queueing system with time-dependent arrival and service rates. Queueing Syst. 1995, 19, 41–62. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Giorno, V.; Nobile, A.G.; Ricciardi, L.M. On the M/M/1 queue with catastrophes and its continuous approximation. Queueing Syst. 2003, 43, 329–347. [Google Scholar] [CrossRef]
- Arns, M.; Buchholz, P.; Panchenko, A. On the numerical analysis of inhomogeneous continuous-time Markov chains. INFORMS J. Comput. 2010, 22, 416–432. [Google Scholar] [CrossRef]
- Taaffe, M.R.; Ong, K.L. Approximating Nonstationary Ph(t)/M(t)/s/c queueing systems. Ann. Oper. Res. 1987, 8, 103–116. [Google Scholar] [CrossRef]
- Clark, G.M. Use of Polya distributions in approximate solutions to nonstationary M/M/s queues. Commun. ACM 1981, 24, 206–217. [Google Scholar] [CrossRef]
- Massey, W.; Pender, J. Gaussian skewness approximation for dynamic rate multiserver queues with abandonment. Queueing Syst. 2013, 75, 243–277. [Google Scholar] [CrossRef]
- Burak, M.R.; Korytkowski, P. Inhomogeneous CTMC Birth-and-Death Models Solved by Uniformization with Steady-State Detection. ACM Trans. Model. Comput. Simul. 2020, 30, 1–18. [Google Scholar] [CrossRef]
- Faddy, M. A note on the general time-dependent stochastic compartmental model. Biometrics 1976, 32, 443–448. [Google Scholar] [CrossRef]
- Zeifman, A.; Korolev, V.; Satin, Y. Two Approaches to the Construction of Perturbation Bounds for Continuous-Time Markov Chains. Mathematics 2020, 8, 253. [Google Scholar] [CrossRef]
- Daleckii, J.L.; Krein, M.G. Stability of solutions of differential equations in Banach space. Am. Math. Soc. 2002, 43, 1024–1102. [Google Scholar]

| n | G | |||
|---|---|---|---|---|
| 4 | 0.02144931153977276 | ≤0.41 | ≤28,903,845 | ≤28,903,846 |
| 5 | 0.02137755886467509 | ≤0.13 | ≤450 | ≤451 |
| 6 | 0.02138771528374614 | ≤0.035 | ≤5 | ≤6 |
| 7 | 0.021386393661019132 | ≤0.009 | ≤0.57 | ≤0.706 |
| 8 | 0.021386550440098923 | ≤0.002 | ≤0.11 | ≤0.245 |
| 9 | 0.021386533366325292 | ≤0.0004 | ≤0.021 | ≤0.157 |
| 10 | 0.02138653508102207 | ≤0.00007 | ≤0.004 | ≤0.14 |
| n | G | ||
|---|---|---|---|
| 4 | ≤4 | ≤0.283 | 21,333 |
| 5 | ≤2 | ≤0.09 | 31 |
| 6 | ≤7 | ≤0.022 | |
| 7 | ≤3 | ≤0.005 | |
| 8 | ≤9.99 | ≤0.002 | |
| 9 | ≤9.99 | ≤0.0002 | |
| 10 | ≤9.99 | ≤0.00004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satin, Y.; Razumchik, R.; Usov, I.; Zeifman, A. Numerical Computation of Distributions in Finite-State Inhomogeneous Continuous Time Markov Chains, Based on Ergodicity Bounds and Piecewise Constant Approximation. Mathematics 2023, 11, 4265. https://doi.org/10.3390/math11204265
Satin Y, Razumchik R, Usov I, Zeifman A. Numerical Computation of Distributions in Finite-State Inhomogeneous Continuous Time Markov Chains, Based on Ergodicity Bounds and Piecewise Constant Approximation. Mathematics. 2023; 11(20):4265. https://doi.org/10.3390/math11204265
Chicago/Turabian StyleSatin, Yacov, Rostislav Razumchik, Ilya Usov, and Alexander Zeifman. 2023. "Numerical Computation of Distributions in Finite-State Inhomogeneous Continuous Time Markov Chains, Based on Ergodicity Bounds and Piecewise Constant Approximation" Mathematics 11, no. 20: 4265. https://doi.org/10.3390/math11204265
APA StyleSatin, Y., Razumchik, R., Usov, I., & Zeifman, A. (2023). Numerical Computation of Distributions in Finite-State Inhomogeneous Continuous Time Markov Chains, Based on Ergodicity Bounds and Piecewise Constant Approximation. Mathematics, 11(20), 4265. https://doi.org/10.3390/math11204265







