Abstract
A queuing system having two different servers is under study. Demands enter the system according to a Markov arrival process. Service times have phase-type distribution. Service of demands is possible only if the fixed number of energy units, probably different for two servers, is available in the system at the potential service beginning moment. Energy units arrive in the system also according to a Markov arrival process and are stored in a stock (battery) of a finite capacity. Leakage of energy units from the stock can occur. Demands waiting in the infinite buffer are impatient and can leave the buffer after an exponentially distributed waiting time. One server is the main one and permanently provides service when the buffer is not empty and the required number of energy units is available. The second server is the assistant server and is switched on or off depending on the availability of energy units and queue length according to the hysteresis strategy defined by two thresholds. The assistant server is switched on when the queue length is not less than the greater threshold and is switched off when the queue length becomes smaller than the smaller threshold. The use of the assistant server has to be paid. Thus, the problem of the optimal selection of the thresholds defining the control strategy naturally arises. To solve this problem, the study of the behavior of the system under any fixed values of the parameters of the control strategy is necessary. Such a study is given in this paper. Numerical results are presented. They illustrate the feasibility of computer realization of the developed algorithms for computation of the stationary distribution of the system states and the main key performance indicators as well as the result of solving one of the possible optimization tasks.
Keywords:
hysteresis control; heterogeneous servers; Markov arrival process; phase-type distribution; energy harvesting MSC:
60K25; 60K30; 68M20; 90B22
1. Introduction
This paper contains the analysis of a queuing system that may be potentially useful for the optimal design of a variety of real-world systems. In brief, besides the consideration of arrival processes, which are essentially more general than the stationary Poisson, and service times having become more complicated than those popular in the literature’s exponential distribution, the distinguishing features of the considered system are (i) the necessity of the use of energy units (e.u. for brevity) for the service of demands; (ii) the generation, consumption, and leakage of e.u. during the system operation with their temporal accumulation stored in the battery (stock) with limited capacity; (iii) the availability of two heterogeneous service devices having different parameters of service time distribution and different consumption of e.u.; (iv) the opportunity of the dynamic activation and deactivation of the server, which consumes more energy according to the hysteresis strategy, depending on the current queue length and amount of available energy; (v) the account of impatience pertaining to waiting demands. The simultaneous presence of all the listed features guarantees the novelty of the analyzed system. A very brief overview of the literature about the systems characterized by some of the above features is as follows.
1.1. Short Literature Overview
1.1.1. Single-Server Queues with Variable Service Rates
The simplest kind of management of the service or arrival rate and the number of active service devices in queuing models is the threshold-type strategy. It is defined by a number called a threshold. Parameters of the system operation are changed when the number of demands in the system crosses up or down this threshold. It is considered quite a general single-server system with the batch Markov Arrival Process (), the general service time distribution, and the multi-threshold control by the service time all being considered in [1]. A disadvantage of the threshold strategy of control is the possibility of many changes in the service rate (oscillation) when the number of demands in the system admits values around the threshold. This may be undesirable in situations when the change in the rate is charged or is implemented non-instantaneously. The hysteresis-type control suggests that a threshold is replaced with two thresholds. The use of the higher service rate begins when the queue length increases up to the larger threshold. The use of the slower service rate begins when the queue length drops below the smaller threshold. When the length of the queue remains between two thresholds, no change in the current service rate is performed. Such a type of control gives a possibility to reduce the number of rate switching compared to the threshold-type control. The hysteresis-type control using the queuing system operation was introduced in 1960 and is often applied to different queuing systems. As early works in this direction, the following papers can be mentioned: [2,3,4]. More references can be found, e.g., in [5,6,7,8] and the references therein.
1.1.2. Multi-Server Queues with a Variable Number of Homogeneous Active Service Devices
In the context of control via the number of active service devices, the following results can be mentioned. In [9], a two-service device queue with identical service devices and a threshold control of activation of an additional service device is analyzed. In [10,11], a more general system with many identical service devices and hysteresis control via the number of active service devices is considered. A similar model but with significantly less restrictive assumptions about the arrival and service processes was investigated in [12]. A more detailed survey of the relevant research is given there. In [13], hysteresis-type control via service device reservation was applied to a multi-server priority queuing system describing the operation of a cognitive radio system.
1.1.3. Multi-Server Queues with a Variable Number of Heterogeneous Service Devices
The all above mentioned multi-server queues have identical service devices. The analysis of systems with distinct servers is essentially more complicated than the analysis of systems with identical servers. This is evidently explained as follows. In the case of identical servers, the service process in the system at an arbitrary moment is defined by the number of active servers. When service time distribution has exponential distribution, the number of active servers completely defines the total service rate at a given moment. In the case of non-identical servers, the service process at an arbitrary moment is not defined by the number of active servers. Keeping track of which servers namely are active and which are idle is required to build the Markov chain describing the behavior of the system. Consideration of a multi-dimensional process (number of active servers and indicators of which servers are active) instead of a one-dimensional process (just the number of active servers) is clearly a more difficult task.
The situation in the study of systems with distinct service devices is as follows. In [14], a system with two heterogeneous service devices and a threshold policy of control via the number of used service devices is considered. The practical motivation of model consideration is given and the invariant distribution of the system states is calculated. In [15], the optimality of the threshold-type strategy, which is used in [14], is proven. Non-optimality of such a strategy in the case of more than two service devices is forecasted. In [16], the task of finding the optimal thresholds defining the hysteresis-type strategy for the two-server system providing service to the demands arriving in batches is solved. In [17], the optimality of the threshold-type control in a system with many heterogeneous service devices is proven and a numerical study of the model is implemented. The results from [18,19,20,21] are obtained as further development of the results from [17]. In [11,22], the application of the hysteresis strategy in a system with many heterogeneous service devices is also discussed.
1.1.4. Queuing Systems with Energy Consumption and Harvesting
In the above mentioned papers, no aspects related to the consumption of the e.u. during service of demands are touched. Meanwhile, this aspect is very important in many real-world systems because more e.u. can be required to provide a higher service rate and it is desirable to reduce its use due to economical and ecological reasons. In particular, this aspect is very important in the management of the operation of wireless sensor networks. Sensors designed for monitoring the state of some objects can be installed in hard-to-reach areas and they can collect and transfer information only if they succeed in receiving (harvesting) enough e.u. The e.u. can be earned from sources, such as solar panels, and is accumulated in a small battery whose low charge makes it impossible for the transmission of information. Such situations are considered using queuing models with energy harvesting, see, e.g., [23,24,25,26,27,28,29]. In such models, it is assumed that e.u. arrive in the system during its operation according to a stationary Poisson process. E.u. are stored in a finite stock and service of any demand can start only in the presence of a minimal required number of e.u. in the stock. Similar queues have been studied in the literature for about seventy years and they are called assembly-like systems; queues with paired demands; taxi/passenger queues; matching systems; double-ended queues; systems with passive service devices; systems with demands’ arrival in sessions, etc. Queuing/inventory models (see, e.g., [30,31,32]) very close to such models are popular now. The distinction is that these models usually assume some standard replenishment policies for increasing the number of e.u. (inventory units), but not the arrival of these units in some random input flow. Aspects relating to the service rate control, depending on the amount of the harvested e.u., are considered very rare and, as such, they deserve attention. We can mention the paper [33] where the threshold strategy for service rate selection depending on the available amount of e.u. is analyzed. When the number of available e.u. increases (or decreases), higher (or lower) service rates can be used.
1.1.5. Queuing Systems with Demand Impatience
An important peculiarity of the model under study is that it takes into account the impatience of demands. Such impatience is typical in many real-world systems including communications systems, call centers, etc. Impatience means that a demand waiting for service in a buffer can renege from the system if the service is not started during some period. In the context of sensor networks, impatience is caused by the useless transmission of a signal to the coordinating node of the network due to the obsolescence of information contained in this signal. Lists of related research on queues with impatient demands can be found, e.g., in recent papers [34,35,36,37,38,39]. Account of the impatience frequently causes essential complications in the analysis because the behavior of the random process describing the dynamics of the system becomes level-dependent and the corresponding process does not belong to the classes of processes or - and -type structures that Markov chains were used to exhaustively investigate by M. Neuts, see [40,41].
1.2. Contributions of the Paper
As far as we know, this paper is the first one where the system with e.u. harvesting and heterogeneous service devices are considered. Two service devices differ by the service rate and the number of e.u. required for service providing. We suggest the hysteresis-type control via the activation and deactivation of the service device that consumes more energy. This service device is activated if the queue length is not below the larger threshold and enough e.u. is available. The service device is deactivated if the queue length becomes less than the smaller threshold or the number of available e.u. is not sufficient to begin service. Arrivals of demands and e.u. are described by the s, which allows us to catch the possible correlation and high variability of inter-arrival times typical for many real-world systems. We assume the service times by both service devices have phase-type () distribution that allows it to fit well with an arbitrary distribution, see [42], or, at least, several initial moments of service time distribution. Possible leakage of e.u. from the stock and the reneging of waiting demands from the buffer are taken into account.
The dynamic of the system is determined via a multidimensional continuous-time Markov chain that is a level-dependent (Quasi-Birth-and-Death) process. The generator of this is written down as the block matrix with sizes of blocks depending on the relation of the level of the chain with the thresholds of the control policy and the relation of the component of the chain describing both the number of e.u. and the number required for a demand service. Ergodicity conditions of the chain in the cases when demands are impatient and absolutely patient are presented and the invariant distribution of the chain is computed. Expressions for the computation of various performance measures are derived. The feasibility of the obtained algorithms for the computation of invariant distribution and performance measures is illustrated by several examples.
1.3. Possible Applications of the Model
Additional items required for demands’ service, which are interpreted in the paper as e.u., may have a meaning of any other resource, e.g., computer memory, service assistants, any other kind of resources (workpiece, place in a warehouse, service device, money, etc.). Therefore, the analyzed model can be used for the performance evaluation and optimization of operation of any real-world object where service of demand requires the use, besides the service device, of some additional resources and available service devices require a different amount of resources, provide different service rates, and have a different cost. In particular, the model fits for the description of the work of the node of a sensor e.u. harvesting network, which has the main, low cost, and low e.u. consuming, transmitter, and reserve transmitter that should be used only in situations when there is enough energy, and there is also a risk of information loss due to its obsolescence. The results can be used for managing the system with the use of the best values of the thresholds of control policy by verifying the ability of the system to provide the required quality of service or the desired revenue in the case of the optimal choice of control strategy.
1.4. Structure of the Text
The mathematical model under study is fully described in Section 2. A multidimensional level-dependent Markov chain () with floating cardinality of blocks that determines the dynamics of the system is introduced in Section 3. The infinitesimal generator of this chain is presented. The ergodicity condition for the system and the procedure for the computation of its stationary distribution in the case of absolute patient demands are presented in Section 4. Analogous results in the case of impatient demands are given in Section 5. Expressions for the computation of the performance indicators of the system based on the invariant distribution of are reported in Section 6. Section 7 deals with the results of some numerical experiments and a short illustration of the possibility of a solution to the optimization problem. Appendix A contains a brief explanation of the blocks of the generator.
2. Mathematical Model
We consider a queuing model having two heterogeneous service devices and an infinite buffer for temporal storing of the demands. The scheme of the system operation is displayed in Figure 1.
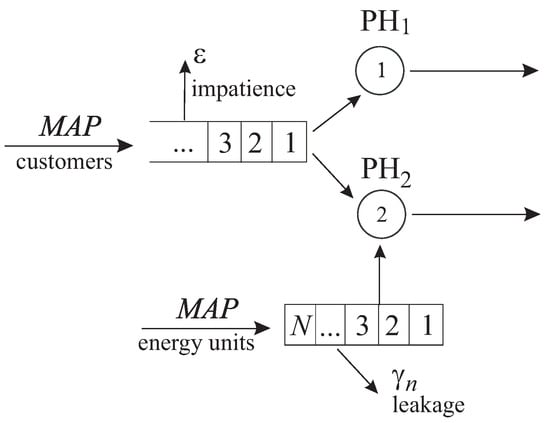
Figure 1.
Scheme of the system operation.
We assume that the flow of demands arrives for service in the system. This flow is defined by the underlying process with the state space and matrices being and , respectively, of size . The average arrival rate of demands is defined by the formula
where the invariant probability vector of the process satisfies the system
where and symbol denotes the operation of transposition of the vector.
More information about the its characteristics, particular cases, and importance for an adequate description of flows in real-life systems can be found, e.g., in [43,44,45,46]. The key benefit of the over the widely used stationary Poisson process model is the possibility to fit real flow with any value of the coefficients of variation and correlation of successive inter-arrival times. The stationary Poisson process does not give any freedom in fitting, except on account of the mean arrival rate. The coefficients of variation and correlation of inter-arrival times in the stationary Poisson process are equal to 1 and 0, correspondingly.
If service devices are unavailable at the arrival moment, the demand joins the buffer of an unlimited capacity and will be processed later on. Otherwise, the demand may try to start the receiving service.
The start of service of any demand requires the presence of a fixed number of e.u. E.u. arrive in the flow defined by the underlying process , with the state space and matrices being and , respectively. The average arrival rate of e.u. is defined by the formula
where the row vector is defined as the unique solution to the system
The e.u. are stored in the stock (battery) of a finite capacity If the stock is full upon the new e.u. arrival moment, this e.u. is permanently lost. Otherwise, it joins the stock. Leakage of e.u. from the stock occurs with rate when n e.u. stay in the stock, We assume that
Service to demands can be provided via two service devices. The rth service device requires e.u. for a demand service. We assume that , i.e., the second service device consumes more e.u. than the first one. The contrary case can be analyzed analogously.
Service time via the rth service device has the distribution defined by the underlying with the state space being of transient states. The state is the absorbing one. It is said that such service time has an irreducible representation Transition rates to the absorbing state are defined by the column vector The service rate is denoted by More useful information about the distribution and its properties can be found, e.g., in [40].
If the required service beginning number of e.u. is unavailable, the service device suspends the work until the required number of e.u. will be accumulated in the stock. After that, the service device may immediately begin service. At the moment of the service beginning, the used service e.u. immediately disappear from the stock.
We consider the first service device as the main one. It cannot stay idle if the buffer is not empty and at least e.u. are available in the stock. The second service device is the reserved, assistant service device. The mechanism of its activation or deactivation is as follows. The thresholds j and k are assumed to be fixed, An idle second service device is switched on if two conditions are simultaneously fulfilled: the number of demands in the queue is not less than k and at least e.u. are available.
Interruption of service is not allowed. The second service device is switched off at the moment of service completion if (i) the queue length is below the value j or (and) (ii) e.u. required for service of the next demand are not available.
The switching-on of the idle second service device occurs when the queue length is not less than k and the number of available e.u. is not less than In other words, there are two scenarios of switching on (activating) the idle second service device: (i) there were not less than e.u., where the number of demands in the system was equal to and a new demand arrives; (ii) there were not less than k demands in the system, where there were e.u. and new e.u. arrives. We will suppose that The contrary case of a small buffer capacity N can be analyzed similarly to the analysis implemented here.
Demands residing in the buffer are, generally speaking, impatient. The patience time of a demand is exponentially distributed with rate After this time finishes, the demand departs from the buffer, independently of other demands, and is considered lost.
We aim to analyze the behavior of this system and solve the optimization problem: to find thresholds j and k providing the minimum to the cost function. This function includes the charge for demands waiting in the buffer and the charges paid for both the use of the assistant service device during a unit of time and each activation of this device.
3. The Process Describing the Dynamics of the System and Its Generator
The dynamics of the described system are determined via the multidimensional with continuous time
where at time
- is the number of demands in the buffer,
- is the number of e.u. in the stock,
- is the state of the underlying process of the of demands,
- is the state of the underlying process of the of e.u.,
- vector process defines the states of the underlying processes of service in the devices. We will distinguish four macro-states of the process : the first macro-state means that both service devices are idle; the second macro-state contains the states when the first service device is busy while the second service device is idle; the third macro-state contains the states when the second service device is busy while the first one is idle; and the fourth macro-state contains the states when both service devices are busy. Here, denotes the current state of the underlying process of service in the rth service device,
Here and below the notation means that the parameter n admits the values from the set
Note that the state space of the vector process defined by Formula (1) depends on the values of the components as follows.
If or and then all macro-states of the process are feasible and the cardinality of its state space is equal to
If and then the first and the third macro-states 0 of the process are not feasible because the first service device cannot stay idle when the queue is not empty and not less than e.u. are available. Correspondingly, the cardinality of the state space of the process is equal to
Finally, if then for , the second macro-state of the process is also not feasible and the cardinality of the state space of the process is equal to In the following, when we say that the process currently has four macro-states, we mean all four possible macro-states described above. When we say that the process has two macro-states, we mean the second and fourth macro-states. When we say that the process has one macro-state, we mean the fourth macro-state.
To simplify the formulas, we will use the following notation:
- is the elements’ number of the state space of the components of the
- ⊗ and ⊕ mean the operations of the Kronecker product and the sum for the matrices, see, e.g., [47];
- is the diagonal matrix with the diagonal entries given in the brackets;
- is equal to 1 if and equal to 0 if ;
- ;
- ;
- sub-generator of the formdescribing the rates of the vector process transition when all of its states are feasible and which do not cause service completions;
- matrix of the formdescribing the rates of the vector process transition when all of its states are feasible and which cause service completion in the first service device;
- matrix of the formdescribing the rates of the vector process transition when all of its states are feasible and which cause service completion in the second service device;
- matrix of the formdescribing the probabilities of the vector process transition when all of its states are feasible and service begins in the first service device;
- matrix of the formdescribing the probabilities of the vector process transition when all of its states are feasible and service begins in the second service device;
- matrices defining the transitions of the vector process when it transits from the group of the states consisting of r macro-states to the group of the states consisting of macro-states:
- matrices defining the transitions of the vector process when service by the second service device starts and the process transits from the group of the states consisting of r macro-states to the group of the states consisting of macro-states:
- matrices defining the transitions of the vector process when the first service device completes service and starts the new one and the process transits from the group of the states consisting of r macro-states to the group of the states consisting of macro-states:
- matrices defining the transitions of the vector process when service by the second service device finishes service and starts the new one and the process transits from the group of the states consisting of r macro-states to the group of the states consisting of macro-states:
- matrix defining the transitions of the vector process when service by the second service device finishes service and the new service does not start, so the process continues to stay in the group of the states consisting of two macro-states:
Let also define the matrices having blocks defined by the following formulas:
- square matrix of size has:the diagonal blocksthe sub-diagonal blocks given bythe up-diagonal blocks given byblocks given byblocks given by
Remark 1.
If we presented above two different expressions for the matrix (formulas for the matrix and ). This happens because the number decrease in e.u. can occur either due to the leakage of e.u. or due to the service of a demand. In this and other similar cases, we merge two formulas into one formula via the summation of right-hand sides:
- matrix has only diagonal blocks.If this matrix is defined byIf the formula is changed to
- Matrices are square matrices of size if and size ifMatrices are the block-tridiagonal ones. Their diagonal blocks are defined as follows.If then for allIf then for allIf then for , we havefor , we haveand for , we haveThe sub-diagonal blocks for are given byFor these blocks have the formThe up-diagonal blocks for have the following form:The blocks for are given by
- Matrix ’s non-zero blocks are already defined by the formulas above (when ) and it has the complementary non-zero blocks
- Matrices have the entries caused by the demands’ departure from the queue due to impatience and also non-zero blockswhich have different sizes and forms in the following three cases: , and The size is equal to for for , and forIn the case of the matrix is the sum of both the matrix and the matrix having the non-zero blocksdefined below:For there exist the blocksFor , blocks for are equal to zero.In the case of the matrix is the sum of both the matrix and the matrix having the non-zero blocksdefined below:Formulas for have different forms depending on the relation between the numbers , andIn the case of , the formula is:In the case of , we have the formula:Formulas for have the following form:As it was already stated above, the matrix is not square. Its size for is It is defined by the formula:where the matrix has the blocks given byand the matrix is defined as follows:Formulas for have different forms depending on the relation between the numbers andIn the case of , the formula is:In the case of , we have the formula:Formulas for have the following form:
- Matrix has different forms for various values of the threshold k: and Its form is not obtained from the above formula for via formal setting because level 0 of the chain has another cardinality than the other levels.In the case of the size of this matrix is and the matrix is equal to the sum of the matrix where the matrix has the blocks defined by the formulaand the matrix has the following non-zero blocks:Block is defined byBlocks are defined by the formulaIf the matrix of size is equal to the sum of the matrix whereand the matrix has the following non-zero blocks:Blocks are defined by the formula
- Matrix has different sizes and forms in the three cases: , and The size is equal to for for , and forIn the case of is the block diagonal matrix of size with the diagonal blocks defined byIn the case of it is the matrix of size , with the blocks defined byIn the case of matrix is a square matrix of size , with the diagonal blocks defined by
Let us arrange all states of the defined by Formula (1) in the direct lexicographic order of its components and call the group of the states of the having the value i of the first component as level i of the chain. The group of the states having the value of the first two components is called the mini-level
The cardinality of level 0 is equal to The cardinality of the mini-levels is The cardinality of the mini-levels is The cardinality of the mini-levels for is The cardinality of the mini-levels for is
Let be the generator of
Theorem 1.
The infinitesimal generator has the block-tridiagonal structure:
where the square blocks, have the following meaning.
The matrix defines (except the diagonal elements of the matrix ) transition rates from level i to level The diagonal elements of the matrix are negative. The modules of these elements specify the departure rate of the from the respective state of belonging to level In turn, the matrix consists of the blocks that define the rates of the chain transition from the mini-level to the mini-level An explicit form of the blocks is given by Formulas (2)–(41).
Proof of Theorem 1 is given in Appendix A.
Having explicit formulas for the blocks of the generator of the we have an opportunity to analyze its stationary behavior.
4. The Case of Absolutely Patient Demands—The Ergodicity Condition of the System and Its Stationary Distribution
Due to the control by the number of active service devices, the dynamics of the is level-dependent. However, if the demands are patient (i.e., ), this dependence disappears for levels higher than k. Therefore, the can be treated as level-independent with many boundary states. It follows from [40] that the ergodicity criterion for this is formulated as follows.
Let
Theorem 2.
The criterion for the ergodicity of is the fulfillment of the inequality
where the vector satisfies the system
The vector has a finite size and the solution of the system (43) is easily implementable on the computer. After the computation of this vector, the validity of inequality can also easily be obtained.
Let us now suppose that the parameters of the system are such that inequality (42) holds good.
Then the limits
which are called stationary probabilities exist and the minimal non-negative solution of the quadratic matrix equation
for the matrix exists as well.
Let be the row vector of stationary probabilities of the states of that belong to the level
Denote
Theorem 3.
The probability vectors are computed as follows.
The vectors are computed as
where the matrix is the solution of Equation (44) having a spectral radius less than 1, while the vector is found as the solution to the finite system of equations
and matrix is given by Formula (45).
Proof of Theorem 3 immediately follows from [40].
5. The Case of Impatient Demands—The Ergodicity Condition of the System and Its Stationary Distribution
Theorem 4.
If the demands are impatient, i.e., then the is ergodic for any choice of the system parameters.
Proof.
If then the dependence of the blocks of generator on the level does not disappear as in the previous section. In this situation, it is feasible to prove that the belongs to the class of asymptotically quasi-Toeplitz Markov chains (), which was defined in [48].
Indeed, the definition of given in [48] requires the existence of limiting matrices
where and where ∘ is the Hadamard product of matrices symbol, see, e.g., [49].
Using the above-obtained explicit expressions for the blocks of generator , it is easy to demonstrate that if then for the , the matrices , and exist and are equal to I, O, and respectively. Thus, the belongs to the class of
It is proven in [48] that the condition sufficient for the ergodicity of the is the fulfillment of inequality
where the row-vector satisfies the system:
Taking into account that , and inequality (46) turns to the trivial inequality Therefore, in the case of impatient demands, the is ergodic for any choice of the system parameters. Therefore, Theorem 4 is proven. □
The statement of this theorem is intuitively clear because, due to impatience, the departure rate of demands from the system unboundedly increases when the length of a queue increases. Therefore, the queue length never becomes infinite.
Let us introduce the stationary probabilities of the and row vectors in the same way as in the previous section.
These vectors are defined as the unique solution of the infinite system of equilibrium equations
In contrast to the case of the absolutely patient demands, in which generator for large values has the block Toeplits-like structure, here the solution of this system does not have a matrix-geometric form. In general case, the solution of such systems is not possible. Some kinds of direct or soft truncation methods are applied to obtain approximate solutions. The most popular in the kind of soft truncation in the literature is described in [50]. However, the truncation methods may not lead to success because a good quality of approximation can be achieved only for large values of the truncation levels and the existing computer memory is not enough to solve the corresponding finite truncated system.
As it was shown above, the Markov chain belongs to the class of of which the system of equilibrium equations can be solved via the corresponding algorithm proposed in [48]. An effective and numerically stable algorithm for solving this system, which exploits the block tri-diagonal form of generator was elaborated in [51]. We use this algorithm below for the numerical study of the system.
6. Performance Measures
With vectors computed, the values of several system performance metrics may be calculated.
The mean number of demands in the buffer is calculated as
The mean number of e.u. in the stock is calculated as
Denote
The probability that the first service device is occupied at any time is calculated as
The probability that the second service device is occupied at any time is calculated as
The probability that both service devices are occupied at any time is given by
The probability that both service devices are not occupied at any time is calculated as
The probability that the system is empty at any time is calculated as
The mean number of demands in service at any time is calculated as
The mean number of demands in the system at any time is calculated as
The probability of any e.u. loss due to the battery overflow is calculated as
The share of arriving energy, which is leaked from the battery, is calculated as
It is worth noting here that the size of the vector in this and similar formulas is not constant. It depends on the size of the vector , which is defined by the cardinality of the corresponding mini-level
The share of the accumulated e.u., which is leaked from the battery is calculated as
The probability of an arbitrary demand loss due to impatience is calculated as
The departure rate of demands that received service is calculated as
Remark 2.
Since the generator of the considered is quite cumbersome, it is necessary to manage some kind of control by using the accuracy of the theoretical derivations and computer implementation of the construction of the generator of the and the computation of its steady-state distribution. We present here a few of the existing possibilities used for such a control.
It is clear that the following relation must be fulfilled:
The departure rate of demands that received service by the first service device is calculated as
The departure rate of demands that received service by the second service device is calculated as
The share of demands that received service by the first service device is calculated as
The share of demands that received service by the second service device is calculated as
The rate of switching off the second service device is calculated as
The first summands here define the rate of switching off the second service device because the number of demands in the buffer at the service completion epoch is below the threshold The last summand is the rate of switching off the second service device because the number of demands in the buffer at the service completion epoch is not below the threshold but there is not enough e.u. to start a new service.
The rate of switching on the second service device is calculated as
Remark 3.
According to the formula of the total probability, the mean number of e.u. spent for service of one demand is equal to It is clear that all which are not lost or leaked e.u. in the stationary operating system is spent for demands service.
Therefore, the following relation should be fulfilled and can be used for the accuracy of computation control:
Also, it is obvious that in the stationary operating system, the relation
must be fulfilled.
7. Numerical Examples and Optimization Problem
Let us provide some findings from numerical experiments to demonstrate the influence of various system parameters on its performance metrics.
7.1. Dependence of Performance Measures on Demands’ Arrival Rate for Different Values of e.u. Arrival Rate
Let us fix the following set of system parameters.
The of demands is defined by the matrices
This has the rate and the coefficient of the correlation of successive inter-arrival times is equal to 0.0864406. The coefficient of the variation is 6.33639.
The of e.u. is defined by the matrices
This has the rate and the coefficient of the correlation of successive inter-arrival times is equal to 0.153007. The coefficient of the variation is 9.85627. To vary in the experiments of the arrival rates and , we multiply the matrices by the corresponding constants.
distribution of service time by the first service device has the irreducible representation where
The mean service rate is The squared coefficient of variation is equal to 1.44291.
distribution of service time by the second service device has the irreducible representation where
The mean service rate is . The squared coefficient of variation is equal to 0.5.
The number of e.u. required for a demand service by the first service device is equal to 1. The number of e.u. required for a demand service by the first service device is equal to 3. The rate of demands reneging due to impatience is equal to 0.01. The energy leakage rate does not depend on the number of the e.u. in the stock and is equal to 0.05.
Let control parameters j and k be fixed as 1 and 3. This means that the second service device is activated (conditional that the required amount of e.u. is available) when the queue length reaches a value of 3. This service device is deactivated only when it finishes service when the queue is empty.
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show the reliance of certain system performance indicators on the arrival rate for different values of the e.u. arrival rate
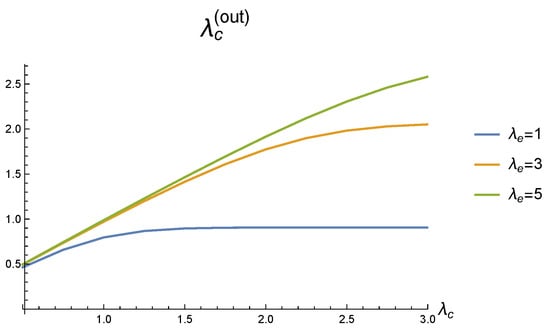
Figure 2.
Dependence of the output rate of serviced demands on the arrival rate for different values of e.u. arrival rate .
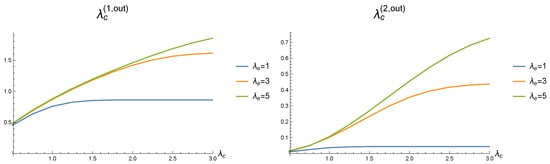
Figure 3.
Dependence of the output rate of demands from the first service device and rate from the second service device on arrival rate for different values of e.u. arrival rate .
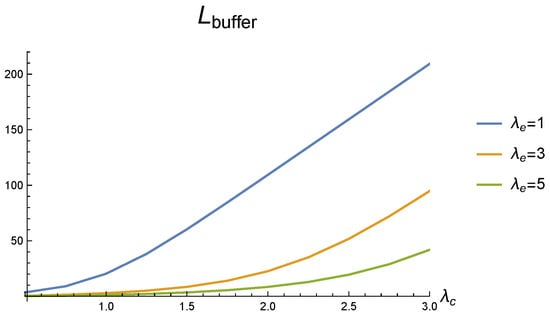
Figure 4.
Dependence of the mean number of demands in the buffer on arrival rate for different values of e.u. arrival rate .
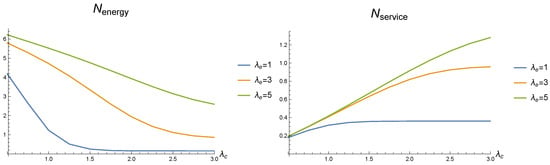
Figure 5.
Dependence of the mean number of e.u. in the stock and the mean number of demands in service on arrival rate for different values of e.u. arrival rate .
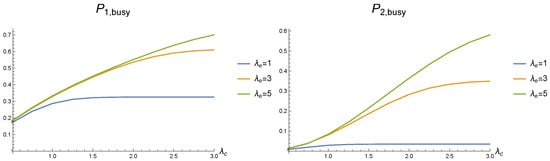
Figure 6.
Dependence of the probability that the first service device and the probability that the second service device is busy on arrival rate for different values of e.u. arrival rate .
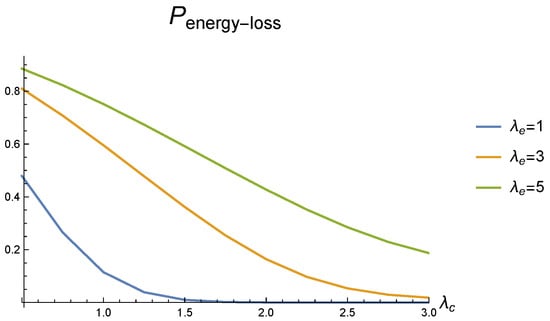
Figure 7.
Dependence of the probability of e.u. loss on arrival rate for different values of e.u. arrival rate .
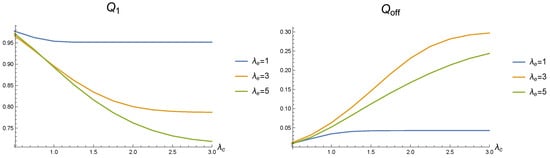
Figure 8.
Dependence of the share of demands, which obtain service by the first service device, and the rate of deactivation of the second service device on arrival rate for different values of e.u. arrival rate .
It is evident from Figure 2 and Figure 3 that the output rate of serviced demands increases along with the increase in demands’ arrival rate . However, for a small rate of e.u. arrival, this output becomes practically constant for It is explained by the lack of e.u. for the activation of the second service device. This is clearly seen in Figure 3 that the second service device is practically not used. This implies the sharp increase in the queue length observed in Figure 4. This increase, however, is smoothed by the mass exodus of demands from the system due to their impatience.
Figure 5, on the left, illustrates the behavior of the mean number of e.u. in the stock. This number decreases with the increase in demands’ arrival rate (and higher consumption of energy). For a small value of the e.u. rate, this number is negligible, which implies the very rare use of the second service device and the stabilization of the output rate of serviced demands which we already commented on above. Figure 5, on the right, presents the mean number of demands in service, which also confirms this stabilization. Also, it illustrates the higher involvement of the second service device into demands’ service when the e.u. flow has a higher rate. This involvement explains the increase in the rate of successfully serviced demands with the growth of that we observed in Figure 2.
The essentially higher involvement of the second service device into demands’ service with the increase in when the e.u. flow has a higher rate is demonstrated in Figure 6. Figure 7 shows the decrease in the loss probability of e.u. due to the stock overflow when increases and more e.u. is spent for service. For small (equal to 1), this loss probability becomes practically equal to zero for because all e.u. is quickly used for service. Figure 8, on the left, illustrates the higher involvement of the second service device to provide service when there is enough e.u. and the rate of demands’ arrival increases.
Figure 8, on the right, shows the behavior of the rate of the second service device deactivation. It is interesting to note here that this rate is higher for the middle value (3) of For the rate of the second service device deactivation is small because it is rarely activated (due to the lack of energy). For the rate of the second service device deactivation is relatively small because the queue length is not small and there is enough e.u. to use the second service device for a relatively long time.
Note that the form of the blocks of the generator given in Theorem 1 and the expressions for the system performance measures given in Section 6 are quite complicated. Thus, it is very important to control the accuracy of the analytical derivation of the obtained expressions of these blocks and the computer implementation of the computations of these blocks as well as the stationary probability vectors and the various performance measures of the system. During our experiments, we used many tests for the control, including the ones mentioned in Remarks 2 and 3 above, and all of them were satisfactory with an accuracy of order
7.2. Illustration of the Impact of Correlation in Arrival Processes of Demands and e.u.
In this experiment, we define the s of demands and e.u. by the following matrices.
The of demands is defined by the matrices
This has the rate and the coefficient of the correlation of successive inter-arrival times is equal to 0.312757. The coefficient of the variation is 10.0512.
The of e.u. is defined by the matrices
This has the rate and the coefficient of the correlation of successive inter-arrival times is equal to 0.374795. The coefficient of the variation is 11.6831.
To make clear the importance of correlation in the arrival processes’ account, let us present a comparison of the shapes of dependence of three performance measures on the demand arrival rate for the presented correlated s and for the stationary Poisson arrival processes (having zero correlation) with the rates and correspondingly.
It is obvious from Figure 9 and Figure 10 that the existence of correlation in arrival processes has a significant effect on the system performance indicators. As a result, if the flows in a real-world system described by the model are correlated or have a significant variance in inter-arrival time, using the stationary Poisson process leads to an overly optimistic assessment of the system’s performance characteristics. This clearly motivates the necessity to analyze the systems with the
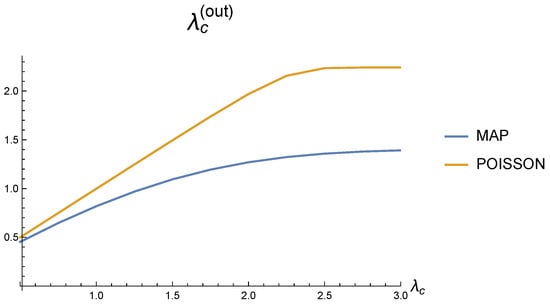
Figure 9.
Dependence of the output rate of serviced demands on the arrival rate for different correlations in demand arrival processes.
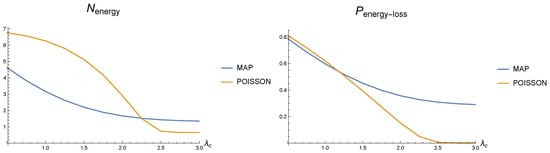
Figure 10.
Dependence of the mean number of e.u. in the stock and the probability of an e.u. loss for different correlations in demand arrival processes on the mean arrival rate .
7.3. Illustration of the Effect of the First Service Device’s Coefficient of Variation in Service Time
An account of the coefficient of variation in service time by the first service device is achieved via the assumption that this time has a distribution. It should be noted that if service time distribution would be assumed exponential (which is a very particular case of ), the analysis implemented above would not become essentially simpler. This is because the main difficulties in the analysis consist of an account of the number of e.u. available at a given moment and the moment just after service begins and also on account of the states of two service devices and the change in cardinality of the levels of M depending on these states. Anyway, it is interesting to look at the influence of the variance of service time distribution. We illustrate such an influence by considering different variances of the service time distribution at the first service device.
We assume the same system’s parameters as in the first experiment and the following three variants of distribution of service time at the first service device having the same mean service rate.
In the first variant, service time has an exponential distribution with the rate It is defined by the irreducible representation where and The squared coefficient of variation in this distribution is equal to 1.
In the second variant, service time has Erlangian distribution with the mean value defined by the vector and sub-generator
The squared coefficient of variation in this distribution is equal to 0.5.
In the third variant, service time has the hyper-exponential distribution with the mean value defined by the vector and sub-generator
The squared coefficient of variation in this distribution is equal to 24.5102.
In Figure 11 and Figure 12, we show the dependencies of the output rate of the serviced demands, the mean number of the demands in the buffer, and the probability of an e.u. loss on the rate for service times at the first service device with different coefficients of variation.
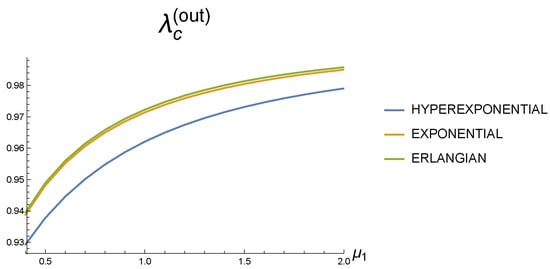
Figure 11.
Dependence of the output rate of serviced demands on the rate for service times with different coefficients of variation.
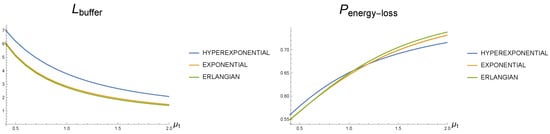
Figure 12.
Dependence of the mean number of demands in the buffer and the probability of an e.u. loss on the rate for service times with different coefficients of variation.
Figure 11 and Figure 12 show that the variance in the service time at the first service device has some impact, but, under the fixed sent of the system parameters, this impact is not very essential, but not negligible. For the mean number of the demands in the buffer, the difference is about 14 percent. A higher coefficient of variation worsens the quality of the system operation.
7.4. Solution of Optimization Problem
We may conceive and solve numerous optimization issues after we have solved the challenge of computing the stationary distribution of the system states and the main performance metrics of the system for an arbitrarily defined set of the thresholds, e.g., let us consider the problem of selection of control parameters that minimize the cost criterion (the economic function representing the system charges during a unit of time) of the form
where b is the charge paid per unit of time for an arbitrary demand waiting in the buffer, is the payment of the system due to the use (lease) of an assistant service device during a unit of time, and is the charge paid for each switching-off of the assistant service device. Evidently, the system obtains a profit from the service of demands and is charged for not enough quick access of demands to the service, for the use of an assistant service device, and for managing its switching on (or off). To maximize the revenue of the system, the cost criterion has to be minimized via the proper choice of the thresholds j and
Let us fix the following parameters of the system. Arrival flows of demands and e.u. are defined by the same matrices and as in the first experiment scaled to provide mean arrival rates and The rate of service by the second service device is assumed to be five times higher () and the impatience rate is assumed to be ten times higher than in the first experiment. The remaining system settings are the same as in the first experiment.
The costs are chosen as follows: and
Figure 13, on the left, depicts the cost criterion dependency on the variable thresholds j and k in the area Figure 13, on the right, shows the same dependence when the arrival flows are replaced with the stationary Poisson flows having the same arrival rate.
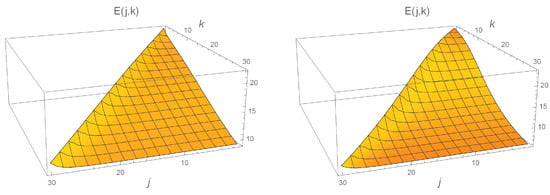
Figure 13.
Dependence of the cost criterion on the thresholds for the correlated arrival processes and stationary Poisson flows of demands and e.u. having the same mean rates.
Some comments on these Figures are as follows. In the case of the flows, the value corresponding to the permanent use of the assistant service device when enough e.u. is available is equal to 21.9769. The value corresponding to the switching on of the assistant service device when the queue reaches the value 30 and switching it off when the number of demands in the buffer drops below 30 is equal to 10.4861. The optimal value of the cost criterion is 9.04651. It is achieved when and This corresponds to the switching on of the assistant service device when the queue reaches the value of 30 and switching it off only when the number of demands in the buffer drops below 1. The absolute profit gained via control defined as is equal to 1.43959. The relative profit gained via control defined as is equal to 15.91%.
In the case of the stationary Poisson flows and the relative profit is 22.98%, i.e., the optimal set of the thresholds is the same, but the relative profit is higher in the case of the stationary Poisson flows. Lower profit in the case of the correlated flows is explained by the fact that periods of the presence of a long queue occur due to the bursty arrivals.
Many other different conditional and unconditional optimization problems with various criteria of quality and restrictions on values of some performance measures can be solved with the use of the presented above analysis, e.g., the cost function may be assumed not user-centric and include the penalty of the system for waiting for the demands as suggested above, but it may be provider-centric and includes the penalty for the loss of demands leading to the decrease in both the throughput of the system and the profit of the service provider.
It is worth noting that we intentionally restricted ourselves from the early beginning to the consideration of a concrete control policy of the hysteresis type defined above. This allowed us to reduce, via consideration of a Markov chain with the generator having quite a complicated form, the problem of the optimization of the cost criterion to the problem of minimization of a function of two integer variables. If a more complicated policy would be considered, the solution of the optimization problem, e.g., via the use of Markov decision processes, looks to be extremely difficult, if feasible.
8. Conclusions
In this paper, we analyzed a queuing system with two distinct service devices providing different service rates and consuming different numbers of e.u. for service of one demand. The main service device cannot stay idle if the buffer of the system is not full and the number of available e.u. is enough for service. The second, assistant service device can start service only when the queue length reaches the high threshold and the number of available e.u. is enough for service. The assistant service device can continue service after a given service completion if the queue length exceeds the low threshold and the number of available e.u. is enough for service. The parameters of the system are quite general: arrivals of demands and e.u. occur according to the s, and the service time distribution is of the type. Demands and e.u. can depart the system after some random waiting time, having the exponential distribution.
Under any fixed pair of the low and high thresholds of the strategy of control via activation and deactivation of the assistant service device, the behavior of the system is described via a multidimensional Markov chain. In the case of absolutely patient demands, this chain belongs to the class of level-independent processes with many boundary levels and its analysis is more or less standard. When the demands are impatient, this chain belongs to the class of Asymptotically Quasi-Toeplitz and its analysis was implemented based on the respective results from [48,51]. The primary system performance measures are computed using non-trivial formulas. Their dependence on some parameters of the system is highlighted via numerical results. An example of solving the problem of optimal selection of the thresholds is presented.
The model under consideration can be utilized for analysis and optimization of real-world systems with service devices that require an online supply from some resource, e.g., it is suitable for modeling the operation of the node of the sensor network with e.u. harvesting.
The presented analysis can be extended to the cases of the correlated marked Markov arrival process of demands and energy, separate stocks for e.u. storing, finite buffer for demands and retrying of demands, disastrous disappearance of demands or (and) energy, service devices breakdowns, etc. An extension of the model to the controlled priority systems, see, e.g., [52], is planned.
Author Contributions
Conceptualization, C.D., A.D. and R.M.; methodology, A.D. and R.M.; software, C.D., M.P.D. and R.M.; validation, M.P.D., A.D. and R.M.; formal analysis, A.D. and R.M.; investigation, C.D., M.P.D., A.D. and R.M.; writing—original draft preparation, A.D. and R.M.; writing—review and editing, A.D. and R.M.; supervision, A.D. and R.M.; project administration, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Theorem 1
Proof of Theorem 1 is carried out via the thorough examination of all potential transitions of the during the infinitesimally tiny span of time. This analysis is quite complicated, first of all, due to the different state spaces of the for different values of the components and and the possible changes in the cardinalities of these state spaces when (a) the number of demands in the buffer i departs from the state 0 and returns to this state, crosses up and down the levels j and k; and (b) the number of e.u. crosses up and down the levels and Due to the possibilities of the different sizes of the jumps of the number of e.u. down (by 1, , and ), it is necessary to keep track of the value of the number of e.u. not only at the moment of a jump but also just after it. This makes some formulas pretty “branching”, requiring consideration of many possible variants of relations between the state of the chain , the thresholds j, and k, and the numbers and .
The three-block diagonal form of the generator is obviously explained by the fact that the number of demands arriving at the system and departing from the system is equal to one. No batch arrivals or services, like in [53], are assumed in this model.
The operation of the Kronecker product of matrices is extremely useful for representing the transition rates of several distinct Markov chains (in our case, the underlying processes of flows of demands and e.u. and the vector process describing the states of the service devices). Transitions of the process are defined by the self-explanatory matrices introduced before the formulation of Theorem 1. Therefore, we present here only a brief proof of the part of the formulas.
The blocks have the diagonal entries, which are negative, and the non-diagonal non-negative entries defining the rates of the transitions of the between its states without the change in the queue length is equal to zero. The diagonal entry modulus specifies the rate of departure from the related state. Form (2) of is explained easily.
The summand
defines the transition rates of (i) the underlying processes of the arrival of demands and e.u. and (ii) the service underlying process without the change in the queue length. The summand defines the rates of transitions of the underlying processes of both the arrival of demands and e.u. and of the process when the first or the second service devices complete the current service (new service does not begin because the queue is empty). The term defines the departure rate o from the respective state due to a leakage of an e.u. The summand corresponds to the arrival and immediate loss of a new e.u. arriving when the stock for e.u. storing is full.
Form (3) of the block is valid when (see Remark 1), which is explained simply by the fact that such a transition occurs only if an e.u. leaks from the storage.
Form (4) of the block is obvious because the component increases its value from n to only when a new e.u. arrives.
The block in the form (5) describes the scenario when the queue is empty, the first service device is idle, and there is enough e.u. to start service by this service device (), and a demand arrives. This demand immediately starts service (without joining the queue), which is reflected by the Kronecker multiplier and e.u. disappear from the stock.
The block in the form (6) corresponds to the scenario when the queue is empty, the first service device is busy, the second service device is idle, there is enough e.u. to start service by the second service device (), the second service device can be switched on when even one demand is present in the system (this is possible only if ), and a demand arrives. This demand immediately starts service (without joining the queue), which is reflected by the Kronecker multiplier and e.u. disappear from the stock.
The block relates to the scenario in which a fresh demand arrives, is not immediately accepted for service, and joins the queues. Correspondingly, nothing can happen at the same moment with the number of accumulated e.u. Therefore, is equal to a zero matrix if If the number of available e.u. is less than nothing can happen with the process along with the demand arrival. Therefore when If , then the arrival of a new demand leads to the change in the cardinality of the state space of the process The states when both service devices are idle and the first service device is idle become impossible. The reduction in the state space is reflected via Kronecker multiplication by the matrix As a result of this consideration, we obtain Formula (7).
This formula was obtained in the assumption that If then when , the arrival of the demand leads to the activation of the idle service device if any. Thus, the arriving demand moves to the queue only when both service devices are busy. The corresponding reduction in the state space of the process is performed via Kronecker multiplication by the matrix
As a result of this consideration, we obtain Formula (8).
Formulas (9)–(13) for the diagonal blocks of the matrices are derived similar to the derivation of Formula (2) for However, several situations have to be treated separately.
In the case of the cardinality of mini-levels is the same as for mini-levels Therefore, Formula (9) repeats Formula (2) up to two modifications: the block appears due to impatience of demands and the block naturally disappears because all values on n in the considered range are not equal to
In the case the state space of the vector process is reduced due to the impossibility of having an idle first service device in the presence of the queue and not less than e.u. The term appears in (10) instead of the term because (a) service completion by the first service device in case implies the immediate start of the next service (and decreasing the value of i to ); and (b) service completion by the second service device, in this case, is not accompanied by the immediate start of the next service due to the lack of the required e.u. ().
Formula (11) is similar to Formula (10). Only here is the possibility of the e.u. loss in case a full stock is accounted for and a new service by the second service device cannot start, not due to the lack of e.u., but because in the considered case , the queue length is below the threshold value
In the case when the second service device can start service, but this will again lead to the decrease in the value of i to Thus, we obtain Formula (12).
In the case when and both service devices are always busy. This implies the decrease in the cardinality of the state space of the process to As a result, we obtain Formula (13).
Formulas (14) and (15) describe the transitions of the considered within the level i caused by the e.u. leakage. Both formulas reflect that the other components of the have no transitions during the leakage moment. But, the cardinality of the state space of the process increases from to M when the number of e.u. drops below the value and this cardinality increases from to when the number of e.u. drops below the value when The change in the cardinality from to M is reflected by the matrix The change in the cardinality from to is reflected by the matrix This explains Formulas (14) and (15).
Formulas (16) and (17) describe the transitions of the within the level i caused by an e.u. arrival. All other components of the have no transitions during the e.u. arrival moment. But, the cardinality of the state space of the process decreases from M to when the number of e.u. reaches the value and this cardinality decreases from to when the number of e.u. reaches the value when The change in the cardinality from M to is reflected by the matrix
The change in the cardinality from to is reflected by the matrix
The form of the complementary non-zero block in the matrix can be commented as follows. This block corresponds to the following scenario. The number of demands in the queue is equal to the second service device is idle, and the number of available e.u. is enough to provide service by this service device. At this moment, a new demand arrives. According to the considered hysteresis strategy of control, this arrival triggers the switching on of the second service device and the service beginning. Simultaneously, e.u. disappear from the stock. Matrix defines the probabilities of the process transition in the case when and, consequently, the number of available e.u. drops below the level and the cardinality of the state space increases from to
Matrix corresponds to the case when i.e., the number of available e.u. becomes not less than and cardinality does not change. Summarizing, we obtain Formula (18).
Transitions of the from level to level correspond to a demand departure from a queue. Such a departure can happen in the following five cases: (a) a demand abandons the queue due to impatience; (b) the first service device was idle, the number of available e.u. was new e.u. arrives, and the first service device starts work (the matrix provides the related rates); (c) the first service device finishes service and starts the new one because the required e.u. is available (the matrix provides the related rates); (d) the first service device was busy while the second one was idle, the number of available e.u. was new e.u. arrives, the queue length is not less than k, and the second service device starts work (the matrix provides the related rates); and (e) the second service device finishes service and starts the new one because the first service device is busy, the required e.u. is available, and the queue length is not less than j (the matrix provides the related rates). The listed blocks
are further called in the case when as
respectively, aiming to stress their explicit independence of i. The form of these blocks is explained below.
Form (19) of the matrix is due to the fact that the e.u. arrival rate is given by the matrix , while the matrix defines the transition of the vector process at the moment of service begins with the first service device.
Matrix has form (20). Here, the matrix contains the rates of transitions of the vector process at the epochs of service completion and beginning by the first service device when the number of available e.u. is not enough to guarantee that the remaining (after service beginning) number of e.u. is sufficient to provide service by the first service device to the next demand, i.e.,
The matrix contains the rates of transitions of the vector process at the moment of service completion and beginning by the first service device when the number of available e.u. allows us to guarantee that the remaining number of e.u. is enough to provide service by the first service device to the next demand, i.e.,
Analogously, the matrices define the rates of transitions of the vector process at the moments of service completion and beginning by the second service device. As a result, we obtain Formula (21).
In the case the blocks
are further called as
respectively. The form of these blocks is explained below.
Formula (22) is the direct analog of Formula (19). Formula (23) describes the scenario when a new e.u. arrival makes it possible to start service by the second service device (while the first one is busy and the queue length i is larger than k).
Recall that for , the state space of the underlying process of service consists of four macro-states if the number of available e.u. is such that ; two macro-states if ; and one macro-state if Formulas (24) and (25) describe the transition rates of the under study when the first server finishes service and begins the new one. During such a transition, the number of available e.u. decreases by Then, the new number of macro-states of the underlying process of service depends also on the relation between the value and the thresholds and , leading to different scenarios of changing the number of macro-states. In the scenario we obtain Formula (24), otherwise Formula (25) holds.
The explanation of Formulas (26)–(41) is similar to the one given for Formulas (2)–(25).
References
- Dudin, A. Optimal multithreshold control for a BMAP/G/1 queue with N service modes. Queueing Syst. 1998, 30, 273–287. [Google Scholar] [CrossRef]
- Gebhard, R. A queuing process with bilevel hysteretic service rate control. Nav. Res. Logist. Q. 1967, 14, 55–67. [Google Scholar] [CrossRef]
- Suzuki, T.; Ebe, M. Decision rules for the queueing system M/G/1 with service depending on queue-length. Mem. Def. Acad. (Jpn.) 1967, 7, 7–13. [Google Scholar]
- Tijms, H. On a switch-over policy for controlling the workload in a queueing system with two constant service rates and fixed switch-over costs. Z. Oper. Res. 1977, 21, 19–32. [Google Scholar] [CrossRef]
- Dudin, A. Optimal control for an Mx/G/1 queue with two operation modes. Probab. Eng. Inf. Sci. 1997, 11, 255–265. [Google Scholar] [CrossRef]
- Neuts, M.; Rao, B. On the design of a finite-capacity queue with phase-type service times and hysteretic control. Eur. J. Oper. Res. 1992, 62, 221–240. [Google Scholar] [CrossRef]
- Rao, B. Waiting times in an exponential queue with hysteretic service rate control: A numerical investigation. Queueing Model. Serv. Manag. 2022, 5, 1–25. [Google Scholar]
- Semenova, O. Optimal hysteresis control for BMAP/SM/1 queue with MAP-input of disasters. Qual. Technol. Quant. Manag. 2007, 4, 395–405. [Google Scholar] [CrossRef]
- Morrison, J. Two-server queue with one server idle below a threshold. Queueing Syst. 1990, 7, 325–336. [Google Scholar] [CrossRef]
- Ibe, O.; Keilson, J. Multi-server threshold queues with hysteresis. Performance Evaluation. Perform. Eval. 1995, 21, 185–213. [Google Scholar] [CrossRef]
- Lui, J.; Golubchik, L. Stochastic complement analysis of multi-server threshold queues with hysteresis. Perform. Eval. 1999, 35, 19–48. [Google Scholar] [CrossRef]
- Kim, C.; Dudin, A.; Dudin, S.; Dudina, O. Hysteresis control by the number of active servers in queueing system MMAP/PH/N with priority service. Perform. Eval. 2016, 101, 20–33. [Google Scholar] [CrossRef]
- Dudin, A.; Dudin, S.; Manzo, R.; Rarità, L. Analysis of multi-server priority queueing system with hysteresis strategy of servers reservation and retrials. Mathematics 2022, 10, 3747. [Google Scholar] [CrossRef]
- Larsen, R.; Agrawala, A. Control of a heterogeneous two-server exponential queueing system. IEEE Trans. Softw. Eng. 1983, 4, 522–526. [Google Scholar] [CrossRef]
- Lin, W.; Kumar, P. Optimal control of a queueing system with two heterogeneous servers. IEEE Trans. Autom. Contr. 1984, 29, 696–703. [Google Scholar] [CrossRef]
- Nobel, R.; Tijms, H. Optimal control of a queueing system with heterogeneous servers and setup costs. IEEE T. Automat. Control 2000, 45, 780–784. [Google Scholar] [CrossRef]
- Rykov, V.; Efrosinin, D. Optimal control of queueing systems with heterogeneous servers. Queueing Syst. 2004, 46, 389–407. [Google Scholar] [CrossRef]
- Efrosinin, D.; Breuer, L. Threshold policies for controlled retrial queues with heterogeneous servers. Ann. Oper. Res. 2006, 141, 139–162. [Google Scholar] [CrossRef]
- Efrosinin, D.; Stepanova, N. Optimal open-loop routing and threshold-based allocation in two parallel queueing systems with heterogeneous servers. Mathematics 2021, 9, 2766. [Google Scholar] [CrossRef]
- Efrosinin, D.; Kochetkova, I.; Samouylov, K.; Stepanova, N. Algorithmic Analysis of a Two-Class Multi-server Heterogeneous Queueing System with a Controllable Cross-Connectivity. In Proceedings of the Analytical and Stochastic Modelling Techniques and Applications. ASMTA 2019. Lecture Notes in Computer Science, Moscow, Russia, 21–25 October 2019; Gribaudo, M., Sopin, E., Kochetkova, I., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Efrosinin, D.; Stepanova, N. On Optimal Control Policy of MAP(t)/M/2 Queueing System with Heterogeneous Servers and Periodic Arrival Process. In Proceedings of the Distributed Computer and Communication Networks. Lecture Notes in Computer Science, Moscow, Russia, 23–27 September 2019; Vishnevskiy, V., Samouylov, K., Kozyrev, D., Eds.; Springer: Cham, Switzerland, 2021. Chapter 11965. [Google Scholar]
- Le Ny, L.; Tuffin, B. A Simple Analysis of Heterogeneous Multi-Server Threshold Queues with Hysteresis; IRISA: Sonoma, CA, USA, 2000. [Google Scholar]
- Ulukus, S.; Yener, A.; Erkip, E.; Simeone, O.; Zorzi, M.; Grover, P.; Huang, K. Energy harvesting wireless communications: A review of recent advances. IEEE J. Sel. Areas Commun. 2015, 33, 360–381. [Google Scholar] [CrossRef]
- Wu, S.; Shin, Y.; Kim, J.; Kim, D. Probability of packet loss in energy harvesting nodes with cognitive radio capabilities. IEEE Commun. Lett. 2016, 20, 978–981. [Google Scholar] [CrossRef]
- De Cuypere, E.; De Turck, K.; Fiems, D. A queueing model of an energy harvesting sensor node with data buffering. Telecommun. Syst. 2018, 67, 281–295. [Google Scholar] [CrossRef]
- Gelenbe, E. Synchronising energy harvesting and data packets in a wireless sensor. Energies 2015, 8, 365–369. [Google Scholar] [CrossRef]
- Gelenbe, E.; Kadioglu, Y. Energy Loss through Standby and Leakage in Energy Harvesting Wireless Sensors. In Proceedings of the 20th International Workshop on Computer Aided Modelling and Design of Communication Links and Networks (CAMAD), Guildford, UK, 7–9 September 2015. [Google Scholar]
- Patil, K.; De Turck, K.; Fiems, D. A two-queue model for optimising the value of information in energy-harvesting sensor networks. Perform. Eval. 2018, 119, 27–42. [Google Scholar] [CrossRef]
- Dudin, S.; Lee, M. Analysis of single-server queue with phasetype service and energy harvesting. Mathematical Problems in Engineering. Math. Probl. Eng. 2016, 2016, 8142743. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Shajin, D.; Viswanath, C. Inventory with Positive Service Time: A Survey. In Queueing Theory 2: Advanced Trends; Anisimov, V., Limnios, N., Eds.; Wiley: London, UK, 2021; Chapter 6. [Google Scholar]
- Krishnamoorthy, A.; Lakshmy, B.; Manikandan, R. A survey on inventory models with positive service time. Opsearch 2011, 48, 153–169. [Google Scholar] [CrossRef]
- Melikov, A.; Molchanov, A. Stock optimization in transportation/storage systems. Cybern. Syst. Anal. 1992, 28, 484–487. [Google Scholar] [CrossRef]
- Kim, C.; Dudin, S.; Dudin, A.; Samouylov, K. Multi-threshold control by a single-server queuing model with a service rate depending on the amount of harvested energy. Perform. Eval. 2018, 127, 1–20. [Google Scholar] [CrossRef]
- Swensen, A. Remaining loads in a PH/M/c queue with impatient customers. Methodol. Comput. Appl. 2023, 25, 25. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q. Matched Queues with Flexible and Impatient Customers. Methodol. Comput. Appl. 2023, 25, 4. [Google Scholar] [CrossRef]
- Bassamboo, A.; Randhawa, R.; Wu, C. Optimally scheduling heterogeneous impatient customers. Manuf. Serv. Oper. Manag. 2023, 25, 811–1208. [Google Scholar] [CrossRef]
- Satin, Y.; Razumchik, R.; Kovalev, I.; Zeifman, A. Ergodicity and related bounds for one particular class of Markovian time—Varying queues with heterogeneous servers and customer’s impatience. Mathematics 2023, 11, 1979. [Google Scholar] [CrossRef]
- Heng-li, L.; Quan-lin, L.I. Performance analysis of a MAP/PH/1 queueing system with impatient customers. J. Syst. Sci. Math. Sci. 2023, 43, 1819–1836. [Google Scholar]
- D’Arienzo, M.; Dudin, A.; Dudin, S.; Manzo, R. Analysis of a retrial queue with group service of impatient customers. J. Ambient Intell. Humaniz. Comput. 2019, 11, 2591–2599. [Google Scholar] [CrossRef]
- Neuts, M. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; Courier Corporation: Chelmsford, MA, USA, 1994. [Google Scholar]
- Neuts, M. Structured Stochastic Matrices of M/G/1 Type and Their Applications; Marcel Dekker: New York, NY, USA, 1989. [Google Scholar]
- Asmussen, S. Applied Probability and Queues; Springer: New York, NY, USA, 2003; Volume 2. [Google Scholar]
- Lucantoni, D. New results on the single server queue with a batch Markovian arrival process. Commun. Stat. 1991, 7, 1–46. [Google Scholar] [CrossRef]
- Chakravarthy, S. Introduction to MatrixAnalytic Methods in Queues 1: Analytical and Simulation Approach—Basics; ISTE Ltd.: London, UK; John Wiley and Sons: New York, NY, USA, 2022. [Google Scholar]
- Chakravarthy, S. Introduction to Matrix-Analytic Methods in Queues 2: Analytical and Simulation Approach—Queues and Simulation; ISTE Ltd.: London, UK; John Wiley and Sons: New York, NY, USA, 2022. [Google Scholar]
- Chakravarthy, S. The batch Markovian Arrival Process: A Review and Future Work. In Advances in Probability Theory and Stochastic Processes; Krishnamoorthy, A., Ed.; Notable Publications, Inc.: Branchburg, NJ, USA, 2001; Chapter 10; pp. 21–49. [Google Scholar]
- Graham, A. Kronecker Products and Matrix Calculus with Applications; Ellis Horwood: Chichester, UK, 1981. [Google Scholar]
- Klimenok, V.; Dudin, A. Multi-dimensional asymptotically quasi-Toeplitz Markov chains and their application in queueing theory. Queueing Syst. 2006, 54, 245–259. [Google Scholar] [CrossRef]
- Horn, R.; Johnson, C. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Neuts, M.; Rao, B.M. Numerical investigation of a multiserver retrial model. Queueing Syst. 1990, 7, 169–189. [Google Scholar] [CrossRef]
- Dudin, S.; Dudina, O. Retrial multi-server queuing system with PHF service time distribution as a model of a channel with unreliable transmission of information. Appl. Math. Model. 2019, 65, 676–695. [Google Scholar] [CrossRef]
- D’Apice, C.; Dudin, A.; Dudin, S.; Manzo, R. Priority queueing system with many types of requests and restricted processor sharing. J. Ambient Intell. Humaniz. Comput. 2023, 14, 12651–12662. [Google Scholar] [CrossRef]
- Dudin, A.; Manzo, R.; Piscopo, R. Single server retrial queue with group admission of customers. Comput. Oper. Res. 2015, 61, 89–99. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).