Faster Implementation of The Dynamic Window Approach Based on Non-Discrete Path Representation
Abstract
:1. Introduction
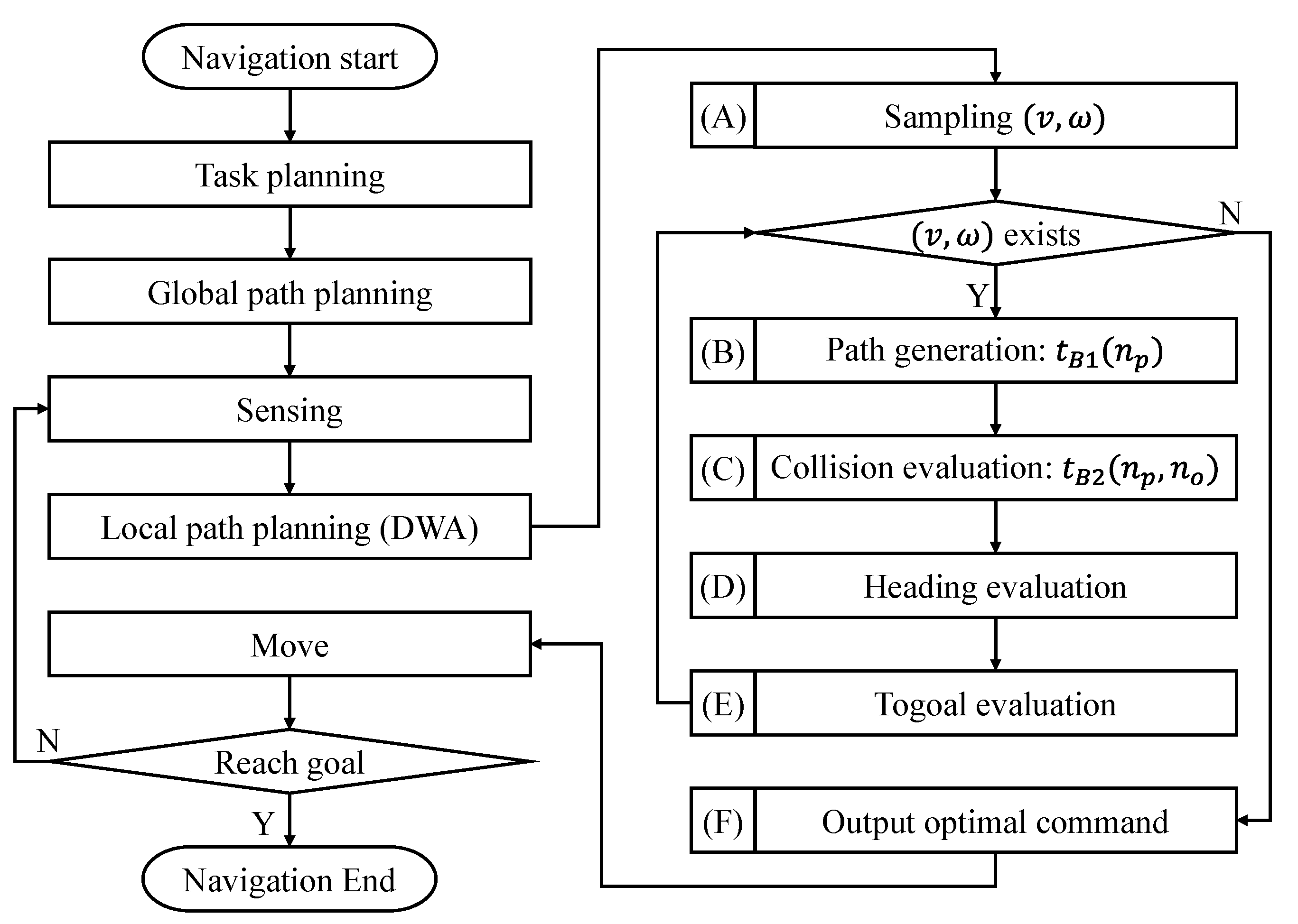
2. Dynamic Window Approach
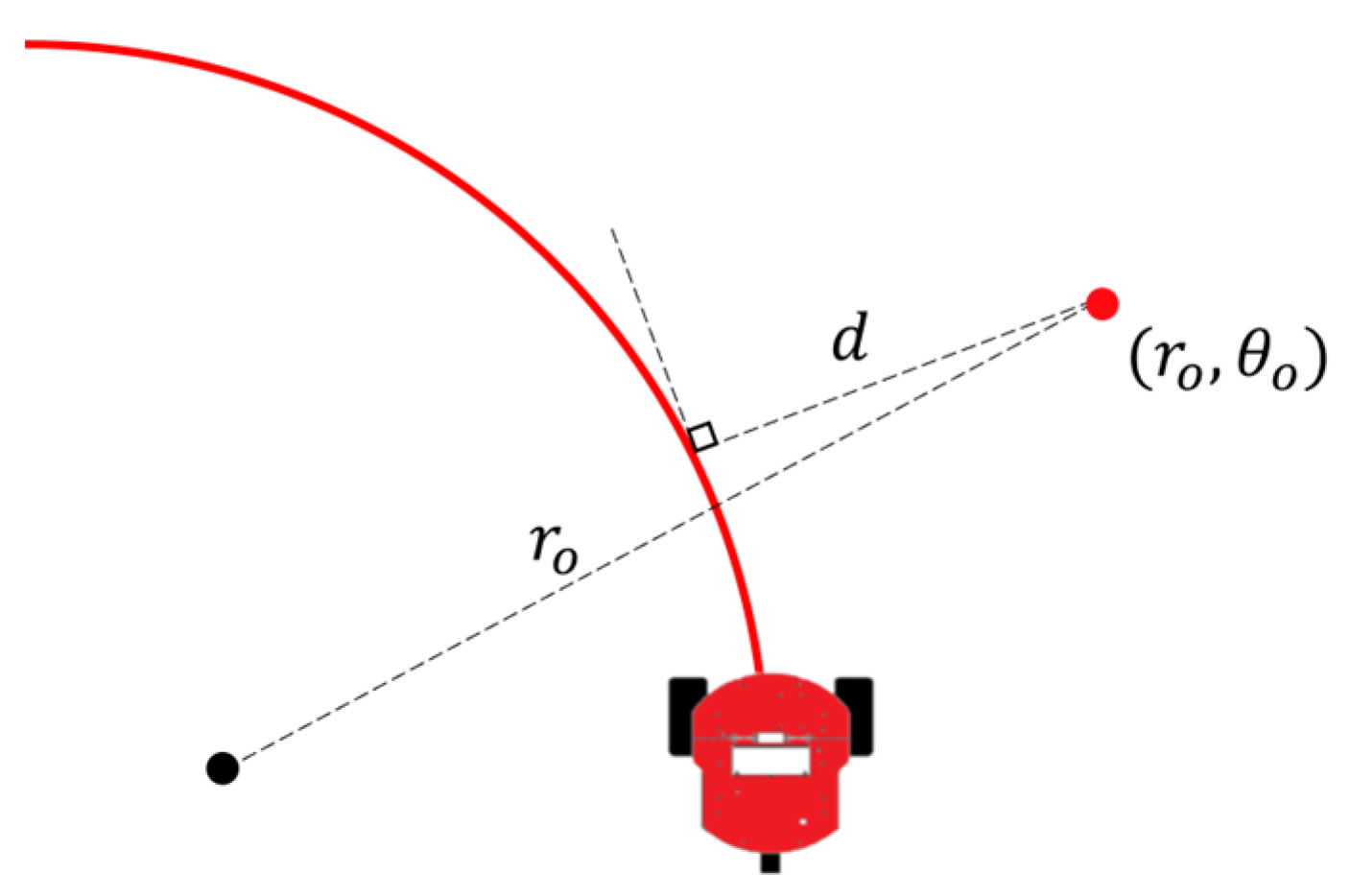
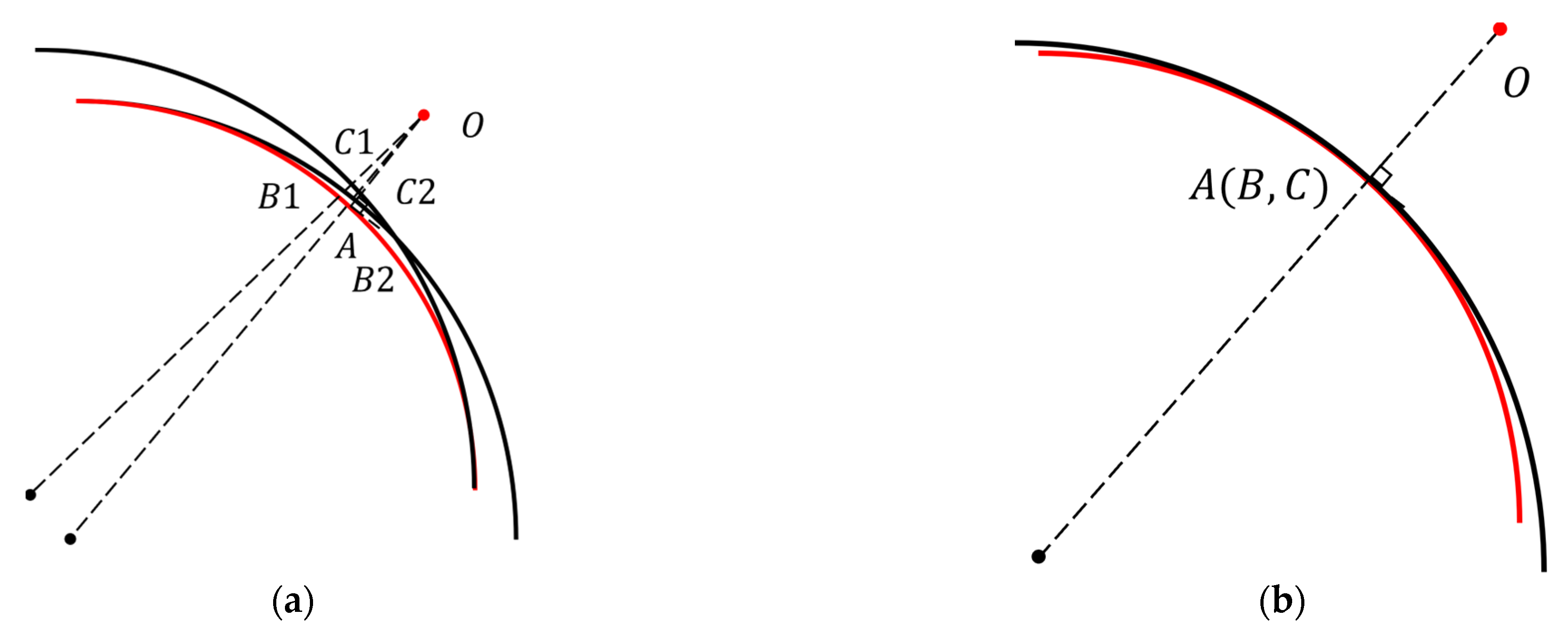
3. Proposed Method
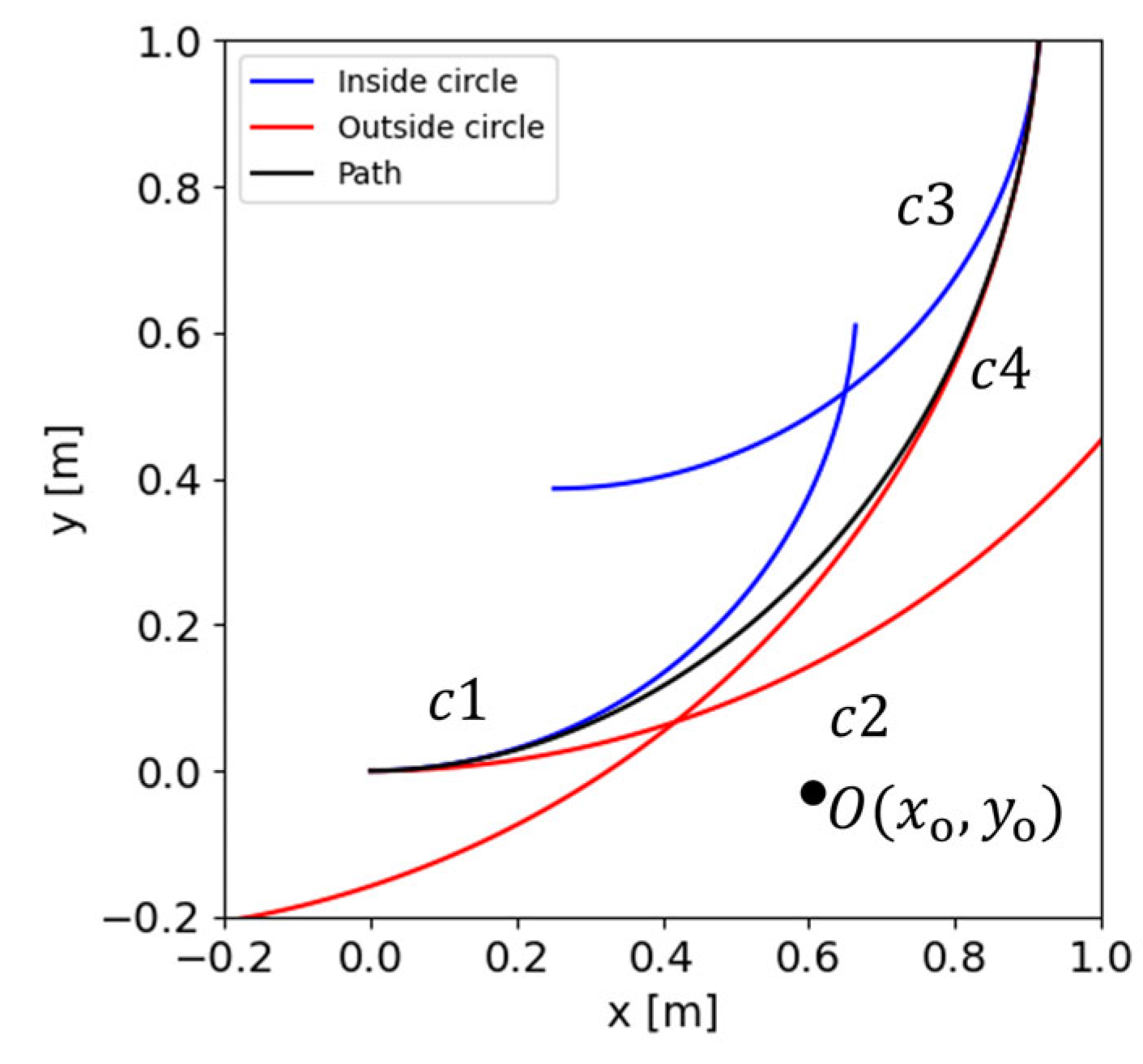
3.1. Proposed Method for Constant Velocity Model
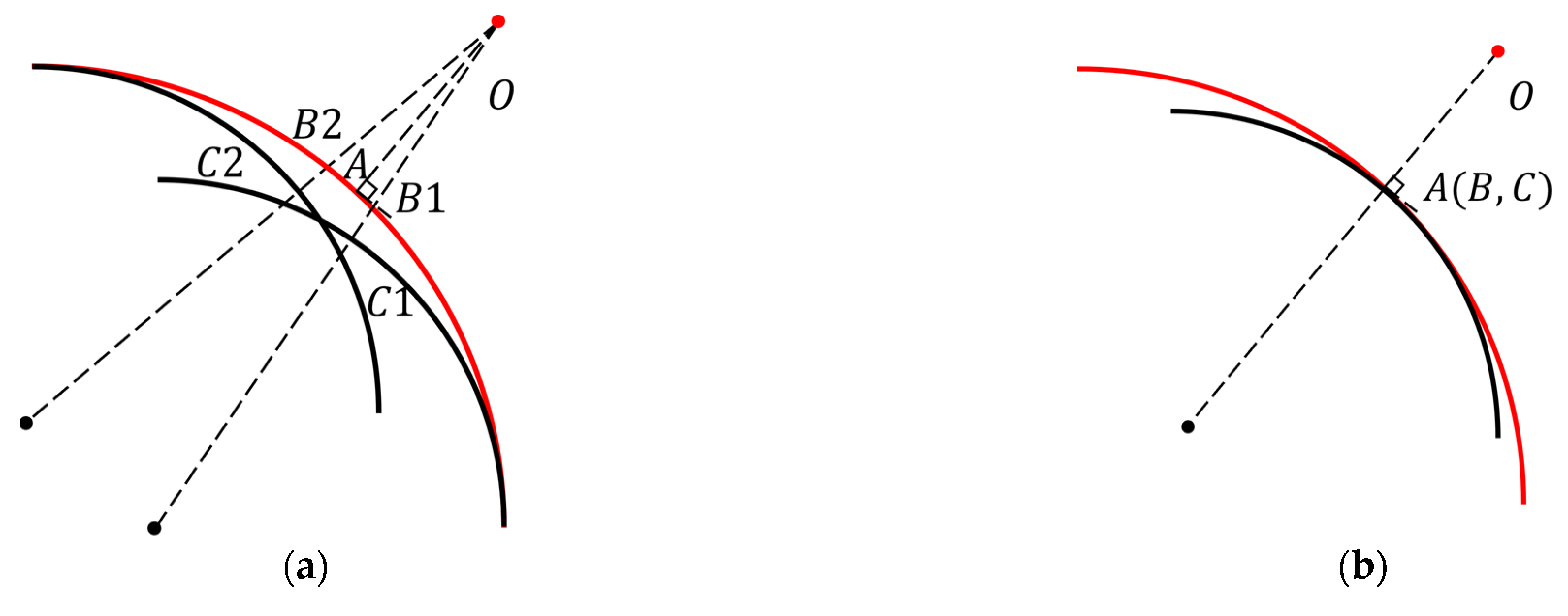
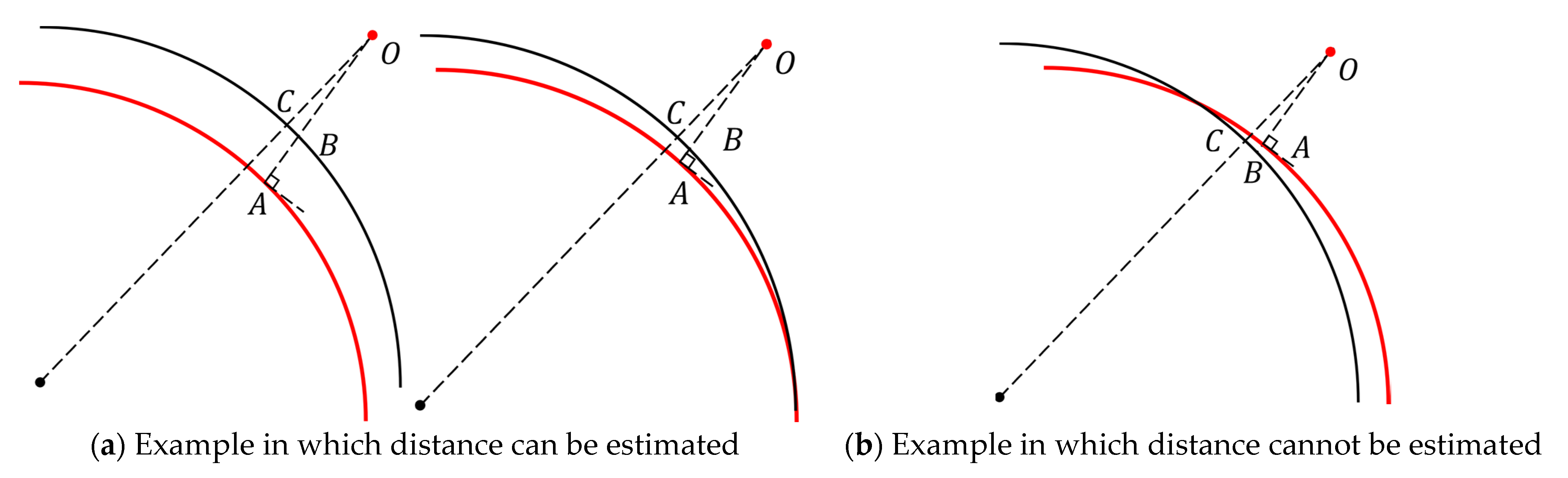
3.2. Proposed Method for the Variable Velocity Model
3.3. Computations
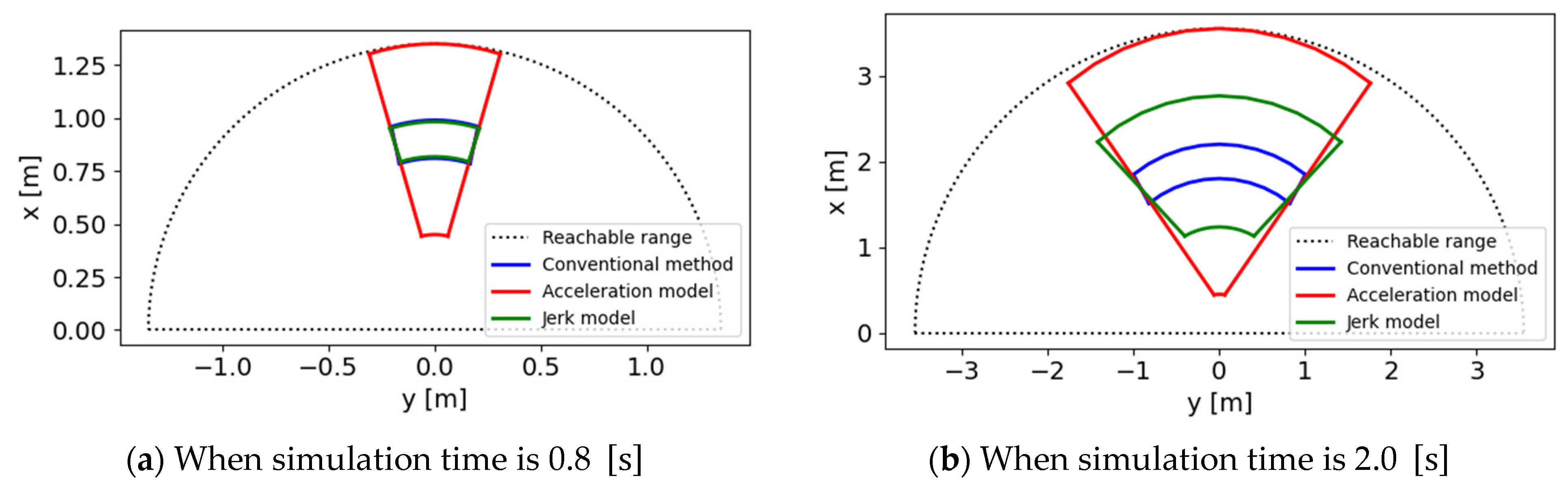
4. Experiment
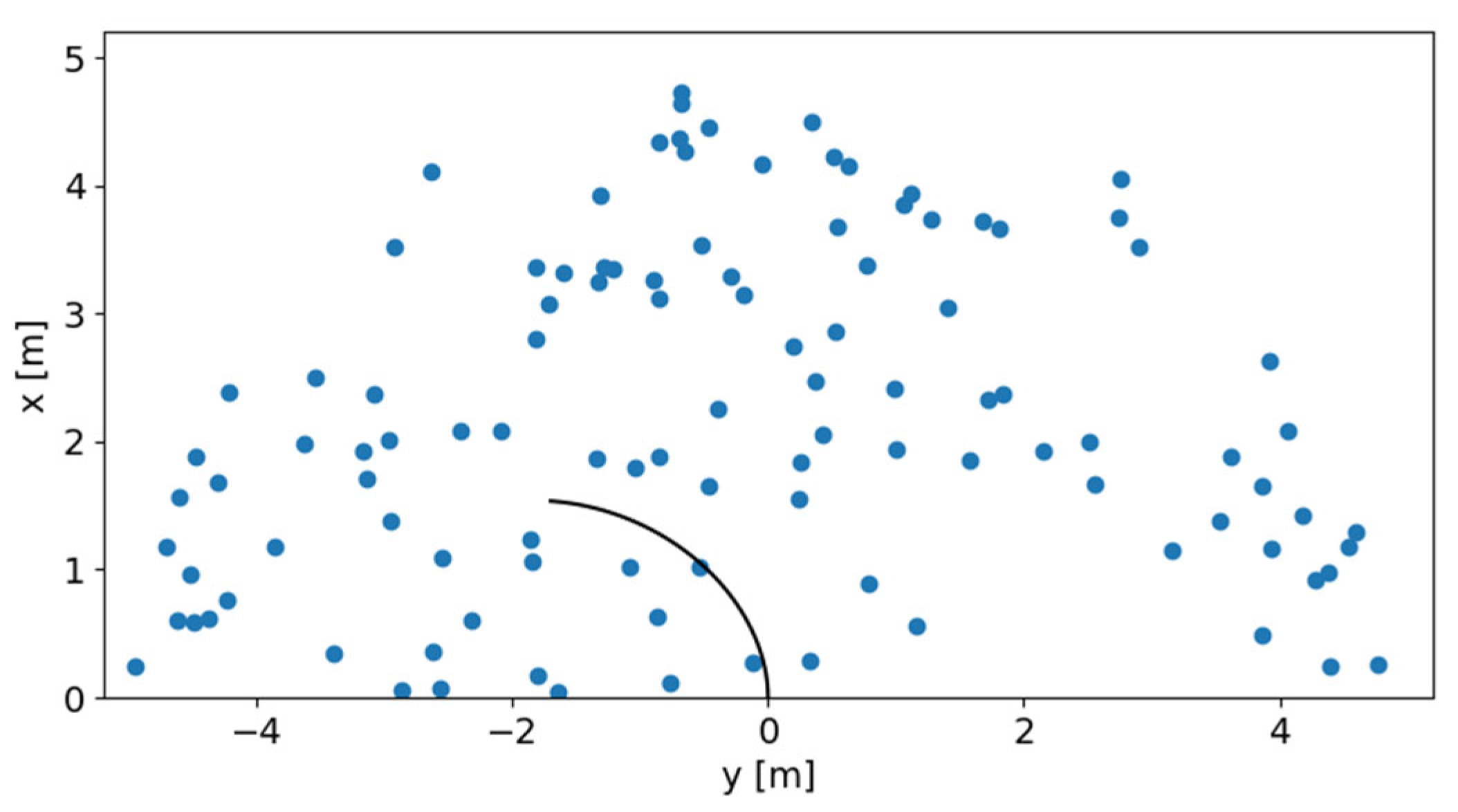
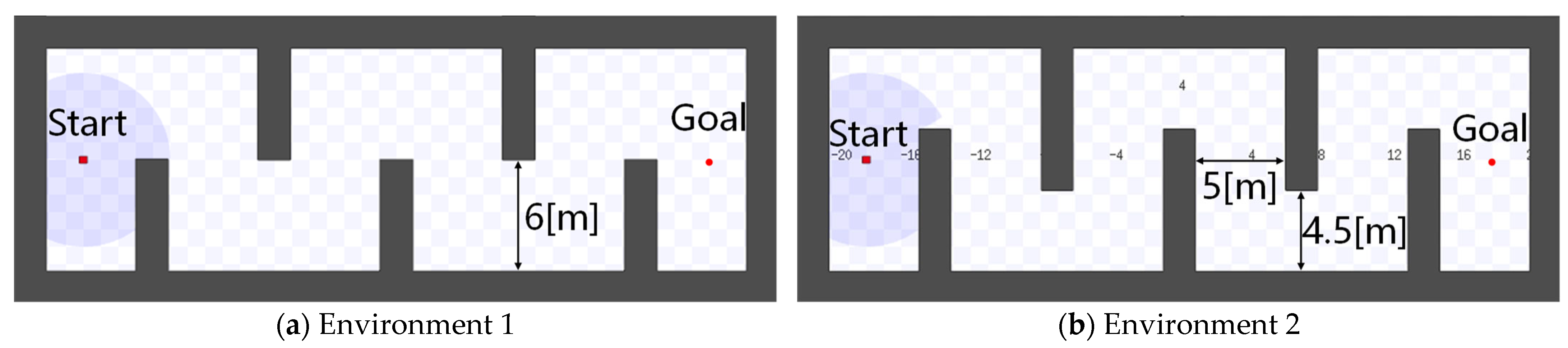
4.1. Conditions of Distance Calculation Accuracy Experiment
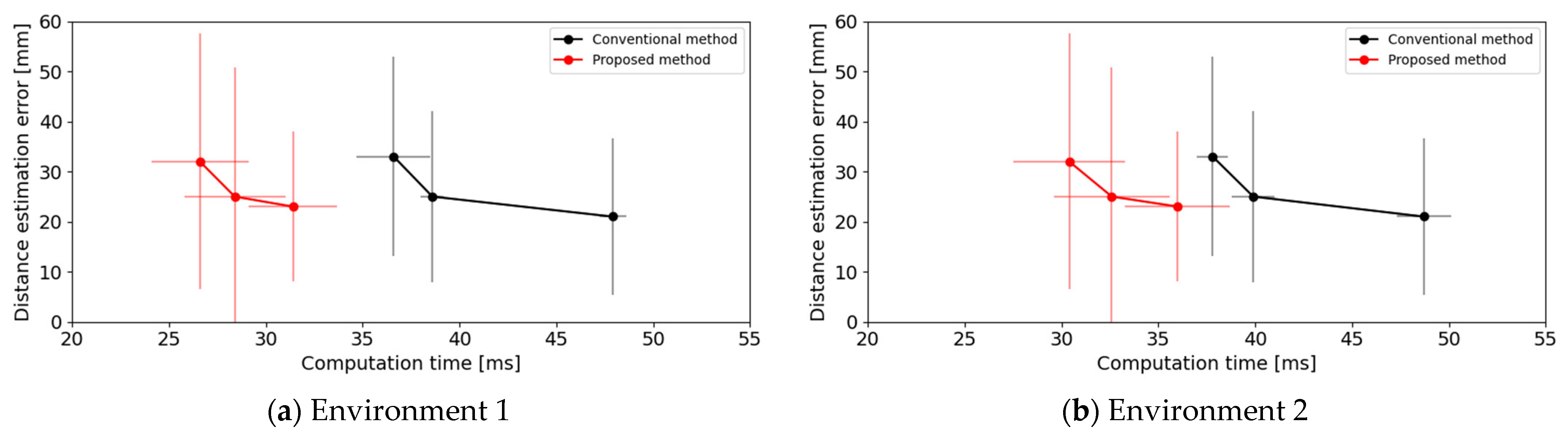
4.2. Results of Distance Calculation Accuracy Experiment
4.3. Conditions of Navigation Experiment
4.4. Results of Navigation Experiment
4.5. Overall Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.F.; Liu, H.Z.; Lin, S.X.; Chen, Y.K. Design and implementation of a multiple AGV scheduling algorithm for a job-shop. Int. J. Simul. Model. 2020, 19, 134–145. [Google Scholar] [CrossRef]
- Reis, W.; Junior, O. Sensors applied to automated guided vehicle position control. Int. J. Adv. Manuf. Technol. 2021, 113, 21–34. [Google Scholar] [CrossRef]
- Ramalepa, L.P.; Jamisola, R.S. A Review on Cooperative Robotic Arms with Mobile or Drones Bases. Int. J. Autom. Comput. 2021, 18, 536–555. [Google Scholar] [CrossRef]
- Suparjon, S. Evaluation of Layout Design, Operation and Maintenance of Multi Automated Systems Guided Vehicles (AGV): A Review. Int. J. Mech. Eng. Technol. Appl. 2022, 3, 1–7. [Google Scholar] [CrossRef]
- Thanh, V.N.; Vinh, D.P.; Nghi, N.T.; Nam, L.H.; Toan, D.L.H. Restaurant serving robot with double line sensors following approach. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019. [Google Scholar]
- Moshayedi, A.J.; Roy, A.S.; Sambo, S.K.; Zhong, Y.; Liao, L. Review On: The Service Robot Mathematical Model. EAI Endorsed Trans. AI Robot. 2022, 1, 1–19. [Google Scholar] [CrossRef]
- Liu, S.; Tian, G.; Zhang, Y.; Duan, P. Scene recognition mechanism for service robot adapting various families: A cnn-based approach using multi-type cameras. IEEE Trans. Multimed. 2021, 24, 2392–2406. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, Y.; Wu, C. An overview of current situations of robot industry development. In Proceedings of the 4th Annual International Conference on Wireless Communication and Sensor Network, Wuhan, China, 15–17 December 2017. [Google Scholar]
- Tzafestas, S.G. Mobile robot control and navigation: A global overview. J. Intell. Robot. Syst. 2018, 91, 35–58. [Google Scholar]
- Atiyah, A.N.; Adzhar, N.; Jaini, N.I. An overview: On path planning optimization criteria and mobile robot navigation. J. Phys. Conf. Ser. 2021, 1988, 1–10. [Google Scholar] [CrossRef]
- Nessrine, K.; Nahla, K.; Safya, B. Reinforcement Learning for Mobile Robot Navigation: An overview. In Proceedings of the 2022 IEEE Information Technologies & Smart Industrial Systems (ITSIS), Paris, France, 15–17 July 2022. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994. [Google Scholar]
- Karaman, S.; Frazzoli, E. Incremental sampling-based algorithms for optimal motion planning. Robot. Sci. Syst. VI 2010, 104, 267–274. [Google Scholar]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. Real-time obstacle avoidance for fast mobile robots. IEEE Trans. Syst. Man Cybern. 1989, 19, 1179–1187. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. The vector field histogram-fast obstacle avoidance for mobile robots. IEEE Trans. Robot. Autom. 1991, 7, 278–288. [Google Scholar] [CrossRef]
- de Lima, D.A.; Pereira, G.A.S. Navigation of an autonomous car using vector fields and the dynamic window approach. J. Control Autom. Electr. Syst. 2013, 24, 106–116. [Google Scholar] [CrossRef]
- Ballesteros, J.; Urdiales, C.; Velasco, A.B.M.; Ramos-Jimenez, G. A biomimetical dynamic window approach to navigation for collaborative control. IEEE Trans. Hum. Mach. Syst. 2017, 47, 1123–1133. [Google Scholar] [CrossRef]
- Missura, M.; Bennewitz, M. Predictive collision avoidance for the dynamic window approach. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, Canada, 20–24 May 2019. [Google Scholar]
- Lin, Z.; Taguchi, R. Improved dynamic window approach using the jerk model. In Proceedings of the 22nd International Conference on Control, Automation and Systems, Busan, Republic of Korea, 27–30 November 2022. [Google Scholar]
- Stefek, A.; Van Pham, T.; Krivanek, V.; Pham, K.L. Energy comparison of controllers used for a differential drive wheeled mobile robot. IEEE Access 2020, 8, 170915–170927. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, C.; Han, Z.; Ma, Z. Research on SLAM navigation of wheeled mobile robot based on ROS. In Proceedings of the 5th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 18–20 September 2020. [Google Scholar]
- Hassan, N.; Saleem, A. Analysis of Trajectory Tracking Control Algorithms for Wheeled Mobile Robots. In Proceedings of the 2021 IEEE Industrial Electronics and Applications Conference (IEACon), Georgetown, Malaysia, 22–23 November 2021. [Google Scholar]
- Wen-lan, W.; Bai, X. P and Feedforward Control for Mobile Robot. In Proceedings of the 2nd International Conference on Electrical Engineering and Computer Technology (ICEECT 2022), Suzhou, China, 23–25 September 2022. [Google Scholar]
- Liu, Y.; Bai, K.; Wang, H.; Fan, Q. Autonomous Planning and Robust Control for Wheeled Mobile Robot with Slippage Disturbances Based on Differential Flat. IET Control. Theory Appl. 2023. [Google Scholar] [CrossRef]
- Yang, D.; Bi, S.; Wang, W.; Yuan, C.; Qi, X.; Cai, Y. DRE-SLAM: Dynamic RGB-D encoder SLAM for a differential-drive robot. Remote Sens. 2019, 11, 380. [Google Scholar] [CrossRef]
- Jiang, H.; Sun, Y. Research on global path planning of electric disinfection vehicle based on improved A* algorithm. Energy Rep. 2021, 7, 1270–1279. [Google Scholar] [CrossRef]
- Khan, M.A.; Baig, D.-E.; Ali, H.; Ashraf, B.; Khan, S.; Wadood, A.; Kamal, T. Efficient System Identification of a Two-Wheeled Robot (TWR) Using Feed-Forward Neural Networks. Electronics 2021, 11, 3584. [Google Scholar] [CrossRef]
- Mushtaq, Z.; Qureshi, M.; Zohaib, A.; Akmal, M. Estimation of Real-Time Wheeled Mobile Robot (Differential Drive) Motion & Pose with Obstacle Avoidance. In Proceedings of the 2022 19th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 16–20 August 2022. [Google Scholar]
- Zhao, Y.; Zhu, Y.; Zhang, P.; Gao, Q.; Han, X. A Hybrid A* Path Planning Algorithm Based on Multi-objective Constraints. In Proceedings of the 2022 Asia Conference on Advanced Robotics, Automation, and Control Engineering (ARACE), Qingdao, China, 26–28 August 2022. [Google Scholar]
- Gong, K.; Xu, Z.; Zhang, X. Bounded-DWA: An Efficient Local Planner for Ackermann-driven Vehicles on Sandy Terrain. In Proceedings of the 2023 IEEE International Conference on Real-time Computing and Robotics (RCAR), Datong, China, 17–20 July 2023. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. Ros: An open-source robot operating system. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Vaughan, R. Massively multi-robot simulation in stage. Swarm Intell. 2008, 2, 189–208. [Google Scholar] [CrossRef]
- An Index of ROS Robots. Available online: https://robots.ros.org/ (accessed on 18 October 2023).
- Mobile Industrial Robots. Automate Your Internal Transportation. Available online: https://www.mobile-industrial-robots.com/ (accessed on 19 October 2023).
- Moving Robot. Available online: https://www.hansrobot.net/product-center/yidongjiqiren/ (accessed on 19 October 2023).
- Automated & Autonomous Mobile Robots|Robotnik®. Available online: https://robotnik.eu/products/mobile-robots/ (accessed on 19 October 2023).
- AITEN AGV (China) Official Site|—Satisfying Every Real Demand in Factory. Available online: https://www.szaiten.com/en/ProductIndex/ (accessed on 19 October 2023).
- AMR Autonomous Mobile Robots|AMS, Inc. Available online: https://www.ams-fa.com/autonomous-mobile-robots/ (accessed on 19 October 2023).







| Trans acc. | |||||||
|---|---|---|---|---|---|---|---|
| s | m | e | s + m | s + e | m + e | s + m + e | |
| −1.0 | 34 | 28 | 181 | 29 | 30 | 29 | 31 |
| −0.5 | 102 | 22 | 84 | 16 | 19 | 27 | 13 |
| 0.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 98 | 30 | 161 | 33 | 30 | 47 | 30 |
| 1.0 | 55 | 78 | 317 | 46 | 81 | 71 | 42 |
| Mean | 58 | 32 | 148 | 25 | 32 | 35 | 23 |
| Std | 38.9 | 25.5 | 105.6 | 15.7 | 27.0 | 23.6 | 14.9 |
| Trans acc. | ||||||
|---|---|---|---|---|---|---|
| Tangent | Secant | Tangent | Secant | Tangent | Secant | |
| −1.0 | 55 | 51 | 42 | 40 | 34 | 33 |
| −0.5 | 23 | 18 | 12 | 9 | 5 | 4 |
| 0.0 | 32 | 1 | 16 | 1 | 7 | 1 |
| 0.5 | 78 | 39 | 51 | 32 | 36 | 28 |
| 1.0 | 104 | 52 | 69 | 43 | 48 | 38 |
| Mean | 59 | 33 | 38 | 25 | 26 | 21 |
| Std | 29.5 | 19.9 | 21.5 | 17.1 | 17.1 | 15.6 |
| System Configuration | Details |
|---|---|
| OS | Ubuntu 18.04.5 LTS |
| ROS | Melodic 1.14.9 |
| Stage | 4.3.0 |
| CPU | Intel Core i7-8700 3.20Ghz×12 |
| Numpy | 1.16.4 |
| Scipy | 1.3.0 |
| Laser Rangefinder Resolution [nums/°] | 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|---|
| Number of Detected Obstacle Points per Frame | |||||||
| Travel Distance [m] | Travel Time [s] | Travel Distance [m] | Travel Time [s] | Travel Distance [m] | Travel Time [s] | ||
| Conventional DWA | 90.6 | 79.9 | 90.4 | 79.9 | 89.4 | 79.9 | |
| 44.8 | 26.7 | 44.4 | 26.5 | 43.0 | 25.5 | ||
| 39.2 | 23.4 | 39.4 | 23.1 | 39.0 | 23.5 | ||
| 39.0 | 23.6 | 39.2 | 23.5 | 39.2 | 23.6 | ||
| 39.0 | 25.0 | 39.0 | 25.2 | 39.0 | 25.0 | ||
| 39.0 | 24.8 | 39.0 | 25.0 | 39.6 | 23.6 | ||
| Proposed method | 38.4 | 21.5 | 38.4 | 21.6 | 38.4 | 21.5 | |
| 38.4 | 21.6 | 38.0 | 21.3 | 38.1 | 21.4 | ||
| 39.1 | 25.1 | 39.0 | 24.9 | 39.1 | 25.0 | ||
| Laser Rangefinder Resolution [nums/°] | 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|---|
| Number of Detected Obstacle Points per Frame | |||||||
| Travel Distance [m] | Travel Time [s] | Travel Distance [m] | Travel Time [s] | Travel Distance [m] | Travel Time [s] | ||
| Conventional DWA | 86.0 | 79.9 | 85.2 | 79.9 | 87.6 | 79.9 | |
| 66.2 | 52.7 | 63.4 | 46.8 | 61.2 | 42.9 | ||
| 60.8 | 42.5 | 61.2 | 41.6 | 61.2 | 41.5 | ||
| 53.4 | 30.7 | 53.6 | 31.4 | 53.8 | 30.9 | ||
| 53.6 | 32.1 | 53.2 | 32.5 | 53.6 | 32.2 | ||
| 55.8 | 31.7 | 56.0 | 31.8 | 55.6 | 31.5 | ||
| Proposed method | 51.6 | 30.5 | 54.3 | 31.6 | 52.6 | 31.1 | |
| 53.1 | 31.4 | 54.4 | 32.2 | 53.6 | 31.7 | ||
| 53.6 | 31.7 | 54.1 | 32.0 | 54.3 | 32.1 | ||
| Laser Rangefinder Resolution [nums/°] | 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|---|
| Number of Detected Obstacle Points per Frame | |||||||
| Mean | p | Mean | p | Mean | p | ||
| Conventional DWA | 16.1 | - | 20.6 | - | 24.0 | - | |
| 17.8 | - | 21.3 | - | 23.8 | - | ||
| 25.4 | - | 30.9 | - | 32.9 | - | ||
| 34.6 | - | 36.1 | - | 39.1 | - | ||
| 37.8 | * | 38.7 | * | 39.3 | |||
| 47.3 | ** | 47.5 | ** | 48.8 | ** | ||
| Proposed method | 24.7 | - | 25.0 | - | 30.1 | - | |
| 25.1 | 28.7 | 31.5 | |||||
| 29.4 | * | 30.2 | 34.7 | ||||
| Laser Rangefinder Resolution [nums/°] | 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|---|
| Number of Detected Obstacle Points per Frame | |||||||
| Mean | p | Mean | p | Mean | p | ||
| Conventional DWA | 21.0 | 25.6 | 29.7 | ||||
| 21.9 | 32.7 | 35.5 | |||||
| 31.0 | 36.0 | 37.6 | |||||
| 36.7 | 38.3 | 38.5 | |||||
| 37.8 | 40.1 | 40.2 | |||||
| 46.8 | ** | 49.1 | ** | 50.0 | ** | ||
| Proposed method | 28.1 | 28.7 | 34.5 | ||||
| 28.8 | 32.9 | 36.1 | |||||
| 33.7 | * | 34.6 | 39.8 | * | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Taguchi, R. Faster Implementation of The Dynamic Window Approach Based on Non-Discrete Path Representation. Mathematics 2023, 11, 4424. https://doi.org/10.3390/math11214424
Lin Z, Taguchi R. Faster Implementation of The Dynamic Window Approach Based on Non-Discrete Path Representation. Mathematics. 2023; 11(21):4424. https://doi.org/10.3390/math11214424
Chicago/Turabian StyleLin, Ziang, and Ryo Taguchi. 2023. "Faster Implementation of The Dynamic Window Approach Based on Non-Discrete Path Representation" Mathematics 11, no. 21: 4424. https://doi.org/10.3390/math11214424
APA StyleLin, Z., & Taguchi, R. (2023). Faster Implementation of The Dynamic Window Approach Based on Non-Discrete Path Representation. Mathematics, 11(21), 4424. https://doi.org/10.3390/math11214424





