Emission Reduction and Channel Decisions in a Two-Echelon Supply Chain Considering Service Spillovers
Abstract
:1. Introduction
- (1)
- How do consumers’ low-carbon preferences and service sensitivity affect suppliers’ emission reduction and channel selection decisions?
- (2)
- Under a dual-channel structure, how do service spillovers affect the decision-making of supply chain members?
- (3)
- When suppliers exploit online channels to introduce competition, which decisions can retailers make to respond to showrooming?
- (4)
- What effect do carbon cap-and-trade (CCT) mechanisms and/or low-carbon policies have on the realization of a win-win outcome?
2. Literature Review
3. The Model
4. Equilibrium Solutions and Discussions in Four Scenarios
4.1. Single-Channel Structure
4.2. Dual-Channel Structure
4.2.1. No Service Spillovers
4.2.2. Service Spillover
- (i)
- ;
- (ii)
- if , otherwise ;
- (iii)
- and if , while and if .
5. Service Strategy
5.1. Channel Decision
5.2. Service Strategy
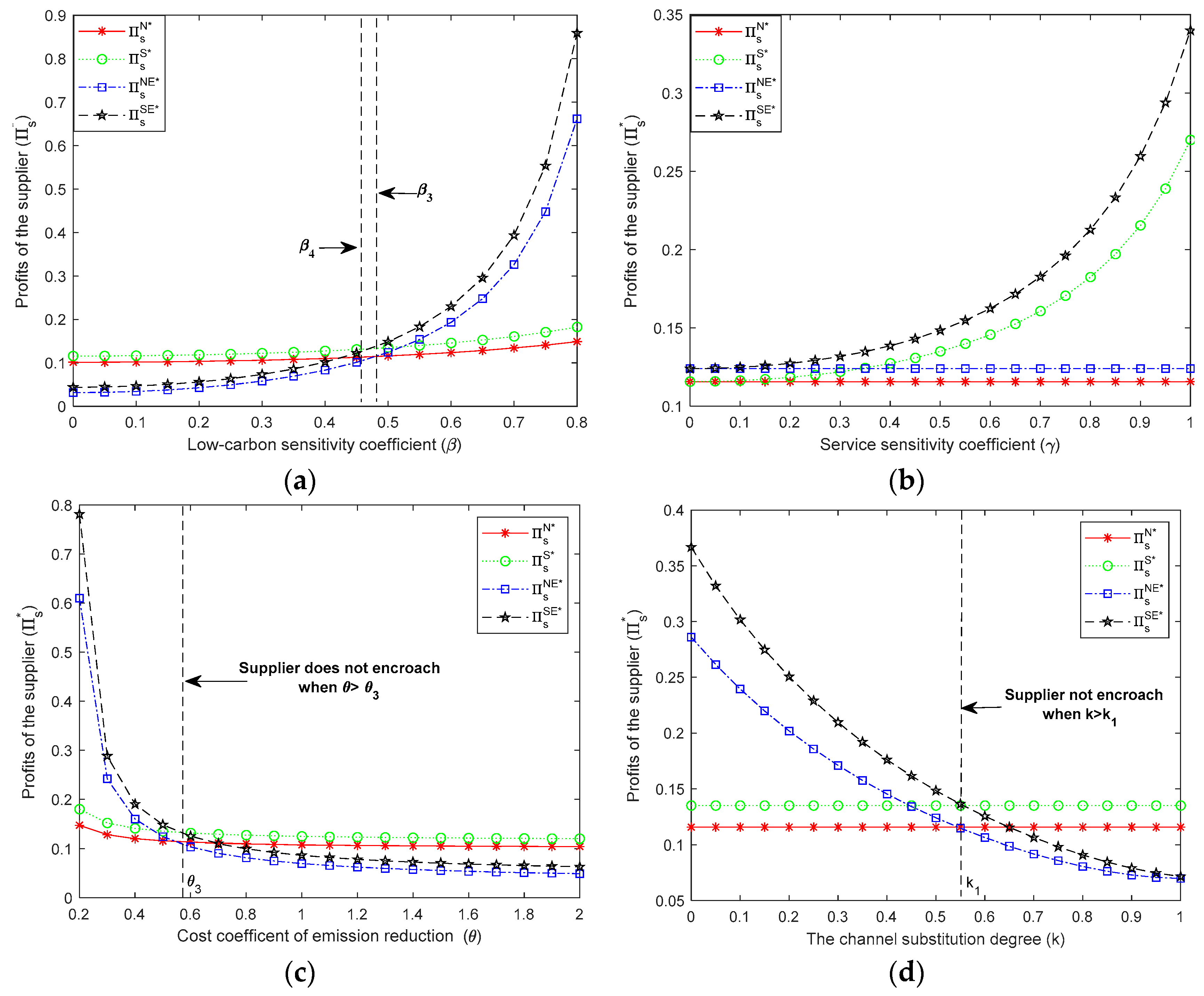
6. Extended Discussion
- (i)
- ;
- (ii)
- and if , while and , if , Where, ;
- (iii)
- , .
7. Conclusions
- (1)
- The channel decisions of the supplier primarily depend on the costs of the direct channel. The supplier prefers to encroach on the market when the cost of opening a direct channel is relatively low; otherwise, she will employ the single-channel strategy, which only distributes through the retail channel. Furthermore, a higher degree of service spillovers motivates supplier encroachment when retail services are available.
- (2)
- When consumers have both low-carbon preference and service sensitivity, the purpose of dual-channel distribution is not to eliminate the traditional channel but to increase total demand by taking advantage of service spillovers and green production. Thus, if the retailer decides to provide retail services in the dual-channel supply chain, the supplier always has the incentive to reduce emissions.
- (3)
- By comparing the optimal service strategies of the retailer in the single-channel and dual-channel supply chains, we reach three interesting conclusions. Firstly, supplier encroachment could motivate the retailer to enhance his service level and help him get more returns from providing retail services, as long as the degree of service spillover is above a threshold. Secondly, compared with service sensitivity, consumers’ low-carbon preference plays a more decisive role in the retailer’s service strategies under a dual-channel structure. Thirdly, if supplier encroachment induces intensive channel competition, although the emission reduction level of the supplier is still better than that under the single-channel structure, the retailer’s margins and service inputs will diminish. Therefore, the optimal decision of emission abatement levels and retail service levels are not positively correlated under supplier encroachment.
- (4)
- The implementation of CCT regulation is beneficial for the retailer to achieve profit growth from the supplier encroachment, which also contributes to achieving a win-win situation under the dual-channel structure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Lemma 1
Appendix A.2. Proof of Proposition 1
Appendix A.3. Proof of Corollary 1
Appendix A.4. Proof of Lemma 2
Appendix A.5. Proof of Proposition 2
Appendix A.6. Proof of Corollary 2
Appendix A.7. Proof of Lemma 3
Appendix A.8. Proof of Proposition 3
Appendix A.9. Proof of Proposition 4
Appendix A.10. Proof of Corollary 3
Appendix A.11. Proof of Lemma 4
Appendix A.12. Proof of Proposition 5
Appendix B
References
- Zhen, Z.; Qi, L.; Tiantian, Y.; Feiyan, L. How do the quality assurance mechanism influence the online sale of experiential products on an e-commerce platform. Manag. Rev. 2023, 35, 181–190. [Google Scholar]
- Xia, J.; Niu, W. Adding clicks to bricks: An analysis of supplier encroachment under service spillovers. Electron. Commer. Res. Appl. 2019, 37, 100876. [Google Scholar] [CrossRef]
- Mehra, A.; Kumar, S.; Raju, J.S. Competitive strategies for brick-and-mortar stores to counter “showrooming”. Manag. Sci. 2018, 64, 3076–3090. [Google Scholar] [CrossRef]
- Zhang, L.-H.; Yao, J.; Xu, L. Emission reduction and market encroachment: Whether the supplier opens a direct channel or not? J. Clean. Prod. 2020, 269, 121931. [Google Scholar] [CrossRef]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chains: Insights from simple models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Yang, H.; Luo, J.; Zhang, Q. Supplier encroachment under nonlinear pricing with imperfect substitutes: Bargaining power versus revenue-sharing. Eur. J. Oper. Res. 2018, 267, 1089–1101. [Google Scholar] [CrossRef]
- Cai, G. Channel Selection and Coordination in Dual-Channel Supply Chains. J. Retail. 2010, 86, 22–36. [Google Scholar] [CrossRef]
- Huang, S.; Guan, X.; Chen, Y.-J. Retailer Information Sharing with Supplier Encroachment. Prod. Oper. Manag. 2018, 27, 1133–1147. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, D.; He, L. Contracting emission reduction for supply chains considering market low-carbon preference. J. Clean. Prod. 2016, 120, 72–84. [Google Scholar] [CrossRef]
- Zhou, Y.-W.; Guo, J.; Zhou, W. Pricing/service strategies for a dual-channel supply chain with free riding and service-cost sharing. Int. J. Prod. Econ. 2018, 196, 198–210. [Google Scholar] [CrossRef]
- Arya, A.; Mittendorf, B. The changing face of distribution channels: Partial forward integration and strategic investments. Prod. Oper. Manag. 2013, 22, 1077–1088. [Google Scholar] [CrossRef]
- Che, Y.-K.; Hausch, D.B. Cooperative investments and the value of contracting. Am. Econ. Rev. 1999, 89, 125–147. [Google Scholar] [CrossRef]
- Chiang, W.-Y.; Chhajed, D.; Hess, J.D. Direct Marketing, Indirect Profits: A Strategic Analysis of Dual-Channel Supply-Chain Design. Manag. Sci. 2003, 49, 1–20. [Google Scholar] [CrossRef]
- Jamali, M.-B.; Rasti-Barzoki, M. A game theoretic approach for green and non-green product pricing in chain-to-chain competitive sustainable and regular dual-channel supply chains. J. Clean. Prod. 2018, 170, 1029–1043. [Google Scholar] [CrossRef]
- Xu, L.; Wei, J.; Choi, T.-M.; Wang, W. Managing online channel and optimization in supply chain systems with different channel leaderships. IEEE Trans. Syst. Man Cybern.-Syst. 2021, 51, 7177–7190. [Google Scholar] [CrossRef]
- Li, H.; Chai, J. Strategic service investment by retailers confronted by manufacturer encroachment. J. Ind. Manag. Optim. 2023, 19, 3255–3286. [Google Scholar] [CrossRef]
- Ghosh, D.; Shah, J. A comparative analysis of greening policies across supply chain structures. J. Int. J. Prod. Econ. 2012, 135, 568–583. [Google Scholar] [CrossRef]
- Hong, Z.; Guo, X. Green product supply chain contracts considering environmental responsibilities. Omega 2019, 83, 155–166. [Google Scholar] [CrossRef]
- Zhao, S.; Zhu, Q. A risk-averse marketing strategy and its effect on coordination activities in a remanufacturing supply chain under market fluctuation. J. Clean. Prod. 2018, 171, 1290–1299. [Google Scholar] [CrossRef]
- Bernstein, F.; Song, J.-S.; Zheng, X. Free riding in a multi-channel supply chain. Nav. Res. Logist. (NRL) 2009, 56, 745–765. [Google Scholar] [CrossRef]
- Hua, G.; Cheng, T.C.E.; Wang, S. Managing carbon footprints in inventory management. Int. J. Prod. Econ. 2011, 132, 178–185. [Google Scholar] [CrossRef]
- Amit Kumar, G. Framing a model for green buying behavior of Indian consumers: From the lenses of the theory of planned behavior. J. Clean. Prod. 2021, 295, 1026487. [Google Scholar] [CrossRef]
- Feng, L.; Govindan, K.; Li, C. Strategic planning: Design and coordination for dual-recycling channel reverse supply chain considering consumer behavior. Eur. J. Oper. Res. 2017, 260, 601–612. [Google Scholar] [CrossRef]
- Liu, Z.; Anderson, T.D.; Cruz, J.M. Consumer environmental awareness and competition in two-stage supply chains. Eur. J. Oper. Res. 2012, 218, 602–613. [Google Scholar] [CrossRef]
- Peng, H.; Pang, T.; Cong, J. Coordination contracts for a supply chain with yield uncertainty and low-carbon preference. J. Clean. Prod. 2018, 205, 291–302. [Google Scholar] [CrossRef]
- Ranjan, A.; Jha, J.K. Pricing and coordination strategies of a dual-channel supply chain considering green quality and sales effort. J. Clean. Prod. 2019, 218, 409–424. [Google Scholar] [CrossRef]
- Tao, F.; Zhou, Y.; Bian, J.S.; Lai, K.K. Agency selling or reselling? Channel selection of green products with consumer environmental awareness. Int. J. Logist.-Res. Appl. 2022. [Google Scholar] [CrossRef]
- Liu, G.; Sheng, W. Pricing and carbon emission reduction decision in dual-channel supply chain with carbon tax and consumer preference. Inf. Syst. Econ. 2023, 4, 21–29. [Google Scholar]
- Shin, J. How does free riding on customer service affect competition? Mark. Sci. 2007, 26, 488–503. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; Sun, Y. Implementing coordination contracts in a supplier Stackelberg dual-channel supply chain. Omega 2012, 40, 571–583. [Google Scholar] [CrossRef]
- Jing, B. Showrooming and webrooming: Information externalities between online and offline sellers. Mark. Sci. 2018, 24, 89–109. [Google Scholar] [CrossRef]
- Flavián, C.; Gurrea, R.; Orús, C. Combining channels to make smart purchases: The role of webrooming and showrooming. J. Retail. Consum. Serv. 2020, 52, 101923. [Google Scholar] [CrossRef]
- Yalabik, B.; Fairchild, R.J. Customer, regulatory, and competitive pressure as drivers of environmental innovation. Int. J. Prod. Econ. 2011, 131, 519–527. [Google Scholar] [CrossRef]
- Adaman, F.; Karalı, N.; Kumbaroğlu, G.; Or, İ.; Özkaynak, B.; Zenginobuz, Ü. What determines urban households’ willingness to pay for CO2 emission reductions in Turkey: A contingent valuation survey. Energy Policy 2011, 39, 689–698. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, Z.; Yang, L. Carbon emission reduction decisions in the retail-/dual-channel supply chain with consumers’ preference. J. Clean. Prod. 2017, 141, 852–867. [Google Scholar] [CrossRef]
- Yoon, D.-H. Supplier encroachment and investment spillovers. Prod. Oper. Manag. 2016, 25, 1839–1854. [Google Scholar] [CrossRef]
- Xia, L.; Hao, W.; Qin, J.; Ji, F.; Yue, X. Carbon emission reduction and promotion policies considering social preferences and consumers’ low-carbon awareness in the cap-and-trade system. J. Clean. Prod. 2018, 195, 1105–1124. [Google Scholar] [CrossRef]
- Xu, L.; Wang, C.X. Sustainable manufacturing in a closed-loop supply chain considering emission reduction and remanufacturing. Resour. Conserv. Recycl. 2018, 131, 297–305. [Google Scholar] [CrossRef]
- Du, S.; Zhu, L.; Liang, L.; Ma, F. Emission-dependent supply chain and environment-policy-making in the ‘cap-and-trade’ system. Energy Policy 2013, 57, 61–67. [Google Scholar] [CrossRef]
- Yi, Y.; Li, J. The effect of governmental policies of carbon taxes and energy-saving subsidies on enterprise decisions in a two-echelon supply chain. J. Clean. Prod. 2018, 181, 675–691. [Google Scholar]
- Yuan, K.; Wu, G.; Dong, H.; He, B.; Wang, D. Differential Pricing and Emission Reduction in Remanufacturing Supply Chains with Dual-Sale Channels under CCT-Mechanism. Sustainability 2020, 12, 8150. [Google Scholar] [CrossRef]
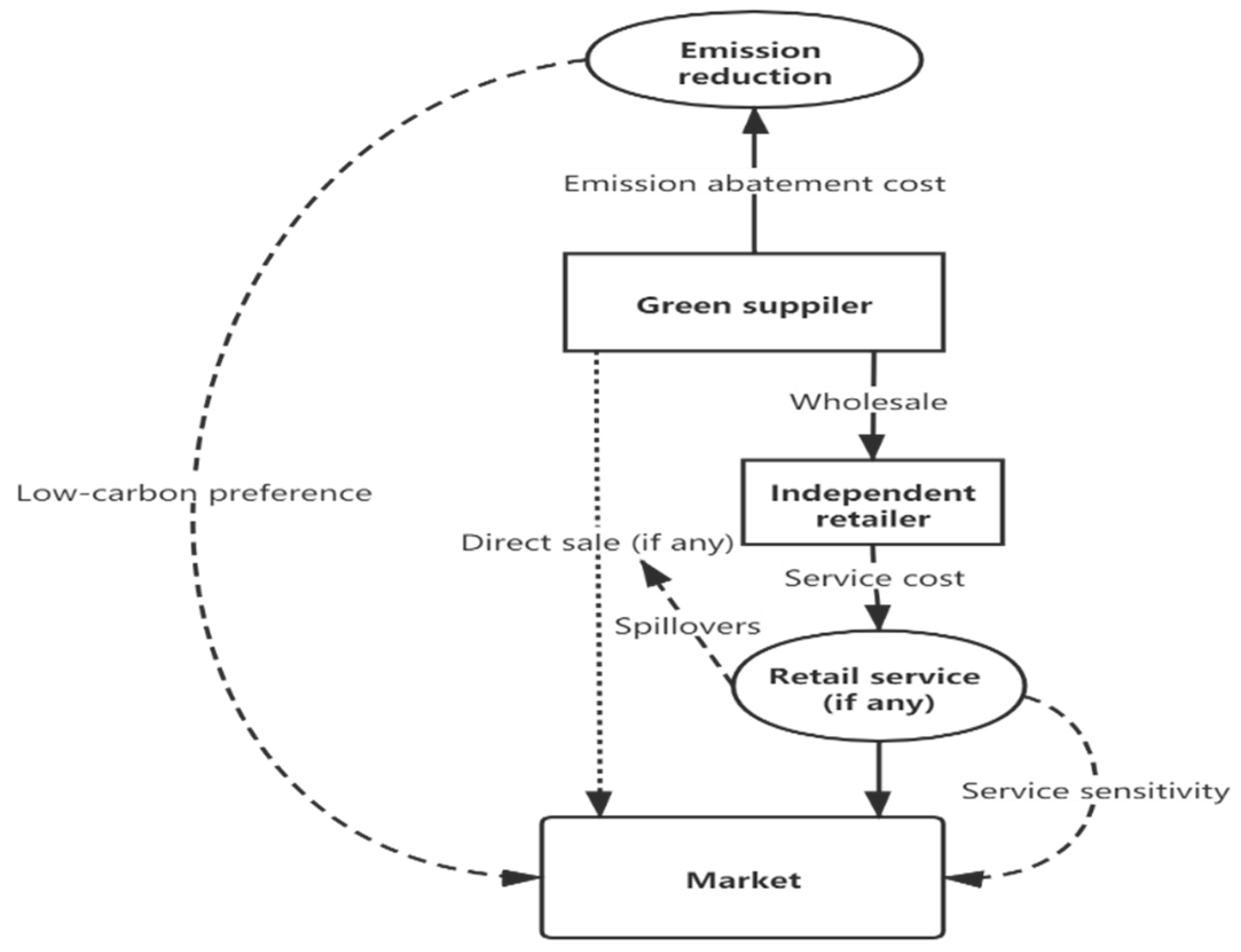

| Model Parameters | |
|---|---|
| Potential demand of market | |
| Low-carbon preference coefficient | |
| Service sensitivity coefficient | |
| Unit production cost (a nonnegative constant) | |
| Cost coefficient of emission reduction | |
| Fixed cost of the direct channel | |
| The substitution degree between dual channels | |
| Degree of service spillover | |
| Unit retail/direct price | |
| Unit carbon price | |
| Initial unit amount of carbon emissions from production process | |
| Total carbon quotas | |
| Decision variables | |
| Order/output quantity | |
| Emission reduction level | |
| Retail service level | |
| Unit wholesale price | |
| — |
| ) | ) | |
|---|---|---|
| — | ||
| — |
| ) | ) | |
|---|---|---|
| — | ||
| — | ||
| The supplier’s channel decision: encroach on the market by opening an internet channel. The retailer’s service strategy: diminish service inputs. | The supplier’s channel decision: encroach on the market by opening an internet channel. The retailer’s service strategy: raise the service level. | |
| The supplier’s channel decision: distribute through the retail channel only. The retailer’s service strategy: diminish service inputs. | The supplier’s channel decision: distribute through the retail channel only. The retailer’s service strategy: raise the service level. |
| ) | ) | |
|---|---|---|
| — | ||
| — | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, J.; Xu, P.; Walker, T.; Yang, G. Emission Reduction and Channel Decisions in a Two-Echelon Supply Chain Considering Service Spillovers. Mathematics 2023, 11, 4423. https://doi.org/10.3390/math11214423
Chen X, Wang J, Xu P, Walker T, Yang G. Emission Reduction and Channel Decisions in a Two-Echelon Supply Chain Considering Service Spillovers. Mathematics. 2023; 11(21):4423. https://doi.org/10.3390/math11214423
Chicago/Turabian StyleChen, Xiaoxu, Jingwei Wang, Peng Xu, Thomas Walker, and Guoqiang Yang. 2023. "Emission Reduction and Channel Decisions in a Two-Echelon Supply Chain Considering Service Spillovers" Mathematics 11, no. 21: 4423. https://doi.org/10.3390/math11214423
APA StyleChen, X., Wang, J., Xu, P., Walker, T., & Yang, G. (2023). Emission Reduction and Channel Decisions in a Two-Echelon Supply Chain Considering Service Spillovers. Mathematics, 11(21), 4423. https://doi.org/10.3390/math11214423






