Default Probabilities and the Credit Spread of Mexican Companies: The Modified Merton Model

Abstract

This study aims to identify the model that best approximates the credit spread that should be fixed on debt instruments issued by both companies listed on the Mexican Stock Market, considering the particularities of the Mexican market. Five models were analyzed: Merton’s model, Brownian Motion Model, Power Law Brownian Motion Model, Bloomberg’s model, and the model presented in this paper, which includes the conformable derivatives, taking as a reference the change in the variable as other authors have done, and the Bloomberg corporate default risk model (DRSK) for publics firms. We concluded that the modified Merton model approximates, to a greater extent, the credit spreads that fix on a prime rate on the loans granted to Mexican non-financial companies.

1. Introduction

The Bank of Mexico’s position after the economic contraction generated by the health measures to tackle the COVID-19 pandemic to encourage consumption and investment would be to lower its monetary policy to complement the liquidity implemented in the financial system to stimulate the economy through the credit channel. To do so, it is necessary to know how much the Bank of Mexico could reduce this rate without negatively affecting inflationary dynamics (Sánchez and Lopez-Herrera [1]).

In addition, as pointed out by Ozili and Arun [2], due to the pressures derived from the trade war between the latter country and Brexit, economic forecasts in 2019 were for moderate growth in the world economy by 2020. The immediate consequences in the affected countries were already apparent, as reported by Nicola et al. [3], including job losses and a drop in demand for manufacturing companies and other goods, in contrast to an increase in demand for medical supplies.

According to Gopinath [4], during the pandemic, there were shocks to aggregate supply due to a decrease in production level, while on the aggregate demand side, the shocks were due to the reluctance of consumers and businesses to spend.

Decreased consumption in the more developed countries implied a sharp decrease in the prices of their export products for Latin America, producing exchange losses and recessionary effects given the economy’s sensitivity to those prices, as pointed out by Schimtt-Grohé and Uribe [5].

Furman and Summers [6], Odendahl and Sprinford [7], as well as Gall [8] pointed out various possible risks, including financial risks such as corporate bankruptcies, lack of liquidity, and bank insolvency.

Sánchez and López-Herrera [1] stated that the COVID-19 effect added to the economic contraction that had been occurring in Mexico. They pointed out that the nominal interest rate went from 8.3% during the first quarter of 2019 to 7.4% in 2020. Meanwhile, inflation remained at low levels. They also stated that the real interest rate had a downward trend, which showed that the Bank of Mexico decided to reduce interest rates to reduce the fall in economic activity and lessen the effects of the financial crisis experienced at that time.

It should be noted that although there has already been a substantial increase in interest rates, to this day in Mexico, there is a large gap between lending rates and borrowing rates at which both banks and extensive corporations finance, which is why there is a financial gain at the expense of the liquidity of the end customer.

According to Article 81 Bis of the Mexican Law on Credit Institutions [9], credit institutions must have guidelines and policies for knowing information about their customers. According to their profile, they set the interest rate and credit spread that the institution considers appropriate so that there is no concordance between the credit risk calculated by a credit rating agency and that determined by a credit institution. In addition, there is no independence between large corporations and credit institutions, as members of corporate boards of directors also serve as directors of lending institutions. So, there is an imbalance between the credit spread they lend and the risk of default.

As Xi and Jiang [10] pointed out, the COVID-19 pandemic has led to the collapse of global economic activity, people have remained highly uncertain, and the economy still faces downward risks such as the COVID-19 persistence, financial turmoil, and further disruption of the global trade and supply chains.

Xi and Jiang [10] stated that many governments have resorted to unconventional economic stimulus measures to mitigate the negative impact of economic uncertainty (Hu and Liu [11]), such as a negative interest rate policy (NIRP). According to the Bank for International Settlements (BIS), major economies have made interest rate cuts mandatory to reduce the corporate debt burden, to ensure the security of the capital chain, and to mitigate the impact of uncertainty on economic and financial operations. Economic uncertainty has resulted in the introduction of extraordinary monetary policies (Ulate [12]). Therefore, central banks in many countries have introduced outstanding monetary policies, including NIRP, and have used monetary and interest rate policy tools to stimulate economic growth.

It is important to emphasize that the analysis we carried out in this research is financial microeconomics, not macroeconomics, which is why we have yet to study sovereign debt or the political impact of the country’s indebtedness and the effects of monetary policy.

Analyzing a firm’s financial performance requires thoroughly evaluating its financial health and knowing its strengths and weaknesses. This, in turn, leads to adequate decision making and adaptability to the ever-changing business environment. According to [5], firms must be willing to pay the market price for whatever goods and services they employ in their economic activities, irrespective of their sector. All these expenses, in turn, must be finance balanced, allowing for present performance and future development. As is well known, there are three primary sources of financial resources, i.e., inner resources generated by a firm during its activities, cash inflows coming from stakeholders, and financial resources obtained using debt, be it short or long term. As a rule, the debt ratios of a firm depend not only on the goods and services it produces or distributes but also on the stage of the business development plan, the type of market within which it operates, and legal and fiscal restrictions, among others.

The interest rate governing such debts is often determined using credit scores from rating agencies such as Moody’s Investor Service (henceforth Moody’s). Often, this score will also define the yield a bond emitted by the company should offer. Nonetheless, credit ratings are usually restricted to public companies with greater purchasing power, which leaves smaller firms with the complicated task of evaluating the real opportunity cost of debt. This is the case for many Mexican firms. The overall proportion of public firms in the Mexican market is relatively small. Further complicating this matter is a debt between peers, which can hardly be graded or rated, and a credit spread could be fixed outside the scope of the market value principle. Consequently, methodologies must show that the cost of debt is directly proportional to the risk of default.

Merton’s model in [13] can be used to directly estimate the risk-neutral default probabilities and the credit spreads to be added to the base interest rate. Also, the Brownian Motion (BM) model and the Power Law Brownian Motion (PLBM) model of [14] allow estimation of the risk-neutral default probability; and thus, the credit spreads using the default frequencies. These models both share features with structural and reduced-form settings. In this work, we use these three models to estimate the cost of debt in different loans. Moreover, we propose a novel, modified Merton’s model to the same end and analyze and compare all four models. Our application focuses on Mexican firms. It is worth noting that there is no secondary corporate debt market in Mexico and no public data on loan recovery rates or credit ratings. To establish this comparison, we follow the definitions in [6] to estimate the rate of loan recovery where needed.

The modification we propose to Merton’s model consists of incorporating the conformable derivatives in the company’s market value into the partial differential equation, effecting a change in variables, and then solving the equation to arrive at the traditional Black–Scholes and Merton solution.

The rest of the paper is organized as follows: Section 2 reviews the existing literature. Section 3 gives a theoretical presentation of all the models used in the analysis and introduces the modified Merton’s model. Section 4 presents the results of our empirical study of Mexican firms. Finally, in Section 5, we offer our conclusions.

2. Literature Review

Ballester et al. [15] systematically reviewed the literature worldwide. They found that most of the indexed and refereed articles referring to the role of corporate governance mechanisms on credit risk have been developed for the United States, followed by some cases for China and developed economies such as Japan, Korea, Canada, Australia, and the United Kingdom, In particular, studies are scarce for non-developed economies (Switzer et al. [16]) and there are practically nonexistent references to Latin America and even less for Colombia specifically, or at least in journals of high international prestige.

The literature on this topic is scarce for emerging markets, which has resulted in a barrier in the analysis of literature reviewed previously, so there are still exciting opportunities for more in-depth study. From the literature review conducted, the case studies described below stand out.

One of the first articles that studied the topic in question is that of Daily and Dalton [17] who analyzed whether there was an impact on the probability of bankruptcy when considering the structure and composition of the Board of Directors above. They compared the results of 57 bankrupt companies and 57 surviving companies. For the surviving companies, they found that the results suggested a relationship between governance structure and the probability of bankruptcy, since 37.5% had dual ownership structures; however, for the bankrupt companies, this value rose to 59.5%. It should be clarified that the authors recognized that these results should be taken with caution and that it was also confirmed that for the companies analyzed that had gone bankrupt, the financial indicators of one year before the event allowed 95% of the cases to be sure that the situation would arise, so that intervention on the ownership structure at that time could do little to change these results.

In addition, Ashbaugh-Skaife et al. [18] investigated whether firms with strong corporate governance obtained higher credit ratings than those with weaker authority. Using a sample of U.S. firms, they identified that credit ratings were negatively associated with the number of shareholders and also with the power of the chief executive officer (management) and positively related to takeover defenses, board independence, and board experience. They found that going from the bottom quartile to the top quartile in the corporate governance variables doubled the probability of a company obtaining an investment grade rating, going from 0.46 to 0.93.

Also noteworthy is the work of Manzaneque et al. [19], who analyzed the impact of some corporate governance mechanisms (ownership and board characteristics) on the probability of business failure for firms listed on the Spanish stock exchange through a study of 308 observations of bankrupt and non-bankrupt firms. They found a negative relationship between board size and the probability of bankruptcy; however, they did not identify significant effects of ownership concentration on the probability of default in the Spanish case.

Similarly, Switzer et al. [16] investigated Canadian entities and found that the corporate governance structure impacted financial and non-financial firms differently.

Focusing only on non-financial companies in Colombia, the authors found that, for non-financial companies, more independent boards of directors were associated with lower credit risk; however, they did not find a significant relationship between ownership structure (institutional shareholders and majority shareholders) and default risk.

For the Latin American case, we highlight the work of Esparza and Soto [20], who considered a sample of family firms in Mexico for the period 2012–2016. By applying a modified Altman Z-Score index, they found that “the size of the board of directors significantly influences a higher probability of incurring insolvency risk, as well as a differentiation by sector”. Ballester et al. [15] systematically reviewed the literature worldwide. They found that most of the indexed and refereed articles referring to the role of corporate governance mechanisms on credit risk have been developed for the United States, followed by some cases for China and developed economies such as Japan, Korea, Canada, Australia, and the United Kingdom, being particularly scarce for non-developed economies (Switzer et al. [15]), and practically nonexistent references to Latin America at least in journals of high international prestige.

According to [21], the development in advanced economies indicates that successful business management can increase a firm’s performance. Also, following [22], corporate performance bears a causal link with the results of a firm, but an exact formula to compare the success of a corporate firm, be it with its past results or those of other firms, does not exist. For this reason, financial ratios, including debt indicators [23], are primary tools for assessing a firm as they help to assess financial health [24]. Debt ratios can determine the extent that external and internal resources are financing a firm and can help to evaluate the risk of default.

The probability of default is determined by several factors, including the size of the firm, its industrial sector, whether it pays dividends, the fiscal policy in the country where it operates, the inflation rate, interest rates, exchange rates, and the overall economic outlook, among others. According to [25], models that employ data to predict the occurrence of a default event have evolved into three distinct types: structural, reduced form, and mixed. The first group, pioneered by Merton [13], base their calculations on a firm’s market value. A structural model uses the Black–Scholes option pricing model to approximate a firm’s market value. It then uses this information to develop a default model and compare how likely it is that a firm will default.

Reduced-form models do not explicitly include the default and firm characteristics relationships. A default is viewed as an accidental, unanticipated event that can result from diverse situations in the financial and economic markets. In this way, an exogenous factor is included to help model default. This exogenous factor is often modeled as a jump process or is driven by some underlying stochastic process [25].

Research on the relation between the probability of default and credit spread includes that of Eberhart [26]. The author studied the models by Merton [13], Leland [27], and Anderson et al. [28] and concluded that Merton’s model strongly and consistently underestimated the credit spread. In contrast, the other two models offered a better fit for accurate data on credit spreads. On the one hand, Ericsson and Reneby [29] also concluded that the risk of default and the liquidity premium were correlated with significant variations in credit spreads. The authors see this relation as causal. On the other hand, more minor variations in credit spread did not seem to be highly correlated with the probability of default. They mostly considered the effect of unknown and unmodeled factors, i.e., statistical noise.

Eom et al. [30] tested and compared five models that are conventionally used to price bonds and corporate firms, namely, those by Merton [1], Geske [31], Longstaff and Schwartz [32], Leland and Toft [33], and Collin-Dufresne and Goldstein [34]. The authors showed that using stochastic interest rates in the models did not significantly affect their valuations’ accuracies. They also argued that all the proposed models were prone to substantial prediction errors, but the errors varied in magnitude and sign among the models. More specifically, when used on safer bonds (low leverage and volatility), all the models underestimated credit spread, and the opposite was true for riskier bonds. It is worth noting that Geske’s model outperformed Merton’s model by including different types of debt. Additionally, Leland and Toft’s model overestimated credit spread, and this phenomenon did not seem solvable by parameter variation. Finally, it was seen that the assumptions on the recovery rates may strongly affect the prediction variance for credit spreads.

Another study by Teixeira [35] showed that Merton’s model overestimated bond prices by approximately 11% and underestimated credit spreads by 76%.

Heynderickx, Carboni, Schoutens and Smits [36] empirically quantified the relationship between default probabilities under the risk-neutral measure $\left(\mathbb{Q}\right)$ and the actual measure $\left(P\right)$ for European corporates. They concluded that, in general, the ratio between $PDs$ under $\mathbb{Q}$ and $P$, which they called the coverage ratio, was larger than one. For average credit quality (Aa-Baa), the coverage ratio was between two and five before the financial and sovereign crises. For highly distress bonds (high actual intensity or $PD$) it converged toward one. The credit risk premium is a decreasing function of credit quality, i.e., the higher the credit quality, the higher the coverage ratio.

Coval, Jurek, and Stafford [37] analyzed a structural model to investigate investment-grade credit risk pricing during financial crises. Their analysis suggested that the dramatic recent widening of credit spreads is highly consistent with the declining equity market, its volatility increase, and an improved investor appreciation of the risks embedded in structured products.

Anderson and Sundaresan [28] studied reduced-form models, and highlighted some limitations. They argued that such models (i) strongly depended on the functional form chosen and (ii) did not consider other firms. Specifically, market risk and how it correlated to any given firm was separate from the model compared to the reduced form and structural models shown in [28]. The authors argued that by treating default as an accidental, unexpected event, reduced-form models lose focus on s firm’s structure, balance sheet, etc. Focused on computing the default and probability rates using observed market credit spreads, these models neither depend upon nor provide economic or financial insight regarding default.

The PLBM model has been seen to better approximate credit spread in an empirical study by Denzler et al. [14]. Model accuracy and quality were evaluated by comparing the results obtained using each model with the observed spread through a measure henceforth denoted by G.

The existing literature is consistent in its conclusions. However, it must be considered that these studies have primarily been based on fully developed and stable economies and financial markets. The problem of evaluating these models in emerging economies is still open. This paper addresses this problem and includes a novel model based on Merton’s model of [13] and conformable calculus.

Although our research aims to carry out an analysis from a non-macroeconomic financial point of view, we analyze the debts of the Mexican companies listed on the stock exchange; we do not analyze the sovereign debt. According to Xin and Jiang [10], due to the economic crisis resulting from COVID-19, scholars have concluded that uncertainty shocks can inhibit output growth, but how uncertainty affects inflation is yet to be completed. Some scholars consider that the impact of uncertainty shocks on the economy is deflation. For example, using a calibrated stochastic general equilibrium (DSGE) model, Leduc and Liu [38] showed that price stickiness led to economic deflations following uncertainty shock with U.S. data. Haque and Magnusson [39] estimated a time-varying parameter VAR using U.S. data and found the response of inflation to be negative in the post-World War II period. Other scholars have argued that the uncertainty shock has no significant effect on inflation.

It is essential to point out that there are no analyses like the one conducted in this research, much less in Latin America. There are macroeconomic analyses of sovereign debt credit ratings, as well as the influence of corporate governance on corporate behavior. But the added value of this analysis is that, from a financial point of view, the credit rating per company is obtained, as well as the probability of default and its consequent credit spread through different models. However, it should be noted that this paper’s objective is not to study the correlation between default probabilities and Mexican or world economic performance. The implication that financial markets lack efficiency is conclusive.

3. Methods

This section describes the theoretical models that estimate credit spread using default probabilities as input. We describe the following models: the Merton’s and Vasicek and Kealhofer’s (VK) model, the Brownian motion (BM) model, the power law Brownian motion (PLBM) model, the corporate default risk model for public firms, and the modified Merton model. Following financial theory, the cost of debt should be directly related, among other factors, to the financial situation of the entity issuing it, the economic landscape of the country in which it operates, and the features of the industry sector to which it belongs. All these factors should, therefore, be reflected by the interest rate at which the debt is bought.

Following Crosbie and Bohn [40], the risk of default is defined as the uncertainty that a firm may not have the means to pay its debt. However, before the facts, there is no exact way to determine if a given firm will or will not default in each period. Estimating default probabilities becomes an important endeavor. It is well known that due to this uncertainty, firms are compelled to offer a risk premium, i.e., an excess return as compared to a risk-free interest rate, and that this risk premium is, broadly speaking, directly proportional to the probability of default.

From an accounting point of view, the risk of default increases as the value of the assets approaches the book value of the debt, since a firm defaults when the value of its assets is less than the total debt. Nonetheless, Crosbie and Bohn [40] found that the actual moment of default strongly depends on the ratio of short-term debt to long-term debt. According to the authors, the probability of default is an increasing function of this ratio. To state this differently, remember that the relevant net value of a firm (net market value) is obtained by subtracting the point of default from the total market value of its assets. Then, a firm is in default when its net market value is equal to zero. Thus, a measure of the risk involved is the volatility of its assets or, more precisely, of the percentual change in its market price.

The former concepts can be combined into a single concept known as the distance to default (DD) that compares the net market value of a firm to its volatility using the formula:

$$DD=\frac{\left[Marketvalueofassets\right]-\left[Pointofdefaullt\right]}{\left[Marketvalueofassets\right]\left[Volatilituofassets\right]}.$$

(1)

The distance to default combines vital elements to estimate the risk of default, i.e., the market value of a firm’s assets and their volatility, and indirectly, industry and firm risks, geographical risks, company size, and other factors that can be correlated to the market value of the assets. Using this measure, the probability of default can be estimated. Such estimation depends upon the probability distribution of the price of the firm’s assets but may also be derived from known empirical relations between default and the DD.

3.1. Merton’s Model, Vasicek, and Kealhofer

Next, we briefly explain the model by Vasicek and Kealhofer in [21], hereafter abbreviated VK, which serves as a preamble to better understand Merton’s model in [13]. The authors of [41] extended the option valuation model initially developed in [13] to compute default probabilities. Similar to Merton’s model, a firm’s equity is considered to be a perpetual option in the VK model. The point of default acts as a barrier to the firm’s value; if the value of equity attains this value, the firm will no longer be able to pay its debts. Under this model, debt and equity are considered to be derivatives, with the firm’s value as the underlying asset.

According to [41], default probability depends on six variables, namely, the current value of a firm’s assets; the probability distribution of said assets at time t; the volatility of the value of the assets, estimated using the VK model at time t; the point of default; the book value of the debt; the expected growth rate for the asset’s worth; and the time horizon. Also, according to [41], default probability represents the possibility that the value of the assets is below the point of default, also known as the expected default frequency and abbreviated as EDF.

The users from Moody’s system can obtain the EDF. The platform predicts the yearly probability of default for the year to come. In Moody’s approach, the best grade for a firm or instrument is Aaa, meaning an almost certain payment or a practically null probability of default. Next are rates Aa, A, Baa, Ba, B, and Caa, each representing a greater risk than its predecessor. To facilitate a finer analysis, each category has been segmented. We, thus, have Aa1, Aa2, Aa2, A1, A2, A3, and so on, until reaching the riskiest Caa.

Having determined the EDF, the next step is to mutate this probability into the credit spread to be added to the risk-free rate, considering the risk particular to a firm. More specifically, diverse methods exist to compute the credit spread, such as the Brownian motion model, the power law Brownian motion model, the modified Merton model (proposed in this paper), and Merton’s model.

According to Merton [13], the valuation of financial options can be applied to corporate instruments, such as actions and debt. In this scenario, the underlying asset corresponds to the value of a firm’s help, and the diffusion process to be used will be the Brownian motion as follows:

$$dV=\left(\mu -q\right)Vdt+{\sigma }_{V}dZ.$$

(2)

where μ represents the expected return on the firm’s investment; q is the rate of dividends, coupons, and interests paid by the firm to stakeholders; ${\sigma }_V$ is the volatility on the value of the assets; and dZ represents integration concerning a traditional Wiener process.

Merton affirms, in [13], that a shareholder has a residual right on the economic flows generated by a firm. If the debt is due on t = 0, they will receive the difference between the free cash flow and the total amount of repayable debt. If a firm with assets of a value of V and a nominal B debt satisfies V > B, the shareholders will obtain a total of E = V − B. On the contrary, if B > V, the shareholder will not receive any cash flow since all of V will be allocated to pay the debt. Finally, the shareholder gets nothing again if V = B and E = 0. As can be inferred, the value of a firm at time T equals the sum of its debt B and its equity capital E. Furthermore, equity can be compared to a call option on the value of the firm’s assets V_T with an exercise price equal to B since:

$$E_T=\max \left(V_T-B,0\right).$$

(3)

It uses the Black–Scholes formula of [42] to evaluate European options. It takes as the volatility the underlying variance of a company’s returns, and the market value of the company must be cleared by forming a system of equations as follows:

$$E_0\left(V,T;B\right)=V_0\varphi \left(d_1\right)-B{e}^{-rT}\varphi \left(d_2\right),$$

(4)

$$d_1=\frac{\mathit{ln}\left(\frac{V_0}{B}\right)+\left(r+\frac{{{\sigma }_V}^2}{2}\right)T}{{\sigma }_V\sqrt{T}},$$

(5)

$$d_2=d_1-{\sigma }_V\sqrt{T}.$$

(6)

where $V_0$ is the total market value of the firm’s assets at time $t_0$ and $V_T$ represents the same value at time T. E is the market value of the share capital, i.e., the share price times the number of ordinary shares in circulation at the initial time; B is the value of the interests and money to be paid at time T; r is the risk-free interest rate, representing the volatility of the firm’s assets (which are assumed homoscedastic). Furthermore, ${\sigma }_E$ is the volatility of the shareholders’ equity, $\varphi$(*) is the standard normal cumulative distribution function, and T is the debt’s due date.

According to this model, the current value of the debt equals the difference between $V_0$and $E_0$, and the risk-neutral default probability can be computed as $\varphi$($-d_2$). Knowing the market value of all the company assets and their volatility is necessary to add this probability. Unfortunately, these values are not directly observable or present in a firm’s financial reports. However, if the firm is public, the market value can be computed by multiplying the number of shares by the market value per share, and its volatility can also be calculated.

In this paper, we estimate the volatility using the GJR-GARCH model of [43], extending the traditional GARCH process by including asymmetries in the volatility. The following equation shows the relationship between a firm’s asset value volatility $\left({\sigma }_V\right)$ and its equity volatility $\left({\sigma }_E\right)$:

$${\sigma }_E{E}_0=\frac{\partial E}{\partial V}{\sigma }_V{V}_0,$$

(7)

$${\sigma }_E=\left(\frac{V_0}{E_0}\right)N{{(d}_1)\sigma }_V.$$

(8)

Solving the nonlinear Equations (4) and (8) simultaneously provides the value $V_0$ and the volatility $\left({\sigma }_V\right)$. The credit spread can be computed with these values, following the procedure in [22], as follows:

$$Creditspread=\frac{1}{T}ln\left[\mathsf{\varphi }\left(d_2+\frac{V_0}{B{e}^{-rT}}\mathsf{\Phi }\left(d_1\right)\right)\right].$$

(9)

3.2. Brownian Motion (BM) and Power Law Brownian Motion Models

3.2.1. An Introduction at Brownian Model

Before explaining the BM and PLBM models, it is essential to detail the calculation of parameters used by both models, such as, among others, the annualized default risk-neutral probability, the recovery rate, and the credit spread.

Under an argument like that used in the valuation of financial options, Denzler et al. [14] calculated the risk-neutral probability of default if one has invested in a coupon base risk-free $F$ and the other risk $\overline{F},$both with a maturity date of $T_j$. In the case of the risk-free bond, the flow to maturity is equal to the expected value of the flows of the risky bond multiplied by the risk-neutral probability of default and the recovery rate as shown below:

$$E\left[F\right]=q_{ji}R\overline{F}+\left(1-q_{ji}\right)\overline{F.}$$

(10)

where $E\left[F\right]$ is the expected value of $F$, a riskless bond at maturity; $q_{ji}$ is the risk-neutral probability of default at time $t_1$ with maturity at $T_j$; and R is the recovery rate.

As expressed by Denzler et al. [14], the essence of pricing under risk neutrality is that both investments offer the same return, such that the expected value under the risk-neutral probability of default of a risky zero-coupon bond with maturity at $T_j$ discounted at a market rate free of credit risk (${\overline{Y}}_{ji}$) is equal to the value of a risky bond discounted at a rate that includes default risk ($Y_{ji}$) (Equation (11)). Substituting Equation (10) into (11) and doing some algebra, we arrive at Expressions (12) and (13):

$$\frac{\overline{F}}{{\left(1+Y_{j,i}\right)}^{T_j}}=\frac{E\left[F\right]}{{\left(1+{\overline{Y}}_{j,i}\right)}^{T_j}}$$

(11)

$${\left(1+Y_{j,i}\right)}^{-T_j}=\left[{R+\left(1-R\right)\left(1-q_{j,i}\right)\left(1+{\overline{Y}}_{j,i}\right)}^{-T_j}\right]$$

(12)

$$q_{ji}=\frac{1}{1-R}\left[1-{\left(\frac{1+Y_{j,i}}{1+{\overline{Y}}_{j,i}}\right)}^{-T_j}\right].$$

(13)

It should be noted that $q_{j,i}$ represents the risk-neutral probability of default during the remaining term to maturity of the debt instrument, which in some cases can be greater or less than one year. Therefore, to perform some analyses, in [2], they suggest annualizing this probability as shown in Equation (14); the credit spread can be obtained with the neutral probability of default as shown in (15):

$${\tilde{q}}_{j,i}=1-{\left(1-q_{j,i}\right)}^{\frac{1}{T_j}},$$

(14)

$$s_{j,i}=Y_{j,i}-{\overline{Y}}_{j,i}\ge 0,$$

$$s_{j,i}=\frac{1+{\overline{Y}}_{j,i}}{{\left[R+\left(1-R\right){\tilde{q}}_{j,i}\right]}^{1/T_j}}-{\overline{Y}}_{j,i}.$$

(15)

where, $s_{j,i}$ represents the base credit spread plus the credit risk-free rate.

The actual risk-neutral probability of default can be derived if the recovery rate (R) is known. Hull [44] defined a bond’s recovery rate as the bond’s market value immediately after default as a percentage of face value. In general terms, a generic value of 40% is assumed for all instruments based on empirical studies by Frye [35], Altman and Kishore [45], Acharya [46], and Hamilton [47]. Despite this, imposing a fixed recovery rate is different from reality since there is evidence that this recovery rate has significant variations concerning the average loan rate [47].

Hull [44], for his part, stated that recovery rates were negatively correlated with default rates. In fact, in [47], they performed an analysis with data on U.S. bonds for the period from 1983 to 2004, and arrived at the following linear relationship:

Average recovery rate 0.52 (–) 6.9 (Average default rate).

(16)

The most appropriate way to calculate the credit spread would be to obtain the real recovery rate for Mexican entities according to the type of loan (senior or junior) or the credit rating; however, since this information was not available, the recovery rate was calculated using the conditional default probabilities.

According to Hull [44], the conditional probabilities of default represent the possibility that an entity will not pay in a period of time ∆t, given that if it paid in t. This probability is called the default intensity at time $t$, where $\overline{\lambda }$ represents the average default intensity between 0 and t. If we denoted the default probability at time $t$ as $Q\left(t\right)$, we obtained the default intensity using Equation (17).

$$Q\left(t\right)=1-e^{-\overline{\lambda }t},$$

(17)

If we denote the EDF as $P\left(t\right)$ and assume that $P\left(t\right)=Q\left(t\right)$, then, on the one hand, we can define $\overline{\lambda }$ as shown in Equation (18). On the other hand, Hull [44] proposed another way to calculate the neutral probability of conditional default per year, given that the entity did not default previously. This approach starts from the premise that the only reason a corporate bond can be sold at a lower price than a risk-free bond with the same characteristics is because of the possibility of default in the payment of the former. Therefore, this probability of default would be calculated as shown in Equation (19):

$$\overline{\lambda }={\overline{\lambda }}_p-\frac{\ln \left(1-P\left(t\right)\right)}{t}=-\frac{\ln \left(1-EDF\right)}{t},$$

(18)

$$\overline{\lambda }=\frac{s}{1-R}$$

(19)

where s is the corporate bond yield spread over the risk-free instrument and R is the expected recovery rate. Now, if we consider the one-year EDF, as well as the definitions of $\overline{\lambda }$ given by Equations (18) and (19), we can arrive at the following approximation of R (20):

$$R=1-\frac{s}{{\overline{\lambda }}_p\left(1+{\overline{Y}}_{j,i}+s\right)}.$$

(20)

The probability of default and the consequent credit spread cannot be readily determined for companies not listed on stock exchanges. Hence, Denzler et al. [14] suggested two models for calculating them, i.e., the Brownian motion (BM) model and the power law Brownian motion (PLBM) model, which will be briefly explained below. These models, as mentioned by the authors, incorporate characteristics of the structural and reduced-form models.

3.2.2. Brownian Motion (BM) Model

The BM model takes as its basis the valuation of debt instruments with the theory of financial options proposed by Black–Scholes [41] and Merton [13], as well as the migration models of credit ratings and credit transition probabilities (Markov chains). Denzler et al. [14] modeled the credit rating, as well as the distance to default ($X_t$) as a general Brownian motion, with an initial level equal to $x_0$, such that $x_0>0$, i.e.:

$$X_t=x_0+{\sigma }_X{W}_{t0}.$$

(21)

where ${\sigma }_X$ is the volatility of the process $X$ and $W_t$ is a Wiener process.

In [2], they also assumed a minimum barrier corresponding to the default level d; once a company reaches this level, it cannot recover. To facilitate the calculation, this level is defined as zero $\left(d=0\right)$, and consequently, the initial level of $x_0$ is transferred. They also believed that the process$X,$ never touched the level d during the entire instrument life. According to the formal development made by Karatzas and Shreve [48], Harrison [49], as well as Janeblanc and Rutkowsky [50], the following propositions are established:

Proposition 1. 

The probability of touching the default barrier during the interval [0,T] starting at $t_0$ is as follows:

$$p\left(t\right)=2\left[1-\varphi \left(\frac{x_0}{{\sigma }_x\sqrt{T}}\right)\right]$$

Inverting the above equation, the initial value of the process  $x_0$ would be equal to:

$$x_0={\sigma }_X\sqrt{T}{\varphi }^{-1}\left(1-\frac{p\left(T\right)}{2}\right).$$

where  $T$ is the maturity date of the debt instrument, $p\left(T\right)$ is the probability or frequency of default (EDF) at maturity T, $\varphi \left(*\right)$ is the cumulative standard normal distribution, and ${\varphi }^{-1}\left(*\right)$ is the inverse cumulative standard normal distribution.

Proposition 2. 

The actual probability of default at $T_j$ is equal to:

$$p(T_j)=2\Phi \left[\sqrt{\frac{T_1}{T_j}}{\Phi }^{-1}\left(\frac{p\left(T_1\right)}{2}\right)\right].$$

where $p\left(T_1\right)$, is the expected default frequency (EDF) with maturity in one year and, is the expected default frequency (EDF) with maturity in $T_j$.

In [2], they assumed that the actual probability would be transformed to the neutral probability default $q_{j,i}$. Since their objective was to derive the neutral default frequency, they obtained that this probability could be calculated as follows.

$$q_{j,i}=2\varphi \left[\sqrt{\frac{T_1}{T_j}}{\varphi }^{-1}\left(\frac{p_i}{2}\right)\right].$$

(22)

where $p_i$ corresponds to the expected annual default frequency (EDF) and $q_{j,i}$is the neutral probability of default until maturity of the instrument at $T_j$. This probability can be annualized by applying Equation (14).

Considering these deficiencies, in [14], they developed another model that considered the possibility of sudden changes in credit quality through a Gaussian diffusion model called the power law Brownian motion (PLBM) model, which is explained in the following section.

3.2.3. Power Law Brownian Motion (PLBM) Model

This model considers the possibility of sudden instrument degradation and credit rating asymmetry. The PLBM model includes additional parameters to the previous equation arriving at (23):

$${\tilde{q}}_{j,i}=2\varphi \left[c_i{\left(\frac{T_1}{T_j}\right)}^{{\alpha }_i}{\varphi }^{-1}\left(\frac{p_i}{2}\right)\right].$$

(23)

where${\alpha }_i$ and $c_i$ $\in R$ are to be estimated and, at each point in time, $0<{\alpha }_i<1$ describes the empirical behavior of firms in the market. It mainly captures all movements (including explosive scaling law movements) of neutral probabilities. Concerned due date, $c_i\in R$ describes the total expected level of default probabilities for the whole market; it can be interpreted as the market premium for credit risk.

In [14], they estimated both parameters at each point in time $t_i$ by running the following linear regression, considering all maturities of the instruments. Such that, $ln\left(T_1/T_j\right)$ is used as the independent variable and $\mathit{ln}\left[\frac{{\Phi }^{-1}\left(\frac{{\tilde{q}}_{j,i}}{2}\right)}{{\Phi }^{-1}\left(\frac{p_i}{2}\right)}\right]$ as dependent variable:

$$\mathit{ln}\left[\frac{{\Phi }^{-1}\left(\frac{{\tilde{q}}_{j,i}}{2}\right)}{{\Phi }^{-1}\left(\frac{p_i}{2}\right)}\right]=\mathit{ln}{c}_i+{\alpha }_i\mathit{ln}\left(\frac{T_1}{T_j}\right)+{\epsilon }_{j.}$$

(24)

where ${\epsilon }_j$ is an independent random variable with $E\left({\epsilon }_j\right)=0$ and $Var\left({\epsilon }_j\right)={\sigma }_{e_j}^2$.

It is important to note that this formula directly calculates the risk-neutral probability of annual default, whereby the credit spread would be obtained by substituting the value of this probability into Equation (24) $s_{j,i}=\frac{1+{\overline{Y}}_{j,i}}{{\left[R+\left(1-R\right){\tilde{q}}_{j,i}\right]}^{1/T_j}}-{\overline{Y}}_{j,i}.$

3.3. The Bloomberg Corporate Default Risk Model (DRSK) for Public Firms

The DRSK is a hybrid model combining a statistical approach with structural models. Bondolini et al. [51] used logistic regression to estimate the probability of default events based on factors that best capture credit risk.

As mentioned in the previous paragraph, the DRSK estimates real-world default probabilities (DP) using a logistic regression of historically realized defaults against the structural model DD and additional risk factors such as profitability and insolvency. Specifically, the real-world default probabilities for a firm $F$ at tenor $t$ can be modeled as:

$$DP=p\left(B\left(F,t\right)\right)=\frac{1}{1+exp\left(-f\left(B\left(F,t\right)\right)\right)},$$

(25)

$$f\left(B\left(F,t\right)\right)={\beta }_0^t+{\beta }_1^{t}DD\left(F,t\right)+\sum _i{\beta }_i^t{\beta }_i.$$

(26)

where $iϵ\left\{ReturnonAssets-Performingloans,DD,Interestcoverage\right\}$.

The model is calibrated by logistic regression of the model’s factors against the default indicator operation set. Using marginal $DPs$ from the logistic regression, one can obtain cumulative $DPs$ for each tenor$ϵ\left\{0.25,0.5,0.75,\mathrm{1,2},3,4,5\right\}$ in the years as follows in [51]. In the same way, annualized $DP\prime$ can be obtained as follows in Equations (27) and (28):

$${DP}_i^{cumulative}=1-\prod _{j=3m}^i\left(1-{DP}_j^{marginal}\right),$$

(27)

$${DP}_i^{annualized}=1-{\left(1-{DP}_i^{cumulative}\right)}^{\frac{1}{t}}.$$

(28)

The cumulative and annualized $DPs$ are used by [4] to evaluate a firm’s default probability per different horizons. They help compare and validate stylized facts between samples within different grades of credit quality.

The DRSK is calibrated to historical financials over a 20 year period containing records for over 65,000 firms. The models achieve high-performance levels in adjusted pseudo-R squared (e.g., between 34% and 47%) [51]. The model $DP$ is predictive of credit events up to a horizon of five years and tracks the realized default rates closely over time. According to Bondoli et al. [51], the model is responsive to market conditions; default probabilities drop during economic expansions and rise during economic contractions.

3.4. Modified Merton Model

3.4.1. Fractional and Conformable Derivatives

Fractional derivatives arise from a concern to generalize the derivate exponent $n$ to a real or complex function.

Khalil, Al Horani, Yousef, and Sababheh [52] presented a new definition of the fractional derivative whose objective was to facilitate the calculations; additionally, they stated that the fractional derivatives for 0 < α < 1, were local by nature. They also stated that given a function $f:\left[0,\mathrm{\infty }\right)\to \mathbb{R}$ and $t>0,$ the conformable fractional derivative of $f$ of order α can be defined as $T_{\alpha }\left(f\right)\left(t\right)={lim}_{\epsilon \to 0}\frac{f\left(t+{\epsilon t}^{1-\alpha }\right)-f\left(t\right)}{\epsilon }$ for all $t>0,\mathrm{a}\mathrm{n}\mathrm{d}$ $\frac{d^{n}y}{{dx}^n}$ of order “n” from an integer to a non-integer, where “n” can be a fraction, an irrational, or a complex.

Khalil et al. [52] presented a new definition of a fractional derivative whose goal was to facilitate calculations. Additionally, they stated that fractional derivatives for $0<\alpha <1$ were local by nature. They also stated that given a function $f:\left[0,\mathrm{\infty }\right)\to \mathbb{R}$ and $t>0,$ the conformable fractional derivative of order $\alpha$ was found to be defined as $T_{\alpha }\left(f\right)\left(t\right)={lim}_{\epsilon \to 0}\frac{f\left(t+{\epsilon t}^{1-\alpha }\right)-f\left(t\right)}{\epsilon }$for all $t>0$ and $\alpha ϵ\left(\mathrm{0,1}\right)$. If f was α-differentiable in some $\left(0,a\right)$, $a>0$, and the ${lim}_{t\to 0^{+}}{f}^{\alpha }\left(t\right)$ there exist, it is defined as $f^{\left(\alpha \right)}\left(0\right)={lim}_{t\to 0^{+}}{f}^{\left(\alpha \right)}\left(t\right)$. Similarly, Anderson, Camrud, and Ulness [53], mentioned that if the conformable fractional derivative, denoted as $f^{\alpha }\left(t\right)$ or $T_{\alpha }\left(f\right)\left(t\right)$, existed, it was said to be α-differentiable, derived from which they presented the following theorem:

Theorem 1. 

If a function $f:[0,\infty )\to \mathbb{R}$ f is α-differentiable in, $t_0>0$ $\alpha \in \left(\mathrm{0,1}\right]$, then $T_{\alpha }\left(f\right)\left(t\right)=t^{1-\alpha }\frac{\partial f}{\partial t}\left(t\right).$

To analyze the equivalence between conformable and fractional derivatives, Anderson et al. [54] applied only a change of variable, such that $u=\frac{x^{\alpha }}{\alpha }$ reached the same result as Khalil et al. [52], as presented in Equations (32) and (33).

In [54], have the following properties, this definition yields the following results (from Theorem 2, 3 of Katugampola [43]):

• $D^{\alpha }\left[af+bg\right]=a{D}^{\alpha }\left[f\right]+b{D}^{\alpha }\left[g\right]$, linearity;
• $D^{\alpha }\left[fg\right]$ = $f{D}^{\alpha }\left[g\right]+g{D}^{\alpha }\left[f\right]$, product rule;
• $D^{\alpha }\left[f\left(g\right)\right]=\frac{df}{dg}{D}^{\alpha }\left[g\right]$, chain rule.

$$D^{\alpha }\left[f\right]=x^{1-\alpha }{f}^{\prime },where{f}^{\prime }=\frac{df}{dx}$$

According to [54], to see the equivalence of the conformable derivate and considering the change of variable $u=\raisebox{1ex}{$x^{\alpha }$}\!\left/ \!\raisebox{-1ex}{$\alpha $}\right.$ the direct substitution and then applying the chain rule in+:

$$D^{\alpha }\left[f\right]=x^{1-\alpha }\frac{df}{dx}$$

(29)

$$x^{1-\alpha }\frac{df}{dx}=x^{1-\alpha }\frac{df\left(u\right)}{du}\frac{du}{dx}=x^{1-\alpha }\frac{df\left(u\right)}{du}{x}^{\alpha -1}=\frac{df\left(u\right)}{du}$$

(30)

The steps followed by Morales-Bañuelos et al. [55] and Anderson et al. [54] to transform a traditional second-order linear differential equation, known by its acronym SOLDE (second order linear differential equation) into a conformable equation, by changing the variable are the following: Equation (30) in [3,29] obtained the expression shown in (34). Finally, they stated the second order linear conformable differential equation as follows:

$$p\left(u\right)\frac{d^{2}y\left(u\right)}{d{u}^2}+q\left(u\right)\frac{dy\left(u\right)}{du}+r\left(u\right)y\left(u\right)=s\left(u\right)$$

(31)

Now, let

$u=\frac{x^{\alpha }}{\alpha }$ and $\frac{du}{dx}=x^{\alpha -1}$, so $du=x^{\alpha -1}dx$, [40,55] calculated the second derivative of $\frac{{\partial }^{2}y\left(u\right)}{\partial u}$ and obtained:

$$\begin{array}{cc}\frac{d^{2}y\left(u\right)}{du}\hfill & =\frac{d}{du}\left(\frac{dy\left(u\right)}{du}\right)=\frac{d}{du}\left(\frac{dy\left(\frac{x^{\alpha }}{\alpha }\right)}{dx}·\frac{dx}{du}\right)=\frac{d^{2}y\left(u\right)}{d{x}^2}{\left(\frac{dx}{du}\right)}^2+\frac{dy\left(\frac{x^{\alpha }}{\alpha }\right)}{dx}\left(\frac{d^{2}x}{d{u}^2}\right)\hfill \\ & =x^{2-2\alpha }\frac{d^{2}y\left(u\right)}{d{x}^2}+\frac{dy\left(u\right)}{dx}·\frac{d^{2}x}{d{u}^2}=x^{2-2\alpha }\frac{d^{2}y\left(u\right)}{d{x}^2}+\left(1-\alpha \right)x^{-\alpha }{x}^{1-\alpha }\frac{dy\left(u\right)}{dx}\hfill \\ & ={\widehat{C}}_{2\alpha }y\left(\frac{x^{\alpha }}{\alpha }\right),\hfill \end{array}$$

(32)

$${\widehat{C}}_{2\alpha }y\left(\frac{x^{\alpha }}{\alpha }\right)=x^{2-2\alpha }\frac{d^{2}y\left(u\right)}{d{x}^2}+\left(1-\alpha \right)x^{1-2\alpha }\frac{dy\left(u\right)}{dx},$$

(33)

Therefore, Equation (34) becomes:

$$p\left(\frac{x^{\alpha }}{\alpha }\right){\widehat{C}}_{2\alpha }y\left(\frac{x^{\alpha }}{\alpha }\right)+q\left(\frac{x^{\alpha }}{\alpha }\right)D_x^{\alpha }y\left(\frac{x^{\alpha }}{\alpha }\right)+r\left(\frac{x^{\alpha }}{\alpha }\right)y\left(\frac{x^{\alpha }}{\alpha }\right)=s\left(\frac{x^{\alpha }}{\alpha }\right).$$

(34)

The interpretation of the conformable derivative is a change of variable $\frac{x^{\alpha }}{\alpha }$, which generates a dependence in the form of the power of the independent variable $x$, where the exponent $\alpha$ is the order of the derivative. This transformation is locally differentiable, and its inverse is also locally differentiable in the independent variable $x$. Its dominion is in the strictly positive real numbers (see [53]).

3.4.2. Proposed Model

As mentioned above, the objective of this work is to solve the Black, Scholes, and Merton (BSM) partial differential equation [13,41] taking as a reference the change of variable proposed by Anderson et al. [54] to obtain an equation with which to calculate the credit spread, incorporating the conformable derivative in the firm value parameter.

Solving the Black, Scholes, and Merton Equation by Conformable Derivatives

Following the proposal of Morales-Bañuelos et al. [55], for the purpose of solving the traditional BSM partial differential equation [13,41], we performed the change of variable in the signature value parameter, such that $u=\frac{V^{\alpha }}{\alpha }$ and $\frac{\partial u}{\partial V}=V^{\alpha -1}\to \partial u=V^{\alpha -1}\partial V$, such that $0<\alpha \le 1$, and the first derivative of the function of $u$ with respect to $u$ is equal to Equation (35).

$$\frac{\partial f\left(u\right)}{\partial u}=\frac{\partial f\left(\frac{V^{\alpha }}{\alpha }\right)}{\partial V}·\frac{\partial V}{\partial u}=V^{1-\alpha }\frac{\partial f\left(u\right)}{\partial V}=D^{\alpha }f\left(V\right).$$

(35)

Subsequently, the second derivative of the function of $u$, concerning $u$, was calculated, again incorporating the change of variable $u=\frac{V^{\alpha }}{\alpha }$, and we arrived at Equation (36). If these derivatives are substituted into the original equation developed by Black, Scholes, and Merton [13,41], the partial differential equation would be represented as shown in (37) and (38). According to [54], Equation (36) is a parabolic partial differential equation for $u=V^{\alpha }/\alpha$, which must be satisfied by any security whose value can be written as a function of the value of the firm and time, like in this case:

$$\begin{array}{cc}\frac{{\partial }^{2}f\left(u\right)}{{\partial u}^2}\hfill & =\frac{\partial }{\partial u}\left(\frac{\partial f\left(u\right)}{\partial u}\right)=\frac{\partial }{\partial u}\left(\frac{\partial f\left(u\right)}{\partial V}·\frac{\partial V}{\partial u}\right)=\frac{{\partial }^{2}f\left(\frac{V^{\alpha }}{\alpha }\right)}{{\partial V}^2}·{\left(\frac{\partial V}{\partial u}\right)}^2+\frac{\partial f\left(\frac{V^{\alpha }}{\alpha }\right)}{\partial V}.\hfill \\ & =\frac{{\partial }^{2}f\left(u\right)}{{\partial u}^2}+\frac{\partial f\left(u\right)}{\partial u}·\frac{{\partial }^{2}V}{\partial u^2}\hfill \\ & =V^{2-2\alpha }\frac{{\partial }^{2}f\left(u\right)}{{\partial S}^2}\hfill \\ & +\left(1-\alpha \right)V^{1-2\alpha }\frac{\partial f\left(u\right)}{\partial V}\hfill \end{array}$$

(36)

$$\frac{\partial f}{\partial t}+rV\left(V^{1-\alpha }\frac{\partial \left(u\right)}{\partial V}\right)+\frac{1}{2}{\sigma }^2{V}^2\left(V^{2-2\alpha }\frac{{\partial }^{2}f\left(u\right)}{{\partial V}^2}+\left(1-\alpha \right)V^{1-2\alpha }\frac{\partial f\left(u\right)}{\partial V}\right)-rf=0$$

(37)

$$\frac{\partial f}{\partial t}+rV\left(\frac{\partial f\left(u\right)}{\partial u}\right)+\frac{1}{2}{\sigma }^2{V}^2\left(\frac{{\partial }^{2}f\left(u\right)}{{\partial u}^2}\right)-rf=0$$

(38)

Similarly, we examined a simple case of corporate debt pricing, i.e., a single class of debt and residual claim equity. We suppose in the same way as [13] that the indenture of the bond issue contains the following provisions and restrictions: (1) The firm promises to pay a total of $F$ (face value antes previously denoted as $B$) to the bondholders on a specific calendar date $T$. (2) In the event this payment is not met, the bondholders immediately take over the company (and the shareholders receive nothing). (3) The firm can not issue any new senior (or of equivalent rank) claims on the firm nor can it pay cash dividends or do share repurchase before the maturity of the debt. We have the constraint presented in Equation (39).

$$F\left(0,T\right)=E\left(0,T\right)=0$$

(39)

Clearly at time T, the firm will pay the bondholders if $V\left(T\right)-F>0$ and the equity value will be the difference; otherwise, the shareholders receive nothing. So, the final condition is $E\left(V,0\right)=Max(0,V-B)$, As mentioned by [1], there is an isomorphic price relationship between levered equity of the firm and call option, and we can solve the equation as Black and Scholes [42] did, but including the parameter and variable changes: $\widehat{V}=\left(\frac{V^{\alpha }}{\alpha }\right)$. The solution to the modified differential equation is shown in Equations (40)–(42) and Equations (43) and (44) show the solution to parameters $d_1$ and $d_2$, with the change of variable:

$$E\left(0,T\right)=\widehat{V}N\left(d_1\right)-\overline{F}{e}^{-rt}N\left(d_2\right)$$

(40)

$$d_1=\left[\frac{\ln \left(\frac{\widehat{V}}{F}\right)+\left(r+\frac{{\sigma }_{\widehat{V}}^2}{2}\left(T-t\right)\right)}{{\sigma }_V\sqrt{\left(T-t\right)}}\right]$$

(41)

$$d_2=d_1-{\sigma }_V\sqrt{T-t}$$

(42)

$$d_1=\left[\frac{\ln \left(\frac{{\widehat{V}}^{\alpha }}{\alpha F}\right)+\left(r+\frac{{\sigma }_{\widehat{V}}^2}{2}\left(T-t\right)\right)}{{\sigma }_V\sqrt{\left(T-t\right)}}\right]$$

(43)

$$d_2=d_1-{\sigma }_V\sqrt{T-t}$$

(44)

3.4.3. Test Parameter

In order to evaluate the fit of these models and to be able to subsequently perform inference, with the one that gives the best results, Denzler et al. [14] defined a parameter denoted as G. Let $n\in N\mathrm{a}\mathrm{n}\mathrm{d}Z=\left(Z_1\dots \dots Z_n\right)\mathrm{is}$a random vector, with realization $z=\left(z_1\dots \dots z_n\right)\in R^n$, we denote the estimator of $z$ as $\widehat{z}=\left({\widehat{z}}_1\dots \dots {\widehat{z}}_n\right)\in R^n$and the parameter evaluating the goodness-of-fit as presented in Equation (45). This parameter approaches one when the true credit spread and those calculated under each model are very similar. Very large deviations result in very small or even negative G values.

$$G:=1-\frac{\sum _{i=1}^n{\left(z_i-{\widehat{z}}_i\right)}^2}{\sum _{i=1}^n{\left(z_i-{\overline{z}}_i\right)}^2}\infty <G\le 1$$

(45)

$$\overline{z}=\frac{1}{n}\sum _{i=1}^n{z}_i$$

(46)

4. Empirical Results

Data Collection

For this study, we obtained financial information, credit ratings from Bloomberg platform [56], KMV Moody’s platform [57] EDFs, and the annual reports issued by Mexican companies listed on the Mexican Stock Exchange during the year 2022. We evaluated the information of the 92 non-financial companies listed during the year under analysis. The requirement to include a company in the sample was that they had debts referenced to prime rates free of credit risk, and on them, a credit spread was added; we eliminated convertible debts, those issued in foreign currency, and leases of any category.

This filter resulted in a total of 64 companies with 304 debt instruments. Most of the liabilities analyzed were bank loans, stock certificates, unsecured loans, mortgage loans, mortgage loans, secured loans, lines of credit, medium- and long-term notes, syndicated loans, and bonds. We only worked with 64 companies because they represented all the Mexican companies listed on the Mexican Stock Exchange that met all the requirements; for this reason, we could not expand the sample.

Another critical factor we considered for selecting loans was that they were made with third parties to establish credit spreads that compled with the market value principle. Groupings by sector were not made because there was only one company in some cases, such as the energy sector. In contrast, in other cases, such as the industrial and manufacturing sectors, there were more than 20 firms.

Table 1. Companies analyzed by sector during 2022. Millions of Mexican Currency.

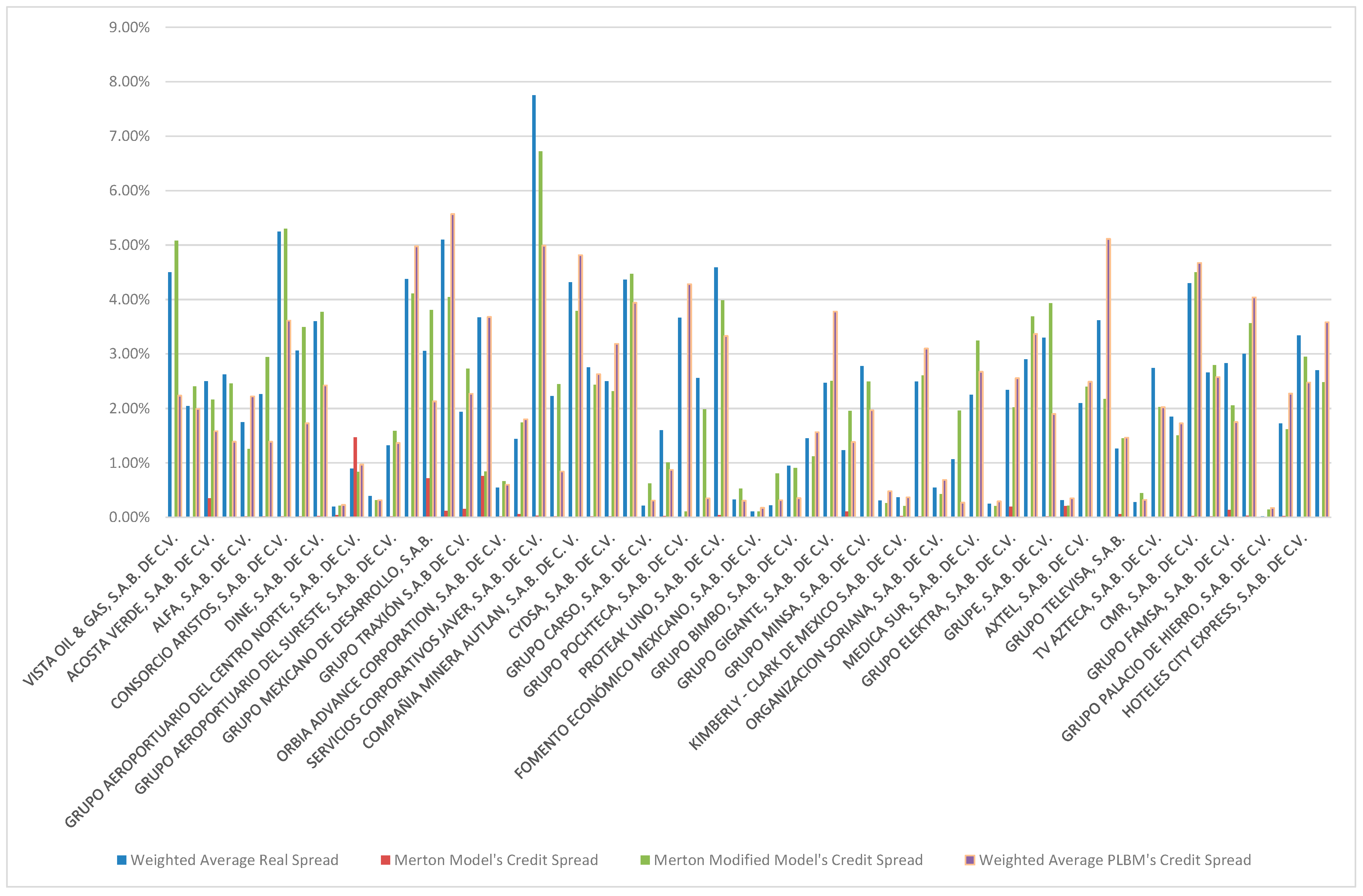
Company	Sector	Total Amount of Debt	Weighted Average Duration	Number of Liabilities	Base Rate		Weighted Average Credit Spread
Vista Oil & Gas, S.A.B. de C.V.	Energy	374	1.56	1	1.29%	plus	4.50%
Accel, S.A.B. de C.V.	Industrial	779	5.66	3	1.29%	plus	2.04%
Acosta Verde, S.A.B. de C.V.	Industrial	3056	7.34	17	4.63%	plus	2.50%
Aleatica, S.A.B. de C.V.	Industrial	6318	5.57	1	1.29%	plus	2.62%
Alfa, S.A.B. de C.V.	Industrial	50	2.36	1	4.63%	plus	1.75%
Consorcio Ara, S.A.B. de C.V.	Industrial	507	5.49	7	4.63%	plus	2.26%
Consorcio Aristos, S.A.B. de C.V.	Industrial	62	4.89	7	4.63%	plus	5.25%
Corpovael S.A.B. de C.V.	Industrial	3092	1.59	22	4.63%	plus	3.06%
Dine, S.A.B. de C.V.	Industrial	210	2.08	1	4.63%	plus	3.60%
Gméxico Transportes, S.A.B. de C.V.	Industrial	64	0.76	3	4.63%	plus	0.20%
Grupo Aeroportuario Del Centro Norte, S.A.B. de C.V.	Industrial	2700	1.91	3	4.63%	plus	0.89%
Grupo Aeroportuario Del Pacifico, S.A.B.de C.V.	Industrial	13,800	2.88	6	4.63%	plus	0.39%
Grupo Aeroportuario Del Sureste, S.A.B. de C.V.	Industrial	5	4.57	2	4.63%	plus	1.32%
Grupo Gicsa, S.A.B. de C.V.	Industrial	4429	4.7	6	4.63%	plus	4.37%
Grupo Mexicano de Desarrollo, S.A.B.	Industrial	65,974	1.46	5	4.63%	plus	3.05%
Grupo TMM, S.A.	Industrial	80	0.53	5	4.63%	plus	5.10%
Grupo Traxión S.A.B de C.V.	Industrial	3781	0.51	8	4.63%	plus	1.94%
Impulsora Del Desarrollo Y El Empleo En America Latina, S.A.B. de C.V.	Industrial	12,794	8.94	7	4.63%	plus	3.67%
Orbia Advance Corporation, S.A.B. de C.V.	Industrial	986	0.5	1	4.63%	plus	0.55%
Promotora Ambiental, S.A.B. de C.V.	Industrial	2255	0.48	4	4.63%	plus	1.44%
Servicios Corporativos Javer, S.A.B. de C.V.	Industrial	2521	2.49	1	4.63%	plus	7.75%
Cemex, S.A.B. de C.V.	Materials	1481	3.76	4	4.63%	plus	2.23%
Compañia Minera Autlan, S.A.B. de C. V.	Materials	3	5.29	4	4.63%	plus	4.32%
Convertidora Industrial, S.A.B. de C.V.	Materials	365	1.7	16	4.63%	plus	2.75%
Cydsa, S.A.B. de C.V.	Materials	2751	10.19	1	4.66%	plus	2.50%
G Collado, S.A.B. de C.V.	Materials	174	0.11	1	4.63%	plus	4.36%
Grupo Carso, S.A.B. de C.V.	Materials	3500	2.25	1	4.63%	plus	0.22%
Grupo Kuo, S.A.B. de C.V.	Materials	711	1.59	2	4.66%	plus	1.60%
Grupo Pochteca, S.A.B. de C.V.	Materials	1975	2.46	2	4.63%	plus	3.67%
Minera Frisco, S.A.B. de C.V.	Materials	7350	2.81	1	4.66%	plus	2.56%
Proteak Uno, S.A.B. de C.V.	Materials	775	1.39	3	1.29%	plus	4.59%
Arca Continental	Products Of Frequent Consumption	12	3.23	9	4.65%	plus	0.32%
Fomento Económico Mexicano, S.A.B. de C.V.	Products Of Frequent Consumption	5662	3.47	3	4.63%	plus	0.11%
Gruma, S.A.B. de C.V.	Products Of Frequent Consumption	1050	0.54	2	4.63%	plus	0.22%
Grupo Bimbo, S.A.B. de C.V.	Products Of Frequent Consumption	35,500	3.04	2	4.63%	plus	0.95%
Grupo Comercial Chedraui, S.A.B. de C.V.	Products Of Frequent Consumption	17,568	3.25	6	4.63%	plus	1.46%
Grupo Gigante, S.A.B. de C.V.	Products Of Frequent Consumption	9	4.86	6	4.63%	plus	2.47%
Grupo Herdez, S.A.B. de C.V.	Products Of Frequent Consumption	3500	0.54	7	4.66%	plus	1.23%
Grupo Minsa, S.A.B. de C.V.	Products Of Frequent Consumption	100	2.15	7	4.63%	plus	2.77%
Industrias Bachoco, S.A.B. de C.V.	Products Of Frequent Consumption	1500	3.44	1	4.63%	plus	0.31%
Kimberly-Clark De Mexico S.A.B. de C.V.	Products Of Frequent Consumption	6000	3.2	2	4.63%	plus	0.37%
Organización Cultiba, S.A.B. de Cv	Products Of Frequent Consumption	752	2.95	6	4.63%	plus	2.49%
Organizacion Soriana, S.A.B. de C.V.	Products Of Frequent Consumption	8538	1.82	4	4.63%	plus	0.55%
Genomma Lab Internacional, S.A.B. de C.V.	Health	97,790	2.01	20	4.63%	plus	1.06%
Medica Sur, S.A.B. de C.V.	Health	1200	1.6	2	4.63%	plus	2.25%
El Puerto de Liverpool, S.A.B. de C.V.	Non-Commodity Goods and Services	1500	0.67	1	4.63%	plus	0.25%
Grupo Elektra, S.A.B. de C.V.	Non-Commodity Goods and Services	13,080	0.75	10	4.63%	plus	2.34%
Grupo Vasconia S.A.B.	Non-Commodity Goods and Services	145	1.3	1	4.63%	plus	2.90%
Grupe, S.A.B. de C.V.	Non-Commodity Goods and Services	1365	7.32	3	4.63%	plus	3.30%
America Movil, S.A.B. de C.V.	Telecommunications Services	34,080	0.51	10	4.93%	plus	0.32%
Axtel, S.A.B. de C.V.	Telecommunications Services	3205	5.5	2	4.63%	plus	2.10%
Grupo Radio Centro, S.A.B. de C.V.	Telecommunications Services	711	5.45	6	4.63%	plus	3.62%
Grupo Televisa, S.A.B.	Telecommunications Services	17,935	0.47	4	4.63%	plus	1.26%
Megacable Holdings, S.A.B. de C.V.	Telecommunications Services	6823	0.58	4	4.63%	plus	0.28%
Tv Azteca, S.A.B. de C.V.	Telecommunications Services	5708	3.22	4	4.63%	plus	2.74%
Alsea, S.A.B. de C.V.	Non-Commodity Goods and Services	565	1.95	2	4.63%	plus	1.85%
CMR S.A.B. de C.V.	Non-Commodity Goods and Services	1141	3.33	1	4.63%	plus	4.30%
Corporacion Interamericana de Entretenimiento, S.A.B. De C.V.	Non-Commodity Goods and Services	850	0.31	4	4.63%	plus	2.66%
Grupo Famsa, S.A.B. De C.V.	Non-Commodity Goods and Services	4529	0.66	7	4.63%	plus	2.83%
Grupo Hotelero Santa Fe, S.A.B. De C.V.	Non-Commodity Goods and Services	343	2.95	2	4.63%	plus	3.00%
Grupo Palacio de Hierro, S.A.B. De C.V.	Non-Commodity Goods and Services	1	0.86	2	4.63%	plus	0.02%
Grupo Sports World, S.A.B. De C.V.	Non-Commodity Goods and Services	2	0.76	2	4.63%	plus	1.72%
Hoteles City Express, S.A.B. De C.V.	Non-Commodity Goods and Services	5101	3.42	18	4.63%	plus	3.34%
Nemak, S.A.B. De C.V.	Non-Commodity Goods and Services	3788	7.1	1	4.63%	plus	2.70%

shows the companies analyzed, grouped by industry according to the categories used by the Mexican Stock Exchange (Bolsa Mexicana de Valores, from now on BMV), the total amount of their debts, the number of liabilities analyzed for each company, the denomination, the weighted average duration, the prime rate, and the weighted average credit spread.

We should note that we used debt duration instead of time to maturity because it represents the average maturity of that instrument’s cash flows or expresses how long it will take to pay the debt cash flows annually, and we used the volatility of equity capital in the Merton and modified Merton models to clear firm value and firm volatility.

According to the data presented in Table 1, the company with the largest liabilities is Medica Sur, S.A.B. de C.V., which belongs to the health sector, although it has only two liabilities. The company with the most extended duration is CYDSA, S.A.P.I. de C.V., with ten years and one month, while the company with the lowest weighted average period is Grupo Collado, S.A.P.I. de C.V., with only 40 days. In addition, 97% of the liabilities have as prime rate the 28-day Interbank Equilibrium Interest Rate (TIIE), 2% the 91-day TIIE, and less than 1% the 3-month London Interbank Offered Rate (LIBOR). The highest credit spread is paid by Servicios Corporativos Javier, at 7.75%. However, according to Bloomberg and Moody’s, it is not the firm with the highest probability of default; in contrast, Grupo Palacio de Hierro, S.A.B. de C.V. pays the smallest spread of 0.029% and is the lowest risk, according to Bloomberg and KMV Moody’s EDFs. The average credit spread paid by Mexican companies listed on the BMV in 2022 is 2.27%, and the average cost of debt is 6.69% per annum.

Table 2. Analysis of the DRSK, Bloomberg’s credit spread, and the EDF of KMV Moody’s.

Company	DRSK 1 Year	DRSK 2 Years	Bloomberg Credit Spread	EDF 1 Year	KMV Moody’s
Vista Oil & Gas, S.A.B. e C.V.	0.22%	0.97%	2.46%	3.02%	B1
Accel, S.A.B. de C.V.	0.00%	0.00%	0.92%	3.02%	B1
Acosta Verde, S.A.B. de C.V.	0.52%	1.40%	2.75%	1.98%	Ba3
Aleatica, S.A.B. de C.V.	0.48%	2.11%	2.82%	1.67%	Ba
Alfa, S.A.B. de C.V.	0.27%	0.99%	2.67%	2.02%	Baa3
Consorcio Ara, S.A.B. de C.V.	0.03%	0.26%	2.24%	1.67%	Ba2
Consorcio Aristos, S.A.B. de C.V.	1.55%	3.38%	3.15%	35.00%	Caa-C
Corpovael S.A.B. de C.V.	1.66%	4.55%	3.27%	7.58%	B3
Dine, S.A.B. de C.V.	0.00%	0.00%	0.71%	3.02%	B1
Gméxico Transportes, S.A.B. de C.V.	0.79%	2.33%	2.76%	3.02%	B1
Grupo Aeroportuario Del Centro Norte, S.A.B. de C.V.	0.00%	0.05%	1.47%	6.71%	B3
Grupo Aeroportuario Del Pacifico, S.A.B. de C.V.	0.01%	0.17%	1.83%	0.37%	Baa1
Grupo Aeroportuario Del Sureste, S.A.B. de C.V.	0.00%	0.04%	1.56%	6.71%	B3
Grupo Gicsa, S.A.B. de C.V.	3.71%	5.93%	3.31%	1.67%	Ba2
Grupo Mexicano de Desarrollo, S.A.B.	0.35%	1.16%	2.55%	3.02%	B2
Grupo TMM, S.A.	0.58%	1.90%	2.56%	6.71%	B3
Grupo Traxión S.A.B De C.V.	0.30%	1.18%	2.38%	3.02%	B1
Impulsora Del Desarrollo y el Empleo en America Latina, S.A.B. de C.V.	0.00%	0.12%	1.66%	4.35%	B2
Orbia Advance Corporation, S.A.B. de C.V.	0.21%	0.87%	2.39%	0.98%	Ba1
Promotora Ambiental, S.A.B. de C.V.	0.00%	0.03%	1.37%	1.67%	Ba2
Servicios Corporativos Javer, S.A.B. de C.V.	0.00%	0.00%	0.39%	35.00%	Caa-C
Cemex, S.A.B. de C.V.	0.53%	1.75%	2.71%	0.93%	Ba1
Compañia Minera Autlan, S.A.B. de C. V.	0.01%	0.10%	1.87%	6.71%	B3
Convertidora Industrial, S.A.B. de C.V.	0.00%	0.00%	0.74%	0.37%	Baa1
Cydsa, S.A.B. de C.V.	0.01%	0.19%	2.17%	3.52%	Ba2
G Collado, S.A.B. de C.V.	0.04%	0.34%	2.33%	6.71%	B3
Grupo Carso, S.A.B. de C.V.	0.03%	0.35%	2.20%	0.37%	Baa1
Grupo Kuo, S.A.B. de C.V.	0.00%	0.01%	1.41%	0.98%	Ba1
Grupo Pochteca, S.A.B. de C.V.	0.01%	0.19%	1.79%	3.02%	B3
Minera Frisco, S.A.B. de C.V.	0.31%	1.13%	2.48%	0.37%	Baa1
Proteak Uno, S.A.B. de C.V.	0.98%	2.79%	2.69%	6.71%	B3
Arca Continental	0.00%	0.03%	1.66%	0.37%	Baa1
Fomento Económico Mexicano, S.A.B. de C.V.	0.00%	0.01%	1.42%	0.37%	Baa1
Gruma, S.A.B. de C.V.	0.03%	0.35%	2.39%	0.37%	Baa1
Grupo Bimbo, S.A.B. de C.V.	0.03%	0.29%	2.34%	0.38%	Baa2
Grupo Comercial Chedraui, S.A.B. de C.V.	0.01%	0.18%	2.18%	6.71%	B3
Grupo Gigante, S.A.B. de C.V.	0.00%	0.05%	1.60%	3.02%	B1
Grupo Herdez, S.A.B. de C.V.	0.14%	0.76%	2.71%	4.35%	B2
Grupo Minsa, S.A.B. de C.V.	0.00%	0.04%	1.57%	1.98%	Ba3
Industrias Bachoco, S.A.B. de C.V.	0.00%	0.01%	1.42%	0.37%	Baa1
Kimberly-Clark de Mexico S.A.B. de C.V.	0.00%	0.00%	1.08%	0.37%	Baa1
Organización Cultiba, S.A.B. de C.V.	0.00%	0.07%	1.62%	0.37%	Baa1
Organizacion Soriana, S.A.B. de C.V.	0.00%	0.08%	1.86%	0.98%	Ba1
Genomma Lab Internacional, S.A.B. de C.V.	0.04%	0.37%	2.23%	3.02%	B1
Medica Sur, S.A.B. de C.V.	0.43%	1.71%	2.78%	4.35%	B2
El Puerto de Liverpool, S.A.B. de C.V.	0.00%	0.00%	1.06%	0.37%	Baa1
Grupo Elektra, S.A.B. de C.V.	0.00%	0.13%	1.50%	3.02%	B1
Grupo Vasconia S.A.B.	2.41%	4.43%	3.21%	3.02%	B1
Grupe, S.A.B. de C.V.	0.00%	0.00%	0.42%	1.98%	Ba3
America Movil, S.A.B. de C.V.	0.01%	0.18%	1.49%	0.48%	Baa2
Axtel, S.A.B. de C.V.	3.73%	6.51%	2.50%	4.35%	B2
Grupo Radio Centro, S.A.B. de C.V.	0.00%	0.00%	0.28%	6.71%	B3
Grupo Televisa, S.A.B.	0.65%	2.29%	1.99%	1.98%	Ba3
Megacable Holdings, S.A.B. de C.V.	0.01%	0.13%	1.32%	0.37%	Baa1
Tv Azteca, S.A.B. de C.V.	4.08%	5.76%	2.50%	35.00%	Caa-C
Alsea, S.A.B. de C.V.	0.20%	0.86%	2.70%	3.02%	B1
CMR, S.A.B. de C.V.	1.80%	3.06%	3.13%	2.02%	Baa3
Corporacion Interamericana de Entretenimiento, S.A.B. de C.V.	0.00%	0.00%	0.91%	3.02%	Baa3
Grupo Famsa, S.A.B. de C.V.	14.30%	16.07%	4.10%	35.00%	Caa-C
Grupo Hotelero Santa Fe, S.A.B. de C.V.	0.04%	0.34%	2.23%	3.02%	B1
Grupo Palacio de Hierro, S.A.B. de C.V.	0.00%	0.00%	0.38%	0.37%	Baa1
Grupo Sports World, S.A.B. de C.V.	7.53%	10.55%	3.57%	3.20%	B1
Hoteles City Express, S.A.B. de C.V.	0.58%	2.12%	2.89%	6.71%	B3
Nemak, S.A.B. de C.V.	0.30%	1.00%	2.68%	3.20%	B1
Max Bloomberg y Moody’s (Famsa)	14.30%	16.07%	4.10%	35.00%
Min Bloomberg y Moody’s (Palacio de Hierro)	0.00%	0.00%	0.28%	0.37%
Average	0.77%	1.43%	2.05%	4.78%
Correlation Between DRSK 1 year vs. EDF I Year	51%
Correlation Between EDF1 year and Debt Cost calculated by Bloomberg	55%
Correlation Between DRSK 1 year and Debt Cost calculated by Bloomberg	20%

shows no one hundred percent proportional relationship between the default probabilities calculated by Bloomberg with the credit spreads determined through that platform and the one-year EDF determined with the KMV Moody’s platform. The correlation between the two probabilities of default is only 51%. More striking is the lack of consistency between the likelihood of default and the cost of credit spread determined by Bloomberg, as the correlation coefficient between the two series is only 20%. For example, as observed in the table above, Servicios Corporativos Javier, S.A.P. I. de C.V. has a default risk of 0.00% according to Bloomberg; however, KMV Moody’s issues the highest risk rating, which is consistent with the credit spread. However, it should be noted that there still needs to be a perfect correlation between credit rating and the cost of debt.

It is important to note that for the Merton and modified Merton models, loans and duration were grouped by multiplying the proportion of each debt’s duration concerning the total per company, obtaining a weighted debt and a weighted duration. It should also be noted that the risk-free prime rate for the modified Merton model was estimated over time with the Nelson and Siegel model [53]. With the GJR-GARCH model, the stock price returns were calculated, and the value of the stockholders’ equity was obtained by multiplying the stock price by the number of shares outstanding at the study date. These calculations were performed because the EDF is used per firm, not per loan. The firm value and firm volatility were calculated with the Excel Solver routine. The credit spreads per firm were obtained by applying Equation (15).

In contrast, in the BM and PLBM models, credit spreads were obtained for debt, so to compare the results shown in Figure 1, it was necessary to multiply each spread by the proportion that each duration represented for each of the firms. We calculated the recovery with Equations (21)–(23) for these models.

Subsequently, the results were analyzed by model, and the test parameter values were denoted as G. In the first instance, the comparison of the credit spread calculated by Bloomberg vs. the actual spread for each loan is shown; with this, the G were estimated (Equations (47) and (48)). The best fit is obtained when the value of G is close to 1; for Bloomberg, the parameter’s value was −0.174, implying that the fundamental importance of the spreads and the estimated ones are very far from each other, regardless of the actual dispersion between them.

The results are shown in

Table 3. Results of the models applying the value of the fit parameter G.

		Merton	BM	PLBM	Modified
	Bloomberg				Merton
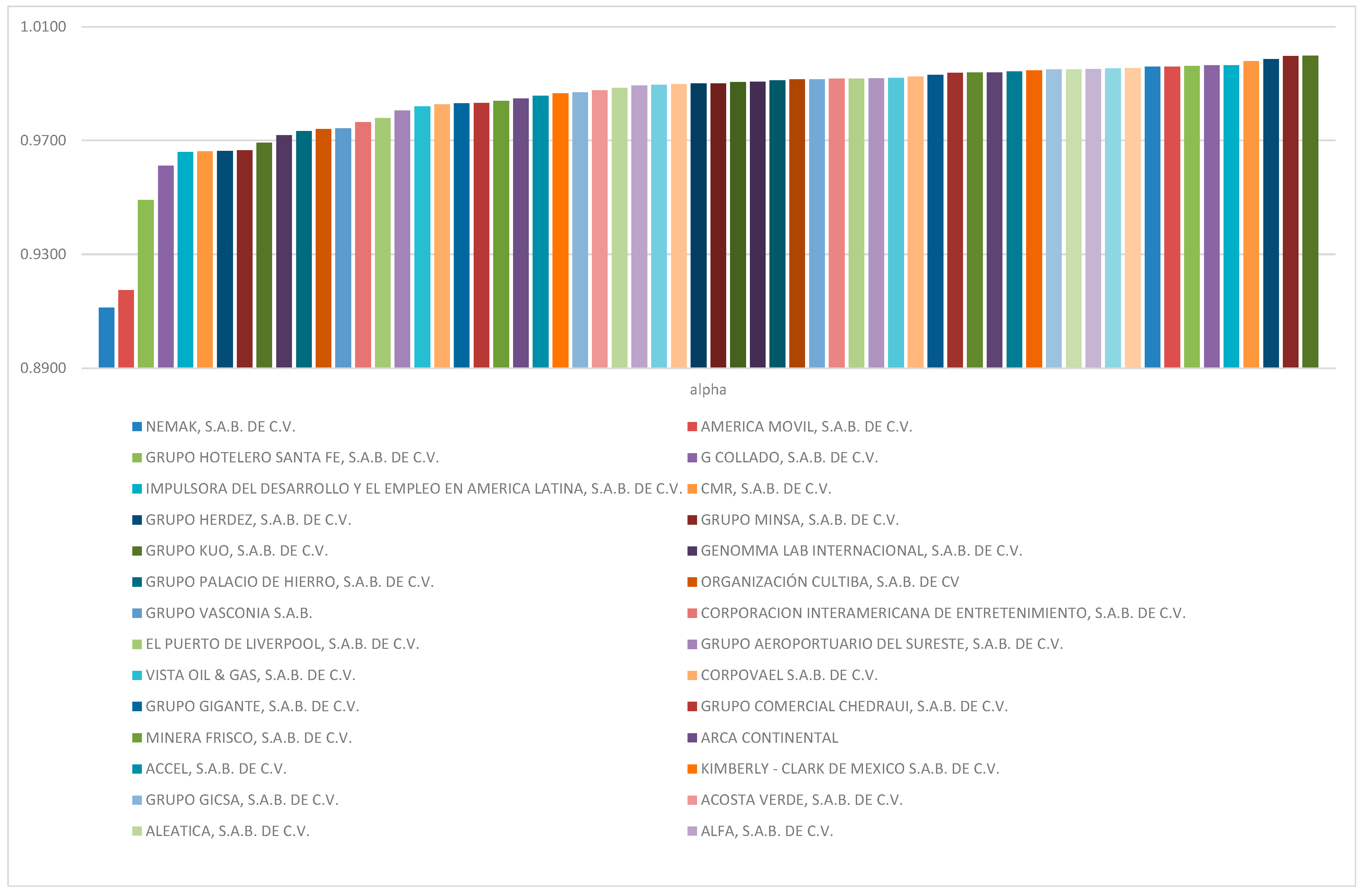
G Value	−0.17	−2.16	−13.105	0.50	0.77

; as can be seen, the modified Merton model is the one that provides the best fit between the actual and estimated credit spreads, with a statistic of 0.767, followed by the PLBM model with 0.504. In contrast, the BM model is the one that has the highest dispersion between the estimated and actual spreads with a G value of −13.105.

As can be seen in Table 3, the traditional Merton’s model, in all cases, underestimates the actual credit spread, as mentioned by Teixeira [35]. In contrast, the results obtained with the BM and PLBM models agree with those shown by Denzler et al. [14]; the BM model strongly overestimates the credit spreads and at other times, underestimates them to a lesser degree, the PLBM model makes a reasonable adjustment; however, the results of the model proposed in this paper make a better estimate. The estimates made by Bloomberg follow a pattern like that of the BM model; in some companies, it overestimates, and in other cases, it underestimates credit spreads.

Figure 1 compares the real credit spreads with those of Merton’s. model, the modified Merton model, and the weighted average PLBM model; in all cases, Merton’s model underestimates the actual spread, agreeing with the results of Teixeira [35]; in contrast, the modified Merton model is the best possible approximation. The PLBM model provides an excellent approximation to the actual spread; however, in most cases, it overestimates slightly, which is consistent with Morales-Bañuelos et al. [55].

A good statistic has good prediction accuracy, in other words, it has a minor prediction error.

We calculated three fit statistics to validate which model provides the best fit. If $\widehat{Y}$ is a vector of n predictions and Y is the vector of valid values, then the (estimated) MSE of the predictor is:

$$MSE=\frac{1}{n}\sum _{i=1}^n{\left(\widehat{Y}-Y\right)}^2.$$

(47)

• In an analogy to the standard deviation, taking the square root of the MSE yields the root mean square error or root mean square deviation (RMSE or RMSD, respectively), which has the same units as the square of the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard deviation.

$$\sqrt{MSE=\frac{1}{n}\sum _{i=1}^n{\left(\widehat{Y}-Y\right)}^2.}$$

(48)

• In statistics, the mean absolute error (MAE) is a measure of errors between paired observations expressing the same phenomenon. For example, Y versus X include comparisons of predicted versus observed. The MAE is calculated as the sum of absolute errors ($e_i)$ divided by the sample size:

$$MAE=\frac{1}{n}\sum _{i=1}^n\left|y_i-x_i\right|=\frac{1}{n}\sum _{i=1}^n⌈e_i⌉$$

(49)

Figure 2 compares the three statistics of predictive accuracy in the sample of real company spreads, with the spreads calculated using Merton’s model, the weighted average Brownian model, the weighted average power law Brownian motion model, and the modified Merton model.

Table 4. Market value of companies. Million Mexican Currency.

	Market Value of Equity Multiplied by the Proportion of Debts Referenced to a Base Rate	Merton’s Modified Model Value of Firm	Traditional Merton’s Model Value of Firm
Vista Oil & Gas, S.A.B. de C.V.	3204	4094	4108
Accel, S.A.B. de C.V.	71	1515	1511
Acosta Verde, S.A.B. de C.V.	4174	5360	5391
Aleatica, S.A.B. de C.V.	4413	19,198	18,777
Alfa, S.A.B. de C.V.	17	83	76
Consorcio Ara, S.A.B. de C.V.	377	1216	1464
Consorcio Aristos, S.A.B. de C.V.	336	648	565
Corpovael S.A.B. de C.V.	5622	10,211	10,025
Dine, S.A.B. de C.V.	367	681	685
Gméxico Transportes, S.A.B. de C.V.	10	87	86
Grupo Aeroportuario Del Centro Norte, S.A.B. de C.V.	1084	4714	4680
Grupo Aeroportuario Del Pacifico, S.A.B. de C.V.	52,297	91,120	90,885
Grupo Aeroportuario Del Sureste, S.A.B. de C.V.	27	51	51
Grupo Gicsa, S.A.B. de C.V.	2308	14,837	14,591
Grupo Mexicano de Desarrollo, S.A.B.	660	85,512	79,305
Grupo TMM, S.A.	12	149	119
Grupo Traxión S.A.B de C.V.	6750	16,585	12,409
Impulsora Del Desarrollo y e Empleo en America Latina, S.A.B. De C.V.	74,219	210,948	202,277
Orbia Advance Corporation, S.A.B. de C.V.	13,675	15,381	15,392
Promotora Ambiental, S.A.B. de C.V.	1012	3884	3664
Servicios Corporativos Javer, S.A.B. de C.V.	1664	5510	5572
Cemex, S.A.B. de C.V.	9573	17,441	17,413
Compañia Minera Autlan, S.A.B. de C. V.	194	16,021	333
Convertidora Industrial, S.A.B. de C.V.	90	511	512
Cydsa, S.A.B. de C.V.	1262	12,891	12,522
G Collado, S.A.B. de C.V.	994	1179	1179
Grupo Carso, S.A.B. de C.V.	7265	16,021	16,021
Grupo Kuo, S.A.B. de C.V.	211	1364	1218
Grupo Pochteca, S.A.B. de C.V.	145	19,002	2778
Minera Frisco, S.A.B. de C.V.	5218	17,726	17,425
Proteak Uno, S.A.B. de C.V.	1630	3081	2977
Arca Continental	26	54	53
Fomento Económico Mexicano, S.A.B. de C.V.	4845	14,962	14,695
Gruma, S.A.B. de C.V.	36,744	39,699	39,707
Grupo Bimbo, S.A.B. de C.V.	41,978	106,305	102,355
Grupo Comercial Chedraui, S.A.B. de C.V.	6614	34,077	34,134
Grupo Gigante, S.A.B. de C.V.	10	30	31
Grupo Herdez, S.A.B. de C.V.	5977	12,087	10,723
Grupo Minsa, S.A.B. de C.V.	173	329	322
Industrias Bachoco, S.A.B. de C.V.	3695	7326	7349
Kimberly-Clark De Mexico S.A.B. de C.V.	13,287	36,864	28,911
Organización Cultiba, S.A.B. de C.V.	389	1576	1563
Organizacion Soriana, S.A.B. de C.V.	1554	12,284	11,843
Genomma Lab Internacional, S.A.B. de C.V.	11,526	21,166	20,834
Medica Sur, S.A.B. de C.V.	3135	4943	4874
El Puerto De Liverpool, S.A.B. de C.V.	1751	3497	3498
Grupo Elektra, S.A.B. de C.V.	14,130	28,042	28,060
Grupo Vasconia S.A.B.	120	307	304
Grupe, S.A.B. de C.V.	875	4192	3827
Axtel, S.A.B. de C.V.	2605	12,247	12,107
Grupo Radio Centro, S.A.B. de C.V.	303	2224	1982
Grupo Televisa, S.A.B.	9937	29,043	30,865
Megacable Holdings, S.A.B. de C.V.	43,799	53,770	53,756
Tv Azteca, S.A.B. de C.V.	2	7854	7865
Alsea, S.A.B. de C.V.	236	909	966
CMR S.A.B. de C.V.	343	1899	1784
Corporacion Interamericana de Entretenimiento, S.A.B. de C.V.	730	1629	1629
Grupo Famsa, S.A.B. de C.V.	137	9160	6937
Grupo Hotelero Santa Fe, S.A.B. de C.V.	210	1117	919
Grupo Palacio de Hierro, S.A.B. de C.V.	1	3	3
Grupo Sports World, S.A.B. de C.V.	10	14	13
Hoteles City Express, S.A.B. de C.V.	1383	10,006	9696
Nemak, S.A.B. de C.V.	1068	7028	8061

shows the company’s values that we obtained with Merton’s model and the modified Merton model; in 70% of the cases, the former underestimated the market amount of the company and overestimated the volatility of the company. Figure 3 shows the α values of the conformable derivative, which were above 0.94 up to 0.98, and which were obtained using the Excel Solver routine, which agrees with the results of Morales-Bañuelos et al. [3].

5. Conclusions

It is very important to point out that there are no analyses like the one conducted in this research, much less in Latin America. There are macroeconomic analyses of sovereign debt credit ratings, as well as the influence of corporate governance on corporate behavior. But the value added by this analysis is from the financial point of view, i.e., the credit rating per company is obtained, as well as the probabilities of default and its consequent credit spread through different models. However, it should be noted that it is not the objective of this paper to study the correlation between default probabilities and Mexican or world economic performance. The implication is conclusive about the lack of efficiency of financial markets.

Another point that is important to highlight for the Mexican case, and which we highlighted after analyzing companies listed on the BMV, is that there is no directly proportional relationship between the actual credit spread assigned to the instruments with the credit rating obtained through the KMV Moody’s platform, which may be due to the lack of pulverization, liquidity, and efficiency of the Mexican capital market.

In fact, according to Salas-Porras [58], in Mexico, “there is still a high concentration of capital in a few families, who even today fear losing control of capital. Despite participating in the stock market, the capital of the largest economic groups belongs to one family in proportions of no less than 60–70%, in most cases”.

Likewise, ref. [58] comments that great financial needs force companies to be listed on the stock markets and to circulate shares. This process is further accelerated by interacting with increasingly complex governmental and international agencies with privileged information networks. These corporate structures participate in the decision-making process, with national and international competition, globalization, and international agreements of different types. In the case of Mexico, this securitization process lags and needs to catch up with that observed in industrialized countries.

Regarding the conclusions of the empirical analysis, according to the information on the Mexican market, we concluded that the modified Merton model, which we developed in this research, was the model that best approximates the actual credit spread. At the same time, according to the analysis performed, the Brownian motion model is the model that presented the worst fit and, additionally, turned out to be the least adequate. Similarly, based on the results, we observed that the BM model’s test parameter (G) value frequently depended on the average loan recovery rate (R).

Our empirical analysis suggests that the modified Merton model provides a better fit to real credit spreads; according to Figure 2, the results of the power law Brownian motion model are close. It should be noted that under all statistical and non-statistical tests, the modified Merton model resulted in the best approximations. Also, it is essential to note that the scale of the mean square error statistic results is tiny in contrast to the root mean square error and the mean absolute error; however, all three statistics show the superiority of the modified Merton model.

According to the results of parameter G and the MSE, RMSE, and MAE statistics, according to Figure 2, the model that provides the worst fit is the Brownian motion model, followed by Merton’s model, and those that provide a very close fit to the real value of the credit spread are the PLBM model and the best model proposed in this research is the modified Merton model.

This paper aims to find a model that Mexican entities can easily apply, because most of them are small- and medium-sized companies that are not listed on stock exchanges, through which they can establish an interest rate on their loans according to their level of default risk. In particular, the results of this research are aimed at organizations that do not have access to a credit rating. For this purpose, five models that could solve this problem were evaluated.

We also conclude that R is not a constant; on the contrary, it is a stochastic variable that depends on the instrument’s characteristics and the probability of default. Future research can analyze a stochastic recovery rate and see how the results change. Another line for future research, since there are no studies in Latin America, would be to analyze sovereign credit ratings and their effects on financial macroeconomic variables, as was done by Athari, et al. For example, it is suggested to compare Mexico with Argentina, Chile, Uruguay, and Brazil, since they are the most similar countries. The aim would be to analyze sovereign credit ratings and their effects on financial macroeconomic variables, as Athari et al. did [59]. According to Athari et al. [59], credit ratings are not only important for investors, but they are also crucial for each country’s rating for political decision makers. It is important to investigate the repercussions in emerging Latin American countries of how changes in country-level credit ratings affect future macroeconomic actions. In fact, when credit ratings are downgraded, it can cause an increase in the yield to maturity of sovereign debt; an imbalance in global portfolios, which varies the flow of capital between countries; as well as increases in volatility that destabilize the financial markets of different countries.