Optimal Control Theory and Calculus of Variations in Mathematical Models of Chemotherapy of Malignant Tumors
Abstract
1. Introduction
2. Materials and Methods
2.1. Dynamics of the Model
- The Gompertz law:where the parameter characterizes the speed of the tumor’s growth, and characterizes the speed of tumor suppression.
- The generalized logistic law:where the parameter again characterizes the speed of the tumor’s growth, characterizes the threshold tumor volume and changes the steepness of the model’s curve.
2.2. The Therapy Function
- A1.
- .
- A2.
- .
- A3.
- .
- A4.
- .
2.3. Optimal Control Problem
- For the Gompertz law (3):
2.4. Value Function and Optimal Synthesis
2.5. The Viability Set
3. Results
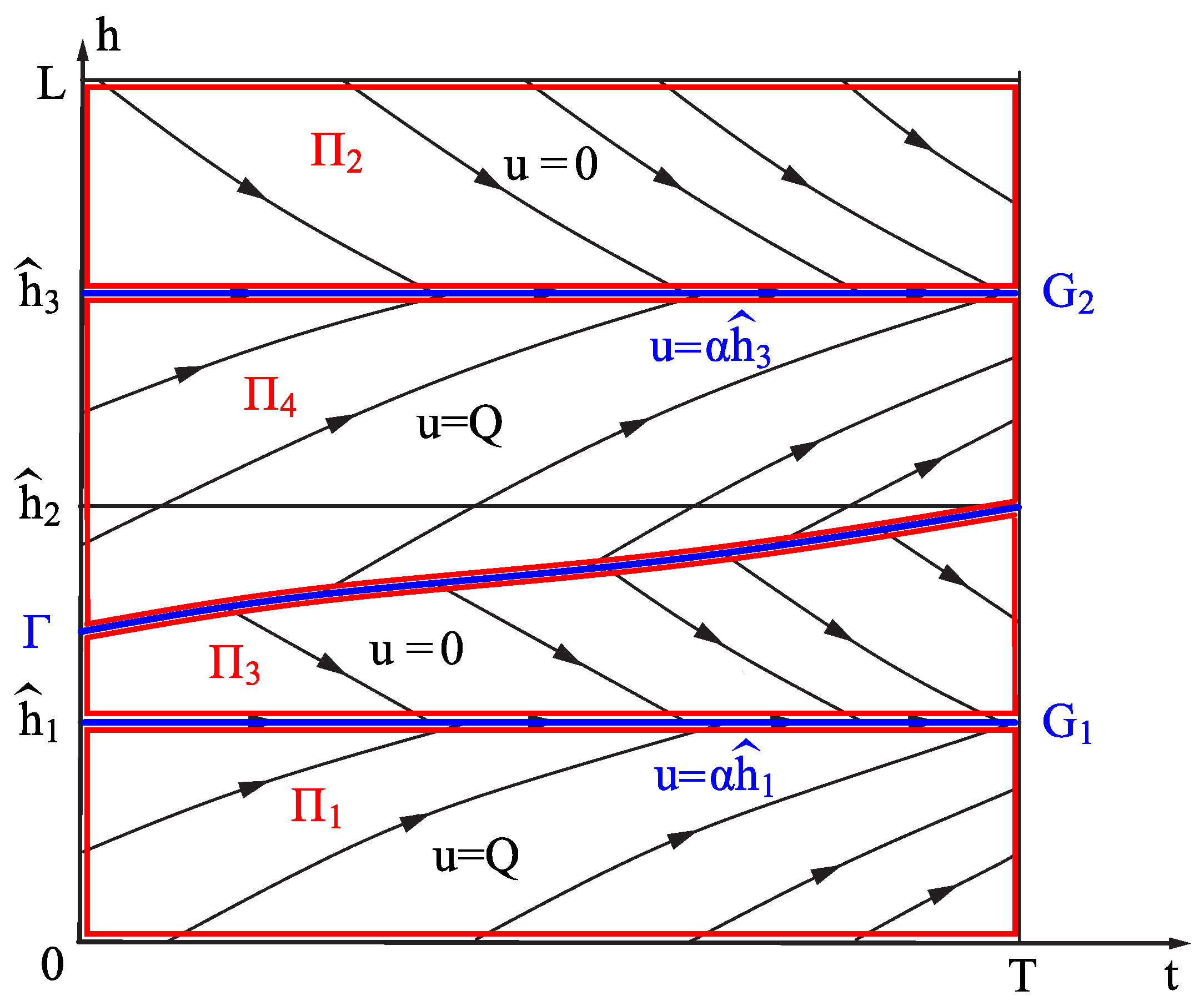
3.1. Construction of Set
- (1)
- Consider the following points:
- (2)
- Consider the following points:
- (3)
- Consider the following points:
- (4)
- Consider the following points:
- (5)
- Consider the following points:
- (6)
- Consider the following points:
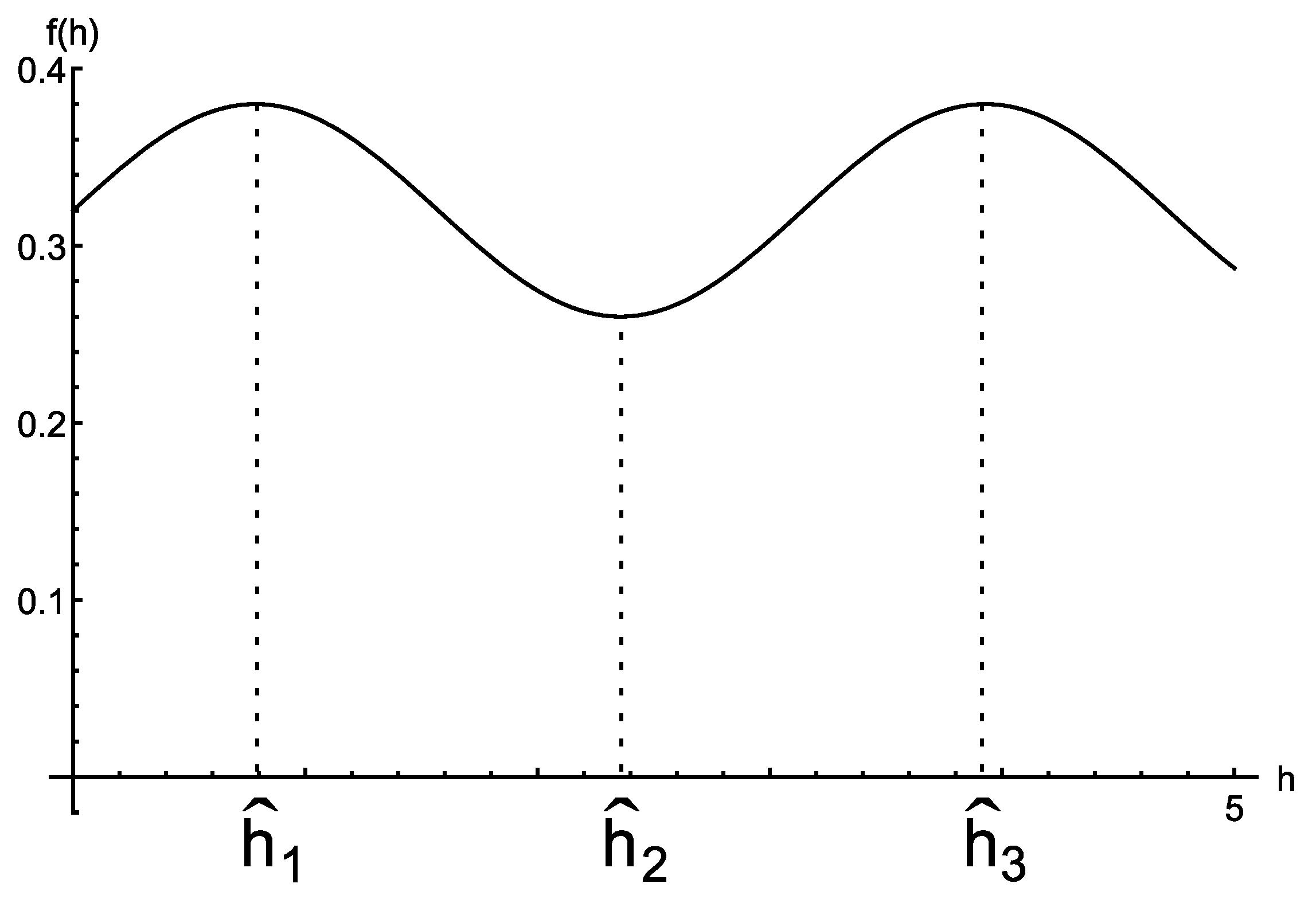
3.2. The Maximal Viability Set
- 1.
- .
- 2.
- Set (19) is weakly invariant with respect to the differential inclusion: , where
- 3.
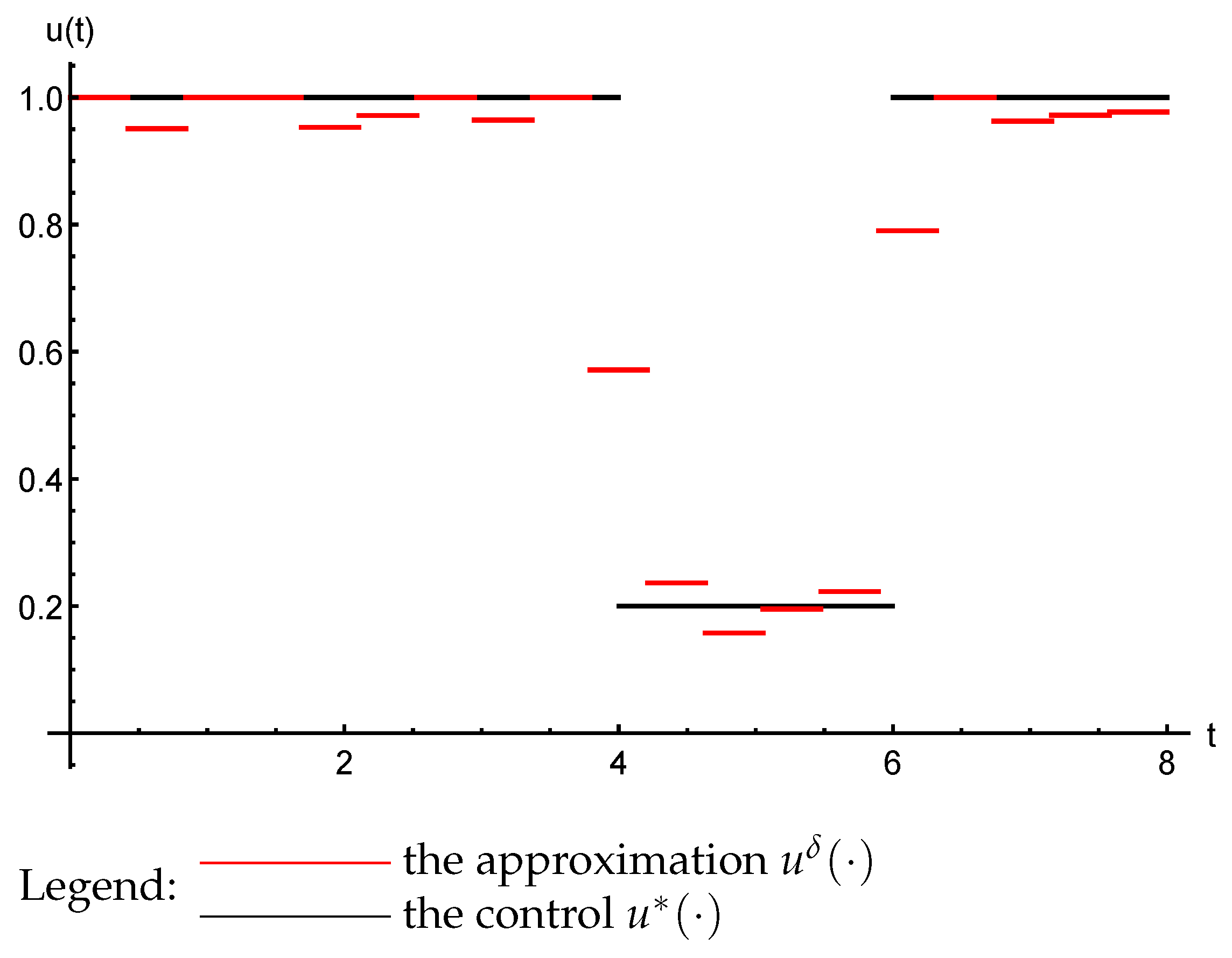
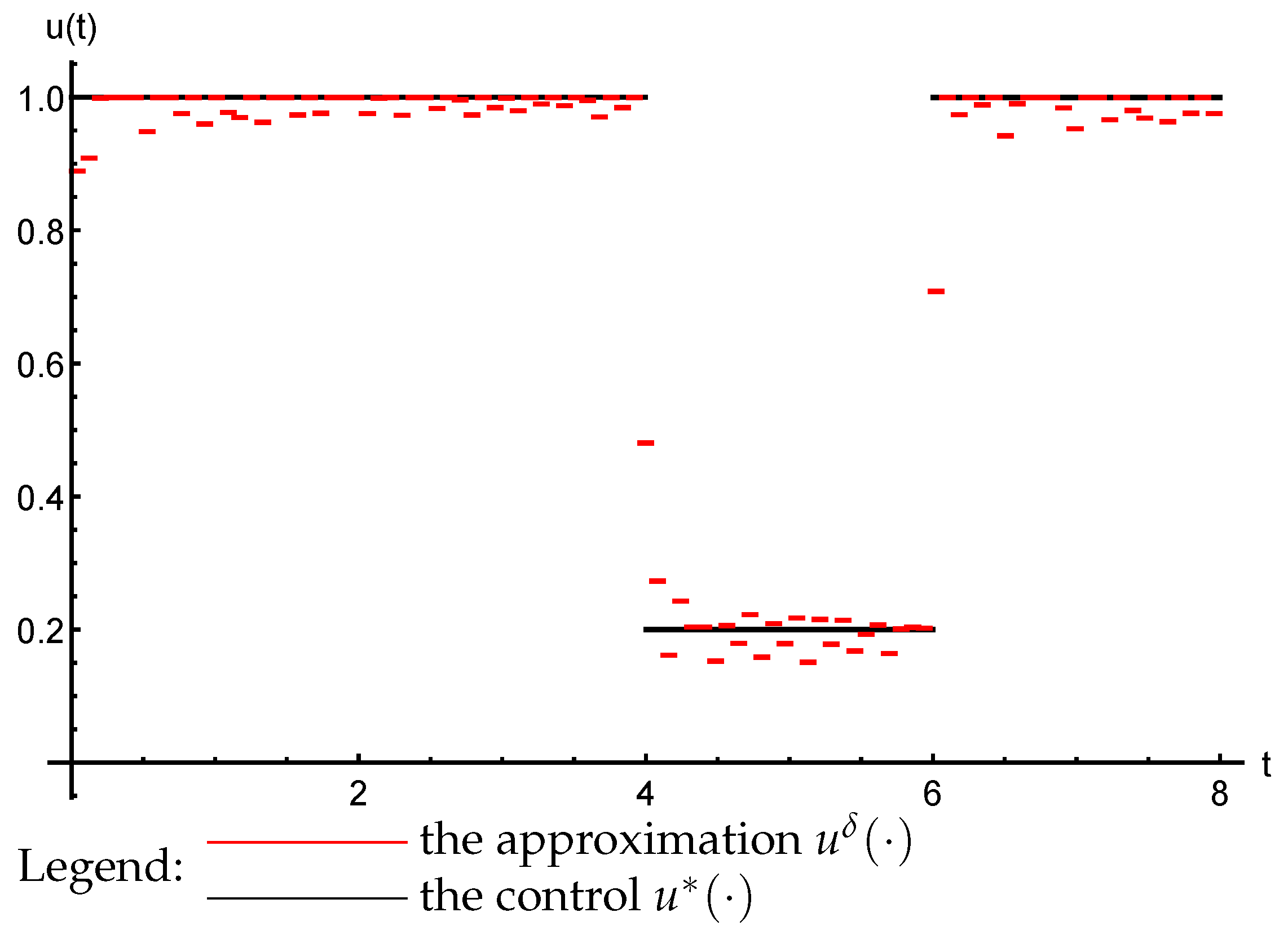
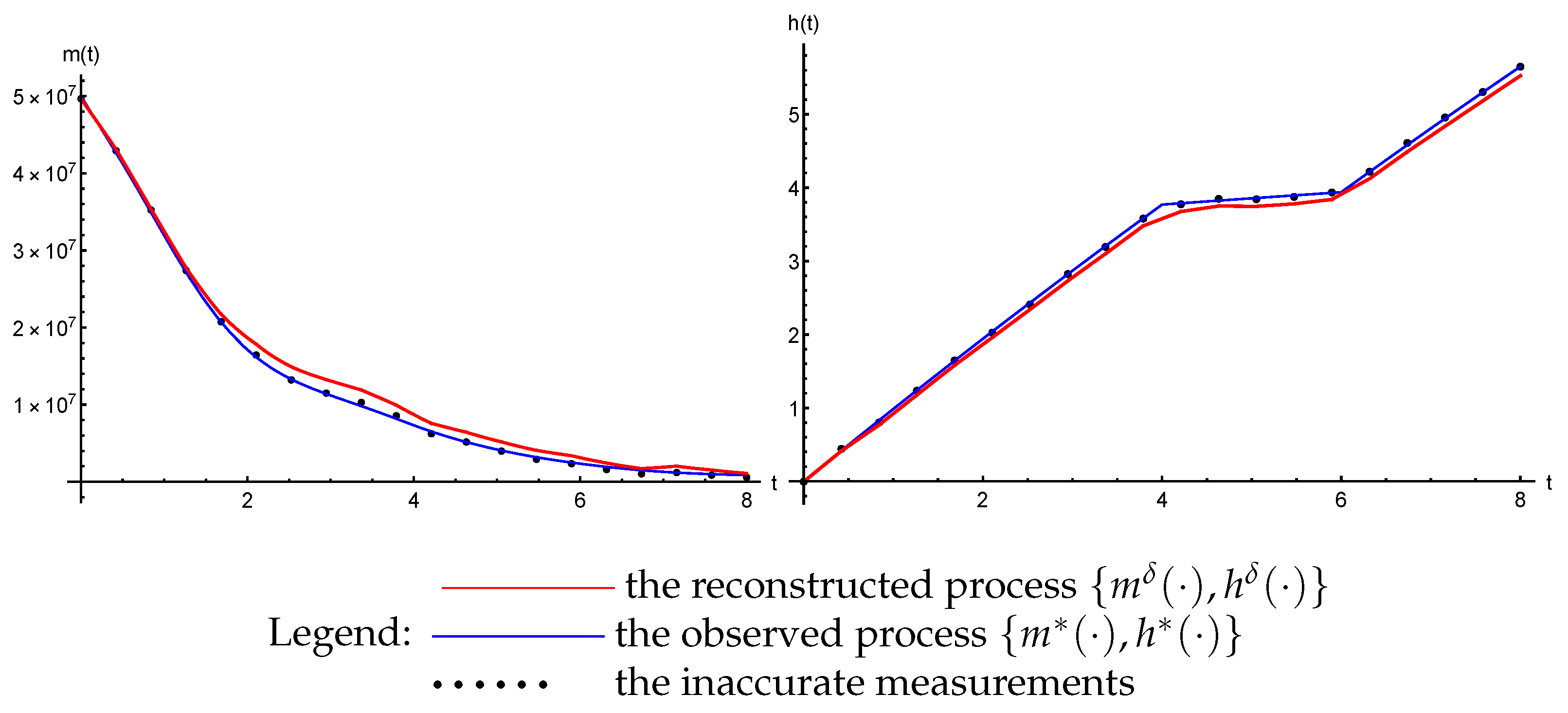
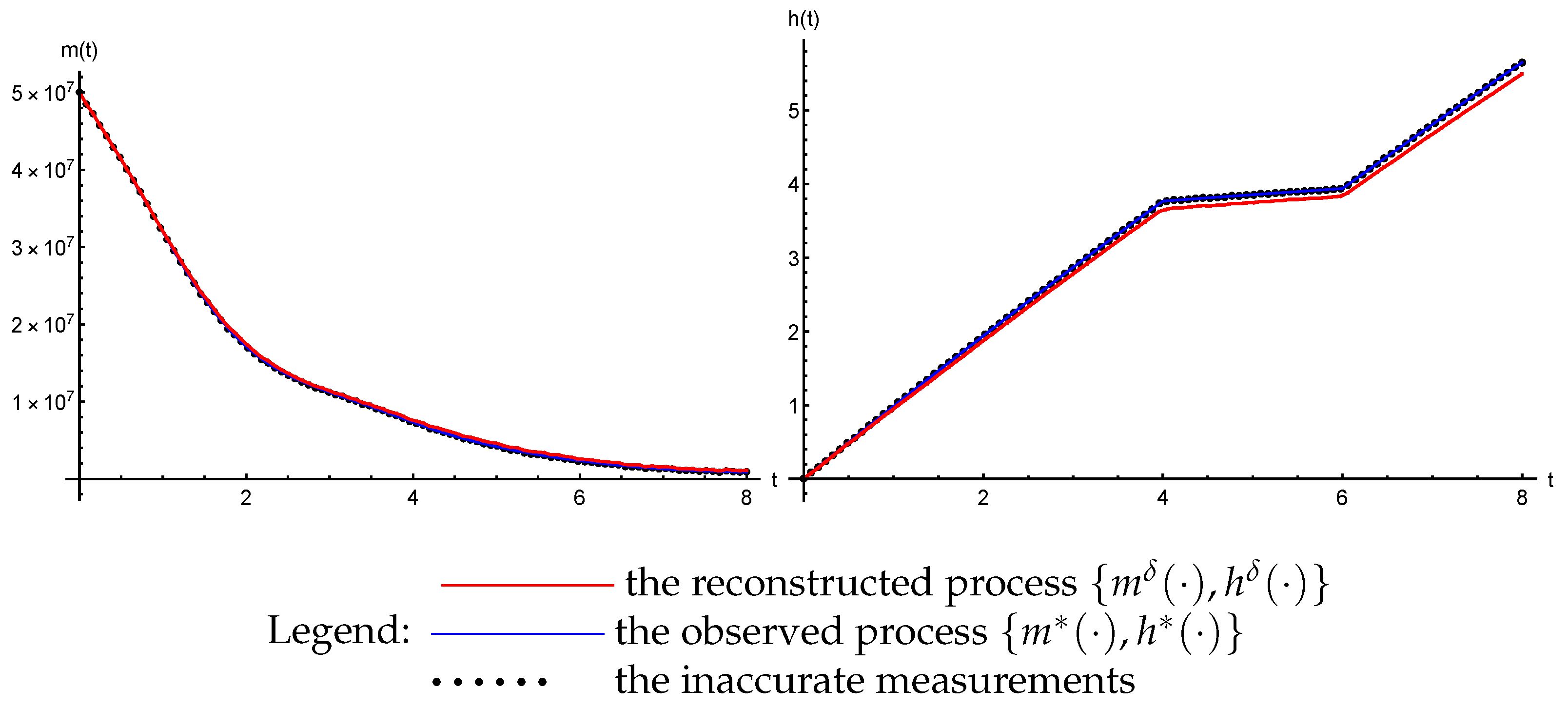
3.3. The Inverse Problem
- ;
- almost everywhere on ;
- ;
- The trajectories () of the system (47) that are generated by the reconstructed parameters ( and ) converge uniformly to the observed process:
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Araujo, R.P.; McElwain, D.L. A history of the study of solid tumour growth: The contribution of mathematical modelling. Bull. Math. Biol. 2004, 66, 1039–1091. [Google Scholar] [CrossRef] [PubMed]
- Marusić, M.; Bajzer, Z.; Freyer, J.P.; Vuk-Pavlović, S. Analysis of growth of multicellular tumour spheroids by mathematical models. Cell Prolif. 1994, 7, 73–94. [Google Scholar] [CrossRef] [PubMed]
- Bratus, A.S.; Chumerina, E.S. Optimal Control Synthesis in Therapy of Solid Tumor Growth. Comp. Math. Math. Phys. 2008, 48, 892–911. [Google Scholar] [CrossRef]
- Kendal, W.S. Gompertzian growth and as a consequence of tumor heterogeneity. Math. Biosci. 1985, 73, 103–107. [Google Scholar] [CrossRef]
- Khailov, E.N.; Grigorenko, N.L.; Grigorieva, E.V.; Klimenkova, A.D. Lotka-Volterra Controlled Systems in the Modeling of Biomedical Processes; MAKS Press: Moscow, Russia, 2021. (In Russian) [Google Scholar]
- Grigorenko, N.L.; Khailov, E.N.; Grigorieva, E.V.; Klimenkova, A.D. Optimal strategies in the treatment of cancers in the Lotka–Volterra mathematical model of competition. Tr. Instituta Mat. Mekhaniki URO RAN 2020, 26, 71–88. [Google Scholar] [CrossRef]
- Grigorenko, N.L.; Khailov, E.N.; Grigorieva, E.V.; Klimenkova, A.D. Lotka–Volterra competition model with nonmonotone therapy function for finding optimal strategies in the treatment of blood cancers. Tr. Instituta Mat. Mekhaniki UrO RAN 2021, 27, 79–98. [Google Scholar] [CrossRef]
- Subbotina, N.N.; Novoselova, N.G. Optimal result in the control problem for a system with piecewise monotonic dynamics. Tr. Instituta Mat. Mekhaniki UrO RAN 2017, 23, 265–280. [Google Scholar]
- Subbotina, N.N.; Novoselova, N.G. On Applications of the Hamilton Jacobi Equations and Optimal Control Theory to Problems of Chemotherapy of Malignant Tumors. Proc. Steklov Inst. Math. 2019, 304, 257–267. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanski, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. Mathematical Theory of Optimal Processes; Interscience Publishers: New York, NY, USA, 1962. [Google Scholar]
- Crandall, G.; Lions, P.L. Viscosity solutions of Hamilton-Jacobi equations. Trans. Am. Math. Soc. 1990, 277, 1–42. [Google Scholar] [CrossRef]
- Subbotin, A.I. Generalized Solutions of First Order PDEs. The Dynamical Optimization Perspective; Birkhäuser: Boston, MA, USA, 1995. [Google Scholar]
- Schättler, H.; Ledzewicz, U. Optimal Control for Mathematical Models of Cancer Therapies: An Applications of Geometric Methods; Springer: New York, NY, USA, 2015. [Google Scholar]
- Moore, H. How to Mathematically Optimize Drug Regimens Using Optimal Control. J. Pharmacokinet. Pharmacodyn. 2018, 45, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Kienle Garrido, M.-L.; Breitenbach, T.; Chudej, K.; Borzì, A. Modeling and Numerical Solution of a Cancer Therapy Optimal Control Problem. Appl. Math. 2018, 9, 985–1004. [Google Scholar] [CrossRef][Green Version]
- Bratus, A.; Yegorov, I.; Yurchenko, D. Dynamic mathematical models of therapy processes against glioma and leukemia under stochastic uncertainties. Mecc. Mater. Strutt. 2016, 6, 131–138. [Google Scholar]
- Bratus, A.S.; Goncharov, A.S.; Todorov, I.T. Optimal control in a mathematical model for leukemia therapy with phase constraints. Moscow Univ. Comput. Math. Cybernet. 2012, 36, 178–182. [Google Scholar] [CrossRef]
- Swan, G.W. Optimal Control Synthesis in Therapy of Solid Tumor Growth. Comp. Math. Math. Phys. 1990, 101, 237–284. [Google Scholar]
- Aubin, J.-P.; Bayen, A.M.; Saint-Pierre, P. Viability Theory: New Directions, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Novoselova, N.G.; Subbotina, N.N. Construction of the viability set in the problem of chemotherapy for a malignant tumor growing according to the Gompertz law. Tr. Instituta Mat. Mekhaniki UrO RAN 2020, 26, 173–181. (In Russian) [Google Scholar]
- Subbotina, N.N.; Krupennikov, E.A. Variational Approach to Solving Control Reconstruction Problems. Lobachevskii J. Math. 2022, 43, 1428–1437. [Google Scholar] [CrossRef]
- Ioffe, A.D.; Tikhomirov, V.M. Theory of Extremal Problems; North-Holland Publishing: New York, NY, USA, 1979. [Google Scholar]
- Strekalovsky, A.S. Elements of Nonconvex Optimization; Nauka: Novosibirsk, Russia, 2003. (In Russian) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subbotina, N.; Novoselova, N.; Krupennikov, E. Optimal Control Theory and Calculus of Variations in Mathematical Models of Chemotherapy of Malignant Tumors. Mathematics 2023, 11, 4301. https://doi.org/10.3390/math11204301
Subbotina N, Novoselova N, Krupennikov E. Optimal Control Theory and Calculus of Variations in Mathematical Models of Chemotherapy of Malignant Tumors. Mathematics. 2023; 11(20):4301. https://doi.org/10.3390/math11204301
Chicago/Turabian StyleSubbotina, Nina, Natalia Novoselova, and Evgenii Krupennikov. 2023. "Optimal Control Theory and Calculus of Variations in Mathematical Models of Chemotherapy of Malignant Tumors" Mathematics 11, no. 20: 4301. https://doi.org/10.3390/math11204301
APA StyleSubbotina, N., Novoselova, N., & Krupennikov, E. (2023). Optimal Control Theory and Calculus of Variations in Mathematical Models of Chemotherapy of Malignant Tumors. Mathematics, 11(20), 4301. https://doi.org/10.3390/math11204301




