Fuzzy Weighted Pareto–Nash Equilibria of Multi-Objective Bi-Matrix Games with Fuzzy Payoffs and Their Applications

Abstract

Based on our previous research, this paper further discusses the multi-objective bi-matrix game with fuzzy payoffs (MBGFP), which is a special case of the fuzzy constrained multi-objective game with fuzzy payoffs. We first prove that any bi-matrix game with interval payoffs (BGIP) has at least one Pareto–Nash equilibrium. Then, with the help of BGIP, we obtain the necessary and sufficient conditions for the existence of fuzzy Pareto–Nash equilibrium of MBGFP. Secondly, based on the bilinear programming method for calculating Nash equilibrium in crisp bi-matrix games, we established a bilinear programming method with parameters for calculating fuzzy Pareto–Nash equilibrium. By considering the importance of each objective to the players, MBGFP is transformed into a bi-matrix game with fuzzy payoffs (BGFP). Furthermore, we obtained the necessary and sufficient conditions for the existence of fuzzy weighted Pareto–Nash equilibrium and its calculation method. Finally, a practical example is used to illustrate the effectiveness of our proposed calculation method.

1. Introduction

Matrix games are widely used in economics, management, sociology, political science, military science, and other fields. In many real-world situations, the information or the payoffs are imprecise, uncertain, or incomplete. In such cases, using the traditional matrix game becomes difficult as it relies on precise and complete information. Since fuzzy numbers can better describe the uncertainty of payoffs, matrix games with fuzzy payoffs are usually considered. Nowadays, the study of matrix games with fuzzy payoffs is an essential branch of game theory that helps in making the analysis and decision-making in various fields more practical and efficient.

Zadeh [1] first introduced the fuzzy set theory. Subsequently, Butnariu [2] first introduced fuzzy sets in non-cooperative games. Dubois and Prade [3] studied the two-player zero-sum game with fuzzy payoffs, and regarded the payoffs in the game as fuzzy numbers, which is an earlier paper on fuzzy matrix games. Campos [4] proposed a fuzzy linear programming method to solve the two-player zero-sum fuzzy game. This method is more suitable for solving the problem that the payoff is a triangular fuzzy number. Maeda [5] discussed the bi-matrix game with fuzzy payoffs. Based on the literature [6,7], Clemente [8] introduced the standard fuzzy orders to compare the fuzzy payoffs, and then studied the Pareto-optimal security strategies of zero-sum matrix games with fuzzy payoffs. Li [9] introduced an approach to computing fuzzy values of matrix games with single objectives and triangular fuzzy payoffs. Chandra and Aggarwal [10] wrote a note on the work of Li [9] for solving the two-player zero-sum games with payoffs of triangular fuzzy numbers and proposed a new methodology for solving such games. For more literature on fuzzy matrix games, see, e.g., Refs. [11,12,13,14,15,16,17,18].

Matrix games with multiple non-comparable objectives are called multi-objective matrix games. Zeleny [19] introduced a parameter vector and a vector with weighting coefficients, and analyzed the multi-objective two-player zero-sum game through parameter changes. Buckley [20] used the decision principles of Bellman and Zadeh [21] in fuzzy environments to formulate multi-objective non-cooperative games under uncertainty. Sakawa and Nishizaki [22] consider multi-objective two-player zero-sum matrix games with fuzzy payoffs and fuzzy goals. Utilizing a degree of attainment of the fuzzy goal, the corresponding max-min strategy of this game is obtained. Fernandez and Puerto [23] showed that a multi-objective zero-sum matrix game corresponds to a multi-objective linear programming problem, and verified that the effective solution set of the linear programming problem is consistent with the Pareto optimal security strategy set for one of the players in the original game. Based on Ref. [22], Nishizaki and Sakawa [24] examined fuzzy bi-matrix games incorporating fuzzy goals in single and multiple objective environments. Bigdeli and Hassanpour [25] discussed the multi-objective zero-sum matrix game with triangular fuzzy numbers. The game is converted to several multi-objective matrix games with interval payoffs by using the $\alpha$-cuts of fuzzy payoffs. For more literature on multi-objective fuzzy matrix games, see, e.g., Refs. [20,22,23,24,25] and references therein. In addition, multi-objective games in which the payoff function is a fuzzy vector-valued function are more general game models. The definition of equilibrium, as well as the existence and stability of equilibrium, hold significant importance in this game. Based on the partial order of fuzzy vectors, Li et al. [26] proposed the concept of fuzzy Pareto–Nash equilibrium in fuzzy constrained multi-objective games with fuzzy payoffs. Furthermore, the existence and stability of fuzzy Pareto–Nash equilibrium are researched.

Moore [27] introduced the concept of interval analysis about interval numbers and functions with interval coefficients. Subsequently, many scholars further developed the theory of interval arithmetic and interval-valued functions, see Refs. [28,29,30,31,32] and references therein. Fei and Li [33] developed an effective bilinear programming method for solving bi-matrix games with interval payoffs. The current application of interval analysis in game theory is mainly to discuss the existence of equilibria for matrix games with interval payoffs and their calculation methods, see, e.g., Refs. [33,34,35,36].

As far as we know, there are few theoretical studies and applications on multi-objective bi-matrix games with fuzzy payoffs (MBGFP). Different from the classic (multi-objective) bi-matrix game, the player’s expected payoff is a (fuzzy vector) fuzzy number in MBGFP. The order on the fuzzy number set is also different from the natural order of real numbers. It is a partial order. There are two existing research ideas on MBGFP. One research idea is to introduce fuzzy goals, construct two attainment degree functions as two players’ payoff functions, and then transform the MBGFP into a two-player crisp game. Another research idea is to use the cut sets of fuzzy numbers to transform the MBGFP into some multi-objective bi-matrix games with interval payoffs, and then use the interval optimization method to solve the interval value of the game. However, there is no literature starting from the partial order on the fuzzy number (vector) set and directly establishing the equilibrium of the MBGFP under this partial order. Based on this, and based on our recent research in Ref. [26], this paper proposes the concept of fuzzy (weighted) Pareto–Nash equilibrium for MBGFP, and obtains calculation methods for these two types of equilibria.

This article is structured as follows. In Section 2, we review some basic terminology and related conclusions. In Section 3, we study the fuzzy Pareto–Nash equilibrium and fuzzy weighted Pareto–Nash equilibrium of MBGFP and show the relationship between them. First, the necessary and sufficient condition for the existence of fuzzy weighted Pareto–Nash equilibrium is given using the existence of Pareto–Nash equilibrium of BGIP. Second, the calculation method of fuzzy weighted Pareto–Nash equilibrium is obtained through the optimal solution of the bilinear programming problem with parameters. Based on Section 3, we specifically discuss the two-type two-company competition problem with triangular fuzzy payoffs in Section 4 and use Lingo software (v.19) to calculate the fuzzy weighted Pareto–Nash equilibrium of the game under a given grade of membership. Finally, the conclusion is presented in Section 5.

2. Preliminaries and Terminology

Throughout this paper, we write $\mathbb{R}$ for the set of all real numbers, $\mathcal{I}\left(\mathbb{R}\right)$ for the set of all closed intervals in $\mathbb{R}$, and $\mathcal{F}\left(\mathbb{R}\right)$ for the set of all fuzzy numbers in $\mathbb{R}$. We first review basic terminology on fuzzy numbers, fuzzy vectors, and some related conclusions. In order to study MBGFP, we will propose the concept of Pareto–Nash equilibrium of a bi-matrix game with interval payoffs (BGIP), and prove that for any BGIP there is at least one Pareto–Nash equilibria in the sense of mixed strategies.

Let X denote a universal set. A fuzzy subset $\tilde{a}$ of X is defined by its membership function ${\mu }_{\tilde{a}}:X\to [0,1]$, which assigns to each element $x\in X$ a real number ${\mu }_{\tilde{a}}\left(x\right)$ in the interval $[0,1]$. Especially, ${\mu }_{\tilde{a}}\left(x\right)$ is the grade of membership of x in the set $\tilde{a}$. The $\alpha$-cut of the fuzzy set $\tilde{a}$, denoted by ${\tilde{a}}^{\alpha }$, is a set defined by

$${\tilde{a}}^{\alpha }=\{x\in X|{\mu }_{\tilde{a}}\left(x\right)\ge \alpha \},$$

when $\alpha \in (0,1]$. And ${\tilde{a}}^0=cl\{x\in X|{\mu }_{\tilde{a}}\left(x\right)>0\}$, where $cl$ denotes the closure of sets. For more about the properties of fuzzy sets, please refer to Refs. [1,3].

Definition 1

(See Ref. [37]). A fuzzy number $\tilde{A}$ is a fuzzy set on $\mathbb{R}$, whose membership function ${\mu }_{\tilde{A}}(·):\mathbb{R}\to [0,1]$ satisfies the following conditions:

1. 

${\mu }_{\tilde{A}}\left(x\right)=0$ for all $x\in (-\infty ,c]$,

2. 

${\mu }_{\tilde{A}}(·)$ is strictly increasing and continuous on $[c,a]$,

3. 

${\mu }_{\tilde{A}}\left(x\right)=1$ for all $x\in [a,b]$,

4. 

${\mu }_{\tilde{A}}(·)$ is strictly decreasing and continuous on $[b,d]$,

5. 

${\mu }_{\tilde{A}}\left(x\right)=0$ for all $x\in [d,+\infty )$,

where $-\infty <c\le a\le b\le d<+\infty$.

For $\tilde{A}\in \mathcal{F}\left(\mathbb{R}\right)$, the $\alpha$-cut of $\tilde{A}$ is a closed interval, i.e., ${\tilde{A}}^{\alpha }=[{\tilde{A}}_L\left(\alpha \right),{\tilde{A}}_R\left(\alpha \right)]$, where ${\tilde{A}}_L\left(\alpha \right)=inf\{x\in \mathbb{R}:{\mu }_{\tilde{A}}\left(x\right)\ge \alpha \}$ and ${\tilde{A}}_R\left(\alpha \right)=sup\{x\in \mathbb{R}:{\mu }_{\tilde{A}}\left(x\right)\ge \alpha \}$.

Suppose that the membership functions of fuzzy numbers $\tilde{A}$ and $\tilde{B}$ are represented as follows:

$${\mu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{ccc}\hfill {\mu }_{\tilde{A}}^L\left(x\right),& \hfill & \hfill x\in [a_1,a_2]\\ \hfill 1,& \hfill & \hfill x\in [a_2,a_3]\\ \hfill {\mu }_{\tilde{A}}^R\left(x\right),& \hfill & \hfill x\in [a_3,a_4]\\ \hfill 0,& \hfill & \hfill \mathrm{otherwise}\end{array}\right.$$

and

$${\mu }_{\tilde{B}}\left(x\right)=\left\{\begin{array}{ccc}\hfill {\mu }_{\tilde{B}}^L\left(x\right),& \hfill & \hfill x\in [b_1,b_2]\\ \hfill 1,& \hfill & \hfill x\in [b_2,b_3]\\ \hfill {\mu }_{\tilde{B}}^R\left(x\right),& \hfill & \hfill x\in [b_3,b_4]\\ \hfill 0,& \hfill & \hfill \mathrm{otherwise}\end{array}\right.$$

where $-\infty <a_1\le a_2\le a_3\le a_4<+\infty$, $-\infty <b_1\le b_2\le b_3\le b_4<+\infty$. Then, the sum of $\tilde{A}$ and $\tilde{B}$ is denoted by $\tilde{A}+\tilde{B}$, whose membership function is defined by

$${\mu }_{\tilde{A}+\tilde{B}}\left(x\right)=\left\{\begin{array}{ccc}\hfill {\mu }_{\tilde{A}+\tilde{B}}^L\left(x\right),& \hfill & \hfill x\in [a_1+b_1,a_2+b_2]\\ \hfill 1,& \hfill & \hfill x\in [a_2+b_2,a_3+b_3]\\ \hfill {\mu }_{\tilde{A}+\tilde{B}}^R\left(x\right),& \hfill & \hfill x\in [a_3+b_3,a_4+b_4]\\ \hfill 0,& \hfill & \hfill \mathrm{otherwise}\end{array}\right.$$

where ${\left({\mu }_{\tilde{A}+\tilde{B}}^L\right)}^{-1}\left(\alpha \right)={\left({\mu }_{\tilde{A}}^L\right)}^{-1}\left(\alpha \right)+{\left({\mu }_{\tilde{B}}^L\right)}^{-1}\left(\alpha \right)$ and ${\left({\mu }_{\tilde{A}+\tilde{B}}^R\right)}^{-1}\left(\alpha \right)={\left({\mu }_{\tilde{A}}^R\right)}^{-1}\left(\alpha \right)+{\left({\mu }_{\tilde{B}}^R\right)}^{-1}\left(\alpha \right)$, for all $\alpha \in [0,1]$.

The product of a scalar k and a fuzzy number $\tilde{A}$, denoted by $k\tilde{A}$, is defined as follows:

Case 1: $k\ge 0$, then

$${\mu }_{k\tilde{A}}\left(x\right)=\left\{\begin{array}{ccc}\hfill {\mu }_{k\tilde{A}}^L\left(x\right),& \hfill & \hfill x\in [k{a}_1,k{a}_2]\\ \hfill 1,& \hfill & \hfill x\in [k{a}_2,k{a}_3]\\ \hfill {\mu }_{k\tilde{A}}^R\left(x\right),& \hfill & \hfill x\in [k{a}_3,k{a}_4]\\ \hfill 0,& \hfill & \hfill \mathrm{otherwise}\end{array}\right.$$

where ${\left({\mu }_{k\tilde{A}}^L\right)}^{-1}\left(\alpha \right)=k·{\left({\mu }_{\tilde{A}}^L\right)}^{-1}\left(\alpha \right)$, ${\left({\mu }_{k\tilde{A}}^R\right)}^{-1}\left(\alpha \right)=k·{\left({\mu }_{\tilde{A}}^R\right)}^{-1}\left(\alpha \right)$, for all $\alpha \in [0,1]$.

Case 2: $k<0$, then

$${\mu }_{k\tilde{A}}\left(x\right)=\left\{\begin{array}{ccc}\hfill {\mu }_{k\tilde{A}}^L\left(x\right),& \hfill & \hfill x\in [k{a}_4,k{a}_3]\\ \hfill 1,& \hfill & \hfill x\in [k{a}_3,k{a}_2]\\ \hfill {\mu }_{k\tilde{A}}^R\left(x\right),& \hfill & \hfill x\in [k{a}_2,k{a}_1]\\ \hfill 0,& \hfill & \hfill \mathrm{otherwise}\end{array}\right.$$

where ${\left({\mu }_{k\tilde{A}}^L\right)}^{-1}\left(\alpha \right)=k·{\left({\mu }_{\tilde{A}}^R\right)}^{-1}\left(\alpha \right)$, ${\left({\mu }_{k\tilde{A}}^R\right)}^{-1}\left(\alpha \right)=k·{\left({\mu }_{\tilde{A}}^L\right)}^{-1}\left(\alpha \right)$, for all $\alpha \in [0,1]$.

From the above definitions, we can see that ${(\tilde{A}+\tilde{B})}^{\alpha }={\tilde{A}}^{\alpha }+{\tilde{B}}^{\alpha }$ and ${\left(k\tilde{A}\right)}^{\alpha }=k{\tilde{A}}^{\alpha }$, for all $\alpha \in [0,1]$. Moreover, the set $\mathcal{F}\left(\mathbb{R}\right)$ is closed under addition and scalar multiplication.

Write $\mathcal{F}{\left(\mathbb{R}\right)}^d$ for the family of all d-dimensional fuzzy vectors. For $\tilde{\mathit{A}}=({\tilde{A}}_1,\dots ,{\tilde{A}}_d)\in \mathcal{F}{\left(\mathbb{R}\right)}^d$ and $\alpha \in [0,1]$. Then the $\alpha$-cut of $\tilde{\mathit{A}}$ is an interval vector, that is,

$${\tilde{\mathit{A}}}^{\alpha }=({\tilde{A}}_1^{\alpha },\dots ,{\tilde{A}}_d^{\alpha })\in \mathcal{I}{\left(\mathbb{R}\right)}^d,$$

where $\mathcal{I}{\left(\mathbb{R}\right)}^d$ is the set of all d-dimensional interval vector. It is worth noting that every ${\tilde{\mathit{A}}}^{\alpha }$ corresponds to two d-dimensional vectors. They are recorded as

$${\tilde{\mathit{A}}}_L\left(\alpha \right)=({\left({\tilde{A}}_1\right)}_L\left(\alpha \right),\dots ,{\left({\tilde{A}}_d\right)}_L\left(\alpha \right))$$

and

$${\tilde{\mathit{A}}}_R\left(\alpha \right)=({\left({\tilde{A}}_1\right)}_R\left(\alpha \right),\dots ,{\left({\tilde{A}}_d\right)}_R\left(\alpha \right)).$$

Similarly, the addition and scalar multiplication of fuzzy vectors are defined for $\tilde{\mathit{A}}=({\tilde{A}}_1,\dots ,{\tilde{A}}_d),\tilde{\mathit{B}}=({\tilde{B}}_1,\dots ,{\tilde{B}}_d)\in \mathcal{F}{\left(\mathbb{R}\right)}^d$, $k\in \mathbb{R}$ by

$$\tilde{\mathit{A}}+\tilde{\mathit{B}}=({\tilde{A}}_1+{\tilde{B}}_1,\dots ,{\tilde{A}}_d+{\tilde{B}}_d)$$

and

$$k·\tilde{\mathit{A}}=(k·{\tilde{A}}_1,\dots ,k·{\tilde{A}}_d).$$

Definition 2

(See Ref. [26]). Let $\tilde{\mathit{A}}$ and $\tilde{\mathit{B}}$ be two elements of $\mathcal{F}{\left(\mathbb{R}\right)}^d$.

1. 

$\tilde{\mathit{A}}$ is said to be dominated by $\tilde{\mathit{B}}$ from below if ${\tilde{\mathit{B}}}_L\left(\alpha \right)\le {\tilde{\mathit{A}}}_L\left(\alpha \right)$ and ${\tilde{\mathit{B}}}_R\left(\alpha \right)\le {\tilde{\mathit{A}}}_R\left(\alpha \right)$ for all $\alpha \in [0,1]$, and we rewrite this property as $\tilde{\mathit{B}}⪯\tilde{\mathit{A}}$. Otherwise, we write $\tilde{\mathit{B}}\tilde{\mathit{A}}$.

2. 

$\tilde{\mathit{A}}$ is said to be strictly dominated by $\tilde{\mathit{B}}$ from below if ${\tilde{\mathit{B}}}_L\left(\alpha \right)<{\tilde{\mathit{A}}}_L\left(\alpha \right)$ and ${\tilde{\mathit{B}}}_R\left(\alpha \right)<{\tilde{\mathit{A}}}_R\left(\alpha \right)$ for all $\alpha \in [0,1]$, and we rewrite this property as $\tilde{\mathit{B}}\prec \tilde{\mathit{A}}$. Otherwise, we write $\tilde{\mathit{B}}\nprec \tilde{\mathit{A}}$.

In particular, when $d=1$, the partial order ⪯ in Definition 2 is precisely equivalent to the fuzzy maximum order in Ref. [7].

Next, consider a bi-matrix games with interval payoffs (BGIP)

$$(\mathcal{A},\mathcal{B})=\left(\begin{array}{cccc}(a_{11},b_{11})& (a_{12},b_{12})& \cdots & (a_{1n},b_{1n})\\ (a_{21},b_{21})& (a_{22},b_{22})& \cdots & (a_{2n},b_{2n})\\ \cdots & \cdots & \cdots & \cdots \\ (a_{m1},b_{m1})& (a_{m2},b_{m2})& \cdots & (a_{mn},b_{mn})\end{array}\right)$$

where $a_{ij}=[{\underline{a}}_{ij},{\overline{a}}_{ij}],b_{ij}=[{\underline{b}}_{ij},{\overline{b}}_{ij}](i=1,\dots ,m;j=1,\cdots ,n)$. Let $\underline{\mathcal{A}}={\left({\underline{a}}_{ij}\right)}_{n\times m}$, $\overline{\mathcal{A}}={\left({\overline{a}}_{ij}\right)}_{n\times m}$, $\underline{\mathcal{B}}={\left({\underline{b}}_{ij}\right)}_{n\times m}$ and $\overline{\mathcal{B}}={\left({\overline{b}}_{ij}\right)}_{n\times m}$. The sets of all mixed strategies for Players I and II are defined as ${\mathcal{S}}^m=\{(x_1,\dots ,x_m)\in {\mathbb{R}}^m|{\sum }_{i=1}^m{x}_i=1,x_i\ge 0,i=1,\dots ,m\}$ and ${\mathcal{S}}^n=\{(y_1,\dots ,y_n)\in {\mathbb{R}}^n|{\sum }_{j=1}^n{y}_j=1,y_j\ge 0,j=1,\dots ,n\}$. The interval-valued expected payoffs for Players I and II are defined as $x^T\mathcal{A}y=[x^T\underline{\mathcal{A}}y,x^T\overline{\mathcal{A}}y]$ and $x^T\mathcal{B}y=[x^T\underline{\mathcal{B}}y,x^T\overline{\mathcal{B}}y]$ for $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$, where $x^T\underline{\mathcal{A}}y={\sum }_{i=1}^m{\sum }_{j=1}^n{\underline{a}}_{ij}{x}_i{y}_j$, $x^T\overline{\mathcal{A}}y={\sum }_{i=1}^m{\sum }_{j=1}^n{\overline{a}}_{ij}{x}_i{y}_j$, $x^T\underline{\mathcal{B}}y={\sum }_{i=1}^m{\sum }_{j=1}^n{\underline{b}}_{ij}{x}_i{y}_j$, and $x^T\overline{\mathcal{B}}y={\sum }_{i=1}^m{\sum }_{j=1}^n{\overline{b}}_{ij}{x}_i{y}_j$.

For $a=[\underline{a},\overline{a}]$, $b=[\underline{b},\overline{b}]$, if $\underline{a}\le \underline{b}$ and $\overline{a}\le \overline{b}$, then we write $a⪯b$. If $\underline{a}<\underline{b}$ and $\overline{a}<\overline{b}$, then we write $a\prec b$. The relation ⪯ is a partial order on $\mathcal{I}\left(\mathbb{R}\right)$. However, two intervals with true inclusion relations are incomparable under the partial order ⪯. For example, $[3,4]\subset [2,5]$, but $[3,4]⋠[2,5]$ and $[2,5]⋠[3,4]$. So, $[3,4]$ and $[2,5]$ are incomparable.

Now we will introduce the equilibrium of bi-matrix games with interval payoffs $(\mathcal{A},\mathcal{B})$.

Definition 3.

A strategy profile $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is called a Pareto–Nash equilibrium of $(\mathcal{A},\mathcal{B})$, if for each $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ such that

$$x^{*T}\underline{\mathcal{A}}{y}^{*}\ge x^T\underline{\mathcal{A}}{y}^{*}(or{x}^{*T}\overline{\mathcal{A}}{y}^{*}\ge x^T\overline{\mathcal{A}}{y}^{*})$$

and

$$x^{*T}\underline{\mathcal{B}}{y}^{*}\ge x^{*T}\underline{\mathcal{B}}y(or{x}^{*T}\overline{\mathcal{B}}{y}^{*}\ge x^{*T}\overline{\mathcal{B}}y).$$

Lemma 1.

Assume that $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a Nash equilibrium to one of the four crisp bi-matrix games $(\underline{\mathcal{A}},\underline{\mathcal{B}})$, $(\underline{\mathcal{A}},\overline{\mathcal{B}})$, $(\overline{\mathcal{A}},\underline{\mathcal{B}})$ and $(\overline{\mathcal{A}},\overline{\mathcal{B}})$. Then, $(x^{*},y^{*})$ is also a Pareto–Nash equilibrium of BGIP $(\mathcal{A},\mathcal{B})$.

Proof. 

Without loss of generality, assume that $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a Nash equilibrium of the crisp bi-matrix game $(\underline{\mathcal{A}},\underline{\mathcal{B}})$. Then

$$x^{*T}\underline{\mathcal{A}}{y}^{*}=\underset{x\in {\mathcal{S}}^m}{max}{x}^T\underline{\mathcal{A}}{y}^{*}and{x}^{*T}\underline{\mathcal{B}}{y}^{*}=\underset{y\in {\mathcal{S}}^n}{max}{x}^{*T}\underline{\mathcal{B}}y.$$

That is, for each $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$, we have $x^{*T}\underline{\mathcal{A}}{y}^{*}\ge x^T\underline{\mathcal{A}}{y}^{*}$ and $x^{*T}\underline{\mathcal{B}}{y}^{*}\ge x^{*T}\underline{\mathcal{B}}y$. From Definition 3, it follows that $(x^{*},y^{*})$ is a Pareto–Nash equilibrium of BGIP $(\mathcal{A},\mathcal{B})$. Similarly, the other three cases can be verified. □

In the sense of mixed strategies, any crisp bi-matrix game must have a Nash equilibrium [38]. According to Lemma 1, there are at least four Pareto–Nash equilibria for any bi-matrix game with interval payoffs.

3. Multi-Objective Bi-Matrix Games with Fuzzy Payoffs

In this section, we discuss the fuzzy Pareto–Nash equilibrium (FPNE) and fuzzy weighted Pareto–Nash equilibrium (FWPNE) of MBGFP. Moreover, we obtain the relationship between FPNE and FWPNE, and provide the necessary and sufficient conditions for the existence of these two equilibria and their calculation methods, respectively.

We focus on the multi-objective bi-matrix game with fuzzy payoffs (MBGFP) $\Gamma ={\left\{({\mathcal{A}}_k,{\mathcal{B}}_k)\right\}}_{k\in \{1,\dots ,d\}}$ given by

$$({\mathcal{A}}_k,{\mathcal{B}}_k)=\left(\begin{array}{cccc}({\tilde{a}}_{11}^k,{\tilde{b}}_{11}^k)& ({\tilde{a}}_{12}^k,{\tilde{b}}_{12}^k)& \cdots & ({\tilde{a}}_{1n}^k,{\tilde{b}}_{1n}^k)\\ ({\tilde{a}}_{21}^k,{\tilde{b}}_{21}^k)& ({\tilde{a}}_{22}^k,{\tilde{b}}_{22}^k)& \cdots & ({\tilde{a}}_{2n}^k,{\tilde{b}}_{2n}^k)\\ \cdots & \cdots & \cdots & \cdots \\ ({\tilde{a}}_{m1}^k,{\tilde{b}}_{m1}^k)& ({\tilde{a}}_{m2}^k,{\tilde{b}}_{m2}^k)& \cdots & ({\tilde{a}}_{mn}^k,{\tilde{b}}_{mn}^k)\end{array}\right)\mathrm{for}k=1,\cdots ,d,$$

where all the components $({\tilde{a}}_{ij}^k,{\tilde{b}}_{ij}^k)\in \mathcal{F}\left(\mathbb{R}\right)\times \mathcal{F}\left(\mathbb{R}\right)$. The sets of all mixed strategies for Players I and II are, respectively,

$${\mathcal{S}}^m=\{(x_1,\dots ,x_m)\in {\mathbb{R}}^m|\sum _{i=1}^m{x}_i=1,x_i\ge 0,i=1,\dots ,m\}$$

and

$${\mathcal{S}}^n=\{(y_1,\dots ,y_n)\in {\mathbb{R}}^n|\sum _{i=1}^n{y}_i=1,y_i\ge 0,i=1,\dots ,n\}.$$

Moreover, the fuzzy-vector-valued expected payoffs for Players I and II are given, respectively, by

$${\tilde{F}}_1(x,y)=(x^T{\mathcal{A}}_{1}y,\dots ,x^T{\mathcal{A}}_{d}y)$$

and

$${\tilde{F}}_2(x,y)=(x^T{\mathcal{B}}_{1}y,\dots ,x^T{\mathcal{B}}_{d}y),$$

for $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$. Clearly, $({\mathcal{S}}^m,{\mathcal{S}}^n,{\tilde{F}}_1,{\tilde{F}}_2)$ is a two-player multi-objective game with fuzzy payoffs.

For ${\alpha }_1,{\alpha }_2\in [0,1]$, let ${\mathcal{A}}_k^{{\alpha }_1}={({({\tilde{a}}_{ij}^k)}^{{\alpha }_1})}_{m\times n}$ and ${\mathcal{B}}_k^{{\alpha }_2}={({({\tilde{b}}_{ij}^k)}^{{\alpha }_2})}_{m\times n}$. Then $\Gamma ({\alpha }_1,{\alpha }_2)={\left\{({\mathcal{A}}_k^{{\alpha }_1},{\mathcal{B}}_k^{{\alpha }_2})\right\}}_{k\in \{1,\dots ,d\}}$ constitutes a multi-objective bi-matrix game with interval payoffs (MBGIP). The interval-vector-valued expected payoffs for Players I and II are

$${\tilde{F}}_1^{{\alpha }_1}(x,y)=([x^T{\underline{\mathcal{A}}}_1^{{\alpha }_1}y,x^T{\overline{\mathcal{A}}}_1^{{\alpha }_1}y],\dots ,[x^T{\underline{\mathcal{A}}}_d^{{\alpha }_1}y,x^T{\overline{\mathcal{A}}}_d^{{\alpha }_1}y])$$

and

$${\tilde{F}}_2^{{\alpha }_2}(x,y)=([x^T{\underline{\mathcal{B}}}_1^{{\alpha }_2}y,x^T{\overline{\mathcal{B}}}_1^{{\alpha }_2}y],\dots ,[x^T{\underline{\mathcal{B}}}_d^{{\alpha }_2}y,x^T{\overline{\mathcal{B}}}_d^{{\alpha }_2}y])$$

respectively, where for $k=1,\dots ,d$,

$$x^T{\underline{\mathcal{A}}}_k^{{\alpha }_1}y=\sum _{i=1}^m\sum _{j=1}^n{\left({\tilde{a}}_{ij}^k\right)}_L\left({\alpha }_1\right)x_i{y}_j,x^T{\overline{\mathcal{A}}}_k^{{\alpha }_1}y=\sum _{i=1}^m\sum _{j=1}^n{\left({\tilde{a}}_{ij}^k\right)}_R\left({\alpha }_1\right)x_i{y}_j$$

and

$$x^T{\underline{\mathcal{B}}}_k^{{\alpha }_2}y=\sum _{i=1}^m\sum _{j=1}^n{\left({\tilde{b}}_{ij}^k\right)}_L\left({\alpha }_2\right)x_i{y}_j,x^T{\overline{\mathcal{B}}}_k^{{\alpha }_2}y=\sum _{i=1}^m\sum _{j=1}^n{\left({\tilde{b}}_{ij}^k\right)}_R\left({\alpha }_2\right)x_i{y}_j.$$

3.1. Fuzzy Pareto–Nash Equilibria

We require the following definition of the fuzzy Pareto–Nash equilibrium of MBGFP.

Definition 4. 

A strategy profile $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is called a FPNE of Γ, if for all $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$, such that

$${\tilde{F}}_1(x^{*},y^{*})\nprec {\tilde{F}}_1(x,y^{*})and{\tilde{F}}_2(x^{*},y^{*})\nprec {\tilde{F}}_2(x^{*},y).$$

Theorem 1. 

A strategy profile $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a FPNE of $\Gamma ={\left\{({\mathcal{A}}_k,{\mathcal{B}}_k)\right\}}_{k\in \{1,\dots ,d\}}$ if and only if there exist ${\alpha }_1,{\alpha }_2\in [0,1]$ and $s,t\in \{1,\dots ,d\}$ such that $(x^{*},y^{*})$ is a Pareto–Nash equilibrium of a BGIP $({\mathcal{A}}_s^{{\alpha }_1},{\mathcal{B}}_t^{{\alpha }_2})$.

Proof. 

Assume that $(x^{*},y^{*})$ is a FPNE of $\Gamma$. By Definition 4, for each $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$, we have

$${\tilde{F}}_1(x^{*},y^{*})\nprec {\tilde{F}}_1(x,y^{*})and{\tilde{F}}_2(x^{*},y^{*})\nprec {\tilde{F}}_2(x^{*},y).$$

Added Definition 2, there exist ${\alpha }_1,{\alpha }_2\in [0,1]$ such that

$${\left({\tilde{F}}_1^{{\alpha }_1}\right)}_L(x^{*},y^{*})\nless {\left({\tilde{F}}_1^{{\alpha }_1}\right)}_L(x,y^{*})\left(\mathrm{or}{\left({\tilde{F}}_1^{{\alpha }_1}\right)}_R(x^{*},y^{*})\nless {\left({\tilde{F}}_1^{{\alpha }_1}\right)}_R(x,y^{*})\right)$$

and

$${\left({\tilde{F}}_2^{{\alpha }_2}\right)}_L(x^{*},y^{*})\nless {\left({\tilde{F}}_2^{{\alpha }_2}\right)}_L(x^{*},y)\left(\mathrm{or}{\left({\tilde{F}}_2^{{\alpha }_2}\right)}_R(x^{*},y^{*})\nless {\left({\tilde{F}}_2^{{\alpha }_2}\right)}_R(x^{*},y)\right).$$

Furthermore, there exist $s,t\in \{1,\cdots ,d\}$ such that

$$x^{*T}{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\ge x^T{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}(\mathrm{or}{x}^{*T}{\overline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\ge x^T{\overline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*})$$

and

$$x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}\ge x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}y(\mathrm{or}{x}^{*T}{\overline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}\ge x^{*T}{\overline{\mathcal{B}}}_t^{{\alpha }_2}y),$$

for all $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$. So $(x^{*},y^{*})$ is a Pareto–Nash equilibrium of $({\mathcal{A}}_s^{{\alpha }_1},{\mathcal{B}}_t^{{\alpha }_2})$.

Finally, the sufficient part is obvious, according to Definitions 3 and 4. □

Fei and Li [33] proposed a bilinear programming method to solve the Nash equilibrium of the crisp bi-matrix game. With the help of Theorem 1 and Lemma 1, we obtain the following calculation method for FPNE.

Theorem 2. 

The strategy profile $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a FPNE of $\Gamma ={\left\{({\mathcal{A}}_k,{\mathcal{B}}_k)\right\}}_{k\in \{1,\dots ,d\}}$, if and only if there exist ${\alpha }_1,{\alpha }_2\in [0,1]$ and $s,t\in \{1,\dots ,d\}$, such that it is an optimal solution to one of the following four bilinear programming models with two parameters:

$$\begin{array}{cc}\hfill \max & \{x^T{\underline{\mathcal{A}}}_s^{{\alpha }_1}y+x^T{\underline{\mathcal{B}}}_t^{{\alpha }_2}y-\underline{\mu }\left({\alpha }_1\right)-\underline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\underline{\mathcal{A}}}_s^{{\alpha }_1}y\le \underline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\underline{\mathcal{B}}}_t^{{\alpha }_{2}T}x\le \underline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \max & \{x^T{\underline{\mathcal{A}}}_s^{{\alpha }_1}y+x^T{\overline{\mathcal{B}}}_t^{{\alpha }_2}y-\underline{\mu }\left({\alpha }_1\right)-\overline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\underline{\mathcal{A}}}_s^{{\alpha }_1}y\le \underline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\overline{\mathcal{B}}}_t^{{\alpha }_{2}T}x\le \overline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \max & \{x^T{\overline{\mathcal{A}}}_s^{{\alpha }_1}y+x^T{\underline{\mathcal{B}}}_t^{{\alpha }_2}y-\overline{\mu }\left({\alpha }_1\right)-\underline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\overline{\mathcal{A}}}_s^{{\alpha }_1}y\le \overline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\underline{\mathcal{B}}}_t^{{\alpha }_{2}T}x\le \underline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \max & \{x^T{\overline{\mathcal{A}}}_s^{{\alpha }_1}y+x^T{\overline{\mathcal{B}}}_t^{{\alpha }_2}y-\overline{\mu }\left({\alpha }_1\right)-\overline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\overline{\mathcal{A}}}_s^{{\alpha }_1}y\le \overline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\overline{\mathcal{B}}}_t^{{\alpha }_{2}T}x\le \overline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(4)

where $e^m={\left(\underset{m}{\underbrace{1,1,\cdots ,1}}\right)}^T$ and $e^n={\left(\underset{n}{\underbrace{1,1,\cdots ,1}}\right)}^T$.

Proof. 

Assume that $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a FPNE of $\Gamma$. By Theorem 1, there are ${\alpha }_1,{\alpha }_2\in [0,1]$ and $s,t\in \{1,\dots ,d\}$, such that $(x^{*},y^{*})$ is a Pareto–Nash equilibrium of BGIP $({\mathcal{A}}_s^{{\alpha }_1},{\mathcal{B}}_t^{{\alpha }_2})$. That is, for each $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$, at least one of the following four conditions are satisfied:

(1)

$x^{*T}{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\ge x^T{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}$ and $x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}\ge x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}y$;

(2)

$x^{*T}{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\ge x^T{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}$ and $x^{*T}{\overline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}\ge x^{*T}{\overline{\mathcal{B}}}_t^{{\alpha }_2}y$;

(3)

$x^{*T}{\overline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\ge x^T{\overline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}$ and $x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}\ge x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}y$;

(4)

$x^{*T}{\overline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\ge x^T{\overline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}$ and $x^{*T}{\overline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}\ge x^{*T}{\overline{\mathcal{B}}}_t^{{\alpha }_2}y$.

Without loss of generality, we assume that (1) holds. Let

$${\underline{\mu }}^{*}\left({\alpha }_1\right)=x^{*T}{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*},{\overline{\mu }}^{*}\left({\alpha }_1\right)=x^{*T}{\overline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}$$

and

$${\underline{\nu }}^{*}\left({\alpha }_2\right)=x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*},{\overline{\nu }}^{*}\left({\alpha }_2\right)=x^{*T}{\overline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}.$$

Therefore, $(x^{*},y^{*},{\underline{\mu }}^{*}\left({\alpha }_1\right),{\underline{\nu }}^{*}\left({\alpha }_2\right))$ is an optimal solution of (1).

Conversely, assume that $(x^{*},y^{*})$ associated with $({\underline{\mu }}^{*}\left({\alpha }_1\right),{\underline{\nu }}^{*}\left({\alpha }_2\right))$ is an optimal solution of (1). For each $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$, we have

$$x^T{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\le {\underline{\mu }}^{*}\left({\alpha }_1\right)and{x}^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}y\le {\underline{\nu }}^{*}\left({\alpha }_2\right).$$

(5)

Furthermore,

$$x^{*T}{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}+x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}-\underline{{\mu }^{*}}\left({\alpha }_1\right)-\underline{{\nu }^{*}}\left({\alpha }_2\right)\le 0.$$

If the objective function value of (1) is 0 at $(x^{*},y^{*},{\underline{\mu }}^{*}\left({\alpha }_1\right),{\underline{\nu }}^{*}\left({\alpha }_2\right))$, then

$${\underline{\mu }}^{*}\left({\alpha }_1\right)=x^{*T}{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}and{\underline{\nu }}^{*}\left({\alpha }_2\right)=x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}.$$

(6)

For each $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$, from (5) and (6) it follows that

$$x^{*T}{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}\ge x^T{\underline{\mathcal{A}}}_s^{{\alpha }_1}{y}^{*}and{x}^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}{y}^{*}\ge x^{*T}{\underline{\mathcal{B}}}_t^{{\alpha }_2}y.$$

Therefore, $(x^{*},y^{*})$ is a Pareto–Nash equilibrium of BGIP $({\mathcal{A}}_s^{{\alpha }_1},{\mathcal{B}}_t^{{\alpha }_2})$. According to Theorem 1, $(x^{*},y^{*})$ is a FPNE of $\Gamma$.

The other three cases can be verified in the same way. □

Remark 1. 

According to the proof of the sufficiency of Theorem 2, we can obtain that the optimal solution that makes the objective function value of (1) equal to 0 is the FPNE of Γ. The other three bilinear programming models have similar conclusions.

3.2. Fuzzy Weighted Pareto–Nash Equilibria

Next, we consider the fuzzy weighted Pareto–Nash equilibrium in MBGFP. Suppose that

$$\Lambda =\}({\lambda }_1,\dots ,{\lambda }_d)\in {\mathbb{R}}^d|\sum _{k=1}^d{\lambda }_k=1,{\lambda }_k\ge 0,k=1,\cdots ,d\}.$$

For $\lambda ,\eta \in \Lambda$, the fuzzy weighted expected payoff for Player I is defined by

$${\tilde{F}}_{1\lambda }(x,y)=\sum _{k=1}^d{x}^T\left({\lambda }_k{\mathcal{A}}_k\right)y,$$

where each component ${\lambda }_k$ of the vector $\lambda$ can be interpreted as the relative importance of the k-th objective to Player I.

Similarly, the fuzzy weighted expected payoff for Player II is defined by

$${\tilde{F}}_{2\eta }(x,y)=\sum _{k=1}^d{x}^T\left({\eta }_k{\mathcal{B}}_k\right)y,$$

where the component ${\eta }_k$ of the vector $\eta$ can be interpreted as the relative importance of the k-th objective to Player II.

Let $\mathcal{A}={\sum }_{k=1}^d{\lambda }_k{\mathcal{A}}_k$ and $\mathcal{B}={\sum }_{k=1}^d{\eta }_k{\mathcal{B}}_k$. Then, ${\Gamma }_{\lambda \eta }=(\mathcal{A},\mathcal{B})$ is a bi-matrix game with fuzzy payoffs (BGFP). A fuzzy Pareto–Nash equilibrium of $(\mathcal{A},\mathcal{B})$ is called a fuzzy weighted Pareto–Nash equilibrium of $\Gamma$ with weights $\lambda$ and $\eta$. In particular, if $\lambda =e_s$, $\eta =e_t$ ($s,t\in \{1,\dots ,d\}$), then $\mathcal{A}={\mathcal{A}}_s$ and $\mathcal{B}={\mathcal{B}}_s$, where $e_s$ and $e_t$ are the standard unit vectors in ${\mathbb{R}}^d$. For this case, the fuzzy weighted Pareto–Nash equilibrium of $\Gamma$ is its fuzzy Pareto–Nash equilibrium. Thus, a fuzzy Pareto–Nash equilibrium of $\Gamma$ is a special fuzzy weighted Pareto–Nash- equilibrium of $\Gamma$ with weights $e_s$ and $e_t$.

Theorem 3. 

A strategy profile $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a FWPNE of Γ with weights λ and η if and only if there exist ${\alpha }_1,{\alpha }_2\in [0,1]$ such that $(x^{*},y^{*})$ is a Pareto–Nash equilibrium of $({\mathcal{A}}^{{\alpha }_1},{\mathcal{B}}^{{\alpha }_2})$.

Proof. 

Assume that $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a FWPNE of $\Gamma$ with weights $\lambda$ and $\eta$, that is, $(x^{*},y^{*})$ is a FPNE of $(\mathcal{A},\mathcal{B})$. By Definition 4, we have

$${\left(x^{*}\right)}^T\mathcal{A}{y}^{*}\nprec x^T\mathcal{A}{y}^{*}and{\left(x^{*}\right)}^T\mathcal{B}{y}^{*}\nprec {\left(x^{*}\right)}^T\mathcal{B}y,$$

for all $(x,y)\in {\mathcal{S}}^m\times {\mathcal{S}}^n$. From Definition 2, there is ${\alpha }_1,{\alpha }_2\in [0,1]$ such that

$$x^{*T}{\underline{\mathcal{A}}}^{{\alpha }_1}{y}^{*}\ge x^T{\underline{\mathcal{A}}}^{{\alpha }_1}{y}^{*}(\mathrm{or}{x}^{*T}{\overline{\mathcal{A}}}^{{\alpha }_1}{y}^{*}\ge x^T{\overline{\mathcal{A}}}^{{\alpha }_1}{y}^{*})$$

and

$$x^{*T}{\underline{\mathcal{B}}}^{{\alpha }_2}{y}^{*}\ge x^{*T}{\underline{\mathcal{B}}}^{{\alpha }_2}y(\mathrm{or}{x}^{*T}{\overline{\mathcal{B}}}^{{\alpha }_2}{y}^{*}\ge x^{*T}{\overline{\mathcal{B}}}^{{\alpha }_2}y).$$

Then, $(x^{*},y^{*})$ is a Pareto–Nash equilibrium of $({\mathcal{A}}^{{\alpha }_1},{\mathcal{B}}^{{\alpha }_2})$. Finally, the sufficient part is obvious, according to Definition 4. □

Theorem 4. 

A strategy profile $(x^{*},y^{*})\in {\mathcal{S}}^m\times {\mathcal{S}}^n$ is a FWPNE of Γ with weights λ and η if and only if there exist ${\alpha }_1,{\alpha }_2\in [0,1]$ such that it is an optimal solution to one of the following four bilinear programming models with two parameters:

$$\begin{array}{cc}\hfill \max & \{x^T{\underline{\mathcal{A}}}^{{\alpha }_1}y+x^T{\underline{\mathcal{B}}}^{{\alpha }_2}y-\underline{\mu }\left({\alpha }_1\right)-\underline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\underline{\mathcal{A}}}^{{\alpha }_1}y\le \underline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\underline{\mathcal{B}}}^{{\alpha }_{2}T}x\le \underline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \max & \{x^T{\underline{\mathcal{A}}}^{{\alpha }_1}y+x^T{\overline{\mathcal{B}}}^{{\alpha }_2}y-\underline{\mu }\left({\alpha }_1\right)-\overline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\underline{\mathcal{A}}}^{{\alpha }_1}y\le \underline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\overline{\mathcal{B}}}^{{\alpha }_{2}T}x\le \overline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \max & \{x^T{\overline{\mathcal{A}}}^{{\alpha }_1}y+x^T{\underline{\mathcal{B}}}^{{\alpha }_2}y-\overline{\mu }\left({\alpha }_1\right)-\underline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\overline{\mathcal{A}}}^{{\alpha }_1}y\le \overline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\underline{\mathcal{B}}}^{{\alpha }_{2}T}x\le \underline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \max & \{x^T{\overline{\mathcal{A}}}^{{\alpha }_1}y+x^T{\overline{\mathcal{B}}}^{{\alpha }_2}y-\overline{\mu }\left({\alpha }_1\right)-\overline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & {\overline{\mathcal{A}}}^{{\alpha }_1}y\le \overline{\mu }\left({\alpha }_1\right)e^m,\hfill \\ \hfill & {\overline{\mathcal{B}}}^{{\alpha }_{2}T}x\le \overline{\nu }\left({\alpha }_2\right)e^n,\hfill \\ \hfill & x^T{e}^m=1,\hfill \\ \hfill & y^T{e}^n=1,\hfill \\ \hfill & x,y\ge 0,\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(10)

where $e^m={\left(\underset{m}{\underbrace{1,1,\cdots ,1}}\right)}^T$ and $e^n={\left(\underset{n}{\underbrace{1,1,\cdots ,1}}\right)}^T$.

Proof. 

The argument is similar to that of Theorem 2. □

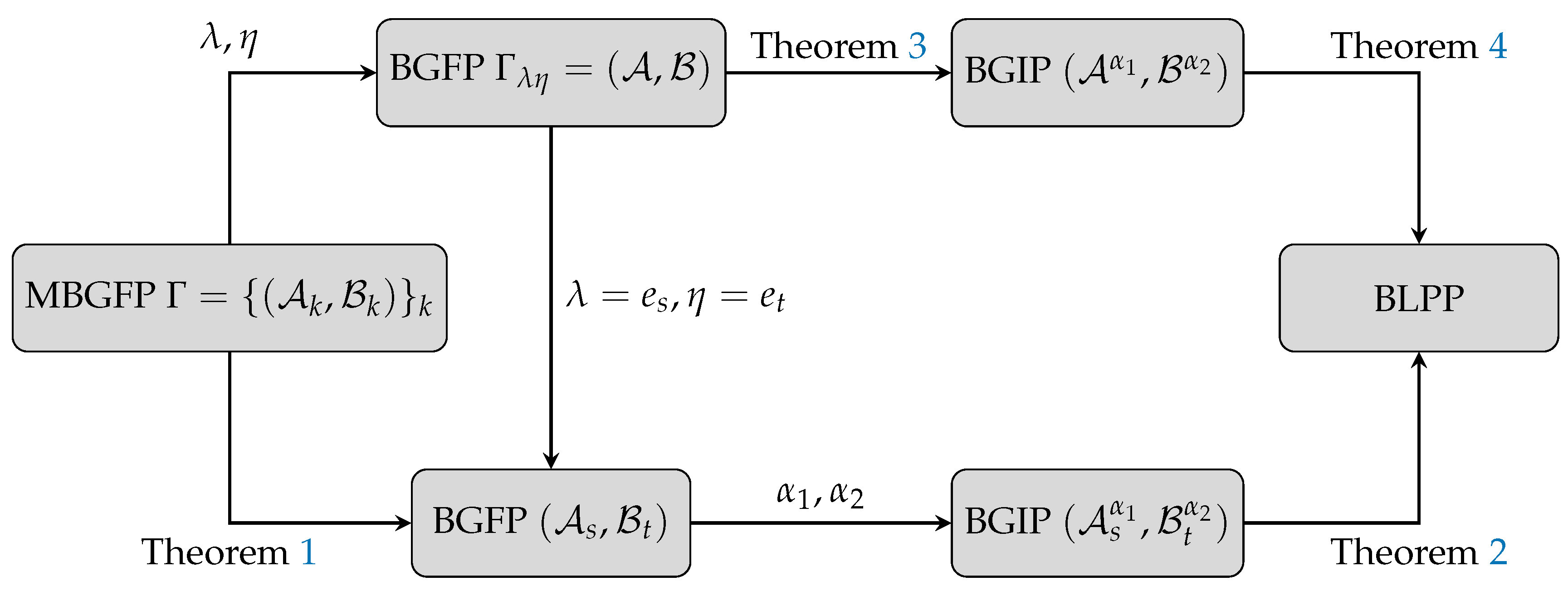
Theorems 1 and 3 illustrate that both the FWPNE and FPNE of MBGFP can be converted into the Pareto–Nash equilibrium of a certain BGIP. From Lemma 1, the Pareto–Nash equilibrium of BGIP can be transformed into four Nash equilibria of crisp bi-matrix games. Through the bilinear programming method, Theorems 2 and 4 further provide the calculation methods for FWPNE and FPNE, which aim to solve bilinear programming problems with parameters (BLPP). The relationship between FWPNE and FPNE, and their calculation methods are presented in Figure 1.

Remark 2. 

Multi-objective matrix games with fuzzy payoffs have been discussed in the literature [24,25], but the idea of obtaining fuzzy (weighted) Pareto–Nash equilibrium based on fuzzy maximum order has never appeared.

1. 

Bigdeli and Hassanpour [25] researched the multi-objective zero-sum matrix games with triangular fuzzy numbers. They first transformed the multi-objective zero-sum matrix game into a multi-objective interval mathematical programming problem. By considering the weight of each objective to the player and the satisfactory crisp equivalent form of interval inequality constraints, the multi-objective interval mathematical programming problem is converted into two linear programming problem. Finally, an interactive algorithm is presented to obtain the satisfactory strategy of the player. However, the interactive algorithm is only applicable when the payoffs are triangular fuzzy numbers. The multi-objective zero-sum matrix game is a special case of multi-objective bi-matrix game. Using the method given in Section 3, we reanalyze and calculate numerical example in [25], see Appendix A.

2. 

Nishizaki and Sakawa [24] mainly discussed multi-objective bi-matrix games with triangular fuzzy numbers (symmetric fuzzy numbers). By introducing the fuzzy goal (linear fuzzy number) of the player, the attainment functions of two players are constructed. Furthermore, the game is transformed into a two-player crisp game. Since the attainment function is nonlinear, the mathematical programming model is relatively complex, and the equilibrium solution of the game is difficult to calculate in practical applications.

4. Application

In this section, we consider how two companies (Company I and Company II) maximize their profits. They produce two identical clothing types: Type I (casual and natural) and Type II (intellectual elegance). In order to increase profits, they have two strategies: Strategy I (to reduce the price) and Strategy II (advertisement).

Because of the lack of information, managers cannot accurately assess the profits obtained by various clothing types. To handle an uncertain situation, triangular fuzzy numbers are used to represent the profit obtained by each clothing type. Therefore, the problem can be regarded as a two-objective bi-matrix game with fuzzy payoffs. That is, Companies I and II are considered as Players I and II, and two clothing types are considered as the two objectives of Players I and II, respectively.

Example 1. 

The market research departments of Companies I and II have respectively established the following fuzzy payoff matrices:

$$\begin{array}{cc}& {\gamma }_1{\gamma }_2\\ {\mathcal{A}}_1=\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}& \left(\begin{array}{cc}(13.25,14.00,14.80)& (14.25,15.00,15.50)\\ (15.75,16.00,16.25)& (13.50,14.00,14.70)\end{array}\right)\end{array}$$

$$\begin{array}{cc}& {\gamma }_1{\gamma }_2\\ {\mathcal{A}}_2=\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}& \left(\begin{array}{cc}(12.80,13.00,13.50)& (14.45,15.00,15.55)\\ (13.45,14.00,14.50)& (12.60,13.00,13.80)\end{array}\right)\end{array}$$

$$\begin{array}{cc}& {\gamma }_1{\gamma }_2\\ {\mathcal{B}}_1=\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}& \left(\begin{array}{cc}(12.60,13.00,13.75)& (13.50,14.00,14.55)\\ (13.55,14.00,14.25)& (12.30,13.00,13.60)\end{array}\right)\end{array}$$

$$\begin{array}{cc}& {\gamma }_1{\gamma }_2\\ {\mathcal{B}}_2=\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}& \left(\begin{array}{cc}(15.25,16.00,16.80)& (17.35,18.00,18.20)\\ (17.20,18.00,18.50)& (14.50,15.00,15.45)\end{array}\right),\end{array}$$

where ${\beta }_1$, ${\beta }_2$ are two strategies for Company I, and ${\gamma }_1$, ${\gamma }_2$ are two strategies for Company II, respectively.

The MBGFP $\Gamma ={\left\{({\mathcal{A}}_k,{\mathcal{B}}_k)\right\}}_{k\in \{1,2\}}$ with weights $\lambda$ and $\eta$ can be transformed into the following BGFP ${\Gamma }_{\lambda \eta }=(\mathcal{A},\mathcal{B})$, where $\lambda$ and $\eta$ respectively represent the relative importance of two clothing types. Let $\lambda =(0.7,0.3)$ and $\eta =(0.4,0.6)$, then

$$\mathcal{A}=0.7{\mathcal{A}}_1+0.3{\mathcal{A}}_2=\left(\begin{array}{cc}(13.115,13.700,14.410)& (14.310,15.000,15.515)\\ (15.060,15.400,15.725)& (13.230,13.700,14.430)\end{array}\right)$$

and

$$\mathcal{B}=0.4{\mathcal{B}}_1+0.6{\mathcal{B}}_2=\left(\begin{array}{cc}(14.190,14.800,15.580)& (15.810,16.400,16.740)\\ (15.740,16.400,16.800)& (13.620,14.200,14.710)\end{array}\right).$$

The fuzzy-valued expected payoffs for Companies I and II are, respectively

$${\tilde{F}}_{1\lambda }(x,y)=x^T\mathcal{A}y=(x^T{A}_{1}y,x^T{A}_{2}y,x^T{A}_{3}y)$$

and

$${\tilde{F}}_{2\eta }(x,y)=x^T\mathcal{B}y=(x^T{B}_{1}y,x^T{B}_{2}y,x^T{B}_{3}y),$$

for $(x,y)\in {\mathcal{S}}^2\times {\mathcal{S}}^2$, where

$$\begin{array}{cc}\hfill x^T{A}_{1}y=& 13.115x_1{y}_1+14.310x_1{y}_2+15.060x_2{y}_1+13.230x_2{y}_2,\hfill \\ \hfill x^T{A}_{2}y=& 13.700x_1{y}_1+15.000x_1{y}_2+15.400x_2{y}_1+13.700x_2{y}_2,\hfill \\ \hfill x^T{A}_{3}y=& 14.410x_1{y}_1+15.515x_1{y}_2+15.725x_2{y}_1+14.430x_2{y}_2,\hfill \\ \hfill x^T{B}_{1}y=& 14.190x_1{y}_1+15.810x_1{y}_2+15.740x_2{y}_1+13.620x_2{y}_2,\hfill \\ \hfill x^T{B}_{2}y=& 14.800x_1{y}_1+16.400x_1{y}_2+16.400x_2{y}_1+14.200x_2{y}_2,\hfill \\ \hfill x^T{B}_{3}y=& 15.580x_1{y}_1+16.740x_1{y}_2+16.800x_2{y}_1+14.710x_2{y}_2.\hfill \end{array}$$

For ${\alpha }_1,{\alpha }_2\in [0,1]$, the BGFP ${\Gamma }_{\lambda \eta }$ can be transformed into the BGIP ${\Gamma }_{\lambda \eta }({\alpha }_1,{\alpha }_2)=({\mathcal{A}}_1^{\alpha },{\mathcal{B}}_2^{\alpha })$, where

$${\mathcal{A}}^{{\alpha }_1}=\left(\begin{array}{cc}[13.115+0.585{\alpha }_1,14.410-0.710{\alpha }_1]& [14.310+0.690{\alpha }_1,15.515-0.515{\alpha }_1]\\ [15.060+0.340{\alpha }_1,15.725-0.325{\alpha }_1]& [13.230+0.470{\alpha }_1,14.430-0.730{\alpha }_1]\end{array}\right)$$

and

$${\mathcal{B}}^{{\alpha }_2}=\left(\begin{array}{cc}[14.190+0.610{\alpha }_2,15.580-0.780{\alpha }_2]& [15.810+0.590{\alpha }_2,16.740-0.340{\alpha }_2]\\ [15.740+0.660{\alpha }_2,16.800-0.400{\alpha }_2]& [13.620+0.580{\alpha }_2,14.710-0.510{\alpha }_2]\end{array}\right).$$

From Theorem 3 and Lemma 1, for each ${\alpha }_1,{\alpha }_2\in [0,1]$, MBGFP $\Gamma$ has four FWPNEs. Due to Theorem 4, we only need to calculate FWPNEs of $\Gamma$. From (7)–(10), four bilinear programming models with two parameters are constructed as follows:

$$\begin{array}{cc}\hfill \max & \{(27.305+0.585{\alpha }_1+0.61{\alpha }_2)x_1{y}_1+(30.12+0.69{\alpha }_1+0.59{\alpha }_2)x_1{y}_2+\hfill \\ \hfill & (30.8+0.34{\alpha }_1+0.66{\alpha }_2)x_2{y}_1+(26.85+0.47{\alpha }_1+0.58{\alpha }_2)x_2{y}_2-\underline{\mu }\left({\alpha }_1\right)-\underline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & (13.115+0.585{\alpha }_1)y_1+(14.31+0.69{\alpha }_1)y_2\le \underline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (15.06+0.34{\alpha }_1)y_1+(13.23+0.47{\alpha }_1)y_2\le \underline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (14.19+0.61{\alpha }_2)x_1+(15.74+0.66{\alpha }_2)x_2\le \underline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & (15.81+0.59{\alpha }_2)x_1+(13.62+0.58{\alpha }_2)x_2\le \underline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & x_1+x_2=1,y_1+y_2=1,\hfill \\ \hfill & x_1,x_2,y_1,y_2\ge 0,{\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \max & \{(28.695+0.585{\alpha }_1-0.78{\alpha }_2)x_1{y}_1+(31.05+0.69{\alpha }_1-0.34{\alpha }_2)x_1{y}_2+\hfill \\ \hfill & (31.86+0.34{\alpha }_1-0.4{\alpha }_2)x_2{y}_1+(27.94+0.47{\alpha }_1-0.51{\alpha }_2)x_2{y}_2-\underline{\mu }\left({\alpha }_1\right)-\overline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & (13.115+0.585{\alpha }_1)y_1+(14.31+0.69{\alpha }_1)y_2\le \underline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (15.06+0.34{\alpha }_1)y_1+(13.23+0.47{\alpha }_1)y_2\le \underline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (15.58-0.78{\alpha }_2)x_1+(16.8-0.4{\alpha }_2)x_2\le \overline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & (16.74-0.34{\alpha }_2)x_1+(14.71-0.51{\alpha }_2)x_2\le \overline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & x_1+x_2=1,y_1+y_2=1,\hfill \\ \hfill & x_1,x_2,y_1,y_2\ge 0,{\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \max & \{(28.6-0.71{\alpha }_1+0.61{\alpha }_2)x_1{y}_1+(31.325-0.515{\alpha }_1+0.59{\alpha }_2)x_1{y}_2+\hfill \\ \hfill & (31.465-0.325{\alpha }_1+0.66{\alpha }_2)x_2{y}_1+(28.05-0.73{\alpha }_1+0.58{\alpha }_2)x_2{y}_2-\overline{\mu }\left({\alpha }_1\right)-\underline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & (14.41-0.71{\alpha }_1)y_1+(15.515-0.515{\alpha }_1)y_2\le \overline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (15.725-0.325{\alpha }_1)y_1+(14.43-0.73{\alpha }_1)y_2\le \overline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (14.19+0.61{\alpha }_2)x_1+(15.74+0.66{\alpha }_2)x_2\le \underline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & (15.81+0.59{\alpha }_2)x_1+(13.62+0.58{\alpha }_2)x_2\le \underline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & x_1+x_2=1,y_1+y_2=1,\hfill \\ \hfill & x_1,x_2,y_1,y_2\ge 0,{\alpha }_1,{\alpha }_2\in [0,1].\hfill \end{array}\right.\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \max & \{(29.99-0.71{\alpha }_1-0.78{\alpha }_2)x_1{y}_1+(32.255-0.515{\alpha }_1-0.34{\alpha }_2)x_1{y}_2+\hfill \\ \hfill & (32.525-0.325{\alpha }_1-0.4{\alpha }_2)x_2{y}_1+(29.14-0.73{\alpha }_1-0.51{\alpha }_2)x_2{y}_2-\overline{\mu }\left({\alpha }_1\right)-\overline{\nu }\left({\alpha }_2\right)\}\hfill \\ \hfill s.t.& \left\{\begin{array}{cc}\hfill & (14.41-0.71{\alpha }_1)y_1+(15.515-0.515{\alpha }_1)y_2\le \overline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (15.725-0.325{\alpha }_1)y_1+(14.43-0.73{\alpha }_1)y_2\le \overline{\mu }\left({\alpha }_1\right),\hfill \\ \hfill & (15.58-0.78{\alpha }_2)x_1+(16.8-0.4{\alpha }_2)x_2\le \overline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & (16.74-0.34{\alpha }_2)x_1+(14.71-0.51{\alpha }_2)x_2\le \overline{\nu }\left({\alpha }_2\right),\hfill \\ \hfill & x_1+x_2=1,y_1+y_2=1,\hfill \\ \hfill & x_1,x_2,y_1,y_2\ge 0,{\alpha }_1,{\alpha }_2\in [0,1];\hfill \end{array}\right.\hfill \end{array}$$

(14)

The parameters ${\alpha }_1$ and ${\alpha }_2$ within Formulas (11)–(14) can be controlled by decision makers. Let ${\alpha }_1=0.2,{\alpha }_2=0.5$, we can obtain an optimal solution $(x^{*},y^{*},\underline{\mu }\left(0.2\right),\underline{\nu }\left(0.5\right))$ of (11) using the Lingo software, where $x^{*}=(0.5729,0.4271)$, $y^{*}=(0.3722,0.6278)$, $\underline{\mu }\left(0.2\right)=13.9954$, $\underline{\nu }\left(0.5\right)=15.1676$. In addition, we obtain an optimal solution of (12), where $x^{*}=(0.6085,0.3915)$, $y^{*}=(0.3722,0.6278)$, $\underline{\mu }\left(0.2\right)=13.9954$, $\overline{\nu }\left(0.5\right)=15.7420$; an optimal solution of (13), where $x^{*}=(0.5729,0.4271)$, $y^{*}=(0.4476,0.5524)$, $\overline{\mu }\left(0.2\right)=14.8999$, $\underline{\nu }\left(0.5\right)=15.1676$; and an optimal solution of (14), where $x^{*}=(0.6085,0.3915)$, $y^{*}=(0.4476,0.5524)$, $\overline{\mu }\left(0.2\right)=14.8999$, $\overline{\nu }\left(0.5\right)=15.7420$. Four fuzzy weighted Pareto–Nash equilibria of $\Gamma$ and the corresponding fuzzy-valued expected payoffs of Companies I and II are collected in

Table 1. The FWPNEs and fuzzy expected payoffs for Companies I and II ($\lambda =(0.7,0.3)$, $\eta =(0.4,0.6)$).

${\mathit{x}}_1^{*}$	${\mathit{x}}_2^{*}$	${\mathit{y}}_1^{*}$	${\mathit{y}}_2^{*}$	${\tilde{\mathit{F}}}_{1(0.7,0.3)}({\mathit{x}}^{*},{\mathit{y}}^{*})$	${\tilde{\mathit{F}}}_{2(0.4,0.6)}({\mathit{x}}^{*},{\mathit{y}}^{*})$
0.5729	0.4271	0.3722	0.6278	(13.8848, 14.4378, 15.0218)	(14.8662, 15.4689, 15.9579)
0.6085	0.3915	0.3722	0.6278	(13.8832, 14.4443, 15.0287)	(14.8946, 15.4969, 15.9871)
0.5729	0.4271	0.4476	0.5524	(13.8921, 14.4364, 15.0158)	(14.8645, 15.4707, 15.9751)
0.6085	0.3915	0.4476	0.5524	(13.8824, 14.4349, 15.0162)	(14.8829, 15.4884, 15.9956)

.

Similar to the calculation method of fuzzy weighted Pareto–Nash equilibria, letting $\lambda =(1,0)$, $\eta =(1,0)$, ${\alpha }_1=0.2$, ${\alpha }_2=0.5$, we can obtain fuzzy Pareto–Nash equilibria of $({\mathcal{A}}_1,{\mathcal{B}}_1)$ and the corresponding fuzzy-valued expected payoffs of Companies I and II, see

Table 2. The FWPNEs and fuzzy expected payoffs for Companies I and II ($\lambda =(1,0)$, $\eta =(1,0)$).

${\mathit{x}}_1^{*}$	${\mathit{x}}_2^{*}$	${\mathit{y}}_1^{*}$	${\mathit{y}}_2^{*}$	${\tilde{\mathit{F}}}_{1(1,0)}({\mathit{x}}^{*},{\mathit{y}}^{*})$	${\tilde{\mathit{F}}}_{2(1,0)}({\mathit{x}}^{*},{\mathit{y}}^{*})$
0.5422	0.4578	0.2500	0.7500	(14.0286, 14.6356, 15.2163)	(12.9717, 13.5211, 14.0810)
0.4783	0.5217	0.2500	0.7500	(14.0326, 14.6196, 15.2011)	(12.9294, 13.4892, 14.0435)
0.5422	0.4578	0.3500	0.6500	(14.0774, 14.6729, 15.2493)	(12.9801, 13.5127, 14.0674)
0.4783	0.5217	0.3500	0.6500	(14.1022, 14.6761, 15.2485)	(12.9515, 13.4935, 14.0391)

. Meanwhile, the fuzzy Pareto–Nash equilibria of $({\mathcal{A}}_2,{\mathcal{B}}_2)$, $({\mathcal{A}}_1,{\mathcal{B}}_2)$, and $({\mathcal{A}}_2,{\mathcal{B}}_1)$ are shown in

Table 3. The FWPNEs and fuzzy expected payoffs for Companies I and II ($\lambda =(0,1)$, $\eta =(0,1)$).

${\mathit{x}}_1^{*}$	${\mathit{x}}_2^{*}$	${\mathit{y}}_1^{*}$	${\mathit{y}}_2^{*}$	${\tilde{\mathit{F}}}_{1(0,1)}({\mathit{x}}^{*},{\mathit{y}}^{*})$	${\tilde{\mathit{F}}}_{2(0,1)}({\mathit{x}}^{*},{\mathit{y}}^{*})$
0.5816	0.4184	0.7231	0.2769	(13.2070, 13.6246, 14.1674)	(16.0913, 16.8113, 17.3834)
0.6402	0.3598	0.7231	0.2769	(13.2062, 13.6147, 14.1535)	(16.0549, 16.7753, 17.3560)
0.5816	0.4184	0.6429	0.3571	(13.2461, 13.6844, 14.2396)	(16.0986, 16.8039, 17.3463)
0.6402	0.3598	0.6429	0.3571	(13.2562, 13.6885, 14.2385)	(16.0848, 16.7914, 17.3398)

,

Table 4. The FWPNEs and fuzzy expected payoffs for Companies I and II ($\lambda =(1,0)$, $\eta =(0,1)$).

${\mathit{x}}_1^{*}$	${\mathit{x}}_2^{*}$	${\mathit{y}}_1^{*}$	${\mathit{y}}_2^{*}$	${\tilde{\mathit{F}}}_{1(1,0)}({\mathit{x}}^{*},{\mathit{y}}^{*})$	${\tilde{\mathit{F}}}_{2(0,1)}({\mathit{x}}^{*},{\mathit{y}}^{*})$
0.5816	0.4184	0.2500	0.7500	(14.0262, 14.6454, 15.2256)	(16.1346, 16.7678, 17.1649)
0.6402	0.3598	0.2500	0.7500	(14.0225, 14.6601, 15.2395)	(16.2313, 16.8704, 17.2608)
0.5816	0.4184	0.3500	0.6500	(14.0621, 14.6709, 15.2498)	(16.1255, 16.7770, 17.2111)
0.6402	0.3598	0.3500	0.6500	(14.0394, 14.6680, 15.2505)	(16.1940, 16.8503, 17.2809)

and

Table 5. The FWPNEs and fuzzy expected payoffs for Companies I and II ($\lambda =(0,1)$, $\eta =(1,0)$).

${\mathit{x}}_1^{*}$	${\mathit{x}}_2^{*}$	${\mathit{y}}_1^{*}$	${\mathit{y}}_2^{*}$	${\tilde{\mathit{F}}}_{1(0,1)}({\mathit{x}}^{*},{\mathit{y}}^{*})$	${\tilde{\mathit{F}}}_{2(1,0)}({\mathit{x}}^{*},{\mathit{y}}^{*})$
0.5422	0.4578	0.7231	0.2769	(13.2075, 13.6313, 14.1768)	(13.0116, 13.4812, 14.0166)
0.4783	0.5217	0.7231	0.2769	(13.2084, 13.6421, 14.1921)	(13.0342, 13.5097, 14.0229)
0.5422	0.4578	0.6429	0.3571	(13.2394, 13.6816, 14.2403)	(13.0048, 13.4879, 14.0275)
0.4783	0.5217	0.6429	0.3571	(13.2284, 13.6770, 14.2414)	(13.0165, 13.5062, 14.0264)

, respectively.

Through the analysis of Table 1, Table 2, Table 3, Table 4 and Table 5, we see that the fuzzy expected payoffs of Companies I and II in Table 4 are better than other situations. Therefore, Company I give priority to the first objective (Type I: casual and natural), and Company II give priority to the second objective (Type II: intellectual elegance).

Taking Table 4 as an example, we illustrate that four FPNEs cannot be replaced by one of them. For example, Company II chooses $y^{*}=(0.2500,0.7500)$ and Company I changes its strategy $x^{*}$ from $(0.6402,0.3598)$ to $(0.5816,0.4184)$, the corresponding fuzzy expected payoff of Company I does not become better due to $(14.0225,14.6601,15.2395)\nprec (14.0262,14.6454,15.2256)$. Similarly, Company I chooses $x^{*}=(0.5816,0.4184)$ and Company II changes its strategy $y^{*}$ from $(0.2500,0.7500)$ to $(0.3500,0.6500)$. The corresponding fuzzy expected payoff of Company II does not become better due to $(16.1346,16.7678,17.1649)\nprec (16.1255,16.7770,17.2111)$. However, simultaneous changes in the strategies of two companies are not within the scope of FPNE’s definition. In Table 4, since $(14.0262,14.6454,15.2256)\prec (14.0394,14.6680,15.2505)$ and $(16.1346,16.7678,17.1649)\prec (16.1940,16.8503,17.2809)$, Company I can choose to strategy $(0.6402,0.3598)$ instead of $(0.5816,0.4184)$, and Company II can also choose to strategy $(0.3500,0.6500)$ instead of $(0.2500,0.7500)$. However, this does not affect the fact that both strategy profiles are FPNE. A company’s own expected payoffs will not be better if it changes its strategy while another company’s strategy remains unchanged. At this time, the strategy combination of the two companies is the FPNE of the competition problem.

5. Conclusions

This paper mainly studies multi-objective bi-matrix games with fuzzy payoffs. This study differs from previous literature in the following two aspects. First, the fuzzy payoff in our game model is a general fuzzy number proposed by Dubois and Prade [37]. Secondly, under the partial order of fuzzy vector values [26], we give the concept of fuzzy Pareto–Nash equilibrium of MBGFP, which is an equilibrium that makes the fuzzy-vector-valued expected payoffs of the players reach Pareto optimality. Furthermore, by considering the weight of each objective in the MBGFP, the weighted MBGFP is transformed into a BGFP, and the concept of fuzzy weighted Pareto–Nash equilibrium is obtained. Finally, the necessary and sufficient conditions for the existence of FPNE and FWPNE of MBGFP and their calculation method are established. This calculation method is feasible for general fuzzy payoffs.

The concepts of FPNE and FWPNE are given based on the fuzzy maximum order. The advantage of this partial order is that it compares two fuzzy numbers while retaining all their characteristics. However, it has relatively high requirements for comparable fuzzy numbers. Some fuzzy numbers that we can intuitively judge as well or bad may not be comparable under this partial order. For example, $\tilde{a}=(1,3,5)$ and $\tilde{b}=(2,3,4)$. We aim to establish a partial order on $\mathcal{F}\left(\mathbb{R}\right)$ that allows for comparisons between more fuzzy numbers while preserving essential characteristics. Furthermore, under the new partial order, we further refine the equilibrium obtained in this article, which is the focus of our future research.