Mathematical Modeling Reveals Mechanisms of Cancer-Immune Interactions Underlying Hepatocellular Carcinoma Development
Abstract
:1. Introduction
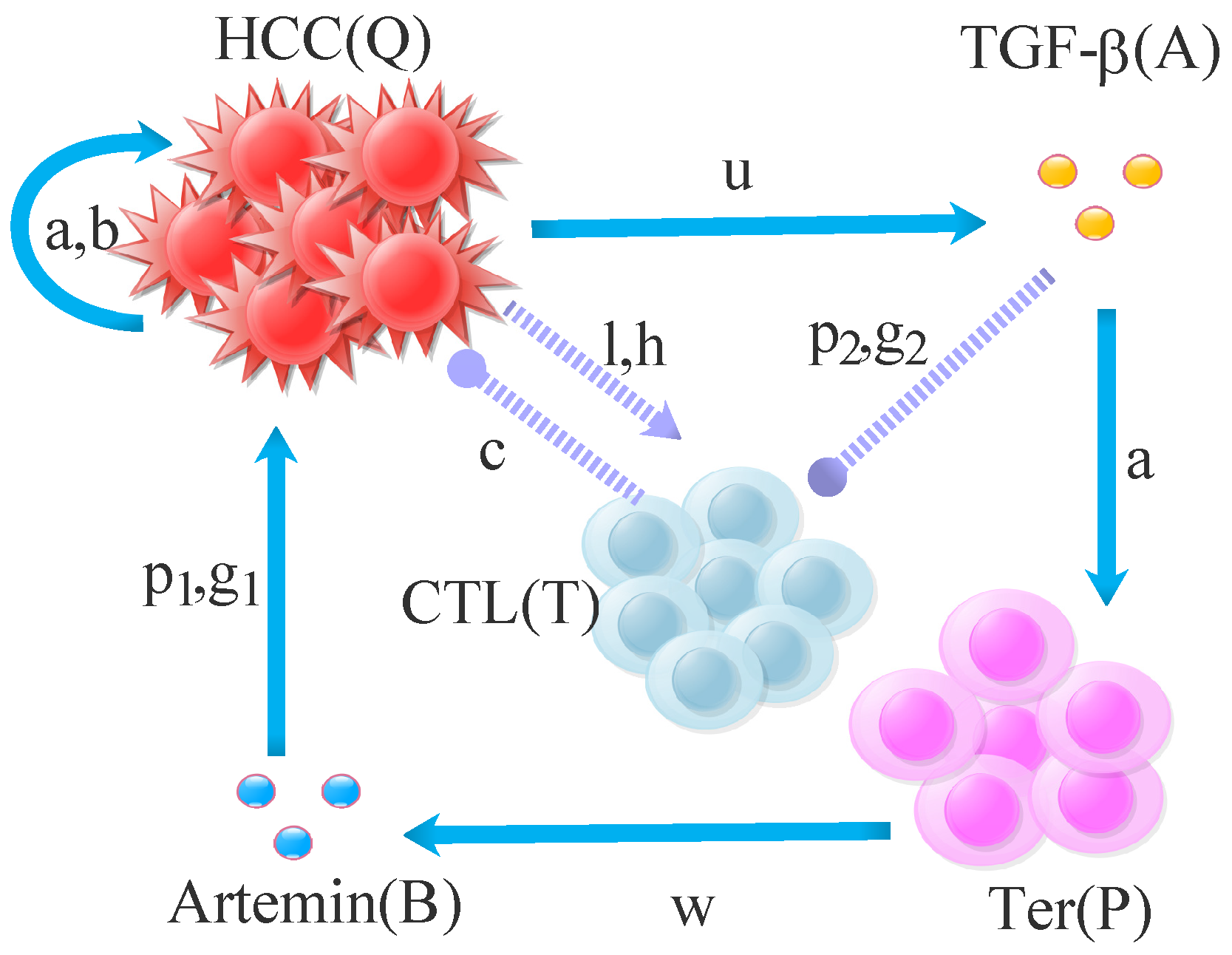
2. Mathematical Modeling
3. Theoretical Properties of the Model
3.1. Nonnegativity of Solutions
3.2. Nonnegative Invariant
3.3. Existence and Local Stability of Equilibrium Points
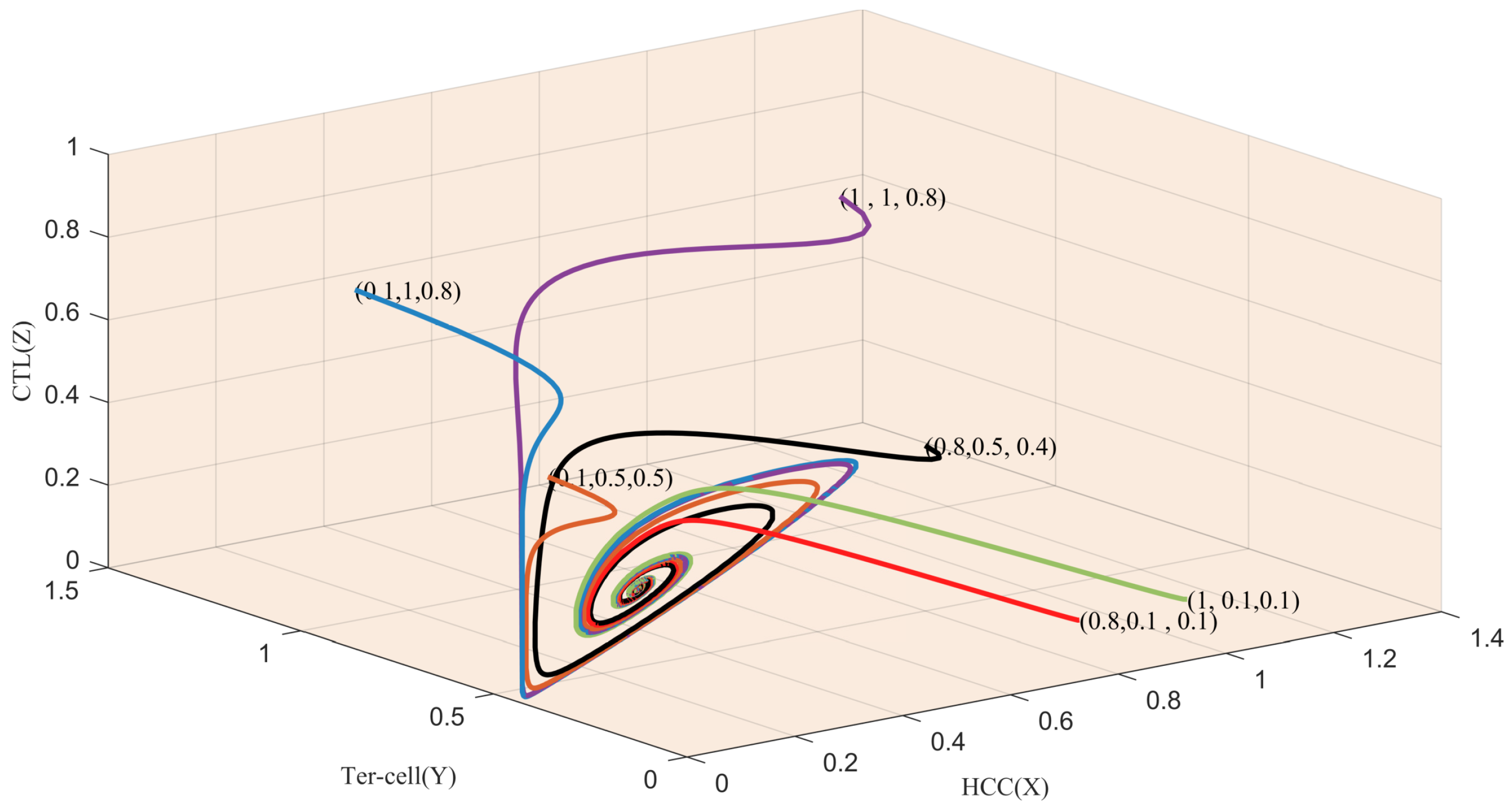
4. Numerical Results
4.1. Sensitivity Analysis of Parameters
4.2. Numerical Simulations Reveal Possible Methods of Cancer Treatment
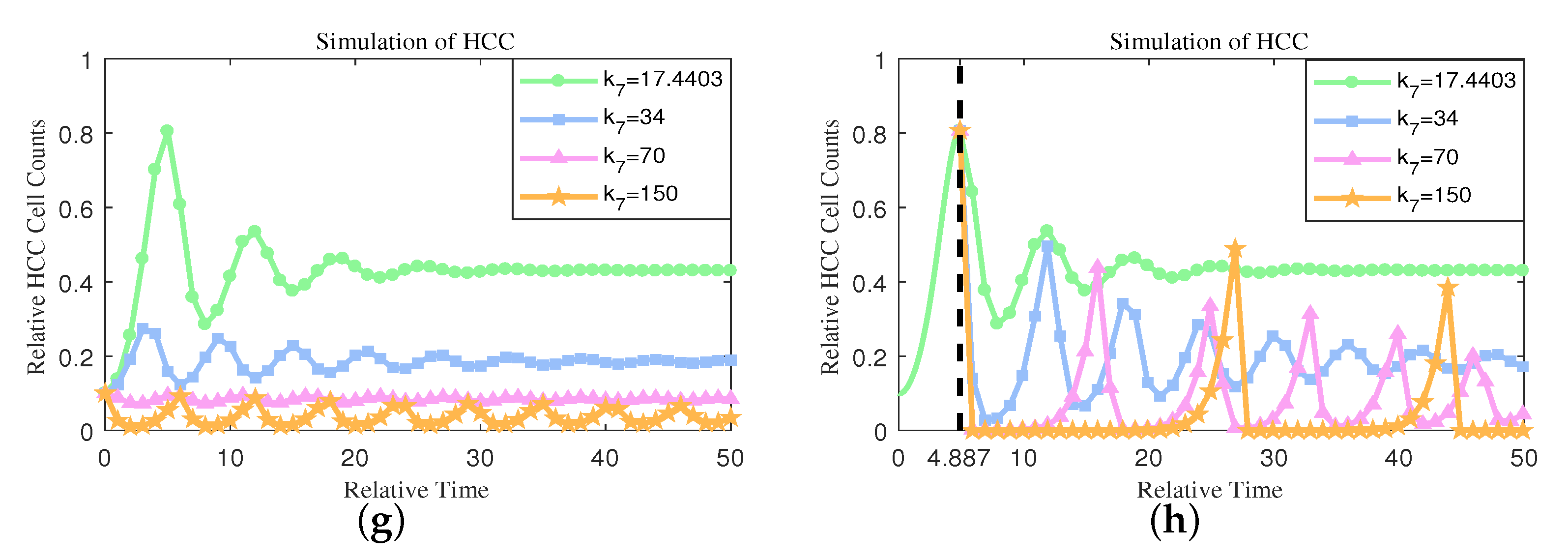
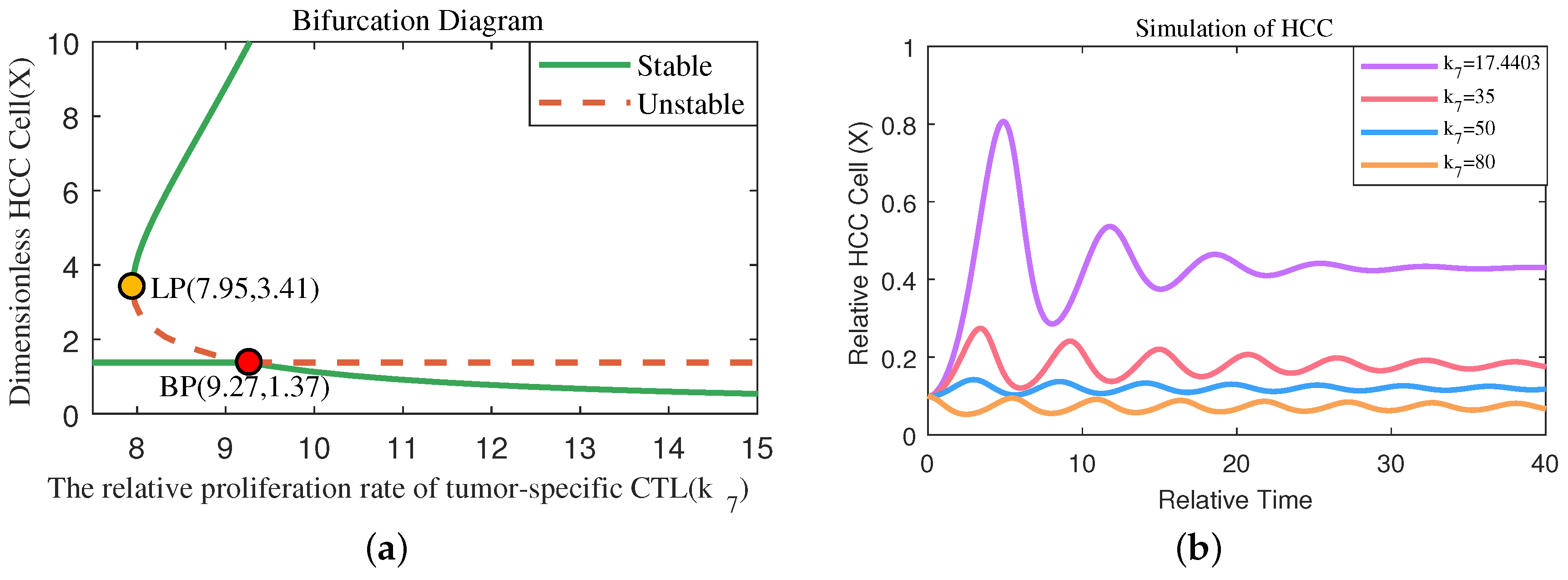
4.3. One-Parameter Bifurcation Analysis Reveals the Significant Effect of Immunity Activation
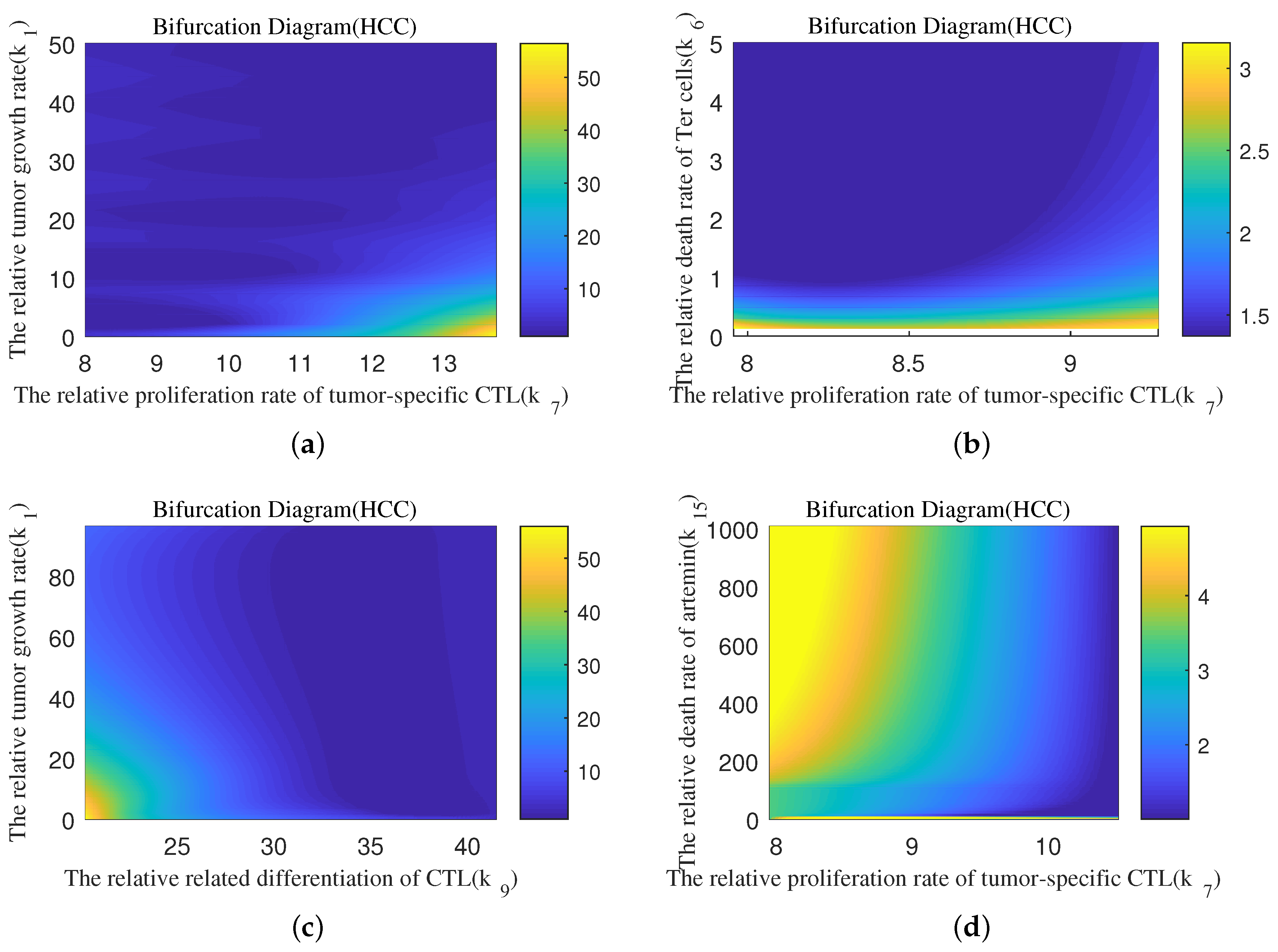
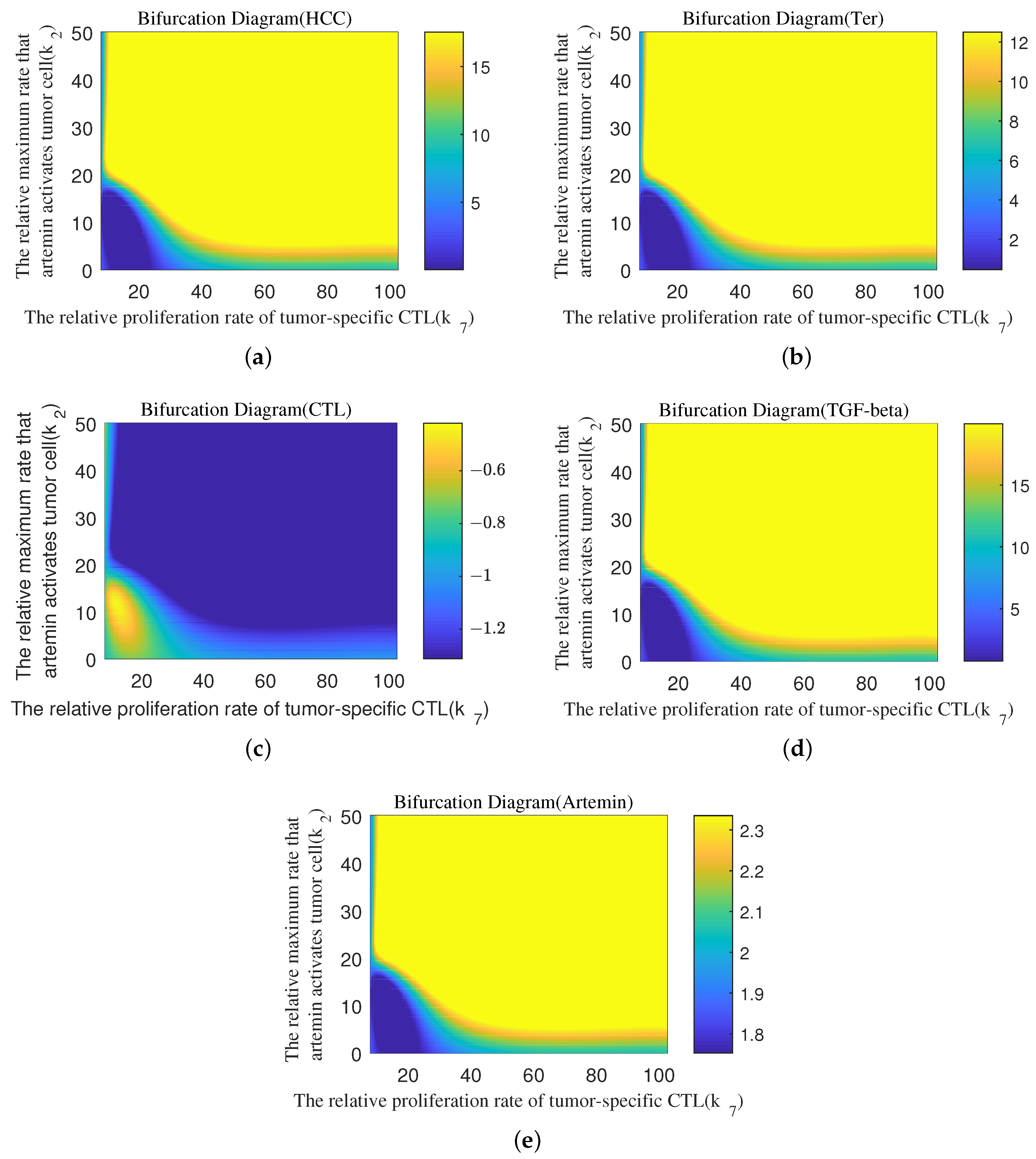
4.4. Quantitative Analysis of Parameter Interactions
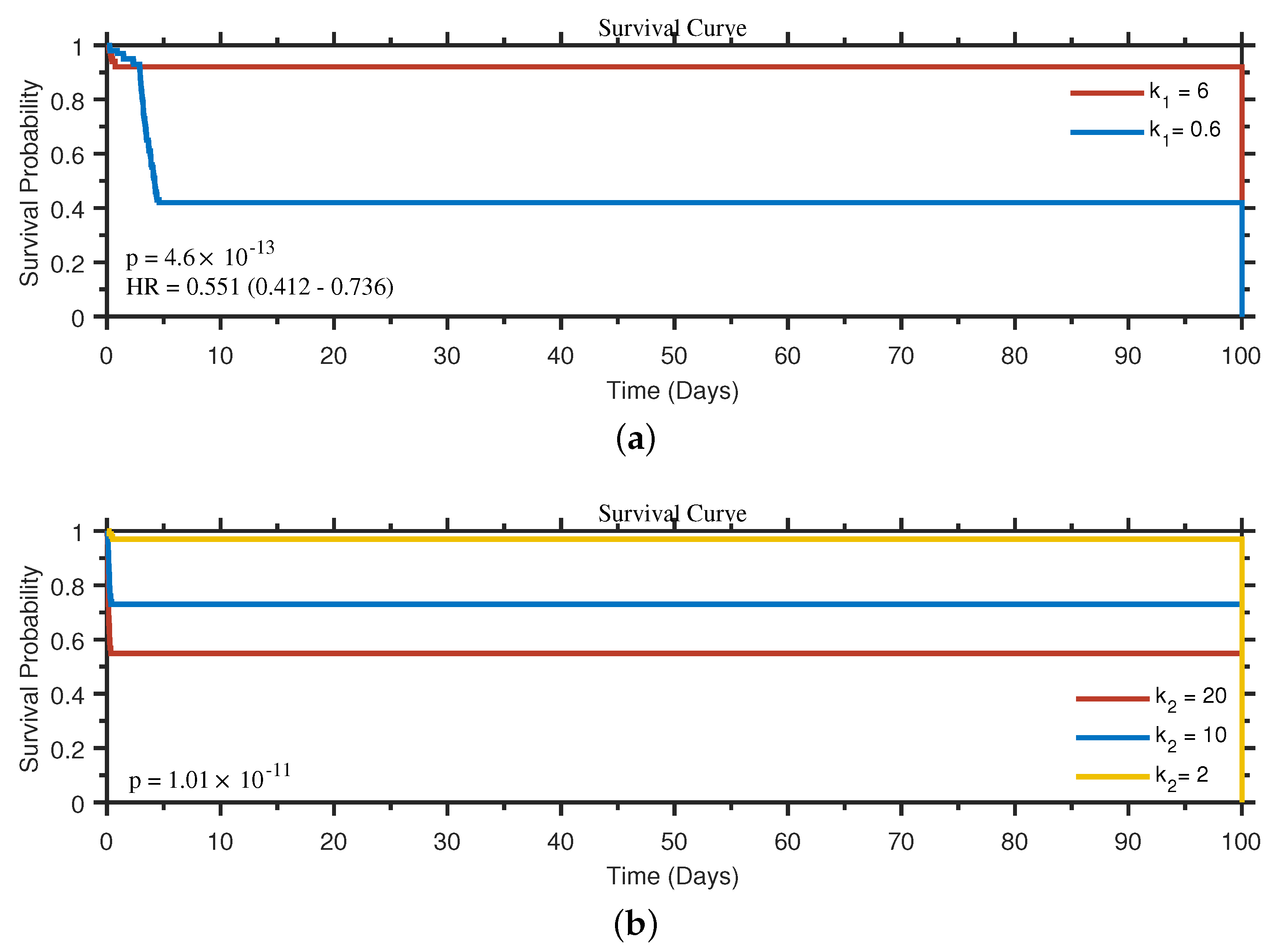
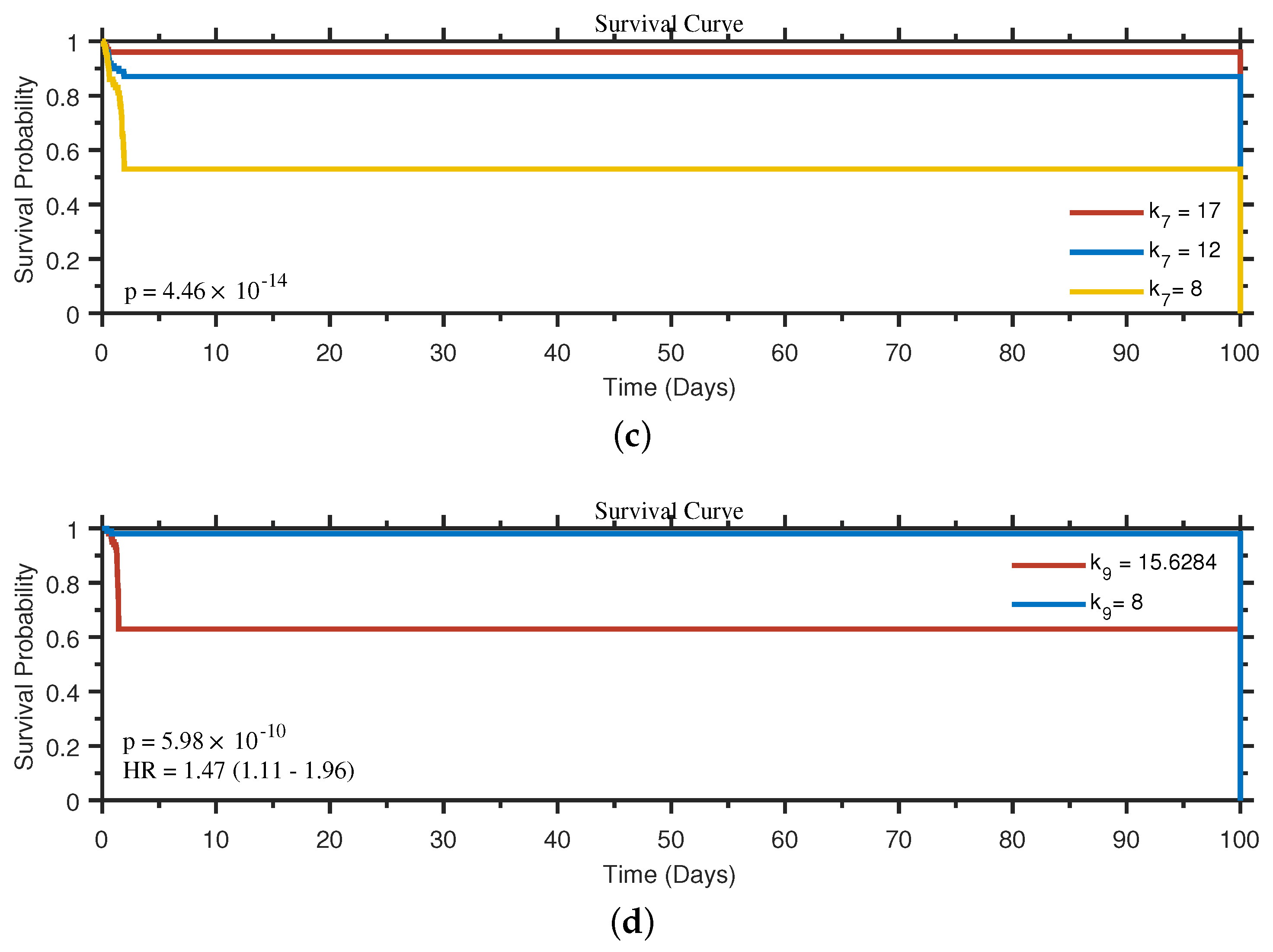
4.5. Survival Analysis Based on the Influence of Biological Processes
5. Conclusions & Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameters
| Symbol | Units | Biological Meanings |
|---|---|---|
| a | Tumor growth rate | |
| b | tumor carrying capacity | |
| c | Killing rate of T cells on tumor cells | |
| The maximum rate that artemin activates tumor cell | ||
| Steepness coefficient of the HCC proliferation curve | ||
| Rate at which Ter cells are generated by TGF- | ||
| r | Death rate of Ter cells | |
| l | The proliferation rate of tumor-specific CTL | |
| h | Number of HCC when the producing rate reaches half of l | |
| TGF- related differentiation of CTL | ||
| Coefficient of CTL differentiation | ||
| e | Death rate of CTL | |
| u | Producing rate of TGF- by HCC | |
| v | Death rate of TGF- | |
| w | Producing rate of artemin by Ter cell | |
| k | Death rate of artemin | |
| Initial concentration of TGF- | ||
| Initial Concentration artemin | ||
| Production rate of TGF- | ||
| Production rate of artemin |
| Symbol | Values | Biological Meanings | Range |
|---|---|---|---|
| 0.690266 | The relative tumor growth rate | [0, 20] | |
| 2.75862 | The relative maximum rate that artemin activates tumor cell | [0, 20] | |
| 17.2953 | The relative steepness coefficient of the HCC proliferation curve | [0, 20] | |
| 8.48557 | The relative killing rate of T cells on tumor cells | [0, 20] | |
| 11.3891 | The relative rate at which Ter cells are generated by TGF- | [0, 20] | |
| 18.1833 | The relative death rate of Ter cells | [0, 20] | |
| 17.4403 | The relative proliferation rate of tumor-specific CTL | [0, 20] | |
| 3.56506 | The relative number of HCC when the producing rate reaches half of l | [0, 20] | |
| 15.6284 | The relative TGF- related differentiation of CTL | [0, 20] | |
| 19.6051 | The relative coefficient of CTL differentiation | [0, 20] | |
| 16.6884 | The relative producing rate of TGF- by HCC | [0, 20] | |
| 15.1812 | The relative death rate of TGF- | [0, 20] | |
| 10.4961 | The relative production rate of TGF- | [0, 20] | |
| 0.526655 | The relative producing rate of artemin by Ter cell | [0, 20] | |
| 10.8804 | The relative death rate of artemin | [0, 20] | |
| 18.8239 | The relative production rate of artemin | [0, 20] |
Appendix B. Bifurcation Diagram





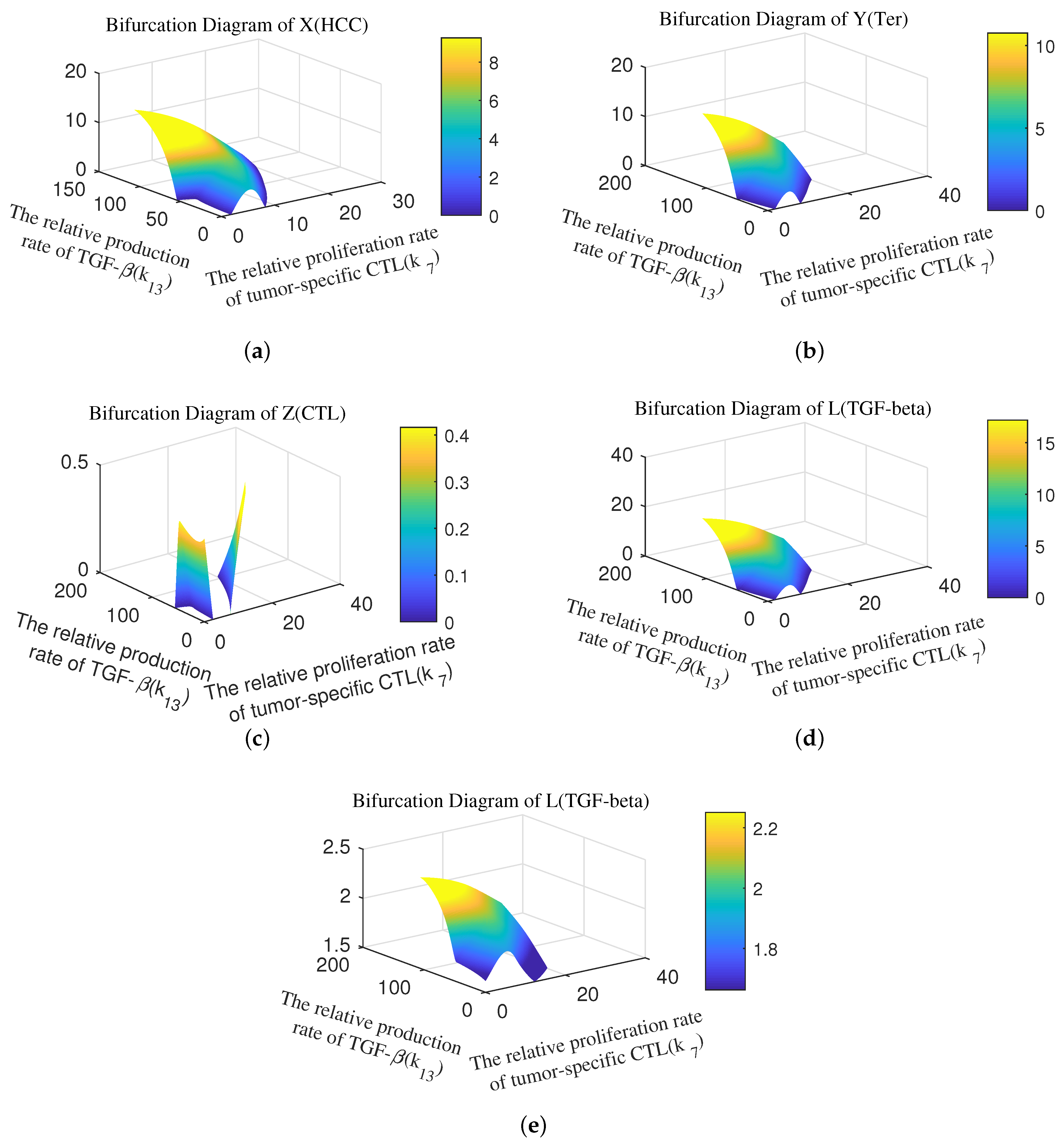
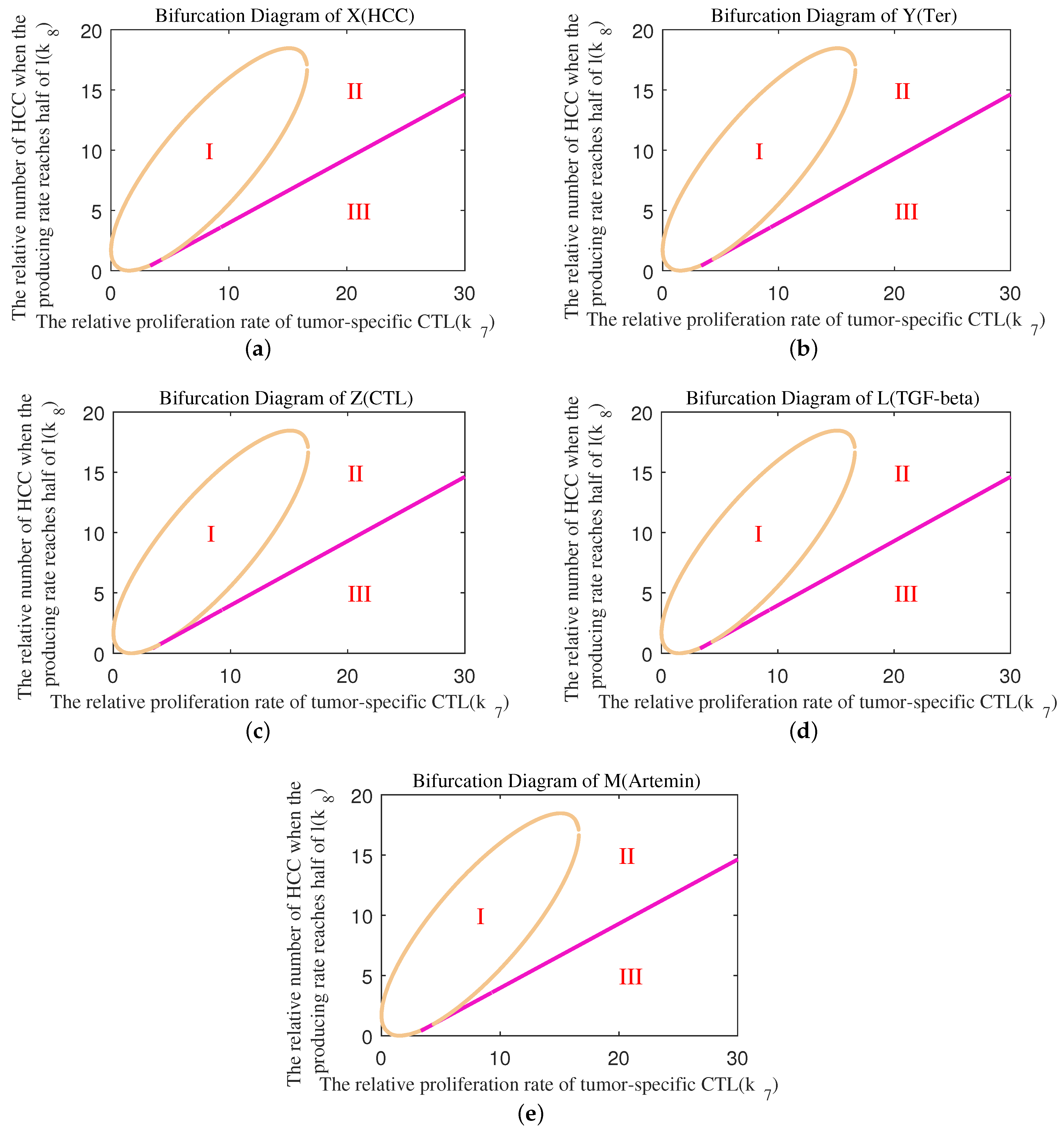
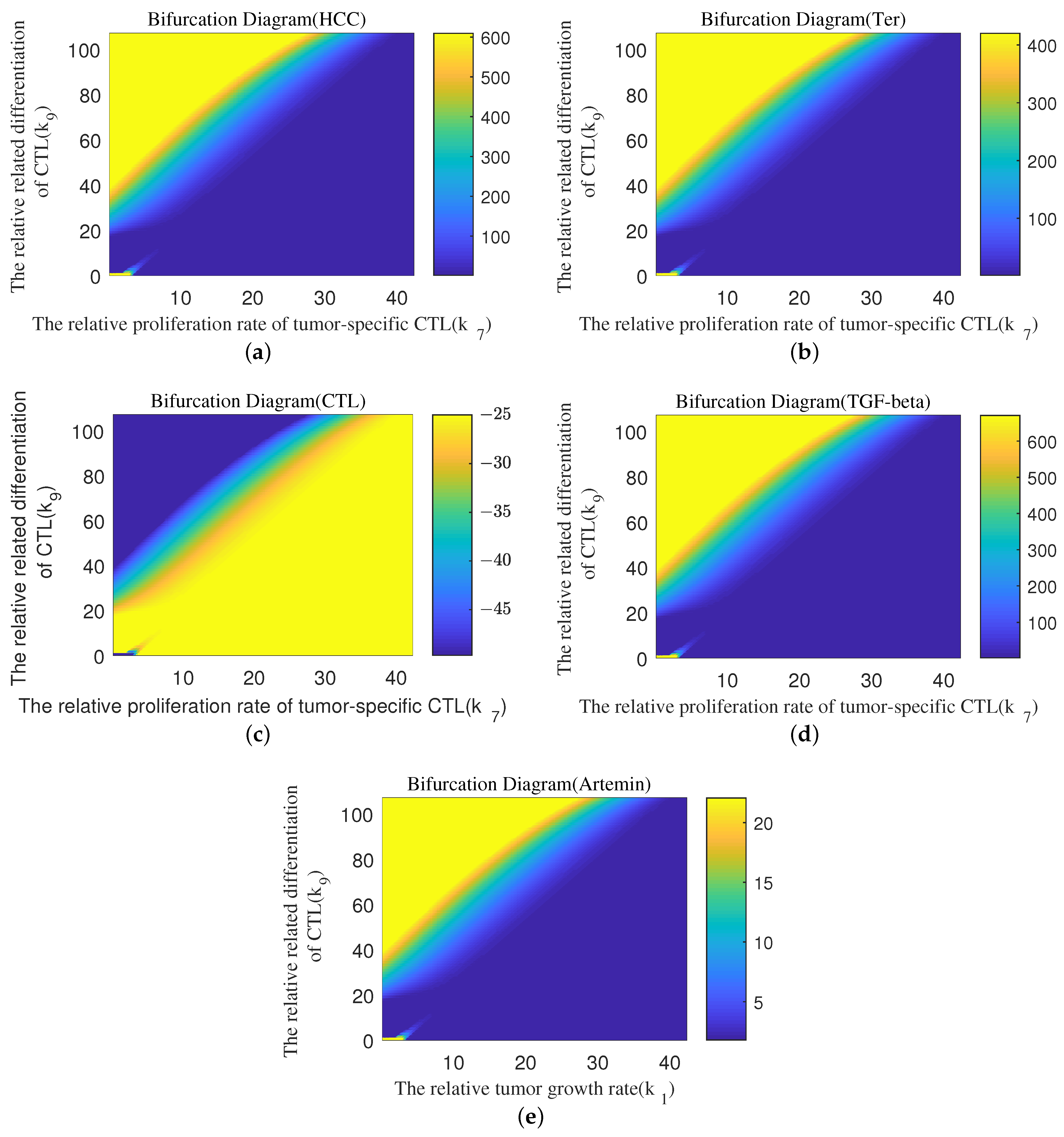
References
- Llovet, J.M.; Kelley, R.K.; Villanueva, A.; Singal, A.G.; Pikarsky, E.; Roayaie, S.; Lencioni, R.; Koike, K.; Zucman-Rossi, J.; Finn, R.S. Hepatocellular carcinoma. Nat. Rev. Dis. Prim. 2021, 7, 6. [Google Scholar] [CrossRef]
- Vogel, A.; Meyer, T.; Sapisochin, G.; Salem, R.; Saborowski, A. Hepatocellular carcinoma. Lancet 2022, 400, 1345–1362. [Google Scholar] [CrossRef] [PubMed]
- Gingold, J.A.; Zhu, D.; Lee, D.F.; Kaseb, A.; Chen, J. Genomic Profiling and Metabolic Homeostasis in Primary Liver Cancers. Trends Mol. Med. 2018, 24, 395–411. [Google Scholar] [CrossRef]
- The Cancer Genome Atlas Research Network. Comprehensive and integrative genomic characterization of hepatocellular carcinoma. Cell 2017, 176, 1327–1341.e23. [Google Scholar] [CrossRef]
- Lin, H.; Xie, Y.; Kong, Y.; Yang, L.; Li, M. Identification of molecular subtypes and prognostic signature for hepatocellular carcinoma based on genes associated with homologous recombination deficiency. Sci. Rep. 2021, 11, 24022. [Google Scholar] [CrossRef] [PubMed]
- Hajibabaie, F.; Abedpoor, N.; Haghjooy Javanmard, S.; Hasan, A.; Sharifi, M.; Rahimmanesh, I.; Shariati, L.; Makvandi, P. The molecular perspective on the melanoma and genome engineering of T-cells in targeting therapy. Environ. Res. 2023, 237, 116980. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, J.S.; Teng, M.W.; Smyth, M.J. Cancer immunoediting and resistance to T cell-based immunotherapy. Nat. Rev. Clin. Oncol. 2019, 16, 151–167. [Google Scholar] [CrossRef]
- Łuksza, M.; Sethna, Z.M.; Rojas, L.A.; Lihm, J.; Bravi, B.; Elhanati, Y.; Soares, K.; Amisaki, M.; Dobrin, A.; Hoyos, D.; et al. Neoantigen quality predicts immunoediting in survivors of pancreatic cancer. Nature 2022, 606, 389–395. [Google Scholar] [CrossRef]
- Gubin, M.M.; Vesely, M.D. Cancer Immunoediting in the Era of Immuno-oncology. Clin. Cancer Res. 2022, 28, 3917–3928. [Google Scholar] [CrossRef]
- Sangro, B.; Sarobe, P.; Hervás-Stubbs, S.; Melero, I. Advances in immunotherapy for hepatocellular carcinoma. Nat. Rev. Gastroenterol. Hepatol. 2021, 18, 525–543. [Google Scholar] [CrossRef] [PubMed]
- Pinato, D.J.; Guerra, N.; Fessas, P.; Murphy, R.; Mineo, T.; Mauri, F.A.; Mukherjee, S.K.; Thursz, M.; Wong, C.N.; Sharma, R.; et al. Immune-based therapies for hepatocellular carcinoma. Oncogene 2020, 39, 3620–3637. [Google Scholar] [CrossRef]
- Ruf, B.; Heinrich, B.; Greten, T.F. Immunobiology and immunotherapy of HCC: Spotlight on innate and innate-like immune cells. Cell. Mol. Immunol. 2021, 18, 112–127. [Google Scholar] [CrossRef]
- Tsuchiya, N.; Sawada, Y.; Endo, I.; Uemura, Y.; Nakatsura, T. Potentiality of immunotherapy against hepatocellular carcinoma. World J. Gastroenterol. 2015, 21, 10314–10326. [Google Scholar] [CrossRef] [PubMed]
- Hepatobiliary malignancies have distinct peripheral myeloid-derived suppressor cell signatures and tumor myeloid cell profiles. Sci. Rep. 2020, 10, 18848. [CrossRef] [PubMed]
- Mantovani, S.; Oliviero, B.; Varchetta, S.; Mele, D.; Mondelli, M.U. Natural Killer Cell Responses in Hepatocellular Carcinoma: Implications for Novel Immunotherapeutic Approaches. Cancers 2020, 12, 926. [Google Scholar] [CrossRef]
- Kalathil, S.G.; Thanavala, Y. Natural Killer Cells and T Cells in Hepatocellular Carcinoma and Viral Hepatitis: Current Status and Perspectives for Future Immunotherapeutic Approaches. Cells 2021, 10, 1332. [Google Scholar] [CrossRef] [PubMed]
- Langhans, B.; Nischalke, H.D.; Krämer, B.; Dold, L.; Lutz, P.; Mohr, R.; Vogt, A.; Toma, M.; Eis-Hübinger, A.M.; Nattermann, J.; et al. Role of regulatory T cells and checkpoint inhibition in hepatocellular carcinoma. Cancer Immunol. Immunother. 2019, 68, 2055–2066. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Wang, Y.; Hou, J.; Li, W.; Wang, X.; Xiang, L.; Tan, D.; Wang, W.; Jiang, L.; Claret, F.X.; et al. Tumor-infiltrating immune cells in hepatocellular carcinoma: Tregs is correlated with poor overall survival. PLoS ONE 2020, 15, e0231003. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.L.; Hsu, C.; Chan, S.L.; Choo, S.P.; Kudo, M. Challenges of combination therapy with immune checkpoint inhibitors for hepatocellular carcinoma. J. Hepatol. 2020, 72, 307–319. [Google Scholar] [CrossRef]
- Wu, T.C.; Shen, Y.C.; Cheng, A.L. Evolution of systemic treatment for advanced hepatocellular carcinoma. Kaohsiung J. Med. Sci. 2021, 37, 643–653. [Google Scholar] [CrossRef] [PubMed]
- Finn, R.S.; Zhu, A.X. Evolution of Systemic Therapy for Hepatocellular Carcinoma. Hepatology 2021, 73, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Llovet, J.M.; Pinyol, R.; Kelley, R.K.; El-Khoueiry, A.; Reeves, H.L.; Wang, X.W.; Gores, G.J.; Villanueva, A. Molecular pathogenesis and systemic therapies for hepatocellular carcinoma. Nat. Cancer 2022, 3, 386–401. [Google Scholar] [CrossRef] [PubMed]
- Llovet, J.M.; Castet, F.; Heikenwalder, M.; Maini, M.K.; Mazzaferro, V.; Pinato, D.J.; Pikarsky, E.; Zhu, A.X.; Finn, R.S. Immunotherapies for hepatocellular carcinoma. Nat. Rev. Clin. Oncol. 2022, 19, 151–172. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Q.; Hou, J.; Gu, Y.; Zhang, Y.; Chen, Z.; Fan, J.; Zhou, W.; Qiu, S.; Zhang, Y.; et al. Tumor-Induced Generation of Splenic Erythroblast-like Ter-Cells Promotes Tumor Progression. Cell 2018, 173, 634–648. [Google Scholar] [CrossRef]
- Shen, J.; Yao, Z.; Tan, X.; Zou, X. Mathematical Modeling and Dynamical Analysis for Tumor Cells and Tumor Propagating Cells Controlled by G9a Inhibitors. Int. J. Bifurc. Chaos 2023, 33, 2350006. [Google Scholar] [CrossRef]
- Tu, X.; Zhang, Q.; Zhang, W.; Zou, X. Single-cell data-driven mathematical model reveals possible molecular mechanisms of embryonic stem-cell differentiation. Math. Biosci. Eng. 2019, 16, 5877–5896. [Google Scholar] [CrossRef]
- Ait-Oudhia, S.; Mager, D.E.; Pokuri, V.; Tomaszewski, G.; Groman, A.; Zagst, P.; Fetterly, G.; Iyer, R. Bridging sunitinib exposure to time-to-tumor progression in hepatocellular carcinoma patients with mathematical modeling of an angiogenic biomarker. CPT Pharmacometrics Syst. Pharmacol. 2016, 5, 297–304. [Google Scholar] [CrossRef]
- Saidak, Z.; Giacobbi, A.S.; Louandre, C.; Sauzay, C.; Mammeri, Y.; Galmiche, A. Mathematical modelling unveils the essential role of cellular phosphatases in the inhibition of RAF-MEK-ERK signalling by sorafenib in hepatocellular carcinoma cells. Cancer Lett. 2017, 392, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Sung, W.; Grassberger, C.; McNamara, A.L.; Basler, L.; Ehrbar, S.; Tanadini-Lang, S.; Hong, T.S.; Paganetti, H. A tumor-immune interaction model for hepatocellular carcinoma based on measured lymphocyte counts in patients undergoing radiotherapy. Radiother. Oncol. 2020, 151, 73–81. [Google Scholar] [CrossRef]
- Sung, W.; Hong, T.S.; Poznansky, M.C.; Paganetti, H.; Grassberger, C. Mathematical Modeling to Simulate the Effect of Adding Radiation Therapy to Immunotherapy and Application to Hepatocellular Carcinoma. Int. J. Radiat. Oncol. Biol. Phys. 2022, 112, 1055–1062. [Google Scholar] [CrossRef]
- Unni, P.; Seshaiyer, P. Mathematical Modeling, Analysis, and Simulation of Tumor Dynamics with Drug Interventions. Comput. Math. Methods Med. 2019, 2019, 4079298. [Google Scholar] [CrossRef] [PubMed]
- Wilson, S.; Levy, D. A Mathematical Model of the Enhancement of Tumor Vaccine Efficacy by Immunotherapy. Bull. Math. Biol. 2012, 74, 1485–1500. [Google Scholar] [CrossRef]
- Xue, V.W.; Chung, J.Y.F.; Córdoba, C.A.G.; Cheung, A.H.K.; Kang, W.; Lam, E.W.F.; Leung, K.T.; To, K.F.; Lan, H.Y.; Tang, P.M.K. Transforming Growth Factor-β: A Multifunctional Regulator of Cancer Immunity. Cancers 2020, 12, 3099. [Google Scholar] [CrossRef] [PubMed]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Teng, C.F.; Li, T.C.; Wang, T.; Liao, D.C.; Wen, Y.H.; Wu, T.H.; Wang, J.; Wu, H.C.; Shyu, W.C.; Su, I.J.; et al. Increased infiltration of regulatory T cells in hepatocellular carcinoma of patients with hepatitis B virus pre-S2 mutant. Sci. Rep. 2021, 11, 1136. [Google Scholar] [CrossRef] [PubMed]
- Sachdeva, M.; Arora, S. Prognostic role of immune cells in hepatocellular carcinoma. EXCLI J. 2020, 19, 718–733. [Google Scholar] [CrossRef] [PubMed]
- Cucarull, B.; Tutusaus, A.; Rider, P.; Hernáez-Alsina, T.; Cuño, C.; García de Frutos, P.; Colell, A.; Marí, M.; Morales, A. Hepatocellular Carcinoma: Molecular Pathogenesis and Therapeutic Advances. Cancers 2022, 14, 621. [Google Scholar] [CrossRef] [PubMed]
- Da, B.L.; Suchman, K.I.; Lau, L.; Rabiee, A.; He, A.R.; Shetty, K.; Yu, H.; Wong, L.L.; Amdur, R.L.; Crawford, J.M.; et al. Pathogenesis to management of hepatocellular carcinoma. Genes Cancer 2022, 13, 72–87. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, Y.; Martin-Rufino, J.D.; Weng, C.; Hosseinzadeh, S.; Yang, D.; Pogson, A.N.; Hein, M.Y.; Hoi (Joseph) Min, K.; Wang, L.; et al. Mapping transcriptomic vector fields of single cells. Cell 2022, 185, 690–711.e45. [Google Scholar] [CrossRef]
- Khajanchi, S.; Nieto, J.J. Mathematical modeling of tumor-immune competitive system, considering the role of time delay. Appl. Math. Comput. 2019, 340, 180–205. [Google Scholar] [CrossRef]
- Nouni, A.; Hattaf, K.; Yousfi, N. Dynamics of a mathematical model for cancer therapy with oncolytic viruses. Commun. Math. Biol. Neurosci. 2019, 237. [Google Scholar] [CrossRef]
- Nouni, A.; Hattaf, K.; Yousfi, N. Dynamics of a Virological Model for Cancer Therapy with Innate Immune Response. Complexity 2020, 2020, 8694821. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Xu, C.; Liu, C.; Mu, D.; Xu, M.; Ou, W.; Cui, Q. Bifurcation mechanism and hybrid control strategy of a finance model with delays. Bound. Value Probl. 2023, 2023, 82. [Google Scholar] [CrossRef]
- Li, P.; Gao, R.; Xu, C.; Shen, J.; Ahmad, S.; Li, Y. Exploring the Impact of Delay on Hopf Bifurcation of a Type of BAM Neural Network Models Concerning Three Nonidentical Delays. Neural Process. Lett. 2023. [Google Scholar] [CrossRef]
- Ou, W.; Xu, C.; Cui, Q.; Liu, Z.; Pang, Y.; Farman, M.; Ahmad, S.; Zeb, A. Mathematical study on bifurcation dynamics and control mechanism of tri-neuron bidirectional associative memory neural networks including delay. Math. Methods Appl. Sci. 2023, 1–25. [Google Scholar] [CrossRef]
- Huang, M.; Wu, S.L.; Zhao, X.Q. Propagation Dynamics for Time–Space Periodic and Partially Degenerate Reaction–Diffusion Systems with Time Delay. J. Dyn. Differ. Equat. 2023. [Google Scholar] [CrossRef]
- Malinzi, J.; Soltani, M. Mathematical Analysis of a Mathematical Model of Chemovirotherapy: Effect of Drug Infusion Method. Comput. Math. Methods Med. 2019, 2019, 15–20. [Google Scholar] [CrossRef]
- Li, P.; Peng, X.; Xu, C.; Han, L.; Shi, S. Novel extended mixed controller design for bifurcation control of fractional-order Myc/E2F/miR-17-92 network model concerning delay. Math. Methods Appl. Sci. 2023, 1–21. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Li, P.; Yan, J.; Yao, L. Bifurcation Mechanism for Fractional-Order Three-Triangle Multi-delayed Neural Networks. Neural Process. Lett. 2022, 55, 6125–6151. [Google Scholar] [CrossRef]
- Li, P.; Lu, Y.; Xu, C.; Ren, J. Insight into Hopf Bifurcation and Control Methods in Fractional Order BAM Neural Networks Incorporating Symmetric Structure and Delay. Cogn. Comput. 2023, 1–43. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Tu, X.; Li, Y. Mathematical Modeling Reveals Mechanisms of Cancer-Immune Interactions Underlying Hepatocellular Carcinoma Development. Mathematics 2023, 11, 4261. https://doi.org/10.3390/math11204261
Shen J, Tu X, Li Y. Mathematical Modeling Reveals Mechanisms of Cancer-Immune Interactions Underlying Hepatocellular Carcinoma Development. Mathematics. 2023; 11(20):4261. https://doi.org/10.3390/math11204261
Chicago/Turabian StyleShen, Juan, Xiao Tu, and Yuanyuan Li. 2023. "Mathematical Modeling Reveals Mechanisms of Cancer-Immune Interactions Underlying Hepatocellular Carcinoma Development" Mathematics 11, no. 20: 4261. https://doi.org/10.3390/math11204261
APA StyleShen, J., Tu, X., & Li, Y. (2023). Mathematical Modeling Reveals Mechanisms of Cancer-Immune Interactions Underlying Hepatocellular Carcinoma Development. Mathematics, 11(20), 4261. https://doi.org/10.3390/math11204261






