Propagation Search Algorithm: A Physics-Based Optimizer for Engineering Applications

Abstract

For process control in engineering applications, the fewer the coding lines of optimization algorithms, the more applications there are. Therefore, this work develops a new straightforward metaheuristic optimization algorithm named the propagation search algorithm (PSA), stirred by the wave propagation of the voltage and current along long transmission lines. The mathematical models of the voltage and current are utilized in modeling the PSA, where the voltage and current are the search agents. The propagation constant of the transmission line is the control parameter for the exploitation and exploration of the PSA. After that, the robustness of the PSA is verified using 23 famous testing functions. The statistical tests, comprising mean, standard deviation, and p-values, for 20 independent optimization experiments are utilized to confirm the robustness of the PSA to find the best result and the significant difference between the outcomes of the PSA and those of the compared algorithms. Finally, the proposed PSA is applied to find the optimum design parameters of four engineering design problems, including a three-bar truss, compression spring, pressure vessel, and welded beam. The outcomes show that the PSA converges to the best solutions very quickly, which can be applied to those applications that require a fast response.

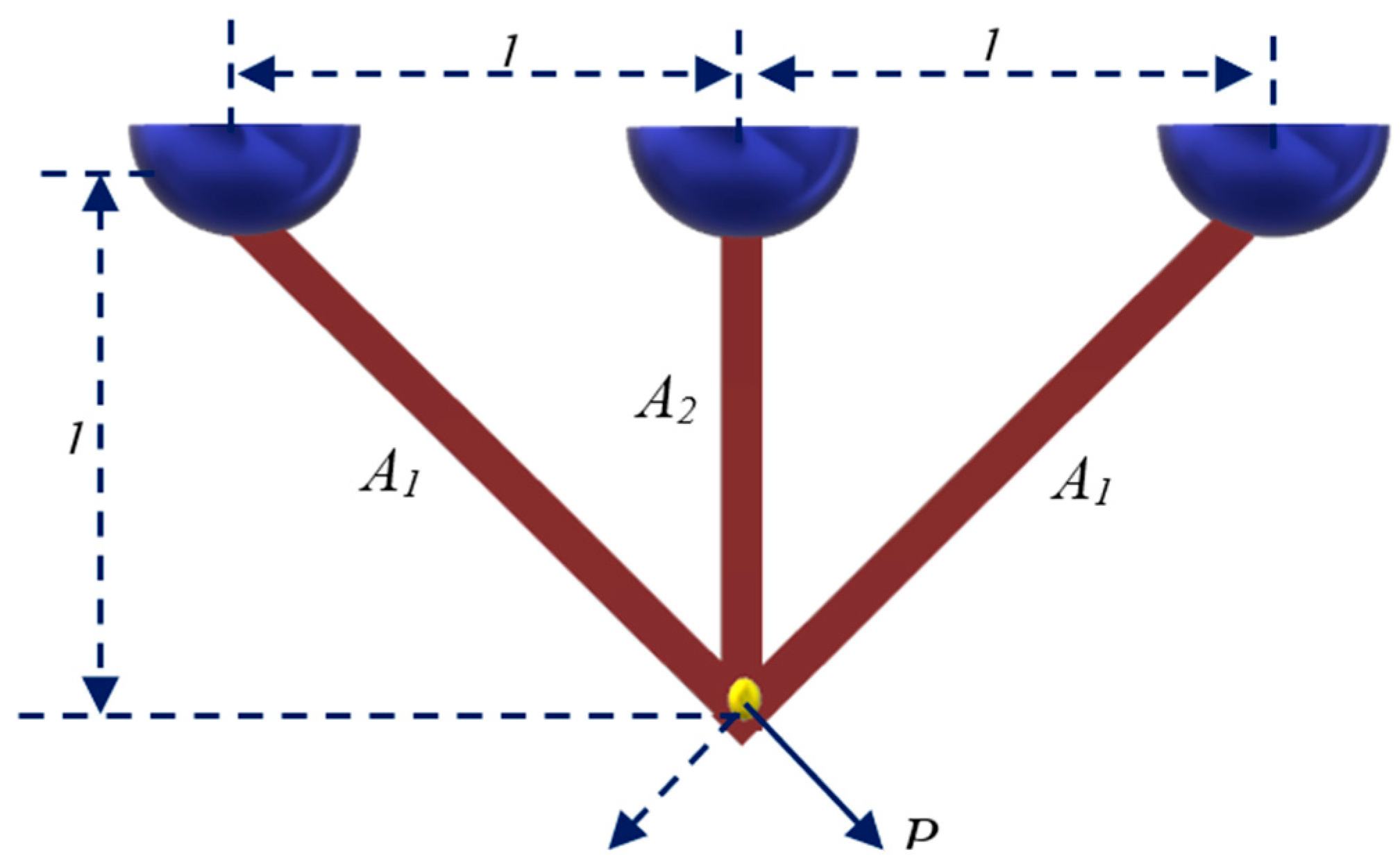
1. Introduction

Metaheuristic optimization algorithms have been extensively utilized in several engineering applications to reduce costs. They have used either an optimal design or online process control. For optimal design problems, it does not pose a significant problem if the optimization algorithm is complex and takes a long time to find the best design parameters. However, for online process control, it is required that optimization algorithms have a fast response and less computation complexity. For example, energy harvesting from solar and wind resources or the optimal power flow in large electrical networks require fast online tracking of power variations, which increases system efficiency. Therefore, particle swarm optimization (PSO) has been utilized in most engineering applications because of its simplicity of coding and capability to find an optimum local or global solution. However, many metaheuristic algorithms with high computational complexity and long codes have recently emerged to achieve optimum solutions, which can be applied to optimal design problems but not in online control processes. Therefore, proposing new metaheuristic algorithms with less computational complexity is very much welcome for engineering applications.

In the literature review, many metaheuristic optimization algorithms have been stimulated by nature, biological behavior, or physical actions. For biological behavior, algorithms are inspired by different behaviors, either social communities, reproduction, food finding, or survival instinct. In 1975, Holland invented the genetic algorithm (GA), the first metaheuristic algorithm version that uses random searches to produce a new set of offspring [1]. After that, in 1995, Kennedy and Eberhart presented a new simple algorithm, the PSO algorithm, stimulated by the swarming performance of birds and fish [2]. Then, in 1995, Dorigo and Caro proposed the ant colony optimization (ACO) algorithm, which is motivated by the manners of ants to find a straight path between the colony and food position [3]. After that, many optimization algorithms emerged, such as the artificial bee colony (ABC) [4], which is stimulated by the swarming deeds of honeybees; firefly algorithm (FA) [5], which is stimulated by the blinking light of fireflies for communicating and attracting prey; and cuckoo search (CS) algorithm [6], which is stimulated by the levy walk and intrusions on the nests of other birds.

Furthermore, there are many recent metaheuristic algorithms that have been stimulated by alive creatures’ behaviors, such as the grey wolf optimizer (GWO), which was stimulated by the hierarchy of guidance and hunting [7]; the whale optimization algorithm (WOA), which was stimulated by producing spiral bubbles around a school of fish [8]; the salp swarm algorithm (SSA), which was stimulated by the teeming of salps to track food [9]; Harris hawk optimization (HHO), which was stimulated by the teeming work of many hawks to attack prey [10]; the mantis search algorithm (MSA), which was inspired by the foraging process of mantises [11]; the nutcracker optimization algorithm (NOA), which was stimulated by the seasonal deeds of nutcrackers in finding, storing, and memorizing food [12]; the Aquila optimizer (AO), which was stimulated by the hunting style of Aquila [13]; the black widow optimizer (BWO), which was stimulated by the mating and flesh-eating of black widow spiders [14]; and the Tunicate swarm algorithm (TSA), which was stimulated by the swarming manners of tunicates in tracking food [15]. Consequently, many algorithms are stimulated by the conduct of living creatures, for example, dolphins [16], white sharks [17], vultures [18], orcas [19], starlings [20], rabbits [21], frogs [22], butterflies [23], hyenas [24], reptiles [25], coati [26], leopards [27], and eagles [28].

Physicists such as Newton, Einstein, etc., were attracted by the physical phenomena in the universe, which led them to find mathematical laws and paradigms after a long study. Therefore, many algorithms have been proposed based on their physical models, such as the annealing process of metals [29]; the law of gravity by Newton [30]; the law of gas by William Henry [31]; the heat transfer between materials and ambient [32]; the collision of bodies [33]; the pull and repulsion forces between atoms [34]; the laws of electrostatic and dynamic charges by Coulomb and Newton [35]; the migrant light between mediums with different intensities [36]; the transient behavior of first- and second-order electrical circuits [37]; the motion and speed of planets by Kepler [38]; the electrical trees and figures of lightning by Lichtenberg [39]; the electromagnetic field [40]; circles geometry [41]; and the electrical field [42]. Moreover, many metaheuristic algorithms were inspired by the gravity effect on the motion of planets and stars [43]; the centrifugal forces and gravity relations [44]; ion motions [45]; and the orbits of electrons around the nucleus inside atoms [46].

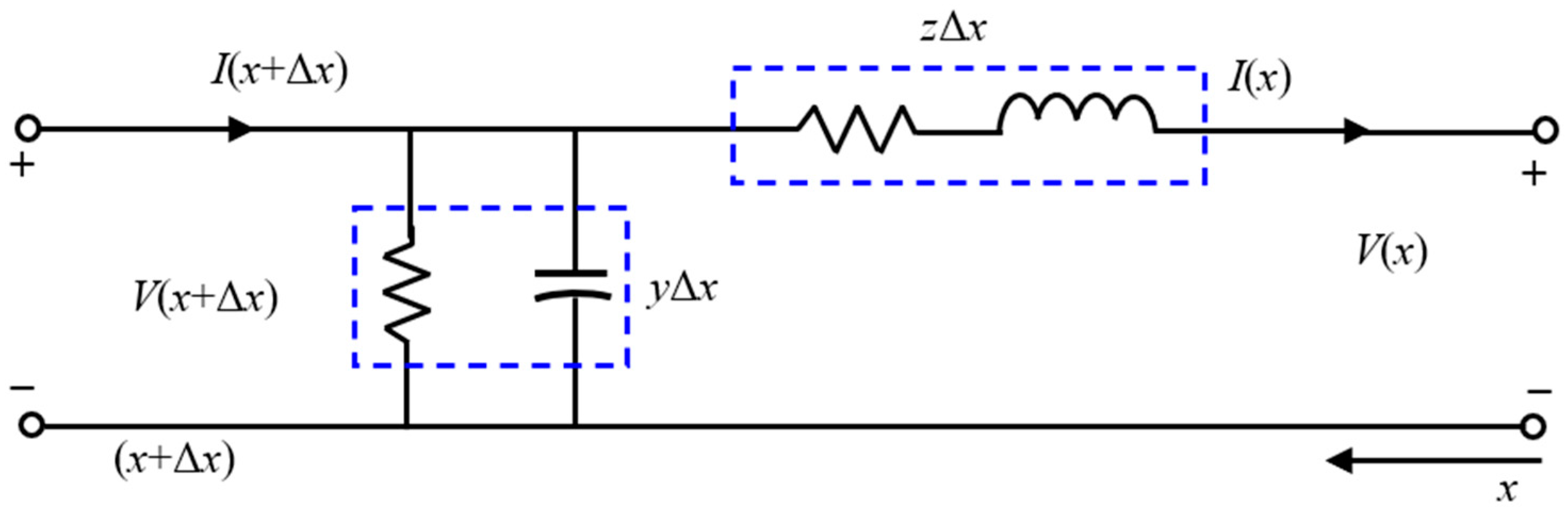
The research gap is defined by the no-free lunch theorem, which states that there is no single algorithm that can succeed in solving all optimization problems. In addition, the mathematical modeling and program coding of some recent metaheuristic algorithms are complex and cannot be easily applied to the online process control of engineering applications. Moreover, some models of algorithms are not investigated by related scientists. Therefore, using a studied mathematical model, simple software code, and fast convergence motivated us to propose a new metaheuristic optimizer called the propagation search algorithm (PSA), stimulated by the propagation of the waveforms of the electrical voltage and current along long transmission lines. Scientists previously offered mathematical voltage and current models at any transmission line section. Then, we adapted these models to be randomized models for random transmission lines with random impedances and admittances. The voltage and current are considered the search agents of the PSA, where they propagate based on their previous values and the propagation constant of the transmission line. These search agents rely on each other’s values, which helps them to encircle the best solution.

The main contributions of this paper are summarized below:

• Developing a new physics-based metaheuristic algorithm called the propagate search algorithm (PSA), inspired by voltage and current waveform propagation along long transmission lines.
• Testing the PSA using the 23 famous testing functions and comparing the outcomes with eight famous metaheuristic algorithms.
• Applying the PSA to find the optimum design of four famous engineering problems and comparing it with other metaheuristic algorithms.

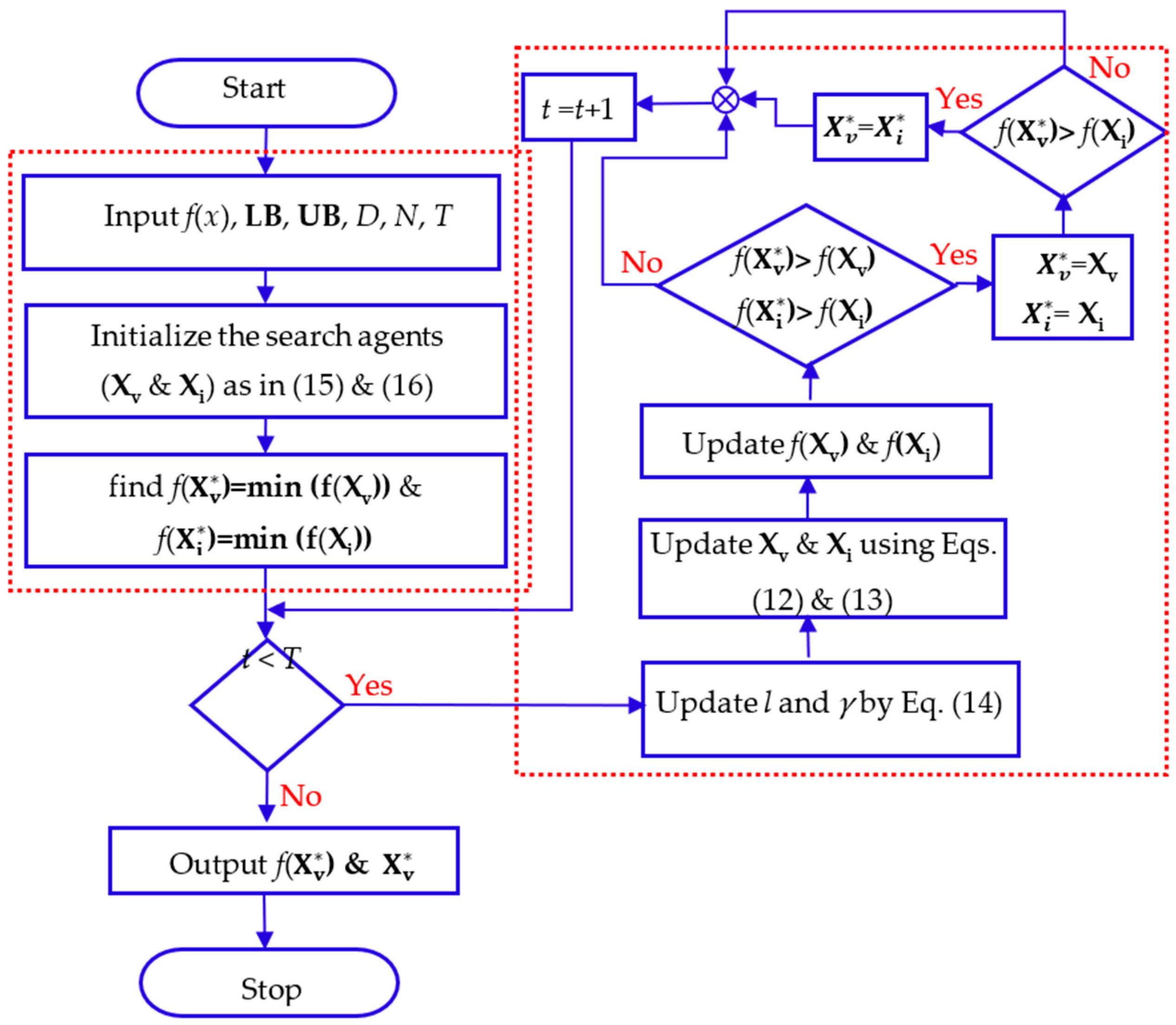
The remainder of this paper is designed as follows: Section 2 describes the background, the mathematical modeling, and the flowchart of the proposed PSA; Section 3 describes the testing results; Section 4 shows the application of the proposed PSA to different engineering applications; and Section 5 presents a brief conclusion about the contribution and the results of this paper.

2. Propagation Search Algorithm

The PSA is a physics-based metaheuristic optimization algorithm that is stimulated by the propagation of electrical voltage (V) and current (I) waveforms along long transmission lines, as shown in Figure 1. The parameters of the transmission line, series impedance (z), and shunt admittance (y) play essential roles in the propagation of the voltage and current. For y > z, V(x + Δx) is higher than I(x + Δx); however, for y < z, V(x + Δx) is lower than I(x + Δx), and for y = z, V(x + Δx) is equal to I(x + Δx), as shown in Figure 2. In this work, we will introduce the mathematical modeling of the presented PSA based on the mathematical modeling of the propagation of the voltage and current along the transmission line.

2.1. Background

For a long transmission line, its impedance (z) and admittance (y) are uniformly distributed along its length and cannot be lumped. Therefore, the voltage (V) and current (I) can be calculated at each line section (Δx), as shown in Figure 1. The voltage at any distance can be calculated using Kirchhoff’s voltage law as follows [47]:

$$V(x+\Delta x)=(z\Delta x)I(x)+V(x)\Rightarrow \frac{V(x+\Delta x)-V(x)}{\Delta x}=zI(x) \Rightarrow \underset{\Delta x\to 0}{\lim }\frac{V(x+\Delta x)-V(x)}{\Delta x}=\frac{dV(x)}{dx}=zI(x)$$

(1)

For electrical current calculation, Kirchhoff’s current law can be applied as follows:

$$I(x+\Delta x)=(y\Delta x)V(x+\Delta x)+I(x)\Rightarrow \frac{I(x+\Delta x)-I(x)}{\Delta x}=yV(x+\Delta x) \Rightarrow \underset{\Delta x\to 0}{\lim }\frac{I(x+\Delta x)-I(x)}{\Delta x}=\frac{dI(x)}{dx}\approx yV(x)$$

(2)

where V(x + Δx) ≈ V(x), by taking the differential of (1) and substituting it in (2), we can obtain the following:

$$\frac{d^{2}V(x)}{d{x}^2}=z\frac{dI(x)}{dx}=zyV(x)\Rightarrow \frac{d^{2}V(x)}{d{x}^2}-zyV(x)=0$$

(3)

Then, the second-order linear differential equation in (3) can be solved to find V(x), as follows [47]:

$$V(x)=A_1{e}^{\sqrt{zy}x}+A_2{e}^{-\sqrt{zy}x}$$

(4)

Then, to find the current expression, we will differentiate (4) and compare it with (1), as follows:

$$\frac{dV(x)}{dx}=A_1\sqrt{zy}{e}^{\sqrt{zy}x}-A_2\sqrt{zy}{e}^{-\sqrt{zy}x}=zI(x)$$

(5)

$$I(x)=\frac{\sqrt{zy}\left(A_1{e}^{\sqrt{zy}x}-A_2{e}^{-\sqrt{zy}x}\right)}{z}=\frac{A_1{e}^{\gamma x}-A_2{e}^{-\gamma x}}{Z_c}$$

(6)

where Z_c is the characteristic impedance of the transmission line, $Z_c=\frac{z}{\sqrt{zy}}$, γ is the propagation constant, $\gamma =\sqrt{zy}$, and A₁ and A₂ are constants that can be obtained by solving (6) and (4) for V(0) =V_R and I(0) = I_R, where V_R and I_R are the receiving end voltage and current, respectively. Then, we achieve A₁ and A₂ as follows:

$$A_1=\frac{V_R+Z_c{I}_R}{2} \& A_2=\frac{V_R-Z_c{I}_R}{2}$$

(7)

Then, substitute (7) into (4) and (6) to obtain the following:

$$V(x)=\left(\frac{V_R+Z_c{I}_R}{2}\right)e^{\gamma x}+\left(\frac{V_R-Z_c{I}_R}{2}\right)e^{-\gamma x}=V_R\left(\frac{e^{\gamma x}+e^{-\gamma x}}{2}\right)+Z_c{I}_R\left(\frac{e^{\gamma x}-e^{-\gamma x}}{2}\right)$$

(8)

$$I(x)=\left(\frac{V_R+Z_c{I}_R}{2Z_c}\right)e^{\gamma x}-\left(\frac{V_R-Z_c{I}_R}{2Z_c}\right)e^{-\gamma x}=\frac{V_R}{Z_c}\left(\frac{e^{\gamma x}-e^{-\gamma x}}{2}\right)+\left(\frac{e^{\gamma x}+e^{-\gamma x}}{2}\right)I_R$$

(9)

Then, the hyperbolic functions can be used to represent the exponential expressions as follows:

$$V(x)=V_R\cosh (\gamma x)+Z_c{I}_R\sinh (\gamma x)$$

(10)

$$I(x)=\frac{V_R}{Z_c}\sinh (\gamma x)+I_R\cosh (\gamma x)$$

(11)

For long transmission lines, the series and shunt resistances can be neglected, and only inductance (L) and capacitor (C) are considered. Therefore, z = jωL and y = jωC, so $Zc=\sqrt{L/C}$ and $\gamma =j\omega \sqrt{LC}$.

2.2. PSA Inspiration

The PSA is a physics-based metaheuristic optimization algorithm stimulated by the propagation performance of the voltage and current waveforms through a long transmission line. The search agents of the PSA imitate the behavior of the voltage and current. The mathematical model of the PSA is developed based on Equations (10) and (11) with some modifications, as in (12) and (13). The modifications assumed that L = C then Z_c = 1 and γ = C, the propagation constant γ is expressed as a random number as in (14), the voltage V_R is expressed as X_v, and the current I_R is expressed as X_i. The length of the transmission line (l) is the shrinking variable that decreases from 1 to 0, as described in (14).

$$X_v(t+1)=\stackrel{V_R}{\overbrace{X_v^{*}(t)-X_v(t)}}\cosh (\gamma l)+\stackrel{I_R}{\overbrace{(X_i^{*}(t)-X_i(t))}}\sinh (\gamma l)$$

(12)

$$X_i(t+1)=\stackrel{I_R}{\overbrace{X_i^{*}(t)-X_i(t)}}\cosh (\gamma l)+\stackrel{V_R}{\overbrace{(X_v^{*}(t)-X_v(t))}}\sinh (\gamma l)$$

(13)

$$l=\left\{\begin{array}{l}1-\sqrt{t/T} t<0.5T\\ \sqrt{1-t/T} t\ge 0.5T\end{array}\right. \& \gamma =\left\{\begin{array}{l}{r}_1\sqrt{\pi r_2} t<0.5T\\ r_n\sqrt{\frac{\pi }{2}{r}_3} t\ge 0.5T\end{array}\right.$$

(14)

where t is the current iteration; T is the total iterations; r₁, r₂, and r₃ are random numbers uniformly distributed between 0 and 1; and r_n is a random number generally distributed with a mean of zero. The search agents of the PSA algorithm are X_v and X_i, and the best agents are $X_v^{*}$ and $X_i^{*}$.

2.2.1. Search Agents Initialization

The PSA first initializes the vector of the search agent randomly between the lower and upper bounds (LB and UB) with the dimension (1 × D) of a cost function. Initialization plays a vital part in successfully helping the proposed algorithm find the global optimum solution. There are two types of initialization: symmetrical and nonsymmetrical methods. For symmetrical initialization, all elements of the search agent vector are multiplied by the same random number. For the nonsymmetrical initialization, every element is multiplied by a different random number. For the PSA, there are two search agent vectors, X_v and X_i, which can be initialized by any initialization method or by both initialization methods, as in (15).

$$X_v=LB+r\times (UB-LB)$$

(15)

$$X_i=LB+R\times (UB-LB)$$

(16)

where X_v = [x_v1, x_v2, x_v3, … x_vd]^T, X_i = [x_i1, x_i2, x_i3, … x_id]^T, UB = [ub₁, ub₂, ub₃, … ub_d]^T, LB = [lb₁, lb₂, lb₃, … lb_d]^T, and R = [r₁, r₂, r₃, … r_d]^T. The initialization can be conducted for a number n of search agents, so the dimension of all search agents is (N × D).

2.2.2. Exploration and Exploitation of PSA

For better exploration, firstly, the search agents X_v and X_i are initialized differently, as in (15) and (16), which will widen the search areas of the PSA. Secondly, these agents are updated using (12) and (13), where they search in opposite directions for V_R ≠ I_R, as shown in Figure 3. For exploitation of the PSA, the changes of both search agents converge to zero for V_R = I_R, as shown in Figure 3. Moreover, both search agents are designed to encircle the best solution due to the presence of V_R =$-X_v$ in (12) and I_R =$-X_i$ in (13). The balance between exploration and exploitation is managed by (14), where the first half of total iterations is used for exploitation, and the second half of iterations is utilized for exploration, where the search agents can be diverted using normally distributed random numbers.

For more explanation about exploitation and exploration, two common functions, the Rosenbrock and Rastrigin functions, are used to test the exploration and exploitation of the PSA. Figure 4 shows how the search agents found the best voltage immediately after 10 iterations for the Rastrigin function; however, they were stuck in a local solution for the Rosenbrock function. After t ≥ 0.5 T (at t = 300), the exploration capability of the PSA was activated, and the search agents moved to the best voltage.

2.2.3. Encircling Behavior of PSA

Even though the search agents X_v and X_i of the PSA go in opposite directions, as shown in Figure 3, in the end, they encircle the best solution (X^*) because each agent relies on the update step of the other best agent, as shown in (12) and (13). We can notice that the term V_R exists in the search agent X_i and the term I_R exists in the search agent X_v. Therefore, both search agents encircle the best position, X^*. The flowchart of the proposed PSA is depicted in Figure 5.

2.2.4. Computational Complexity of PSA

The complexity of the algorithms varies with the number of loops, the number of search agents (N), and the number of fitness function evaluations. Big O Notation is utilized to measure the computational complexity of PSA. As shown in Figure 4, it starts with the loop of initialization for two kinds of search agents, X_v and X_i, and then the PSA has O(2N) complexity. For the update process and function evaluations, the PSA has O(T × 2N). Therefore, the total complexity of the PSA is O(2N + 2T × N), which can be reduced to the term with the largest order, such as O(2T × N).

3. Optimization Results of Testing Functions

First of all, the robustness of the proposed PSA should be tested using the 23 well-known testing functions. These functions are utilized to verify the exploration and exploitation behaviors of all previously published algorithms. Some of these functions are utilized to test the exploitation ability of the algorithms because they are convex and have one lowest solution, such as the unimodal functions (F1–F7) displayed in

Table 1. Unimodal testing functions with unfixed dimensions (d).

No.	Name	Formula	Dimension	[LB, UB]	Minimum
F1	Sphere	${\displaystyle \sum _{i=1}^d{y}_i{}^2}$	d = 30	[−100, 100] d	0
F2	Shwefel 2.22	${\displaystyle \sum _{i=1}^d\left|y_i\right|}+{\displaystyle \prod _{i=1}^d\left|y_i\right|}$	d = 30	[−10, 10] d	0
F3	Shwefel 1.2	${\displaystyle \sum _{i=1}^d{({\displaystyle \sum _{j=1}^i{y}_j})}^2}$	d = 30	[−100, 100] d	0
F4	Schwefel 2.21	${\max }_i\{\left|y_i\right|,1\le i\le d\}$	d = 30	[−100, 100] d	0
F5	Rosenbrock	${\displaystyle \sum _{i=1}^d[100{(y_{i+1}-y_i{}^2)}^2+{(y_i-1)}^2]}$	d = 30	[−30, 30] d	0
F6	Step	${\displaystyle \sum _{i=1}^d{(y_i+0.5)}^2}$	d = 30	[−100, 100] d	0
F7	Quartic Noise	${\displaystyle \sum _{i=1}^{d}i.y_i{}^4+random[0,1)}$	d = 30	[−1.28, 1.28] d	0

. Other functions are utilized to verify the exploration capability of algorithms to escape being trapped in a local minimum solution because they have different local minimum solutions rather than the global minimum solution, such as the multimodal functions (F8–F23) displayed in

Table 2. Multimodal testing functions with unfixed dimensions (d).

No.	Name	Formula	Dimension	[LB, UB]	Minimum
F8	Schwefel 2.26	${\displaystyle \sum _{i=1}^d{y}_i\sin (\sqrt{\left|y_i\right|})}$	d = 30	[−500, 500] d	−418.98 × d
F9	Rastrigin	${\displaystyle \sum _{i=1}^n[y_i{}^2-10\cos (2\pi y_i)}+10]$	d = 30	[−5.12, 5.12] d	0
F10	Ackley	$-20\exp (-0.2\sqrt{\frac{1}{d}{\displaystyle \sum _{j=1}^d{y}_j}})-\exp (\frac{1}{n}\cos (2\pi y_j))+20+e$	d = 30	[−32, 32] d	0
F11	Griewank	$\frac{1}{4000}{\displaystyle \sum _{i=1}^d{y}_i{}^2}-{\displaystyle \prod _{i=1}^d\cos (\frac{y_i}{\sqrt{i}})}+1$	d = 30	[−600, 600] d	0
F12	Penalized	$\begin{array}{l}\frac{\pi }{d}\{10\sin (\pi y_1)+{\displaystyle \sum _{i=1}^d{(y_i-1)}^2[1+10{\sin }^2(\pi y_{i+1})]+{(y_d-1)}^2\}}\\ +{\displaystyle \sum _{i=1}^{d}u(x_i,10,100,4)}\\ y_i=1+\frac{x_i+1}{4} \& u(x_i,a,k,m)=\left\{\begin{array}{l}k{(x_i-a)}^m x_i>a\\ 0 -a<x_i<a\\ k{(-x_i-a)}^m x_i<-a\end{array}\right.\end{array}$	d = 30	[−50, 50] d	0
F13	Generalized Penalized	$\begin{array}{l}0.1\times \{10{\sin }^2(3\pi y_1)+{\displaystyle \sum _{i=1}^d{(y_i-1)}^2[1+{\sin }^2(3\pi y_i+1)]}\\ +{(y_d-1)}^2[1+{\sin }^2(2\pi y_d)]\}+{\displaystyle \sum _{i=1}^{d}u(y_i,5,100,4)}\end{array}$	d = 30	[−50, 50] d	0

and

Table 3. Fixed-dimension (d) multimodal testing functions.

No.	Name	Formula	Dimension	[LB, UB]	Best Solution
F14	De Jong Fifth	$(\frac{1}{500}+{\displaystyle \sum _{i=1}^{25}\frac{1}{i+{\displaystyle \sum _{j=1}^2{(y_i-a_{ij})}^6}}{)}^{-1}}$	d = 2	[−65, 65] d	1
F15		${\displaystyle \sum _{i=1}^{11}{[a_i-\frac{y_i(b_i{}^2+b_i{y}_2)}{b_i{}^2+b_i{y}_3+y_4}]}^2}$	d = 4	[−5, 5] d	0.00030
F16	Six-Hump Camel	$4y_1{}^2-2.1y_1{}^4+\frac{1}{3}{y}_1{}^6+y_1{y}_2-4y_2{}^2+4y_2{}^4$	d = 2	[−5, 5] d	−1.0316
F17	Branins	${(y_2-\frac{5.1}{4{\pi }^2}{y}_1{}^2+\frac{5}{\pi }{y}_1-6)}^2+10(1-\frac{1}{8\pi })\cos (y_1)+10$	d = 2	[−5, 5] d	0.398
F18	Goldstein–Price	$\begin{array}{l}[1+{(y_1+y_2+1)}^2(19-14y_1+3y_1{}^2-14y_2+6y_1{y}_2+3y_2{}^2)]\times \\ [30+{(2y_1-3y_2)}^2\times (18-32y_1+12y_1{}^2\\ +48y_2-36y_1{y}_2+27y_2{}^2)]\end{array}$	d = 2	[−2, 2] d	3
F19	Hartmann 3D	$-{\displaystyle \sum _{i=1}^4{c}_i\exp {(-{\displaystyle \sum _{j=1}^3{a}_{ij}(y_j-p_{ij}})}^2)}$	d = 3	[1, 3] d	−3.86
F20	Hartmann 6D	$-{\displaystyle \sum _{i=1}^4{c}_i\exp {(-{\displaystyle \sum _{j=1}^6{a}_{ij}(y_j-p_{ij}})}^2)}$	d = 6	[0, 1] d	−3.32
F21	Shekel 5	$-{\displaystyle \sum _{i=1}^5{[(Y-a_i){(Y-a_i)}^T+c_i]}^{-1}}$	d = 4	[0, 10] d	−10.1532
F22	Shekel 7	$-{\displaystyle \sum _{i=1}^7{[(Y-a_i){(Y-a_i)}^T+c_i]}^{-1}}$	d = 4	[0, 10] d	−10.4028
F23	Shekel 10	$-{\displaystyle \sum _{i=1}^{10}{[(Y-a_i){(Y-a_i)}^T+c_i]}^{-1}}$	d = 4	[0, 10] d	−10.5363

. Then, the minimum values of these functions found by the PSA are compared with those of other renowned algorithms.

In this section, we used eight metaheuristic optimization algorithms besides the PSA. These are the particle swarm optimization (PSO), grey wolf optimizer (GWO), whale optimization algorithm (WOA), sine-cosine algorithm (SCA), transient search optimization (TSO), salp swarm algorithm (SSA), cuckoo search algorithm (CS), and artificial electric field algorithm (AEFA). These algorithms are carefully selected based on the most popular algorithms applied in different engineering applications, such as PSO, GWO, and the WOA. Some of these algorithms are selected because they are inspired by physical behaviors, such as TSO and the AEFA. The remaining algorithms are selected randomly for more comparisons. The values of the algorithms’ parameters are displayed in

Table 4. The setting of the compared algorithms.

Algorithm	Parameters
Proposed PSA	l decrease from 1 to 0
PSO	weight ω varies between [0.5, 0.3] c1 = c2 = 2
GWO	The variable a changes between [2, 0]
SSA	The probability is 0.5
SCA	a = 2 and p = 0.5
CS	Pa = 0.25, tolerance is 1 × 10−5, beta = 1.5,
WOA	l = 1, a decrease from 2 to 0, a2 decrease from −1 to −2
TSO	t decreases from 2 to 0, K = 1, probability update is 0.5
AFEA	Alfa = 30, K0 = 500;

.

In this work, the testing experiments are implemented using MATLAB R2023a on Windows 10 64 bits on a Core i7, 16 GB RAM laptop. For an unbiased evaluation, all compared algorithms have a similar number of search agents, N = 30, and the same total number of iterations, T = 500, and all algorithms have the same initialized search agents.

3.1. Statistical Analysis

Due to the random operation of all metaheuristic algorithms, we need to test these algorithms in many independent optimization experiments. Therefore, all optimization algorithms are executed 20 times for each testing function in this paper. Then, the robustness of an algorithm is confirmed by applying different statistical methods, for example, mean (m) and standard deviation (σ) and nonparametric testing methods.

Table 5. Mean and standard deviations of 20 independent trials.

No.		GWO	SCA	SSA	CS	WOA	PSO	TSO	AEFA	PSA
F1	m	2.954E−38	4.401E−11	1.204E−07	6.780E−01	1.845E−75	3.772E−07	2.037E−77	1.818E+00	3.507E−81
	σ	4.217E−38	7.184E−11	7.488E−08	3.424E−01	8.119E−75	5.262E−07	9.038E−77	4.526E+00	1.568E−80
F2	m	1.798E−22	4.088E−08	1.919E−01	4.904E−01	4.471E−52	9.866E−04	7.933E−40	9.613E+00	2.814E−42
	σ	2.141E−22	9.436E−08	1.990E−01	1.785E−01	1.355E−51	3.135E−03	3.353E−39	5.891E+00	8.774E−42
F3	m	1.465E−08	1.942E−08	1.891E+02	3.220E+02	2.092E+00	9.432E+02	2.050E−72	8.880E+02	5.964E−81
	σ	5.082E−08	4.062E−08	3.092E+02	2.957E+02	5.104E+00	1.118E+03	9.161E−72	4.508E+02	2.536E−80
F4	m	1.022E−01	8.313E−01	7.620E−01	1.083E+00	1.833E−02	2.120E+00	9.245E−40	1.486E+00	6.223E−43
	σ	2.591E−01	1.103E+00	6.087E−01	6.512E−01	3.710E−02	2.301E+00	4.122E−39	1.199E+00	1.474E−42
F5	m	2.161E+01	5.604E+01	1.991E+01	5.693E+01	7.043E+00	2.968E+01	4.282E+01	6.921E+02	2.507E−02
	σ	1.056E+01	8.190E+01	1.286E+01	4.234E+01	1.228E+01	2.689E+01	1.308E+02	1.143E+03	4.152E−02
F6	m	5.181E−01	5.225E+00	1.006E−06	5.647E−01	6.694E−03	6.793E−07	5.687E−01	1.379E+00	4.303E−02
	σ	3.616E−01	1.234E+00	3.178E−06	3.298E−01	1.232E−02	1.157E−06	6.711E−01	3.051E+00	1.902E−01
F7	m	1.701E−03	5.580E−04	2.901E−02	1.043E−02	7.335E−04	3.340E−02	6.114E−03	2.270E−01	6.207E−05
	σ	1.196E−03	7.296E−04	2.039E−02	1.271E−02	6.587E−04	2.274E−02	1.298E−02	1.791E−01	6.558E−05
F8	m	−1.176E+04	−1.173E+04	−1.239E+04	−1.243E+04	−1.239E+04	−1.234E+04	−1.247E+04	−1.226E+04	−1.257E+04
	σ	1.174E+03	1.161E+03	7.945E+02	2.125E+02	7.951E+02	8.072E+02	2.035E+02	4.015E+02	2.810E−02
F9	m	5.013E+01	2.966E+01	5.970E+00	1.652E+01	0.000E+00	1.323E+01	4.601E−05	3.100E+01	0.000E+00
	σ	4.214E+01	4.088E+01	1.225E+01	1.156E+01	0.000E+00	1.463E+01	1.111E−04	1.977E+01	0.000E+00
F10	m	1.910E−14	2.723E−05	8.452E−01	1.482E+00	3.997E−15	1.493E+00	9.446E−04	1.379E+00	4.441E−16
	σ	3.972E−15	7.773E−05	1.101E+00	8.255E−01	2.577E−15	1.916E+00	1.101E−03	1.058E+00	0.000E+00
F11	m	1.215E−03	6.158E−09	1.418E−02	6.696E−01	0.000E+00	1.746E−02	8.731E−02	6.641E−01	0.000E+00
	σ	3.741E−03	1.751E−08	1.305E−02	1.297E−01	0.000E+00	1.371E−03	1.968E−02	4.874E−01	0.000E+00
F12	m	4.925E−01	1.218E+00	4.070E−02	8.174E−02	1.105E−04	1.371E+00	1.219E−02	2.001E+00	1.433E−05
	σ	1.417E+00	1.462E+00	1.183E−01	7.730E−02	2.800E−04	2.738E+00	2.050E−02	1.659E+00	2.472E−05
F13	m	3.058E−01	2.085E+00	1.750E−01	3.605E−01	1.707E−02	4.397E−03	4.041E−01	1.017E+01	1.076E−02
	σ	2.599E−01	8.328E−01	6.583E−01	4.287E−01	5.871E−02	5.525E−03	9.038E−01	1.078E+01	4.679E−02
F14	m	1.978E+00	1.652E+00	1.048E+00	9.980E−01	1.486E+00	9.980E−01	9.980E−01	3.074E+00	1.147E+00
	σ	2.643E+00	9.196E−01	2.223E−01	7.675E−16	2.184E+00	0.000E+00	4.434E−08	2.259E+00	4.857E−01
F15	m	1.354E−03	5.678E−04	9.093E−04	3.141E−04	3.131E−04	4.319E−04	3.889E−04	1.045E−02	4.438E−04
	σ	4.475E−03	3.540E−04	6.895E−04	6.6833E−06	6.186E−06	1.139E−04	1.244E−04	6.900E−03	2.274E−04
F16	m	−1.032E+00	−1.032E+00	−1.032E+00	−1.032E+00	−1.032E+00	−1.032E+00	−1.032E+00	−1.032E+00	−1.032E+00
	σ	8.071E−08	9.936E−05	1.929E−14	8.823E−17	8.258E−10	2.161E−16	7.439E−06	2.038E−16	2.783E−06
F17	m	3.979E−01	4.020E−01	3.979E−01	3.979E−01	3.979E−01	3.979E−01	3.979E−01	3.979E−01	3.979E−01
	σ	2.293E−06	4.196E−03	9.744E−15	0.000E+00	1.453E−05	0.000E+00	4.011E−05	0.000E+00	3.393E−05
F18	m	3.000E+00	3.000E+00	3.000E+00	3.000E+00	3.000E+00	3.000E+00	3.107E+01	3.056E+00	3.000E+00
	σ	1.935E−05	6.407E−05	1.253E−13	1.585E−15	8.710E−05	9.557E−16	1.209E+00	2.518E−01	2.115E−04
F19	m	−3.860E+00	−3.850E+00	−3.863E+00	−3.863E+00	−3.857E+00	−3.862E+00	−3.731E+00	−3.862E+00	−3.862E+00
	σ	3.312E−03	4.917E−03	9.363E−11	2.040E−15	1.049E−02	1.762E−03	3.073E−01	1.102E−03	1.400E−03
F20	m	−3.298E+00	−2.696E+00	−3.255E+00	−3.322E+00	−3.294E+00	−3.286E+00	−3.275E+00	−3.322E+00	−3.223E+00
	σ	7.242E−02	3.335E−01	1.025E−01	4.843E−09	7.383E−02	6.652E−02	1.799E−01	4.556E−16	8.357E−02
F21	m	−8.318E+00	−7.132E+00	−1.015E+01	−1.015E+01	−9.898E+00	−8.373E+00	−1.013E+01	−7.285E+00	−1.015E+01
	σ	2.229E+00	2.255E+00	3.153E−11	1.500E−08	1.140E+00	2.488E+00	3.212E−02	2.158E+00	6.068E−04
F22	m	−8.548E+00	−7.536E+00	−9.612E+00	−1.040E+01	−1.014E+01	−8.289E+00	−1.038E+01	−9.712E+00	−1.040E+01
	σ	2.445E+00	2.342E+00	1.932E+00	1.765E−08	1.188E+00	2.656E+00	5.051E−02	1.703E+00	8.270E−04
F23	m	−8.912E+00	−7.562E+00	−1.027E+01	−1.054E+01	−9.995E+00	−8.923E+00	−1.051E+01	−1.054E+01	−1.054E+01
	σ	2.200E+00	2.216E+00	1.199E+00	1.223E−07	1.664E+00	2.528E+00	2.716E−02	1.578E−15	2.631E−03

displays the m and σ of 20 independent runs for all 23 testing functions using the offered PSA and other compared algorithms. The outcomes proved that the offered PSA is competitive with different algorithms and obtained the optimum outcomes for 16 functions out of 23. However, the second competitive algorithm is the CS algorithm, which achieves 9 best functions out of 23 functions.

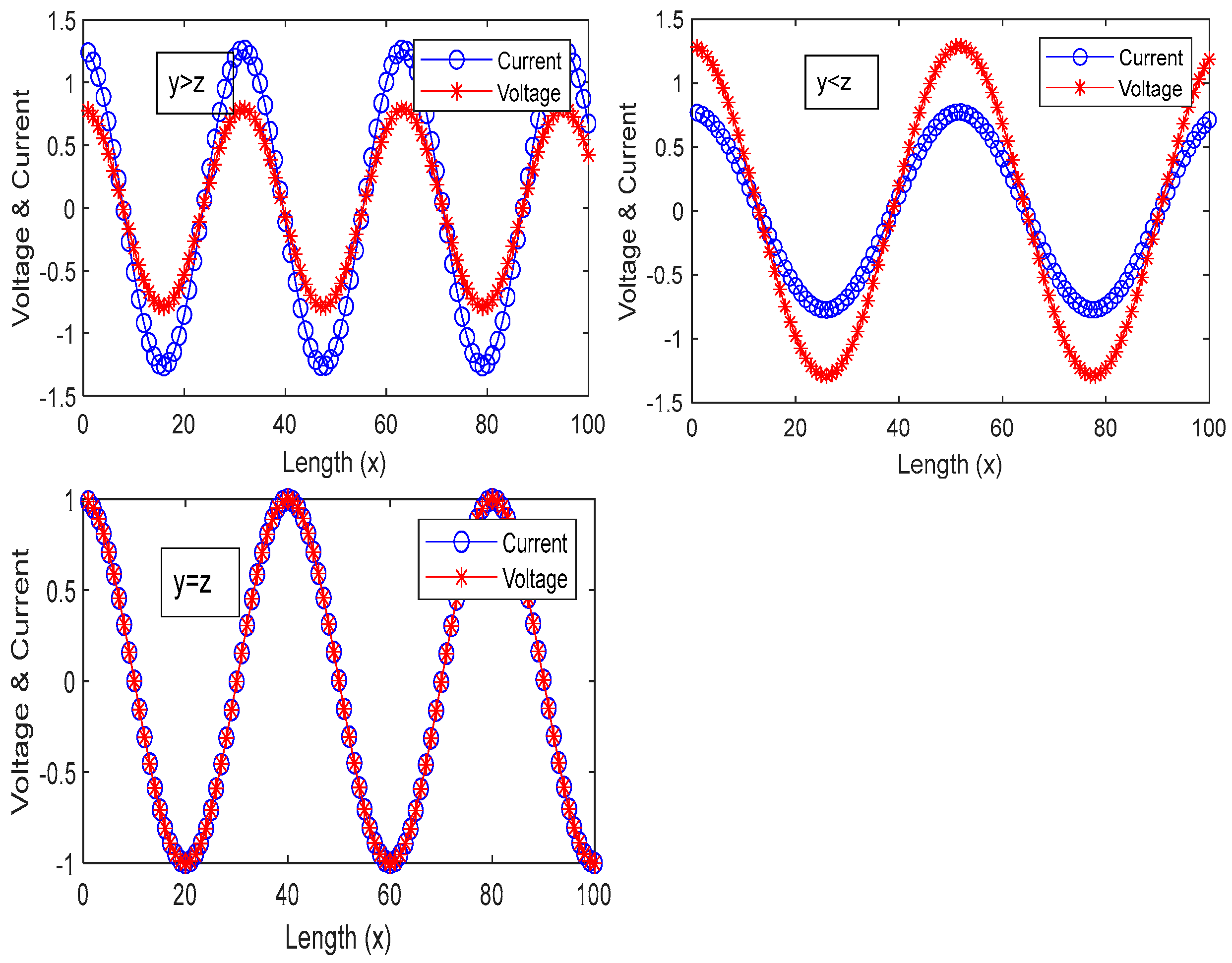
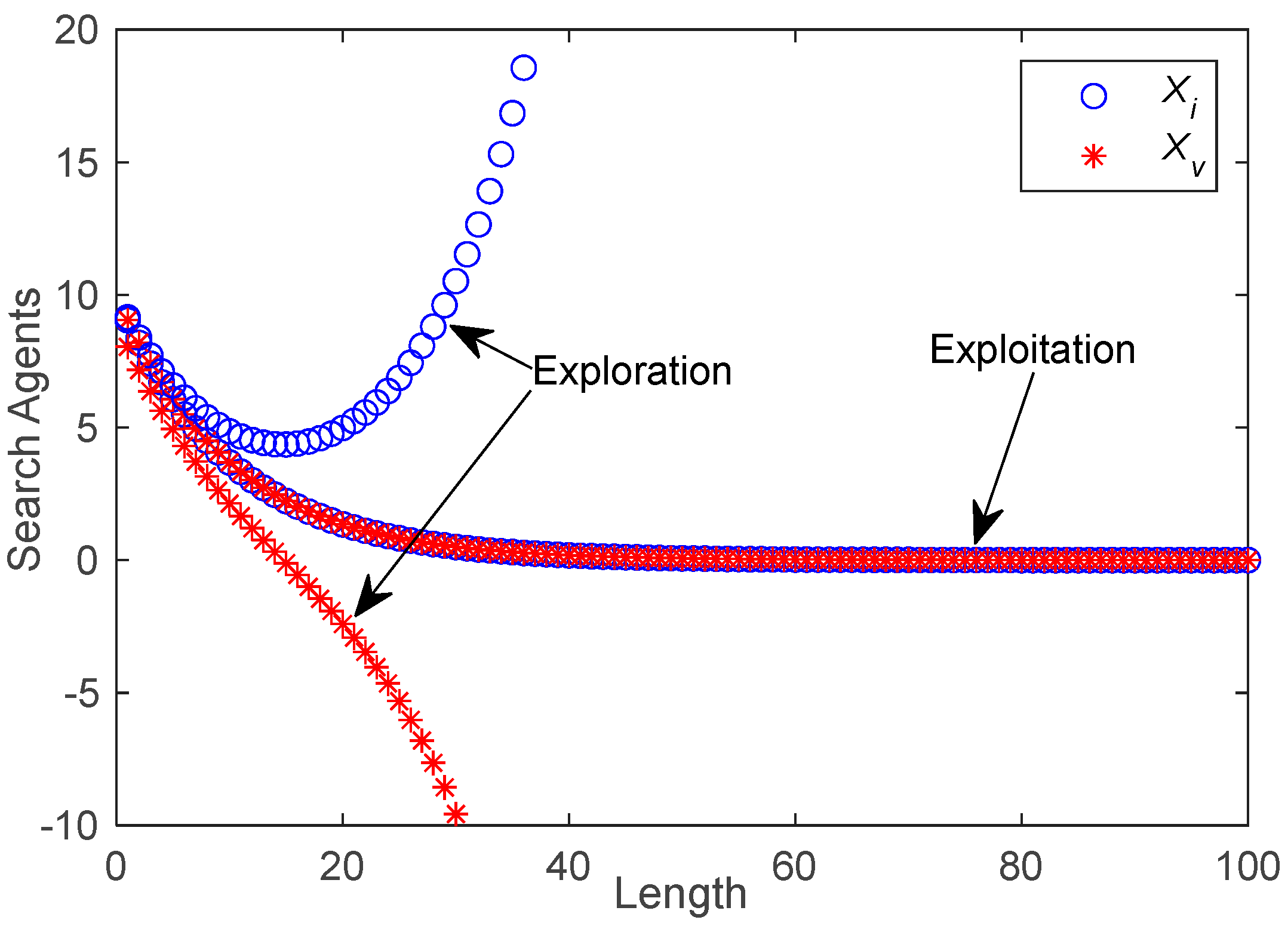
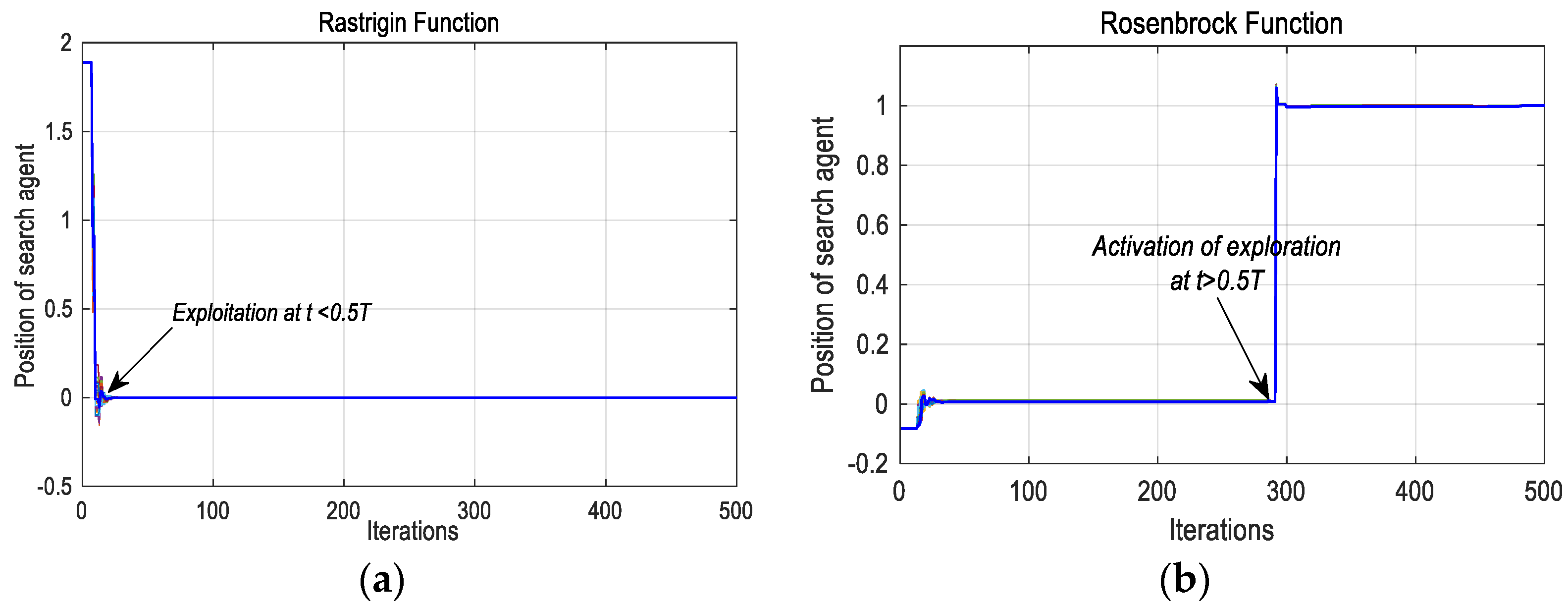
The exploitation of the algorithms is measured using unimodal functions (F1–F8), where the proposed PSA achieved the best outcomes for seven out of eight functions, which proved the exploitation capability of the PSA among other algorithms. On the other side, the exploration capability of the PSA is measured using the multimodal functions (F9–F23). The results show that the PSA obtained the 10 best results out of 15, whereas the CS algorithm achieved second place with the 9 best results out of 15. To check the equilibrium between exploration and exploitation, Rosenbrock (F5) and Rastrigin (F9) are used because they are contrasted, and no algorithm can solve both of them successfully. The results verified that the PSA succeeded in obtaining better results than other algorithms in both types of functions.

Additionally, the Wilcoxon signed-rank test with a 5% significance level is utilized to verify the significance of the PSA among other compared algorithms. This test is a null hypothesis test, which hypothesizes that the results of the PSA and other algorithms are the same if the p-value is higher than 0.05.

Table 6. Wilcoxon signed-rank test.

No.		GWO	SCA	SSA	CS	WOA	PSO	TSO	AEFA
F1	p-value	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05
	h	true	true	true	true	true	true	true	true
F2	p-value	6.683E−05	6.683E−05	6.683E−05	6.683E−05	1.03E−04	6.683E−05	6.683E−05	6.683E−05
	h	true	true	true	true	true	true	true	true
F3	p-value	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05
	h	true	true	true	true	true	true	true	true
F4	p-value	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05	6.683E−05
	h	true	true	true	true	true	true	true	true
F5	p-value	6.683E−05	6.683E−05	6.683E−05	6.683E−05	1.32E−03	1.03E−04	6.683E−05	6.683E−05
	h	true	true	true	true	true	true	true	true
F6	p-value	6.81E−04	6.683E−05	6.683E−05	1.20E−04	3.04E−02	1.03E−04	7.80E−04	2.82E−03
	h	true	true	true	true	true	true	true	true
F7	p-value	6.683E−05	2.54E−04	6.683E−05	6.683E−05	2.19E−04	6.683E−05	1.20E−04	6.683E−05
	h	true	true	true	true	true	true	true	true
F8	p-value	6.683E−05	6.683E−05	1.51E−03	6.683E−05	9.11E−01	7.31E−02	1.03E−04	6.683E−05
	h	true	true	true	true	true	true	true	true
F9	p-value	1.32E−04	4.38E−04	6.683E−05	6.683E−05	trueE+00	6.683E−05	6.683E−05	6.683E−05
	h	true	true	true	true	false	true	true	true
F10	p-value	6.81E−05	6.683E−05	6.683E−05	6.683E−05	6.10E−05	6.683E−05	6.683E−05	6.683E−05
	h	true	true	true	true	true	true	true	true
F11	p-value	5.00E−01	6.683E−05	6.683E−05	6.683E−05	trueE+00	6.683E−05	6.683E−05	6.683E−05
	h	false	true	true	true	false	true	true	true
F12	p-value	6.683E−05	6.683E−05	2.19E−04	6.683E−05	5.75E−01	6.01E−01	6.683E−05	6.683E−05
	h	true	true	true	true	false	false	true	true
F13	p-value	2.19E−04	6.683E−05	1.32E−03	6.683E−05	1.52E−02	4.78E−01	3.90E−04	6.683E−05
	h	true	true	true	true	true	false	true	true
F14	p-value	4.38E−02	7.80E−04	1.16E−03	6.683E−05	3.33E−02	6.683E−05	5.02E−01	3.38E−04
	h	true	true	true	true	true	true	false	true
F15	p-value	1.79E−01	9.30E−02	1.11E−02	2.19E−04	7.80E−04	7.94E−01	5.02E−01	6.683E−05
	h	false	false	true	true	true	false	false	true
F16	p-value	2.54E−04	6.683E−05	6.683E−05	6.683E−05	1.03E−04	6.683E−05	1.87E−02	6.683E−05
	h	true	true	true	true	true	true	true	true
F17	p-value	3.04E−02	6.683E−05	6.683E−05	6.683E−05	1.56E−01	6.683E−05	2.28E−02	6.683E−05
	h	true	true	true	true	false	true	true	true
F18	p-value	1.52E−02	1.79E−01	6.683E−05	6.683E−05	3.33E−02	6.683E−05	6.683E−05	1.51E−03
	h	true	true	true	true	false	true	true	true
F19	p-value	3.32E−01	6.683E−05	6.683E−05	6.683E−05	2.28E−02	1.32E−03	2.19E−04	2.04E−01
	h	false	true	true	true	true	true	true	false
F20	p-value	6.42E−03	6.683E−05	2.63E−01	6.683E−05	2.20E−03	1.24E−02	4.55E−03	6.683E−05
	h	true	true	false	true	true	true	true	true
F21	p-value	6.683E−05	6.683E−05	6.683E−05	6.683E−05	8.52E−01	6.01E−01	6.683E−05	1.03E−04
	h	true	true	true	true	false	false	true	true
F22	p-value	6.683E−05	6.683E−05	7.31E−02	6.683E−05	2.63E−01	3.13E−01	6.683E−05	trueE+00
	h	true	true	false	true	false	false	true	false
F23	p-value	6.683E−05	6.683E−05	1.51E−03	6.683E−05	4.33E−01	trueE+00	1.63E−04	6.683E−05
	h	true	true	true	true	false	false	true	true

shows the p-values and the denial of the null hypothesis (h = true) or acceptance of it (h = false). We can notice that the most dominant decision is h = true, meaning a significant difference exists between the PSA and other algorithms.

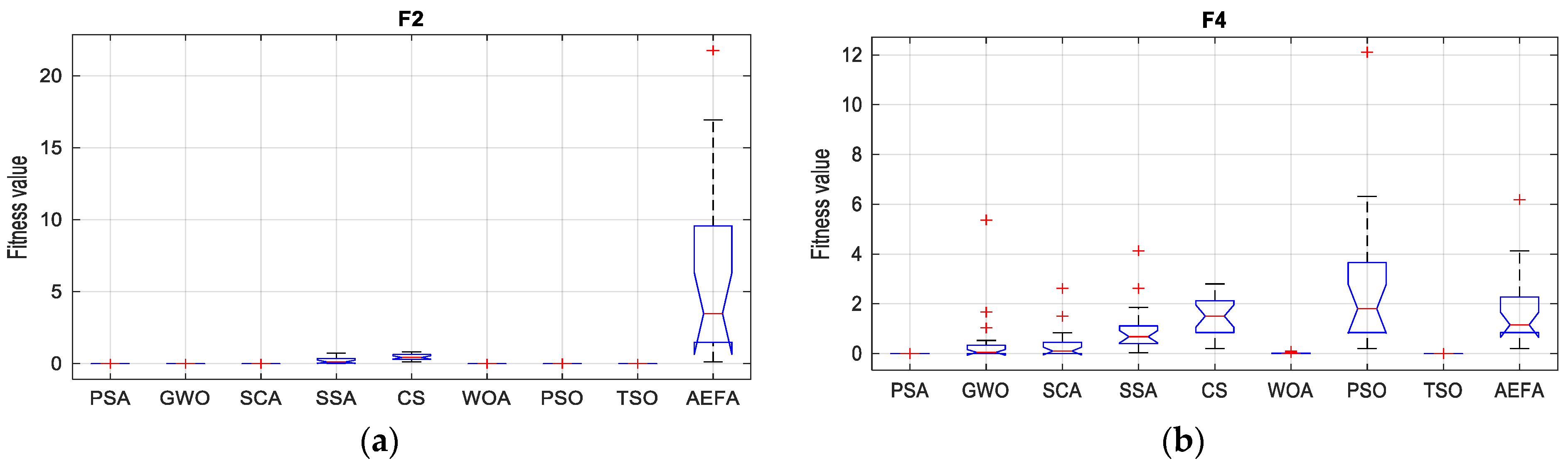
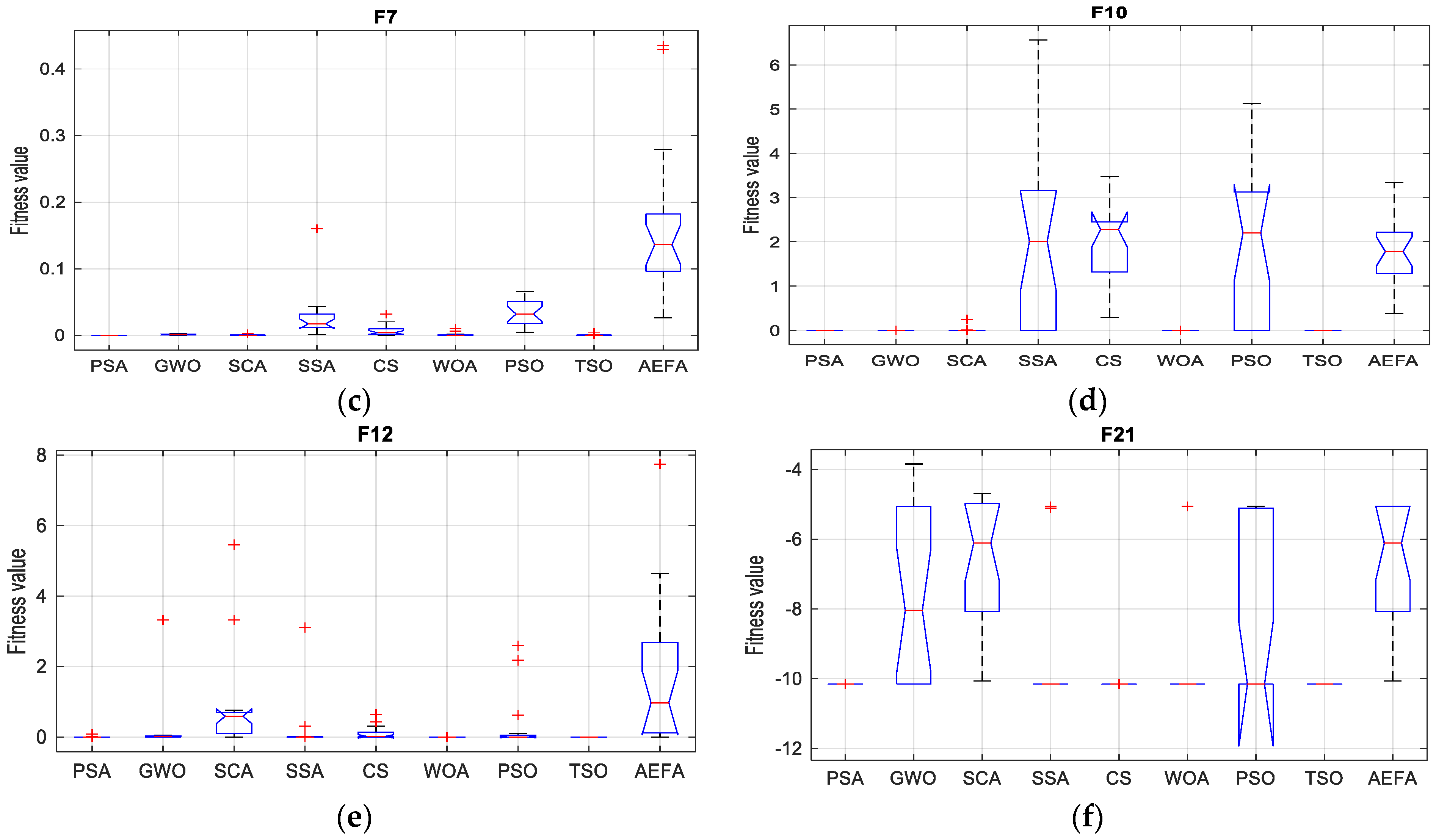
Finally, a boxplot is used for further statistical analysis to verify the performance of the PSA during 20 independent experiments. Figure 6a–f shows the boxplot for six benchmark functions (F2, F4, F8, F10, F12, and F21). The boxplot analysis shows that the PSA has obtained a very small deviation between the maximum and minimum values of 20 experiments. Moreover, it is noticeable that there are outlier points, which are labeled by (+), for all compared algorithm except PSA. Therefore, the boxplot proved the robustness of the PSA over other algorithms.

3.2. Optimization Convergence

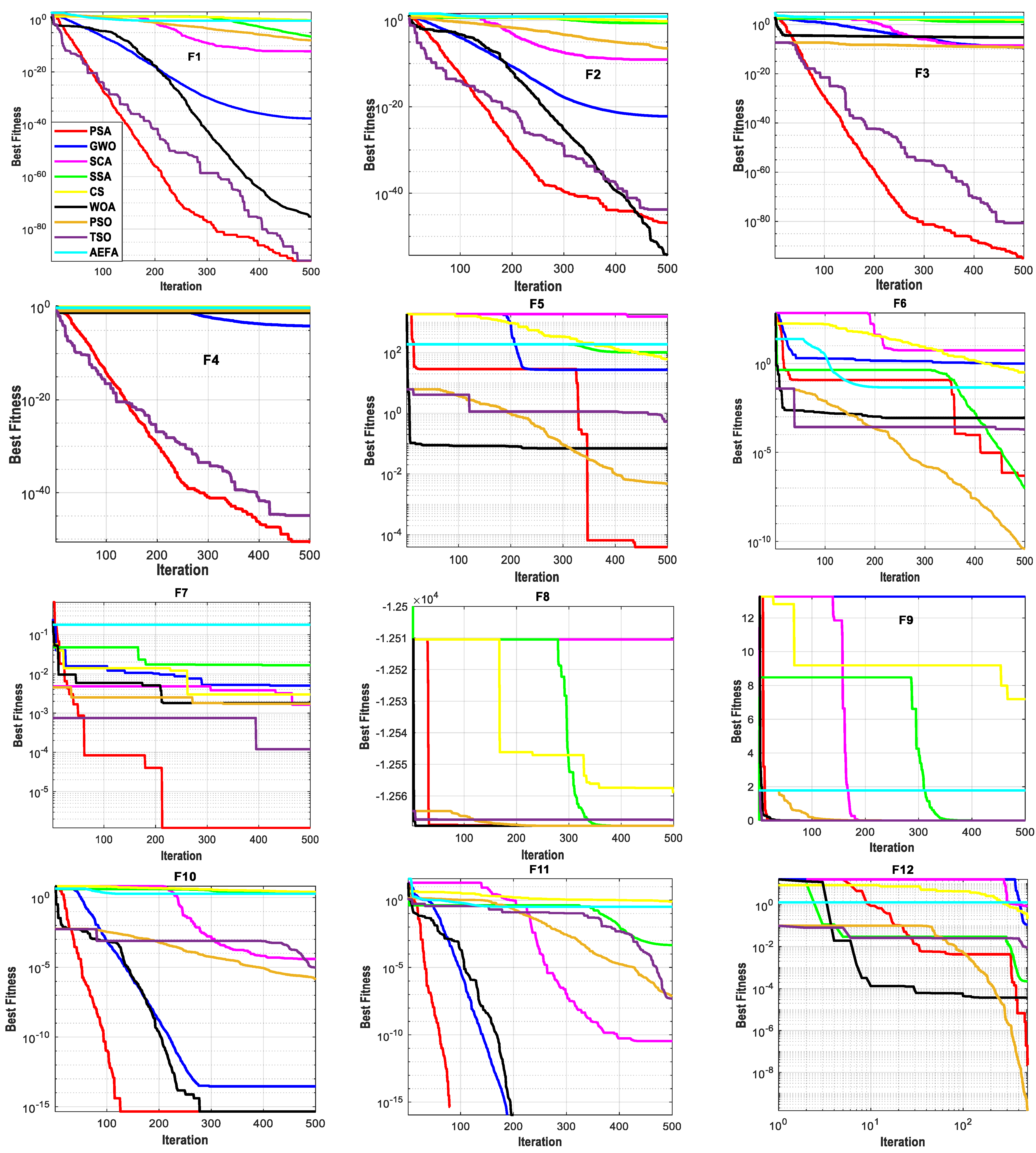
The speed of finding the best solution plays a critical role in control systems, so we need to check the behavior of algorithms with each increment of iterations.

Table 7. Elapsed time in seconds for algorithm execution.

	GWO	SCA	SSA	CS	WOA	PSO	TSO	AEFA	PSA
F1	0.19396	0.12807	0.12076	0.32297	0.07844	0.10489	0.07901	0.70572	0.14529
F3	0.28908	0.25333	0.21823	0.59093	0.21227	0.24697	0.20247	0.5662	0.21162
F5	0.22024	0.14419	0.11669	0.37283	0.09557	0.12428	0.09445	0.74423	0.18258
F7	0.25270	0.27462	0.17785	0.52765	0.18240	0.20720	0.15772	0.58886	0.23347
F9	0.21667	0.14238	0.10190	0.35608	0.09275	0.12364	0.07937	0.70294	0.15709
F11	0.21608	0.15083	0.11007	0.39285	0.09911	0.13238	0.09883	0.75162	0.18998
F13	0.43091	0.37946	0.34172	0.89211	0.32739	0.34480	0.31621	0.71861	0.45095
F15	0.08482	0.06125	0.04754	0.24100	0.04562	0.04603	0.04342	0.19139	0.07792
F17	0.04381	0.05114	0.03805	0.20785	0.03501	0.02629	0.03271	0.14607	0.05805
F19	0.05045	0.05739	0.05281	0.22891	0.05190	0.04391	0.04880	0.17714	0.12969
F21	0.06674	0.06795	0.06347	0.25504	0.05845	0.05484	0.06027	0.21141	0.10314
F23	0.08750	0.08496	0.08194	0.29582	0.07910	0.07160	0.07826	0.22082	0.14134
Sum	2.15295	1.79558	1.47103	4.68403	1.35800	1.52684	1.29151	5.72502	2.08111

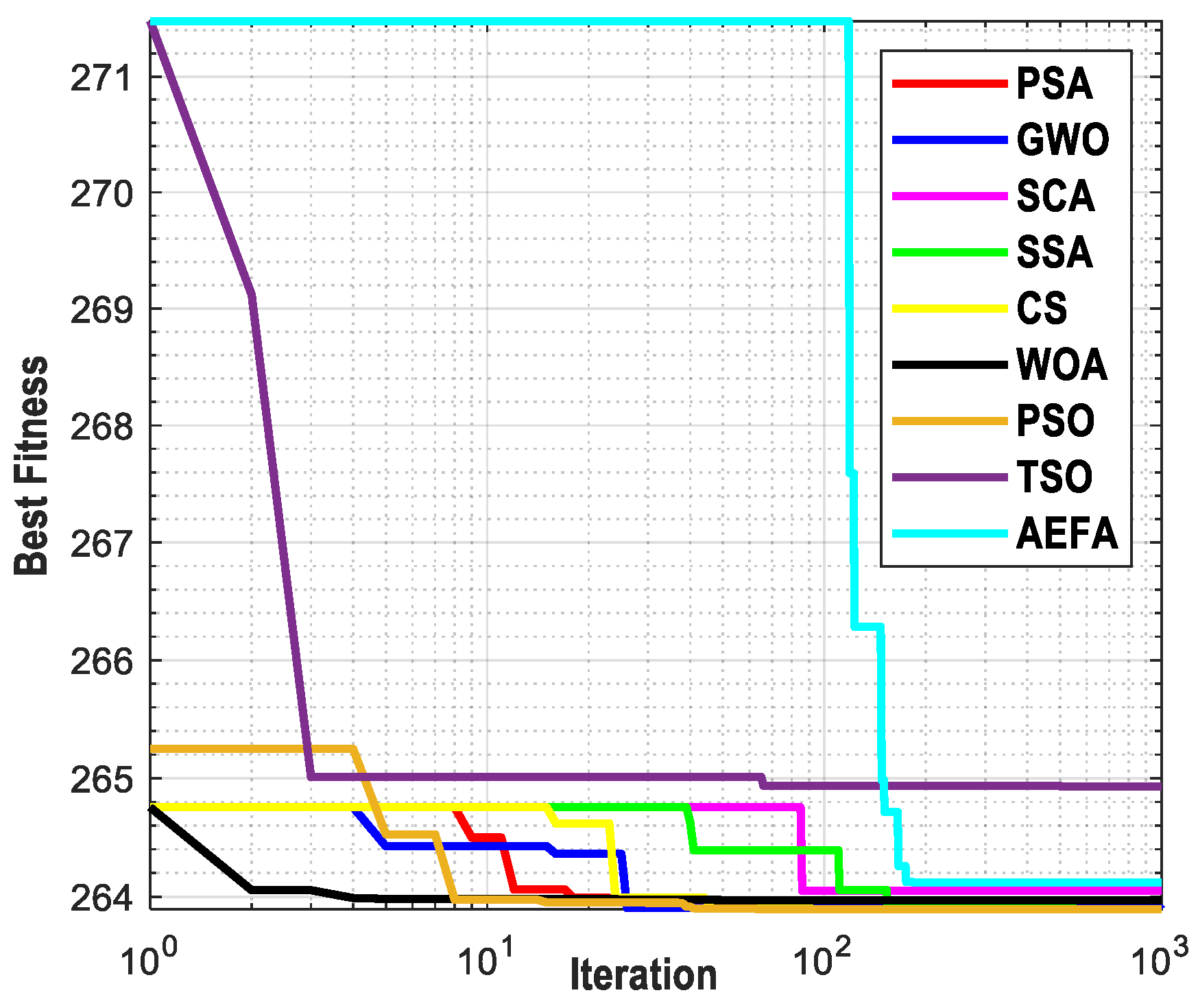
displays the total elapsed time for all compared algorithms during each independent experiment. However, Figure 7 shows the convergence behavior for all compared algorithms toward the best minimum solution. It is noticeable that all algorithms start from the same initial point for unbiased comparison. The proposed PSA shows fast convergence for the testing functions F1–F8, and then at the middle of total iterations (t = 250) it becomes slower because of changes in the values of the propagation constant (γ). For the remaining functions, the PSA competes with the other algorithms in searching for global solutions; particularly, at t = 250 the PSA escapes being trapped in a local solution.

4. Renowned Engineering Problems

In this section, the offered PSA and other algorithms are utilized to obtain the optimum design of four famous engineering problems, including a three-bar truss structure, a compression spring, a pressure vessel, and a welded beam. The optimization experiments are conducted on MATLAB 2023a on a Windows 10 Core-i7 laptop. The number of search agents is 200, and the total number of iterations is 1000. The mean and standard deviation are calculated for 20 independent code runs.

4.1. Three-Bar Truss Design

Figure 8 depicts the structure of this truss, which is constructed of three bars with different cross-sectional areas (A₁, A₂, and A₃), where A₁ = A₃. These bars meet at a common node, where a P load is connected to this node. The dimensions between the supporting points of the three bars are equal, which is l, and the vertical dimension between the supporting points and the common node is l too. Reducing the weight of the truss structure is the chief objective, and the design parameters are A₁ and A₂. The objective function is shown in (17), and the subjected constraints are shown in (18). The PSA is applied to obtain the optimal cross-sectional areas that result in the minimum weight of the three-bar truss.

Table 8. Optimal weight and parameters of three-bar truss design.

	GWO	SCA	SSA	CS	WOA	PSO	TSO	AEFA	PSA
Best	263.8959846	263.9090923	263.9195433	263.8958434	263.8959030	263.8958434	263.8969047	263.9195433	263.8958824
m	263.8964313	263.9553596	264.0115258	263.8958434	263.9431231	263.8958439	265.5472387	264.0115258	263.8984017
σ	4.11448E−04	4.21400E−02	9.00459E−02	0.00000E+00	6.82155E−02	7.34918E−07	1.49798E+00	9.00459E−02	2.21516E−03
x1	0.789005319	0.789674131	0.788484498	0.788675136	0.788960013	0.788681652	0.787476956	0.788484498	0.789351215
x2	0.407315799	0.405555191	0.408787881	0.408248286	0.407443127	0.408229858	0.411647866	0.408787881	0.406573046

displays the outcomes of the optimal areas and the minimum weights obtained using eight algorithms. The statistical results (m and σ) show that the offered PSA has a performance that is comparable with other algorithms, and even better. Moreover, Figure 9 indicates that the PSA converges to the minimum result after only 85 iterations, which is quicker than most of the compared algorithms.

$$\min f(x=[A_1,A_2])=\left(2\sqrt{2}{A}_1+A_2\right)\times l$$

(17)

$$\begin{array}{l}{g}_1(x)=\frac{2\sqrt{2}{A}_1+A_2}{\sqrt{2}{A}_1{}^2+2A_1{A}_2}P-\sigma \le 0 \& g_2(x)=\frac{A_2}{\sqrt{2}{A}_1{}^2+2A_1{A}_2}P-\sigma \le 0\\ g_3(x)=\frac{1}{A_1+\sqrt{2}{A}_2}P-\sigma \le 0 , P=2 \mathrm{kN}, \sigma =2{ \mathrm{kN}/\mathrm{cm}}^2, l=100 \mathrm{cm}\end{array}$$

(18)

4.2. Compression Spring Design

The structure of the compression spring, which is made of steel wire in a spiral form with several coils (N), a material diameter (d), and outer diameter of coil (D), is depicted in Figure 10. Reducing the weight of the compressional spring is the chief objective, where the controlling design parameters are D, d, and N. However, there are constraints to minimizing the weight of the spring, such as the torsional stress, deflection, traveling waves, and dimension. The objective function and the constraint functions of the compression spring design are expressed in (19) and (20). The PSA and other algorithms are applied to find the minimum weight of the compression spring, and the optimal outcomes are presented in

Table 9. Optimal weight and parameters of compression spring design.

	GWO	SCA	SSA	CS	WOA	PSO	TSO	AEFA	PSA
Best	0.0177757	0.0127331	0.0178723	0.0126721	0.0127984	0.0178487	0.0126668	0.0196575	0.0127226
m	0.0177873	0.0128085	0.0219118	0.0126977	0.0136459	0.0179014	0.0139309	0.0336801	0.0132851
σ	0.0000080	0.0000546	0.0082340	0.0000195	0.0011371	0.0000373	0.0015793	0.0137893	0.0006535
D	0.0689962	0.0500000	0.0691542	0.0515176	0.0544458	0.0690812	0.0519697	0.0572892	0.0500000
d	0.9335070	0.3172711	0.9404314	0.3525262	0.4267345	0.9370252	0.3635050	0.5068545	0.3174241
N	2.0000000	14.0532354	1.9739055	11.5439263	8.1174138	1.9914889	10.9019563	9.8167597	14.0323211

. Furthermore, Figure 11 compares the PSA’s convergence speed with other algorithms, showing that the PSA offers a quicker convergence than most of the compared algorithms, and the PSA converges to the minimum solution after 10 iterations only.

$$\min f(x=[D,d,N])=D^{2}d(N+2)$$

(19)

$$\begin{array}{l}{g}_1(x)=1-\frac{d^{3}N}{71785D^4}\le 0 \mathrm{and} g_2(x)=\frac{4d^2-Dd}{12566D^3(d-D)}+\frac{1}{5108D^2}-1\le 0\\ g_3(x)=1-\frac{140.45D}{N{d}^2}\le 0 \mathrm{and} g_4(x)=\frac{D+d}{1.5}-1\le 0\\ 0.05\le D\le 2 \& 0.25\le d\le 1.3 \& 2.00\le N\le 15\end{array}$$

(20)

4.3. Welded Beam Design

The structure of the welded beam, which is made by welding a beam to a rigid support member, is depicted in Figure 12. Therefore, reducing the fabrication cost of the welded beam, including labor and material costs, is the main objective, where the controlling design parameters are the dimensions of welding (h) and (l) and the dimensions of the member bar (t) and (b), as shown in Figure 10. However, there are constraints to lessening the cost of the welded beam, such as the weld stress (τ), bending stress (σ), and bar buckling load (P_c). The objective function and the constraint functions of welded beam design are expressed in (21) and (22). The PSA and other algorithms are utilized to find the minimum cost of the welded beam design, and the optimal outcomes are shown in

Table 10. Optimal cost and parameters of welded beam design.

	GWO	SCA	SSA	CS	WOA	PSO	TSO	AEFA	PSA
Best	1.7261166637	1.7789887672	2.4719864210	1.7318832346	1.7332745737	1.7248523086	1.7338377644	2.4719864210	1.7250306573
m	1.7267581063	1.8287256087	3.0407655957	1.7378652824	1.7947045480	1.7248523088	1.7835502505	3.0407655957	1.7327229652
σ	5.19265E−04	2.34891E−02	3.96367E−01	4.99296E−03	3.61117E−02	5.07366E−10	4.43964E−02	3.96367E−01	5.14617E−03
h	0.2057226591	0.2074198677	0.1534791096	0.2060105624	0.2002029004	0.2057296398	0.1824037798	0.1534791096	0.2056551204
l	3.4718445411	3.6040616975	6.8582665831	3.4837895853	3.5923940636	3.4704886656	4.5358535044	6.8582665831	3.4718699729
t	9.0382895241	9.0678166725	9.5571430874	9.0294913594	9.0419370726	9.0366239104	8.8276280063	9.5571430874	9.0373416776
b	0.2058352914	0.2093402452	0.2391445616	0.2065207396	0.2057031460	0.2057296398	0.2155863505	0.2391445616	0.2057274905

. Furthermore, Figure 13 compares the PSA algorithm’s convergence speed with other algorithms, showing that the PSA offers a faster convergence speed than most different algorithms, and the PSA converges to the best minimum after only 40 iterations.

$$\min f(x=[h l t b])=1.10471\times h^2\times l+0.04811t\times b(14.0+l)$$

(21)

$$\begin{array}{l}{g}_1(x)=\tau -{\tau }_{\max }\le 0 \mathrm{and} g_2(x)=\sigma -{\sigma }_{\max }\le 0\\ g_3(x)=\delta -{\delta }_{\max }\le 0 \mathrm{and} g_4(x)=h-b\le 0\\ g_5(x)=P-P_c\le 0 \mathrm{and} g_6(x)=0.125-h\le 0\\ g_7(x)=0.10471\times h^2+0.04811\times l\times b\times (14.0+l)-5.0\le 0\\ 0.1\le h\le 2 \& 0.1\le l\le 10 \& 0.1\le t\le 10 \& 0.1\le b\le 2\end{array}$$

(22)

where

$$\begin{array}{l}P=6,000 lb;L=14 in;E=30\times {10}^6 psi;G=12\times {10}^6 psi\\ {\tau }_{\max }=13,600 psi;{\sigma }_{\max }=30,000 psi;{\delta }_{\max }=0.25 in\\ M=P(L+\frac{l}{2});R=\sqrt{\frac{l^2}{4}+{(\frac{h+t}{2})}^2};{\tau }^{’}=\frac{P}{\sqrt{2h\times l}};{\tau }^{"}=\frac{MR}{J}\end{array}$$

$$\begin{array}{l}J=2\sqrt{2}h\times l(\frac{l^2}{12}+{(\frac{h+t}{2})}^2);\tau =\sqrt{{\tau }^{’}{}^2+{\tau }^{’}{\tau }^{"}\frac{l}{R}+{\tau }^{"}{}^2}\\ P_c=4.013\frac{E}{L^2}\sqrt{\frac{t^2\times b^6}{36}}(1-\frac{t}{2L}\sqrt{\frac{E}{4G}})\\ \sigma =\frac{6PL}{b\times t^2};\delta =\frac{4P{L}^3}{E\times b\times t^2}\end{array}$$

4.4. Pressure Vessel Design

The structure of the pressure vessel, which is made of stainless steel plates that are welded to form a cylindrical shape, is depicted in Figure 14. Therefore, reducing the weight of the pressure vessel is the chief objective, where the controlling design parameters are the dimensions of the vessel, comprising the thickness of the shell (t_s), thickness of the head (t_h), inner radius (r), and length of the vessel (l). However, there are constraints to minimizing the cost of the pressure vessel design, such as the inner volume and the overall size of the vessel. The cost function and the constraint functions of pressure vessel design are expressed in (23) and (24). The PSA and other algorithms are utilized to find the lowest weight of the pressure vessel, and the optimal outcomes are shown in

Table 11. Optimal weight and parameters of pressure vessel design.

	GWO	SCA	SSA	CS	WOA	PSO	TSO	AEFA	PSA
Best	5889.3161636	6084.9664550	6288.2580937	5886.5458106	6033.9780276	5942.1267062	6713.1969272	26533.6320741	5886.9897087
m	5894.1446757	6307.2406394	7009.5719313	5893.2120452	6631.8600064	6101.1999200	7102.4268313	96354.3822355	6077.8295567
σ	6.1000446	139.9687665	874.9974107	3.8547414	493.3610049	140.4149521	893.3723107	44235.2712807	308.1664002
ts	0.7784311	0.7895409	0.9652823	0.7782347	0.7910326	0.8100689	1.0831728	2.8963402	0.7783762
th	0.3848615	0.3983170	0.4771401	0.3847895	0.4320066	0.4004175	0.5158489	1.1004971	0.3846826
r	40.3285572	40.7806669	50.0145885	40.3216202	40.9557154	41.9724803	54.0592595	64.9921818	40.3199574
l	200.0000000	200.0000000	98.2297744	200.0000000	191.3306399	178.2037836	69.0821101	51.8458794	200.0000000

. Additionally, Figure 15 compares the convergence curve of the PSA with other algorithms, where the PSA offers a quicker convergence than the most of compared algorithms, and the PSA converges to the best minimum after only 50 iterations.

$$\min f(x=[T_s,T_h,R,L])=0.6224T_s{T}_{h}L+1.7781T_h{R}^2+3.1661T_s{}^{2}L+19.84T_s{}^{2}R$$

(23)

$$\begin{array}{l}{g}_1(x)=-T_s+0.0193R\le 0 \& g_2(x)=-T_h+0.00954R\le 0\\ g_3(x)=-\pi R^{2}L-\frac{4}{3}\pi R^3+1,296,000\le 0 \& g_4(x)=L-240\le 0\\ 0\le T_s\le 99 \& 0\le T_h\le 99 \& 10\le R\le 200 \& 10\le L\le 200\end{array}$$

(24)

5. Conclusions

In this work, a new physics-based metaheuristic optimization algorithm named the propagation search algorithm (PSA) is offered and utilized to optimize different engineering design problems. First, the exploration and exploitation capabilities of the PSA are confirmed using 23 famous testing functions. The obtained outcomes for the Rosenbrock and Rastrigin functions have confirmed that the PSA has a balanced capability between exploration and exploitation in the optimization procedure. The propagation constant of the PSA controls this balancing capability. The statistical tests are applied to verify the superiority of the PSA among other compared algorithms. The PSA has succeeded in finding the optimal solution for 17 functions out of 23; however, the second-ranked algorithm solved only 9 functions. The Wilcoxon signed-ranked test is applied to confirm the significance level of the outcomes of the PSA compared with those of other algorithms, where 90% of the computed p-values are less than 5%. The PSA and the compared algorithms are utilized to obtain the optimum design of four famous engineering problems, including the three-bar truss, compression spring, welded beam, and pressure vessel. The PSA has succeeded in finding competitive results and fast convergence to the minimum fitness values. The optimization results have shown that the proposed PSA is a promising optimizer that can be easily applied in engineering fields. Finally, the simple form of the PSA limits its performance in some engineering applications. Therefore, the future work will present different enhancements to the PSA and will apply it in power systems.