An Approach Using the Transfer Matrix Method (TMM) for Mandible Body Bone Calculus

Abstract

This paper presents an original approach for mandible bone calculus by the Transfer Matrix Method (TMM). The role of the mandible bone is very important due to the three functions that it has: mastication, phonation and aesthetics. Due to these functions, there are many studies in this regard. The mandible bone is an unpaired bone and the only movable bone in the skull. For our studies, we separated a part of the mandible bone assimilated with a spring, and due to the symmetry we can only study a quarter of the circle, embedded at the two ends, charged perpendicular to its plane by a concentrated vertical load corresponding to a tooth which is on the studied side. This mandible side under study has eight teeth: two incisors, one canine, two premolars and three molars. The approach by the TMM is very easy to program, especially for extreme cases, when a quick calculus is needed to optimize the shape of the mandible. In the future we hope to be able to publish the calculation and shape optimization program and a related case study.

1. Introduction

The application of a mathematical apparatus and calculus of Material Resistance in medicine are challenges that researchers have undertaken to study. This approach by the Transfer Matrix Method (TMM) is an original calculus for a mathematical model of mandible body bone and that is presented in this work. In current context of evolution for interdisciplinary collaborations, we believe that this study can be considered as an additional step in the study of orthodontics through mathematical methods, in particular through the TMM. Therefore, we think it is appropriate in the current scientific context. Our study is relevant in the fact that the TMM has not been applied to the study of the mandibular bone before. The idea is original, and also the mathematical approach of study through the TMM is original, by considering the mandible body model as a semicircle. Due to the symmetry in relation to the vertical sectioning plane (according to Figure 1), only a quarter circle was studied (according to Figure 2).

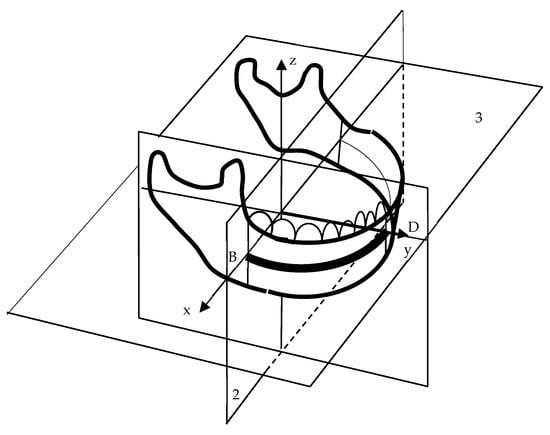
Figure 1. Mandible body separated with two planes.

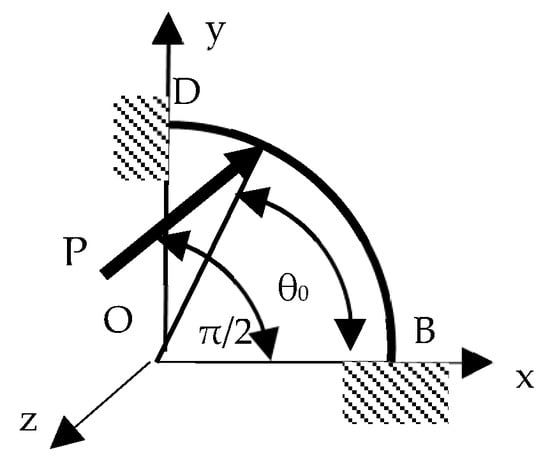
Figure 2. Mathematical model of mandible body as a quarter of a circle loaded with P, a concentrated vertical force which acts perpendicular to the plane of a spring.

The three functions (mastication, phonation and aesthetics) in which the mandible participates are very important for human life and health. The lower jaw or mandible is an unpaired bone and is the only mobile bone of head skeleton, which consists of a body and two branches; each branch has a condyle in the posterior part and the coronoid process takes place in the anterior part. In the glenoid cavity of the temporal bone, the condyle articulates and forms the temporomandibular joint. The body is shaped like a horseshoe, and on the upper part it presents 16 dental alveoli corresponding to the lower teeth. This study presents several works from different fields in which the TMM was used, without being able to include all the works in the TMM field. In addition, some works with other approaches are presented, problems that in the future could be treated with the TMM. The basics of the Transfer Matrix Method are presented in [1], and the strength calculus for springs and curved bars is given in [2]. In the following, we present some bio-engineering and bone engineering studies using different methods (TMM, FEM, etc.). Another approach to the calculus for mandible bone according to a semicircle model by TMM is presented in [3]. A study about a buckling calculus of straight bars in an elastic environment by the Transfer Matrix Method (TMM) for dental implants was conducted in [4], and [5] gives us an analytical study of a dental bridge by the similarity to a beam by the TMM. The Finite Element Method (FEM) is used in [6] for studies on the transmission of masticator forces to the bone substrate via titanium and zirconium implants. In [7] is presented the creation of bone supply for patients with severe atrophy of the mandible for rehabilitation using prosthetic implants. A study on the position of the mandible channel in totally edentulous patients with clinical implications is given in [8]. Human bone marrow stromal cells with in vitro expansion and differentiation for bone engineering are presented in [9]. The authors of [10] present a study of changing geometric characteristics in the proximal femoral bone affected by osteoporosis in compliance with the Singh index. The Matrix Method is applied in the robotics domain in [11]. In [12], the application of a numerical quantum Transfer Matrix approach in randomly diluted quantum spin chains is presented. Applications of a probabilistic Transfer Matrix are presented in [13] and [14]. The evolution of Transfer Matrix elements for multimodal systems is given in [15]. The authors of [16] present an evaluation of a dynamic Transfer Matrix for a hydraulic turbine. The authors of [17] give a matrix approach for analyzing a signal flow graph, and [18] presents the Transfer Matrix of a MIMO system. Furthermore, [19] and [20] show applications of Transfer Matrices in acoustics. A Transfer Matrix analysis of a duct with a gradually varying arbitrary cross-sectional area is presented in [21]. In [22], the adaptable Transfer Matrix Method for fixed-energy finite-width beams is shown. The Transfer Matrix in a Quasiclassical Approximation with Constant and Position-Dependent Mass and Resonant Tunneling is given in [23]. The Transfer Matrix in four-dimensional Causal Dynamical Triangulations is presented in [24], and in [25] is given a Transfer Matrix optimization of a one-dimensional photonic crystal cavity for enhanced absorption of monolayer graphene.

2. Mathematical Model for Mandible Body

The mandibular bone is symmetrical in relation to vertical plane 1 that passes through the middle of the body. The mandible is sectioned with plane 2 in such a way as to isolate of the mandible body from the two branches. For simplicity, the body is considered as a semicircle (Figure 1).

To obtain the semicircle, the mandible body was sectioned with horizontal plane 3, which passes through the middle of the mandible body.

Due to this symmetry, we study a mathematical model in the shape of a quarter circle (Figure 2). Between vertical planes 1 and 2 the quarter circle was obtained, which is the mathematical model used for the TMM approach, embedded at both ends in B and D, and loaded with concentrated vertical forces which act perpendicular to the plane of the spring, forces corresponding to the eight teeth on this quarter circle. In Figure 2, only one force P corresponding to a tooth is represented, the force perpendicular to the plane of the quarter circle, directed along the direction of the Oz axis, which is perpendicular to the plane xOy, the plane containing the quarter circle.

We consider the mathematical model for the mandible body as a quarter circle that is a spring studied by an approach with the TMM.

3. Equations of a Plane Spring Loaded Perpendicular to Its Plane [1]

We consider a plane spring contained in the Oxy plane, subject to the load density

$$\overrightarrow{p}\left(s\right)=p\left(s\right)\cdot \overrightarrow{k},$$

(1)

where s is the curvilinear abscissa of a current point on the considered spring. The spring is determined as a whole in a direct referential Oxyz, in which the axes admit as unit vectors $\overrightarrow{I}$, $\overrightarrow{J}$ and $\overrightarrow{K}$ (Figure 3).

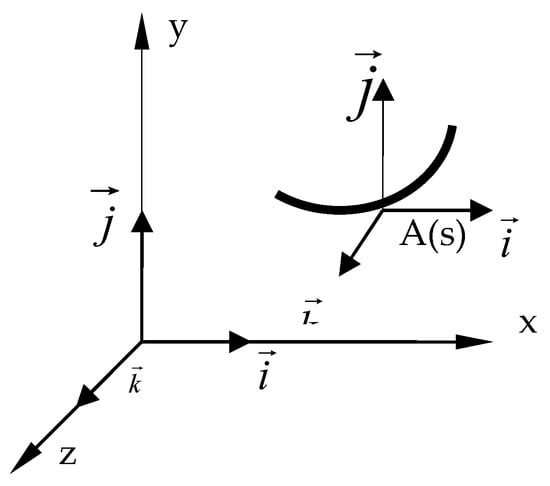
Figure 3. A spring element with axes and unit vectors.

In the current point A(s) of the middle fiber of the spring, the mobile triad $\left(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)$ is directly associated, so that $\overrightarrow{i}$ and $\overrightarrow{j}$ are unit vectors along the tangent and normal to the spring. An element of the spring between the abscissas s and s + ds is isolated (Figure 4).

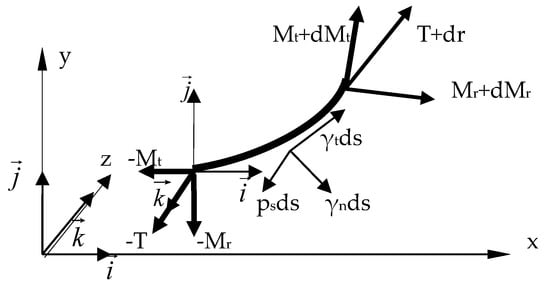
Figure 4. An element of spring between the abscissas s and s + ds.

The external components that act on this element are the following:

$$p\left(s\right)ds\cdot \overrightarrow{k}.$$

(2)

The result on the section with the abscissa s is the following:

• $\left(-T\right)\cdot \stackrel{\rightharpoonup }{k}$.

The resulting moment has the following components:

• (-M_r)on$\overrightarrow{j}\left(s\right)$—radial moment;
• (-M_t)on$\overrightarrow{i}\left(s\right)$—tangential moment.

On the section with abscissa s + ds, we have the following:

• A resultant with module $\left(T+dT\right)\cdot \stackrel{\rightharpoonup }{k}$.

The resultant moment has the following components:

• (-M_r + dM_r) on $\overrightarrow{j}\left(s+ds\right)$;
• (-M_t + dM_t) on $\overrightarrow{i}\left(s+ds\right)$.

It is possible to assume that the spring is subjected to the action of some torques distributed with the respective densities:

• γ_t (s) after tangent;
• γ_n (s) after normal;

which can give rise to possible external loads:

• γ_t (s) ds;
• γ_n (s) ds;

after the tangent and normal in the middle of the element.

It is noted with ψ the oriented angle that the vector $\overrightarrow{i}$ makes relative to the general axis Ox of the base reference.

The balance equations of the element are the following:

• Projection on $\overrightarrow{i}$:

  dM_t + M_r dψ + γ_t ds = 0,

  (3)
• Projection on $\overrightarrow{j}$:

  dM_r + M_t dψ + γ_n ds − Tds = 0,

  (4)
• Projection on $\stackrel{\rightharpoonup }{k}$:

  d T = − p (s) ds.

  (5)

  where R is the radius of the spring curvature at a point in abscissa s, and we know that

  ds = R dψ.

  (6)

With (6), relations (3), (4) and (5) can be written as follows:

$$\frac{d{M}_t}{ds}+\frac{M_r}{R}+{\gamma }_t=0,$$

(7)

$$\frac{d{M}_r}{ds}-\frac{M_t}{R}=T-{\gamma }_n,$$

(8)

$$\frac{dT}{ds}=-p\left(s\right).$$

(9)

By solving the Equations (7)–(9), we can calculate T, M_t and M_r. These quantities must be related to deformations, but deformation due to cutting force is neglected.

We note the following:

• E—Longitudinal modulus of elasticity (Young’s modulus);
• G—Transverse modulus of elasticity;
• I—Moment of inertia around the horizontal axis;
• J—Torsional stiffness inertia.

Thus, displacement of section s + ds in regard to section s is reduced to an elementary rotation $\overrightarrow{\mathsf{\Omega }}ds$ (10) and a translation $\overrightarrow{\lambda }ds$ (11):

$$\frac{d\overrightarrow{\mathsf{\Omega }}}{ds}=\frac{M_t}{GJ}\overline{i}+\frac{M_r}{EI}\overrightarrow{j},$$

(10)

$$\frac{d\overrightarrow{\lambda }}{ds}=\overrightarrow{\mathsf{\Omega }}\wedge \overrightarrow{i}.$$

(11)

The vertical displacement of the spring, considered positive in direction of vector $\overrightarrow{k}$, is noted by v, ω and φ as the angular deformations.

The rotation $\overrightarrow{\mathsf{\Omega }}$ is decomposed according to the direction $\overrightarrow{i}$:

$$\overrightarrow{\mathsf{\Omega }}=\phi \cdot \overrightarrow{i}+\omega \cdot \overrightarrow{j},$$

(12)

which makes (10) become (13) and (14):

$$\frac{d\phi }{ds}-\omega \frac{d\psi }{ds}=\frac{M_t}{GJ},$$

(13)

$$\frac{d\omega }{ds}+\phi \frac{d\psi }{ds}=\frac{M_r}{EI},$$

(14)

and (15) according to the direction $\overrightarrow{j}$:

$$\frac{dv}{ds}=-\omega .$$

(15)

With R at the point with abscissa s, the following system of Equations (16)–(21) can be written

$$\frac{dT}{ds}=-p\left(s\right),$$

(16)

$$\frac{d{M}_t}{ds}+\frac{M_r}{R}+{\gamma }_t=0,$$

(17)

$$\frac{d{M}_r}{ds}-\frac{M_t}{R}+{\gamma }_n=T,$$

(18)

$$\frac{d\phi }{ds}-\frac{\omega }{R}=\frac{M_t}{GJ},$$

(19)

$$\frac{d\omega }{ds}+\frac{\phi }{R}=\frac{M_r}{EI},$$

(20)

$$\frac{dv}{ds}=-\omega .$$

(21)

The conditions are

γ_t = γ_n = 0.

(22)

This system can be integrated, and six integration constants will intervene: T₀, M_t0, M_r0, φ, ω₀ and v₀. For a circular spring with radius R, relation (6) is valid.

Expression (5) can be written

$$T=T_0-{\displaystyle {\int }_0^{s}p\left(\sigma \right)}d\sigma .$$

(23)

It is taken as a parameter angle θ such that

$$d\psi =d\theta .$$

(24)

Relationship (23) can be written as (25):

$$T\left(\theta \right)=T_0-R{\displaystyle {\int }_0^{\theta }p\left(\theta \right)}d\theta ,$$

(25)

or

$$T\left(\theta \right)=T_0-R{p}_1\left(\theta \right),$$

(26)

with

$$p_1\left(\theta \right)={\displaystyle {\int }_0^{\theta }p\left(\theta \right)}d\theta .$$

(27)

Relationships (3) and (4) are derived and expressions (28) and (29) are obtained:

$$\frac{d^2{M}_t}{d{\theta }^2}+M_t=-RT\left(\theta \right),$$

(28)

$$\frac{d^2{M}_r}{d{\theta }^2}+M_r=-R^{2}p\left(\theta \right)$$

(29)

After, it can be written

$$M_t=A_t\cos \theta +B_t\sin \theta -R{\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}\cdot T\left(t\right)dt,$$

(30)

or

$$M_t=A_t\cos \theta +B_t\sin \theta -R{T}_0\left(1-\cos \theta \right)+R^{2}t\left(\theta \right),$$

(31)

with

$$t\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}\cdot p_1\left(t\right)dt.$$

(32)

It can also be written in the same way:

$$M_r=A_r\cos \theta +B_r\sin \theta -R^{2}r\left(\theta \right),$$

(33)

with

$$r\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}\cdot p\left(t\right)dt$$

(34)

If θ = 0, we can write the following:

$$M_t\left(0\right)=M_{t_0}=A_t,$$

(35)

and

$$M_r\left(0\right)=M_{r_0}=A_r.$$

(36)

Then, we can write

$${\left(\frac{d{M}_t}{d\theta }\right)}_{\theta =0}=-M_{r_0}=B_t,$$

(37)

and

$${\left(\frac{d{M}_r}{d\theta }\right)}_{\theta =0}=-M_{t_0}+R{T}_0=B_r.$$

(38)

The integration of Equations (3) and (4) gives (39) and (40):

$$M_t=M_{t_0}\cos \theta +M_{r_0}\sin \theta -R{T}_0\left(1-\cos \theta \right)+R^{2}t\left(\theta \right),$$

(39)

and

$$M_r=M_{r_0}\cos \theta +M_{t_0}\sin \theta +R\sin \theta \cdot T_0-R^{2}r\left(\theta \right),$$

(40)

with

$$t\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}\cdot p_1\left(t\right)dt,$$

(41)

and

$$r\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}\cdot p\left(t\right)dt.$$

(42)

because

$$\frac{d{M}_t}{d\theta }=-M_r,$$

(43)

and

$$\frac{d{M}_r}{d\theta }=M_t+RT,$$

(44)

Relations (19) and (20) are derived, the substitution is applied and the functions are separated, and after the following system of equations for the calculus of angular deformations is obtained:

$$\{\begin{array}{l}\frac{d^2\phi }{d{\theta }^2}+\phi =\frac{R}{GJ}\frac{d{M}_t}{d\theta }+\frac{R}{EI}{M}_r\\ \frac{d^2\omega }{d{\theta }^2}+\omega =\frac{R}{EI}\frac{d{M}_r}{d\theta }-\frac{R}{GJ}{M}_t\end{array},$$

(45)

which can also be written as (46):

$$\{\begin{array}{l}\frac{d^2\phi }{d{\theta }^2}+\phi =R\left(\frac{1}{EI}-\frac{1}{GJ}\right)M_r\\ \frac{d^2\omega }{d{\theta }^2}+\omega =R\left(\frac{1}{EI}-\frac{1}{GJ}\right)M_t+\frac{R^2}{EI}T\end{array}.$$

(46)

We note the following:

$$a=\frac{R}{EI},$$

(47)

and

$$b=\frac{EI}{GJ}.$$

(48)

Thus, the general solutions of the angular deformations (49) and (50) can be written:

$$\phi \left(\theta \right)=A_{\phi }\cos \theta +B_{\phi }\sin \theta +a\left(1-b\right){\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}{M}_r\left(t\right)dt,$$

(49)

and

$$\omega \left(\theta \right)=A_{\omega }\cos \theta +B_{\omega }\sin \theta +a\left(1-b\right){\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}{M}_t\left(t\right)dt+aR{\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)T}\left(t\right)dt.$$

(50)

In addition to the limit conditions, the following conditions are also applied:

$$\phi \left(0\right)={\phi }_0=A_{\phi },$$

(51)

$$\omega \left(0\right)={\omega }_0=A_{\omega }.$$

(52)

$${\left(\frac{d\phi }{d\theta }\right)}_{\theta =0}=-{\omega }_0+\frac{R}{GJ}{M}_{t_0}=B_{\phi }={\omega }_0+ab{M}_{t_0},$$

(53)

$${\left(\frac{d\omega }{d\theta }\right)}_{\theta =0}=-{\phi }_0+\frac{R}{EI}{M}_{r_0}=B_{\omega }={\phi }_0+a{M}_{r_0}.$$

(54)

Knowing

$${\displaystyle {\int }_0^{\theta }\cos t\sin \left(\theta -t\right)}dt=\frac{\theta }{2}\sin \theta ,$$

(55)

$${\displaystyle {\int }_0^{\theta }\sin t\sin \left(\theta -t\right)}dt=\frac{1}{2}\left(\sin \theta -\theta \cos \theta \right),$$

(56)

$${\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}dt=1-\cos \theta ,$$

(57)

and noting with

$$h\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)\cdot }r\left(t\right)dt,$$

(58)

and

$$l\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)}\left[\left(1-b\right)t\left(t\right)-p_1\left(t\right)\right]dt,$$

(59)

the angular deformations can be written with the relations (61) and (62):

$$\begin{array}{l}\phi \left(\theta \right)={\phi }_0\cos \theta +{\omega }_0\sin \theta +\frac{a}{2}\left(1-b\right)\theta \sin \theta \cdot M_{r_0}\\ +\frac{a}{2}\left(\left(1+b\right)\sin \theta -\left(1-b\right)\theta \cos \theta \right)M_{t_o}\\ +\frac{aR}{2}\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)T_0-R^{2}a\left(1-k\right)h\left(\theta \right)\end{array},$$

(60)

and

$$\begin{array}{l}\omega \left(\theta \right)={\omega }_0\cos \theta +{\phi }_0\sin \theta +\frac{a}{2}\left(\left(1+b\right)\sin \theta +\left(1-b\right)\theta \cos \theta \right)M_{r_0}\\ +\frac{a\left(1-b\right)}{2}\theta \sin \theta \cdot M_{t_0}+\frac{aR}{2}\left(\left(1-b\right)\theta \sin \theta +2b\left(1-\cos \theta \right)\right)T_0+R^{2}al\left(\theta \right)\end{array},$$

(61)

To calculate the linear deformation, the expression is integrated as (62):

$$\begin{array}{l}v\left(\theta \right)=v_0-R\sin \theta {\omega }_0+R\left(1-\cos \theta \right){\phi }_0\\ -\frac{aR}{2}\left(\left(1+b\right)\left(1-\cos \theta \right)+\left(1-b\right)\left(\theta \sin \theta +\cos \theta -1\right)\right)M_{r_0}\\ +\frac{aR\left(1-b\right)}{2}\left(\sin \theta -\theta \cos \theta \right)\cdot M_{t_0}\\ -\frac{a{R}^2}{2}\left(\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)+2b\left(\theta -\sin \theta \right)\right)T_0\\ +R^{3}a{\displaystyle {\int }_0^{\theta }l\left(t\right)}dt\end{array}.$$

(62)

Synthetically, we can write the following:

$$\{\begin{array}{l}{M}_r\left(\theta \right)=-M_{r_0}\sin \theta +M_{t_0}\cos \theta -R\left(1-\cos \theta \right)T_0+R^{2}t\left(\theta \right)\\ M_t\left(\theta \right)=M_{r_0}\cos \theta +M_{t_0}\sin \theta +R{T}_0\sin \theta -R^{2}r\left(\theta \right)\\ T\left(\theta \right)=T_0-R{p}_1\left(\theta \right)\\ \phi \left(\theta \right)=\frac{a\left(1-b\right)\theta \sin \theta }{2}{M}_{r_0}+\frac{a\left(\left(1+b\right)\sin \theta -\left(1-b\right)\theta \cos \theta \right)}{2}{M}_{t_0}+\frac{aR\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)}{2}{T}_0\\ \hspace{1em} {{\displaystyle }}_{}^{}{{\displaystyle }}_{}^{}+{\phi }_0\cos \theta +{\omega }_0\sin \theta -a{R}^2\left(1-b\right)h\left(\theta \right)\\ \omega \left(\theta \right)=\frac{a\left(\left(1+b\right)\sin \theta -\left(1-b\right)\theta \cos \theta \right)}{2}{M}_{r_0}-\frac{a\left(1-b\right)\theta \sin \theta }{2}{M}_{t_0}-\frac{a{R}^2\left(\left(1-b\right)\theta \sin \theta +2b\left(1-\cos \theta \right)\right)}{2}{T}_0\\ \hspace{1em} {{\displaystyle }}_{}^{}{{\displaystyle }}_{}^{}+{\phi }_0\sin \theta -{\omega }_0\cos \theta +a{R}^{2}l\left(\theta \right)\\ v\left(\theta \right)=\frac{aR\left(\left(1+b\right)\left(1-\cos \theta \right)+\left(1-b\right)\left(\theta \sin \theta +\cos \theta -1\right)\right)}{2}{M}_{r_0}-\frac{aR\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)}{2}{M}_{t_0}\\ \hspace{1em} {{\displaystyle }}_{}^{}{{\displaystyle }}_{}^{}-\frac{a{R}^2\left(\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)+2b\left(\theta -\sin \theta \right)\right)}{2}{T}_0-a{R}^3{\displaystyle {\int }_0^{\theta }l\left(t\right)dt}\end{array},$$

(63)

4. Transfer Matrix of Spring Model Loaded Perpendicular to Its Plane

4.1. General Expression of the Transfer Matrix

We consider a state vector with the expression (64):

$$\left\{C\left(\theta \right)\right\}={\left\{C\right\}}_{\theta }={\left\{M_r\left(\theta \right),M_t\left(\theta \right),T\left(\theta \right),\phi \left(\theta \right),\omega \left(\theta \right),v\left(\theta \right)\right\}}^{-1},$$

(64)

corresponding to the face from the angle θ.

For the first face, the face from the left end of the spring, or face 0, a state vector of face 0 or a state vector of the origin face, is defined with (65) or (66):

$$\left\{C\left({\theta }_0\right)\right\}=\left\{C_0\right\}={\left\{C\right\}}_0={\left\{M_r\left({\theta }_0\right),M_t\left({\theta }_0\right),T\left({\theta }_0\right),\phi \left({\theta }_0\right),\omega \left({\theta }_0\right),v\left({\theta }_0\right)\right\}}^{-1},$$

(65)

or

$$\left\{C_0\right\}={\left\{C\right\}}_0={\left\{M_{r_0},M_{t_0},T_0,{\phi }_0,{\omega }_0,v_0\right\}}^{-1}.$$

(66)

The state vector of the face at the origin is related to the state vector of the face at angle θ by the Transfer Matrix (67):

$$\left[TM\left(\theta \right)\right]={\left[TM\right]}_{\theta }=\left[\begin{array}{cccccc}t{m}_{11}& t{m}_{12}& t{m}_{13}& t{m}_{14}& t{m}_{15}& t{m}_{16}\\ t{m}_{21}& t{m}_{22}& t{m}_{23}& t{m}_{24}& t{m}_{25}& t{m}_{26}\\ t{m}_{31}& t{m}_{32}& t{m}_{33}& t{m}_{34}& t{m}_{35}& t{m}_{36}\\ t{m}_{41}& t{m}_{42}& t{m}_{43}& t{m}_{44}& t{m}_{45}& t{m}_{46}\\ t{m}_{51}& t{m}_{52}& t{m}_{53}& t{m}_{54}& t{m}_{55}& t{m}_{56}\\ t{m}_{61}& t{m}_{62}& t{m}_{63}& t{m}_{64}& t{m}_{65}& t{m}_{66}\end{array}\right],$$

(67)

and by the matrix relation (68):

$${\left\{C\right\}}_{\theta }={\left[TM\right]}_{\theta }{\left\{C\right\}}_0+{\left\{C_e\right\}}_{\theta },$$

(68)

where {C_e}_θ is the vector of external loads on the element located at angle θ of the shape:

$${\left\{C_e\right\}}_{\theta }=\left\{\begin{array}{l}{R}^{2}t\left(\theta \right)\\ -R^{2}r\left(\theta \right)\\ -R{p}_1\left(\theta \right)\\ -a{R}^2\left(1-b\right)h\left(\theta \right)\\ a{R}^{2}l\left(\theta \right)\\ -a{R}^3{\displaystyle {\int }_0^{\theta }l\left(t\right)dt}\end{array}\right\}$$

(69)

with

$$\{\begin{array}{l}{p}_1\left(\theta \right)={\displaystyle {\int }_0^{\theta }p\left(t\right)dt}\\ r\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)p\left(t\right)dt}\\ t\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)p_1\left(t\right)dt}\\ h\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)r\left(t\right)dt}\\ l\left(\theta \right)={\displaystyle {\int }_0^{\theta }\sin \left(\theta -t\right)\left[\left(1-b\right)t\left(t\right)-p_1\left(t\right)\right]dt}\end{array}.$$

(70)

For {TM]_θ, the elements are the following:

$$\left[\begin{array}{cccccc}\cos \theta & \sin \theta & R\sin \theta & 0& 0& 0\\ -\sin \theta & \cos \theta & -R\left(1-\cos \theta \right)& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ \frac{a\left(1-b\right)\theta \sin \theta }{2}& \frac{a\left(\left(1+b\right)\sin \theta -\left(1-b\right)\theta \cos \theta \right)}{2}& \frac{aR\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)}{2}& \cos \theta & \sin \theta & 0\\ \frac{a\left(\left(1+b\right)\sin \theta -\left(1-b\right)\theta \cos \theta \right)}{2}& \frac{a\left(1-b\right)\theta \sin \theta }{2}& \frac{aR\left(\left(1-b\right)\theta \sin \theta +2b\left(1-\cos \theta \right)\right)}{2}& -\sin \theta & \cos \theta & 0\\ \frac{aR\left(\left(1-b\right)\theta \sin \theta +2b\left(1-\cos \theta \right)\right)}{2}& \frac{aR\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)}{2}& \frac{a{R}^2\left(\left(1-b\right)\left(\sin \theta -\theta \cos \theta \right)+2b\left(\theta -\sin \theta \right)\right)}{2}& R\left(1-\cos \theta \right)& -R\sin \theta & 1\end{array}\right]$$

(71)

4.2. Calculus of Elements for the Vector Corresponding to an External Vertical Concentrate Load in Section at Angle θ = θ₀

It is noted that P is the concentrated external vertical force, which acts in the section where θ = θ₀, perpendicular to the plane of spring (Figure 2). In this case, the charge density p(s) is given by Dirac’s function:

$$p\left(s\right)=P\delta \left(s-s_0\right).$$

(72)

With the help of Heaviside’s function and operators, the cutting force T can be written:

$$T=T_0-{{\displaystyle \int }}_0^{s}P\delta \left(s-s_0\right)ds,$$

(73)

or

$$T=T_0-PY\left(s-s_0\right).$$

(74)

Heaviside’s function is a symbolic function, which allows replacing s with the parameter θ, and we can write it with Heaviside’s operators:

$$R{p}_1\left(\theta \right)=PY\left(\theta -{\theta }_0\right),$$

(75)

where

$$p_1\left(\theta \right)=\frac{P}{R}Y\left(\theta -{\theta }_0\right),$$

(76)

Thus, it can be written

$$r\left(\theta \right)=\frac{P}{R}{\displaystyle {\int }_{{\theta }_0}^{\theta }\sin \left(\theta -t\right)}\cdot \delta \left(t-{\theta }_0\right)dt,$$

(77)

or

$$r\left(\theta \right)=\frac{P}{R}\sin \left(\theta -{\theta }_0\right)\cdot Y\left(\theta -{\theta }_0\right),$$

(78)

and

$$t\left(\theta \right)=\frac{P}{R}Y\left(\theta -{\theta }_0\right){\displaystyle {\int }_{{\theta }_0}^{\theta }\sin \left(\theta -t\right)}dt,$$

(79)

or

$$t\left(\theta \right)=\frac{P}{R}Y\left(\theta -{\theta }_0\right)\left[1-\cos \left(\theta -{\theta }_0\right)\right],$$

(80)

and

$$h\left(\theta \right)=\frac{P}{R}Y\left(\theta -{\theta }_0\right){\displaystyle {\int }_{{\theta }_0}^{\theta }\sin \left(\theta -t\right)\sin \left(t-{\theta }_0\right)}dt,$$

(81)

or

$$h\left(\theta \right)=\frac{P}{2R}Y\left(\theta -{\theta }_0\right)\left[\sin \left(\theta -{\theta }_0\right)-\left(\theta -{\theta }_0\right)\cos \left(\theta -{\theta }_0\right)\right],$$

(82)

and

$$l\left(\theta \right)=-\frac{P}{R}Y\left(\theta -{\theta }_0\right){\displaystyle {\int }_{{\theta }_0}^{\theta }\sin \left(\theta -t\right)\left[b+\left(1-b\right)\cos \left(t-{\theta }_0\right)\right]}dt,$$

(83)

or

$$l\left(\theta \right)=-\frac{P}{R}Y\left(\theta -{\theta }_0\right)\left[b\left(1-\cos \left(\theta -{\theta }_0\right)\right)+\frac{1-b}{2}\left(\theta -{\theta }_0\right)\sin \left(\theta -{\theta }_0\right)\right],$$

(84)

and

$${\displaystyle {\int }_0^{\theta }l\left(t\right)}dt=-\frac{P}{R}Y\left(\theta -{\theta }_0\right)\left[b\left(\theta -{\theta }_0-\sin \left(\theta -{\theta }_0\right)\right)+\frac{1-b}{2}\left(\sin \left(\theta -{\theta }_0\right)-\left(\theta -{\theta }_0\right)\cos \left(\theta -{\theta }_0\right)\right)\right].$$

(85)

We can write the following for {C_e}_θ:

$${\left\{C_e\right\}}_{\theta }={\left\{\begin{array}{l}{R}^{2}t\left(\theta \right)\\ -R^{2}r\left(\theta \right)\\ -R{p}_1\left(\theta \right)\\ -a{R}^2\left(1-b\right)h\left(\theta \right)\\ a{R}^{2}l\left(\theta \right)\\ -a{R}^3{\displaystyle {\int }_0^{\theta }l\left(t\right)dt}\end{array}\right\}}_{\theta }.$$

(86)

and with Heaviside’s function, (86) becomes

$${\left\{C_e\right\}}_{\theta }={\left\{\begin{array}{l}RPY\left(\theta -{\theta }_0\right)\left[1-\cos \left(\theta -{\theta }_0\right)\right]\\ -RP\sin \left(\theta -{\theta }_0\right)Y\left(\theta -{\theta }_0\right)\\ -PY\left(\theta -{\theta }_0\right)\\ aR\frac{\left(1-b\right)}{2}PY\left(\theta -{\theta }_0\right)\left[\sin \left(\theta -{\theta }_0\right)-\left(\theta -{\theta }_0\right)\cos \left(\theta -{\theta }_0\right)\right]\\ -aRPY\left(\theta -{\theta }_0\right)\left[b\left(1-\cos \left(\theta -{\theta }_0\right)\right)+\frac{1-b}{2}\left(\theta -{\theta }_0\right)\sin \left(\theta -{\theta }_0\right)\right]\\ -a{R}^{2}PY\left(\theta -{\theta }_0\right)\left[b\left(\left(\theta -{\theta }_0\right)-\sin \left(\theta -{\theta }_0\right)\right)+\frac{1-b}{2}\left(\sin \left(\theta -{\theta }_0\right)-\left(\theta -{\theta }_0\right)\cos \left(\theta -{\theta }_0\right)\right)\right]\end{array}\right\}}_{\theta },$$

(87)

With Heaviside’s operators and for $\theta =\frac{\pi }{2}$, for the right end of the spring (point D), (87) can be written:

$${\left\{C_e\right\}}_{\theta }={\left\{\begin{array}{l}PR\left[1-\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ -PR\sin \left(\frac{\pi }{2}-{\theta }_0\right)\\ -P\left(\frac{\pi }{2}-{\theta }_0\right)\\ PRa\frac{\left(1-b\right)}{2}\left[\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ -PRa\left[b\left(1-\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right)+\frac{1-b}{2}\left(\frac{\pi }{2}-{\theta }_0\right)\sin \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ -P{R}^{2}a\left[b\left(\left(\frac{\pi }{2}-{\theta }_0\right)-\sin \left(\frac{\pi }{2}-{\theta }_0\right)\right)+\frac{1-b}{2}\left(\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\theta -{\theta }_0\right)\right)\right]\end{array}\right\}}_{\theta },$$

(88)

where θ₀ is the angle where the force P is located. The mathematical formalism with Heaviside’s function and operators allows the function θ ≥ θ₀ to take the value 1 and θ < θ₀ takes the value 0.

5. Application to a Model as a Quarter Circle for Mandible Body by TMM: Results

We consider a spring in the shape of a quarter circle (Figure 2), embedded at both ends and loaded with a vertical concentrated force P acting perpendicular to its plane, in a section at angle θ₀.

The matrix relation (68) can be written as (89):

$$\left\{\begin{array}{l}{M}_r\left(\theta \right)\\ M_t\left(\theta \right)\\ T\left(\theta \right)\\ \phi \left(\theta \right)\\ \omega \left(\theta \right)\\ v\left(\theta \right)\end{array}\right\}={\left[TM\right]}_{\theta }\left\{\begin{array}{l}{M}_{r_0}\\ M_{t_0}\\ T_0\\ {\phi }_0\\ {\omega }_0\\ v_0\end{array}\right\}+{\left\{C_e\right\}}_{\theta },$$

(89)

or

$$\left\{\begin{array}{l}{M}_r\left(\theta \right)\\ M_t\left(\theta \right)\\ T\left(\theta \right)\\ \phi \left(\theta \right)\\ \omega \left(\theta \right)\\ v\left(\theta \right)\end{array}\right\}={\left[TM\right]}_{\theta }\left\{\begin{array}{l}{M}_{r_0}\\ M_{t_0}\\ T_0\\ {\phi }_0\\ {\omega }_0\\ v_0\end{array}\right\}+{\left\{\begin{array}{l}{R}^{2}t\left(\theta \right)\\ -R^{2}r\left(\theta \right)\\ -R{p}_1\left(\theta \right)\\ -a{R}^2\left(1-b\right)h\left(\theta \right)\\ a{R}^{2}l\left(\theta \right)\\ -a{R}^3{\displaystyle {\int }_0^{\theta }l\left(t\right)dt}\end{array}\right\}}_{\theta }.$$

(90)

With Heaviside’s function, (90) becomes (91):

$$\left\{\begin{array}{l}{M}_r\left(\theta \right)\\ M_t\left(\theta \right)\\ T\left(\theta \right)\\ \phi \left(\theta \right)\\ \omega \left(\theta \right)\\ v\left(\theta \right)\end{array}\right\}={\left[TM\right]}_{\theta }\left\{\begin{array}{l}{M}_{r_0}\\ M_{t_0}\\ T_0\\ {\phi }_0\\ {\omega }_0\\ v_0\end{array}\right\}+{\left\{\begin{array}{l}RPY\left(\theta -{\theta }_0\right)\left[1-\cos \left(\theta -{\theta }_0\right)\right]\\ -RP\sin \left(\theta -{\theta }_0\right)Y\left(\theta -{\theta }_0\right)\\ -PY\left(\theta -{\theta }_0\right)\\ aR\frac{\left(1-b\right)}{2}PY\left(\theta -{\theta }_0\right)\left[\sin \left(\theta -{\theta }_0\right)-\left(\theta -{\theta }_0\right)\cos \left(\theta -{\theta }_0\right)\right]\\ -aRPY\left(\theta -{\theta }_0\right)\left[b\left(1-\cos \left(\theta -{\theta }_0\right)\right)+\frac{1-b}{2}\left(\theta -{\theta }_0\right)\sin \left(\theta -{\theta }_0\right)\right]\\ -a{R}^{2}PY\left(\theta -{\theta }_0\right)\left[b\left(\left(\theta -{\theta }_0\right)-\sin \left(\theta -{\theta }_0\right)\right)+\frac{1-b}{2}\left(-\left(\theta -{\theta }_0\right)\cos \left(\theta -{\theta }_0\right)+\sin \left(\theta -{\theta }_0\right)\right)\right]\end{array}\right\}}_{\theta },$$

(91)

and with Heaviside’s operators, for $\theta =\frac{\pi }{2}$, we can write

$$\left\{\begin{array}{l}{M}_r\left(\frac{\pi }{2}\right)\\ M_t\left(\frac{\pi }{2}\right)\\ T\left(\frac{\pi }{2}\right)\\ \phi \left(\frac{\pi }{2}\right)\\ \omega \left(\frac{\pi }{2}\right)\\ v\left(\frac{\pi }{2}\right)\end{array}\right\}={\left[TM\right]}_{\theta }\left\{\begin{array}{l}{M}_{r_0}\\ M_{t_0}\\ T_0\\ {\phi }_0\\ {\omega }_0\\ v_0\end{array}\right\}+{\left\{\begin{array}{l}RP\cdot \left[1-\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ -RP\sin \left(\frac{\pi }{2}-{\theta }_0\right)\\ -P\\ aR\frac{\left(1-b\right)}{2}P\left[\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ -aRP\left[b\left(1-\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right)+\frac{1-b}{2}\left(\frac{\pi }{2}-{\theta }_0\right)\sin \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ -a{R}^{2}P\left[b\left(\left(\frac{\pi }{2}-{\theta }_0\right)-\sin \left(\frac{\pi }{2}-{\theta }_0\right)\right)+\frac{1-b}{2}\left(\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right)\right]\end{array}\right\}}_{\frac{\pi }{2}},$$

(92)

The following conditions are imposed on the limit, on the two embedded supports, for θ = 0 and $\theta =\frac{\pi }{2}$:

$$\{\begin{array}{l}v\left(0\right)=v\left(\frac{\pi }{2}\right)=0\\ \omega \left(0\right)=\omega \left(\frac{\pi }{2}\right)=0\\ \phi \left(0\right)=\phi \left(\frac{\pi }{2}\right)=0\end{array}.$$

(93)

With condition (93), expressions (92) and (86) for $\theta =\frac{\pi }{2}$ become

$$\left\{\begin{array}{l}{M}_r\left(\frac{\pi }{2}\right)\\ M_t\left(\frac{\pi }{2}\right)\\ T\left(\frac{\pi }{2}\right)\\ 0\\ 0\\ 0\end{array}\right\}={\left[TM\right]}_{\frac{\pi }{2}}\left\{\begin{array}{l}{M}_{r_0}\\ M_{t_0}\\ T_0\\ 0\\ 0\\ 0\end{array}\right\}+{\left\{C_e\right\}}_{\frac{\pi }{2}}.$$

(94)

The global Transfer Matrix for our spring (71), for $\theta =\frac{\pi }{2}$, becomes

$$\left[\begin{array}{cccccc}0& 1& R& 0& 0& 0\\ -1& 0& -R& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ \frac{a\left(1-b\right)\pi }{4}& \frac{a\left(1+b\right)}{2}& \frac{aR\left(1-b\right)}{2}& 0& 1& 0\\ \frac{a\left(1+b\right)}{2}& \frac{a\left(1-b\right)\pi }{4}& \frac{aR\left(\left(1-b\right)\pi +4b\right)}{4}& -1& 0& 0\\ \frac{aR\left(\left(1-b\right)\pi +4b\right)}{4}& \frac{aR\left(1-b\right)}{2}& \frac{a{R}^2\left(1+\pi b-3b\right)}{2}& R& -R& 1\end{array}\right],$$

(95)

and expressions (89) and (87) can be written as (96) and (90):

$$\left\{\begin{array}{l}{M}_r\left(\frac{\pi }{2}\right)\\ M_t\left(\frac{\pi }{2}\right)\\ T\left(\frac{\pi }{2}\right)\\ 0\\ 0\\ 0\end{array}\right\}=\left[\begin{array}{cccccc}0& 1& R& 0& 0& 0\\ -1& 0& -R& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ \frac{a\left(1-b\right)\pi }{4}& \frac{a\left(1+b\right)}{2}& \frac{aR\left(1-b\right)}{2}& 0& 1& 0\\ \frac{a\left(1+b\right)}{2}& \frac{a\left(1-b\right)\pi }{4}& \frac{aR\left(\left(1-b\right)\pi +4b\right)}{4}& -1& 0& 0\\ \frac{aR\left(\left(1-b\right)\pi +4b\right)}{4}& \frac{aR\left(1-b\right)}{2}& \frac{a{R}^2\left(1+\pi b-3b\right)}{2}& R& -R& 1\end{array}\right]\cdot \left\{\begin{array}{l}{M}_r{}_0\\ M_t{}_0\\ T_0\\ 0\\ 0\\ 0\end{array}\right\}+{\left\{C_e\right\}}_{\frac{\pi }{2}}.$$

(96)

where ${\left\{C_e\right\}}_{\frac{\pi }{2}}$ is the vector of external loads that act perpendicular to the plane of the spring at angle θ₀.

From (96) and (93) we can write a linear system of six equations with six unknowns:

$$\{\begin{array}{l}{M}_r\left(\frac{\pi }{2}\right)=M_t{}_0+R{T}_0+PR\left[1-\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ M_t\left(\frac{\pi }{2}\right)=M_r{}_0-R{T}_0-PR\sin \left(\frac{\pi }{2}-{\theta }_0\right)\\ T\left(\frac{\pi }{2}\right)=\frac{aR\left(1-b\right)}{2}{T}_0-P\\ 0=\frac{a\left(1-b\right)\pi }{4}{M}_r{}_0+\frac{a\left(1+b\right)}{2}{M}_t{}_0+\frac{aR\left(1-b\right)}{2}{T}_0+aPR\frac{1-b}{2}\left[\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ 0=\frac{a\left(1+b\right)}{2}{M}_r{}_0+\frac{a\left(1-b\right)\pi }{4}{M}_t{}_0+\frac{aR\left[\left(1-b\right)\pi +4b\right]}{4}{T}_0-aPR\frac{1-b}{2}\left[\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ 0=\frac{aR\left[\left(1-b\right)\pi +4b\right]}{4}{M}_r{}_0+\frac{aR\left(1-b\right)}{2}{M}_t{}_0+\frac{a{R}^2\left(1+\pi b-3b\right)}{2}{T}_0-aP{R}^2\left[b\left(\left(\frac{\pi }{2}-{\theta }_0\right)-\sin \left(\frac{\pi }{2}-{\theta }_0\right)\right)+\frac{1-b}{2}\left(\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right)\right]\end{array}.$$

(97)

From the last 3 equations, a linear system of equations with three unknowns can be formed, the unknowns being M_r0, M_t0 and T₀:

$$\{\begin{array}{l}\frac{a\left(1-b\right)\pi }{4}{M}_r{}_0+\frac{a\left(1+b\right)}{2}{M}_t{}_0+\frac{aR\left(1-b\right)}{2}{T}_0\\ =-aPR\frac{1-b}{2}\left[\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ \frac{a\left(1+b\right)}{2}{M}_r{}_0+\frac{a\left(1-b\right)\pi }{4}{M}_t{}_0+\frac{aR\left[\left(1-b\right)\pi +4b\right]}{4}{T}_0\\ =aPR\frac{1-b}{2}\left[\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ \frac{aR\left[\left(1-b\right)\pi +4b\right]}{4}{M}_r{}_0+\frac{aR\left(1-b\right)}{2}{M}_t{}_0+\frac{a{R}^2\left(1+\pi b-3b\right)}{2}{T}_0\\ =aP{R}^2\left[b\left(\left(\frac{\pi }{2}-{\theta }_0\right)-\sin \left(\frac{\pi }{2}-{\theta }_0\right)\right)+\frac{1-b}{2}\left(\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right)\right]\end{array},$$

(98)

or

$$\{\begin{array}{l}{a}_{11}{M}_r{}_0+a_{12}{M}_t{}_0+a_{13}{T}_0=b_1\\ a_{21}{M}_r{}_0+a_{22}{M}_t{}_0+a_{23}{T}_0=b_2\\ a_{31}{M}_r{}_0+a_{32}{M}_t{}_0+a_{33}{T}_0=b_3\end{array},$$

(99)

where

$$\{\begin{array}{l}{a}_{11}=\frac{a\left(1-b\right)\pi }{4}\\ a_{12}=\frac{a\left(1+b\right)}{2}\\ a_{13}=\frac{aR\left(1-b\right)}{2}\\ a_{21}=a_{12}\\ a_{22}=a_{11}\\ a_{23}=\frac{aR\left[\left(1-b\right)\pi +4b\right]}{4}\\ a_{31}=a_{23}\\ a_{32}=a_{13}\\ a_{33}=\frac{a{R}^2\left(1+\pi b-3b\right)}{2}\end{array},$$

(100)

and

$$\{\begin{array}{l}{b}_1=-aPR\frac{1-b}{2}\left[\sin \left(\frac{\pi }{2}-{\theta }_0\right)-\left(\frac{\pi }{2}-{\theta }_0\right)\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ b_2=-b_1\\ b_3=-b_{1}R+aP{R}^{2}b\left[\left(\frac{\pi }{2}-{\theta }_0\right)-\sin \left(\frac{\pi }{2}-{\theta }_0\right)\right]\end{array}.$$

(101)

Thus, the system (96) can be written as follows:

$$\{\begin{array}{l}{a}_{11}{M}_r{}_0+a_{12}{M}_t{}_0+a_{13}{T}_0=b_1\\ a_{12}{M}_r{}_0+a_{11}{M}_t{}_0+a_{23}{T}_0=-b_1\\ a_{23}{M}_r{}_0+a_{13}{M}_t{}_0+a_{33}{T}_0=b_3\end{array},$$

(102)

M_r0 is reduced between the first and second equations of system (102) and between the second and third equations and a system of two equations with two unknowns is obtained, the unknowns being M_t0 and T₀. From the two equations, M_t0 is reduced, and T₀ is obtained:

$$T_0=\frac{b_1\left(a_{11}+a_{12}\right)\left[a_{11}{a}_{23}-a_{12}{a}_{13}-\left(a_{11}-a_{12}\right)\left(a_{23}{b}_1+a_{12}{b}_3\right)\right]}{\left(a_{12}^2-a_{11}^2\right)\left(a_{23}^2-a_{12}{a}_{13}\right)-{\left(a_{11}{a}_{23}-a_{12}{a}_{13}\right)}^2}.$$

(103)

We return to the first two equations of system (102), where T₀ is already known and the other two unknowns M_r0 and M_t0 are determined:

$$M_{r0}=\frac{a_{12}{a}_{13}-a_{11}{a}_{23}}{a_{11}^2-a_{12}^2}{T}_0-\frac{b_1}{a_{11}-a_{12}},$$

(104)

$$M_{t0}=-\frac{a_{11}{a}_{13}-a_{12}{a}_{23}}{a_{11}^2-a_{12}^2}{T}_0+\frac{b_1}{a_{11}-a_{12}}.$$

(105)

At this moment, all six elements of the state vector {C}₀ corresponding to section 0 at the origin are known on the embedded end from the left of the spring extremity.

We consider now the first three equations of system (97) that allow the calculation of the three remaining unknowns from the embedded end of the right spring extremity:

$$\{\begin{array}{l}{M}_r\left(\frac{\pi }{2}\right)=M_t{}_0+R{T}_0+PR\left[1-\cos \left(\frac{\pi }{2}-{\theta }_0\right)\right]\\ M_t\left(\frac{\pi }{2}\right)=M_r{}_0-R{T}_0-PR\sin \left(\frac{\pi }{2}-{\theta }_0\right)\\ T\left(\frac{\pi }{2}\right)=\frac{aR\left(1-b\right)}{2}{T}_0-P\end{array}.$$

(106)

Now, all six elements of the state vector ${\left\{C\right\}}_{\theta =\frac{\pi }{2}}$ of the last section at $\theta =\frac{\pi }{2}$ are known as well. With the matrix relation (91), we can now calculate all state vectors for the spring, in any section of the spring, positioned at a given angle θ, when the external force acts perpendicular to the plane of the spring at an angle θ = θ₀.

This approach is very easy to program for cases when an iterative calculation is necessary to optimize the constructive form of the mandible in extreme situations.

6. Discussion

This approach by the Transfer Matrix Method (TMM) is an original calculus for a mathematical model of mandible body bone and that is presented in this work. This article is an original idea of the TMM approach in the field of orthodontics, a rather restrictive area of approach with mathematical methods, due to the complexity of the problems and, most of the time, due to the urgency with which they must be solved, quickly giving appropriate solutions.

We have two state vectors: for the left section, the origin section, and for the right section, the last section. Matrix relation (91) is relationship that gives the state vector of the certain section θ depending on the state vector of the left section 0 and the state vector of the external forces. In (91), if $\theta =\frac{\pi }{2}$, the matrix relationship (92) is obtained, and that gives the state vector of the last face depending on the state vector of the first face. In (92), one can put the conditions on the two embedded supports in (93), and then solve the linear system of three equations with three unknowns in (102) with the solutions (103), (104) and (105). We return to system (97) and take into account the first three equations, the solutions of which will give the solution (106). At this moment, all the elements of the two vectors on the supports are known. With the matrix expression (91) we can now calculate all state vectors in any section of the spring, in occurrence, for the mandibular bone model considered as a quarter circle, when the external force acts perpendicular to the plane of the spring at an angle of θ = θ₀. This approach by the TMM can be very easy to program for cases when the calculus must be performed rapidly and to optimize the constructive form of the mandible in extreme situations. The mandible bone has a variable and complex geometry. It is also worth noting the simplicity of obtaining some results in form optimization by programming the given algorithm, which will be studied in the future with utility in certain special medical cases. This article is an original idea of the TMM approach in the field of orthodontics, a rather restrictive area of approach with mathematical methods, due to the complexity of the problems and, most of the time, due to the urgency with which they must be solved, quickly giving appropriate solutions. The problem from the point of view of the materials (natural bone or biomedical materials compatible with the mandible bone, such as titanium and its alloys) has not yet been addressed due to the greater complexity of the problem. This study was conducted considering the future research related to biocompatible materials, which, in special medical situations, will be able to replace human bone in order to quickly obtain an optimal shape needed in the respective place in these special situations.

In the future, we hope to publish the calculus program with the TMM for optimizing the shape of the mandibular bone in a case study.