Study of COVID-19 Epidemic Control Capability and Emergency Management Strategy Based on Optimized SEIR Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Public Health Emergency Management during COVID-19
2.2. Application of SEIR System Dynamics Model in Epidemic Public Health Emergency Management
2.3. Case Assumptions and Model Construction
- The exposed (E) is also infectious, but because it does not have symptoms of an illness, the exposed is mixed in with the general susceptible population (S). Identifying the exposed cases from the population through screening tests and isolating them to eliminate the problem of transmission is necessary. With the assumption of the transmission property of the latent person, the average number of contacts per day is , where the probability of encountering a susceptible person is , and the probability of successful disease transmission after contact is . Meanwhile, the exposed individuals who are tested are able to be detected and switched to the symptomatic infected (I) type. Or, the exposed spontaneously develops symptoms without testing and shifting to the infected (I) type, and the probability of this spontaneous state shift is assumed to be .
- The infected (I) is someone with symptomatic manifestations of the disease. Due to the already clearly perceptible symptoms, and with adequate attention to the epidemic, it is assumed that infected individuals will be spontaneously or forcibly isolated, without additional testing, and without mixing into the social population. Nonetheless, even if quarantined, because of the imperfect nature of quarantine itself, it is assumed that the quarantined person may still come into contact with a small number of susceptible people. To distinguish between markers, the average number of people an infected person comes into contact with per day is assumed to be , where the probability of encountering a susceptible person is , and the probability of successfully achieving disease transmission after contact is .
- Assuming that strict official quarantine measures are not enforced, this corresponds to the period in the actual situation when governments do not take coercive measures at the beginning of the epidemic, or the period at the end of the epidemic when officials deregulate the epidemic, but continue to search for the infected and the exposed. It is presumed that the testing facility has a perfect capability to determine whether the virus has been transmitted, and that the false negative and false positive rates of the test are 0%, and that the facility has the capacity to perform multiple K tests per day. The test was performed on a mixed group of exposed (E), and a general susceptible population (S).
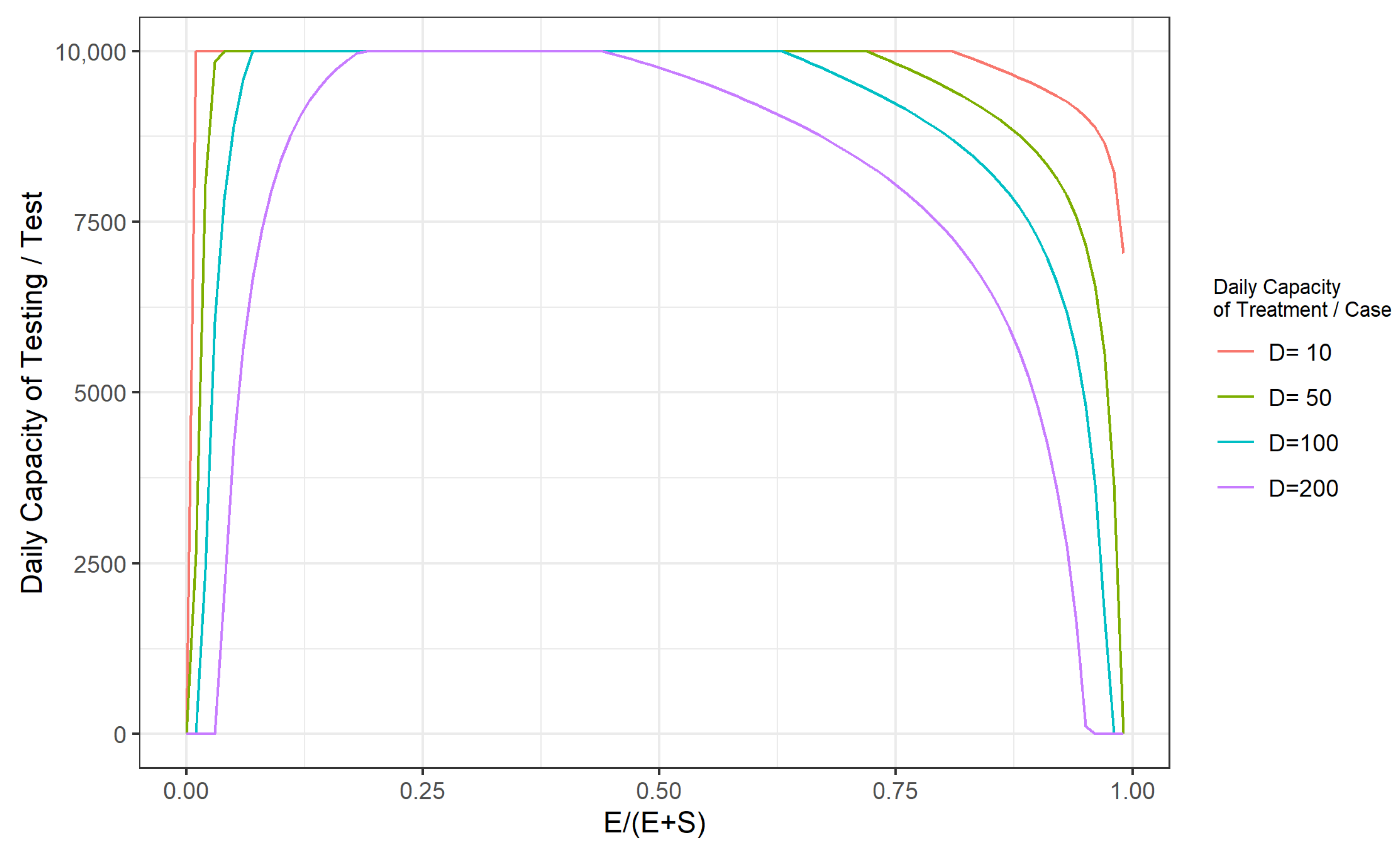
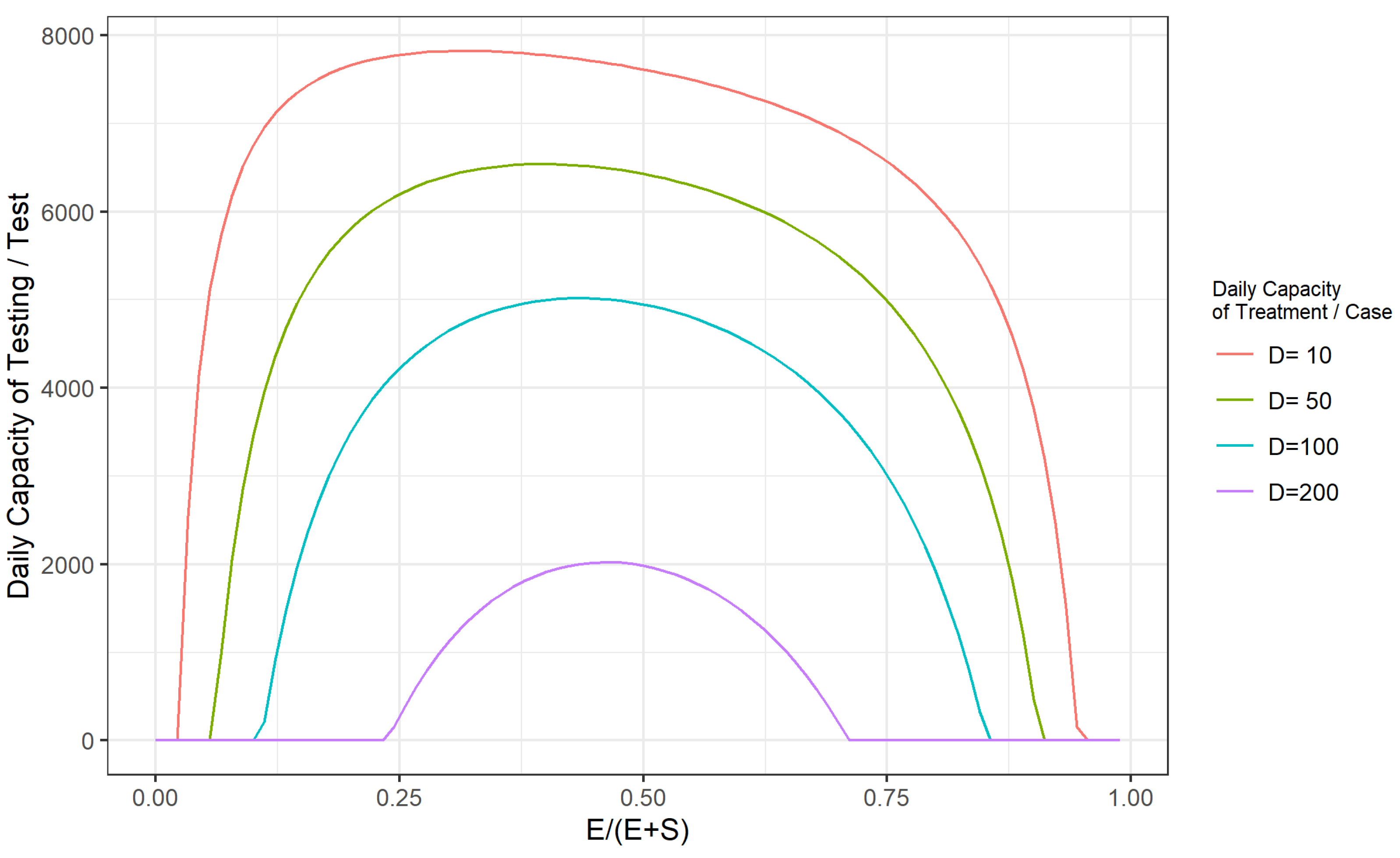
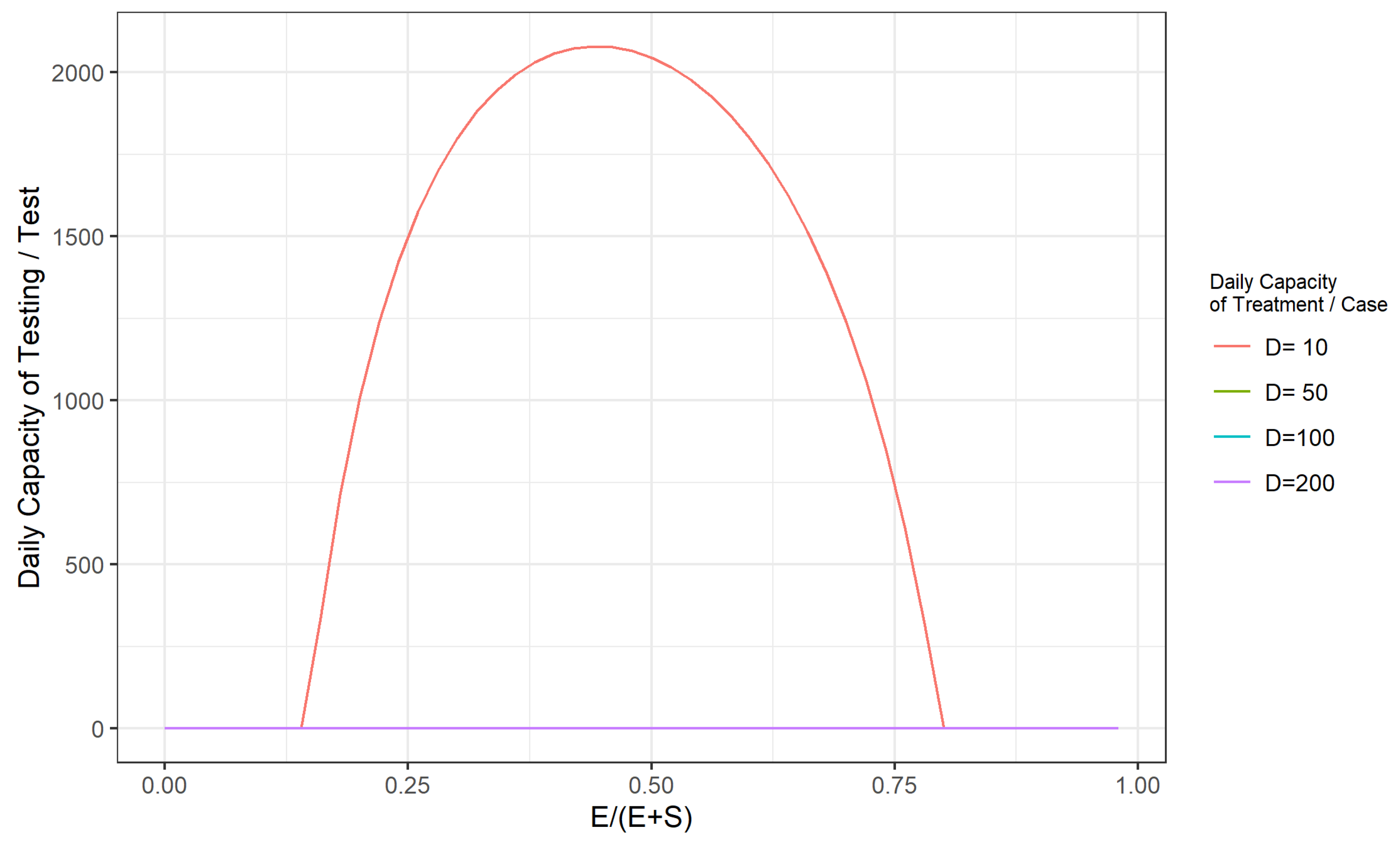
- If the total capacity of the health care system in a region is G (the upper limit of the total number of patients that the health care system can receive at the same time), and assuming that the limit of the daily capacity of the health care system is a constant D. The prevention and control of the epidemic will be achieved by identifying the exposed (E) through extensive sampling, isolating, and treating the infected (I) and the exposed (E) population, and controlling the proportion of the population with the virus so that the sum of the average daily number of infected persons in the population plus the number of infected persons tested on the same day will be lower than the assumed capacity constant (T) of the healthcare system. Therefore, the model can generate a threshold value for when the population base and the number of patients is adequately enough that the capacity of the given health care system (the total capacity G and the daily capacity D) is no longer possible to contain the epidemic, and that value is the outbreak point at which the development of the epidemic is out of control.
3. Results
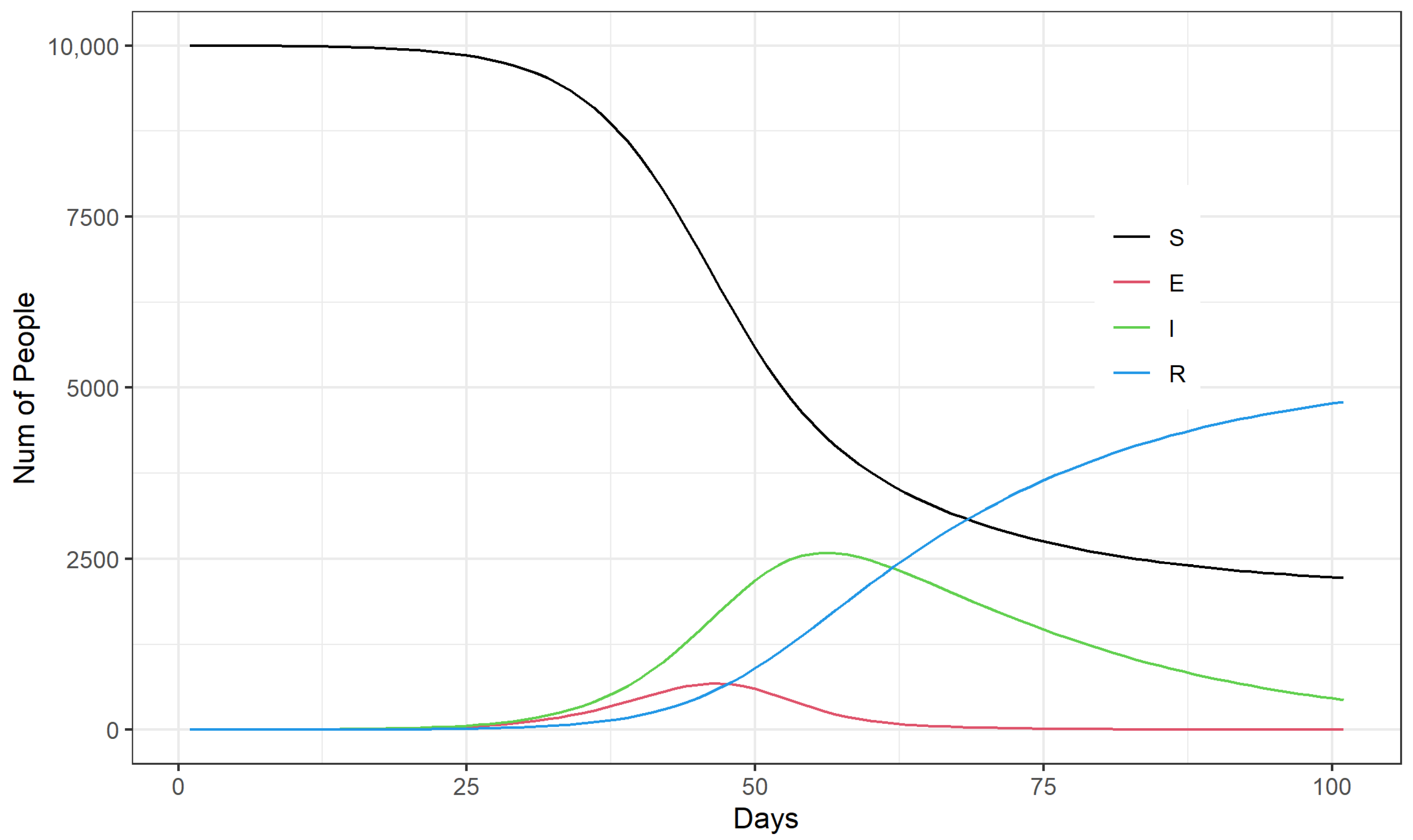
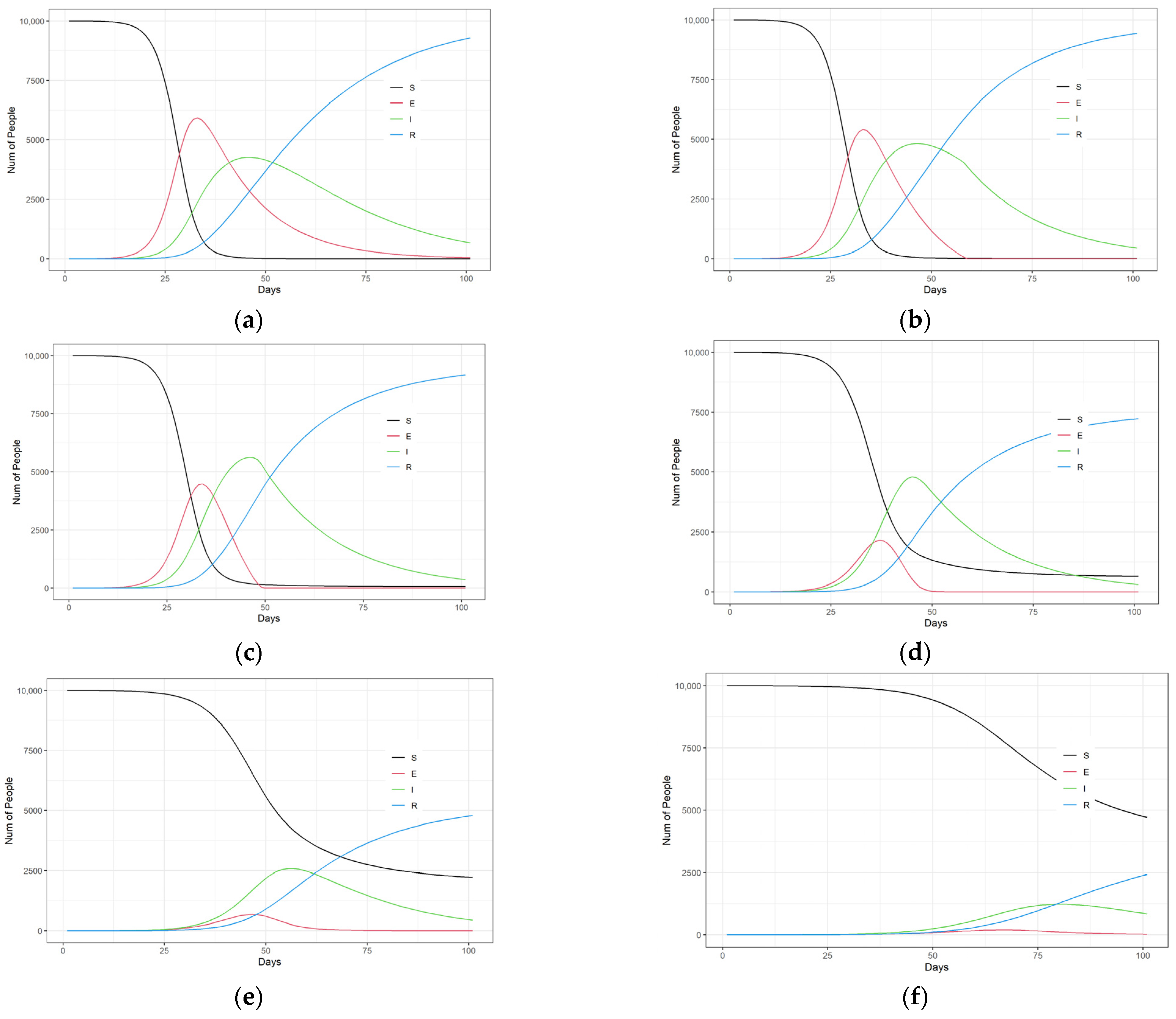
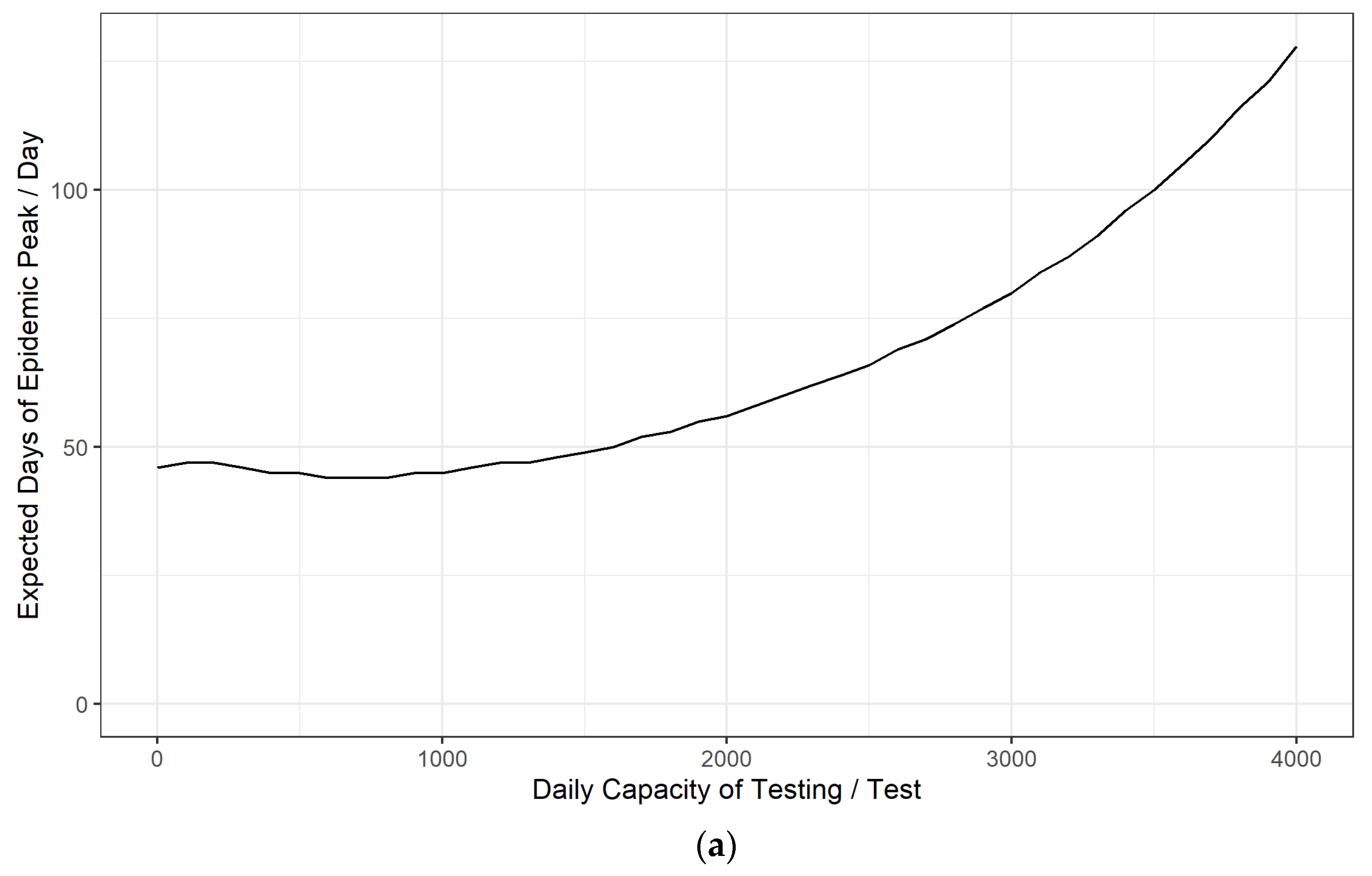
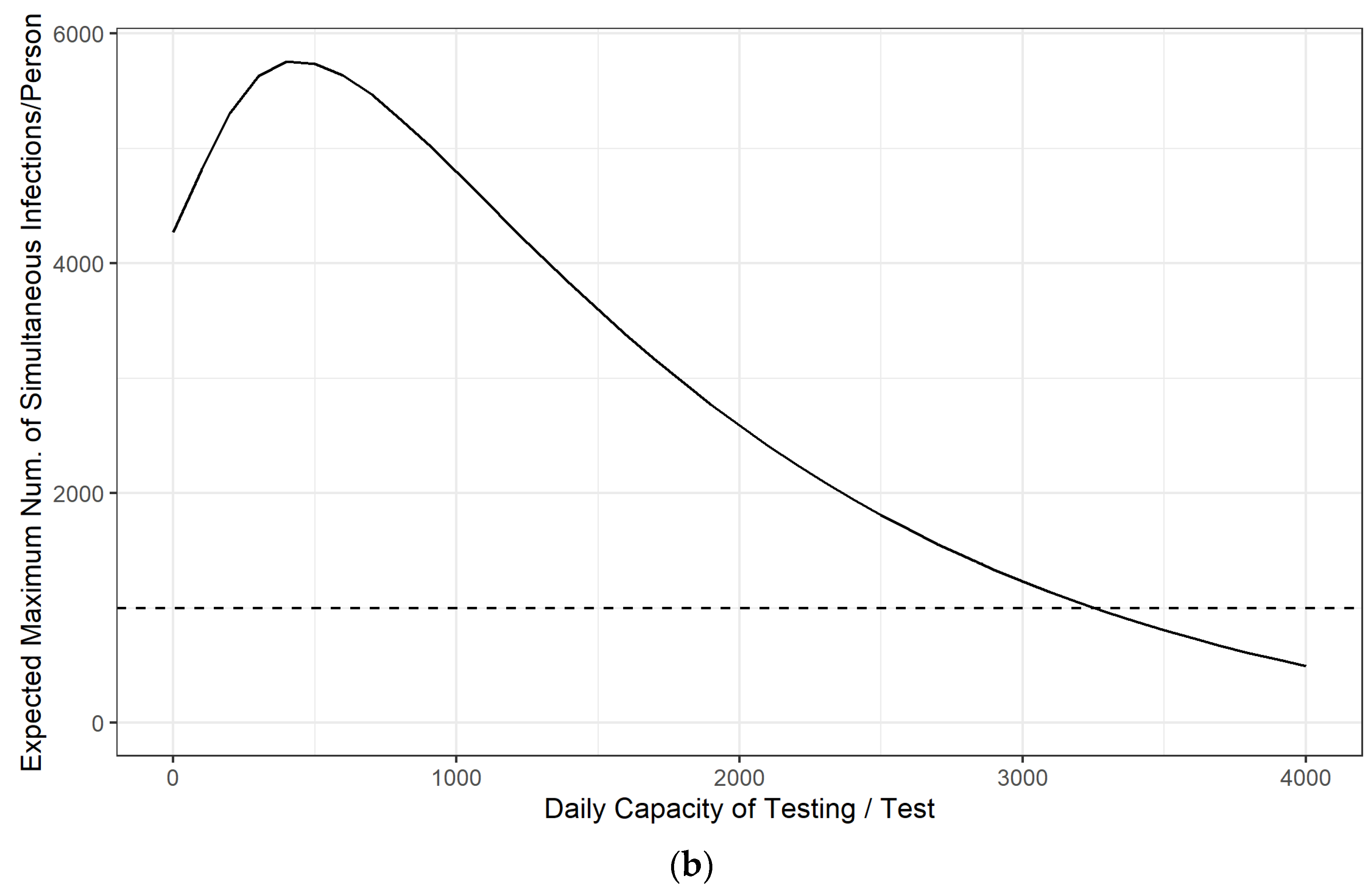
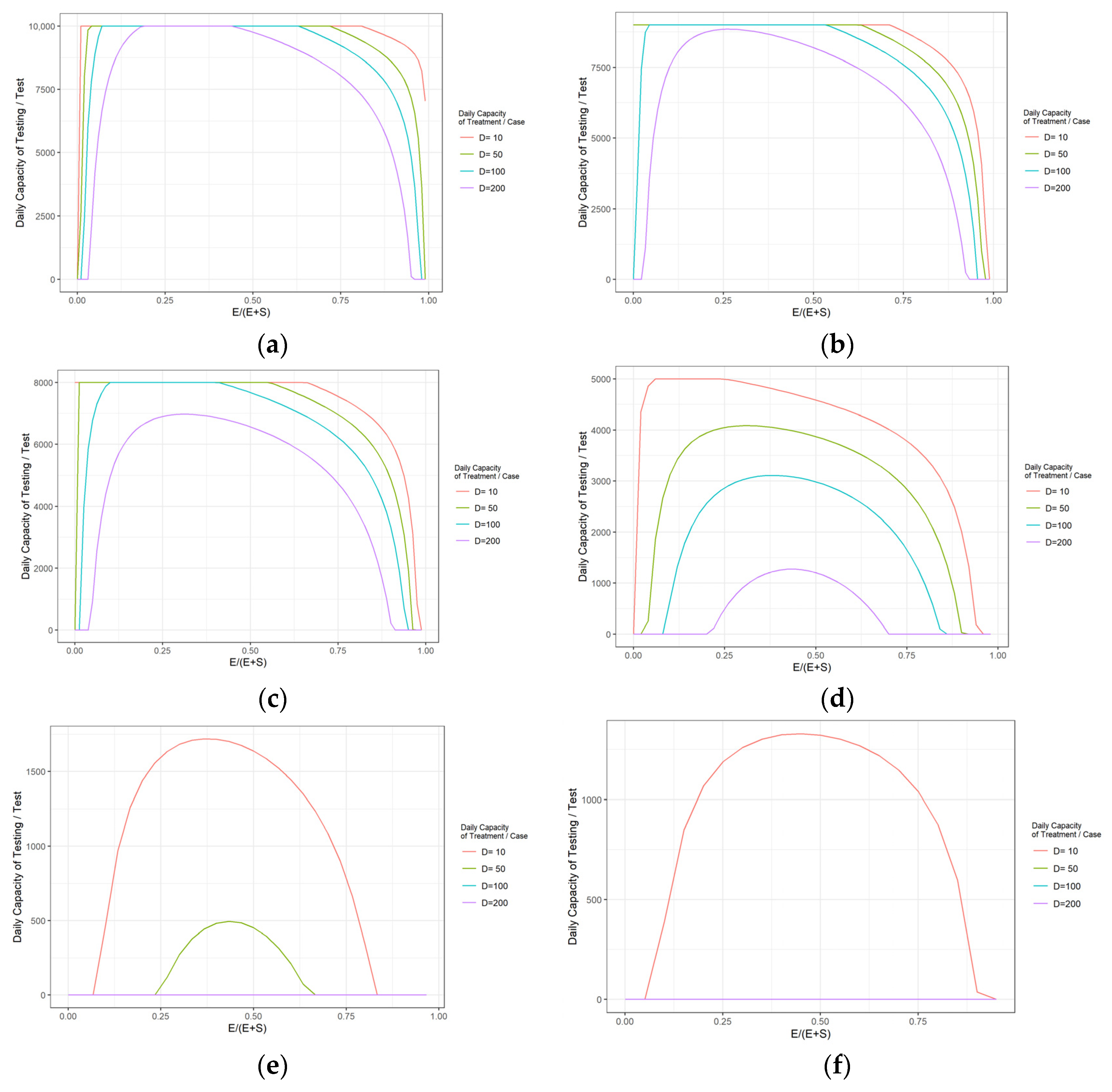
3.1. Simulation Analysis of the Emergency Control Effect of Daily Testing Capacity in the Early Stage of the Epidemic
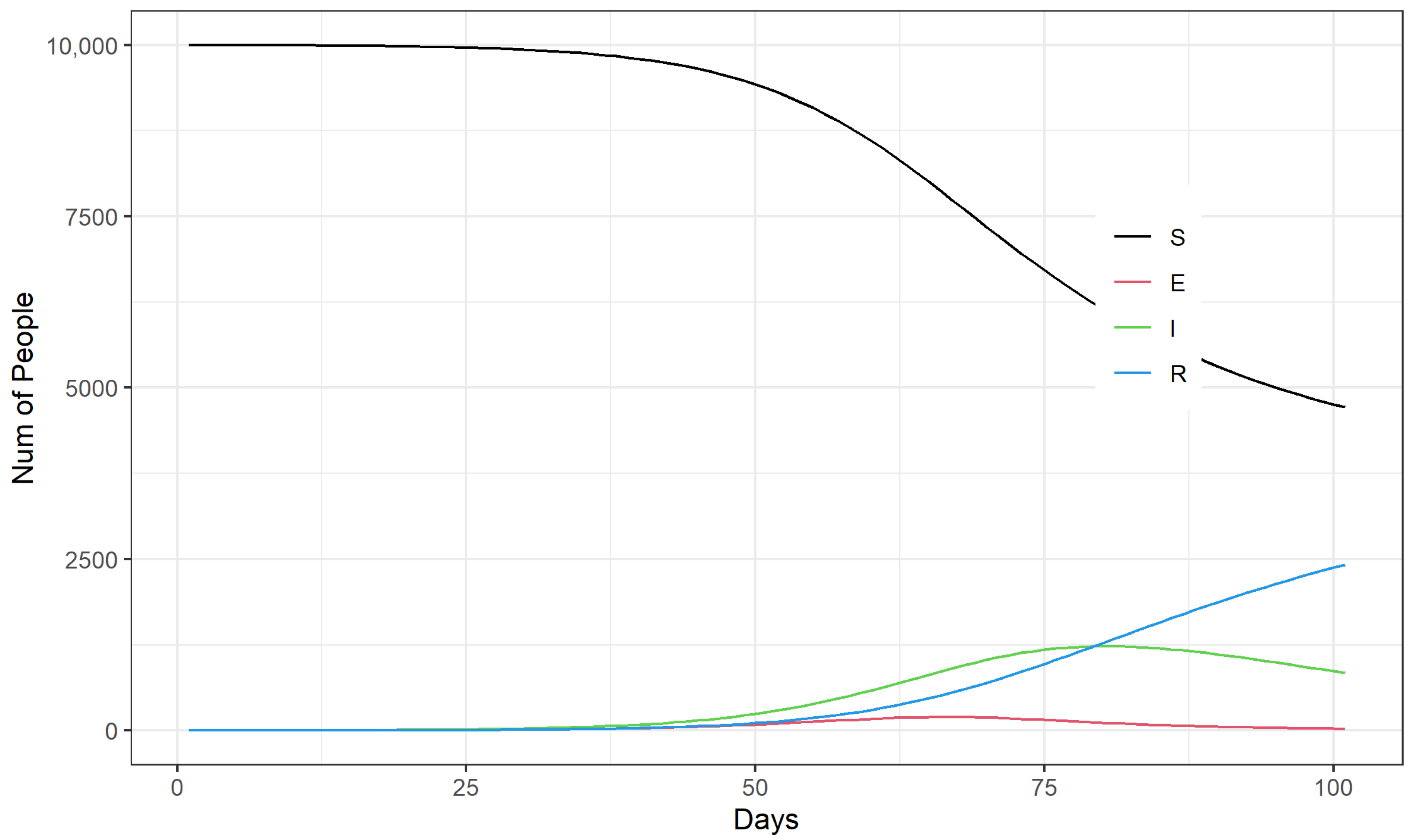
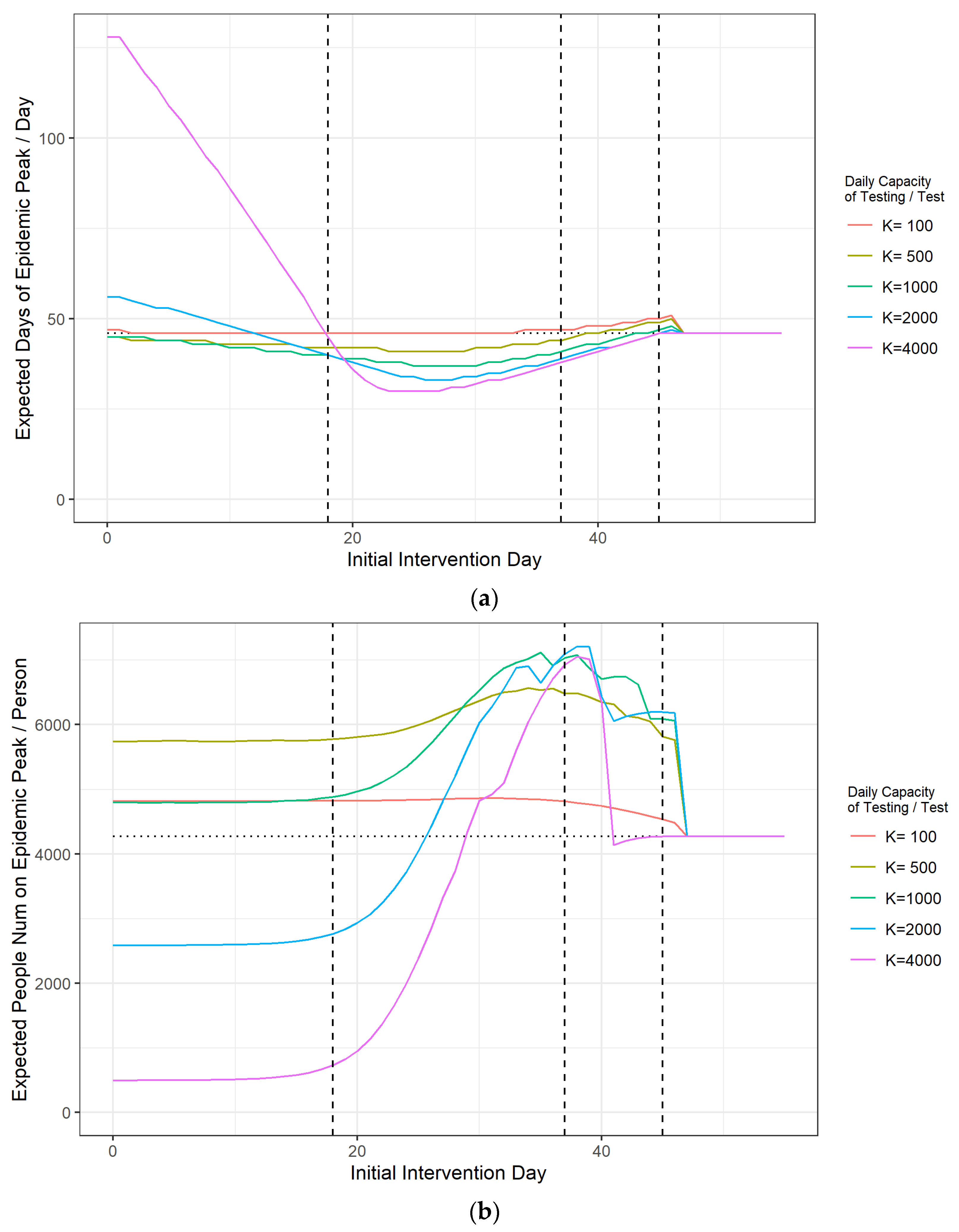
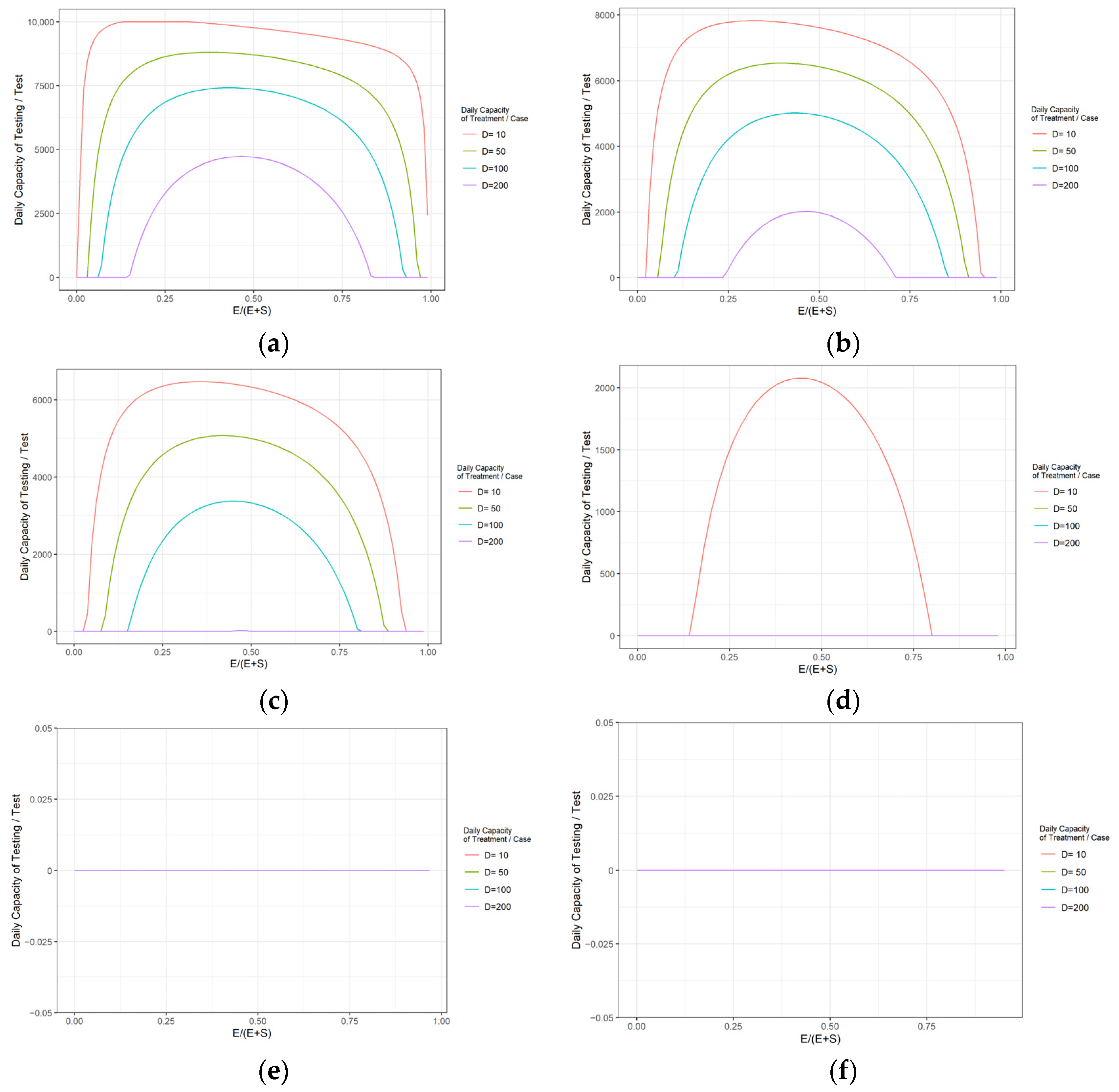
3.2. Simulation Analysis of Timing Options for the Emergency Management of an Outbreak
3.3. Simulation Analysis of Outbreak Control Effectiveness and Emergency Management Decisions during the Peak of COVID-19
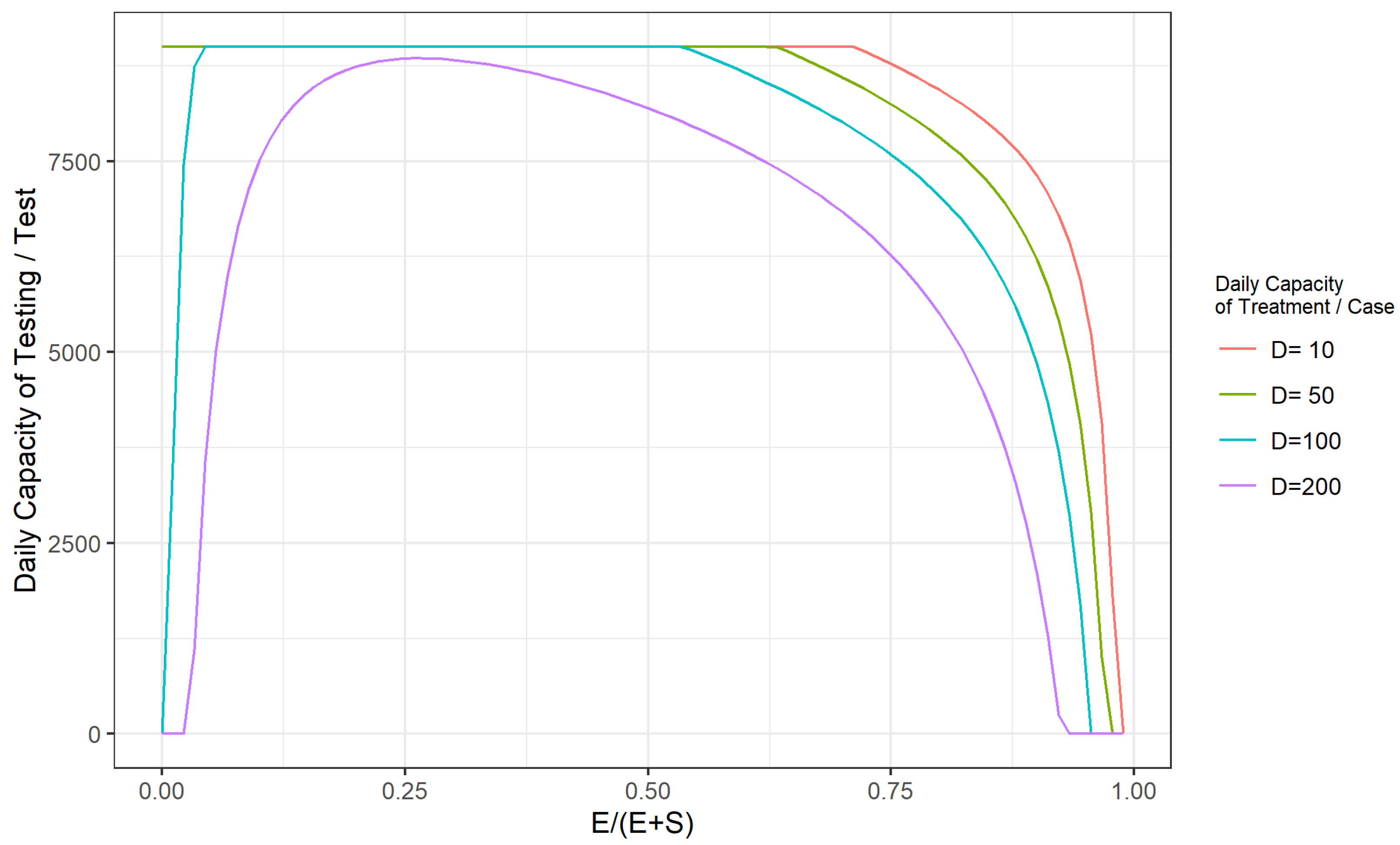
3.4. Decision on the Timing of Resumption of Work and School under the Consideration of Epidemic Control Costs
- The cost of reducing the average number of contacts to one-third or less by reducing the probability of the infected and the exposed people coming into contact with susceptible people through daily preventive and control measures, such as wearing masks, washing hands frequently, reducing social contact between people, and isolating suspected infected persons.
- The cost of establishing a “suspected information tracking system” to locate the exposed (E) mixed in with the crowd.
- The cost associated with expanding local capacity for routine testing.
- The cost of the expansion of the local health care system’s capacity to admit and treat patients, building more hospitals, hospital beds, supporting more equipment, such as ventilators, hiring more doctors and nurses, etc.
4. Discussion
5. Conclusions
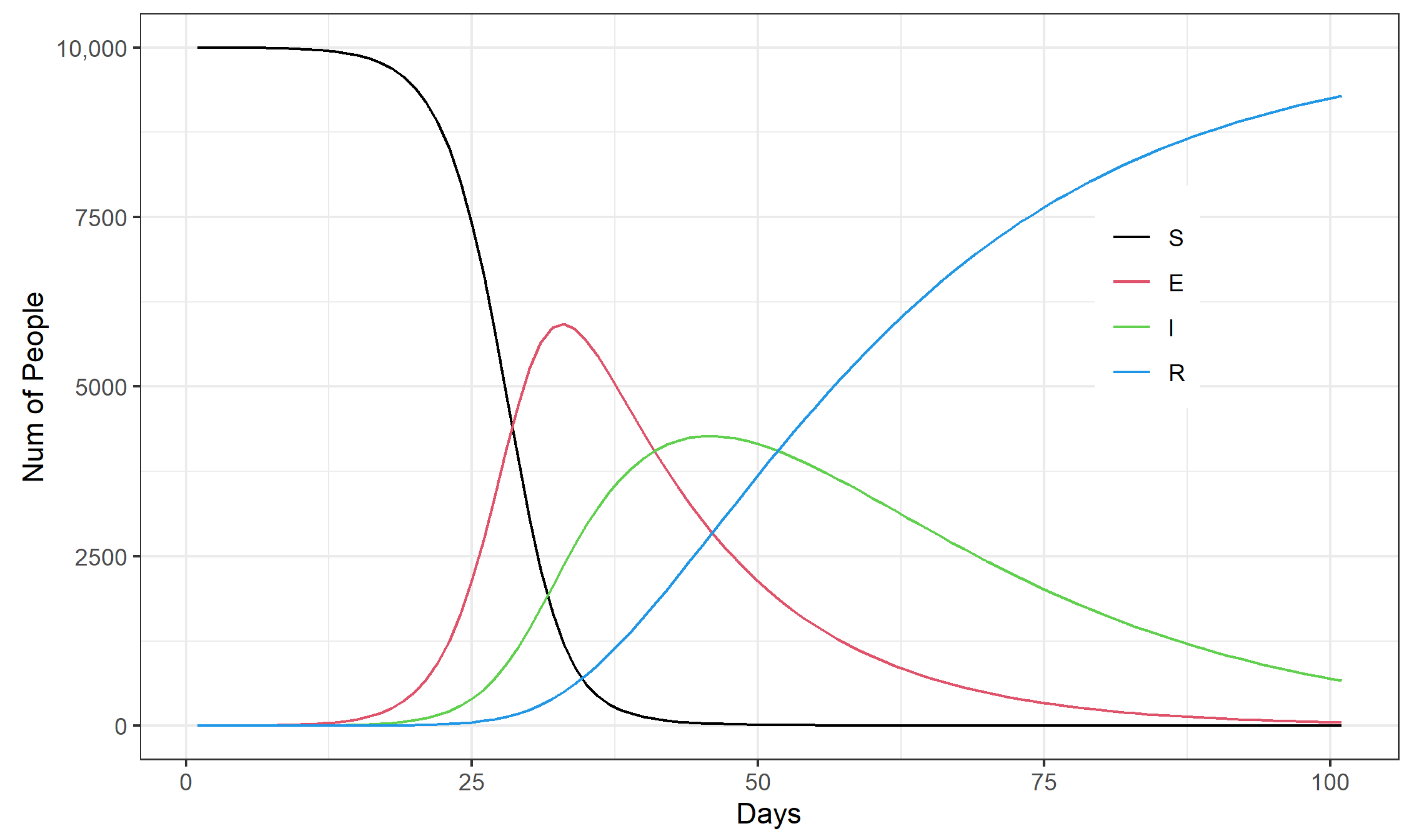
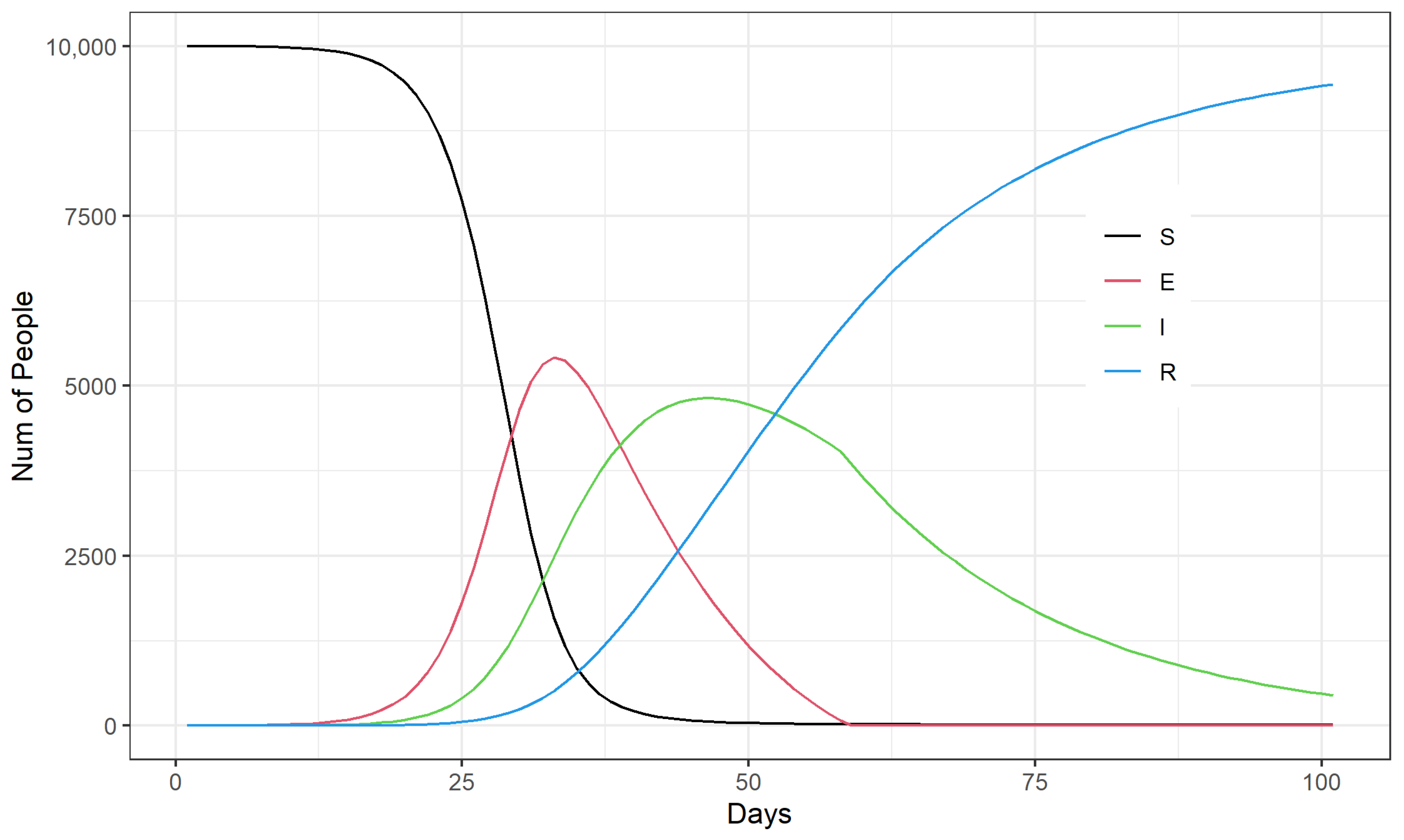
- At the beginning of the COVID-19 epidemic, the increase in the number of outbreak testing can considerably enhance the emergency control capacity of the epidemic, which can significantly delay the arrival of the peak of the epidemic and reduce the number of infected people at the peak of the epidemic development. To conduct the test among approximately 3500 people per 10,000 people per day can effectively control the outbreak and protect the local health care system from being highly stressed.
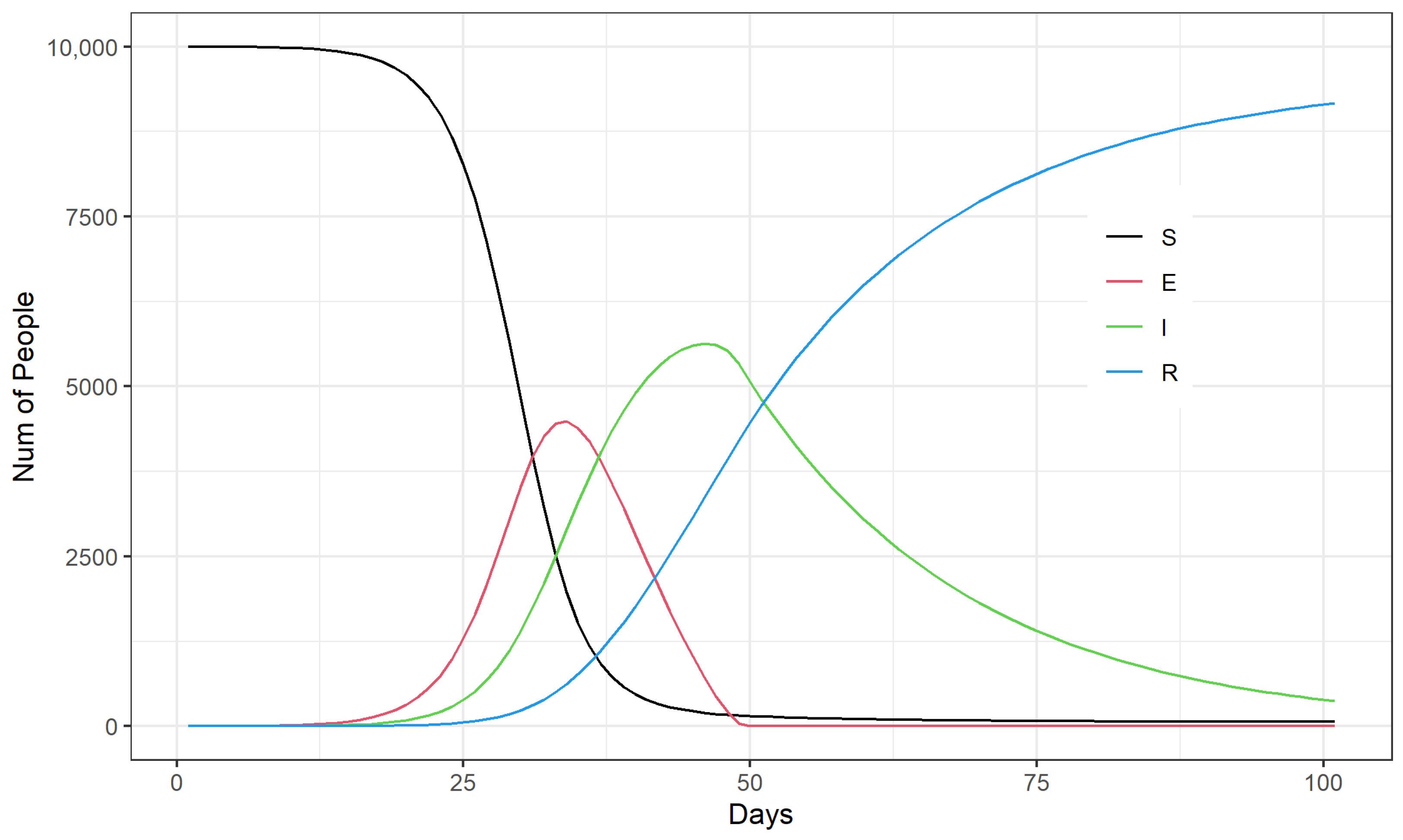
- For the timing of emergency outbreak interventions, mass sampling for example, the implementation of mass testing starting around the 20th to 30th day of the COVID-19 outbreak was most effective in controlling the number of infections at the peak of the outbreak. The final window for limiting the number of infections at the peak of the outbreak through emergency management measures is around day 37 to day 45 of the outbreak.
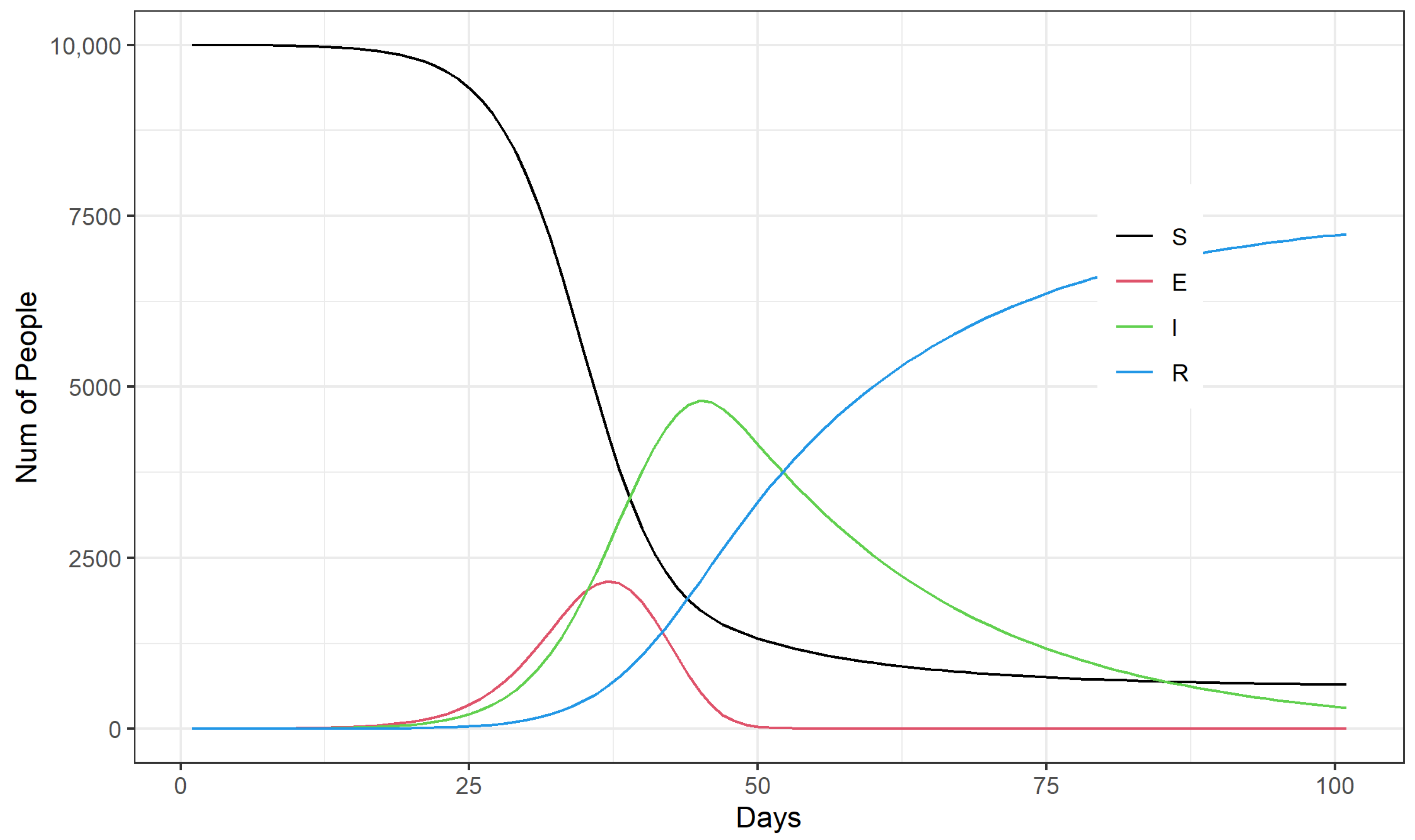
- When the COVID-19 epidemic is in the middle and late stages of development (more than half of the total population has already been infected), it is no longer necessary to perform daily testing when routine protective measures, such as wearing masks and washing hands, are strictly enforced, as long as a daily treatment capacity of 0.5% of the total community population is maintained. Alternatively, reducing the daily treatment capacity to 0.1% of the total community population while maintaining a daily testing capacity at the 1% level of the total community population could achieve effective control of the COVID-19 outbreak at a lower cost.
- The decision on the timing of resumption depends mainly on the magnitude of the total cost of community epidemic prevention and control. This paper summarizes the simulation results of the daily admission capacity and critical testing capacity of the healthcare system generated under different SEIR model parameters, which can be combined with the unit testing cost, unit treatment cost, and actual price level corresponding to different epidemic stages to derive the total cost of epidemic control, and thus decide whether to resume work and school at a particular time.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
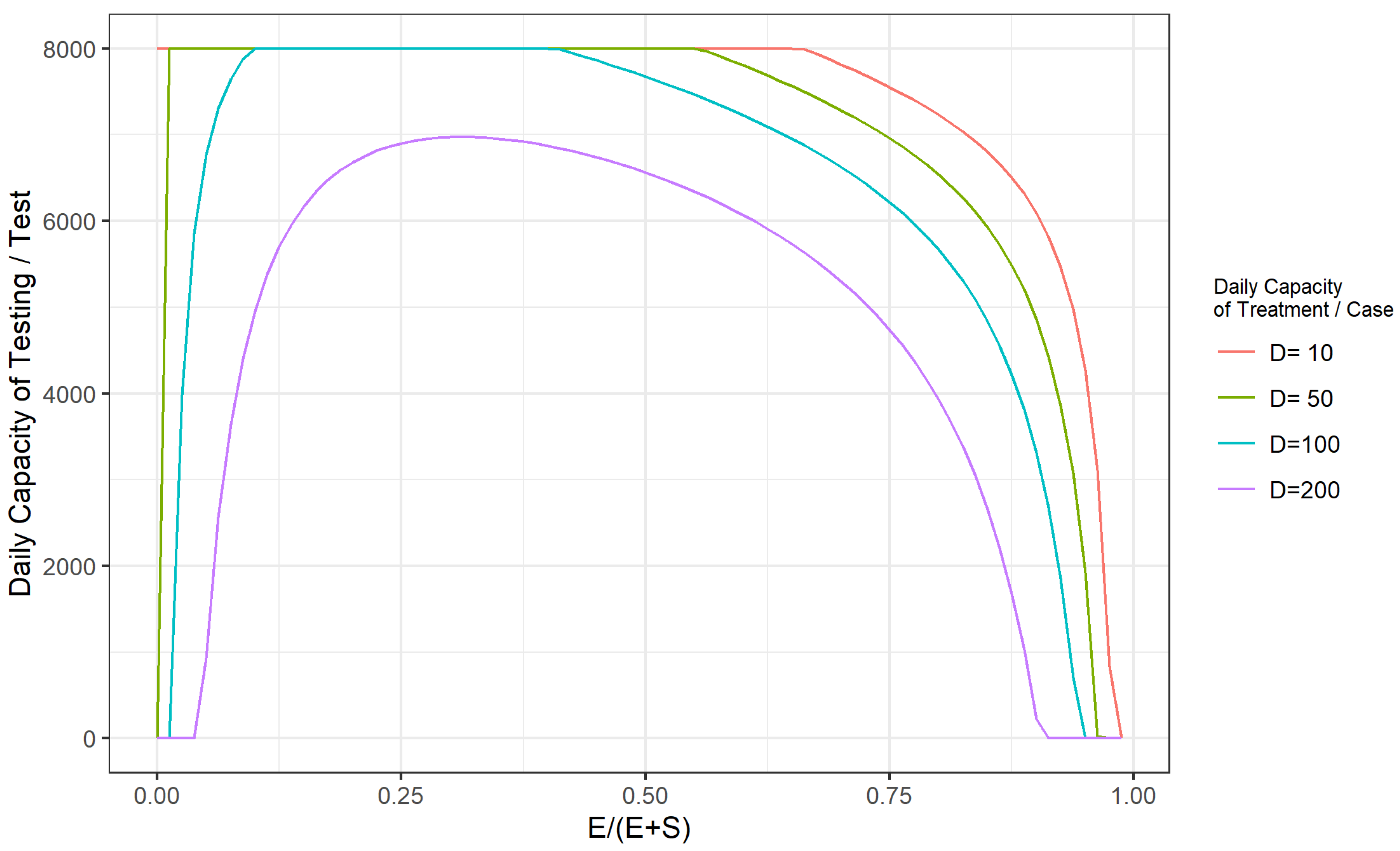
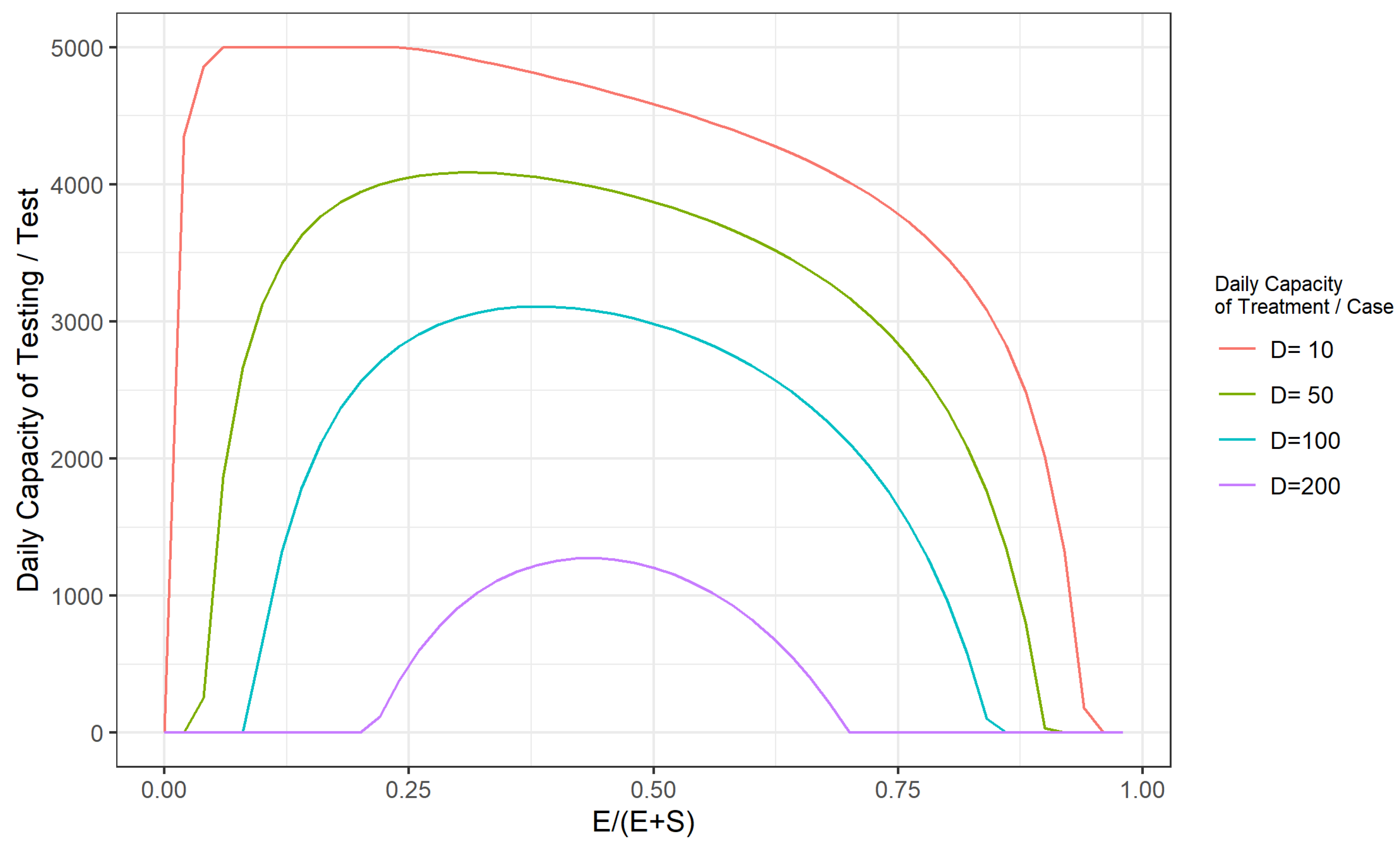

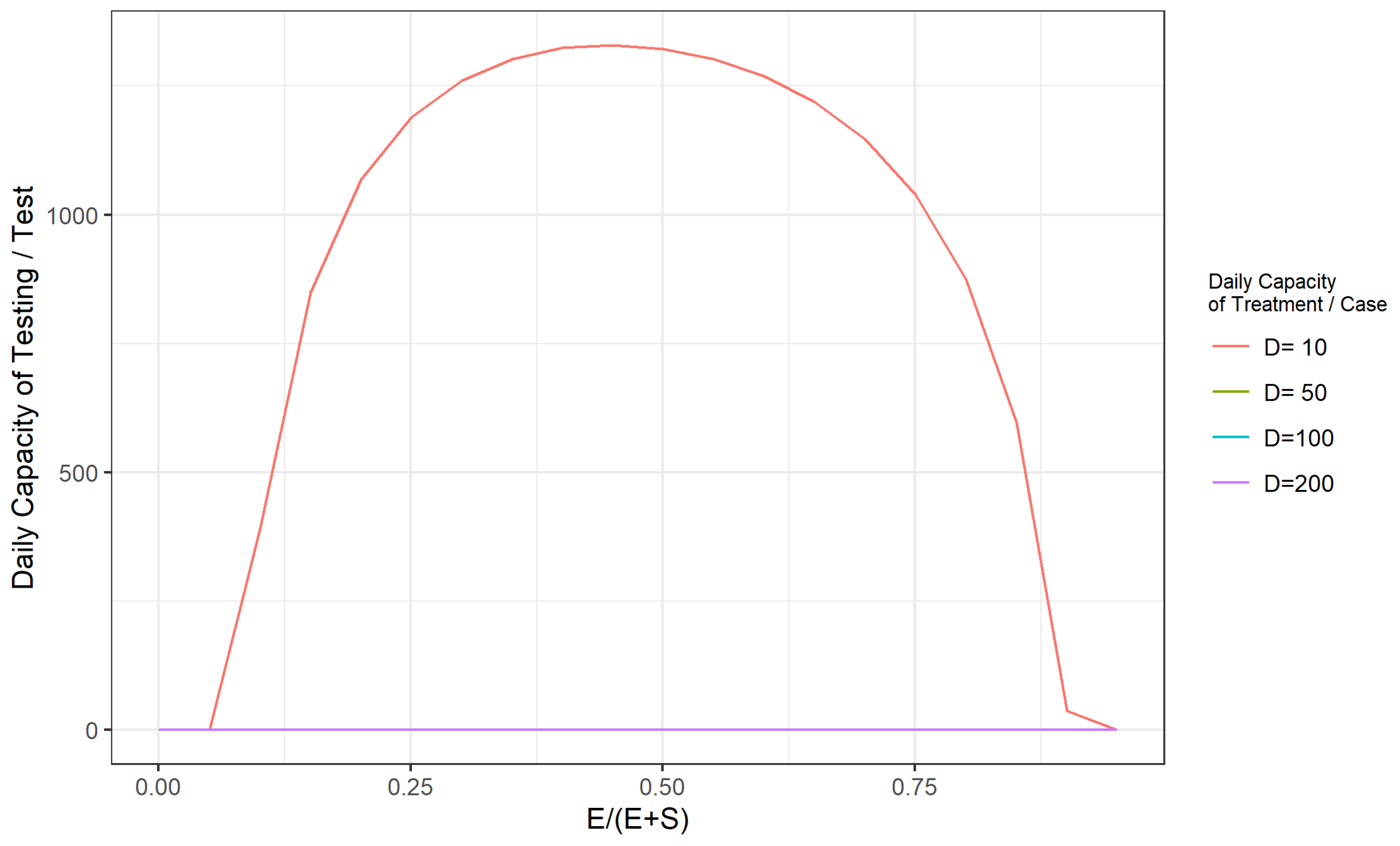
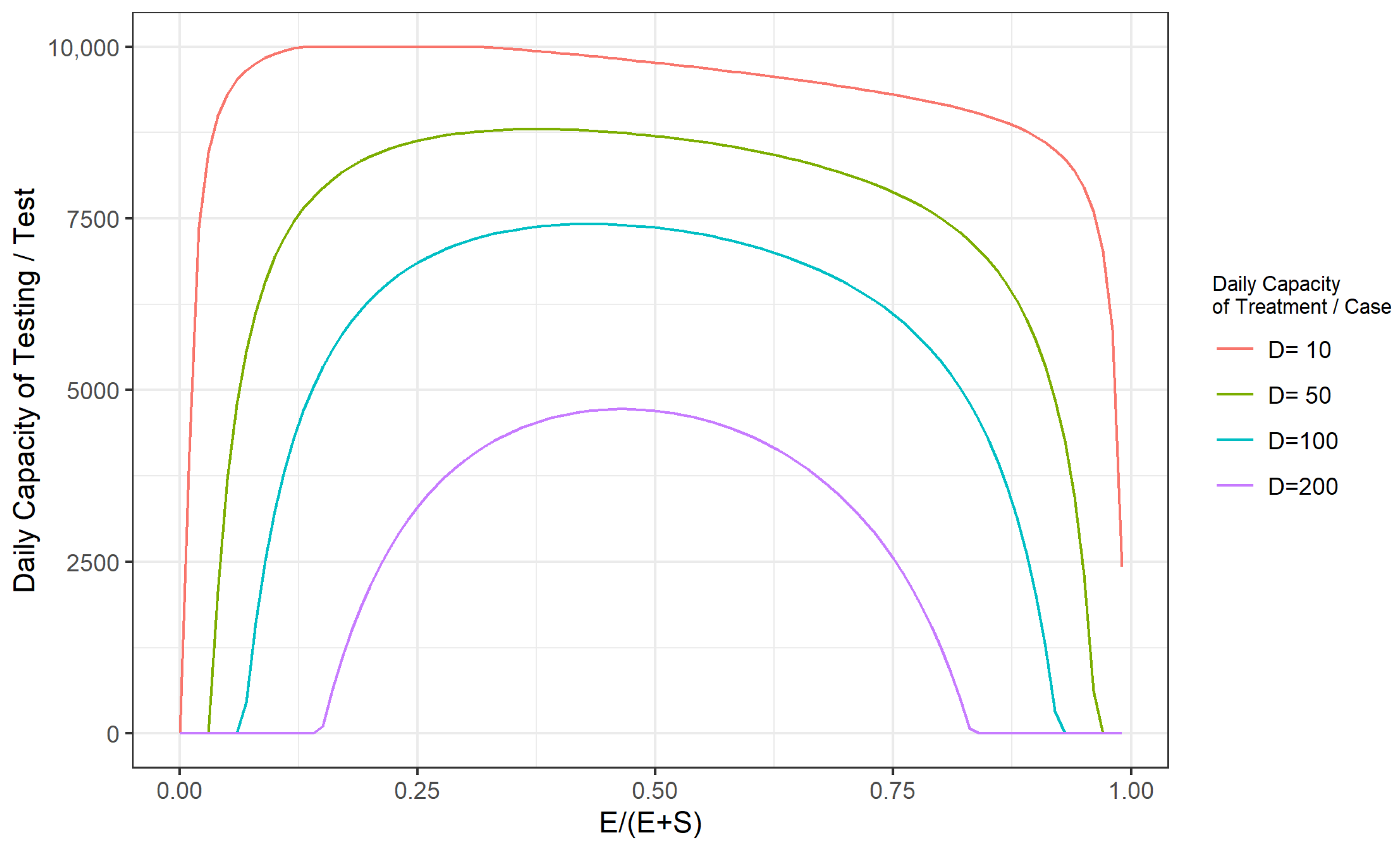

References
- Miao, Q.; Schwarz, S.; Schwarz, G.; Coomes, O.T. Responding to COVID-19: Community volunteerism and coproduction in China. World Dev. 2021, 137, 105128. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Wang, H.; Xi, X.; Boonyasiri, A.; Wang, Y.; Hinsley, W.; Fraser, K.J.; McCabe, R.; Mesa, D.O.; Skarp, J.; et al. Database of epidemic trends and control measures during the first wave of COVID-19 in mainland China. Int. J. Infect. Dis. 2021, 7, 463–471. [Google Scholar] [CrossRef] [PubMed]
- Zeller, M.; Gangavarapu, K.; Anderson, C.; Smither, A.R.; Andersen, K.G. Emergence of an early SARS-CoV-2 epidemic in the United States. Cell 2021, 184, 4939–4952. [Google Scholar] [CrossRef] [PubMed]
- Ghafari, M.; Hejazi, B.; Karshenas, A.; Dascalu, S.; Katzourakis, A. Lessons for preparedness and reasons for concern from the early COVID-19 epidemic in Iran. Epidemics 2021, 9, 100472. [Google Scholar] [CrossRef]
- Hsieh, H.S.; Hsia, H.C. Can continued anti-epidemic measures help post-COVID-19 public transport recovery? Evidence from Taiwan. J. Transp. Health 2022, 9, 101392. [Google Scholar] [CrossRef]
- Cereda, D.; Manica, M.; Tirani, M.; Rovida, F.; Merler, S. The early phase of the COVID-19 epidemic in Lombardy, Italy. Epidemics 2021, 12, 100528. [Google Scholar] [CrossRef]
- Kwok, K.O.; Wan In, W.; Huang, Y.; Wong, A.; Tang, A.; Wong, S.Y.S. Estimation of early phase local-to-local transmissibility and importation hazard of Coronavirus Disease 2019 (COVID-19) epidemic under assorted containment measures in Hong Kong. Travel Med. Infect. Dis. 2022, 1–2, 102226. [Google Scholar] [CrossRef]
- Yang, H.M. Directly transmitted infections modeling considering an age-structured contact rate. Math. Comput. Model. 1999, 29, 39–48. [Google Scholar] [CrossRef]
- Yuan, S.L.; Ma, Z.E.; Han, M.A. Global stability of an SIS epidemic model with time delays. Appl. Math. Lett. 2005, 25, 349–356. [Google Scholar]
- Chen, X.Y.; Ting, W.U. An SIR epidemic model with distributed delay and saturation incidence. J. Fuzhou Univ. 2010, 6, 808–812. [Google Scholar]
- Cha, Y.; Milner, F.A.; Iannelli, M. Existence and uniqueness of endemic states for the age-structured SEIR epidemic model. Math. Biosci. Int. J. 1998, 150, 177–190. [Google Scholar] [CrossRef]
- Wang, H. Public health emergency decision-making and management system sound research using rough set attribute reduction and blockchain. Sci. Rep. 2022, 12, 3600. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.B. Configurable Analysis of America Public Health Emergency Management System. Med. Philos. 2004, 25, 14–15. [Google Scholar]
- Wang, Z. Construction of Urban Public Emergency Management System. J. Soc. Work 2012, 95–96. [Google Scholar]
- Ying-Lian, H.U. Comparative Study of Emergency Management Institution in China——A Focus on Public Health Emergency. J. Univ. Sci. Technol. Beijing (Soc. Sci. Ed.) 2012, 141–146. [Google Scholar]
- Sun, Y.H.; Hao, Y.H.; Qun-Hong, W.U.; Jiao, M.L.; Kang, Z.; Huang, K.G.; Ma, J.C.; Liu, J. Application of risk analysis methods in public health emergency management. Chin. Health Resour. 2013, 1, 20–22. [Google Scholar]
- Cao, Y.; Shan, J.; Gong, Z.; Kuang, J.; Gao, Y. Status and Challenges of Public Health Emergency Management in China Related to COVID-19. Front. Public Health 2020, 5, 250. [Google Scholar] [CrossRef] [PubMed]
- Martinez, E.G.; Zabalegui, A.; Sevilla, G.S. Management and leadership of nursing services in the emergency plan for the pandemic COVID-19: The experience of the Clinic Hospital of Barcelona. Enferm. Clin. (Engl. Ed.) 2021, 10, 12–17. [Google Scholar] [CrossRef]
- Wang, C.; Miao, L.; Wang, Z.; Xiong, Y.; Jiao, Y.; Liu, H. Emergency Management in a Dental Clinic During the Coronavirus Disease 2019 (COVID-19) Epidemic in Beijing. Int. Dent. J. 2021, 71, 32–39. [Google Scholar] [CrossRef]
- Song, X. Coping with COVID-19 in China: Lessons Learned from Japan’s Public Health Emergency Management System. China Emerg. Rescue 2020, 3, 22–28. [Google Scholar]
- Bokler, B. Chaos and complexity in measles models: A comparative numerical study. Math. Med. Biol. 1993, 10, 83–95. [Google Scholar]
- Lin, J.F. Assessment and Prediction of COVID-19 Based on SEIR Model with Undiscovered People. J. Univ. Electron. Sci. Technol. 2020, 49, 1–8. [Google Scholar]
- Danon, L.; Brooks-Pollock, E.; Bailey, M.; Keeling, M.J. A spatial model of covid-19 transmission in England and Wales: Early spread and peak timing. medRxiv 2020, 376, 20200272. [Google Scholar] [CrossRef]
- Ku, C.C.; Ng, T.C.; Lin, H.H. Epidemiological benchmarks of the covid-19 outbreak control in china after wuhan’s lockdown: A modelling study with an empirical approach. SSRN Prepr. 2020, 3544127. [Google Scholar] [CrossRef]
- Deguen, S.; Thomas, G.; Chau, N.P. Estimation of the contact rate in a seasonal SEIR model: Application to chickenpox incidence in France. Stat. Med. 2000, 19, 1207–1216. [Google Scholar] [CrossRef]
- Li, G.; Jin, Z. Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period. Chaos Solitons Fractals 2005, 25, 1177–1184. [Google Scholar] [CrossRef]
- Prin, M.; Wunsch, H. International comparisons of intensive care: Informing outcomes and improving standards. Curr. Opin. Crit. Care 2012, 18, 700–706. [Google Scholar] [CrossRef]
- Rhodes, A.; Ferdinande, P.; Flaatten, H.; Guidet, B.; Metnitz, P.G.; Moreno, R.P. The variability of critical care bed numbers in Europe. Intensive Care Med. 2012, 38, 1647–1653. [Google Scholar] [CrossRef]
- Subbiah, S.; Hussain, S.A.; Kumar, M.S. Managing cancer during COVID pandemic–Experience of a tertiary cancer care center. Eur. J. Surg. Oncol. 2020, 47, 1220–1224. [Google Scholar] [CrossRef]
- Berger, D.W.; Herkenhoff, K.F.; Mongey, S. An SEIR Infectious Disease Model with Testing and Conditional Quarantine; Staff Report 597; Federal Reserve Bank of Minneapolis: Minneapolis, MI, USA, 2020. [Google Scholar] [CrossRef]
- Chen, Z.; Kong, G. Hospital admission and social distancing: An SEIR model with constrained medical resources. Prod. Oper. Manag. 2022. [Google Scholar] [CrossRef]
- David, B.; Kyle, H.; Chengdai, H.; Simon, M. Testing and reopening in an SEIR model. Rev. Econ. Dyn. 2022, 43, 1–21. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Xia, Z. Study of COVID-19 Epidemic Control Capability and Emergency Management Strategy Based on Optimized SEIR Model. Mathematics 2023, 11, 323. https://doi.org/10.3390/math11020323
Wang W, Xia Z. Study of COVID-19 Epidemic Control Capability and Emergency Management Strategy Based on Optimized SEIR Model. Mathematics. 2023; 11(2):323. https://doi.org/10.3390/math11020323
Chicago/Turabian StyleWang, Weibin, and Zeyu Xia. 2023. "Study of COVID-19 Epidemic Control Capability and Emergency Management Strategy Based on Optimized SEIR Model" Mathematics 11, no. 2: 323. https://doi.org/10.3390/math11020323
APA StyleWang, W., & Xia, Z. (2023). Study of COVID-19 Epidemic Control Capability and Emergency Management Strategy Based on Optimized SEIR Model. Mathematics, 11(2), 323. https://doi.org/10.3390/math11020323




