Abstract
An effective MPPT approach plays a significant role in increasing the efficiency of a PV system. Solar energy is a rich renewable energy source that is supplied to the earth in surplus by the sun. Solar PV systems are designed to utilize sunlight in order to meet the energy needs of the user. Due to unreliable climatic conditions, these PV frames have a non-linear characteristic that has a significant impact on their yield. Moreover, PSCs also affect the performance of PV systems in yielding maximum power. A significant progression in solar PV installations has resulted in rapid growth of MPPT techniques. As a result, a variety of MPPT approaches have been used to enhance the power yield of PV systems along with their advantages and disadvantages. Thus, it is essential for researchers to appraise developed MPPT strategies appropriately on regular basis. This study is novel because it provides an in-depth assessment of the current state of MPPT strategies for PV systems. On account of novelty, the authors analyzed the successive growth in MPPT strategies along with working principles, mathematical modeling, and simplified flow charts for better understanding by new learners. Moreover, the taxonomy and pro and cons of conventional and AI-based MPPT techniques are explored comprehensively. In addition, a comparative study based on key characteristics of PV system of all MPPT algorithms is depicted in a table, which can be used as a reference by various researchers while designing PV systems.
MSC:
68W50
1. Introduction
As our civilization advances in technology, it necessitates a greater use of energy in today’s world. Renewable energy sources have the potential to cater the increasing demand for energy in various forms. In near future, demand for renewable energy will rise in all sectors, including heating, power, and transportation, etc. Solar power is more admired than other renewable energy sources due to its widespread availability and well-established technology. This is because of recent developments in increasing accuracy and tracking speed for maximum energy harvesting [1].
Direct current is generated when photons from sunlight strike the solar cells. A series-parallel combination of these cells gives rise to a PV module, which when further combined together forms a PV array. The literature reveals that the characteristics of solar cells are non-linear [2], which degrades their conversion efficiency. Therefore, it is required to extract all the power accessible from the PV module. Moreover, a PV module does not supply power constantly on account of various factors such as temperature, irradiance, geographical conditions, and so on [3].
The P–V curve of any solar module has an optimal point, i.e., the global maximum power point (GMPP), that varies depending on temperature and solar irradiance. The PV module produces the most power at that point [4]. To confirm that the PV module is always operating at GMPP, MPPT techniques come into picture. MPPT techniques are algorithms that are implemented via software and power electronics hardware combination in any solar controller. These algorithms aid in ensuring that the output of solar array is always at its peak. MPPT techniques perform this task by continuous power tracking methodology to determine the best operating power point from solar array. Since the maximum power of a solar array varies in accordance with many environmental conditions, tracking this power is crucial for utmost utilization of solar energy. The MPPT system’s aim is to sample the output of the PV array and apply the appropriate resistance to obtain maximum power for any given environmental conditions. Thus, these techniques function as an impedance-matching device between the array and load with the help of varying the duty cycle of the DC-DC converter. The whole process is controlled by software and a micro-controller. MPPT-equipped controllers have numerous advantages over other controllers, such as the following:
- More efficiency;
- Capability of optimizing voltage differences as well as DC load optimization;
- Best for larger systems where solar panel output exceeds battery voltage by a significant margin;
- Enhances the system’s output and hence its capacity.
There are several approaches to achieving MPPT, which are discussed in this article.
Many researchers have published their findings on MPPT algorithms. Refs. [5,6,7] compare various MPPT approaches for uniform irradiance and PSCs for solar PV systems, whereas [8,9] focus specifically on PSCs. Traditional MPPT techniques such as P&O [10], INC [11], and HC [12] are proficient for uniform irradiance with a unique peak. They are unsuitable when the PV system is subjected to PSCs. The researchers attempted to improve on traditional MPPT algorithms by combining them with advanced strategies [13,14,15]. Figure 1a,b show a generalized block diagram of standalone and grid-connected PV systems.
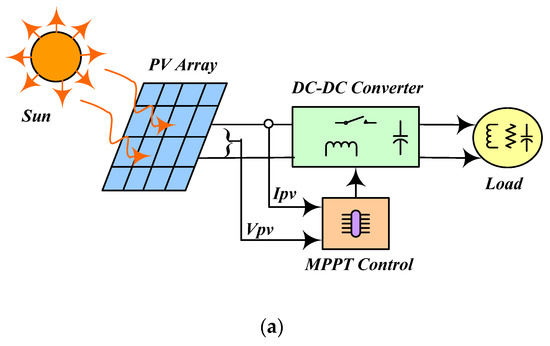

Figure 1.
Generalized block diagram of (a) standalone PV system and (b) grid-connected PV system.
However, the choice of a specific MPPT approach is still an ambiguity. As a result, there is strong need to investigate and reassess the developed strategies on regular basis, as this will help in the selection of a specific technique based on the context. Different conventional and AI-based meta-heuristic MPPT techniques are reviewed and compared in this article based on a variety of factors such as tracking time, complexity, oscillations around GMPP, implementation cost, and so on. BI [16,17], SI [18,19], ANN, FLC, and ECI are explained and reviewed by authors on various parameters.
The novelty of this work can be summarized as an approach to presenting qualitative comparative analysis and set-theoretic research, with emphasis on tabular presentation (technical datasheet presentation) of the chief attributes of conventional and AI-based MPPT techniques.
This data positioning approach is most appropriate format for reading and understanding the data. Quantifying these data helps in comprehensive analysis and comparing different data sets, thereby bringing out the most important and widely used conventional, metaheuristic, and other AI-based MPPT techniques, wherein various parameters such as array size, irradiance levels, techniques considered, % boost in GMPP using best technique, and tracking time, etc., are considered.
This research work is novel from other aspects as well, such as the following:
- Ease of representation: In distinct sections, the work summarizes the main characteristics of traditional and AI-based metaheuristic techniques in a simplified style using simplified flowcharts;
- Ease of analysis: A technical datasheet was created after reviewing all the major attributes required to design any PV system of recently reported conventional MPPT techniques, AI-based metaheuristic approaches, and other AI-based MPPT techniques. This datasheet provides a bare-bones description that facilitates even a new learner to understand the performances of these metaheuristic MPPT techniques, particularly PV systems in PSCs;
- Ease of modification: The technical datasheet highlights the pros and cons of all reviewed works of each category, which enables the user to identify the research gap as discussed above and helps them to modify a particular algorithm to meet the requirement of good PV system;
- Qualitative comparative analysis: The technical datasheet facilitates comparison of all MPPT approaches based on the key characteristics required while incorporating them in any PV system, which helps the readers to select the most suitable technique for any particular application.
Structure of this work is as follows: The modeling of the PV cell is elaborated upon in Section 2 along with the effects of environmental factors. The partial shading effect is discussed in Section 3. MPPT techniques and their classification are elaborated upon in Section 4. Research gap findings are reported in Section 5. Challenges and further scope of the conducted effort are pointed out in Section 6, and paper is concluded in Section 7.
2. Modeling of PV Cell
Ideally, a parallel combination of a current source and a diode represents a solar cell. For practical applications, the model also incorporates shunt and series resistances to take into account manufacturing defects and contact resistances [20], as illustrated in Figure 2a.

Figure 2.
Solar cell: (a) single-diode model and (b) double-diode model.
The current generated by the solar cell can be computed by Equation (1).
The Shockley equation and Ohm’s law can be used to calculate the current through a diode and shunt resistor, as shown in Equations (2) and (3), respectively.
Thus, the distinctive Equation of solar cell output current can be written as
The ideality factor “n” is assumed to be constant in single-diode model, but this factor is a function of voltage at the device terminals. Its value is close to one at high voltages and becomes two at low voltages because of recombination in junction. This effect can be modelled by connecting another diode in parallel with the first diode, giving rise to the double-diode model, as shown in Figure 2b. The ideality factor is set to “2” for the double-diode model.
Figure 3 shows the PV module (I–V) and (P–V) characteristic curves. It details the solar energy conversion capability and efficiency for a particular atmospheric condition. Since short- and open-circuit circumstances have no effect on power generation, there must be a point somewhere in the middle where the solar module produces most power and is located close to the bend in the characteristic curves. is generated by a specific combination of voltage and current, and the combination’s coordinates represent the MPP.
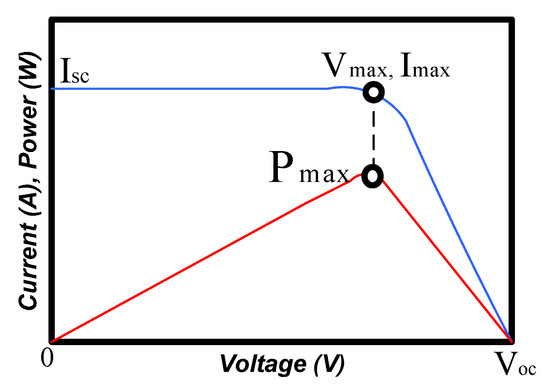
Figure 3.
PV module characteristic curves (I–V) and (P–V).
A slight change in atmospheric temperature and irradiance affects the module’s performance. Since module Voc decreases as temperature rises [21], the power output yield of the PV system will decrease. Figure 4a,b show the temperature variation effect on PV module (I–V) and (P–V) curves.

Figure 4.
Temperature variations effect on PV module: (a) I–V curve and (b) P–V Similarly, the output of PV modules is also affected by the change in solar irradiance “W w/m2”, as the output current of PV module depends on irradiance. As irradiance increases, the PV module output current also increases. Thus, the PV module can generate more output power. Figure 5a,b show the effect of irradiance change on PV module (I–V) and (P–V) curves.
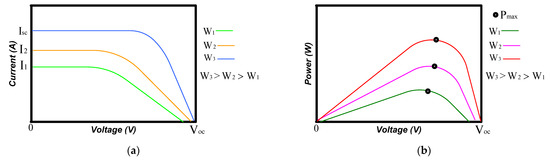
Figure 5.
Irradiance variation effect on PV module: (a) I–V curve and (b) P–V curve.
3. Partial shading Effect
PV systems are extremely susceptible to partial shading. On account of various environmental conditions such as rain, clouds, and storms, it is not possible to obtain uniform irradiance at all times. In addition, PV array also suffers shading from nearby buildings and trees. This shading effect leads the PV module to yield less output power [22]. PSCs can lead to the following:
- Non-linear PV module (I–V) characteristic curve with multiple LMPP. As a result, shading causes hot spots and damages the solar cells;
- Current and voltage mismatch in PV array;
- Many peaks in the (P–V) characteristic curve with an increase in shading conditions.
Shading one cell results in a drop of current flowing through it when compared to the unshaded cells of its string. As a result, unshaded cells are forced to carry high current, and shaded cells will be restricted to the string current. This leads to a drop in the output power of the PV string. A bypass diode is connected across the shaded cell string to moderate the effect of shading. Through this, unidirectional flow of current is achieved. Figure 6a,b shows the effect of partial shading on (I–V) and (P–V) characteristics of PV system.

Figure 6.
Characteristics of (a) I–V and (b) P–V under PSCs.
4. MPPT Algorithms
Each PV module has a different MPP in different atmospheric conditions. Thus, to extract maximum power from it, MPPT algorithms are used. These algorithms are imposed through electronic converters. Though these techniques enhance the performance of PV system, designers are generally concerned about tracking GMPP under PSCs. These algorithms are implemented through microcontrollers. The duty ratio of the DC converter employed is adjusted by these algorithms after frequent sampling of some PV module parameters. This changes the impedance seen by the PV module, resulting in achieving maximum power. These MPPT techniques are classified as shown in Figure 7. The following sections explain the basics of these techniques comprehensively, while recent advancements in each are listed in the tables at the end of each classification separately.

Figure 7.
MPPT Techniques Classifications.
4.1. Conventional MPPT Techniques
4.1.1. Perturb and Observe
The P&O MPPT technique is widely used due to its simplicity, ease of implementation, fewer sensor requirements, and low actualized costs [23,24]. It is an iterative method of tracking MPP. This technique works on the principle of minor change in PV array voltage and monitors the resulting impact on power. This is achieved by varying the duty cycle of the DC–DC converter employed in the system. With these perturbations, the change in power can be determined. If power is increased by increasing the voltage, the operating point of the PV module is on the left side of the P–V curve. If, on the other hand, power is reduced with the increase in voltage, the PV module operating point is on the right side of the P–V curve. As a result, for tracking MPP, the direction of perturbation must be such that it converges towards a precise end. Thereafter, this iteration process is continued until MPP is reached. Though the conventional P&O technique works well in stable environmental conditions, it fails to track MPP in PSCs [25]. To overcome this drawback, P&O are modified, as reported in [26]. Steps to demonstrate the working of this technique are shown in Figure 8.

Figure 8.
P&O-based MPPT technique [24].
4.1.2. Incremental Conductance
This technique is an improved version of P&O and can track MPP in a rapidly changing environment [27,28]. The principle fact of this technique is based on computing the slope of power “p” on the P–V curve. Since instantaneous power is given as the product of instantaneous voltage and current,
The P–V curve slope can be computed as
The following conditions can be drawn from Equation (6):
| If | At MPP | |
| If | At the right side of MPP | |
| If | At the left side of MPP |
As a result, the INC approach tracks MPP by comparing incremental conductance with instantaneous one [28]. Although INC can show zero oscillations in steady state, it acts the same as the P&O technique in transition states. Figure 9 shows the flowchart of the INC approach for tracking MPP.

Figure 9.
INC-based MPPT technique [27].
4.1.3. Fractional Open-Circuit Voltage Technique
FOCV MPPT technique is an indirect scheme to track MPP and can be utilized for low-power functions. This technique utilizes the principle that shows linear relationship between :
“b” lies in a range of 0.71 < b < 0.78 [29]. Its value is mainly dependent on module and environmental conditions. Although the technique is simple, FOCV suffers from power loss while sampling . A flowchart of the FOCV method is shown in Figure 10.

Figure 10.
FOCV-based MPPT technique [29].
4.1.4. Fractional Short-Circuit Current Technique
This technique is also an indirect method for tracking MPP and is similar to FOCV. The FSCC technique utilizes the fact that there exists a linear association between and :
The range of “d” lies in 0.78 < d < 0.92 [30]. This technique also suffers from the drawback of power loss while measuring during MPPT. A flowchart of the FSCC technique is shown in Figure 11.

Figure 11.
FSCC-based MPPT technique [30].
These conventional techniques are still used as a baseline for tracking GMPP in PSCs. Table 1 summarizes recently reported works based on these principles, followed by a discussion of their pros and cons in Table 2.

Table 1.
Taxonomy on recent reported work on conventional techniques to track GMPP.

Table 2.
Pros and cons of recent work based on conventional techniques.
4.2. Swarm Intelligence MPPT Techniques
This section of the paper explains various swarm intelligence MPPT techniques in detail and reports the recent work done with these techniques to enhance MPPT along with their pros and cons in Table 3 and Table 4 respectively.
4.2.1. Ant colony Optimization
Ants’ cooperative search behavior for the shortest path between source food and their colony motivates ACO. Firstly, ants scurry about aimlessly. When any ant finds a food source, they return to their home along with the food, leaving pheromone trails at their back. This pheromone is composed of particular artificial compounds that are received by living organisms to send messages or codes to other members of the same class. If other colony ants come across such a route, they will follow it to the food source rather than roaming randomly.
They leave pheromones when they return to their territory, boosting the existing pheromone strength. The potency of the pheromone is condensed as pheromone dissipates over time. The ants ultimately regulate and find the shortest path to the food source.
The procedure starts with a single colony of (artificial) ants that has been randomly positioned in that colony. Suppose ants are represented by N parameters. Each ant in the colony uses its magnetic power to entice another ant. They travel from the lower potency zone to the higher potency zone on the basis of attractive force. The attractive power resolute after each iteration cycle and the ants travel in the direction of the best option based on the results.
Consider a problem in which “n” artificial ants (parameters) must be tuned so that A n. The solution register stores “A”, which represents the primarily created arbitrary solutions. The result afterwards sited according to their fitness significance, f (si), is shown in Equation (9):
Similarly, fresh arrangements are created to determine the placements of these ants with the help of Gaussian kernel function sampling for ith dimensions and kth solution as [46]
, can be evaluated as
The investigative cycle will be continual depending on the quantity of parameters that needs to be improved. First, we generate “B” novel solutions that sum up the initial “A” solutions. Afterwards, A + B solutions must be placed in the search box. Soon after, A’s most effective arrangements are re-established. The entire cycle is thus re-hashed for the required amount of iterations [47]. Effective tracking of GMPP, high convergence rate, and a lesser number of iteration makes ACO more advantageous than traditional MPPT techniques. A flowchart of ACO is shown in Figure 12.

Figure 12.
ACO-based MPPT technique [47].
4.2.2. Particle Swarm Optimization
PSO is a random search technique. It utilizes the principle of maximizing nonlinear continuous function. It follows the rules of natural manner of fish schooling and flock gathering. Several combined birds are used in this technique, each of which represents a particle. In search space, every particle has a fitness value mapped by a vector of position and velocity. The direction and steps of every particle are determined by their fitness value. Following that, all particles present a solution by combining the information gathered during their own search process to arrive at the optimal solution. This technique starts with random solution groups based on particles position and velocity in the search area. With the help of cerebral and social trade-off, the fitness value of particles is adjusted after each iteration. Because of the trade off, shifts in individual and community best position are obtained. Individual particles’ best position is also remembered by every particle while also accumulating the global best position [48].
After each cycle, the swarm tries to determine the optimum solution by stimulating the position and velocity. Following that, a global maximum is swiftly achieved by each particle. For the cycle, the nth molecule refreshes the condition with position “Y” and velocity “v” as given below
If, with an improvised scenario as in Equation (16), the initialization requirement is satisfied, the technique update is in line with Equation (17):
“” must be maximized. Figure 13 shows the flowchart of the PSO algorithm to track GMPP.

Figure 13.
PSO-based MPPT technique [48].
4.2.3. Artificial Bee Colony
The ABC approach is based on honey bees’ foraging intelligence. This approach is a sensible, modern, and speculative global optimization technique. Honey bees reside inside their hives and use a chemical exchange (pheromones) and the shake dance for their communication. If a bee finds a honey source (food), it takes food back to its hive by performing a shake dance to trade off the food-source site. The potency and duration of the shake dance show the richness of the food source discovered.
Three classes of artificial bee are formed by ABC algorithm, i.e., employed, scouts, and spectator bees. The hive is divided equally between employed and spectator bees. The main aim of whole bees group is to find the best honey source. Employed bees seek out a honey source (food) initially. They revisit their hive and communicate their findings with other groups of bees through shake dance movements. By carefully examining the shake dance of employee bees, spectator bees try to find the food source, while scout bees imprecisely search for new food sources. Thus, with this communication and coordination amongst them, artificial honey bees arrive at ideal solutions in the possible shortest time [49,50]. The ABC algorithm uses five phases to track GMPP as discussed below.
Phase 1: Initialization phase
First, create food sources at random in the hunt arena. The algorithm’s performance improves with the increase in size of the group. Each solution is an n-dimensional vector that dispenses the entire employed bee equivalent to each distinctive source of food as per Equation (18) with n optimization parameter numbered as
Phase 2: Employed bee phase
The goal is to chase the food source location in the exploration region with the most nectar accessible (i.e., GMPP). Every employed bee progresses to its new position (Xi, k) in the immediate space by means of the previous position value (Yi) to maintain the previous position value (Yi) securely in memory according to Equation (19):
is other than i.e., and ranges from [−1, 1].
A gluttonous assortment method is adopted by employed bees after they search a new food source. The quantity of nectar present at the previous and latest sites is compared in this technique. As a result, a better option is preserved.
Phase 3: Spectator bee phase
On the basis of the information of the food source obtained by spectator bees from employed bees with their shake dance, spectator bees use a probabilistic selection mechanism in order to identify food sources (solutions) with f(x) fitness factor according to Equation (20).
Phase 4: Scout bee phase
Scout bees can locate fresh feasible solutions on the basis of Equation (20) in the vicinity of the chosen food source. In any event, even after a thorough investigation of the entire investigated area by employed and spectator bees, the food-source fitness value remains unaffected for the existing step. The same employed bees turn into scout bees, and the scout bees use Equation (18) to hunt for new possible solutions in the next step.
Phase 5: Conclusion phase
In case that output power does not show any further improvement, the method comes to an end. The procedure, on the other hand, will restart when there is a fluctuation in output power on account of various factors. Irradiance variation is one amongst them, and such changes can be represented as
If Equation (21) is satisfied, ABC again starts searching GMPP. Hence, ABC works well in PSCs. Figure 14 shows a flowchart of the ABC technique.

Figure 14.
ABC-based MPPT technique [50].
4.2.4. Grey Wolf Optimization
The GWO technique was proposed in 2014. It is motivated by social stratification and the gray wolf’s behavioral hunting personality [51]. Grey wolves, as a whole, live in packs with typical size of around 5–12. According to the hierarchical chain shown in Figure 15, grey wolves are classified into four categories based on their community supremacy. Alpha (α) wolves are the pioneer at the peak and are thus regarded as the best sources of solutions for a given optimization problem. Beta (β) wolves pursue the (α) and assist them in fulfilling their tasks. They take (α) wolves’ position if the (α) wolves die. The delta (δ) wolves make up the pack’s hunters, keepers, and explorers and are the second end-class. As a result, (β) and (δ) wolves represent the second- and third-best solutions, correspondingly. Omega (ω) wolves are the last group, which make up the youngest members and therefore stand for the residual solution [52].

Figure 15.
Grey wolves hierarchy sequence.
The supremacy of wolves is reduced as the position of the wolves lowers in the hierarchical order from top to bottom. Aside from the community order of wolves, the grey wolf’s social behavior is also heavily influenced by aggregation hunting. On the basis of this, the GWO algorithm’s mathematical model analyzes the following measure [52]:
Step-1: Social Hierarchy
The GWO technique presumes (α) as the fittest solution, followed by (β) and (δ) as the second- and third-finest solutions, to simulate the hierarchical system of wolves. (ω) is thought to represent the left-over contender solutions. Thus α, β and δ wolves guide the hunting process with ω wolves trailing behind.
Step-2: Tracking and Encircling the Prey
Grey wolves frequently encircle prey all through the hunting phase, expressed mathematically by Equations (22) and (23) (with iteration “i”). Equation (22) calculates a wolf’s distance vector from prey with current iteration.
ranges between [0, 1], and = linearly decreases from 2 to 0 during each iteration.
Step-3: Hunting
Using arbitrary vectors , any place in between the points can be reached by a wolf. The first three best solutions (i.e., α, β, and δ wolves’ locations) are initially saved. Other probing wolves alter their locations based on the top solution knowledge. As a result, a grey wolf can use this technique to improve its position in any arbitrary direction.
Step-4: Attack the Prey
Since in each cycle, the drops linearly from 2 to 0, therefore, when is achieved, the prey comes to a standstill in an unchanging position, and the grey wolves attack it.
Step-5: Searches for Prey
If condition is achieved, grey wolves are compelled to look for the prey. The exploration approach is depicted in this procedure where the wolves wander away from each other in search of prey, then return to attack the prey.
In addition to this, a flowchart to explain the operation of the GWO-based MPPT technique is depicted in Figure 16.

Figure 16.
GWO-based MPPT technique [52].
4.2.5. Salp Swarm Algorithm (SSA)
SSA was proposed in 2017 and mimics the salps’ swarm behavior. Salps are barrel-shaped, jellylike zooplankton with jellylike bodies, and they live in the deep, warm waters of the ocean. It moves by swimming with its gelatinous body, which pumps water all the way through it. It moves by constructing a chain formation of one leader, and rest follow in the chain [53]. Figure 17 shows its flowchart.
At first, a candidate solution for the leader is updated and then for the followers with the solutions found for the leaders. Let the entire chain’s primary solution be given by , where represent salp chain size and verdict variable numbers, respectively. The leader’s candidate solutions are rationalized by
Random numbers are distributed evenly between [0, 1], as per the following Equation:
where i= current iteration, and I= iterations maximum count.
This solution aids in updating the followers’ candidate solutions:
If, after modifying the candidate solutions as recommended in Equations (26), (27), and (29), the entire chain candidate solutions still breach the minimum and maximum standards of verdict variables, the candidate solutions must be reinitialized at the appropriate minimum and maximum values of verdict variables.

Figure 17.
SSA-based MPPT technique [46].

Table 3.
Taxonomy on recent reported work on swarm intelligence techniques to track GMPP.
Table 3.
Taxonomy on recent reported work on swarm intelligence techniques to track GMPP.
| Authors [Reference No.] | Optimization Techniques | Best Optimization Techniques | PV Module Pm (W) | PV System Size | GMPP (W) | Improved GMPP (%) | Irradiance (W/m2) | Shading Patterns | Tracking Time (s) |
|---|---|---|---|---|---|---|---|---|---|
| Krishnan SG et al. [54] | Proposed, ACO, PSO, P&O | Proposed ACO | 20 | 4 × 4 3 × 6 | 63, 48.75 | 1.00, 32.29 | NA | Non uniform | 1.5, 1.56 |
| Sridhar R et al. [55] | ACO, P&O | ACO | NA | 3 PV module in series | 61.4 | 261.1 | NA | Non uniform | 0.076 |
| Alshareef M et al. [56] | APSO, PSO, P&O | APSO | NA | NA | 40.56, 73.33, 76.51 | 13.07, 4.29, 73.49 | NA | NA | 1.9–2.4 |
| Panda KP et al. [57] | Modified PSO PSO, P&O | Modified PSO | 60 | 4 × 1 | 116.4 | 105.3 | 1000–400 | Non uniform | 0.9 |
| Gopalakrishnan SG et al. [58] | Proposed PSO PSO, P&O | Proposed PSO | 20 | 4 × 4 3 × 6 | 56.25, 48.75 | 18.42, 32.29 | NA | Non uniform | 1.9, 1.7 |
| Mao M et al. [59] | Proposed, PSO | Proposed | 83.2824 | 3 × 1 | 245.31, 60.8, 148.38 | −0.28, 32.83, 1.54 | 1000–300 | Non uniform | 0.012–0.016 |
| Koad RBA et al. [60] | LIPSO, P&O INC, PSO | LIPSO | NA | 4 × 1 | 60.64, 48.76, 36.58, 24.29, 11.67 | 4.98, 12.79, 8.80, 16.23 | 1000–200 | Uniform | NA |
| Belghith OB et al. [61] | PSO Fuzzy_TS P&O | PSO | 150 | 1 PV module | 148.46, 122.81, 55.67 | 1.48, 2.36, 5.69 | 1000–400 | Non uniform | 0.003–0.043 |
| Obukhov S et al. [62] | VCPSO, CFPSO | VCPSO | 320.4 | 3 PV module in series, 4 PV module in series, 8 PV module in series | 960.2, 478.8, 477.8, 312.3 | 0.376, 0.041, 0.378, 0.192 | 1000–100 | Non uniform | 0.48–0.66 |
| Li H et al. [63] | OD-PSO Firefly, P&O-PSO | OD-PSO | 101.3 | 3 PV module in series | 112.85, 110.85 | −10.48, 4.00 | 1000–300 | Non uniform | 1.64, 2.08 |
| Suhardi D et al. [64] | GWO INC | GWO | 200 | NA | 203.2, 142.2, 35.9 | 112.19, 54.76, −50.72 | 1000–400 | Non uniform | 0.55 |
| Kumar CS [65] | EGWO GWO PSO | EGWO | 200 | 4 PV module in series, 2 × 2 | 522.629, 401.044, 522.763, 401.027 | 0.938, 2.707, −0.05, 7.91 | 1000–400 | Non uniform | 3.6–4.8 |
| Shi JY et al. [66] | P&O, PSO GWO, GWO-P&O GWO-GSO | GWO-GSO | 60 | 4 × 1 | 100.72 | 100.95 | 1000–300 | Non uniform | 0.64 |
| Ilyas M [67] | Modified GWO GWO | Modified GWO | 100 | 4 PV module in series, 2 × 2 | 444.65, 435.76 | 0.234, 0.045 | NA | Non uniform | 0.189, 0.21 |
| Kraiem H et al. [68] | PSO, GWO | PSO | 249 | 4 PV module in series | 645.6, 633.9, 359.1 | 0.077, 0.939, 0.447 | 1000–200 | Non uniform | 0.0561–0.071 |
| Jamaludin MNI et al. [69] | SSA PSO GOA GWO BOA HC | SSA | 59.85 | 4 × 1 | 136.3, 114.3, 176.9 | 23.5, 107.7, 58.93 | 1000–500 | Non uniform | 0.22, 2.3, 4.2 |
| Dagal I et al. [70] | Hybrid SSPSO P&O FA DE ISSA | SSPSO | 60 | 4 PV module in series | 124.09 | 6.55 | 1000–400 | Non uniform | 0.29 |
| Krishnan S et al. [71] | SSO WOA GWO | SSO | 220.5 | 3 PV module in series 2X2 | 294.8, 41.8, 525.4, 38.5, 445.2, 02.7 | 5.58, 10.04, 39.92, 14.67, 14.97, 28.43 | 750–500 | Non uniform | 0.0245–0.0749 |
| Farzaneh J et al. [72] | P&O, FFA, PSO, DE, SSA, ISSA | ISSA | 60 | 4 PV module in series | 115.59 | 6.53 | 1000–400 | Non uniform | 1.22 |
| Ali MHM [73] | P&O, SSO | SSO | NA | NA | 843.5 | 2.55 | 200 | Uniform | 0.72 |
| Balaji V et al. [74] | Hybrid SSPO SS, PO | Hybrid SSPO | 50 | 4 PV module in series | 50.3, 85.1, 78.2, 96.1 | 27.66, 0.09, 24.32, 51.10 | 1000–200 | Non uniform | 0.52–0.57 |
| Restrepo C et al. [75] | ABC-P&O GMPPT P&O | ABC-P&O | 200.143 | 4 PV module in series | 597.95 | 54.19 | 900–120 | Non uniform | NA |
| Sawant PT et al. [76] | ABC, PSO | ABC | 75 | NA | 74, 61 | 2.77, 3.38 | 1000–800 | Non uniform | NA |
| Li N et al. [77] | P&O, PSO ABC, MABC | Modified MABC | NA | 2 PV module in series | 850 | 70.68 | 1000–800 | Non uniform | 0.39 |
| Wan Y et al. [78] | SSA-GWO, P&O, PSO, SSA | SSA-GWO | 35 | 3 PV module in series | 104.88, 44.55, 69.32 | 0.788, 28.60, 1.612 | 1000–300 | Non uniform | 0.46, 0.53, 0.47 |
| Hayder W et al. [79] | IPSO, PSO-P&O, ANN-PSO | IPSO | 120 | NA | 119.9720, 69.9888, 94.9073, 45.3924 | NA | 1000–400 | Non uniform | 1.5 |
| Almutairi A et al. [80] | OGWO, P&O | OGWO | 60 | NA | 60, 47.8, 23 | 32.77 | NA | Non uniform | 0.5, <1, |
| Sharma A et al. [81] | TSA-PSO, FPA, GWO, TSA, PSO, P&O | TSA-PSO | 85 | 3 PV module in series | 103.36, 122.88, 156.84 | 22.20, 5.97, 13.11 | 1000–300 | Non uniform | 0.38, 0.54, 0.40 |
| Chao K-H et al. [82] | I-ABC, PSO, P&O, ABC | I-ABC | 20 | 4 × 3 | 246.6, 198.6, 148.8, 107.1, 77.1 | 0.08, 2.00, 0.881, 17.43, 66.88 | NA | Non uniform | 0.38, 0.63, 0.89, 1.48, 1.14 |
| Alaraj M et al. [83] | HGWO, PSO, INC | HGWO | 450 | 5 × 5 | 8256, 6441, 6347, 5567 | 13.23, 13.09, 20.50, 22.86 | 1000–400 | Non uniform | 0.08, 0.07 |
| Windarko N A et al. [84] | Proposed, DE, FF, PSO, GWO | Proposed | 100 | 3 PV module in series | 172.9, 170.9, 80.9 | 5.81, 65.60, 226.2 | 1000–100 | Non uniform | 0.45, 0.41, 0.52 |
| Chawda G S et al. [85] | ICPSO, P&O, INC, GA-based FLC, PSO-based FLC PSO-GA-FLC | ICPSO | NA | NA | 97.3, 60, 94.2 | 7.955, 11.77 | 1000–300 | Non uniform | 0.1 |

Table 4.
Pros and cons of recent work based on swarm intelligence techniques.
Table 4.
Pros and cons of recent work based on swarm intelligence techniques.
| Authors [Reference No.] | Pros | Cons |
|---|---|---|
| Krishnan SG et al. [54] |
|
|
| Sridhar R et al. [55] |
|
|
| Alshareef M et al. [56] |
|
|
| Pandal KP et al. [57] |
|
|
| Gopalakrishnan SK et al. [58] |
|
|
| Mao M et al. [59] |
|
|
| Koad RBA et al. [60] |
|
|
| Belghith OB et al. [61] |
|
|
| Obukhov S et al. [62] |
|
|
| Li H et al. [63] |
|
|
| Suhardi D et al. [64] |
|
|
| Kumar CS et al. [65] |
|
|
| Shi JY et al. [66] |
|
|
| Ilyas M et al. [67] |
|
|
| Kraiem H et al. [68] |
|
|
| Jamaludin MNI et al. [69] |
|
|
| Dagal I et al. [70] |
|
|
| Krishnan S et al. [71] |
|
|
| Farzaneh J et al. [72] |
|
|
| Ali MHM [73] |
|
|
| Balaji V et al. [74] |
|
|
| Restrepo C et al. [75] |
|
|
| Sawant PT et al. [76] |
|
|
| Li N et al. [77] |
|
|
| Wan Y et al. [78] |
|
|
| Hayder W et al. [79] |
|
|
| Almutairi A et al. [80] |
|
|
| Sharma A et al. [81] |
|
|
| Chao K-H et al. [82] |
|
|
| Alaraj M et al. [83] |
|
|
| Windarko N A et al. [84] |
|
|
| Chawda G S et al. [85] |
|
|
4.3. Bio Inspired Techniques
This part of the paper elaborates various MPPT techniques inspired by biological behavior of different organism. Additionally, various recent works done to track MPP incorporating these techniques are tabulated in Table 5 and Table 6.
4.3.1. Firefly MPPT Algorithm
Fireflies are beetles emitting light in the night and communicate amongst themselves using a special light pattern. The light color formed by each species is unique. The FFA’s hunting tactic is governed by firefly attraction, which is equivalent to brightness. A dimmer firefly approaches a brighter one, and if their brightness level is the same as that of a certain firefly, it will shift at random [86]. The key purpose of flashing in the FFA tactic is to allure other fireflies and attract their target. The charm of fireflies is governed by the intensity of the firefly along with the objective function value. The value of attraction “µ” is resolute by the evaluation of other fireflies and is diverge on the basis of “i” and “j” fireflies’ distance . Both can be evaluated as per Equations (30) and (31), with “D” as the distance between two fireflies, as an arbitrary constant that lies between 0.1 and 10, and as the dimension number.
is taken in MPPT problems because it is a one-dimensional case. A flowchart of FFA is shown in Figure 18.
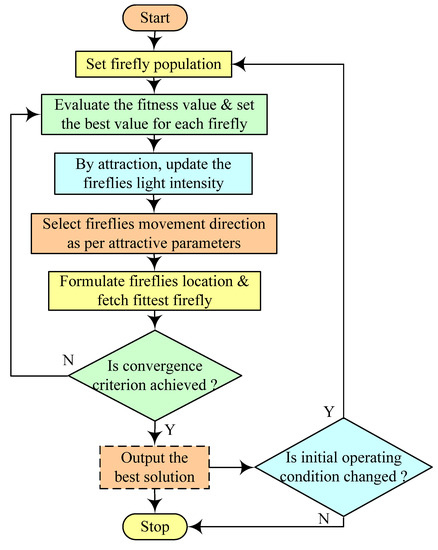
Figure 18.
FFA-based MPPT technique [46].
4.3.2. Cuckoo Search
This bio-inspired technique was reported in 2009 and is inspired by the cuckoo species’ parasitic imitation tactic (brood-parasitism) [87]. Certain birds, such as cuckoos (Tapera), engage in social parasitism. The Tapera is a knowledgeable winged creature that fits in with the host fowls, and with this tactic, next-generation endurance is encouraged. Rather than building its own nest, the cuckoo places its eggs in the nests of other flying species. Primarily, the cuckoo bird (female) flies erratically in search of a nest with similar egg characteristics to their own. After finding the best nest, cuckoo eggs have the utmost opportunity of hatching, ensuring the new generation. The cuckoo makes a few attempts by assisting the incubating bird in laying their eggs in a suitable location and hence gives itself a better chance. The cuckoo may occasionally throw the eggs of the host species from the nest because host birds could be readily duped into recognizing the strange eggs. If the host bird comes to know about the foreign eggs, the eggs will definitely be dumped outside the nest. The host bird may even demolish the nest.
For optimization objectives, the CS approach is an effective meta-heuristic method. Three idealized principles used to accomplish this strategy are as follows:
- Every cuckoo bird merely lays one egg at a time in a hastily chosen host nest;
- The cuckoos’ subsequent generation will be carried on by the superior eggs’ nest (i.e., the best solutions);
- In the hunt area, the entire number of reachable host nests is fixed.
Cuckoo birds represent the particles relegated to find the solution in the CS strategy implementation, and their eggs indicate the current iteration’s solution to an optimization problem. Searching for a nest is comparable to searching for food, and in CS, it is described by Levy flight. A Levy flight is an arbitrary stride where Levy distribution is used to evaluate sizes of steps by using a power law [88]:
Thus, has an infinite variance. The new cuckoo solution for ith iteration cycle “i” and the nth particle “n” can be generated as
is a mathematical operator that represents the multidimensional problem’s entry-wise multiplication.
In each iteration cycle, all particles transmit Levy flights until they find GMPP. Figure 19 shows the flowchart of the CS algorithm to track GMPP.

Figure 19.
CS-based MPPT technique [87].
4.3.3. Flying Squirrel Search Optimization
This bio-inspired optimization approach to track GMPP was introduced in 2020 and mimics the highly effective hunting tactic used by southern flying squirrels [89]. This approach also mimics the squirrels’ manner of buoyant headways in the air. The posture of FS is referenced to as the feasible outcome vector and the comparable wellness is typical food source, respectively.
The posture is divided into three districts addressing sets based on wellness value:
- BS (hickory nut tree);
- CBS (acorn nut tree);
- US (ordinary tree).
Following assumptions are made while incorporating FSSO [89] in tracing GMPP:
The food supply point is similar to the power yield from PV;
DC converter duty ratio () in the MPPT approach is regarded as option variable, i.e., the posture;
To reduce the tracking time, the FSSO approach is custom-fitted by eliminating the occurrence of hunters.
The following steps are taken into account while implementing the FSSO technique.
Starting: Initially, FSs “N” numbers are placed at various locations. In the solution area, the duty ratio of the DC converter can be estimated for “i” iteration count by these points as follows:
Wellness evaluation: The DC converter employed is gradually running with each duty ratio in this progression (i.e., with each FS posture). Each food source feature shows instantaneous power yield PV () for each . This sequence is repeated for all , whereas MPPT goal wellness function can be determined as
- Declaration and categorization: The duty cycle at which the system yields maximum power is considered as hickory tree, while acorn trees are considered as the most excellent FS positions;
- Posture update: After the examination of occasional observing situation, the duty cycle is updated, and wellness is assessed from that point.
Important conditions followed in FSSA are as follows:
Occasional observing conditions: These conditions help FSSA to avoid being stuck in LMPP. The cyclic constant () and its base value () for a single-dimensional space with as the count of the present and maximum number of cycles allowed are
For investigating the superior search area, Levy distribution is employed. As a result, the OTFS duty cycle is relocated.
- Groove contemporized: Squirrels of hickory tree maintain their position. The squirrels on acorn tree, on the other hand, find a way to access the hickory tree. The arbitrarily chosen squirrel (ATFS) from normal trees chooses the hickory tree, while the leftover (NTFS-ATFS) is pressed to the acorn tree. The duty cycle is changed:
- Convergence Resolution: If the utmost number of iterations has been reached, the algorithm is terminated and gives the duty cycle at the point where the converter follows GMPP.
- Re-initialization: In rapidly changing environmental conditions, the duty ratio (FSs posture) is reinitialized to hunt new GMPP in accordance with Equation (41).
The complete steps of FSSO algorithm in tracking GMPP are depicted in Figure 20.

Figure 20.
FSSO-based MPPT technique [89].

Table 5.
Taxonomy on recent reported work on bio-inspired techniques to track GMPP.
Table 5.
Taxonomy on recent reported work on bio-inspired techniques to track GMPP.
| Authors [Reference No.] | Optimization Techniques | Best Optimization Techniques | PV Module Pm (W) | PV System Size | GMPP (W) | Improved GMPP (%) | Irradiance (W/m2) | Shading Patterns | Tracking Time (s) |
|---|---|---|---|---|---|---|---|---|---|
| Saad W et al. [90] | Proposed FA, P&O | Proposed | 200 | 1PV module | 201.7 37.7 | 2.40, 8.02 | 1000 and 200 | Non uniform | NA |
| Farzaneh J et al. [91] | MFA, P&O PSO, FA | MFA | 200.143 | 4 PV module in series | 397.52 | 9.41 | 1000–400 | Non uniform | 2.22 |
| Nusaif AI et al. [92] | MFA, P&O PSO, FA | MFA | 265.737 | 3 × 3 | 1264, 1206, 1582, 834 | 1.77, 31.08, 17.70, 27.91 | 1000–100 | Non uniform | 0.085–0.124 |
| Abo-Khalil AG et al. [93] | OFA, FA P&O | OFA | NA | NA | 48, 36.5, 29 | 0.418, 2.24, 34.88 | NA | Non uniform | 0.2–0.33 |
| Shi J-Y [94] | INC-FA, P&O INC, FA | INC-FA | 60 | 4 × 1 | 81.4 | 76.19 | 1000–100 | Non uniform | 0.98 |
| Omar FA et al. [95] | Proposed FA P&O | Proposed FA | NA | 3 PV module in series | 100,150,200, 300,400,500 | 25.00, 2.04, 108.33, 100, 110.52, 170.27 | NA | Non uniform | 1.3 |
| Chitra A et al. [96] | INC, FA, MFA | MFA | 200.143 | 2 PV module in series | 330, 255 | 6.24, 3.23 | 1000–600 | Non uniform | 0.0018–0.0064 |
| Mosaad MI et al. [97] | CS, NN, INC | CS | 59.9 | 1PV module | 60.47, 48.24 | 2.68, 3.36 | 1000–800 | uniform | NA |
| Shi J-Y et al. [98] | ICS, CS PSO, P&O | ICS | 60 | 4 PV module in series | 87.547 | 74.97 | 1000–200 | Non uniform | 0.88 |
| Hidayat T et al. [99] | CSA, P&O | CSA | 72 | 2 PV module in series | 97, 107.92, 107.63, 114.94, 124.56, 74.53, 72.58 | 45.86, 70.75, 63.99, 77.89, 81.52, 5.40, 0.276 | 944–495 | Non uniform | NA |
| Bilgin N et al. [100] | FFO, PSO, CSO, BOA | FFO | NA | 3 PV module in series | 531.46, 377.63 | 5.73, 4.26 | 1000–278 | Non uniform | NA |
| Ibrahim A-W et al. [101] | CSA, MPSO, MP&O, ANN | CSA | 250 | 4 PV module in series | 699.6, 928.5, 534.7, 694.7 | 67.93, 29.40, 13.25, 4.215 | 1000–400 | Non uniform | 0.5–0.7 |
| Bentata K et al. [102] | DCSA, CSA | DCSA | 249 | 2 × 2, 4 PV module in series, 3 × 2, 6 PV module in series | 989.29, 482.06, 797.3, 656.45 | 0.00, 13.31, 6.40, 16.09 | 1000–200 | Non uniform | 0.046- 0.085 |
| Singh N et al. [103] | FSSO, P&O, PSO, GWO | FSSO | 40 | 4 PV module in series, 2 × 2 | 61.66, 48.65, 79.75, 35.37 | 107.53, 85.68, 61.73, 3.23 | 900–100 | Non uniform | 0.3–1.8 |
| Fares D et al. [104] | ISSA, SSA, PSO, GA | ISSA | 135 | 3 PV module in series | 227.83, 142.82, 98.79 | 0.065, 0.098, 0.050 | 900–100 | Non uniform | 0.2 |
| Al-Shammaa A A et al. [105] | CS, PSO | CS | NA | 4 PV module in series | 293.57, 415.38, 578.96 | 0.00, 0.67, 0.52 | 1000–200 | Non uniform | 1.32, 1.29, 1.28 |
| Watanabe R B et al. [106] | FF, P&O | FF | 213.15 | 3 PV module in series | 638.7, 553.1, 316.9 | 0.251, 31.87, 58.05 | 1000–300 | Non uniform | 0.18, 0.22, 0.21 |

Table 6.
Pros and cons of recent work based on bio-inspired techniques.
Table 6.
Pros and cons of recent work based on bio-inspired techniques.
| Authors [Reference No.] | Pros | Cons |
|---|---|---|
| Saad W et al. [90] |
|
|
| Farzaneh J et al. [91] |
|
|
| Nusaif AI et al. [92] |
|
|
| Abo-Khalil AG et al. [93] |
|
|
| Shi JY [94] |
|
|
| Omar FA et al. [95] |
|
|
| Chitra A et al. [96] |
|
|
| Mosaad MI et al. [97] |
|
|
| Shi J-Y et al. [98] |
|
|
| Hidayat T et al. [99] |
|
|
| Bilgin N et al. [100] |
|
|
| Ibrahim A-W et al. [101] |
|
|
| Bentata K et al. [102] |
|
|
| Singh N et al. [103] |
|
|
| Fares D et al. [104] |
|
|
| Al-Shammaa A A et al. [105] |
|
|
| Watanabe R B et al. [106] |
|
|
4.4. Other AI-Based MPPT
This section of the paper explains other artificial intelligence methods applied in the field of tracking maximum power from the PV array along with a report of the various latest research performed concerning it in Table 7 and Table 8 respectively.
4.4.1. Fuzzy Logic Control
FLC converts its analog input to digital values. This technique examines the output power of PV array for every sample. If the change fraction is greater than zero, voltage is enhanced by FLC by adjusting the duty cycle and vice versa. As a result, the maximum power ratio is zero. FLC inputs error and its change with samples in time can be computed as
Figure 21 shows a block diagram of FLC control. The input variables are changed to linguistic variables by using different distinct membership functions. Thereafter, they are manipulated on the basis of the “if-then” rule by applying the required conduct of the scheme. Finally, they are converted to their numerical equivalent [107]. This approach shows fewer oscillations, fast response [108], and high tracking efficiency in contrast to conventional MPPT approaches. However, it suffers from high computational complexity.

Figure 21.
Block representation of FLC-based MPPT.
4.4.2. Artificial Neural Network
An ANN is a set of static learning models. For anticipating a precise output for each input, this approach simulates a biological neural system. Figure 22 shows the three-layered structure of ANN in which the neuron quantity in each layer varies depending on the situation.
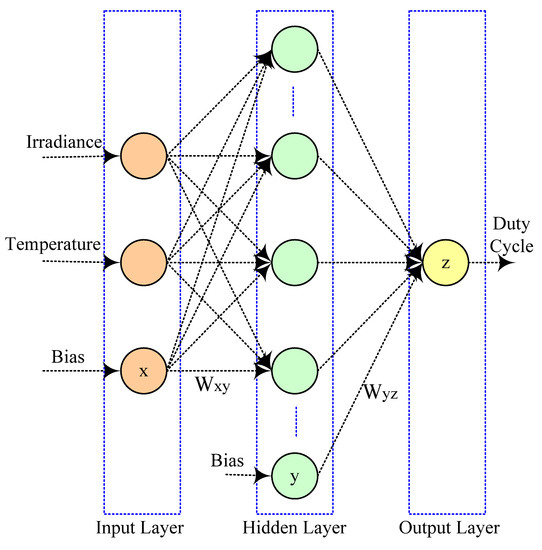
Figure 22.
Three-layer structure of ANN [109].
These networks are used as an MPP system to predict the best possible values of power or voltage that can be produced at a given time. These values act as base values in deciding the converter’s duty cycle. The PV module parameters and atmospheric parameters are included in the input variables and then processed by hidden layers in the network. The procreation algorithm is retroactive and grades in a mishap. Thereafter, utilizing neurons of center layer, it feeds back the output through the input neurons. The following Equation is used to calculate the presence of hidden neurons:
A complete experimental setup assists in data collection. The dataset is then obtained by feeding atmospheric conditions and array parameters into the ANN to find output Vm and Pm. This set is then transformed into an instructional one, which moves into the premeditated ANN, where it is taught how to perform. Moreover, the functions of input data serve as instruction data for the ANN model that was created. Then, the model learns how to execute on its own. The assessment datasets examine the performance of the constructed ANN after the instruction phase, and the errors are sent back to the ANN until all of the neurons’ weights are changed correctly. MPPT using ANN is more accurate and shows less oscillation around MPP [109]. These algorithms suffer from the drawback of high computational complexity.
4.4.3. Evolutionary Computational Techniques
Evolutionary computation is an area of artificial intelligence and soft computing that studies a family of algorithms for global optimization inspired by biological evolution. GA and DE are ones amongst them used to track MPP.
GA is a computer model that is inspired by evolution and consists of chromosomes. These chromosomes include information on a potential solution to a problem. Each chromosome has its own set of characteristics. This algorithm is used in wide applications. In contrast to tracking MPP, it is able to boost the PV voltage, which represents the chromosomes and their fitness value that corresponds to PV power. The main idea is to make genetic changes to a population of people and discover the ideal ones corresponding to the fitness function. Figure 23 shows the flowchart of GA.

Figure 23.
Flowchart of GA [110].
DE is another evolutionary computational algorithm applied to problems based on global optimization. It is applicable to track GMPP in PSCs due to its simpler execution and wide search freedom. The DC converter duty cycle is used as a target vector by this approach. Initially, the target vector with two dimensions is initialized as for each iteration and generation as the population. It chooses three random particles after one generation in order to reduce the execution time. Following that, the selected duty cycles are used to calculate the PV array’s associated powers . is picked as the maximum power in the set of , and is chosen as the corresponding . The weight difference between any two target vectors is then used by a mutation factor (M) and forms the mutated particle by adding this difference to the remaining target vector. The mutated particle is also called the donor vector . The mutation’s way should be towards . Following mutation, donor and target vectors are combined by a crossover procedure to create trial vector and estimate the PV array’s power.

Table 7.
Taxonomy on recent reported work on other artificial intelligence techniques to track GMPP.
Table 7.
Taxonomy on recent reported work on other artificial intelligence techniques to track GMPP.
| Authors [Reference No.] | Optimization Techniques | Best Optimization Techniques | PV Module Pm (W) | PV System Size | GMPP (W) | Improved GMPP (%) | Irradiance (W/m2) | Shading Patterns | Tracking Time (s) |
|---|---|---|---|---|---|---|---|---|---|
| Verma P et al. [111] | AFLC, FLC P&O | AFLC | 360 | 3 PV module in series | 521.5, 250.6, 198.1 | 7.30, 0.642, 4.26 | 900–100 | Non uniform | 0.1–0.19 |
| Rahman MM et al. [112] | PSO-ANN PSO | PSO-ANN | 60.53 | 4 PV module in series | 135.9, 202.1 | 0.00, −0.04 | 900–400 | Non uniform | 0.22, 0.21 |
| Farzaneh J [113] | Proposed P&O, PSO | Proposed | 60 | 3 PV module in series | 87.12, 116.74 | 46.00, 94.17 | 1000–300 | Non uniform | 0.15, 0.1 |
| Manikandan PV [114] | Proposed P&O | Proposed | 320 | 1 PV module | 36.88, 37.2, 37.66 | 53.73, 50.12, 51.36 | 1200–400 | Non uniform | NA |
| Al-Majidi SDet al. [115] | ANFIS FLC, P&O | ANFIS | 185 | 5 PV module in series | 924 | 0.2168 | 1000 | Uniform | 0.07 |
| Aymen J et al. [116] | Neuro fuzzy Fuzzy | Neuro fuzzy | 60 | 1PV module | 50.262, 45.736, 40.856, 35.633, 30.156 | 0.001, −0.004, 0.0171, 0.0533, 0.0763 | 1000–600 | Non uniform | NA |
| Farajdadian S [117] | AF-FA AF-PSO SF, PSO, P&O | AF-FA | 220.7 | NA | 220.5, 175.1, 124.3 | 1.37, 20.26, 72.87 | 1000–600 | Non uniform | NA |
| Eltamalya AM et al. [118] | GWO-FLC PSO | GWO-FLC | 185.22 | NA | 54.6, 92.8 | 40.00, 20.51 | 1000–200 | Non uniform | NA |
| Chen Y-T et al. [119] | Proposed fixed-step INC FLC-HC ASVSS | Proposed | 60 | NA | 157.3,46.83 | 5.92, 2.51 | 1000 and 300 | Non uniform | 0.42, 0.52 |
| Raj A et al. [120] | ANN-INC INC, P&O | ANN-INC | NA | NA | 450 | 6.13 | NA | Non uniform | NA |
| Abdellatif WSE et al. [121] | FB, P&O, INC | FB | 305.226 | NA | 100.38, 80.17, 59.87 | 3.14, 3.13, 3.11 | 1000–600 | Non uniform | NA |
| Mohammed SS et al. [122] | GA fuzzy Fuzzy ANFICS | GA fuzzy | 60 | 1 PV module | 44.17, 36.11, 41.68, 41.70, 24.07 | 0.546, 5.64, 0.506, 0.870, 11.22 | 791–481.1 | Non uniform | NA |
| Tandel BG et al. [123] | GA, P&O | GA | 200.143 | 16 PV module in series | 1319.12 | 81.16 | 1000–250 | Non uniform | NA |
| Karthika S et al. [124] | GA-tuned PI PI | GA-tuned PI | 200 | 7 × 7 | 7020 | 56.69 | 1000 and 200 | Non uniform | 0.001 |
| Dehghani M et al. [125] | PSO-GA PSO, GA INC, P&O | PSO-GA | 1S | NA | 98.85, 78.69, 58.64 | 9.67, 9.30, 9.23 | 1000–600 | Non uniform | < 0.3 |
| Bendary FM et al. [126] | ANFIS-GA ANFIS, NN, FLC | ANFIS-GA | 40.9081 | NA | 40.90, 27.78, 19.28 | 15.24, 0.908, 1.10 | 1000–500 | Non uniform | < 0.3 |
| Firmanza AP et al. [127] | Proposed DE PSO | Proposed DE | 100 | 2 PV module in series | 170.5, 87.9, 152, 130.9 | 1.66, −0.34, 0.462, 0.383 | 1000–400 | Non uniform | 0.233- 0.371 |
| Neethu M. et al. [128] | DE PSO | DE | 215 | 4 PV module in series | 663.8 | 81.41 | 900–600 | Non uniform | 366 |
| Kamaruddina NI et al. [129] | DE, P&O | DE | 125 | 3 × 3 | 489.3, 497.2 | 39.87, 56.40 | 1000–250 | Non uniform | NA |
| Joisher M et al. [130] | Proposed, PSO, DE | Proposed | 95 | 2 PV module in series | 11, 20.33, 13.88 | 120.0, 18.40, 16.5 | NA | Non uniform | 1.0 |
| Algarín C R et al. [131] | FLC P&O | FLC | 65 | 1 PV module | 11.7, 24.4, 37.7, 51.3, 64.9 | 0.00 | 1000–200 | Non uniform | NA |
| Cheng P-C et AL. [132] | Asymmetrical FLC, Symmetrical FLC, P&O | Asymmetrical FLC | 220 | NA | 44.12, 222.18 | 6.134, 04.53 | 1000 and 200 | Non uniform | 0.7, 5.6 |
| Liu C-L et al. [133] | Asymmetrical FLC, Symmetrical FLC, P&O | Asymmetrical FLC | 220 | NA | 222.69 | 7.63 | 1000 | Uniform | 0.91 |
| Kececioglu O F et al. [134] | Proposed, AIC | Proposed | 250 | 1 PV module | 249.4, 244.2 | 0.605, 0.825, | 1000–600 | Non uniform | 0.008 |
| Hayder W et al. [135] | NN-P&O IPSO | NN-P&O | 120 | 1 PV Module | 90.2943, 55.2495, 73.076, 98.6604 | 0.00 | 1100–600 | Uniform | 0.2003, 0.0003, 0.7003, 0.0003 |
| Hua C-C et al. [136] | Proposed, P&O+PSO, GA | Proposed | 21.31 | 3 PV module in series | 42.90, 37.38, 32.56, 26.73, 22.06 | 2.21, 0.402, 0.618, 0.074, 5.499 | 1000–300 | Non uniform | 12, 15, 16 |
| Zhang P et al. [137] | Improved DE, DE, PSO | Improved DE | NA | 4X3 | 644.57, 857.56 | 0.041, 0.282 | 800–350 | Non uniform | 0.019, 0.02 |
| Bakkar M et al. [138] | DSM-based FLC, FLC | DSM-based FLC | 80 | 1 PV module | 80 | 122.2 | 700 | Non uniform | NA |
| Batainesh K et al. [139] | Hybrid, FLC+P&O, FLC | Hybrid FLC+P&O | 270 | 1 PV module | 127.9, 57.9, 126.2, 46.1 | 4.40, 3.02, 18.16, 21.31 | 1000–100 | Non uniform | NA |
| Guerra M I S et al. [140] | ANIFS, P&O, ANN, Fuzzy | ANN | 245 | NA | 956.6, 1674, 2190, 1631 | 0.525, 0.600, 0.274, 0.803 | 548–303 | Non uniform | NA |

Table 8.
Pros and cons of recent work based on other artificial intelligence techniques.
Table 8.
Pros and cons of recent work based on other artificial intelligence techniques.
| Authors [Reference No.] | Pros | Cons |
|---|---|---|
| Verma P et al. [111] |
|
|
| Rahman MM et al. [112] |
|
|
| Farzaneh J [113] |
|
|
| Manikandan PV [114] |
|
|
| Al-Majidi SD et al. [115] |
|
|
| Aymen J et al. [116] |
|
|
| Farajdadian S [117] |
|
|
| Eltamalya AM et al. [118] |
|
|
| Chen Y-T et al. [119] |
|
|
| Raj A et al. [120] |
|
|
| Abdellatif WSE et al. [121] |
|
|
| Mohammed SS et al. [122] |
|
|
| Tandel BG et al. [123] |
|
|
| Karthika S et al. [124] |
|
|
| Dehghani M et al. [125] |
|
|
| Bendary FM et al. [126] |
|
|
| Firmanza AP et al. [127] |
|
|
| Neethu M. et al. [128] |
|
|
| Kamaruddina NI et al. [129] |
|
|
| Joisher M et al. [130] |
|
|
| Algarín C R et al. [131] |
|
|
| Cheng P-C et al. [132] |
|
|
| Liu C-L et al. [133] |
|
|
| Kececioglu O F et al. [134] |
|
|
| Hayder W et al. [135] |
|
|
| Hua C-C et al. [136] |
|
|
| Zhang P et al. [137] |
|
|
| Bakkar M et al. [138] |
|
|
| Batainesh K et al. [139] |
|
|
| Guerra M I S et al. [140] |
|
|
After having the deep analysis of all these MPPT techniques, a concluded comparative study has been depicted in Table 9 for better understanding as

Table 9.
Comparative analysis of various MPPT.
5. Research Gap and Findings
There are total 16 techniques reported in this paper. In 23 papers conventional MPPT techniques, 42 papers swarm intelligence MPPT techniques, 21 papers bio-inspired, and in 35 papers other AI-based techniques are discussed. Therefore, a total of 121 papers were mainly studied, which are focused on these MPPT techniques. The remaining 23 out of 144 papers were used in other important sections. The classification of papers focusing on different techniques can be seen in Figure 24.

Figure 24.
Papers focused on different MPPT techniques.
The authors are mainly classified concerning conventional MPPT techniques, metaheuristic AI techniques, and other AI-based techniques. Further, conventional MPPT techniques are classified as perturb and observe, incremental conductance, fractional open-circuit voltage, and fractional short-circuit current; particle swarm optimization, artificial bee colony, grey wolf optimization, and salp swarm algorithm fall under swarm intelligence MPPT techniques; and firefly MPPT algorithm, cuckoo search, and flying squirrel search optimization techniques are classified as bio-inspired techniques [141,142,143,144]. While swarm intelligence and bio-inspired techniques are metaheuristic AI techniques, other AI-based MPPT techniques are fuzzy logic control, artificial neural network, and evolutionary computational techniques (genetic algorithm and differential evolution).
After conducting a thorough analysis of metaheuristic MPPT approaches based on conventional and AI techniques in this paper, one can easily find the following gaps in this area:
- Despite the fact that conventional techniques are simpler and work better in unshaded spaces, they have the downside of slow response. In their findings, oscillations around GMPP are observed;
- Even though these methods are frequently modified, power loss still occurs while monitoring open-circuit voltage or short-circuit current. Additionally, these methods need a large number of sensors to function, but those numbers can be decreased;
- In PSCs, AI approaches are effective, but they have the disadvantage of having high computational complexity;
- These methods require a great deal of time to track GMPP because of the large number of iterations. Despite the fact that many of these are only tested on virtual platforms, real-world validation is still crucial;
- Most of the reported work ignores the effect of load variation, which is crucial for building any PV system.
6. Challenges and Future Work
This paper comprehensively elaborates many recently reported works to track GMPP in PSCs in detail along with their pros and cons. Presently, over eighty MPPT optimization techniques have been published, and more than four new techniques are published each year. This article covers the recent findings in each MPPT technique in a tabular form. Because there are so many optimization strategies in the literature, picking one becomes quite challenging. Avoiding local MPP and local hotspots of PV array is critical for any optimization strategy. Moreover, when these algorithms are built, there is a requirement to manage energy. Research on efficient MPPT techniques can be rationalized in the future by considering many other critical factors such as local hotspots, array reconfigurations, and cell materials, which contribute to producing maximum power during PSCs. With the aid of smartphones, an MPPT application can also be set to work at any time via the Internet.
7. Conclusions
Solar PV systems are regarded as the most capable energy source in renewable power-generation systems due to the copious availability of sunlight. However, unpredictable weather makes their working efficiency low. Thus, MPPT techniques are used to yield maximum power from these systems in any weather conditions. Much research has been done till now in this field, but selecting an appropriate technique for specific circumstances has always been difficult. For the mentioned reason, this study reassesses the art of various MPPT optimization strategies developed by various researchers so far in a different manner. Conventional and AI-based MPPT techniques are elaborated separately with simplified flowcharts in respective sections with the aim to understand their basic principles in detail for new learners. Following the appropriate evaluation of each study, a tabular summary was created on important attributes of PV systems under PSCs, such as array size, % improvement in GMPP, level of irradiance, and tracking time, forming novel datasheets. In this paper, the reported taxonomy of MPPT techniques can help new learners, researchers, amd professional engineers to interpret the performance of each MPPT approach under different climatic scenarios. After careful analysis, it is easy to conclude that traditional techniques are less complex and work well in unshaded environmental conditions. However, they have the disadvantage of slow response. AI techniques perform well in PSCs with negligible oscillations in a steady state, with high accuracy and high tracking efficiency, but they suffer from high computational complexity. With the tabulated pros and cons of each reviewed article, new learners can easily find the research gaps that still exist in this field. With the help of the comparison table based on important parameters, while incorporating any MPPT in PV system, one can select most appropriate MPPT approach in a specific application. Furthermore, this analysis reveals that AI-based MPP controllers are the best option to deal with PSCs. As a result, a large research area has opened up for new researchers. To summarize, this review paper will be a useful resource for researchers or industrialists to utilize in choosing the most appropriate MPPT method for a certain objective.
Author Contributions
Conceptualization, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Data curation, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Formal analysis, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Funding acquisition, H.M., M.A.A. and F.P.G.M.; Investigation, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Methodology, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Project administration, H.M., M.A.A. and F.P.G.M.; Resources, H.M., M.A.A. and F.P.G.M.; Software, H.M., M.A.A. and F.P.G.M.; Supervision, H.M., M.A.A., R.K.P.; S.C. and F.P.G.M.; Validation, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Visualization, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Writing – original draft, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M.; Writing – review & editing, A.K.S., R.K.P., S.C., A.F.M., M.A.A., H.M. and F.P.G.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work reported here in has been financially supported by the Intelligent Prognostic Private Limited Delhi, India under Research Grant XX-02/2022.
Data Availability Statement
Data will be provided on request.
Acknowledgments
This study was supported by the Universiti Teknologi Malaysia—“Development of Adaptive and Predictive ACMV/HVAC Health Monitoring System Using IoT, Advanced FDD, and Weather Forecast Algorithms” (Q.J130000.3823.31J06). The authors would like to acknowledge the support from Ingenium Research Group, Universidad Castilla-La Mancha, 13071 Ciudad Real, Spain, support from Integral University, Lucknow, support from Universiti Teknologi Malaysia (UTM), and support from Intelligent Prognostic Private Limited Delhi, India researcher’s supporting Project.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| MPPT | Maximum power point tracking | PV | Photovoltaic |
| PSCs | Partial shading conditions | RES | Renewable energy sources |
| P–V | Power–voltage | GMPP | Global maximum power point |
| P&O | Perturb and observe | INC | Incremental conductance |
| HC | Hill climbing | BI | Bio-inspired |
| SI | Swarm intelligence | AI | Artificial intelligence |
| ANN | Artificial neural networks | FLC | Fuzzy logic control |
| ECI | Evolutionary computational intelligence | I–V | Current–voltage |
| MPP | Maximum power point | LMPP | Local maximum power points |
| DC | Direct current | CS | Cuckoo search |
| FOCV | Fractional open-circuit voltage | FSCC | Fractional short-circuit current |
| ACO | Ant colony optimization | ACO-P&O | Ant colony optimization–perturb and observe |
| SP-INC | Self-predictive incremental conductance | SPC | Semi pilot cell |
| PC | Pilot cell | CSAM | Current Sensorless Method with Auto-modulation |
| VSS | Variable step size | PSO | Particle swarm optimization |
| ABC | Artificial Bee Colony | GWO | Grey wolf optimization |
| SSA | Salp swarm algorithm | APSO | Accelerated PSO |
| LIPSO | Lagrange interpolation PSO | TS | Takagi–Sugeno |
| VCPSO | Variable coefficients PSO | CFPSO | Constriction factor-based PSO |
| OD-PSO | Overall distribution PSO | P&O-PSO | Perturb and observe-PSO |
| EGWO | Enhanced GWO | GWO-GSO | GWO–golden-section optimization |
| GWO-P&O | GWO–Perturb and observe | GOA | Grasshopper optimization algorithm |
| BOA | Bat algorithm | SSPSO | Series salp PSO |
| FA | Firefly elgorithm | ISSA | Improved salp swarm algorithm |
| DE | Differential Evolution | WOA | Whale optimization algorithm |
| SSO | Salp swarm optimization | ISSA | Improved salp swarm algorithm |
| SSPO | Hybrid salp swarm–perturb and observe | ABC-P&O | Artificial bee colony–perturb and observe |
| GMPPT | Global maximum power point tracking | MABC | Modified artificial bee colony |
| AIC | Angle of incremental conductance | IPSO | Improved particle swarm optimization |
| OGWO | Opposition-based learning GWO | DFO | Dragonfly optimization |
| TSA-PSO | Tunicate swarm algorithm with PSO | IABC | Improved artificial bee colony |
| SPF-P&O | Surface-sased polynomial fitting P&O | HGWO | Hybrid grey wolf optimization |
| DSM | Dynamic safty margin | ICPSO | Incremental conductance-based PSO |
| FSSO | Flying squirrel search optimization | BS | Best solution |
Nomenclature
| PV output current | |
| Photocurrent | |
| Shunt current | |
| Diode current | |
| Diode reverses saturation current | |
| Electron charge | |
| Number of cells in series | |
| Boltzmann constant | |
| Temperature | |
| PV output voltage | |
| Series resistance | |
| Shunt resistance | |
| Maximum power | |
| Open-circuit voltage | |
| Short-circuit current | |
| Change in power | |
| Change in voltage | |
| Change in current | |
| Voltage at maximum power point | |
| Proportionality constant | |
| Current at maximum power point | |
| Constant current factor | |
| Maximum power | |
| Gaussian kernel solution | |
| Sub-Gaussian function | |
| Mean value | |
| Standard deviation | |
| Weight factor | |
| Best optimal operating solution | |
| Convergence rate | |
| Individual best position | |
| Swarm optimum position | |
| particle position | |
| particle velocity | |
| Inertia burden | |
| Social and cognitive acceleration coefficients | |
| Arbitrary variables that are uniformly distributed between zero and one in terms of their assessments | |
| Target function | |
| -dimension maximum and minimum values. | |
| Arbitrarily selected food source | |
| Arbitrary number between | |
| Prey vector | |
| Position vector of grey wolf | |
| Coefficient vectors | |
| Random variables | |
| -rationalized candidate solution | |
| Position of food source | |
| Decemberision variables maximum and minimum value | |
| Initial call | |
| fireflies spatial coordinate components | |
| Step length | |
| Variance | |
| Maximum and minimum duty cycle | |
| Squirrels’ posture address at hickory and acorn trees | |
| Hovering constant (~1.90) | |
| Hovering distance | |
| PV output power | |
| Maximum voltage | |
| Hidden neuron numbers | |
| Injected input neurons numbers | |
| Output neurons numbers | |
| Instruction samples numbers |
References
- Kermadi, M.; Salam, Z.; Eltamaly, A.M.; Ahmed, J.; Mekhilef, S.; Larbes, C.; Berkouk, E.M. Recent Developments of MPPT Techniques for PV Systems under Partial Shading Conditions: A Critical Review and Performance Evaluation. IET Renew. Power Gener. 2020, 17, 3401–3417. [Google Scholar] [CrossRef]
- Singh, N.; Goswami, A. Study of P-V and I-V Characteristics of Solar Cell in MATLAB/Simulink. Int. J. Pure Appl. Math. 2018, 118, 24. [Google Scholar]
- Selvan, S.; Nair, P.; Umayal, A. Review on Photo Voltaic MPPT Algorithms. Int. J. Electr. Comput. Eng. 2016, 6, 567–582. [Google Scholar]
- Xu, L.; Cheng, R.; Yang, J. A New MPPT Technique for Fast and Efficient Tracking under Fast Varying Solar Irradiation and Load Resistance. Int. J. Photoenergy 2020, 2020, 6535372. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chauhan, Y.K.; Pachauri, R.K. A comparative investigation of maximum power point tracking methods for solar PV system. Sol. Energy 2016, 136, 236–253. [Google Scholar] [CrossRef]
- Baba, A.O.; Liu, G.; Chen, X. Classification and Evaluation Review of Maximum Power Point Tracking Methods. Sustain. Futures 2020, 2, 100020. [Google Scholar] [CrossRef]
- Belhachat, F.; Larbes, C. A review of global maximum power point tracking techniques of photovoltaic system under partial shading conditions. Renew. Sustain. Energy Rev. 2018, 92, 513–553. [Google Scholar] [CrossRef]
- Podder, A.K.; Roy, N.K.; Pota, H.R. MPPT methods for solar PV systems: A critical review based on tracking nature. IET Renew. Power Gener. 2019, 13, 1615–1632. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Agrawal, R.; Sawle, Y.; Kumar, A. A Different Approach for Maximum Power Point Tracking (MPPT) Using Impedance Matching through Non-Isolated DC-DC Converters in Solar Photovoltaic Systems. Electronics 2022, 11, 1053. [Google Scholar] [CrossRef]
- Szemes, P.T.; Melhem, M. Analyzing and modeling PV with “P&O” MPPT Algorithm by MATLAB/SIMULINK. In Proceedings of the 3rd International Symposium on Small-Scale Intelligent Manufacturing Systems (SIMS) 2020, Gjovik, Norway, 10–12 June 2020; pp. 1–6. [Google Scholar]
- Christopher, I.W.; Ramesh, R. Comparative Study of P&O and InC MPPT Algorithms. Am. J. Eng. Res. 2013, 2, 402–408. [Google Scholar]
- Jately, V.; Azzopardi, B.; Joshi, J.; Venkateswaran, B.V.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Ali, A.; Almutairi, K.; Padmanaban, S.K.; Tirth, V.; Algarni, S.; Irshad, K.; Islam, S.; Zahir, M.H.; Shafiullah, M.; Malik, M.Z. Investigation of mppt techniques under uniform and non-uniform solar irradiation condition-a retrospection. IEEE Access 2020, 8, 127368–127392. [Google Scholar] [CrossRef]
- Batarseh, M.G.; Za’ter, M.E. Hybrid maximum power point tracking techniques: A comparative survey, suggested classification and uninvestigated combinations. Sol. Energy 2018, 169, 535–555. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Vigneshkumar, V.; Palani, S. Development of a hybrid genetic algorithm/perturb and observe algorithm for maximum power point tracking in photovoltaic systems under non-uniform insolation. IET Renew. Power Gener. 2015, 9, 757–765. [Google Scholar] [CrossRef]
- Li, G.; Jin, Y.; Akram, M.W.; Chen, X.; Ji, J. Application of bio-inspired algorithms in maximum power point tracking for PV systems under partial shading conditions—A review. Renew. Sustain. Energy Rev. 2018, 81, 840–873. [Google Scholar] [CrossRef]
- Pathy, S.; Subramani, C.; Sridhar, R.; Thentral, T.M.T.; Padmanaban, S. Nature-Inspired MPPT Algorithms for Partially Shaded PV Systems: A Comparative Study. Energies 2019, 12, 1451. [Google Scholar] [CrossRef]
- Pilakkat, D.; Kanthalakshmi, S.; Navaneethan, S. A comprehensive review of swarm optimization algorithms for MPPT control of PV systems under partially shaded conditions. Electronics 2020, 24, 3–14. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A.; Abdelaziz, A.Y. A comparison of different global MPPT techniques based on meta-heuristic algorithms for photovoltaic system subjected to partial shading conditions. Renew. Sustain. Energy Rev. 2017, 74, 377–386. [Google Scholar] [CrossRef]
- Tamrakar, R.; Gupta, A. A Review: Extraction of solar cell modelling parameters. Int. J. Innov. Res. Electr. Electron. Instrum. Control Eng. 2015, 3, 55–60. [Google Scholar]
- Singh, P.; Vinay, T.R.; Balyan, A.; Gangadhara; Sandeep, P.M. P-V and I-V Characteristics of Solar Cell. Design Eng. 2021, 6, 520–528. [Google Scholar]
- Bayrak, F.; Ertürk, G.; Oztop, H.F. Effects of partial shading on energy and exergy efficiencies for photovoltaic panels. J. Clean. Prod. 2017, 164, 58–69. [Google Scholar] [CrossRef]
- Nkambule, M.; Hasan, A.; Ali, J.A. Proportional study of Perturb & Observe and Fuzzy Logic Control MPPT Algorithm for a PV system under different weather conditions. In Proceedings of the IEEE 10th GCC Conference and Exhibition, Kuwait City, Kuwait, 19–23 April 2019. [Google Scholar]
- Reddy, D.C.K.; Satyanarayana, S.; Ganesh, V. Design of Hybrid Solar Wind Energy System in a Microgrid with MPPT Techniques. Int. J. Electr. Comput. Eng. 2018, 8, 730–740. [Google Scholar]
- Hajighorbani, S.; Amran, M.; Radzi, M.; Kadir, M.Z.A.A.; Shafie, S. Dual Search Maximum Power Point (DSMPP) Algorithm Based on Mathematical Analysis under Shaded Conditions. Energies 2015, 8, 12116–12146. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Modified P&O Maximum Power Point Tracking Method with Reduced Steady-State Oscillation and Improved Tracking Efficiency. IEEE Trans. Sustain. Energy 2016, 7, 1506–1515. [Google Scholar]
- Sera, D.; Kerekes, T.; Teodorescu, R.; Blaabjerg, F. Improved MPPT Algorithms for Rapidly Changing Environmental Conditions. In Proceedings of the 2006 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 1614–1619. [Google Scholar]
- Bouksaim, M.; Mekhfioui, M.; Srifi, M.N. Design and Implementation of Modified INC, Conventional INC, and Fuzzy Logic Controllers Applied to a PV System under Variable Weather Conditions. Designs 2021, 5, 71. [Google Scholar] [CrossRef]
- Babu, C.S.; Kumari, J.S.; Kullayappa, T.R. Design and Analysis of Open Circuit Voltage Based Maximum Power Point Tracking for Photovoltaic System. Int. J. Adv. Sci. Technol. 2011, 2, 51–60. [Google Scholar]
- Kumari, J.S.; Ch, S.B.; Yugandhar, J. Design and Investigation of Short Circuit Current Based Maximum Power Point Tracking for Photovoltaic System. Int. J. Res. Rev. Electr. Comput. Eng. 2011, 1, 63–68. [Google Scholar]
- Numan, B.A.; Shakir, A.M.; Ahmed, B.M. Enhancement of P&O algorithm for MPPT for partially shading PV systems. In Proceedings of the Academicsera International Conference, Antalya, Turkey, 21–22 January 2021. [Google Scholar]
- Gil-Velasco, A.; Aguilar-Castillo, C. A modification of the perturb and observe method to improve the energy harvesting of PV systems under partial shading conditions. Energies 2021, 14, 2521. [Google Scholar] [CrossRef]
- Efendi, M.Z.; Suhariningsih Murdianto, F.D.; Inawati, E. Implementation of modified P&O method as power optimizer of solar panel under partial shading condition for battery charging system. AIP Conf. Proc. 2018, 1977, 020002. [Google Scholar]
- Shang, L.; Guo, H.; Zhu, W. An improved MPPT control strategy based on incremental conductance algorithm. Prot. Control. Mod. Power Syst. 2020, 5, 14. [Google Scholar] [CrossRef]
- Zand, S.J.; Hsia, K.H.; Eskandarian, N.; Mobayen, S. Improvement of Self-Predictive Incremental Conductance Algorithm with the Ability to Detect Dynamic Conditions. Energies 2021, 14, 1234. [Google Scholar] [CrossRef]
- Baimel, D.; Tapuchi, S.; Levron, Y.; Belikov, J. Improved fractional open circuit voltage MPPT methods for PV systems. Electronics 2019, 8, 321–340. [Google Scholar] [CrossRef]
- Hua, C.; Chen, W.; Fang, Y. A hybrid MPPT with adaptive step-size based on single sensor for photovoltaic systems. In Proceedings of the 2014 International Conference on Information Science, Electronics and Electrical Engineering, Sapporo, Japan, 26–28 April 2014; pp. 441–445. [Google Scholar]
- Nadeem, A.; Sher, H.A.; Murtaza, A.F. Online fractional open-circuit voltage maximum output power algorithm for photovoltaic modules. IET Renew. Power Gener. 2020, 14, 188–198. [Google Scholar] [CrossRef]
- Fapi, C.B.N.; Wira, P.; Kamta, M. Real-time experimental assessment of a new MPPT algorithm based on the direct detection of the short-circuit current for a PV system. In Proceedings of the 19th International Conference on Renewable Energies and Power Quality (ICREPQ’21), Almeria, Spain, 28–30 July 2021. [Google Scholar]
- Sarika, E.P.; Jacob, J.; Mohammed, S.; Paul, S. A novel hybrid maximum power point tracking technique with zero oscillation based on P&O algorithm. Int. J. Renew. Energy Res. 2020, 10, 1962–1973. [Google Scholar]
- Li, C.; Chen, Y.; Zhou, D.; Liu, J.; Zeng, J. A High-Performance Adaptive Incremental Conductance MPPT Algorithm for Photovoltaic Systems. Energies 2016, 9, 288. [Google Scholar] [CrossRef]
- Owusu-Nyarko, I.; Elgenedy, M.A.; Abdelsalam, I.; Ahmed, K.H. Modified Variable Step-Size Incremental Conductance MPPT Technique for Photovoltaic Systems. Electronics 2021, 10, 2331. [Google Scholar] [CrossRef]
- Sarwar, S.; Javed, M.Y.; Jaffery, M.H.; Arshad, J.; Ur Rehman, A.; Shafiq, M.; Choi, J.-G. A Novel Hybrid MPPT Technique to Maximize Power Harvesting from PV System under Partial and Complex Partial Shading. Appl. Sci. 2022, 12, 587. [Google Scholar] [CrossRef]
- Hafeez, M.A.; Naeem, A.; Akram, M.; Javed, M.Y.; Asghar, A.B.; Wang, Y. A Novel Hybrid MPPT Technique Based on Harris Hawk Optimization (HHO) and Perturb and Observer (P&O) under Partial and Complex Partial Shading Conditions. Energies 2022, 15, 5550. [Google Scholar]
- González-Castaño, C.; Restrepo, C.; Revelo-Fuelagán, J.; Lorente-Leyva, L.L.; Peluffo-Ordóñez, D.H. A Fast-Tracking Hybrid MPPT Based on Surface-Based Polynomial Fitting and P&O Methods for Solar PV under Partial Shaded Conditions. Mathematics 2021, 9, 2732. [Google Scholar]
- Verma, P.; Alam, A.; Sarwar, A.; Tariq, M.; Vahedi, H.; Gupta, D.; Ahmad, S.; Mohamed, A.S.N. Meta-Heuristic optimization techniques used for maximum power point tracking in solar PV system. Electronics 2021, 10, 2419. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.L.; Patra, J.C. A novel ant colony optimization-based maximum power point tracking for photovoltaic systems under partially shaded conditions. Energy Build. 2013, 58, 227–236. [Google Scholar] [CrossRef]
- Oliveira, F.M.; da Silva, S.A.O.; Durand, F.R.; Sampaio, L.P. Application of PSO method for maximum power point extraction in photovoltaic systems under partial shading conditions. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar]
- Benyoucef, A.S.; Chouder, A.; Kara, K.; Silvestre, S.; Sahed, O.A. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Rezaei, H.; Bozorg-Haddad, O.; Chu, X. Grey Wolf Optimization (GWO) Algorithm. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2017; pp. 81–91. [Google Scholar]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar] [CrossRef]
- Faris, H.; Mirjalili, S.; Aljarah, I.; Mafarja, M.; Heidari, A.A. Salp Swarm Algorithm: Theory, Literature Review, and Application in Extreme Learning Machines. In Nature-Inspired Optimizers. Studies in Computational Intelligence; Springer: Cham, Switzerland, 2019; Volume 811, pp. 185–199. [Google Scholar]
- Krishnan, G.S.; Kinattingal, S.; Simon, S.P.; Nayak, P.S.R. MPPT in PV systems using ant colony optimisation with dwindling population. IET Renew. Power Gener. 2020, 14, 1105–1112. [Google Scholar] [CrossRef]
- Sridhar, R.; Vishnuram, P.; Bindu, D.H.; Divya, A. Ant Colony Optimization based Maximum Power Point Tracking (MPPT) for Partially Shaded Standalone PV System. IJCTA 2016, 9, 8125–8133. [Google Scholar]
- Alshareef, M.; Lin, Z.; Ma, M.; Cao, W. Accelerated Particle Swarm Optimization for Photovoltaic Maximum Power Point Tracking under Partial Shading Conditions. Energies 2019, 12, 623. [Google Scholar] [CrossRef]
- Panda, K.P.; Anand, A.; Bana, P.R.; Panda, G. Novel PWM Control with Modified PSO-MPPT Algorithm for Reduced Switch MLI Based Standalone PV System. Int. J. Emerg. Electr. Power Syst. 2018, 19, 20180023. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.K.; Kinattingal, S.; Simon, S.P. MPPT in PV Systems Using PSO Appended with Centripetal Instinct Attribute. Electr. Power Compon. Syst. 2020, 48, 881–891. [Google Scholar] [CrossRef]
- Mao, M.; Zhang, L.; Duan, Q.; Oghorada, O.J.K.; Duan, P.; Hu, B. A Two-Stage Particle Swarm Optimization Algorithm for MPPT of Partially Shaded PV Arrays. Int. J. Green Energy 2017, 4, 694–702. [Google Scholar] [CrossRef]
- Koad, R.B.A.; Zobaa, A.F.; El-Shahat, A. A Novel MPPT Algorithm Based on Particle Swarm Optimization for Photovoltaic Systems. IEEE Trans. Sustain. Energy 2017, 8, 468–476. [Google Scholar] [CrossRef]
- Belghith, O.B.; Sbita1, L.; Bettaher, F. MPPT Design Using PSO Technique for Photovoltaic System Control Comparing to Fuzzy Logic and P&O Controllers. Energy Power Eng. 2016, 8, 349–366. [Google Scholar]
- Obukhov, S.; Ibrahim, A.; Zaki Diab, A.A.; Al-Sumaiti, A.S.; Aboelsaud, R. Optimal Performance of Dynamic Particle Swarm Optimization Based Maximum Power Trackers for Stand-Alone PV System Under Partial Shading Conditions. IEEE Access 2020, 8, 20770–20785. [Google Scholar] [CrossRef]
- Li, H.; Yang, D.; Su, W.; Lü, J.; Yu, X. An Overall Distribution Particle Swarm Optimization MPPT Algorithm for Photovoltaic System Under Partial Shading. IEEE Trans. Ind. Electron. 2019, 66, 265–275. [Google Scholar] [CrossRef]
- Suhardi, D.; Syafaah, L.; Irfan, M.; Yusuf, M.; Effendy, M.; Pakaya, I. Improvement of maximum power point tracking (MPPT) efficiency using grey wolf optimization (GWO) algorithm in photovoltaic (PV) system. IOP Conf. Ser. Mater. Sci. Eng. 2019, 674, 012038. [Google Scholar] [CrossRef]
- Kumar, C.S.; Rao, R.S. Enhanced Grey Wolf Optimizer Based MPPT Algorithm of PV System Under Partial Shaded Condition. Int. J. Renew. Energy Dev. 2017, 6, 203–212. [Google Scholar]
- Shi, J.Y.; Zhang, D.Y.; Ling, L.T.; Xue, F.; Li, Y.J.; Qin, Z.J.; Yang, T. Dual-Algorithm Maximum Power Point Tracking Control Method for Photovoltaic Systems based on Grey Wolf Optimization and Golden-Section Optimization. J. Power Electron. 2018, 18, 841–852. [Google Scholar]
- Ilyas, M.; Ghazal, H.K.E. Design of a MPPT System Based on Modified Grey Wolf Optimization Algorithm in Photovoltaic System under Partially Shaded Condition. Int. J. Comput. 2021, 40, 36–49. [Google Scholar]
- Kraiem, H.; Aymen, F.; Yahya, L.; Triviño, A.; Alharthi, M.; Ghoneim, S.S.M. A Comparison between Particle Swarm and GreyWolf Optimization Algorithms for Improving the Battery Autonomy in a Photovoltaic System. Appl. Sci. 2021, 11, 7732. [Google Scholar] [CrossRef]
- Jamaludin, M.N.I.; Tajuddin, M.F.N.; Ahmed, J.; Azmi, A.; Azmi, S.A.; Ghazali, N.H.; Babu, T.S.; Alhelou, H.H. An Effective Salp Swarm Based MPPT for Photovoltaic Systems Under Dynamic and Partial Shading Conditions. IEEE Access 2021, 9, 34570–34589. [Google Scholar] [CrossRef]
- Dagal, I.; Akın, B.; Akboy, E. A novel hybrid series salp particle Swarm optimization (SSPSO) for standalone battery charging applications. Ain Shams Eng. J. 2022, 13, 101747. [Google Scholar] [CrossRef]
- Krishnan, S.; Sathiyasekar, K. A Novel Salp Swarm Optimization MPP Tracking Algorithm for the Solar Photovoltaic Systems under Partial Shading Conditions. J. Circuits Syst. Comput. 2020, 29, 2050017. [Google Scholar] [CrossRef]
- Farzaneh, J.; Karsaz, A. Application of Improved Salp Swarm Algorithm Based on MPPT for PV Systems under Partial Shading Conditions. Int. J. Ind. Electron. Control Optim. 2020, 3, 415–429. [Google Scholar]
- Ali, M.H.M.; Mohamed, M.M.S.; Ahmed, N.M.; Zahran, M.B.A. Comparison between P&O and SSO techniques based MPPT algorithm for photovoltaic systems. Int. J. Electr. Comput. Eng. 2022, 12, 32–40. [Google Scholar]
- Balaji, V.; Fathima, A.P. Enhancing the Maximum Power Extraction in Partially Shaded PV Arrays Using Hybrid Salp Swarm Perturb and Observe Algorithm. Int. J. Renew. Energy Res. 2020, 10, 898–911. [Google Scholar]
- Restrepo, C.; Yanez-Monsalvez, N.; González-Castaño, C.; Kouro, S.; Rodriguez, J. A Fast Converging Hybrid MPPT Algorithm Based on ABC and P&O Techniques for a Partially Shaded PV System. Mathematics 2021, 9, 2228. [Google Scholar]
- Sawant, P.T.; Tejasvi, P.C.; Bhattar, L.; Bhattar, C.L. Enhancement of PV System Based on Artificial Bee Colony Algorithm under dynamic Conditions. In Proceedings of the IEEE International Conference on Recent Trends In Electronics Information Communication Technology 2016, Bangalore, India, 20–21 May 2016; pp. 1251–1255. [Google Scholar]
- Li, N.; Mingxuan, M.; Yihao, W.; Lichuang, C.; Lin, Z.; Qianjin, Z. Maximum Power Point Tracking Control Based on Modified ABC Algorithm for Shaded PV System. In Proceedings of the 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 2–4 July 2019; pp. 1–5. [Google Scholar]
- Wan, Y.; Mao, M.; Zhou, L.; Zhang, Q.; Xi, X.; Zheng, C. A Novel Nature-Inspired Maximum Power Point Tracking (MPPT) Controller Based on SSA-GWO Algorithm for Partially Shaded Photovoltaic Systems. Electronics 2019, 8, 680. [Google Scholar] [CrossRef]
- Hayder, W.; Ogliari, E.; Dolara, A.; Abid, A.; Hamed, M.B.; Sbita, L. Improved PSO: A Comparative Study in MPPT Algorithm for PV System Control under Partial Shading Conditions. Energies 2020, 13, 2035. [Google Scholar] [CrossRef]
- Almutairi, A.; Abo-Khalil, A.G.; Sayed, K.; Albagami, N. MPPT for a PV Grid-Connected System to Improve efficiency under Partial Shading Conditions. Sustainability 2020, 12, 10310. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, A.; Jately, V.; Averbukh, M.; Rajput, S.; Azzopardi, B. A Novel TSA-PSO Based Hybrid Algorithm for GMPP Tracking under Partial Shading Conditions. Energies 2022, 15, 3164. [Google Scholar] [CrossRef]
- Chao, K.-H.; Li, J.-Y. Global Maximum Power Point Tracking of Photovoltaic Module Arrays Based on Improved Artificial Bee Colony Algorithm. Electronics 2022, 11, 1572. [Google Scholar] [CrossRef]
- Alaraj, M.; Kumar, A.; Alsaidan, I.; Rizwan, M.; Jamil, M. An Advanced and Robust Approach to Maximize Solar Photovoltaic Power Production. Sustainability 2022, 14, 7398. [Google Scholar] [CrossRef]
- Windarko, N.A.; Nizar Habibi, M.; Sumantri, B.; Prasetyono, E.; Efendi, M.Z.; Taufik, A. New MPPT Algorithm for Photovoltaic Power Generation under Uniform and Partial Shading Conditions. Energies 2021, 14, 483. [Google Scholar] [CrossRef]
- Chawda, G.S.; Mahela, O.P.; Gupta, N.; Khosravy, M.; Senjyu, T. Incremental Conductance Based Particle Swarm Optimization Algorithm for Global Maximum Power Tracking of Solar-PV under Nonuniform Operating Conditions. Appl. Sci. 2020, 10, 4575. [Google Scholar] [CrossRef]
- Teshome, D.F.; Lee, C.H.; Lin, Y.W.; Lian, K.L. A Modified Firefly Algorithm for Photovoltaic Maximum Power Point Tracking Control Under Partial Shading. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 661–671. [Google Scholar] [CrossRef]
- Nugraha, D.A.; Lian, K.L.; Suwarno. A Novel MPPT Method Based on Cuckoo Search Algorithm and Golden Section Search Algorithm for Partially Shaded PV System. Can. J. Electr. Comput. Eng. 2019, 42, 173–182. [Google Scholar] [CrossRef]
- Assis, A.; Mathew, S. Cuckoo Search Algorithm Based Maximum Power Point Tracking For Solar PV Systems. Int. J. Adv. Electr. Power Syst. Inf. Technol. 2016, 2, 20–28. [Google Scholar]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm and Evolutionary Computation 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Saad, W.; Hegazy, E.; Shokair, M. Maximum power point tracking based on modified firefly scheme for PV system. SN Appl. Sci. 2022, 4, 94. [Google Scholar] [CrossRef]
- Farzaneh, J.; Keypour, R.; Khanesar, M.A. A New Maximum Power Point Tracking Based on Modified Firefly Algorithm for PV System Under Partial Shading Conditions. Technol. Econ. Smart Grids Sustain. Energy 2018, 3, 9. [Google Scholar] [CrossRef]
- Nusaif, A.I.; Mahmood, A.L. MPPT Algorithms (PSO, FA, and MFA) for PV System Under Partial Shading Condition, Case Study: BTS in Algazalia, Baghdad. Int. J. Smart Grid 2020, 10, 100–110. [Google Scholar]
- Abo-Khalil, A.G.; Alharbi, W.; Al-Qawasmi, A.R.; Alobaid, M.; Alarifi, I.M. Maximum Power Point Tracking of PV Systems under Partial Shading Conditions Based on Opposition-Based Learning Firefly Algorithm. Sustainability 2021, 13, 2656. [Google Scholar] [CrossRef]
- Shi, J.-Y.; Ling, L.-T.; Xue, F.; Qin, Z.-J.; Li, Y.-J.; Lai, Z.-X.; Yang, T. Combining incremental conductance and firefly algorithm for tracking the global MPP of PV arrays. J. Renew. Sustain. Energy 2017, 9, 023501. [Google Scholar] [CrossRef]
- Omar, F.A.; Kulaksiz, A.A. Experimental evaluation of a hybrid global maximum power tracking algorithm based on modified firefly and perturbation and observation algorithms. Neural Comput. Appl. 2021, 33, 17185–17208. [Google Scholar] [CrossRef]
- Chitra, A.; Yogitha, G.; Sivaramakrishnan, K.; Sultana, W.R.; Sanjeevikumar, P. Modified Firefly-Based Maximum Power Point Tracking Algorithm for PV Systems Under Partial Shading Conditions. In Artificial Intelligent Techniques for Electric and Hybrid Electric Vehicles; Scrivener Publishing LLC: Beverly, MA, USA, 2020; pp. 143–164. [Google Scholar]
- Mosaad, M.I.; Abed el-Raouf, M.O.; Al-Ahmar, M.A.; Banakher, F.A. Maximum Power Point Tracking of PV system Based Cuckoo Search Algorithm; review and comparison. Energy Procedia 2019, 162, 117–126. [Google Scholar] [CrossRef]
- Shi, Y.-J.; Xue, F.; Qin, Z.-J.; Zhang, W.; Ling, L.-T.; Yang, T. Improved Global Maximum Power Point Tracking for Photovoltaic System via Cuckoo Search under Partial Shaded Conditions. J. Power Electron. 2016, 16, 287–296. [Google Scholar] [CrossRef]
- Hidayat, T.; Efendi, M.Z.; Murdianto, F.D. Maximum Power Point Tracking Interleaved Boost Converter Using Cuckoo Search Algorithm on The Nano Grid System. J. Adv. Res. Electr. Eng. 2021, 5, 41–46. [Google Scholar] [CrossRef]
- Bilgin, N.; Yazici, I. Comparison of Maximum Power Point Tracking Methods Using Metaheuristic Optimization Algorithms for Photovoltaic Systems. Sak. Univ. J. Sci. 2021, 25, 1075–1085. [Google Scholar] [CrossRef]
- Ibrahim, A.-W.; Fang, Z.; Ameur, K.; Min, D.; Shafik, M.B.; Al-Muthanna, G. Comparative Study of Solar PV System Performance under Partial Shaded Condition Utilizing Different Control Approaches. Indian J. Sci. Technol. 2021, 14, 1864–1893. [Google Scholar] [CrossRef]
- Bentata, K.; Mohammedi, A.; Benslimane, T. Development of rapid and reliable cuckoo search algorithm for global maximum power point tracking of solar PV systems in partial shading condition. Arch. Control Sci. 2021, 31, 495–526. [Google Scholar]
- Singh, N.; Gupta, K.K.; Jain, S.K.; Dewangan, N.K.; Bhatnagar, P. A Flying Squirrel Search Optimization for MPPT Under Partial Shaded Photovoltaic System. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4963–4978. [Google Scholar] [CrossRef]
- Fares, D.; Fathi, M.; Shams, I.; Mekhilef, S. A novel global MPPT technique based on squirrel search algorithm for PV module under partial shading conditions. Energy Convers. Manag. 2021, 230, 113773. [Google Scholar] [CrossRef]
- Al-Shammaa, A.A.; Abdurraqeeb, A.M.; Noman, A.M.; Alkuhayli, A.; Farh HM, H. Hardware-In-the-Loop Validation of Direct MPPT Based Cuckoo Search Optimization for Partially Shaded Photovoltaic System. Electronics 2022, 11, 1655. [Google Scholar] [CrossRef]
- Watanabe, R.B.; Ando Junior, O.H.; Leandro PG, M.; Salvadori, F.; Beck, M.F.; Pereira, K.; Brandt MH, M.; De Oliveira, F.M. Implementation of the Bio-Inspired Metaheuristic Firefly Algorithm (FA) Applied to Maximum Power Point Tracking of Photovoltaic Systems. Energies 2022, 15, 5338. [Google Scholar] [CrossRef]
- Pandey, A.K.; Singh, V.; Jain, S. Chapter eleven—Study and comparative analysis of perturb and observe (P&O) and fuzzy logic based PV-MPPT algorithms. In Applications of AI and IOT in Renewable Energy; Academic Press: Cambridge, MA, USA, 2022; pp. 193–209. [Google Scholar]
- Almajid, S.; Al-Raweshidy, H.; Abbod, M. A Novel Maximum Power Point Tracking Technique based on Fuzzy logic for Photovoltaic Systems. Int. J. Hydrogen Energy 2018, 43, 14158–14171. [Google Scholar] [CrossRef]
- Jyothy, L.P.N.; Sindhu, M.R. An Artificial Neural Network based MPPT Algorithm for Solar PV System. In Proceedings of the 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 375–380. [Google Scholar]
- Selivanov, S.G.; Poezjalova, S.N.; Gavrilova, O.A. The Use of Artificial Intelligence Methods of Technological Preparation of Engine-Building Production. Am. J. Ind. Eng. 2014, 2, 10–14. [Google Scholar]
- Verma, P.; Garg, R.; Mahajan, P. Asymmetrical fuzzy logic control-based MPPT algorithm for stand-alone photovoltaic systems under partially shaded conditions. Sci. Iran. 2020, 27, 3162–3174. [Google Scholar]
- Rahman, M.M.; Islam, M.S. PSO and ANN Based Hybrid MPPT Algorithm for Photovoltaic Array under Partial Shading Condition. Eng. Int. 2020, 8, 9–24. [Google Scholar] [CrossRef]
- Farzaneh, J. A Hybrid Modified FA-ANFIS-P&O Approach for MPPT in Photovoltaic Systems under PSCs. Int. J. Electron. 2019, 107, 703–718. [Google Scholar]
- Manikandan, P.V.; Selvaperuma, S. EANFIS-based Maximum Power Point Tracking for Standalone PV System. IETE J. Res. 2022, 68, 4218–4231. [Google Scholar] [CrossRef]
- Al-Majidi, S.D.; Abbod, M.F.; Al-Raweshidy, H.S. Design of an Efficient Maximum Power Point Tracker Based on ANFIS Using an Experimental Photovoltaic System Data. Electronics 2019, 8, 858. [Google Scholar] [CrossRef]
- Aymen, J.; Ons, Z.; Crăciunescu, A.; Popescu, M. Comparison of Fuzzy and Neuro-Fuzzy Controllers for Maximum Power Point Tracking of Photovoltaic Modules. Renew. Energy Power Qual. J. 2016, 1, 796–800. [Google Scholar] [CrossRef]
- Farajdadian, S.; Hosseini, S.M.H. Design of an optimal fuzzy controller to obtain maximum power in solar power generation system. Sol. Energy 2019, 182, 161–178. [Google Scholar] [CrossRef]
- Eltamalya, A.M.; Farh, H.M.H. Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC. Sol. Energy 2019, 177, 306–316. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Jhang, Y.-C.; Liang, R.-H. A fuzzy-logic based auto-scaling variable step-size MPPT method for PV systems. Sol. Energy 2016, 126, 53–63. [Google Scholar] [CrossRef]
- Raj, A.; Gupta, M. Numerical Simulation and Performance Assessment of ANN-INC Improved Maximum Power Point Tracking System for Solar Photovoltaic System Under Changing Irradiation Operation. Ann. Rom. Soc. Cell Biol. 2021, 25, 790–797. [Google Scholar]
- Abdellatif, W.S.E.; Mohamed, M.S.; Barakat, S.; Brisha, A. A Fuzzy Logic Controller Based MPPT Technique for Photovoltaic Generation System. Int. J. Electr. Eng. Inform. 2021, 13, 394–417. [Google Scholar]
- Mohammed, S.S.; Devaraj, D.; Ahamed, T.P.I. GA-Optimized Fuzzy-Based MPPT Technique for Abruptly Varying Environmental Conditions. J. Inst. Eng. Ser. B 2021, 102, 497–508. [Google Scholar] [CrossRef]
- Tandel, B.G.; Vora, D.R. MPP Detection Based on Genetic Algorithm for PV System in Partial Shading Condition. Int. J. Res. Dev. Technol. 2016, 5, 107–115. [Google Scholar]
- Karthika, S.; Rathika, P.; Devaraj, D. Evaluation of GA Tuned PI Controller for Maximum Power Point Tracking for Solar PV System under Partially Shaded Conditions Based on Two Diode Model. World Appl. Sci. J. 2017, 35, 2580–2590. [Google Scholar]
- Dehghani, M.; Taghipour, M.; Gharehpetian, G.B.; Abedi, M. Optimized Fuzzy Controller for MPPT of Grid-connected PV Systems in Rapidly Changing Atmospheric Conditions. J. Mod. Power Syst. Clean Energy 2021, 9, 376–383. [Google Scholar] [CrossRef]
- Bendary, F.M.; Saied, E.M.; Mohamed, W.A.; Afifi, Z.E. Optimal Maximum Power Point Tracking of PV Systems based Genetic-ANFIS Hybrid Algorithm. Int. J. Sci. Eng. Res. 2016, 7, 830–836. [Google Scholar]
- Firmanza, A.P.; Habibi, M.N.; Windarko, N.A.; Yanaratri, D.S. Differential Evolution-based MPPT with Dual Mutation for PV Array under Partial Shading Condition. In Proceedings of the 2020 10th Electrical Power, Electronics, Communications, Controls and Informatics Seminar (EECCIS), Malang, Indonesia, 26–28 August 2020; pp. 198–203. [Google Scholar]
- Neethu, M.; Senthilkumar, R. Comparison Method of PSO and DE Optimization for MPPT in PV Systems under Partial Shading Conditions. Int. Energy J. 2020, 20, 291–298. [Google Scholar]
- Kamaruddina, N.I.; Haron, A.R.; Chua, B.L.; Tan, M.K.; Lim, K.G.; Teo, K.T.K. Differential Evolution Based Maximum Power Point Tracker for Photovoltaic Array Under Non-Uniform Illumination Condition. ICTACT J. Soft Comput. 2020, 10, 2076–2083. [Google Scholar]
- Joisher, M.; Singh, D.; Taheri, S.; Espinoza-Trejo, D.R.; Pouresmaeil, E.; Taheri, H. A Hybrid Evolutionary-Based MPPT for Photovoltaic Systems Under Partial Shading Conditions. IEEE Access 2020, 8, 38481–38492. [Google Scholar] [CrossRef]
- Algarín, C.R.; Giraldo, J.T.; Álvarez, O.R. Fuzzy Logic Based MPPT Controller for a PV System. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Cheng, P.-C.; Peng, B.-R.; Liu, Y.-H.; Cheng, Y.-S.; Huang, J.-W. Optimization of a Fuzzy-Logic-Control-Based MPPT Algorithm Using the Particle Swarm Optimization Technique. Energies 2015, 8, 5338–5360. [Google Scholar] [CrossRef]
- Liu, C.-L.; Chen, J.-H.; Liu, Y.-H.; Yang, Z.-Z. An Asymmetrical Fuzzy-Logic-Control-Based MPPT Algorithm for Photovoltaic Systems. Energies 2014, 7, 2177–2193. [Google Scholar] [CrossRef]
- Kececioglu, O.F.; Gani, A.; Sekkeli, M. Design and Hardware Implementation Based on Hybrid Structure for MPPT of PV System Using an Interval Type-2 TSK Fuzzy Logic Controller. Energies 2020, 13, 1842. [Google Scholar] [CrossRef]
- Hayder, W.; Sera, D.; Ogliari, E.; Lashab, A. On Improved PSO and Neural Network P&O Methods for PV System under Shading and Various Atmospheric Conditions. Energies 2022, 15, 7668. [Google Scholar]
- Hua, C.-C.; Zhan, Y.-J. A Hybrid Maximum Power Point Tracking Method without Oscillations in Steady-State for Photovoltaic Energy Systems. Energies 2021, 14, 5590. [Google Scholar] [CrossRef]
- Zhang, P.; Sui, H. Maximum Power Point Tracking Technology of Photovoltaic Array under Partial Shading Based on Adaptive Improved Di_erential Evolution Algorithm. Energies 2020, 13, 1254. [Google Scholar] [CrossRef]
- Bakkar, M.; Aboelhassan, A.; Abdelgeliel, M.; Galea, M. PV Systems Control Using Fuzzy Logic Controller Employing Dynamic Safety Margin under Normal and Partial Shading Conditions. Energies 2021, 14, 841. [Google Scholar] [CrossRef]
- Bataineh, K.; Eid, N. A Hybrid Maximum Power Point Tracking Method for Photovoltaic Systems for Dynamic Weather Conditions. Resources 2018, 7, 68. [Google Scholar] [CrossRef]
- Guerra MI, S.; Ugulino de Araújo, F.M.; Dhimish, M.; Vieira, R.G. Assessing Maximum Power Point Tracking Intelligent Techniques on a PV System with a Buck–Boost Converter. Energies 2021, 14, 7453. [Google Scholar] [CrossRef]
- Minai, A.F.; Khan, A.A.; Pachauri, R.K.; Malik, H.; Márquez, F.P.G.; Jiménez, A.A. Performance Evaluation of Solar PV-Based Z-Source Cascaded Multilevel Inverter with Optimized Switching Scheme. Electronics 2022, 11, 3706. [Google Scholar] [CrossRef]
- Minai, A.F.; Malik, H. Metaheuristics Paradigms for Renewable Energy Systems: Advances in Optimization Algorithms. Springer Nature Book: Metaheuristic and Evolutionary Computation: Algorithms and Applications. In Metaheuristic and Evolutionary Computation: Algorithms and Applications; Studies in Computational Intelligence; Springer: Singapore, 2020; pp. 35–61. [Google Scholar]
- Chankaya, M.; Hussain, I.; Ahmad, A.; Fausto, P.; García, M. Multi-Objective Grasshopper Optimization Based MPPT and VSC Control of Grid-Tied PV-Battery System. Electronics 2021, 10, 2770. [Google Scholar] [CrossRef]
- Tajjour, S.; Chandel, S.S.; Alotaibi, M.A.; Ustun, T.S.A. Novel Metaheuristic Approach for Solar Photovoltaic Parameter Extraction Using Manufacturer Data. Photonics 2022, 9, 858. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
