Asymptotic Sample Size for Common Test of Relative Risk Ratios in Stratified Bilateral Data
Abstract
:1. Introduction
2. Donner’s Model and Common Test
2.1. Likelihood Ratio Test
2.2. Score Test
2.3. Wald-Type Test
2.4. Pooled MLE-Based Wald-Type Test
2.5. Pooled MLE-Based Log-Transformation Test
3. Sample Size Determination
3.1. Asymptotic Sample Size
3.2. The Iterative Method
- (i)
- Given and , . The initial values of sample size , the step size and flag .
- (ii)
- The th update of is . The 10,000 replicates are randomly generated under , where follows a trinomial distribution
- (iii)
- Calculate empirical power based on random samples generated in step (ii) at a given significance level . The empirical power can be computed by dividing the number of times rejecting by 10,000. The empirical power is denoted as .
- (iv)
- Compare with given power . If , return to step (ii). Otherwise, and return to step (ii).
- (v)
- Repeat the steps (ii)–(iv) until closes to before d becomes a decimal.
4. Simulation for Asymptotic Power and Sample Size
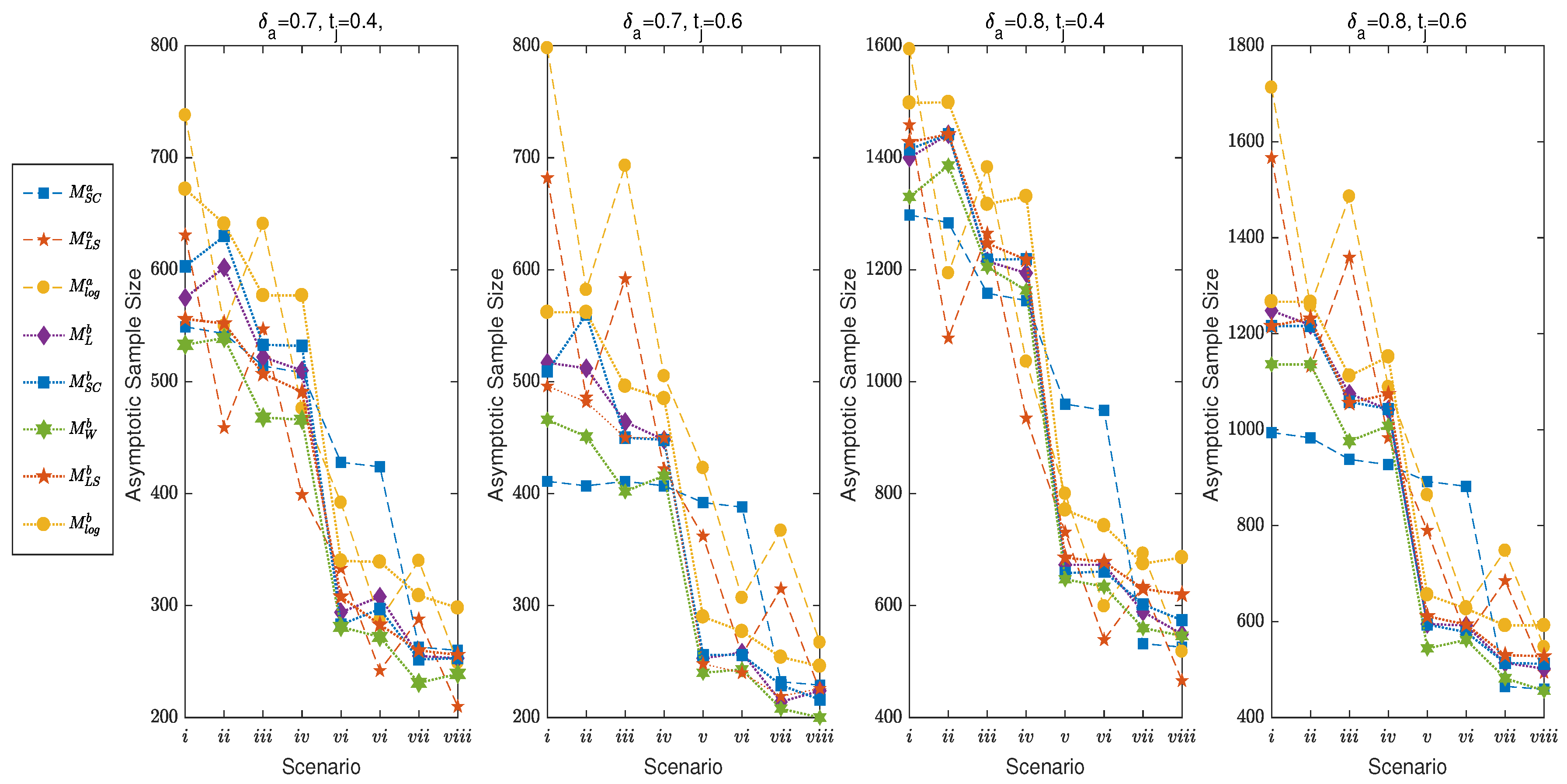
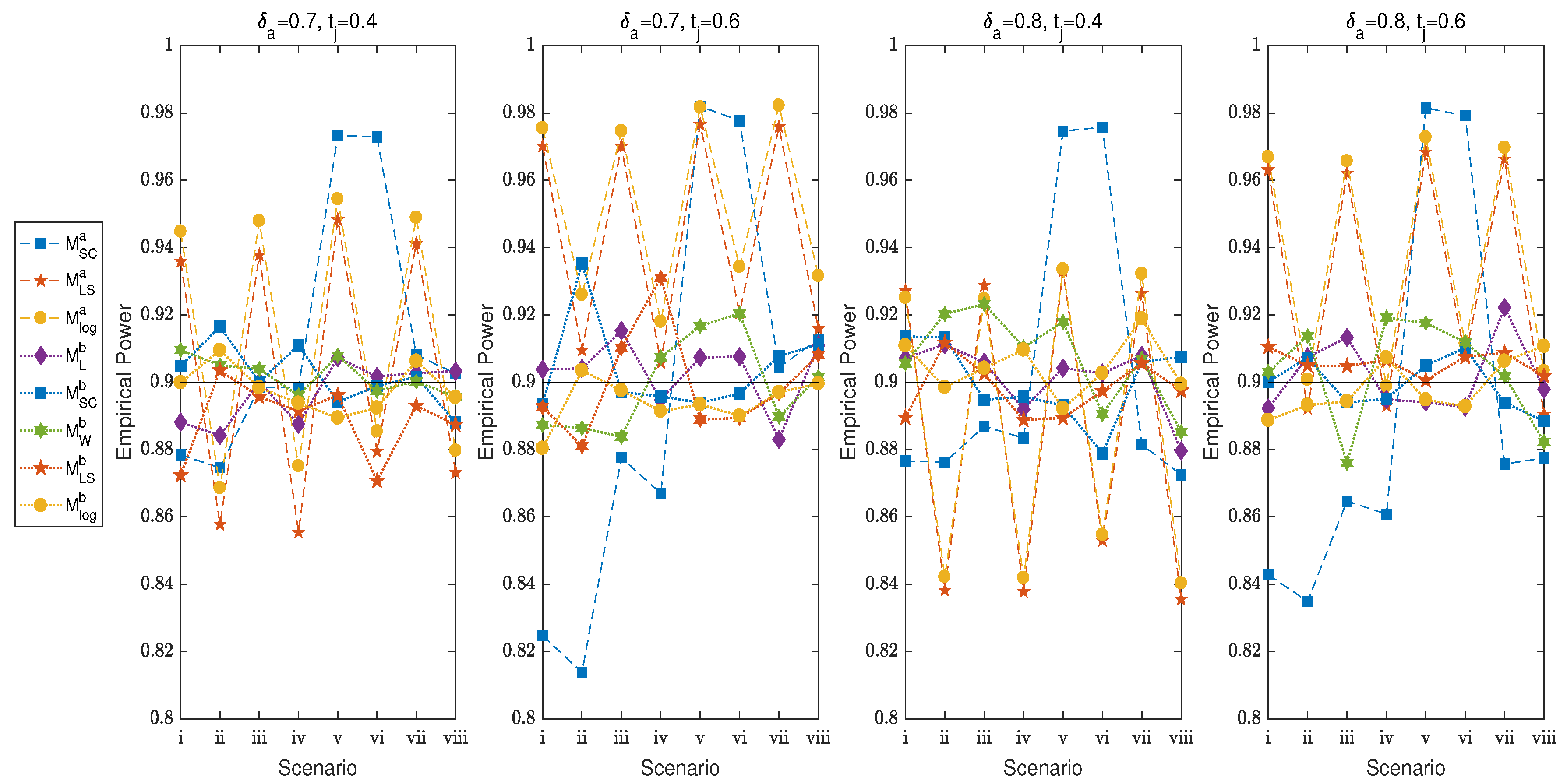
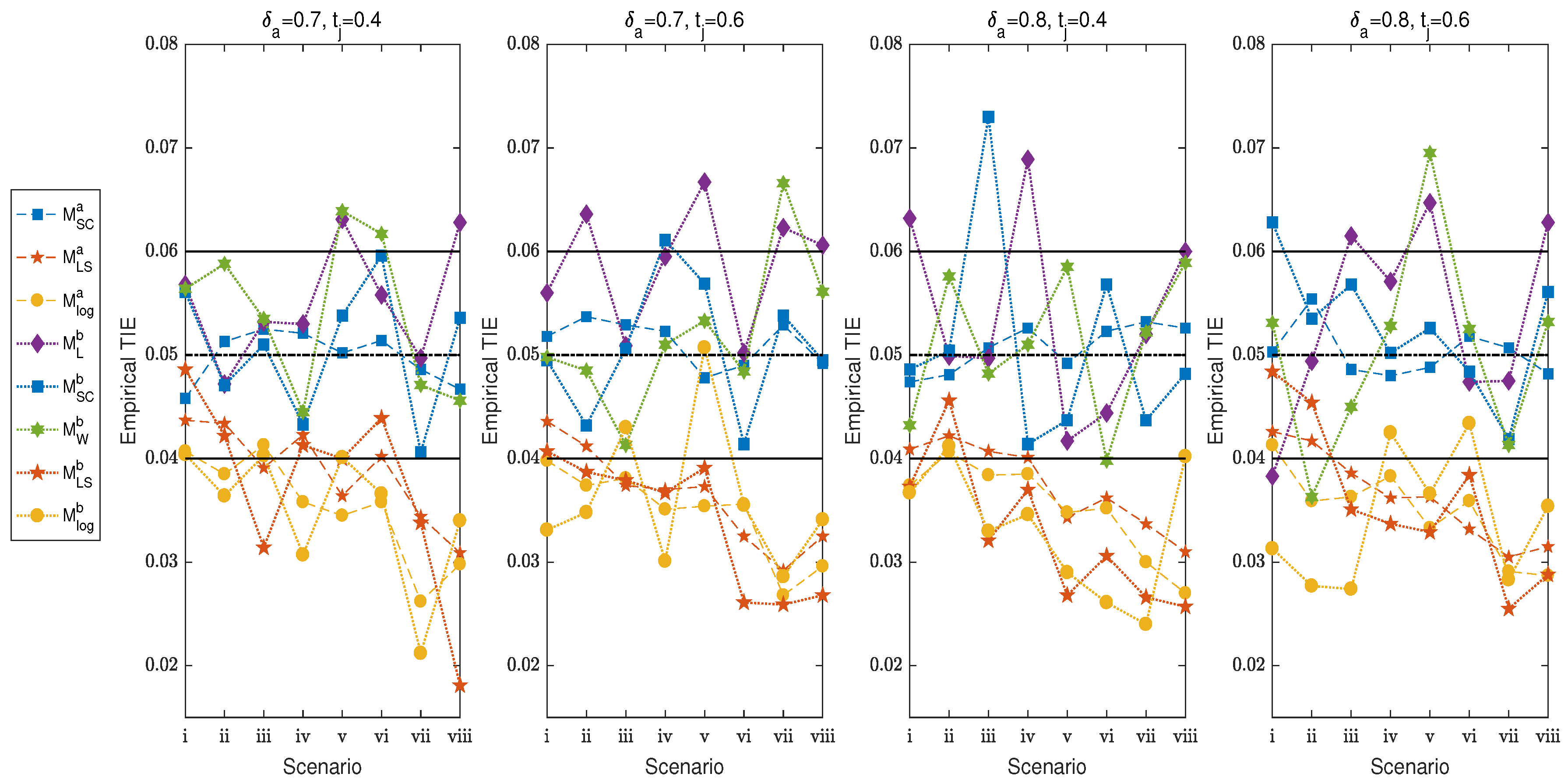
4.1. Asymptotic Sample Size, Power and TIE
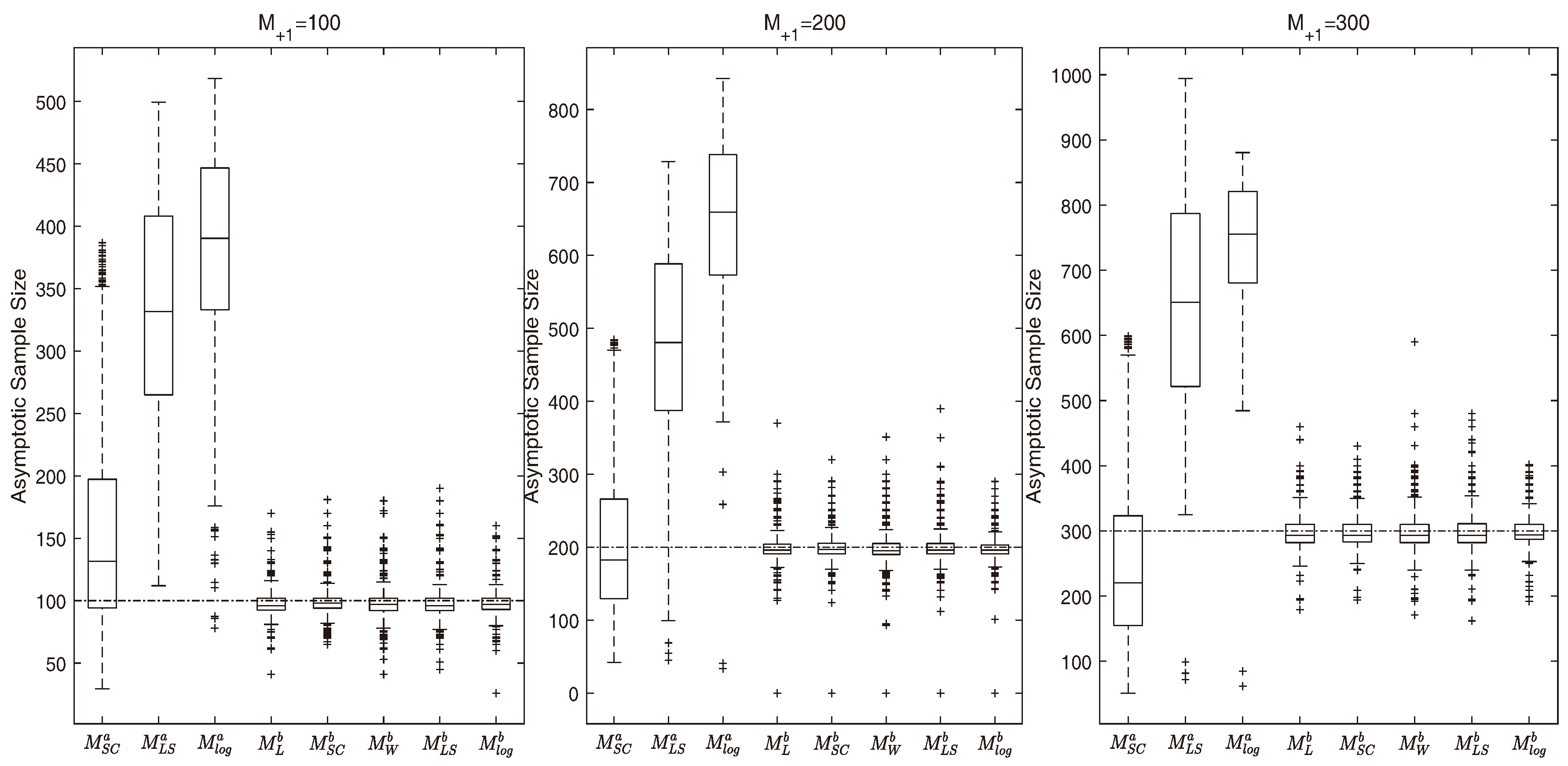
4.2. Accuracy
4.3. The Effect of Parameters
5. A Real Example
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation for the Log-Likelihood Function under H0
Appendix B. Derivation for Score Statistic
References
- Rosner, B. Statistical methods in ophthalmology: An adjustment for the correlation between eyes. Biometrics 1982, 38, 105–114. [Google Scholar] [CrossRef]
- Dallal, G. Paired Bernoulli trials. Biometrics 1988, 44, 253–257. [Google Scholar] [CrossRef]
- Donner, A. Statistical methods in ophthalmology: An adjusted chi-square approach. Biometrics 1989, 45, 605–611. [Google Scholar] [CrossRef]
- Tang, N.; Tang, M.; Qiu, S. Testing the equality of proportions for correlated otolaryngologic data. Comput. Stat. Data Anal. 2008, 52, 3719–3729. [Google Scholar] [CrossRef]
- Pei, Y.; Tang, M.; Wong, W.; Tang, N. Testing equality of correlations of two paired binary responses from two treated groups in a randomized trial. J. Biopharm. Stat. 2011, 21, 511–525. [Google Scholar] [CrossRef]
- Mou, K.; Ma, C.; Li, Z. Homogeneity test of relative risk ratios for stratified bilateral data under different algorithms. J. Appl. Stat. 2023, 50, 1060–1077. [Google Scholar] [CrossRef]
- Tang, N.; Qiu, S. Homogeneity test, sample size determination and interval construction of difference of two proportions in stratified bilateral-sample designs. J. Stat. Plan. Inference 2012, 142, 1242–1251. [Google Scholar] [CrossRef]
- Tang, M.; Tang, N.; Carey, V. Sample size determination for 2-step studies with dichotomous response. J. Stat. Plan. Inference 2006, 136, 1166–1180. [Google Scholar] [CrossRef]
- Tang, M.; Tang, N.; Rosner, B. Statistical inference for correlated data in ophthalmologic studies. Stat. Med. 2006, 25, 2771–2783. [Google Scholar] [CrossRef]
- Liu, X.; Shan, G.; Tian, L.; Ma, C. Exact methods for testing homogeneity of proportions for multiple groups of paired binary data. Commun. Stat.-Simul. C 2017, 46, 6074–6082. [Google Scholar] [CrossRef]
- Shan, G. Exact approaches for testing non-inferiority or superiority of two incidence rates. Stat. Probab. Lett. 2014, 85, 129–134. [Google Scholar] [CrossRef]
- Tang, N.; Qiu, S.; Tang, M.; Pei, Y. Asymptotic confidence interval construction for proportion difference in medical studies with bilateral data. Stat. Methods Med. Res. 2011, 20, 233–259. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; Tang, M.; Wong, W.; Gao, J. Confidence intervals for correlated proportion differences from paired data in a two-arm randomised clinical trial. Stat. Methods Med. Res. 2012, 21, 167–187. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Poon, W.; Tang, M. Sample size determination for disease prevalence studies with partially validated data. Stat. Methods Med. Res. 2012, 25, 37–63. [Google Scholar] [CrossRef]
- Qiu, S.; Zeng, X.; Tang, M.; Pei, Y. Test procedure and sample size determination for a proportion study using a doublesampling scheme with two fallible classifiers. Stat. Methods Med. Res. 2019, 28, 1019–1043. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Li, Z.; Jiang, H. Homogeneity test and sample size of risk difference for stratified unilateral and bilateral data. Commun. Stat.-Simul. C 2022, 1–24. [Google Scholar] [CrossRef]
- Lloyd, C.; Ripamonti, E. comprehensive open-source library for exact required sample size in binary clinical trials. Contemp. Clin. Trials 2021, 107, 106491. [Google Scholar] [CrossRef]
- Tang, N.; Yu, B. Bayesian sample size determination in a three-arm non-inferiority trial with binary endpoints. J. Biopharm. Stat. 2022, 32, 768–788. [Google Scholar] [CrossRef]
- Pilz, M. Sample size calculation for one-armed clinical trials with clustered data and binary outcome. Biom. J. 2023, 28, e2300123. [Google Scholar] [CrossRef]
- Zhuang, T.; Tian, G.; Ma, C. Homogeneity test of ratio of two proportions in stratified bilateral data. Stat. Biopharm. Res. 2019, 11, 200–209. [Google Scholar] [CrossRef]
- Mandel, E.; Bluestone, C.; Rockette, H.; Blatter, M.; Reisinger, K.; Wucher, F.; Harper, J. Duration of effusion after antibiotic treatment for acute otitis media: Comparison of Cefaclor and Amoxicillin. Pediatr. Infect. Dis. J. 1982, 1, 310–316. [Google Scholar] [CrossRef] [PubMed]

| Number of Responses | Group | Total | |
|---|---|---|---|
| 1 | 2 | ||
| 0 | () | () | |
| 1 | () | () | |
| 2 | () | () | |
| Total | |||
| Number of Responses | Group | Total | |
|---|---|---|---|
| 1 | 2 | ||
| 0 | |||
| 1 | |||
| 2 | |||
| Total | M | ||
| Scenario | k | ||
|---|---|---|---|
| i | 0.4 | 0.5 | (1/3, 1/3, 1/3) |
| 0.4 | 0.5 | (0.5, 0.3, 0.2) | |
| 0.4 | 0.3 | (1/3, 1/3, 1/3) | |
| 0.4 | 0.3 | (0.5, 0.3, 0.2) | |
| v | 0.6 | 0.5 | (1/3, 1/3, 1/3) |
| 0.6 | 0.5 | (0.5, 0.3, 0.2) | |
| 0.6 | 0.3 | (1/3, 1/3, 1/3) | |
| 0.6 | 0.3 | (0.5, 0.3, 0.2) |
| Number of OME-Free Ears | <2 yr | 2–5 yr | >5 yr | Total | |||
|---|---|---|---|---|---|---|---|
| Cefaclor | Amoxicillin | Cefaclor | Amoxicillin | Cefaclor | Amoxicillin | ||
| 0 | 8 | 11 | 6 | 3 | 0 | 1 | 29 |
| 1 | 2 | 2 | 6 | 1 | 1 | 0 | 12 |
| 2 | 8 | 2 | 10 | 5 | 3 | 6 | 34 |
| Total | 18 | 15 | 22 | 9 | 4 | 7 | 75 |
| Age | Stratum | |||
|---|---|---|---|---|
| <2 yr | 1 | 0.377 | 0.736 | 0.937 |
| 2–5 yr | 2 | 0.606 | 0.532 | 0.937 |
| >5 yr | 3 | 0.885 | 0.624 | 0.937 |
| Power | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.80 | 70 | 127 | 67 | 43 | 43 | 53 | 86 | 53 |
| 0.90 | 81 | 153 | 82 | 53 | 62 | 72 | 100 | 77 | |
| 0.95 | 88 | 170 | 91 | 70 | 74 | 86 | 122 | 94 | |
| 0.6 | 0.80 | 129 | 213 | 134 | 77 | 79 | 91 | 151 | 120 |
| 0.90 | 151 | 259 | 163 | 100 | 110 | 122 | 182 | 154 | |
| 0.95 | 164 | 285 | 180 | 132 | 132 | 146 | 218 | 192 |
| Result | ||||||
|---|---|---|---|---|---|---|
| 0.5 | Value | 8.8475 | 6.9551 | 8.2666 | 4.2853 | 4.6490 |
| p-value | 0.0029 | 0.0084 | 0.0040 | 0.0384 | 0.0311 | |
| 0.6 | Value | 4.3363 | 3.8767 | 4.9158 | 1.6514 | 1.7826 |
| p-value | 0.0373 | 0.0490 | 0.0266 | 0.1988 | 0.1818 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, K.; Li, Z.; Ma, C. Asymptotic Sample Size for Common Test of Relative Risk Ratios in Stratified Bilateral Data. Mathematics 2023, 11, 4198. https://doi.org/10.3390/math11194198
Mou K, Li Z, Ma C. Asymptotic Sample Size for Common Test of Relative Risk Ratios in Stratified Bilateral Data. Mathematics. 2023; 11(19):4198. https://doi.org/10.3390/math11194198
Chicago/Turabian StyleMou, Keyi, Zhiming Li, and Changxing Ma. 2023. "Asymptotic Sample Size for Common Test of Relative Risk Ratios in Stratified Bilateral Data" Mathematics 11, no. 19: 4198. https://doi.org/10.3390/math11194198
APA StyleMou, K., Li, Z., & Ma, C. (2023). Asymptotic Sample Size for Common Test of Relative Risk Ratios in Stratified Bilateral Data. Mathematics, 11(19), 4198. https://doi.org/10.3390/math11194198








