An Efficient and Fast Sparse Grid Algorithm for High-Dimensional Numerical Integration
Abstract
1. Introduction
2. Preliminaries
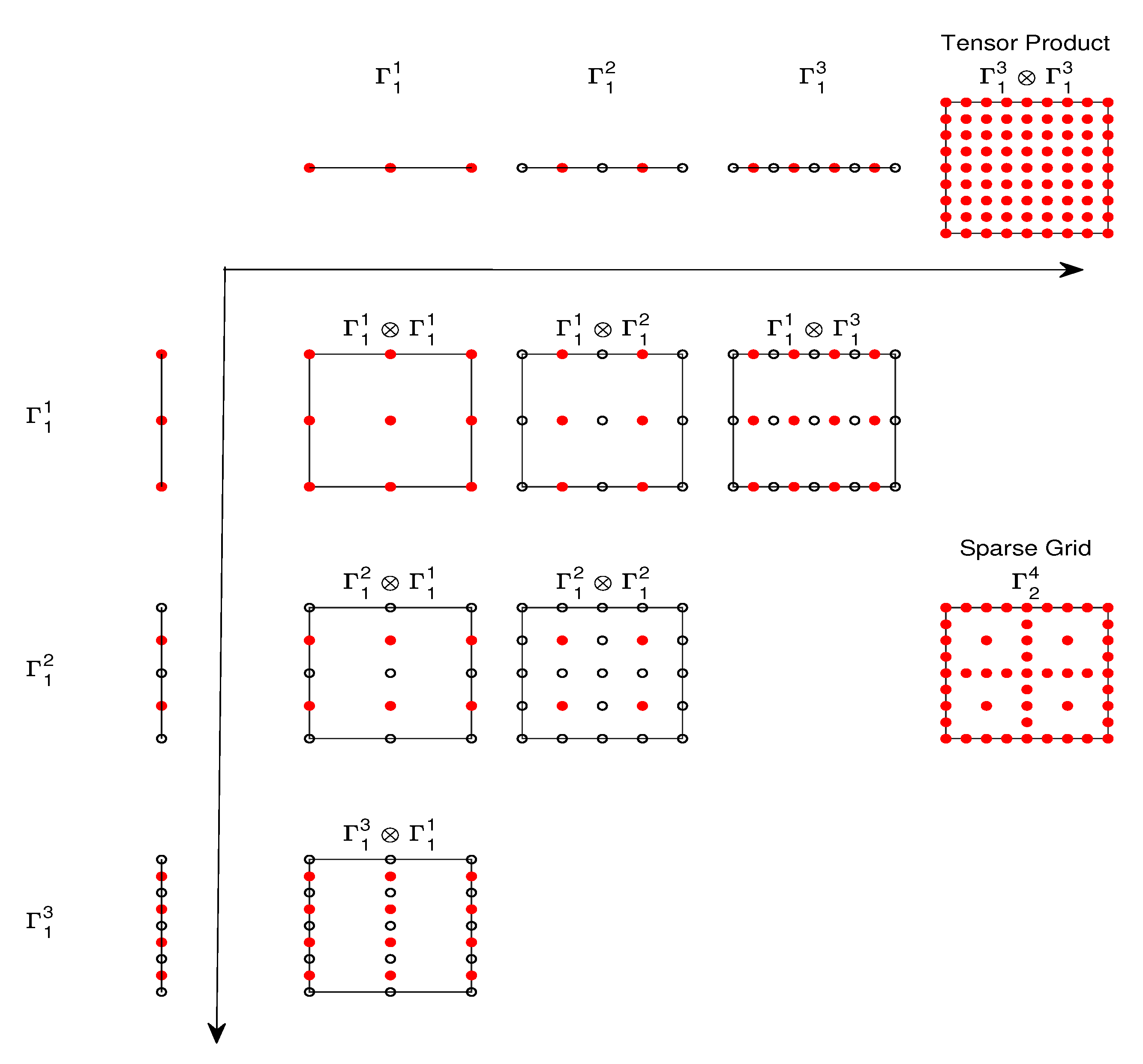
2.1. The Sparse Grid Method
2.2. Examples of Sparse Grid Methods
3. The MDI-SG Algorithm
3.1. Formulation of the MDI-SG Algorithm in Two Dimensions
3.2. Formulation of the MDI-SG Algorithm in Three Dimensions
| Algorithm 1: 2d-MDI-SG (f, ) |
|
| Algorithm 2: 3d-MDI-SG(f, ) |
|
3.3. Formulation of the MDI-SG Algorithm in Arbitrary d-Dimensions
- If , set MDI-SG, which is computed by using the one-dimensional quadrature rule (5);
- If , set MDI-SG 2d-MDI-SG;
- If , set MDI-SG 3d-MDI-SG.
| Algorithm 3: MDI-SG |
4. Numerical Performance Tests
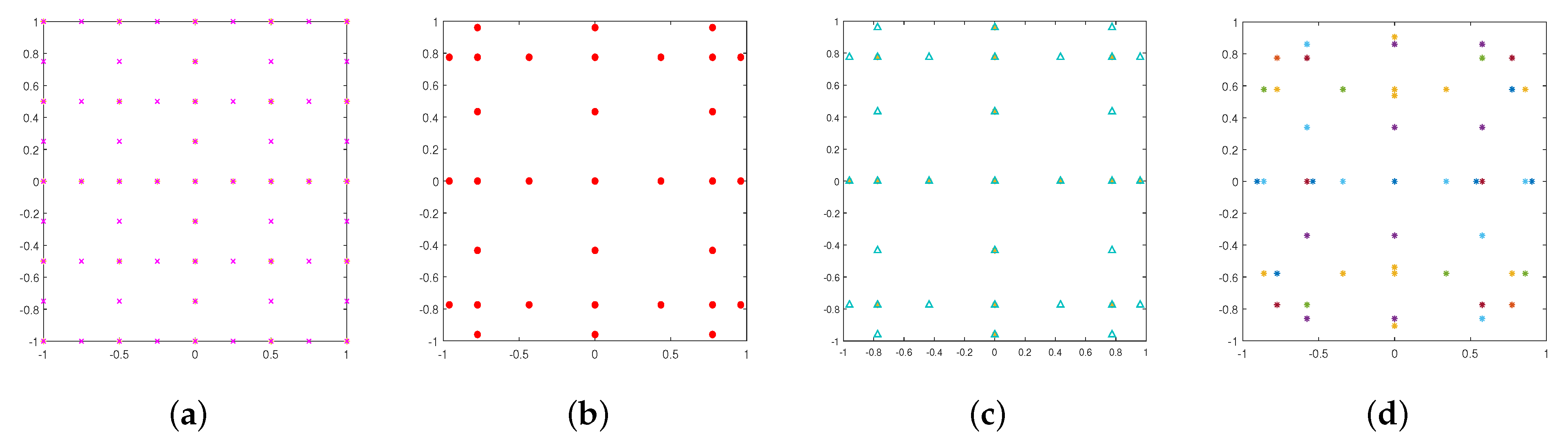
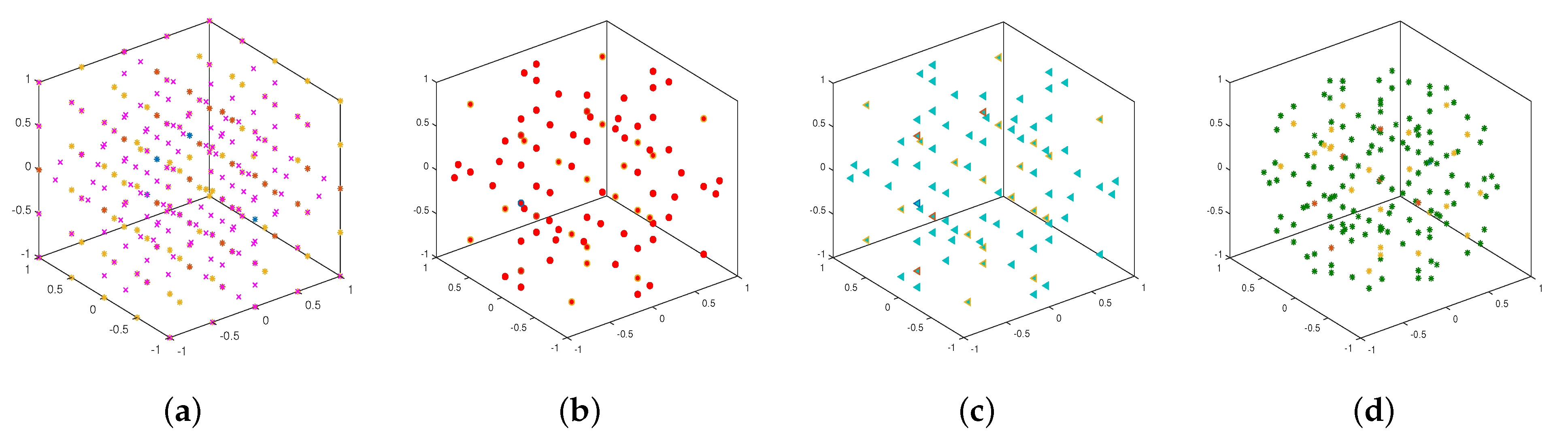
4.1. Two- and Three-Dimensional Tests
4.2. High-Dimensional Tests
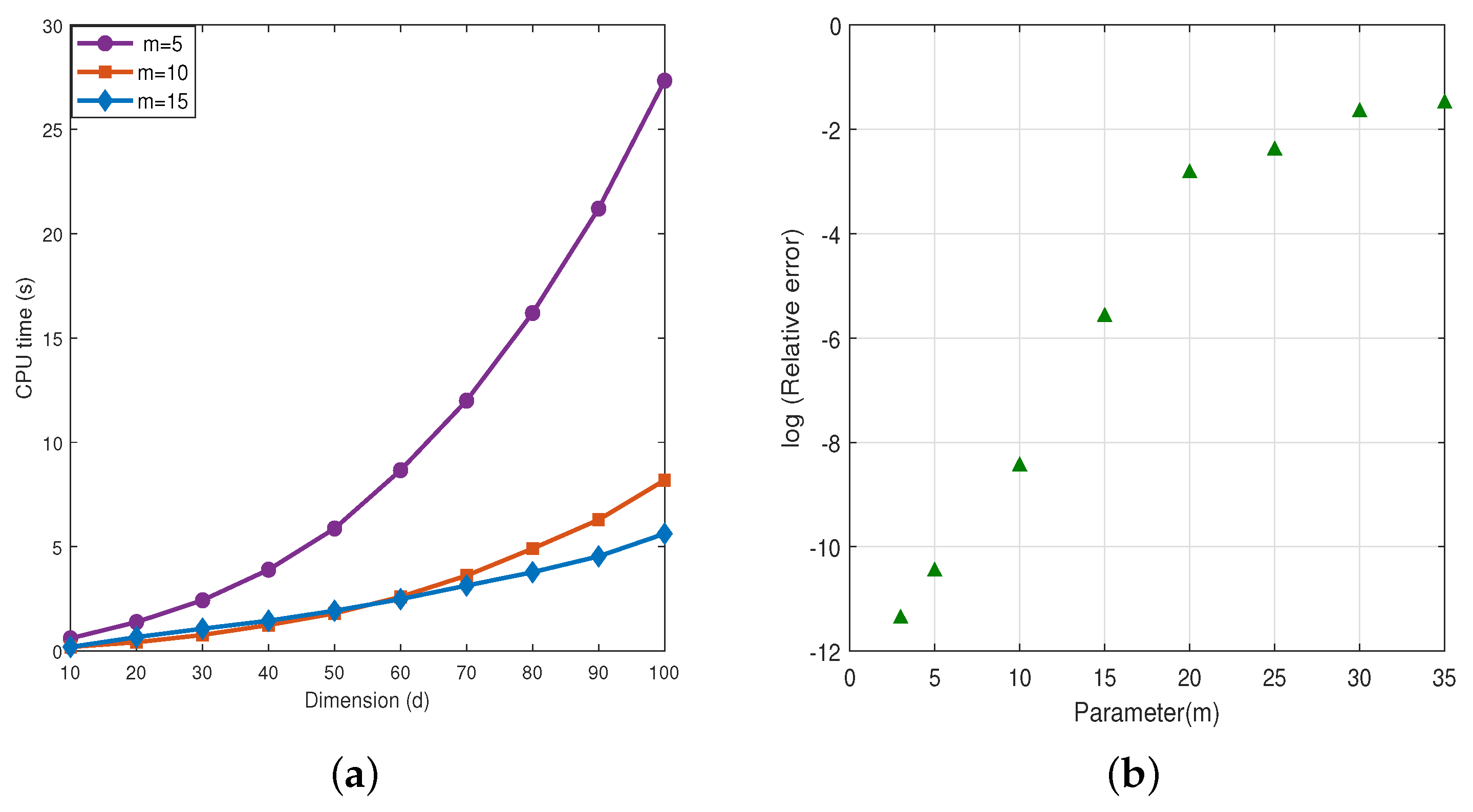
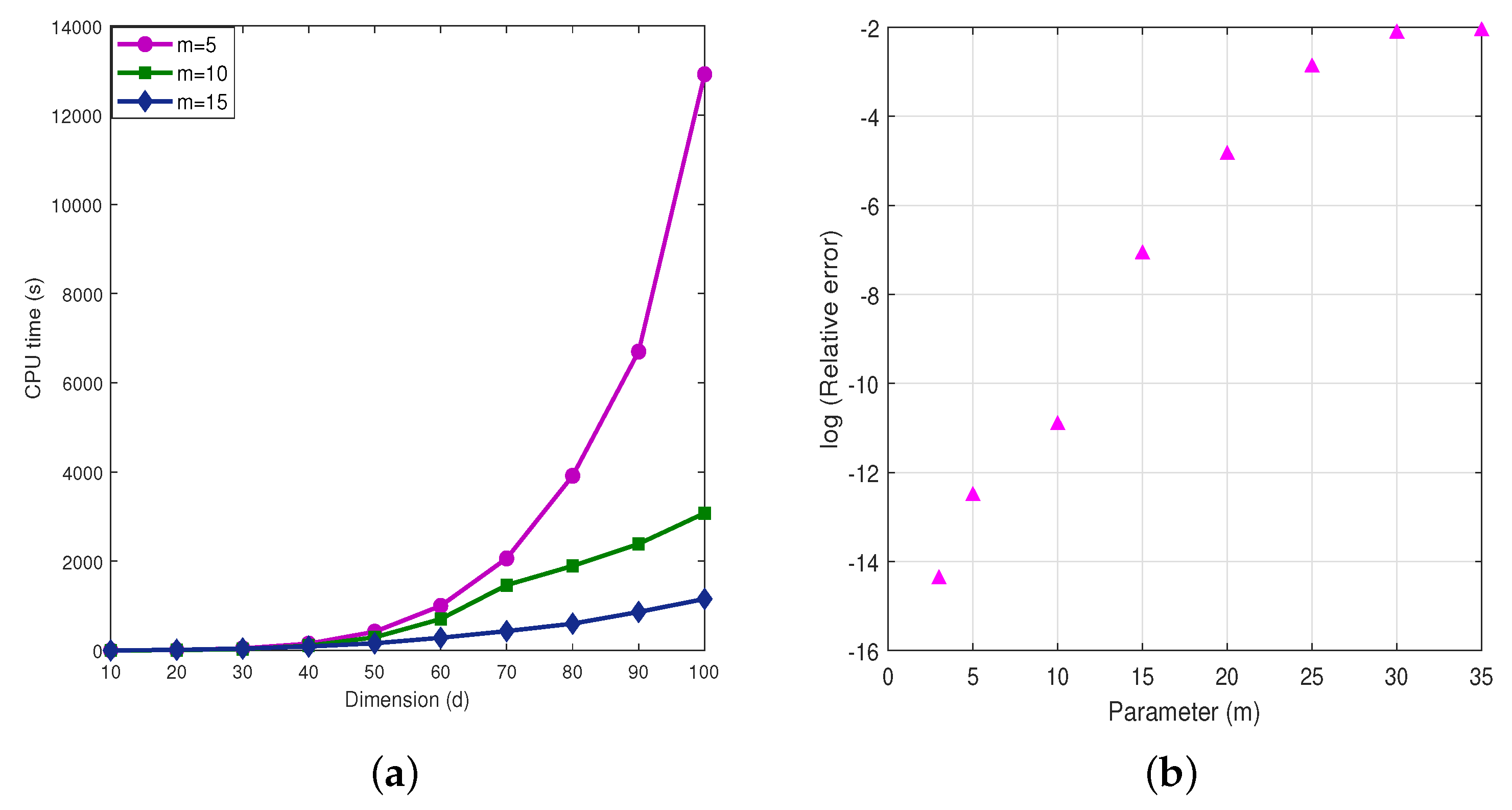
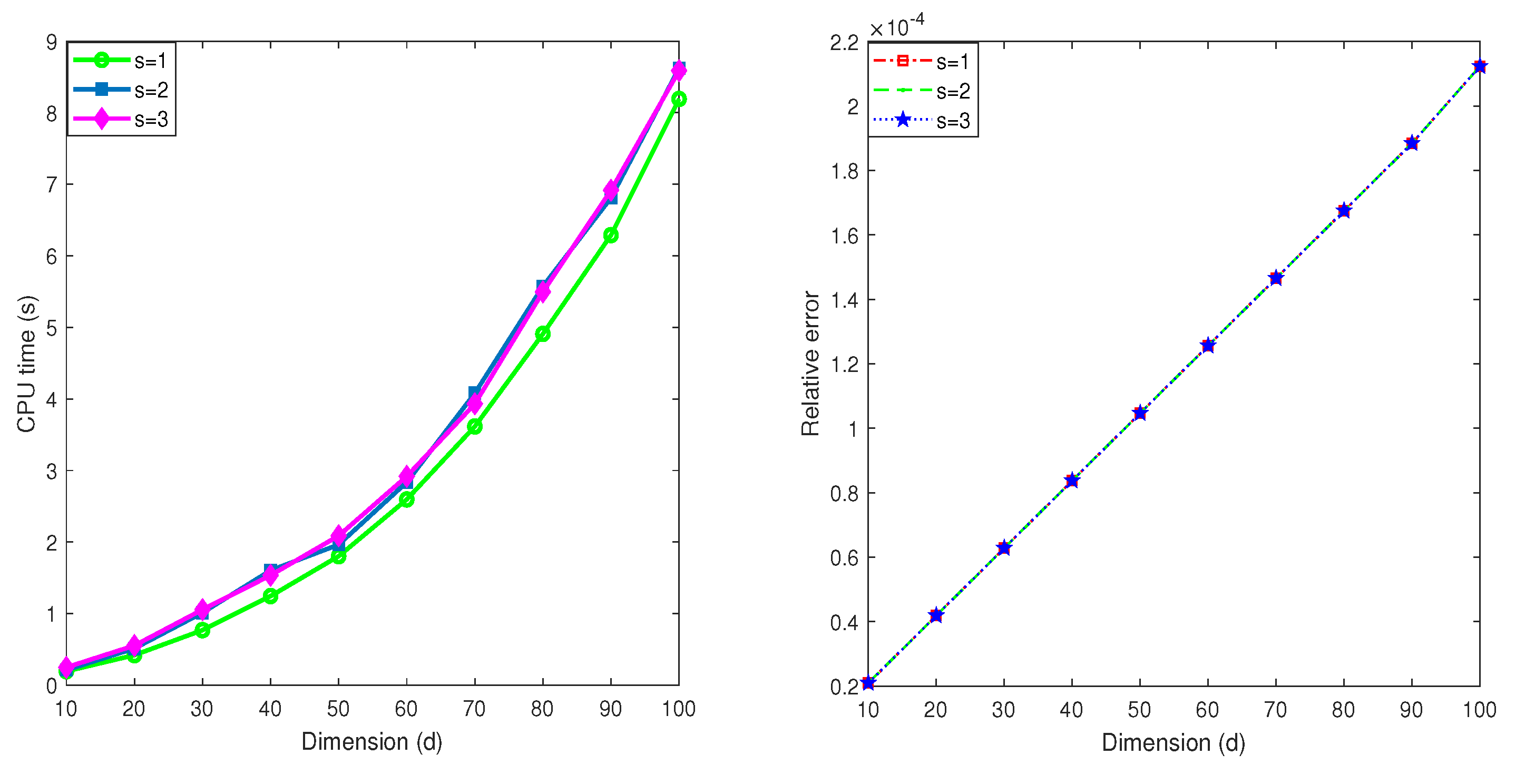
5. Influence of Parameters
5.1. Influence of Parameter r
5.2. Influence of Parameter m
5.3. Influence of the Parameter s
5.4. Influence of the Parameter q or N
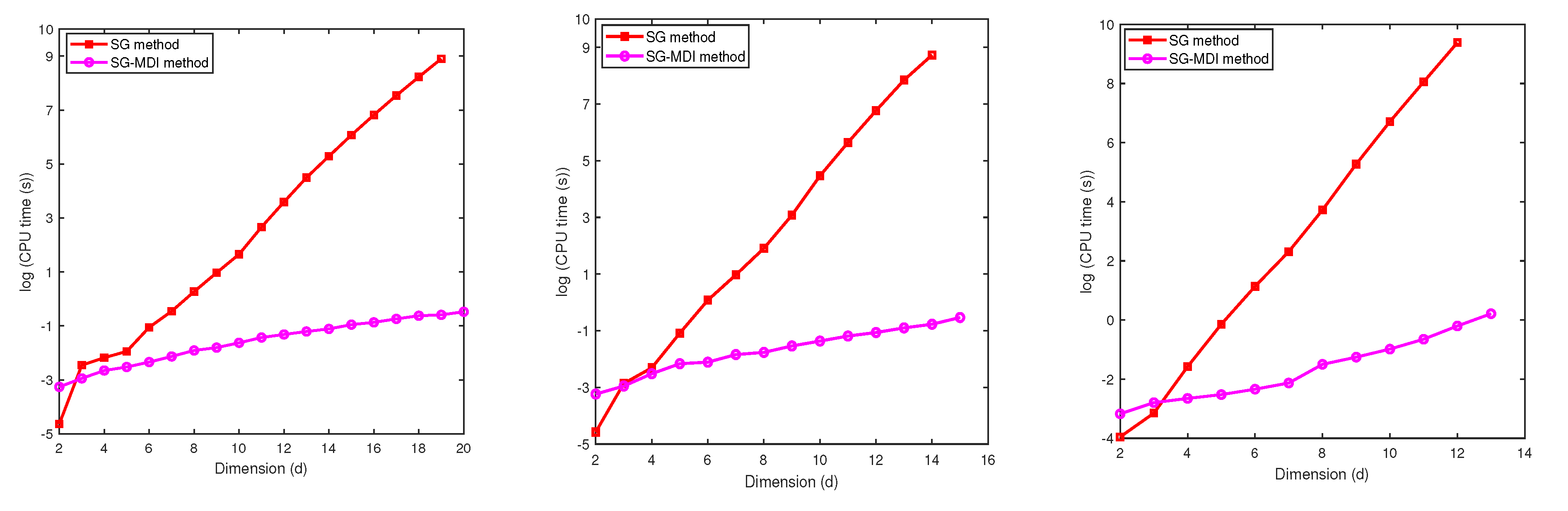
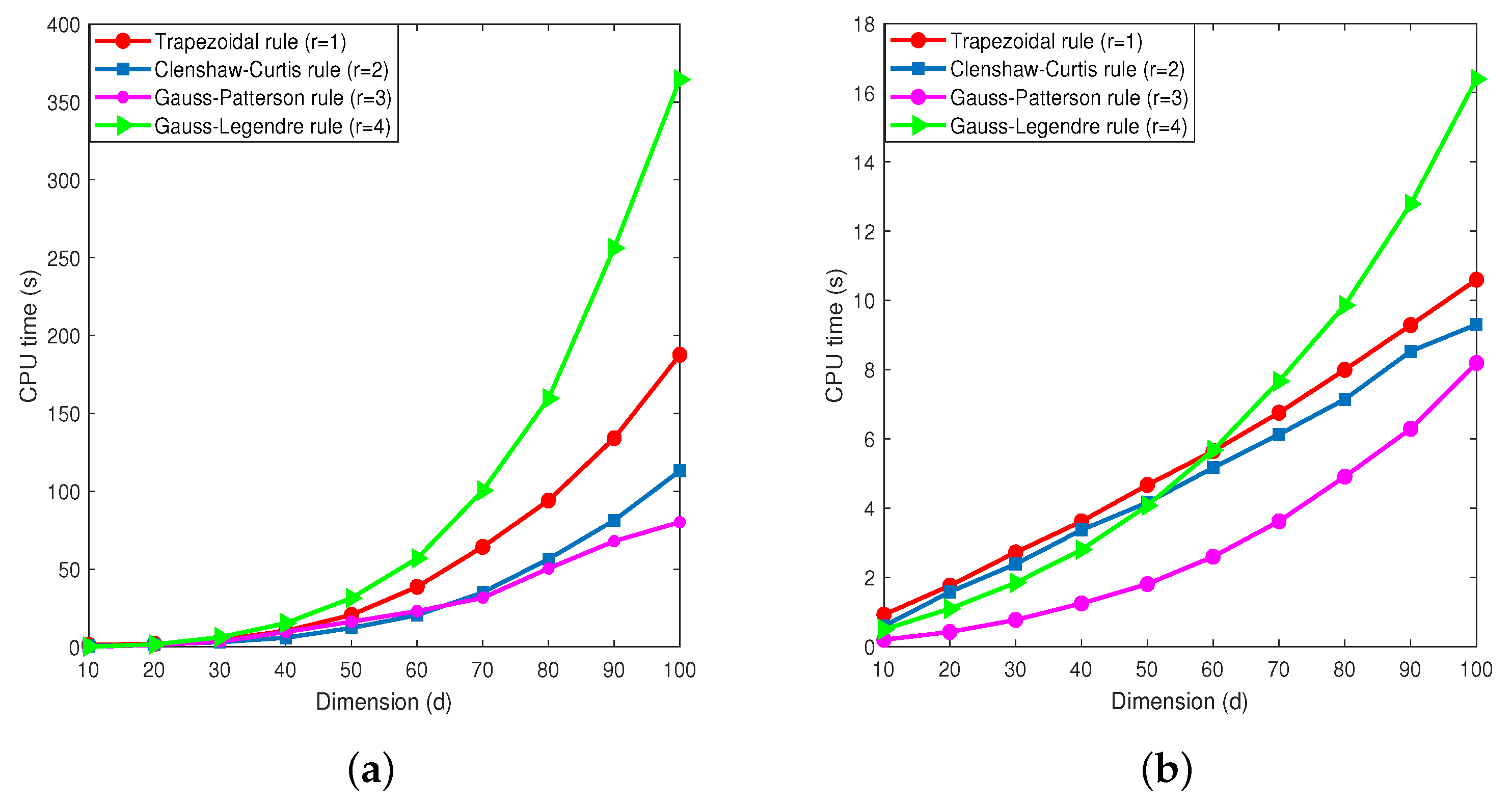
6. Computational Complexity
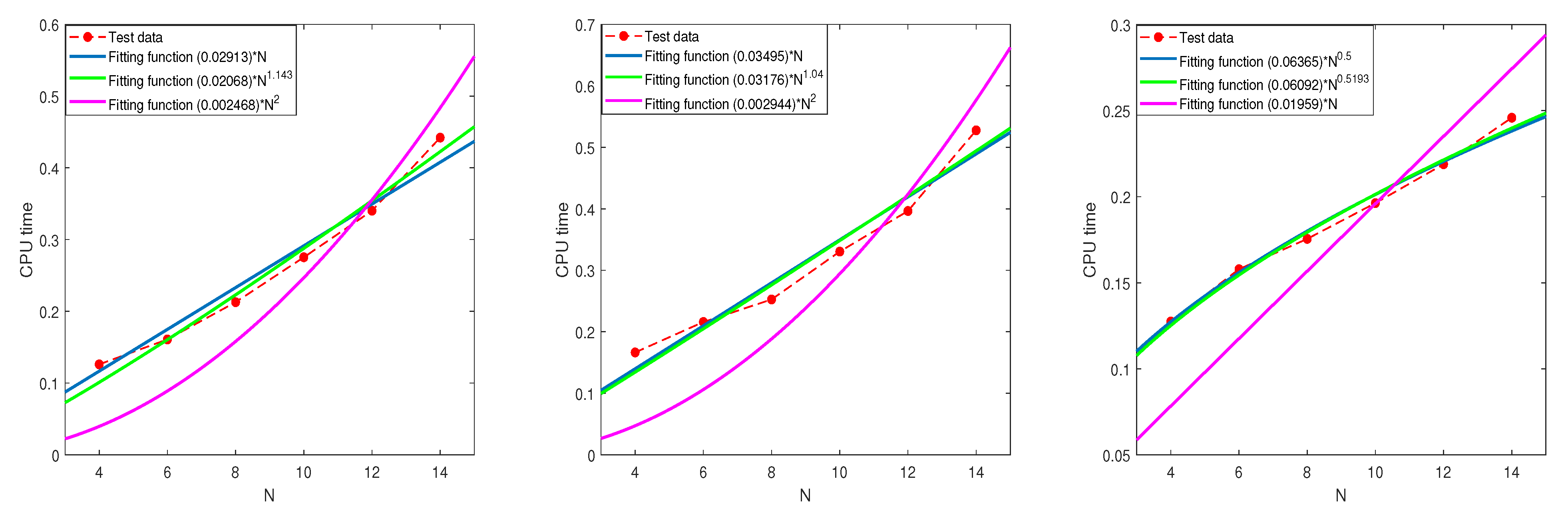
6.1. The Relationship between the CPU Time and N
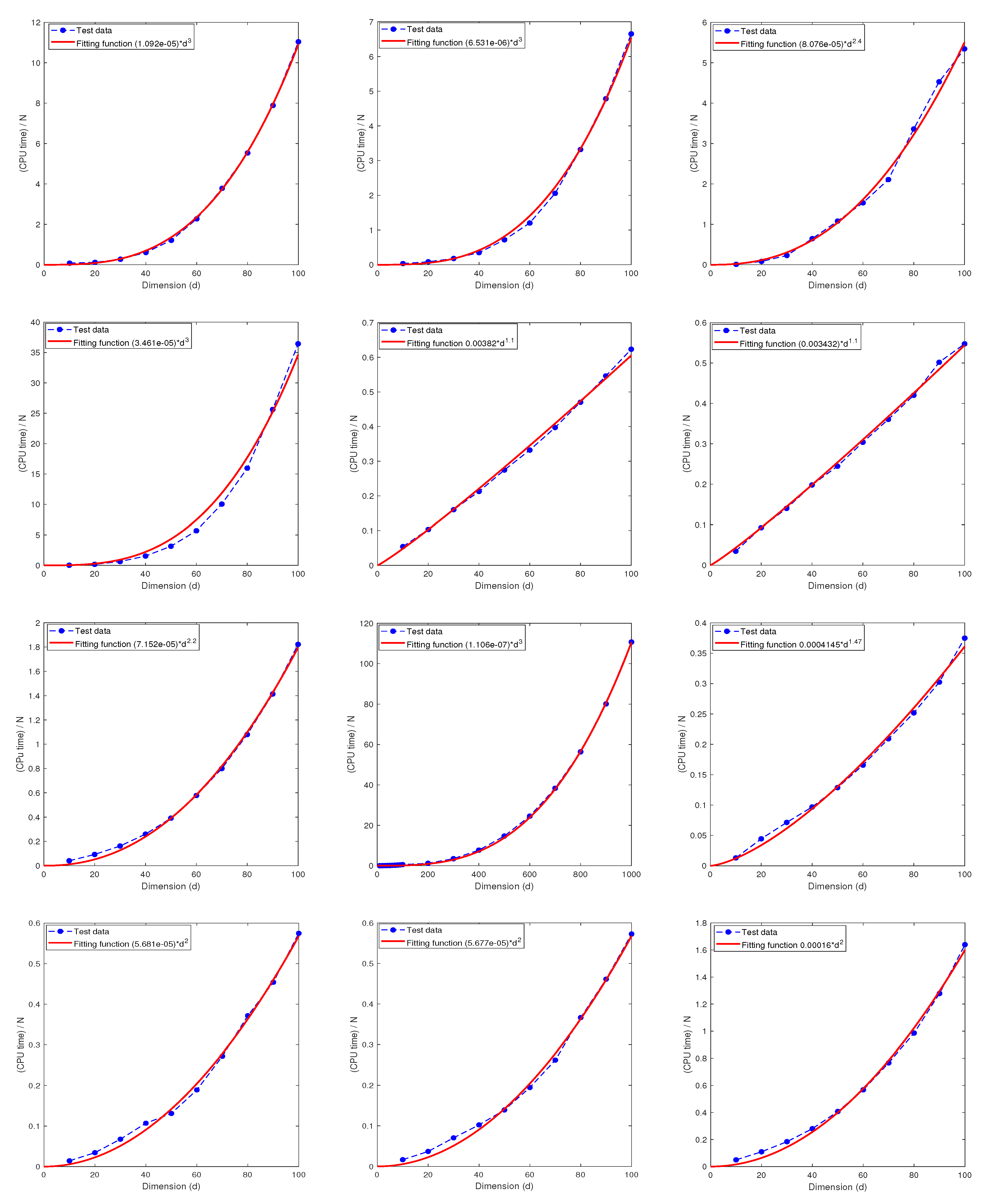
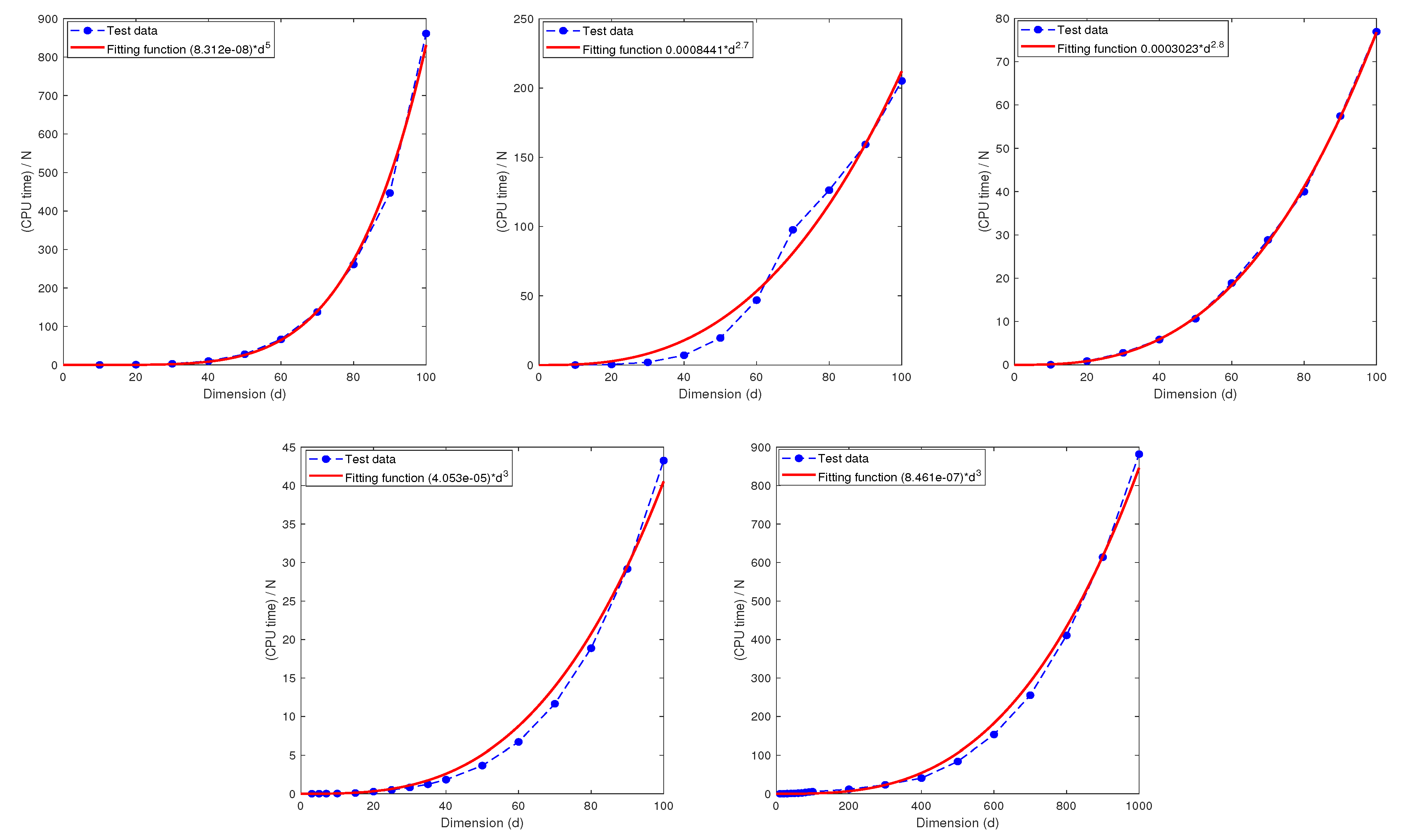
6.2. The Relationship between the CPU Time and the Dimension d
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Griebel, M.; Holtz, M. Dimension-wise integration of high-dimensional functions with applications to finance. J. Complex. 2010, 26, 455–489. [Google Scholar] [CrossRef]
- LaValle, S.M.; Moroney, K.J.; Hutchinson, S.A. Methods for numerical integration of high-dimensional posterior densities with application to statistical image models. IEEE Trans. Image Process. 1997, 6, 1659–1672. [Google Scholar] [CrossRef] [PubMed]
- Barraquand, J.; Martineau, D. Numerical valuation of high dimensional multivariate American securities. J. Financ. Quant. Anal. 1995, 30, 383–405. [Google Scholar] [CrossRef]
- Quackenbush, J. Extracting biology from high-dimensional biological data. J. Exp. Biol. 2007, 210, 1507–1517. [Google Scholar] [CrossRef] [PubMed]
- Azevedo, J.D.S.; Oliveira, S.P. A numerical comparison between quasi-Monte Carlo and sparse grid stochastic collocation methods. Commun. Comput. Phys. 2012, 12, 1051–1069. [Google Scholar] [CrossRef]
- Gerstner, T.; Griebel, M. Numerical integration using sparse grids. Numer. Algorithms 1998, 18, 209–232. [Google Scholar] [CrossRef]
- Bungartz, H.-J.; Griebel, M. Sparse grids. Acta Numer. 2014, 13, 147–269. [Google Scholar] [CrossRef]
- Caflisch, R.E. Monte Carlo and quasi-Monte Carlo methods. Acta Numer. 1998, 7, 1–49. [Google Scholar] [CrossRef]
- Ogata, Y. A Monte Carlo method for high dimensional integration. Numer. Math. 1989, 55, 137–157. [Google Scholar] [CrossRef]
- Dick, J.; Kuo, F.Y.; Sloan, I.H. High-dimensional integration: The quasi-Monte Carlo way. Acta Numer. 2013, 22, 133–288. [Google Scholar] [CrossRef]
- Hickernell, F.J.; Müller-Gronbach, T.; Niu, B.; Ritter, K. Multi-level Monte Carlo algorithms for infinite-dimensional integration on RN. J. Complexity 2010, 26, 229–254. [Google Scholar] [CrossRef][Green Version]
- Kuo, F.Y.; Schwab, C.; Sloan, I.H. Quasi-Monte Carlo methods for high-dimensional integration: The standard (weighted Hilbert space) setting and beyond. ANZIAM J. 2011, 53, 1–37. [Google Scholar] [CrossRef]
- Lu, J.; Darmofal, L. Higher-dimensional integration with Gaussian weight for applications in probabilistic design. SIAM J. Sci. Comput. 2004, 26, 613–624. [Google Scholar] [CrossRef]
- Wipf, A. High-Dimensional Integrals. In Statistical Approach to Quantum Field Theory; Springer Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 100, pp. 25–46. [Google Scholar]
- E, W.; Yu, B. The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems. Commun. Math. Stat. 2018, 6, 1–12. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Han, J.; Jentzen, A.E.W. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef]
- Xu, J. Finite neuron method and convergence analysis. Commun. Comput. Phys. 2020, 28, 1707–1745. [Google Scholar] [CrossRef]
- Feng, X.; Zhong, H. A fast multilevel dimension iteration algorithm for high dimensional numerical integration. arXiv 2022, arXiv:2210.13658. [Google Scholar]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 10th ed.; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Smolyak, S.A. Quadrature and Interpolation Formulas for Tensor Products of Certain Classes of Functions; Russian Academy of Sciences: Saint Petersburg, Russia, 1963; Volume 148, pp. 1042–1045. [Google Scholar]
- Maruri-Aguilar, H.; Wynn, H. Sparse polynomial prediction. Stat. Pap. 2023, 64, 1233–1249. [Google Scholar] [CrossRef]
- Deluzet, F.; Fubiani, G.; Garrigues, L.; Guillet, C.; Narski, J. Sparse grid reconstructions for Particle-In-Cell methods. ESAIM: Math. Model. Numer. Anal. 2022, 56, 1809–1841. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, D.; Jiang, C. On reliability analysis method through rotational sparse grid nodes. Mech. Sys. Signal Process. 2021, 147, 107106. [Google Scholar] [CrossRef]
- Baszenki, G.; Delvos, F.-J. Multivariate Boolean Midpoint Rules, Numerical Integration IV; Birkhäuser: Basel, Switzerland, 1993; pp. 1–11. [Google Scholar]
- Paskov, S.H. Average case complexity of multivariate integration for smooth functions. J. Complex. 1993, 9, 291–312. [Google Scholar] [CrossRef]
- Bonk, T. A new algorithm for multi-dimensional adaptive numerical quadrature. In Adaptive Methods—Algorithms, Theory and Applications; Vieweg/Teubner Verlag: Wiesbaden, Germany, 1994; pp. 54–68. [Google Scholar]
- Novak, E.; Ritter, K. The curse of dimension and a universal method for numerical integration. In Multivariate Approximation and Splines; Birkhäuser: Basel, Switzerland, 1997; pp. 177–187. [Google Scholar]
- Novak, E.; Ritter, K. High dimensional integration of smooth functions over cubes. Numer. Math. 1996, 75, 79–97. [Google Scholar] [CrossRef]
- Patterson, T.N.L. The optimum addition of points to quadrature formulae. Math. Comp. 1968, 22, 847–856. [Google Scholar] [CrossRef]
- Novak, E.; Ritter, K. Simple Cubature Formulas for d-Dimensional Integrals with High Polynomial Exactness and Small Error; Report; Institut für Mathematik, Universität Erlangen–Nürnberg: Nürnberg, Germany, 1997. [Google Scholar]

| MDI-SG | SG | ||||
|---|---|---|---|---|---|
| Accuracy Level | Total Nodes | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 6 | 33 | 0.0512817 | 0.0078077 | ||
| 7 | 65 | 0.0623538 | 0.0084645 | ||
| 9 | 97 | 0.0644339 | 0.0095105 | ||
| 10 | 161 | 0.0724491 | 0.0106986 | ||
| 13 | 257 | 0.0913161 | 0.0135131 | ||
| 14 | 321 | 0.1072016 | 0.0155733 | ||
| MDI-SG | SG | ||||
|---|---|---|---|---|---|
| Accuracy Level | Total Nodes | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 9 | 97 | 0.0767906 | 0.0098862 | ||
| 10 | 161 | 0.0901238 | 0.0102700 | ||
| 13 | 257 | 0.1025934 | 0.0152676 | ||
| 14 | 321 | 0.1186194 | 0.0144737 | ||
| 16 | 449 | 0.1353691 | 0.0177445 | ||
| 20 | 705 | 0.1880289 | 0.0355606 | ||
| MDI-SG | SG | ||||
|---|---|---|---|---|---|
| Accuracy Level | Total Nodes | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 9 | 495 | 0.0669318 | 0.0235407 | ||
| 10 | 751 | 0.0886774 | 0.0411750 | ||
| 11 | 1135 | 0.0902602 | 0.0672375 | ||
| 13 | 1759 | 0.1088353 | 0.0589584 | ||
| 14 | 2335 | 0.1381728 | 0.0704032 | ||
| 15 | 2527 | 0.1484829 | 0.0902680 | ||
| 16 | 3679 | 0.1525743 | 0.1143728 | ||
| MDI-SG | SG | ||||
|---|---|---|---|---|---|
| Accuracy Level | Total Nodes | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 12 | 1135 | 0.0921728 | 0.0495310 | ||
| 13 | 1759 | 0.1031632 | 0.0644124 | ||
| 15 | 2527 | 0.1771094 | 0.0891040 | ||
| 16 | 3679 | 0.1957219 | 0.1159222 | ||
| 17 | 4447 | 0.2053174 | 0.1443184 | ||
| 19 | 6495 | 0.4801467 | 0.2259950 | ||
| 20 | 8031 | 0.6777698 | 0.2632516 | ||
| MDI-SG | SG | ||||
|---|---|---|---|---|---|
| Dimension () | Total Nodes | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 2 | 161 | 0.0393572 | 0.0103062 | ||
| 4 | 2881 | 0.0807326 | 0.0993984 | ||
| 8 | 206465 | 0.1713308 | 6.7454179 | ||
| 10 | 1041185 | 0.2553576 | 86.816883 | ||
| 12 | 4286913 | 0.3452745 | 866.1886366 | ||
| 14 | 5036449 | 0.4625503 | 6167.3838002 | ||
| 15 | 12533167 | 0.5867914 | failed | failed | |
| MDI-SG | SG | ||||
|---|---|---|---|---|---|
| Dimension () | Total Nodes | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 2 | 161 | 0.0418615 | 0.0191817 | ||
| 4 | 6465 | 0.0704915 | 0.2067346 | ||
| 6 | 93665 | 0.0963325 | 3.1216913 | ||
| 8 | 791169 | 0.2233707 | 41.3632962 | ||
| 10 | 5020449 | 0.3740873 | 821.6461622 | ||
| 12 | 25549761 | 0.8169479 | 11,887.797686 | ||
| 13 | 29344150 | 1.2380811 | failed | failed | |
| MC | MDI-SG | |||
|---|---|---|---|---|
| Dimension () | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 5 | 62.1586394 | 0.0938295 | ||
| 10 | 514.1493073 | 0.1945813 | ||
| 20 | 1851.0461899 | 0.4204564 | ||
| 30 | 15,346.222011 | 0.7692118 | ||
| 35 | failed | 0.9785784 | ||
| 40 | 1.2452577 | |||
| 60 | 2.5959174 | |||
| 80 | 4.9092032 | |||
| 100 | 8.1920274 | |||
| MC | MDI-SG | |||
|---|---|---|---|---|
| Dimension () | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
| 5 | 85.2726354 | 0.0811157 | ||
| 10 | 978.1462121 | 0.295855 | ||
| 20 | 2038.138555 | 6.3939110 | ||
| 30 | 16,872.143255 | 29.5098187 | ||
| 35 | failed | 62.0270714 | ||
| 40 | 106.1616486 | |||
| 80 | 1893.8402620 | |||
| 100 | 3077.1890005 | |||
| Dimension () | Approximate Total Nodes | Relative Error | CPU Time (s) | Relative Error | CPU Time (s) |
|---|---|---|---|---|---|
| 10 | 0.1541 | 0.1945 | |||
| 100 | 80.1522 | 8.1920 | |||
| 300 | 348.6000 | 52.0221 | |||
| 500 | 1257.3354 | 219.8689 | |||
| 700 | 3827.5210 | 574.9161 | |||
| 900 | 9209.119 | 1201.65 | |||
| 1000 | 13225.14 | 1660.84 | |||
| Approximate Total Nodes | Relative Error | CPU Time (s) | Approximate Total Nodes | Relative Error | CPU Time (s) | |
|---|---|---|---|---|---|---|
| 4 (4) | 241 | 0.1260 | 1581 | 0.3185 | ||
| 6 (6) | 2203 | 0.1608 | 40405 | 0.4546 | ||
| 8 (8) | 13073 | 0.2127 | 581385 | 0.6056 | ||
| 10 (10) | 58923 | 0.2753 | 5778965 | 0.7479 | ||
| 12 (12) | 218193 | 0.3402 | 44097173 | 1.0236 | ||
| 14 (14) | 695083 | 0.4421 | 112613833 | 1.2377 | ||
| Approximate Total Nodes | Relative Error | CPU Time (s) | Approximate Total Nodes | Relative Error | CPU Time (s) | |
|---|---|---|---|---|---|---|
| 4 (4) | 241 | 0.1664 | 1581 | 0.3174 | ||
| 6 (6) | 2203 | 0.2159 | 40405 | 0.4457 | ||
| 8 (8) | 13073 | 0.2526 | 581385 | 0.5571 | ||
| 10 (10) | 58923 | 0.3305 | 5778965 | 0.6717 | ||
| 12 (12) | 218193 | 0.3965 | 44097173 | 0.8843 | ||
| 14 (14) | 695083 | 0.5277 | 112613833 | 1.1182 | ||
| Approximate Total Nodes | Relative Error | CPU Time (s) | Approximate Total Nodes | Relative Error | CPU Time (s) | |
|---|---|---|---|---|---|---|
| 4 (4) | 241 | 0.1275 | 1581 | 0.1657 | ||
| 6 (6) | 2203 | 0.1579 | 40405 | 0.2530 | ||
| 8 (8) | 13073 | 0.1755 | 581385 | 0.3086 | ||
| 10 (10) | 58923 | 0.1963 | 5778965 | 0.3889 | ||
| 12 (12) | 218193 | 0.2189 | 44097173 | 0.4493 | ||
| 14 (14) | 695083 | 0.2459 | 112613833 | 0.4864 | ||
| Fitting Function | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Integrand | -Square | -Square | -Square | |||||||
| 5 | 0.0291 | 1 | 0.9683 | 0.0206 | 1.14 | 0.9790 | 0.0024 | 2 | 0.7361 | |
| 5 | 0.0349 | 1 | 0.9564 | 0.0317 | 1.04 | 0.9574 | 0.0029 | 2 | 0.6028 | |
| 5 | 0.0636 | 0.9877 | 0.0609 | 0.52 | 0.9889 | 0.0195 | 1 | 0.3992 | ||
| 10 | 0.0826 | 1 | 0.9692 | 0.0518 | 1.19 | 0.9876 | 0.0070 | 2 | 0.7866 | |
| 10 | 0.0744 | 1 | 0.9700 | 0.0584 | 1.10 | 0.9758 | 0.0062 | 2 | 0.6905 | |
| 10 | 0.0373 | 1 | 0.9630 | 0.0558 | 0.83 | 0.9924 | 0.0109 | 0.6287 | ||
| Integrand | r | m | s | Fitting Function | R-Square | |
|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10(33) | 0.9995 | ||
| 2 | 10 | 1 | 10(33) | 0.9977 | ||
| 3 | 10 | 1 | 10(15) | 0.9946 | ||
| 4 | 10 | 1 | 10(10) | 0.9892 | ||
| 1 | 10 | 1 | 10(33) | 0.9985 | ||
| 2 | 10 | 1 | 10(33) | 0.9986 | ||
| 3 | 5 | 1 | 10(15) | 0.9983 | ||
| 3 | 10 | 1 | 10(15) | 0.9998 | ||
| 3 | 15 | 1 | 10(15) | 0.9955 | ||
| 3 | 15 | 2 | 10(15) | 0.9961 | ||
| 3 | 15 | 3 | 10(15) | 0.9962 | ||
| 4 | 10 | 1 | 10(10) | 0.9965 | ||
| 3 | 5 | 1 | 10(15) | 0.9977 | ||
| 3 | 10 | 1 | 10(15) | 0.9844 | ||
| 3 | 15 | 1 | 10(15) | 0.9997 | ||
| 3 | 10 | 1 | 10(15) | 0.9903 | ||
| 3 | 10 | 1 | 10(15) | 0.9958 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, H.; Feng, X. An Efficient and Fast Sparse Grid Algorithm for High-Dimensional Numerical Integration. Mathematics 2023, 11, 4191. https://doi.org/10.3390/math11194191
Zhong H, Feng X. An Efficient and Fast Sparse Grid Algorithm for High-Dimensional Numerical Integration. Mathematics. 2023; 11(19):4191. https://doi.org/10.3390/math11194191
Chicago/Turabian StyleZhong, Huicong, and Xiaobing Feng. 2023. "An Efficient and Fast Sparse Grid Algorithm for High-Dimensional Numerical Integration" Mathematics 11, no. 19: 4191. https://doi.org/10.3390/math11194191
APA StyleZhong, H., & Feng, X. (2023). An Efficient and Fast Sparse Grid Algorithm for High-Dimensional Numerical Integration. Mathematics, 11(19), 4191. https://doi.org/10.3390/math11194191








