Existence and Uniqueness of Positive Solutions for Semipositone Lane-Emden Equations on the Half-Axis

Abstract

Semipositone Lane–Emden type equations are considered on the half-axis. Such equations have been used in modelling several phenomena in astrophysics and mathematical physics and are often difficult to solve analytically. We provide sufficient conditions for the existence of a positive continuous solution and we describe its global behavior. Our approach is based on a perturbed operator technique and fixed point theorems. Some examples are presented to illustrate the main results.

1. Introduction

In this paper, we consider the semipositone Lane–Emden type equation on the half-axis

$$L_{q}u:=-\frac{1}{A}{\left(A{u}^{\prime }\right)}^{\prime }+qu=\varphi \left(z\right)+\lambda f(z,u),z\in (0,\infty ),$$

(1)

subject to boundary conditions

$$\underset{z\to 0}{lim}\left(A{u}^{\prime }\right)\left(z\right)=0\mathrm{and}\underset{z\to \infty }{lim}u\left(z\right)=0,$$

(2)

where $\lambda \ge 0,$ $f\in C\left(\right(0,\infty )\times \mathbb{R},\mathbb{R}),$ which is allowed taking negative value. In particular, we may have $f(z,0)<0,$ for $z>0$ (i.e., semipositone). The function A satisfies

$\left(H0\right)$$A\in C\left([0,\infty )\right)\cap C^1\left((0,\infty )\right)$ with $A>0$ on $(0,\infty )$ and ${\int }_1^{\infty }\frac{1}{A\left(r\right)}dr<\infty .$

We always assume that q and $\varphi$ are in ${\mathcal{J}}_A$ where

$${\displaystyle {\mathcal{J}}_A:=\{\psi \in C^{+}\left((0,\infty )\right),a_{\psi }:={\int }_0^{\infty }A\left(r\right)\rho \left(r\right)\psi \left(r\right)dr<\infty \},}$$

(3)

and

$$\rho \left(z\right):={\int }_z^{\infty }\frac{1}{A\left(r\right)}dr,\mathrm{for}z>0.$$

(4)

Such problems have been used in modelling many physical and chemical processes such as in chemical reactor theory, astrophysics, mathematical physics and design of suspension bridges (see [1,2,3,4,5,6,7]).

For instance, if $A\left(z\right)\equiv z^{\gamma }(\gamma >1),$$\lambda =1$ and $q\left(z\right)\equiv 0,$ Equation (1) takes the form

$$u^{\prime \prime }\left(z\right)+\frac{\gamma }{z}{u}^{\prime }\left(z\right)+f(z,u)=-\varphi \left(z\right).$$

(5)

Then, Equation (5) with $f(z,u)=e^u,$ $\varphi \left(z\right)=0$ and $\gamma =2$ is known as the Poisson–Boltzmann differential equation. It was used to model the isothermal gas spheres (see [8]). If $f(z,u)=-{\displaystyle \frac{\theta u}{u+k}}$(where $\theta ,k$ are some convenient constants), $\varphi \left(z\right)=0$ and $\gamma =2,$ then Equation (5) is used in the study of steady-state oxygen diffusion in a spherical cell with Michaelis–Menten uptake kinetics (see [9]). On the other hand, from [10], we learned that the heat conduction in human head can be modeled by equation of the form (5) with $f(z,u)=e^{-u},$ $\varphi \left(z\right)=0$ and $\gamma =2.$ Further, Equation (5) with $f(z,u)={(u^2-c)}^{\frac{3}{2}},$ $\varphi \left(z\right)=0$ and $\gamma =2$ was used to model the gravitational potential of a degenerate white-dwarf star (see [11]).

It is also important to observe that equation of the form (1) arises naturally in the study of radially symmetric solutions (ground states) of semi-linear equations, and many works have been conducted in this area; see [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

In [15], Dalmasso, by using the sub-supersolutions method, established an existence result for the semilinear elliptic equation

$$\Delta u+h\left(z\right)u^{-\gamma }=0,\mathrm{in}{\mathbb{R}}^n,$$

(6)

where $n\ge 3,$ $\gamma >0,$ $h\in C_{loc}^{\nu }\left({\mathbb{R}}^n\right),$ $0<\nu <1,$ and $h>0$ on ${\mathbb{R}}^n\setminus \left\{0\right\}$ such that

$$c{p}_0\left(\left|z\right|\right)\le h\left(z\right)\le p_0\left(\left|z\right|\right),z\in {\mathbb{R}}^n,$$

where $c\in (0,1],$ $p_0\left(r\right):=\underset{\left|z\right|=r}{sup}h\left(z\right),$ for $r\ge 0$ and ${\int }_1^{\infty }{r}^{n-1+\gamma (n-2)}{p}_0\left(r\right)dr<\infty .$

It is worth mentioning that the construction of sub-supersolution to (6) was based on the study of the following radial problem:

$$\frac{1}{z^{n-1}}{\left(z^{n-1}{y}^{\prime }\left(z\right)\right)}^{\prime }+p_0\left(z\right)y^{-\gamma }\left(z\right)=0,z>0,$$

(7)

where $n\ge 3$ and $\gamma >0.$

In [26], by means of a sub-supersolutions argument and a perturbed argument, the author showed the existence of entire solutions to the semilinear elliptic problem

$$\left\{\begin{array}{cc}\Delta u+b\left(z\right)g\left(u\right)=0,\hfill & \mathrm{in}{\mathbb{R}}^n(n\ge 3),\hfill \\ u>0,\hfill & \mathrm{in}{\mathbb{R}}^n,\hfill \\ \underset{\left|z\right|\to \infty }{lim}u\left(z\right)=0,\hfill \end{array}\right.$$

(8)

where $b\in C_{loc}^{\nu }\left({\mathbb{R}}^n\right)$ for some $\nu \in (0,1)$ and $b\left(z\right)>0,$ in ${\mathbb{R}}^n$ such that ${\int }_0^{\infty }r\underset{\left|z\right|=r}{sup}b\left(z\right)dr<\infty .$ Function $g\in C^1((0,\infty ),(0,\infty ))$ is required to be sublinear at both 0 and $\infty .$

In [14], the authors studied to the following problem:

$$\left\{\begin{array}{cc}\frac{1}{A}{\left(A{u}^{\prime }\right)}^{\prime }=uh(z,u),\hfill & \mathrm{in}(0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(A{u}^{\prime }\right)\left(z\right)=0,\hfill & \\ \underset{z\to \infty }{lim}u\left(z\right)=c>0,\hfill \end{array}\right.$$

(9)

where A satisfies $\left(H0\right),$ function $z\to zh(.,z)\in C\left(\right[0,\infty \left)\right)$, and the following:

For each $a>0,$ there exists $q_a\in {\mathcal{J}}_A$ such that

$$zh(r,z)-sh(r,s)\le q_a(z-s),\mathrm{for}0\le s\le z\le a\mathrm{and}r>0.$$

They proved, by means of the monotone convergence theorem, the existence of positive bounded solution $u\in C\left([0,\infty )\right)\cap C^1\left((0,\infty )\right)$ satisfying

$$c_1\le u\left(z\right)\le c_2,\mathrm{for}\mathrm{all}z\in (0,\infty ),$$

where $c_1,c_2$ are positive constants.

Our goal in this paper is to take up the existence and uniqueness of a positive continuous solution to (1) and (2) with global behavior. This problem is more challenging with previous works due to the fact that f may change sign (i.e., semipositone). In fact, the study of positive solutions to (1) subject to (2) turns into a nontrivial question as the zero function is not a subsolution, making the method of sub-supersolutions difficult to apply. Our approach is based on a perturbed operator technique and fixed point theorems.

• Notations:

(i)

${\mathcal{B}}^{+}\left((0,\infty )\right)=\{\psi :(0,\infty )\to [0,\infty ),$ Borel measurable functions}.

(ii)

$C_0\left([0,\infty )\right):=\{\psi \in C\left([0,\infty )\right):$$\underset{z\to \infty }{lim}\psi \left(z\right)=0\}.$

Clearly, $(C_0\left([0,\infty )\right),{∥u∥}_{\infty })$ is a Banach space with the norm

$${∥\psi ∥}_{\infty }:=\underset{z\ge 0}{sup}\left|\psi \left(z\right)\right|.$$

In particular, $(C_0\left([0,\infty )\right),d)$ is a complete metric space, with

$$d({\psi }_1,{\psi }_2):={∥{\psi }_1-{\psi }_2∥}_{\infty }.$$

(iii)

For ${\psi }_1,{\psi }_2\in {\mathcal{B}}^{+}\left((0,\infty )\right),$ we say ${\psi }_1\asymp {\psi }_2,$ if there is $c>0$ such that

$$\frac{1}{c}{\psi }_2\left(z\right)\le {\psi }_1\left(z\right)\le c{\psi }_2\left(z\right),\mathrm{for}\mathrm{all}z>0.$$

(iv)

For $p\in C^{+}\left((0,\infty )\right),$ we let $G_p(z,s))$ be the Green’s function of $u\to L_{p}u$ subjected to $\underset{z\to 0}{lim}\left(A{u}^{\prime }\right)\left(z\right)=0$ and $\underset{z\to \infty }{lim}u\left(z\right)=0.$ We recall (see [19]) that for all $(z,s)\in [0,\infty )\times (0,\infty )$,

$$G_p(z,s)=A\left(s\right)\phi \left(z\right)\phi \left(s\right){\int }_{z\vee s}^{\infty }\frac{1}{A\left(r\right){\phi }^2\left(r\right)}dr,$$

(10)

where $z\vee s:=max(z,s)$ and $\phi$ is the unique solution of $L_{p}u=0$ satisfying $\phi \left(0\right)=1$ and $\left(A{\phi }^{\prime }\right)\left(0\right)=0.$

In particular, if $p\equiv 0,$ then $\phi \equiv 1$ and

$$G(z,s):=G_0(z,s)=A\left(s\right)\rho (z\vee s).$$

(11)

(v)

For $p\in C^{+}\left((0,\infty )\right)$ and $\psi \in {\mathcal{B}}^{+}\left((0,\infty )\right),$ we let

$$V_p\psi \left(z\right):={\int }_0^{\infty }{G}_p(z,r)\psi \left(r\right)dr\mathrm{and}V\psi \left(z\right):={\int }_0^{\infty }G(z,r)\psi \left(r\right)dr,\mathrm{for}z\ge 0.$$

(12)

We note that if $\psi \in {\mathcal{J}}_A,$ then $V\psi \in C_0\left([0,\infty )\right)$ and

$$V\psi \left(0\right)=a_{\psi }={∥V\psi ∥}_{\infty }.$$

(13)

From [19] Theorem 2, we learned that if $\psi \in {\mathcal{J}}_A,$ then $V_p\psi \in C_0\left([0,\infty )\right)$ is the unique solution of problem

$$\left({\mathcal{H}}_{\psi }\right)\left\{\begin{array}{cc}{L}_{p}u=\psi \hfill & \mathrm{in}(0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(A{u}^{\prime }\right)\left(z\right)=0,\hfill & \\ \underset{z\to \infty }{lim}u\left(z\right)=0.\hfill \end{array}\right.$$

(14)

(vi)

For $\psi \in {\mathcal{B}}^{+}\left((0,\infty )\right),$ we let

$${\sigma }_{\psi }:=\underset{z,s\in (0,\infty )}{sup}{\int }_0^{\infty }\frac{G(z,r)G(r,s)}{G(z,s)}\psi \left(r\right)dr.$$

(15)

It can be seen that if $\psi \in {\mathcal{J}}_A,$ then

$${\sigma }_{\psi }=a_{\psi }<\infty .$$

(16)

2. Preliminaries

Lemma 1.

The Green’s function $G(z,s)$ (see (11)) satisfies

(i) 

G is continuous on $[0,\infty )\times (0,\infty ),$ with

$$0\le G(z,s)=A\left(s\right)min\left(\rho \right(z),\rho (s\left)\right),\mathrm{for}\mathrm{all}z,s>0.$$

(17)

In particular, $\underset{z\to \infty }{lim}G(z,s)=0,$ for all $s\ge 0.$

(ii) 

For all $z,s,\varsigma \in (0,\infty ),$

$$\frac{G(z,\varsigma )G(\varsigma ,s)}{G(z,s)}\le A\left(\varsigma \right)\rho \left(\varsigma \right).$$

(18)

Proof. 

Clearly, $\left(i\right)$ holds.

$\left(ii\right)$ From (17), we have, for all $z,s,\varsigma \in (0,\infty ),$

$$\frac{G(z,\varsigma )G(\varsigma ,s)}{G(z,s)}=A\left(\varsigma \right)\frac{min\left(\rho \right(z),\rho (\varsigma \left)\right)min\left(\rho \right(\varsigma ),\rho (s\left)\right)}{min\left(\rho \right(z),\rho (s\left)\right)}.$$

We claim that

$$H(z,\varsigma ,s):=\frac{min\left(\rho \right(z),\rho (\varsigma \left)\right)min\left(\rho \right(\varsigma ),\rho (s\left)\right)}{min\left(\rho \right(z),\rho (s\left)\right)}\le \rho \left(\varsigma \right).$$

By symmetry, we may assume that $z\le s.$ Hence, $\rho \left(z\right)\ge \rho \left(s\right).$

Therefore, we discuss the following cases:

Case 1. If $z\le s\le \varsigma ;$ then,

$$H(z,\varsigma ,s)=\frac{\rho \left(\varsigma \right)\rho \left(\varsigma \right)}{\rho \left(s\right)}\le \rho \left(\varsigma \right).$$

Case 2. If $z\le \varsigma \le s,$ then

$$H(z,\varsigma ,s)=\frac{\rho \left(\varsigma \right)\rho \left(s\right)}{\rho \left(s\right)}=\rho \left(\varsigma \right).$$

Case 3. If $\varsigma \le z\le s,$ then

$$H(z,\varsigma ,s)=\frac{\rho \left(z\right)\rho \left(s\right)}{\rho \left(s\right)}=\rho \left(z\right)\le \rho \left(\varsigma \right).$$

The proof is completed. □

The next Lemma is crucial in the rest of the paper.

Lemma 2

((See [19])). Let $p\in {\mathcal{J}}_A,$ then

(i) 

$$V\psi =V_p\psi +V_p\left(pV\right)\left(\psi \right)=V_p\psi +V\left(p{V}_p\right)\left(\psi \right),\mathrm{for}\psi \in {\mathcal{B}}^{+}\left((0,\infty )\right).$$

(19)

(ii) 

for $z,\varsigma \in [0,\infty ),$

$$e^{-Vp\left(0\right)}G(z,\varsigma )\le G_p(z,\varsigma )\le G(z,\varsigma ).$$

(20)

In particular,

$$e^{-Vp\left(0\right)}V\psi \le V_p\psi \le V\psi ,\mathrm{for}\psi \in {\mathcal{B}}^{+}\left((0,\infty )\right).$$

(21)

Remark 1.

Let $p\in C^{+}\left((0,\infty )\right);$ then,

(i) 

$G_p$ is continuous on $[0,\infty ))\times (0,\infty )$ with $\underset{z\to \infty }{lim}{G}_p(z,\varsigma )=0,$ for all $\varsigma \ge 0.$

(ii) 

For all $z,s,\varsigma \in (0,\infty ),$

$$\frac{G_p(z,\varsigma )G_p(\varsigma ,s)}{G_p(z,s)}\le e^{a_p}A\left(\varsigma \right)\rho \left(\varsigma \right).$$

Lemma 3.

Let $p,h\in {\mathcal{J}}_A$ and $\psi \in {\mathcal{B}}^{+}\left((0,\infty )\right)$; then, ${\sigma }_h<\infty$ and

$$V_p\left(h{V}_p\psi \right)\left(z\right)\le {\sigma }_h{e}^{a_p}{V}_p\psi \left(z\right),\mathit{for}\mathit{z}>0.$$

(22)

Proof. 

Let $h\in {\mathcal{J}}_A$ and $\psi \in {\mathcal{B}}^{+}\left((0,\infty )\right)$; then, from (18), for all $z,s\in (0,\infty ),$

$${\int }_0^{\infty }\frac{G(z,\varsigma )G(\varsigma ,s)}{G(z,s)}h\left(\varsigma \right)d\varsigma \le {\int }_0^{\infty }A\left(\varsigma \right)\rho \left(\varsigma \right)h\left(\varsigma \right)d\varsigma :=a_h<\infty .$$

Therefore,

$${\sigma }_h\le a_h<\infty .$$

(23)

On the other hand, from Lemma 2, the Fubini–Tonelli theorem and (15), obtain, for $z>0,$

$$\begin{array}{ccc}\hfill V_p\left(h{V}_p\psi \right)\left(z\right)& \le & V\left(hV\psi \right)\left(z\right)\hfill \\ & =& {\int }_0^{\infty }G(z,s)h\left(s\right)\left({\int }_0^{\infty }G(s,\varsigma )\psi \left(\varsigma \right)d\varsigma \right)ds\hfill \\ & =& {\int }_0^{\infty }\psi \left(\varsigma \right)\left({\int }_0^{\infty }G(z,s)G(s,\varsigma )h\left(s\right)ds\right)d\varsigma \hfill \\ & \le & {\sigma }_h{\int }_0^{\infty }G(z,\varsigma )\psi \left(\varsigma \right)d\varsigma \hfill \\ & =& {\sigma }_h{e}^{a_p}{V}_p\psi \left(z\right).\hfill \end{array}$$

□

Remark 2.

Let $h\in {\mathcal{J}}_A;$ then, ${\sigma }_h=a_h.$

Indeed, from (23), it remains to be proven that $a_h\le {\sigma }_h.$

To this end, observe that

$$\underset{z\to 0}{lim}\frac{\rho (z\vee \varsigma )\rho (\varsigma \vee s)}{\rho (z\vee s)}=\frac{\rho \left(\varsigma \right)\rho (\varsigma \vee s)}{\rho \left(s\right)}\mathrm{and}\underset{s\to \infty }{lim}\frac{\rho \left(\varsigma \right)\rho (\varsigma \vee s)}{\rho \left(s\right)}=\rho \left(\varsigma \right).$$

Therefore, by Fatou’s lemma, obtain

$$a_h={\int }_0^{\infty }A\left(\varsigma \right)\rho \left(\varsigma \right)h\left(\varsigma \right)d\varsigma \le \underset{s\to \infty }{liminf}{\int }_0^{\infty }A\left(\varsigma \right)\frac{\rho \left(\varsigma \right)\rho (\varsigma \vee s)}{\rho \left(s\right)}h\left(\varsigma \right)d\varsigma$$

and

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }A\left(\varsigma \right)\frac{\rho \left(\varsigma \right)\rho (\varsigma \vee s)}{\rho \left(s\right)}h\left(\varsigma \right)d\varsigma & \le & \underset{z\to 0}{liminf}{\int }_0^{\infty }A\left(\varsigma \right)\frac{\rho (z\vee \varsigma )\rho (\varsigma \vee s)}{\rho (z\vee s)}h\left(\varsigma \right)d\varsigma \hfill \\ & =& \underset{z\to 0}{liminf}{\int }_0^{\infty }\frac{G(z,\varsigma )G(\varsigma ,s)}{G(z,s)}h\left(\varsigma \right)d\varsigma \hfill \\ & \le & {\sigma }_h.\hfill \end{array}$$

Hence, $a_h\le {\sigma }_h.$

Proposition 1.

Let $A\left(r\right)=r^{\gamma }$ with $\gamma >1$ and $\xi <2<\zeta .$

Consider $\varphi \left(r\right)={\displaystyle \frac{1}{r^{\xi }{(1+r)}^{\zeta -\xi }}},$ for $r>0.$ Then, $\varphi \in {\mathcal{J}}_A$ and

$$V\varphi \left(z\right)\asymp \left\{\begin{array}{cc}{\displaystyle \frac{1}{{(1+z)}^{\zeta -2}}}\hfill & \mathit{if}2<\zeta <\gamma +1,\hfill \\ {\displaystyle \frac{log(z+2)}{{(1+z)}^{\gamma -1}}}\hfill & \mathit{if}\zeta =\gamma +1,\hfill \\ {\displaystyle \frac{1}{{(1+z)}^{\gamma -1}}}\hfill & \mathit{if}\zeta >\gamma +1.\hfill \end{array}\right.$$

(24)

Proof. 

Since $A\left(r\right)=r^{\gamma },$ then

$$\rho \left(z\right):={\int }_z^{\infty }\frac{1}{A\left(r\right)}dr=\frac{1}{\gamma -1}{z}^{1-\gamma }.$$

Therefore,

$${\displaystyle a_{\varphi }=\frac{1}{\gamma -1}{\int }_0^{\infty }r\varphi \left(r\right)dr=\frac{1}{\gamma -1}{\int }_0^{\infty }{\displaystyle \frac{1}{r^{\xi -1}{(1+r)}^{\zeta -\xi }}}dr<\infty .}$$

That is, $\varphi \in {\mathcal{J}}_A.$

To prove (24), we proceed as follows:

Case 1. $z\in [0,1].$

Since $z\to V\varphi \left(z\right)\in C\left(\right[0,1\left]\right)$ with $V\varphi >0$ on $[0,1],$ we deduce that

$$V\varphi \left(z\right)\asymp 1,\mathrm{on}[0,1].$$

Case 2. $z\in [1,\infty ).$

On $[1,\infty ),$ we have

$$\begin{array}{ccc}\hfill V\varphi \left(z\right)& \asymp & {\int }_z^{\infty }{s}^{-\gamma }({\int }_0^1{\displaystyle \frac{r^{\gamma -\xi }}{{(1+z)}^{\zeta -\xi }}}dr+{\int }_1^s{r}^{\gamma -\zeta }dr)ds\hfill \\ & \asymp & {\int }_z^{\infty }{s}^{-\gamma }(1+{\int }_1^s{r}^{\gamma -\zeta }dr)ds.\hfill \end{array}$$

(i)

If $2<\zeta <\gamma +1,$ then

$${\int }_1^s{r}^{\gamma -\zeta }dr=\frac{1}{\gamma +1-\zeta }(s^{\gamma +1-\zeta }-1)\asymp (s^{\gamma +1-\zeta }-1).$$

Therefore,

$$V\varphi \left(z\right)\asymp {\int }_z^{\infty }{s}^{1-\zeta }ds\asymp z^{2-\zeta }\asymp {(1+z)}^{2-\zeta }.$$

(ii)

If $\zeta =\gamma +1,$ then

$$(1+{\int }_1^s{r}^{\gamma -\zeta }dr)\asymp log\left(es\right).$$

Hence,

$$\begin{array}{ccc}\hfill V\varphi \left(z\right)& \asymp & {\int }_z^{\infty }{r}^{-\gamma }log\left(er\right)dr\hfill \\ & \asymp & {\int }_{ez}^{\infty }{r}^{-\gamma }log\left(r\right)dr\hfill \\ & \asymp & z^{1-\gamma }log(z+1)\hfill \\ & \asymp & {(1+z)}^{1-\gamma }log(z+2).\hfill \end{array}$$

(iii)

If $\zeta >\gamma +1,$ then

$$1+{\int }_1^s{r}^{\gamma -\zeta }dr\asymp 1.$$

Therefore,

$$V\varphi \left(z\right)\asymp {\int }_z^{\infty }{s}^{-\gamma }ds\asymp z^{1-\gamma }\asymp {(1+z)}^{1-\gamma }.$$

The estimates in (24) follow by combining the two cases. □

3. Main Results

To study Problems (1) and (2), we make the following assumptions on f:

$\left(H1\right)$ $f\in C\left(\right(0,\infty )\times \mathbb{R},\mathbb{R})$ and for some $k\ge 0,$

$$\left|f(z,0)\right|\le k\varphi \left(z\right),\mathrm{for}\mathrm{all}z>0,$$

where $\varphi \in {\mathcal{J}}_A$ with $\varphi \ne 0.$

$\left(H2\right)$ there exists function $g\in {\mathcal{J}}_A$ such that

$$\left|f(z,t)-f(z,r)\right|\le g\left(z\right)\left|t-r\right|,\mathrm{for}\mathrm{all}z>0\mathrm{and}t,r\in \mathbb{R}.$$

The next Lemma is used for existence and uniqueness.

Lemma 4.

Suppose that $\left(H0\right)$–$\left(H2\right)$ hold and let $u\in C_0\left([0,\infty )\right).$ Then, u is a solution of Problems (1) and (2) if and only if

$${\displaystyle u\left(z\right)=V_q\varphi \left(z\right)+\lambda {\int }_0^{\infty }{G}_q(z,\varsigma )f(\varsigma ,u\left(\varsigma \right))d\varsigma ,\mathrm{for}z\ge 0.}$$

(25)

Proof. 

Assume that u satisfies (25).

Since A satisfies $\left(H0\right)$ and $\varphi \in {\mathcal{J}}_A,$ then, from (14), we already know that $V_q\varphi \in C_0\left([0,\infty )\right)$ and it is a solution of

$$\left({\mathcal{H}}_{\varphi }\right)\left\{\begin{array}{cc}{L}_{q}v=\varphi \hfill & \mathrm{in}(0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(A{v}^{\prime }\right)\left(z\right)=0,\hfill & \\ \underset{z\to \infty }{lim}v\left(z\right)=0.\hfill \end{array}\right.$$

(26)

Now, by using $\left(H1\right)$ and $\left(H2\right),$ obtain

$$\begin{array}{ccc}\hfill \left|f(\varsigma ,u(\varsigma \left)\right)\right|& \le & \left|f(\varsigma ,u(\varsigma \left)\right)-f(\varsigma ,0)\right|+\left|f(\varsigma ,0)\right|\hfill \\ & \le & g\left(\varsigma \right)\left|u\left(\varsigma \right)\right|+k\varphi \left(\varsigma \right))\hfill \\ & \le & \beta {∥u∥}_{\infty }g\left(\varsigma \right)+k\varphi \left(\varsigma \right).\hfill \end{array}$$

Since $g,\varphi \in {\mathcal{J}}_A,$ deduce that $\varsigma \to \left|f(\varsigma ,u(\varsigma \left)\right)\right|\in {\mathcal{J}}_A$ and therefore, by [19] Theorem 2, conclude that $\omega :=V_{q}f(.,u)$ belongs to $C_0\left([0,\infty )\right)$ and satisfies

$$\left\{\begin{array}{cc}{L}_q\omega =f(.,u)\hfill & \mathrm{in}(0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(A{\omega }^{\prime }\right)\left(z\right)=0\mathrm{and}\underset{z\to \infty }{lim}\omega \left(z\right)=0.\hfill \end{array}\right.$$

(27)

Hence, from (26) and (27), u is a solution of Problems (1) and (2).

Conversely, assume that u satisfies (1) and (2); then, $w\left(z\right):=u\left(z\right)-V_q\varphi \left(z\right)-\lambda V_{q}f(.,u)\left(z\right),$ verifies

$$\left({\mathcal{H}}_0\right)\left\{\begin{array}{cc}{L}_{q}w=0\hfill & \mathrm{in}(0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(A{w}^{\prime }\right)\left(z\right)=0,\hfill & \\ \underset{z\to \infty }{lim}w\left(z\right)=0.\hfill \end{array}\right.$$

From the uniqueness in [19] Theorem 2, conclude that $w\equiv 0.$ Namely u satisfies (25). □

Theorem 1.

Under conditions $\left(H0\right)$, $\left(H1\right)$ and $\left(H2\right),$ there exists ${\lambda }^{\ast }>0$ such that for $\lambda \in [0,{\lambda }^{\ast })$ Equation (1) subjected to (2) admit a unique solution $u\in C_0\left([0,\infty )\right)$ with

$$\alpha V_q\varphi \left(z\right)\le u\left(z\right)\le \beta V_q\varphi \left(z\right),\mathrm{for}z\ge 0,$$

(28)

where $\alpha ={\displaystyle \frac{2({\lambda }^{\ast }-\lambda (k{\lambda }^{\ast }+e^{a_q}))}{(2{\lambda }^{\ast }-\lambda e^{a_q})}}$ and $\beta ={\displaystyle \frac{2(1+\lambda k){\lambda }^{\ast }}{(2{\lambda }^{\ast }-\lambda e^{a_q})}}.$

Proof. 

Suppose that $\left(H1\right)$ and $\left(H2\right)$ hold and put ${\lambda }^{\ast }=\frac{1}{2a_g}>0.$ For $\lambda \in [0,{\lambda }^{\ast });$ let

$$\alpha :=\frac{1-\lambda (k+2a_g{e}^{a_q})}{1-\lambda a_g{e}^{a_q}}\mathrm{and}\beta =:\frac{1+\lambda k}{1-\lambda a_g{e}^{a_q}}.$$

Consider set

$$\mathrm{\Lambda }=\{v\in C_0\left([0,\infty )\right),\alpha V_q\varphi \left(z\right)\le v\left(z\right)\le \beta V_q\varphi \left(z\right),\mathrm{for}z\ge 0\}.$$

Since $\varphi \in {\mathcal{J}}_A,$ then, from [19] Theorem 2, $V_q\varphi$ belongs to $C_0\left([0,\infty )\right)$ and therefore $V_q\varphi \in \mathrm{\Lambda }.$ Due to the fact that $\mathrm{\Lambda }$ is a closed subset of $(C_0\left([0,\infty )\right),d),$$(\mathrm{\Lambda },d)$ becomes a complete metric space.

Consider T defined on $\mathrm{\Lambda }$ by

$${\displaystyle Tv\left(z\right)=V_q\varphi \left(z\right)+\lambda {\int }_0^{\infty }{G}_q(z,\varsigma )f(\varsigma ,v\left(\varsigma \right))d\varsigma ,z\ge 0.}$$

(29)

We prove that $T\left(\mathrm{\Lambda }\right)\subset \mathrm{\Lambda }.$ Therefore, let v be an element of $\mathrm{\Lambda }$.

By using $\left(H1\right)$ and $\left(H2\right),$ obtain

$$\begin{array}{ccc}\hfill \left|f(\varsigma ,v(\varsigma \left)\right)\right|& \le & \left|f(\varsigma ,v(\varsigma \left)\right)-f(\varsigma ,0)\right|+\left|f(\varsigma ,0)\right|\hfill \\ & \le & \beta g\left(\varsigma \right)V_q\varphi \left(\varsigma \right)+k\varphi \left(\varsigma \right))\hfill \\ & \le & \beta {∥V_q\varphi ∥}_{\infty }g\left(\varsigma \right)+k\varphi \left(\varsigma \right).\hfill \end{array}$$

Since $g,\varphi \in {\mathcal{J}}_A,$ we deduce that $\varsigma \to \left|f(\varsigma ,v(\varsigma \left)\right)\right|\in {\mathcal{J}}_A$ and again by [19] Theorem 2, the function $V_{q}f(.,v)$ becomes in $C_0\left([0,\infty )\right).$

Hence, $Tv\in C_0\left([0,\infty )\right).$

On the other hand, by using, again, $\left(H1\right),$$\left(H2\right)$, Lemma 3 and Remark 2, we deduce that

$$\begin{array}{ccc}\hfill \left|{\displaystyle {\int }_0^{\infty }{G}_q(z,\varsigma )f(\varsigma ,v\left(\varsigma \right))d\varsigma }\right|& \le & {\displaystyle {\int }_0^{\infty }{G}_q(z,\varsigma )(\left|f(\varsigma ,v(\varsigma \left)\right)-f(\varsigma ,0)\right|+\left|f(\varsigma ,0)\right|)d\varsigma }\hfill \\ & \le & \beta V_q\left(g{V}_q\varphi \right)\left(z\right)+k{V}_q\varphi \left(z\right)\hfill \\ & \le & (\beta a_g{e}^{a_q}+k)V_q\varphi \left(z\right)\hfill \\ & \le & \left(\frac{k+a_g{e}^{a_q}}{1-\lambda a_g{e}^{a_q}}\right)V_q\varphi \left(z\right).\hfill \end{array}$$

Hence, $T\left(\mathrm{\Lambda }\right)\subset \mathrm{\Lambda }.$

Next, we aim at proving that T is a contraction operator from $(\mathrm{\Lambda },d)$ into itself.

To this end, take $v_1,v_2\in \mathrm{\Lambda };$ then, by using $\left(H1\right),$ $\left(H2\right),$ (20) and (17), obtain for $z\ge 0$

$$\begin{array}{ccc}\hfill \left|T{v}_1\left(z\right)-T{v}_2\left(z\right)\right|& \le & {\displaystyle \lambda {\int }_0^{\infty }G(z,\varsigma )\left|f(\varsigma ,v_1\left(\varsigma \right))-f(\varsigma ,v_2\left(\varsigma \right))\right|d\varsigma }\hfill \\ & \le & {\displaystyle \lambda {\int }_0^{\infty }A\left(\varsigma \right)\rho \left(\varsigma \right)g\left(\varsigma \right)\left|v_1\left(\varsigma \right)-v_2\left(\varsigma \right)\right|d\varsigma }\hfill \\ & \le & {\displaystyle \lambda d(v_1,v_2){\int }_0^{\infty }A\left(\varsigma \right)\rho \left(\varsigma \right)g\left(\varsigma \right)d\varsigma }\hfill \\ & =& \lambda a_{g}d(v_1,v_2).\hfill \end{array}$$

Hence,

$$d(T{v}_1,T{v}_2)\le \lambda a_{g}d(v_1,v_2).$$

Since $\lambda a_g<\frac{1}{2},$ then, by the Banach’s contraction principle, there exists a unique $u\in \mathrm{\Lambda },$ satisfying

$${\displaystyle u\left(z\right)=V_q\varphi \left(z\right)+\lambda {\int }_0^{\infty }{G}_q(z,\varsigma )f(\varsigma ,u\left(\varsigma \right))d\varsigma .}$$

(30)

From Lemma 4, we conclude that u is the unique solution of Problems (1) and (2) verifying (28). □

Remark 3.

Under the same assumptions as in Theorem 1, we know from the Banach’s contraction principle that for any $u_0\in C_0\left([0,\infty )\right)$ satisfying (28), the iterative sequence ${\displaystyle u_j\left(z\right):=V_q\varphi \left(z\right)+\lambda {\int }_0^{\infty }{G}_q(z,\varsigma )f(\varsigma ,u_{j-1}\left(\varsigma \right))d\varsigma }$ converges uniformly to $u,$ the unique solution of Problems (1) and (2), and we have

$${∥u_j-u∥}_{\infty }\le \frac{{\lambda }^{\ast }}{(2{\lambda }^{\ast }-\lambda )2^{j-1}}{∥u_1-u_0∥}_{\infty }.$$

(31)

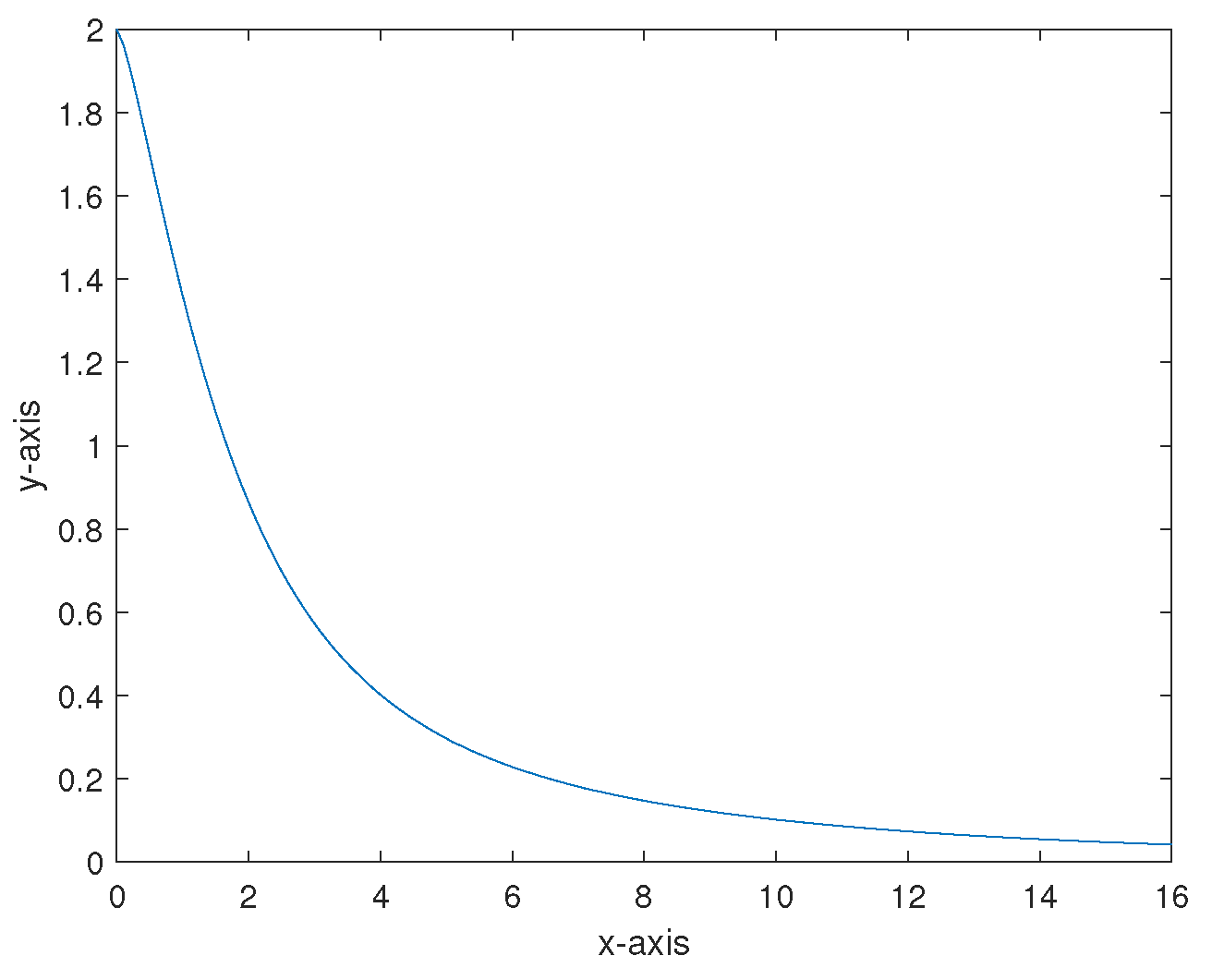
4. Examples

Example 1.

Let $2<\zeta <3$ and consider

$$\varphi \left(z\right):={\displaystyle \frac{1}{z{(1+z)}^{\zeta -1}}},\mathrm{for}z>0.$$

For $\lambda \in [0,\frac{\zeta -2}{2}),$ problem

$$\left\{\begin{array}{cc}-\frac{1}{z^2}{\left(z^2{v}^{\prime }\right)}^{\prime }+e^{-z}v=\varphi \left(z\right)+\lambda \varphi \left(z\right)(cosv-2),\hfill & z\in (0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(z^2{v}^{\prime }\right)\left(z\right)=0\mathrm{and}\underset{z\to \infty }{lim}v\left(z\right)=0,\hfill \end{array}\right.$$

(32)

admits a unique solution v in $C_0\left([0,\infty )\right)$ satisfying

$$v\left(z\right)\asymp {\displaystyle \frac{1}{{(1+z)}^{\zeta -2}}}.$$

(33)

We may apply Theorem 1, with $A\left(z\right):=z^2,$ $q\left(z\right):=e^{-z}$ and $f(z,v)=\varphi \left(z\right)(cosv-2).$

Indeed, clearly, $A\left(z\right)$ satisfies $\left(H0\right)$ and functions $q,$ ϕ belong to ${\mathcal{J}}_A.$

On the other hand, f satisfies $\left(H1\right)$ with $k=1$ and $\left(H2\right)$ with $g\left(z\right)=\varphi \left(z\right)\in {\mathcal{J}}_A.$

By simple computation, we obtain ${\lambda }^{\ast }:=\frac{1}{2a_g}=\frac{1}{2Vg\left(0\right)}=\frac{\zeta -2}{2}.$

Estimates in (33) follow from (28), (21) and Proposition 1.

Example 2.

Let $a<2$ and $b<2.$ Put

$$\varphi \left(z\right):={\displaystyle \frac{1}{z{(1+z)}^3}},\mathrm{for}z>0.$$

For $\lambda \in [0,\frac{1}{\Gamma (2-b)}),$ problem

$$\left\{\begin{array}{cc}-\frac{1}{z^3}{\left(z^3{v}^{\prime }\right)}^{\prime }+z^{-a}{e}^{-z}v=\varphi \left(z\right)+\lambda z^{-b}{e}^{-z}{tan}^{-1}v,\hfill & z\in (0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(z^3{v}^{\prime }\right)\left(z\right)=0\mathrm{and}\underset{z\to \infty }{lim}v\left(z\right)=0\hfill \end{array}\right.$$

(34)

admits a unique solution v in $C_0\left([0,\infty )\right)$ satisfying

$$v\left(z\right)\asymp {\displaystyle \frac{log(z+2)}{{(1+z)}^2}}.$$

(35)

Indeed, in this case we have $A\left(z\right):=z^3,$ $q\left(z\right):=z^{-a}{e}^{-z}$ and $f(z,v):=z^{-b}{e}^{-z}{tan}^{-1}v.$

It is clear that $A\left(z\right)$ satisfies $\left(H0\right)$ and the functions q and ϕ belongs to ${\mathcal{J}}_A.$

Since $f(z,0)=0,$ then $\left(H1\right)$ is valid with $k=0$ and hypothesis $\left(H2\right)$ is satisfied with $g\left(z\right):=z^{-b}{e}^{-z}\in {\mathcal{J}}_A.$

By simple computation we obtain ${\lambda }^{\ast }:=\frac{1}{2a_g}=\frac{1}{2Vg\left(0\right)}=\frac{1}{\Gamma (2-b)}.$

So the conclusion follows from Theorem 1. Estimates in (35) can be obtained from (28), (21) and Proposition 1.

Example 3.

Let $b<3$ and consider

$$\varphi \left(z\right):={\displaystyle \frac{1}{z^2{(1+z)}^4}},\mathrm{for}z>0.$$

For $\lambda \in [0,\frac{3}{2\Gamma (3-b)}),$ the problem

$$\left\{\begin{array}{cc}-\frac{1}{z^4}{\left(z^4{v}^{\prime }\right)}^{\prime }=\varphi \left(z\right)+\lambda z^{-b}{e}^{-z}sin\left(zv\right),\hfill & z\in (0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(z^4{v}^{\prime }\right)\left(z\right)=0\mathrm{and}\underset{z\to \infty }{lim}v\left(z\right)=0,\hfill \end{array}\right.$$

(36)

admits a unique solution v in $C_0\left([0,\infty )\right)$ satisfying

$$v\left(z\right)\asymp {\displaystyle \frac{1}{{(1+z)}^3}}.$$

(37)

Indeed, as in the previous examples, we may apply Theorem 1 with $A\left(z\right):=z^3,$ $q\left(z\right)\equiv 0$ and $f(z,v):=z^{-b}{e}^{-z}sin\left(zv\right).$ In this case, $\left(H0\right)$ and $\left(H1\right)$ are obviously verified and $\left(H2\right)$ is satisfied with $g\left(z\right):=z^{1-b}{e}^{-z}.$ By simple computation we obtain ${\lambda }^{\ast }:=\frac{1}{2a_g}=\frac{1}{2Vg\left(0\right)}=\frac{3}{2\Gamma (3-b)}.$ Estimates in (37) follow as above from (28), (21) and Proposition 1.

Example 4.

Let $A\left(t\right)=e^t$ and $q\in C^{+}\left((0,\infty )\right)\cap L^1\left((0,\infty )\right)\subset {\mathcal{J}}_A.$ For $\lambda \in [0,\frac{1}{4}),$ the problem

$$\left\{\begin{array}{cc}-\frac{1}{A}{\left(A{v}^{\prime }\right)}^{\prime }+qv=\varphi \left(z\right)+\lambda \varphi \left(z\right)\sqrt{1+v^2},\hfill & z\in (0,\infty ),\hfill \\ \underset{z\to 0}{lim}\left(A{v}^{\prime }\right)\left(z\right)=0\mathrm{and}\underset{z\to \infty }{lim}v\left(z\right)=0,\hfill \end{array}\right.$$

(38)

admits a unique solution v in $C_0\left([0,\infty )\right)$ satisfying

$$v\left(z\right)\asymp V_q\varphi \left(z\right)\asymp V\varphi \left(z\right),$$

(39)

where $\varphi \left(z\right):=\frac{e^{-\sqrt{z}}}{\sqrt{z}}\in {\mathcal{J}}_A$ and the graph of $V\varphi \left(z\right)$ is given in Figure 1.

Figure 1. Graph of $V\varphi$.

Indeed, it is clear that $\left(H0\right)$ is satisfied and $\left(H1\right)$ is valid with $k=1.$ Hypotheses $\left(H2\right)$ hold with $g\left(z\right):=\varphi \left(z\right)$ and by computation we obtain ${\lambda }^{\ast }:=\frac{1}{2a_g}=\frac{1}{2Vg\left(0\right)}=\frac{1}{4}.$

So the conlusion follows from Theorem 1 and (21).

5. Conclusions

A semipositone Lane-Emden type equations on the half-axis have been studied. Such problems are more interesting and challenging due to the fact that the nonlinearity can take negative value. We have proved the existence and uniqueness of a positive continuous solution and described its global behavior. The approach is based on a combination of properties of the perturbed operator and some fixed point theorems. It will be interesting to investigate similar problems for others operators.