Bifurcation, Hidden Chaos, Entropy and Control in Hénon-Based Fractional Memristor Map with Commensurate and Incommensurate Orders

Abstract

In this paper, we present an innovative 3D fractional Hénon-based memristor map and conduct an extensive exploration and analysis of its dynamic behaviors under commensurate and incommensurate orders. The study employs diverse numerical techniques, such as visualizing phase portraits, analyzing Lyapunov exponents, plotting bifurcation diagrams, and applying the sample entropy test to assess the complexity and validate the chaotic characteristics. However, since the proposed fractional map has no fixed points, the outcomes reveal that the map can exhibit a wide range of hidden dynamical behaviors. This phenomenon significantly augments the complexity of the fractal structure inherent to the chaotic attractors. Moreover, we introduce nonlinear controllers designed for stabilizing and synchronizing the proposed fractional Hénon-based memristor map. The research emphasizes the system’s sensitivity to fractional-order parameters, resulting in the emergence of distinct dynamic patterns. The memristor-based chaotic map exhibits rich and intricate behavior, making it a captivating and significant area of investigation.

1. Introduction

Discrete fractional calculus has emerged as a captivating research area that has grabbed the interest of mathematicians and scholars in various disciplines over the last decade. Its applications span diverse fields, including biology, ecology, and applied sciences, offering valuable insights into real-world challenges. Fractional systems have demonstrated the ability to describe complex nonlinear phenomena with greater accuracy compared to traditional integer-order systems [1], showcasing their unique properties, including long-term memory, viscosity, and flexibility. Recently, there has been a surge in published articles addressing this intriguing topic. Researchers have been offering various discrete-time fractional operators, conducting stability analyses, and presenting numerous theoretical findings [2,3,4,5,6]. Notably, Wu and Baleanu presented the first study that delves into the modeling of fractional chaotic maps using the left Caputo-like operator and investigates their chaotic characteristics [7]. As a result of these advances, this work paved the way for the emergence of more commensurate- and non-commensurate-order chaotic maps [8,9,10,11,12,13], in addition to exploring diverse control strategies and synchronization schemes that have been developed to synchronize the interactions between different fractional discrete chaotic systems [14,15,16,17]. These studies reflected that the system’s behavior is highly dependent on the chosen fractional order, showcasing its non-linear and complex nature, which makes it a fascinating subject of study in the field of fractional dynamics.

A memory resistor, commonly known as a “memristor”, has been widely recognized as the fourth fundamental circuit element that serves as a link between charge and magnetic flux. The theoretical concept of the memristor was initially forwarded by Chua in 1971 [18]. For an extended period, memristor research remained primarily theoretical until the first physical implementation of a memristor was achieved by HP laboratories in 2008. They successfully developed the first practical memristor using nanomaterials [19]. It has since become an essential component in various applications due to its unique properties and potential to revolutionize memory and computing technologies. Memristors have garnered significant attention and research interest, contributing to the advancement of various fields, including electronics [20], computing [21], nonvolatile memory [22], and neuromorphic systems [23].

In general, memristor-based chaotic systems are commonly designed using differential equations in the continuous-time domain [24]. However, until recent years, discrete-time memristive maps had not been extensively explored or discussed. In practice, discrete chaotic systems offer the advantage of avoiding parameter sensitivity issues present in continuous systems, making them easier to implement using digital hardware circuits [25]. Consequently, there has been a growing realization among researchers of the significance of exploring and understanding discrete memristive maps, leading to promising advancements in understanding the behavior of discrete memristor-based systems and their implications for various applications [26,27,28,29,30]. These studies contribute to exploring the interactions between memristive elements and mathematical functions, providing valuable insights into the dynamics of memristive maps and their potential applications in various fields.

The majority of the previous discrete memristors research has been focused on integer-order systems. Regrettably, the study of discrete fractional memristors remains inadequate, with relatively few studies dedicated to exploring their behavior and characteristics. For instance, Lu et al. [31] developed an innovative 2D discrete memristor map by incorporating a memristor into a 1D Rulkov neuron map. In [32], Peng et al. investigated the chaotic behaviors in the Caputo fractional memristive map, while in [33], the authors conducted an investigation into the multistability and synchronization of fractional maps resulting from the coupling of Rulkov neurons with locally active discrete memristors. Furthermore, Shatnawi et al. [34] recently explored the hidden attractors and multistability in a fractional non-fixed-point discrete memristor-based map. Additionally, the study of the fractional memristor-based discrete chaotic map based on the Grunwald–Letnikov operator and its implementation in digital circuits is presented in [35]. The studies highlight the intricate and rich behavior of the system, emphasizing the significance of fractional components in contributing to the complexity and versatility of memristor-based maps. The aforementioned papers have primarily concentrated on models with commensurate orders within discrete memristor-based maps. However, there appears to be a noticeable gap in the literature concerning the effect of the incommensurate-order case on the dynamics of such maps. This indicates an underexplored area in the field of discrete memristors, particularly in the context of incommensurate fractional memristors. Understanding the behavior and properties of incommensurate fractional memristors could lead to valuable insights and potential applications in various domains. Therefore, further investigation and research in this area are essential to uncovering the unique characteristics and potential benefits of incommensurate fractional memristors.

Inspired by the preceding discussion, the main innovations and contributions of this paper are summarized as follows:

• A new 3D fractional-order Hénon-based memristor map is presented by establishing a connection between the 2D Hénon map and the discrete memristor.
• The rich variety of complex nonlinear dynamical behavior is comprehensively explored, and some basic dynamical characteristics demonstrated by this map, such as phase portraits, bifurcation diagrams, and the maximum Lyapunov exponent, are investigated.
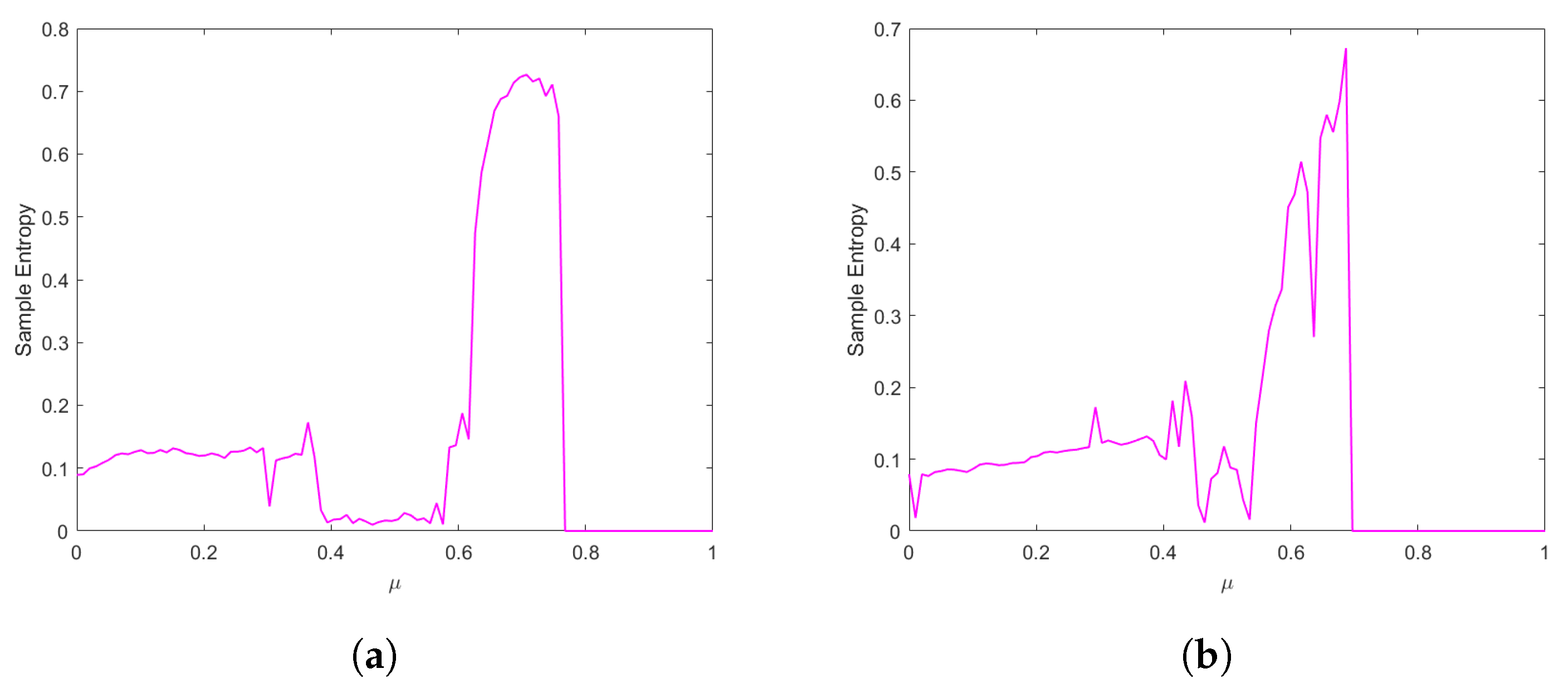
• To measure the complexity and demonstrate the presence of chaos in the proposed memristor map, we give its sample entropy ($SampEn$) test results using a range of fractional values, encompassing both commensurate and incommensurate cases.
• Chaos control and synchronization of the proposed 3D fractional Hénon-based memristor map are realized based on the stability theorem of fractional-order discrete-time linear systems.

The rest of this article is outlined as follows: In Section 2, we introduce essential preliminary concepts related to discrete fractional calculus and we introduce the mathematical model of the 3D fractional Hénon-based memristor map. In Section 3, we delve into an analysis of the dynamic characteristics of the fractional Hénon-based memristor map, focusing on both commensurate and incommensurate scenarios. This exploration is facilitated through phase portrait visualization, Lyapunov exponent analysis and bifurcation diagram plots. Section 4 involves the utilization of the sample entropy test ($SampEn$) to quantitatively measure the complexity and validate the presence of chaos within the map. In Section 5, we propose adaptive nonlinear controllers aimed at stabilizing and synchronizing the proposed 3D fractional Hénon-based memristor map. In conclusion, we provide a concise summary of the most noteworthy findings that we obtained during our study.

2. Preliminaries and Model Description

To elucidate our memristor framework, we first provide a specific overview within the domain of discrete fractional calculus. Then, we proceed to introduce the mathematical construct of the fractional Hénon-based memristor map, which incorporates the Caputo-left difference operator.

2.1. Discrete Fractional Calculus

Definition 1

([2]). The β-th fractional sum for a function Y can be expressed as

$${\Delta }_b^{-\beta }Y\left(\upsilon \right)=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\sum _{l=b}^{b-\beta }{\left(b-1-l\right)}^{\left(\beta -1\right)}Y\left(l\right),$$

(1)

with $\upsilon \in {\mathbb{N}}_{b+\beta },$ $\beta >0$.

Definition 2

([4]). The Caputo-like difference operator for a function $Y\left(\upsilon \right)$ can be stated as

$$\begin{array}{c}{}^C{\Delta }_{\upsilon }^{\beta }Y\left(b\right)={\Delta }_b^{-(m-\beta )}{\Delta }^{m}X\left(\upsilon \right)=\frac{1}{\beta \left(m-\beta \right)}{\sum }_{l=b}^{\upsilon -\left(m-\beta \right)}{\left(\upsilon -l-1\right)}^{\left(m-\beta -1\right)}{\Delta }^{m}Y\left(l\right),\hfill \end{array}$$

(2)

where $\upsilon \in {\mathbb{N}}_{b+m-\beta }$, $\beta \notin \mathbb{N}$ and $m=⌈\beta ⌉+1$. ${\Delta }^{m}Y\left(\upsilon \right)$ and ${\left(\upsilon -l-1\right)}^{\left(m-\beta -1\right)}$ are the m-th integer difference operator and the falling factorial function, respectively, which are written as

$${\Delta }^{m}Y\left(\upsilon \right)=\Delta \left({\Delta }^{m-1}Y\left(\upsilon \right)\right)=\sum _{k=0}^m\left(\begin{array}{c}m\\ k\end{array}\right){(-1)}^{m-k}Y(\upsilon +k),\upsilon \in {\mathbb{N}}_b,$$

(3)

and

$${(\upsilon -1-l)}^{(m-\beta -1)}=\frac{\beta (\upsilon -l)}{\beta (\upsilon +1-l-m+\beta )},$$

(4)

Remark 1.

For $m=1$, we can define the Caputo-like operator by

$$\begin{array}{c}{}^C{\Delta }_b^{\beta }Y\left(\upsilon \right)={\Delta }_b^{-(1-\beta )}\Delta Y\left(\upsilon \right)=\frac{1}{\beta \left(1-\beta \right)}{\sum }_{l=b}^{\upsilon -\left(1-\beta \right)}{\left(\upsilon -1-l\right)}^{\left(-\beta \right)}\Delta Y\left(l\right),\upsilon \in {\mathbb{N}}_{b-\beta +1}\hfill \end{array}$$

(5)

Theorem 1

([7]). The solution of the following fractional difference system

$$\left\{\begin{array}{c}{}^C{\Delta }_b^{\beta }Z\left(\upsilon \right)=Y(\upsilon +\beta -1,Z(\upsilon +\beta -1))\hfill \\ {\Delta }^{j}Z\left(\upsilon \right)=Z_j,m=\lceil \beta \rceil +1,\hfill \end{array}\right.$$

(6)

is expressed by

$$Z\left(\upsilon \right)=Z_0\left(\upsilon \right)+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\sum _{l=m-\beta }^{\upsilon -\beta }{(\upsilon +1-l)}^{(\beta -1)}Y(l-1+\beta ,Z(l-1+\beta )),\upsilon \in {\mathbb{N}}_{b+m},$$

(7)

where

$$Z_0\left(\upsilon \right)=\sum _{j=0}^{m-1}\frac{{(\upsilon -b)}^j}{\mathsf{\Gamma }(j+1)}{\Delta }^{j}Z\left(0\right).$$

(8)

2.2. Fractional-Order Hénon-Based Memristor Map

The original work of Hénon [36] introduced the 2D Hénon map, which is written as

$$\left\{\begin{array}{cc}\hfill & y_1(r+1)=1-{\rho }_1{\left(y_1\left(r\right)\right)}^2+y_2\left(r\right),\hfill \\ \hfill & y_2(r+1)={\rho }_2{y}_1\left(r\right),\hfill \end{array}\right.$$

(9)

where ${\rho }_1$ and ${\rho }_2$ are adjustable parameters.

The memristor is a two-terminal nonlinear device that displays a pinched hysteresis in response to the application of any periodic voltage or current stimulation. Diverse memristors with discrete memristance values have been suggested through the use of differential modeling theory [37]. As per the concept presented in reference [38], the discrete memristor can be defined by

$$\left\{\begin{array}{cc}\hfill & v_r=M\left(q_r\right)i_r,\hfill \\ \hfill & q_{r+1}=q_r+k{i}_r,\hfill \end{array}\right.$$

(10)

where $v_r$ represents the output voltage, $i_r$ is the input current, and $q_r$ is the internal state of the discrete memristor at step r. $M\left(q_r\right)$ denotes the value of the discrete memristance function, which is equal, in this study, to

$$M\left(q_r\right)=tanh{q}_r.$$

Thus, the mathematical model for the discrete memristor (10) is formulated by

$$\left\{\begin{array}{cc}\hfill & v_r=tanh\left(q_r\right)i_r,\hfill \\ \hfill & q_{r+1}=q_r+k{i}_r.\hfill \end{array}\right.$$

(11)

Rong et al. [26] expanded the dimension of the Ikeda map by incorporating the discrete memristor model (11) into the map (9), yielding the following 3D Hénon-based memristor map:

$$\left\{\begin{array}{cc}\hfill & y_1(r+1)=1-{\rho }_1{\left(y_1\left(r\right)\right)}^2+y_2\left(r\right),\hfill \\ \hfill & y_2(r+1)={\rho }_2{y}_1\left(r\right)+\mu tanh\left(y_3\left(r\right)\right)y_2\left(r\right),\hfill \\ \hfill & y_3(r+1)=y_3\left(r\right)+y_2\left(r\right).\hfill \end{array}\right.$$

(12)

where $\mu$ is the controller parameter. Figure 1 illustrates the bifurcation diagram and Lyapunov exponent, as well as the phase attractor of the 3D Hénon-based memristor map, while varying $\mu$ from 0 to 1. The evidence presented in Figure 1 provides that the model demonstrates chaotic dynamics for a significant range of values, specifically within the interval $\rho \in (0.448,0.531)\cup (0.722,0.986)$.

In this investigation, we extend the integer-order Hénon-based memristor map to generate the fractional-order Hénon-based memristor map by employing the Caputo difference operator. The formula representing the first-order difference of the Hénon-based memristor map is as follows:

$$\left\{\begin{array}{cc}\hfill & \Delta y_1\left(r\right)=1-{\rho }_1{\left(y_1\left(r\right)\right)}^2+y_2\left(r\right)-y_1\left(r\right),\hfill \\ \hfill & \Delta y_2\left(r\right)={\rho }_2{y}_1\left(r\right)+\left(\mu tanh\left(y_3\left(r\right)\right)-1\right)y_2\left(r\right),\hfill \\ \hfill & \Delta y_3\left(r\right)=y_2\left(r\right),\hfill \end{array}\right.$$

(13)

where $\Delta y\left(r\right)=y(r+1)-y\left(r\right)$ is the standard difference operator. In the aforementioned system, if we substitute $\Delta$ with the Caputo-like operator ${}^c{\Delta }_b^{\beta }$ and replace r with $\varrho =\upsilon +\beta -1$, the resulting system becomes a fractional-order difference system:

$$\left\{\begin{array}{cc}\hfill & {}^c{\Delta }_b^{\beta }{y}_1\left(\upsilon \right)=1-{\rho }_1{\left(y_1\left(\varrho \right)\right)}^2+y_2\left(\varrho \right)-y_1\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{\beta }{y}_2\left(\upsilon \right)={\rho }_2{y}_1\left(\varrho \right)+\left(\mu tanh\left(y_3\left(\varrho \right)\right)-1\right)y_2\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{\beta }{y}_3\left(\upsilon \right)=y_2\left(\varrho \right),\hfill \end{array}\right.$$

(14)

where $\upsilon \in {\mathbb{N}}_{b+1-\beta }$, b is the initial point, and $0<\beta \le 1$ represents the fractional order.

The fixed points of the fractional-order Henon-based memristor map (14) are the values of $(y_1^{\ast },y_2^{\ast },y_3^{\ast })$ that fulfill the following set of equations:

$$\left\{\begin{array}{cc}\hfill & 1-{\rho }_1{\left(y_1^{\ast }\right)}^2+y_2^{\ast }-y_1^{\ast }=0,\hfill \\ \hfill & {\rho }_2{y}_1^{\ast }+\left(\mu tanh\left(y_3^{\ast }\right)-1\right)y_2^{\ast }=0,\hfill \\ \hfill & y_2^{\ast }=0.\hfill \end{array}\right.$$

(15)

It is clear that, from the third equation of (15), $y_2^{\ast }=0$. Substituting $y_2^{\ast }$ in the second equation, we obtain $y_1^{\ast }=0$. Moreover, upon substituting $y_1^{\ast }$ and $y_2^{\ast }$ into the first equation of (15), it becomes apparent that the system (15) does not have a solution. This signifies that the fractional-order Henon-based memristor map (14) does not possess any fixed points. Consequently, as indicated in reference [39], all attractors produced by the fractional-order Henon-based memristor map (14) are hidden. This means that they are not visible in the traditional plots of the map’s phase space.

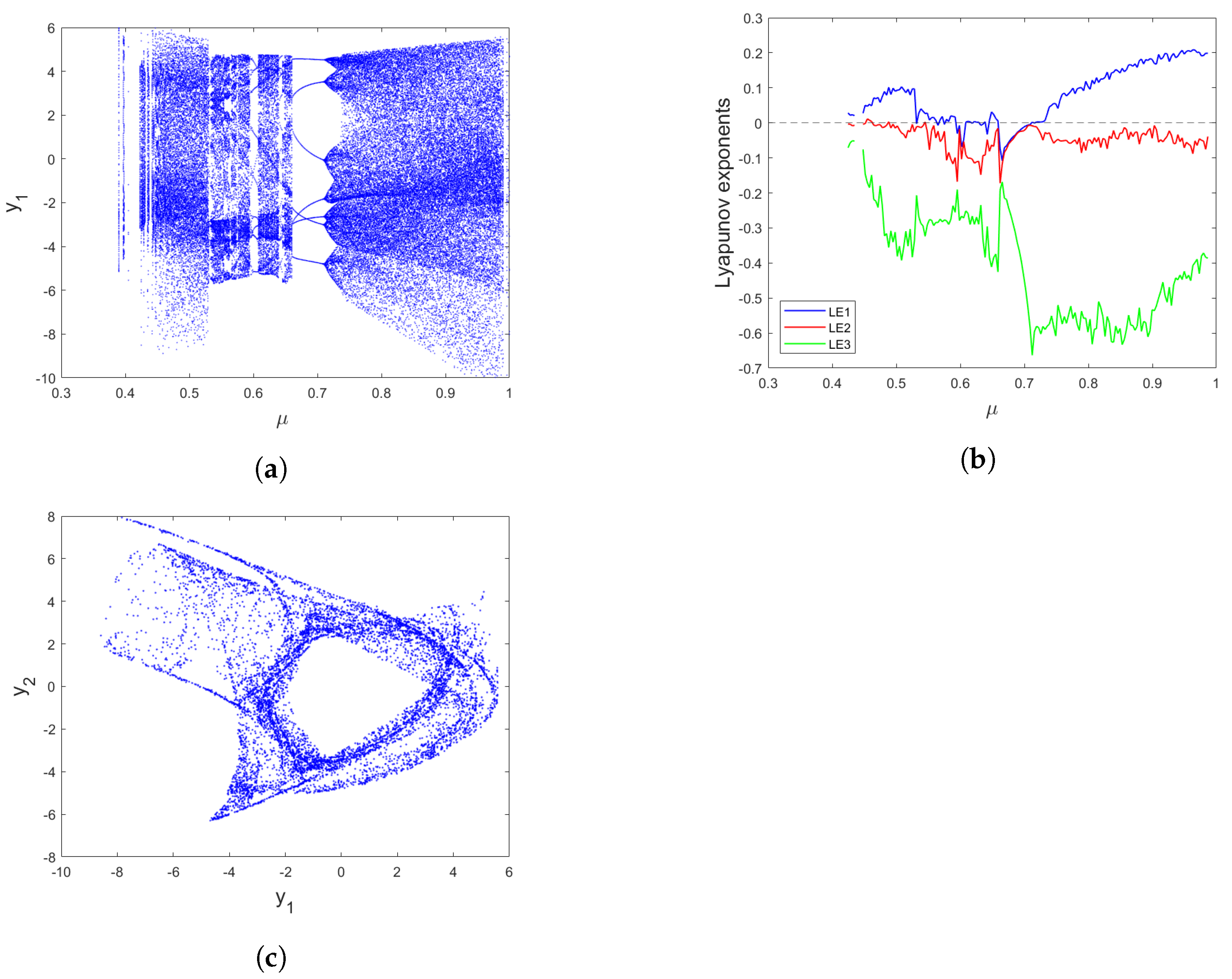
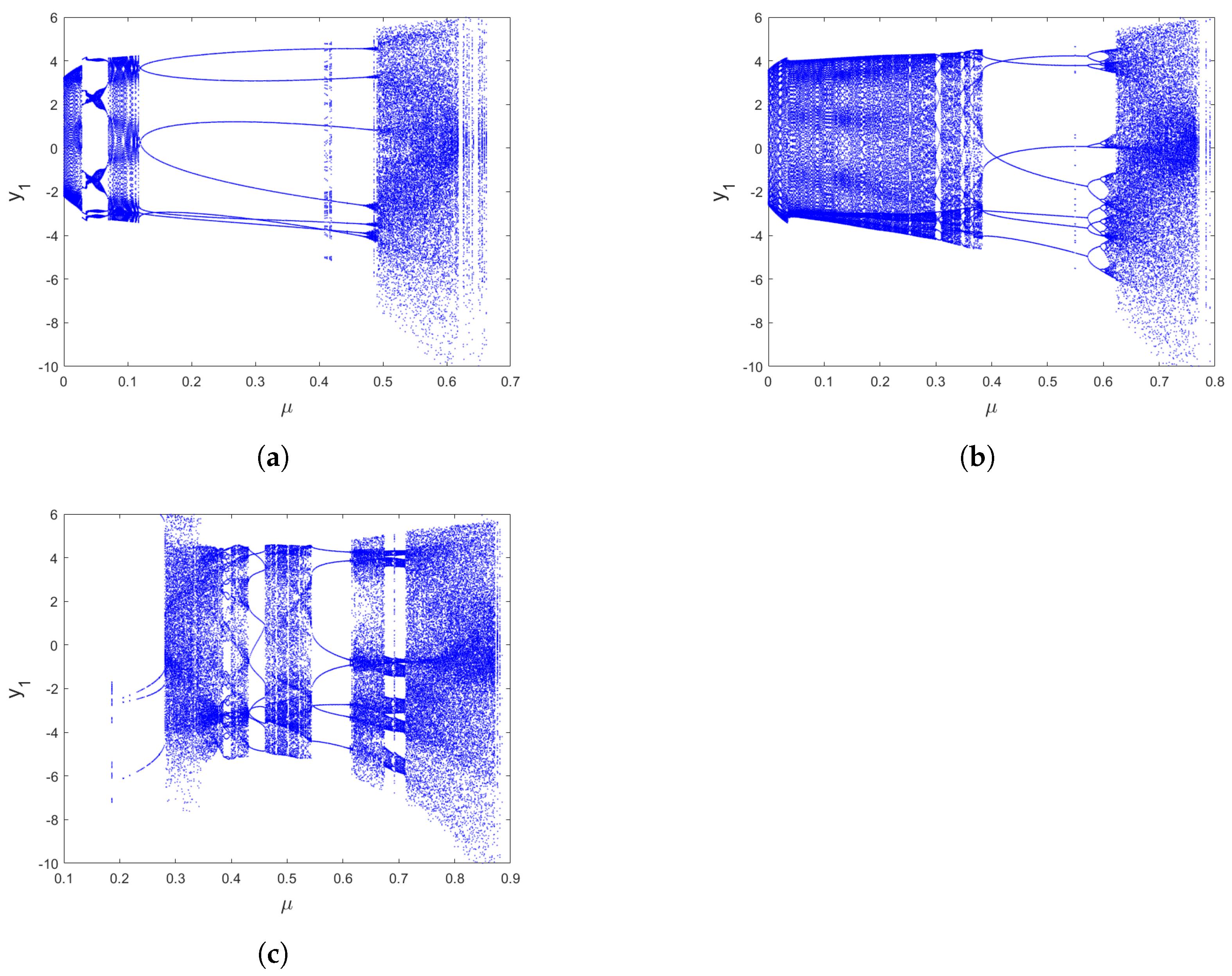
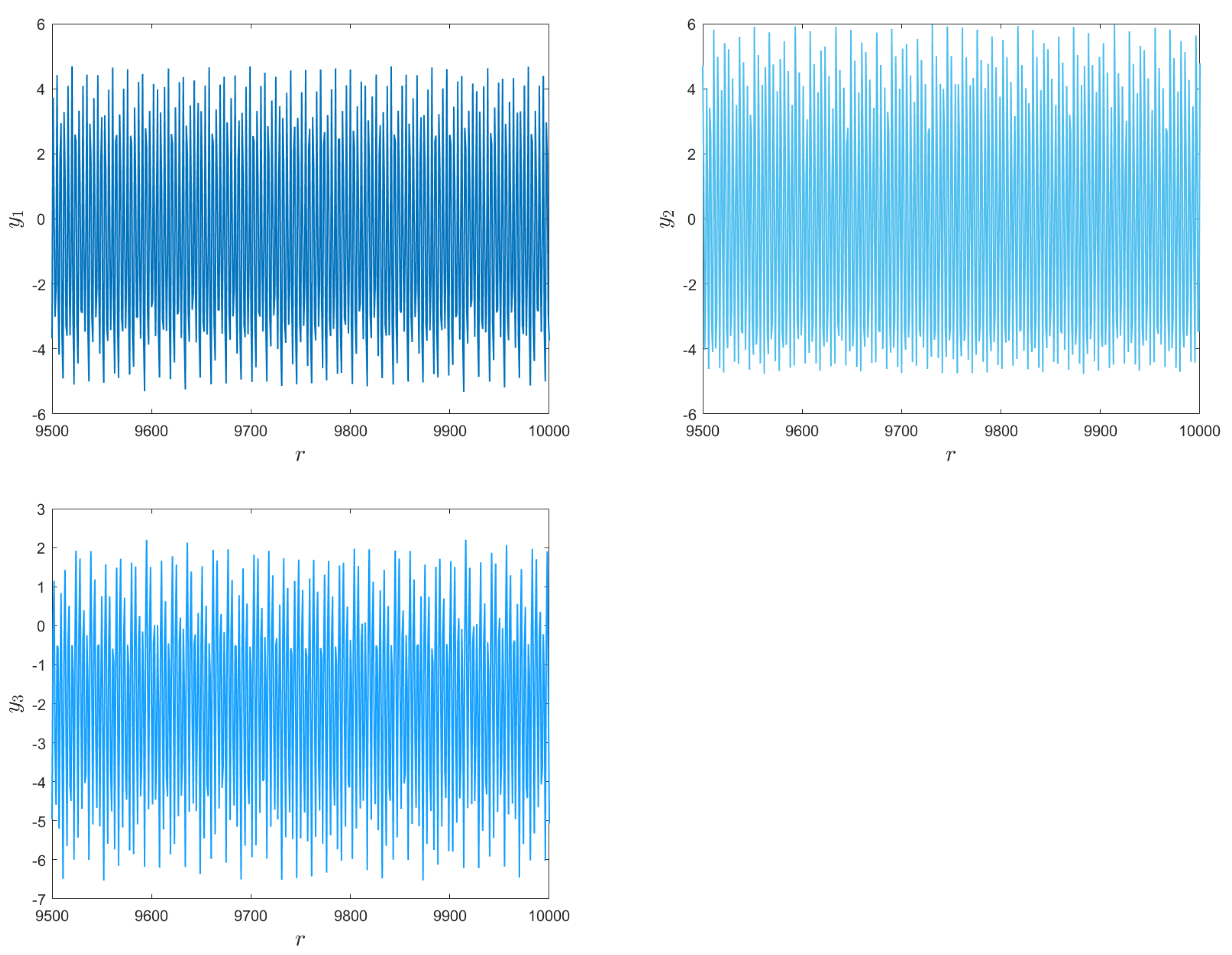
3. Nonlinear Dynamics of the Fractional-Order Hénon-Based Memristor Map

In this section, we conduct an analysis of the behaviors of the 3D fractional-order Hénon-based memristor map (14). The analysis is carried out across commensurate and incommensurate orders. We employ a range of numerical tools, such as visualizing phase portraits, illustrating bifurcations, and estimating the maximum Lyapunov exponent ($L{E}_{max}$).

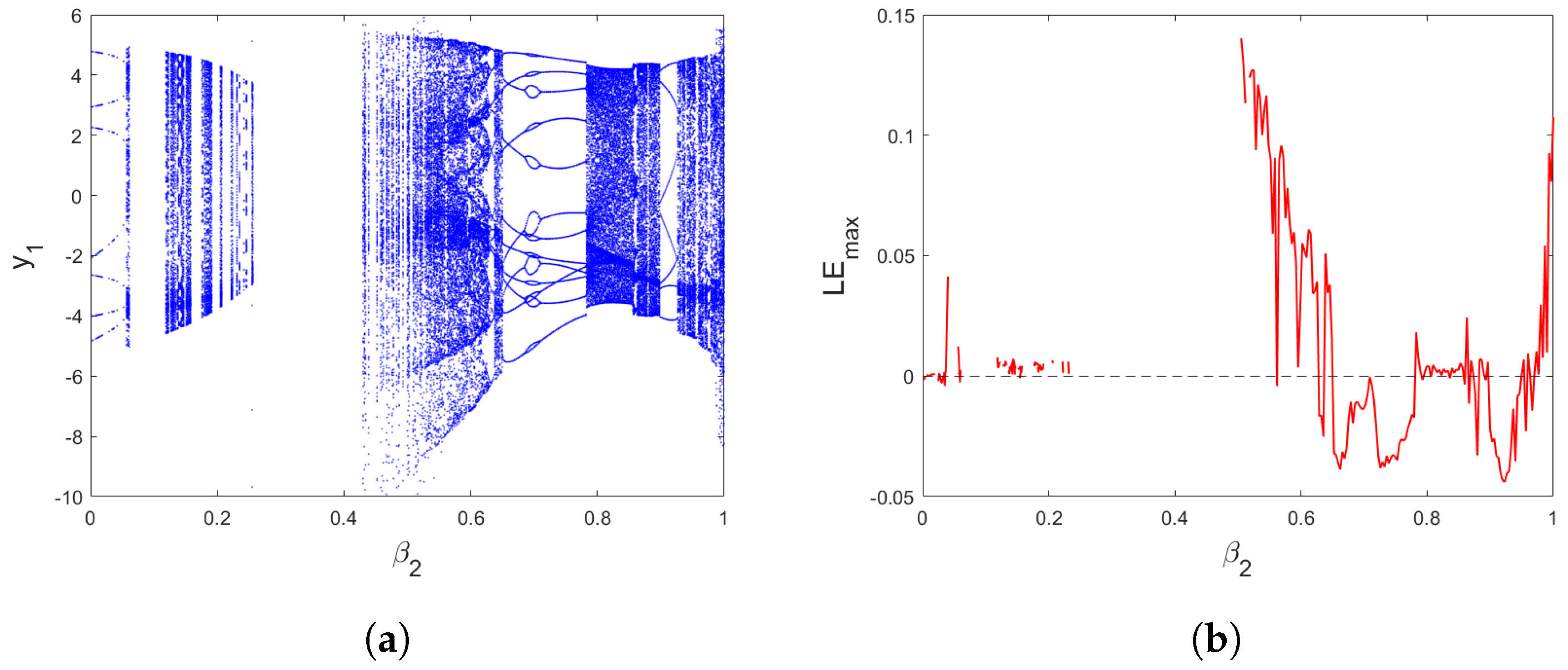
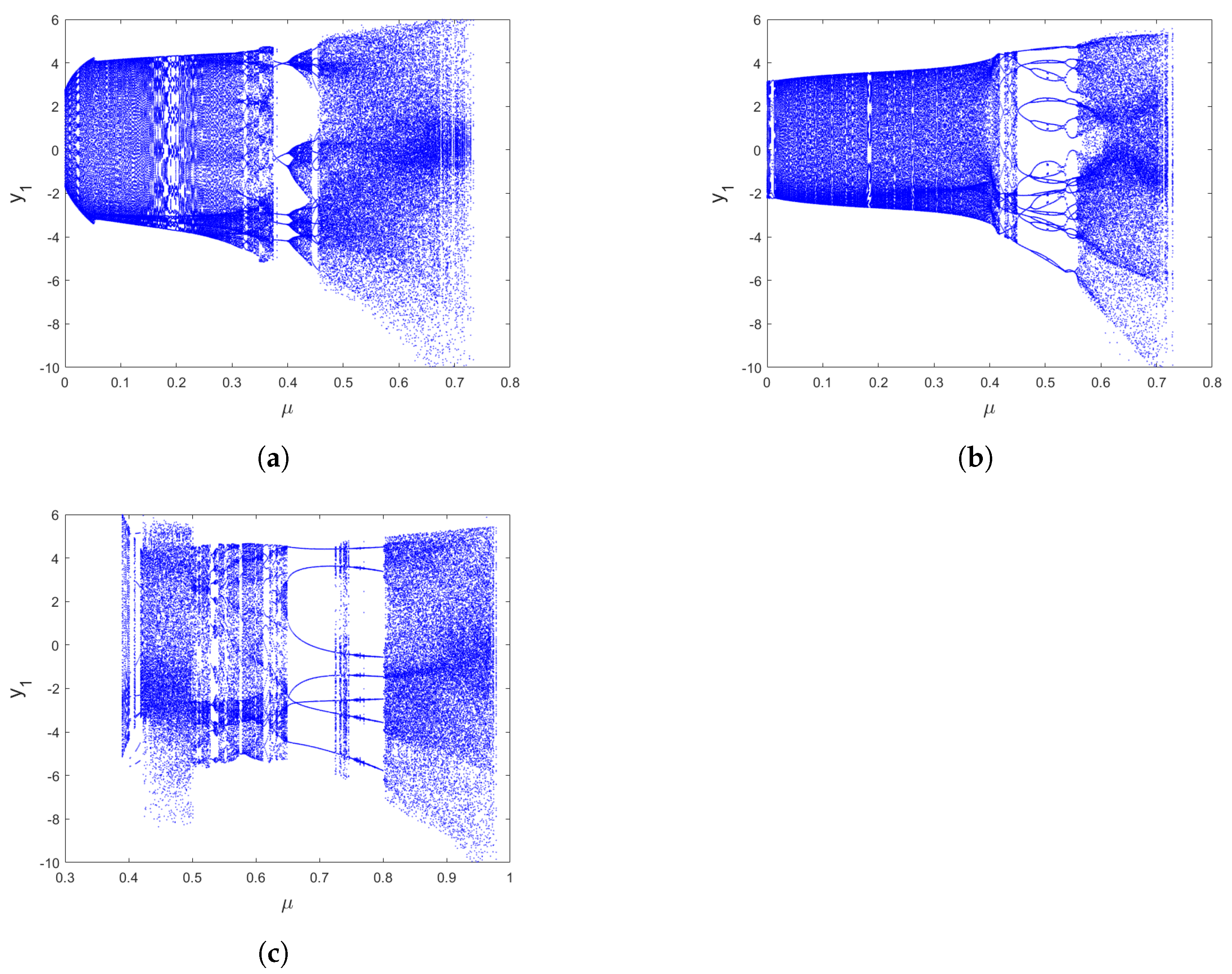
3.1. Commensurate-Order Fractional Hénon-Based Memristor Map

In this part, our focus is on elaborating on the different characteristics of the commensurate-order 3D fractional Hénon-based memristor map. It is important to recognize that a commensurate-order fractional system is comprised of equations that possess identical orders. To this end, we will now supply the numerical formula, which is presented in the following manner and is derived from Theorem 1:

$$\left\{\begin{array}{c}{y}_1\left(r\right)=y_1\left(0\right)+{\displaystyle \sum _{j=0}^{r-1}}\frac{\mathsf{\Gamma }(r-j-1+\beta )}{\mathsf{\Gamma }\left(\beta \right)\mathsf{\Gamma }(r-j)}\left(1-{\rho }_1{\left(y_1\left(j\right)\right)}^2+y_2\left(j\right)-y_1\left(j\right)\right),\hfill \\ y_2\left(r\right)=y_2\left(0\right)+{\displaystyle \sum _{j=0}^{r-1}}\frac{\mathsf{\Gamma }(r-j-1+\beta )}{\mathsf{\Gamma }\left(\beta \right)\mathsf{\Gamma }(r-j)}\left({\rho }_2{y}_1\left(j\right)+\left(\mu tanh\left(y_3\left(j\right)\right)-1\right)y_2\left(j\right)\right),\hfill \\ y_3\left(r\right)=y_3\left(0\right)+{\displaystyle \sum _{j=0}^{r-1}}\frac{\mathsf{\Gamma }(r-j-1+\beta )}{\mathsf{\Gamma }\left(\beta \right)\mathsf{\Gamma }(r-j)}\left(y_2\left(j\right)\right),\hfill \end{array}\right.$$

(16)

Setting $y_1\left(0\right)=y_2\left(0\right)=t_3\left(0\right)=0$ and the parameters ${\rho }_1=0.15$, ${\rho }_2=-1.05$ and $\mu =0.5$, the bifurcation diagram is used to show the variations in the behaviors of the commensurate 3D fractional Hénon-based memristor map (14), as the order $\beta$ is varied from 0.8 to 1 with a step size of 0.0005. Figure 2 depicts the bifurcation and $L{E}_{max}$. By adjusting the commensurate-order $\beta$, we are able to explore a rich set of dynamic characteristics (hidden chaotic and regular) of the fractional map. In more detail, the system exhibits both chaotic and periodic oscillations in distinct regions of its phase space. More specifically, when $\beta \in (0.804,0.855)$, the trajectories of the commensurate 3D fractional Hénon-based memristor map (14) exhibit hidden chaotic behavior, while as $\beta$ transitions to the range of $\beta \in (0.855,0.931)$, periodic windows with 7-period orbits appear, indicating the stability of the states of the map. However, when the commensurate-order $\beta$ falls within the range of $\beta \in (0.932,0.984)$, we can observe oscillations between the chaotic and regular trajectories in the states of the 3D fractional Hénon-based memristor map (14). During this range, the Lyapunov exponent (LE) also fluctuates between positive and negative values, indicating transitions between chaotic and non-chaotic behaviors in the system. Subsequently, for larger values of $\beta$, chaotic motions reappear, characterized by a positive maximum Lyapunov exponent ($L{E}_{m}ax$), indicating chaotic dynamics in the trajectories of the commensurate-order 3D Hénon-based memristor map. These described dynamic features are further confirmed by the Lyapunov exponent shown in Figure 2, providing additional evidence for the system’s complex and diverse behavior and confirming the sensitivity of the map to changes in the commensurate-order parameter $\beta$. Furthermore, based on the observation of the maximum Lyapunov exponent, it can be concluded that when the maximum Lyapunov exponent is not positive, the commensurate 3D fractional Hénon-based memristor map exhibits regular oscillations. Conversely, the presence of chaotic oscillations is inferred when the exponent is positive.

Now, considering $\mu$ as the critical parameter, we plot three bifurcations of (14) associated with $\mu \in [0,1]$ as shown in Figure 3, which correspond to the commensurate orders $\beta =0.85,\beta =0.9$ and $\beta =0.95$. It is evident that both the parameter’s system $\mu$ and the commensurate order $\beta$ have an effect on the states of the commensurate fractional Hénon-based memristor map (14). Indeed, as the commensurate fractional-order $\beta$ and parameter $\rho$ increases, the commensurate 3D fractional Hénon-based memristor map (14) displays a more extended hidden chaotic region. This leads to the emergence of more complex oscillations and increased unpredictability in the system’s behavior. The interplay between the fractional order and the system parameter has a significant impact on the dynamical behavior, and these changes can result in a richer range of chaotic patterns and intricate trajectories within the 3D Hénon-based memristor map (14). In order to achieve a comprehensive understanding of these characteristics, Figure 4 displays the discrete time evolution of the states $y_1$, $y_2$, and $y_3$ in the suggested commensurate map. We can observe that the trajectories are not regular or predictable. Instead, they display irregular patterns, which is a hallmark of chaotic behavior, where small differences in the initial conditions lead to vastly different trajectories. Additionally, Figure 5 illustrates the phase portraits for various values of the commensurate-order $\beta$ ($\beta =0.1$, $\beta =0.4$, $\beta =0.6$, $\beta =0.9$, $\beta =0.98$, and $\beta =1$). From the figures, the observed trajectories in the proposed commensurate map switch between hidden chaotic oscillations and periodic behaviors as the commensurate-order $\beta$ varies. This observation emphasizes the sensitivity of the system to changes in $\beta$ and demonstrates the richness and complexity of the dynamical properties in the commensurate-order 3 D Hénon-based memristor map (14).

3.2. Incommensurate-Order Fractional Hénon-Based Memristor Map

In this section, we delve into the dynamics of the incommensurate-order fractional Hénon-based memristor map. The concept of the incommensurate order entails utilizing different fractional orders for each equation within the system. The representation of the incommensurate-order fractional Hénon-based memristor map is as follows:

$$\left\{\begin{array}{cc}\hfill & {}^c{\Delta }_b^{{\beta }_1}{y}_1\left(\upsilon \right)=1-{\rho }_1{\left(y_1\left(\varrho \right)\right)}^2+y_2\left(\varrho \right)-y_1\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{{\beta }_2}{y}_2\left(\upsilon \right)={\rho }_2{y}_1\left(\varrho \right)+\left(\mu tanh\left(y_3\left(\varrho \right)\right)-1\right)y_2\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{{\beta }_3}{y}_3\left(\upsilon \right)=y_2\left(\varrho \right),\hfill \end{array}\right.$$

(17)

By utilizing Theorem 1, we can express the numerical representation of the incommensurate fractional 3D Hénon-based memristor map (17) as follows:

$$\left\{\begin{array}{c}{y}_1\left(r\right)=y_1\left(0\right)+{\displaystyle \sum _{j=0}^{r-1}}\frac{\mathsf{\Gamma }(r-j-1+{\beta }_1)}{\mathsf{\Gamma }\left({\beta }_1\right)\mathsf{\Gamma }(r-j)}\left(1-{\rho }_1{\left(y_1\left(j\right)\right)}^2+y_2\left(j\right)-y_1\left(j\right)\right),\hfill \\ y_2\left(r\right)=y_2\left(0\right)+{\displaystyle \sum _{j=0}^{r-1}}\frac{\mathsf{\Gamma }(r-j-1+{\beta }_2)}{\mathsf{\Gamma }\left({\beta }_2\right)\mathsf{\Gamma }(r-j)}\left({\rho }_2{y}_1\left(j\right)+\left(\mu tanh\left(y_3\left(j\right)\right)-1\right)y_2\left(j\right)\right),\hfill \\ y_3\left(r\right)=y_3\left(0\right)+{\displaystyle \sum _{j=0}^{r-1}}\frac{\mathsf{\Gamma }(r-j-1+{\beta }_3)}{\mathsf{\Gamma }\left({\beta }_3\right)\mathsf{\Gamma }(r-j)}\left(y_2\left(j\right)\right),\hfill \end{array}\right.$$

(18)

We analyze the dynamics and characteristics of this map to understand its unique behavior and explore the implications of employing distinct fractional orders in the system’s equations. These investigations offer a deeper understanding of how the fractional orders impact the system dynamics and underscore the importance of considering incommensurate orders in the analysis of the model’s behavior. In Figure 6, we observe the variation of the order ${\beta }_1$ from 0.7 to 1 with a step size of $\Delta {\beta }_1=0.0005$. These figures illustrate the bifurcation and its corresponding Lyapunov exponent of the incommensurate-order 3D fractional Hénon-based memristor map (17) for ${\beta }_2=0.9$ and ${\beta }_3=1$, the parameters value ${\rho }_1=0.15$, ${\rho }_2=-1.05$, $\mu =0.5$, and the initial conditions $(y_1\left(0\right)=y_2\left(0\right)=y_3\left(0\right))=0$. From Figure 6a, it is evident that the state of the incommensurate Hénon-based memristor map (17) exhibits periodic behavior for larger values of ${\beta }_1$ as evidenced by negative Lyapunov exponents as shown in Figure 6b. On the other hand, as ${\beta }_1$ decreases, hidden chaotic behaviors emerge with positive values of $L{E}_{max}$. As the incommensurate-order ${\beta }_1$ decreases further, the trajectories undergo a transition state, and as ${\beta }_1$ drops below 0.745, the states of the fractional Hénon-based memristor map (17) exhibit a divergence towards infinity. In addition, the bifurcation chart and its corresponding largest Lyapunov exponent ($L{E}_{max}$), where the parameter ${\beta }_3$ is varied within the range $(0,1)$, are presented in Figure 7. In this analysis, we maintain the incommensurate orders as ${\beta }_1={\beta }_3=1$. From Figure 7, it is evident that, unlike the previous case, the trajectories of the incommensurate model exhibit hidden chaotic behavior when the order ${\beta }_2$ takes larger values as indicated by the positive values of $L{E}_{max}$. When ${\beta }_2$ decreases, the trajectories transition from chaotic to regular motion, where the states of the incommensurate-order fractional Hénon-based memristor map (17) become stable within the interval ${\beta }_2\in (0.65,0.78)\cup (0.897,0.97)$. The Lyapunov exponent ($L{E}_{max}$) displayed in Figure 7b fluctuates between positive and negative values when ${\beta }_1$ lies within the region ${\beta }_2\in (0.87,0.897)$. This outcome indicates the presence of chaotic behavior with the emergence of periodic windows. Additionally, as ${\beta }_2$ decreases even further, the maximum Lyapunov exponent values increase until they reach their highest value, indicating that the fractional Hénon-based memristor map becomes chaotic. We also see that when the incommensurate-order ${\beta }_3$ continues to decrease, the map shows transition states, and the trajectories go to infinity. The observed changes in the largest Lyapunov exponent and the corresponding dynamic patterns illustrate the system’s sensitivity to variations in the parameter ${\beta }_2$, highlighting the complexity and versatility of the incommensurate-order 3D fractional Hénon-based memristor map.

Now, to provide a more detailed illustration of the influence of incommensurate orders on the behaviors of the Hénon-based memristor map, further investigation is carried out. These investigations offer a deeper understanding of how the fractional orders impact the system dynamics and underscore the importance of considering incommensurate orders in the analysis of the model’s behavior. The three bifurcation diagrams presented in Figure 8 demonstrate the behaviors of the incommensurate Hénon-based memristor map (17) as the parameter $\mu$ varies within the range [0, 1]. The simulations are conducted with the value of parameters ${\rho }_1=0.15$ and ${\rho }_2=-1.05$, and the initial conditions $(y_1\left(0\right)=y_2\left(0\right)=y_3\left(0\right))=0$. It is evident that these diagrams exhibit distinct patterns, indicating that the change in fractional orders $({\beta }_1,{\beta }_2,{\beta }_3)$ significantly impacts the states of the incommensurate-order 3D fractional Hénon-based memristor map (17). For instance, when $({\beta }_1,{\beta }_2,{\beta }_3)$ = $(0.85,0.9,1)$, the system’s states evolve from periodic to hidden chaotic behavior as the parameter $\mu$ increases. On the other hand, when $({\beta }_1,{\beta }_2,{\beta }_3)$ = $(1,0.7,1)$, oscillatory motion is observed, with trajectories remaining stable for small values of $\mu$ and becoming chaotic for large values of $\mu$. In the case of $({\beta }_1,{\beta }_2,{\beta }_3)$ = $(1,1,0.9)$, a hidden chaotic region is evident throughout the interval, except for some periodic regions, where the model exhibits regular oscillations, especially when $\mu \in (0.66,0.81)$. These results emphasize the sensitivity of the incommensurate 3D fractional Hénon-based memristor map (17) to changes in the orders ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$, resulting in a diverse range of hidden dynamic behaviors, including hidden chaotic and periodic motion. This highlights the significance of incommensurate orders in shaping the system’s dynamics. Additionally, the phase portraits of the state variables of the incommensurate fractional Hénon-based memristor map (17) as shown in Figure 9 further support the notion that incommensurate orders more accurately represent the system’s behaviors. Overall, the study emphasizes the intricate and diverse nature of the incommensurate-order 3D fractional Hénon-based memristor map and the significance of the choice of fractional orders in modeling and characterizing its dynamics.

4. The Sample Entropy Test ($\mathit{SampEn}$)

In this study, we employ the sample entropy ($SampEn$) method to assess the complexity of both the commensurate-order 3D fractional IHénon-based memristor map (14) and the incommensurate-order 3D fractional Hénon-based memristor map (17). Unlike approximate entropy (ApEn), SampEn can effectively measure the irregularity of time series regardless of the embedding dimension (m) and the similarity coefficient (r). Consequently, SampEn provides a more consistent and unbiased measure compared to ApEn [40]. The $SampEn$ values indicate the complexity level of the time series, with higher values corresponding to higher complexity [41]. The calculation of $SampEn$ is performed as follows:

$$SampEn=-log\frac{{\mathsf{\Psi }}^{j+1}\left(r\right)}{{\mathsf{\Psi }}^j\left(r\right)},$$

(19)

where ${\mathsf{\Psi }}^j\left(r\right)$ is expressed as

$${\mathsf{\Psi }}^j\left(r\right)=\frac{1}{m-j+1}\sum _{i=1}^{m-j+1}log{C}_i^j\left(r\right).$$

(20)

and $r=0.2std\left(C\right)$ is the tolerance defined, and $std\left(C\right)$ represents the standard deviation.

The sample entropy results for the commensurate-order 3D fractional Hénon-based memristor map (14) and the incommensurate-order 3D fractional Hénon-based memristor map (17) are presented in Figure 10, with the initial conditions set as $(y_1\left(0\right),y_2\left(0\right),Y_3\left(0\right))=(0,0.0)$ and parameter values ${\rho }_1=0.15$ and ${\rho }_1=-1.05$. The obtained $SampEn$ values indicate the complexity levels of the time series, with larger values corresponding to higher complexity. The results demonstrate that both the commensurate and incommensurate fractional Hénon-based memristor maps exhibit higher complexity as indicated by their larger $SampEn$ values. These findings align with the results obtained from the maximum Lyapunov exponent analysis, further confirming the chaotic nature of the dynamics in the proposed fractional map. The higher complexity and chaotic behavior support the significance of fractional orders in capturing the rich dynamics of the proposed fractional Hénon-based memristor map.

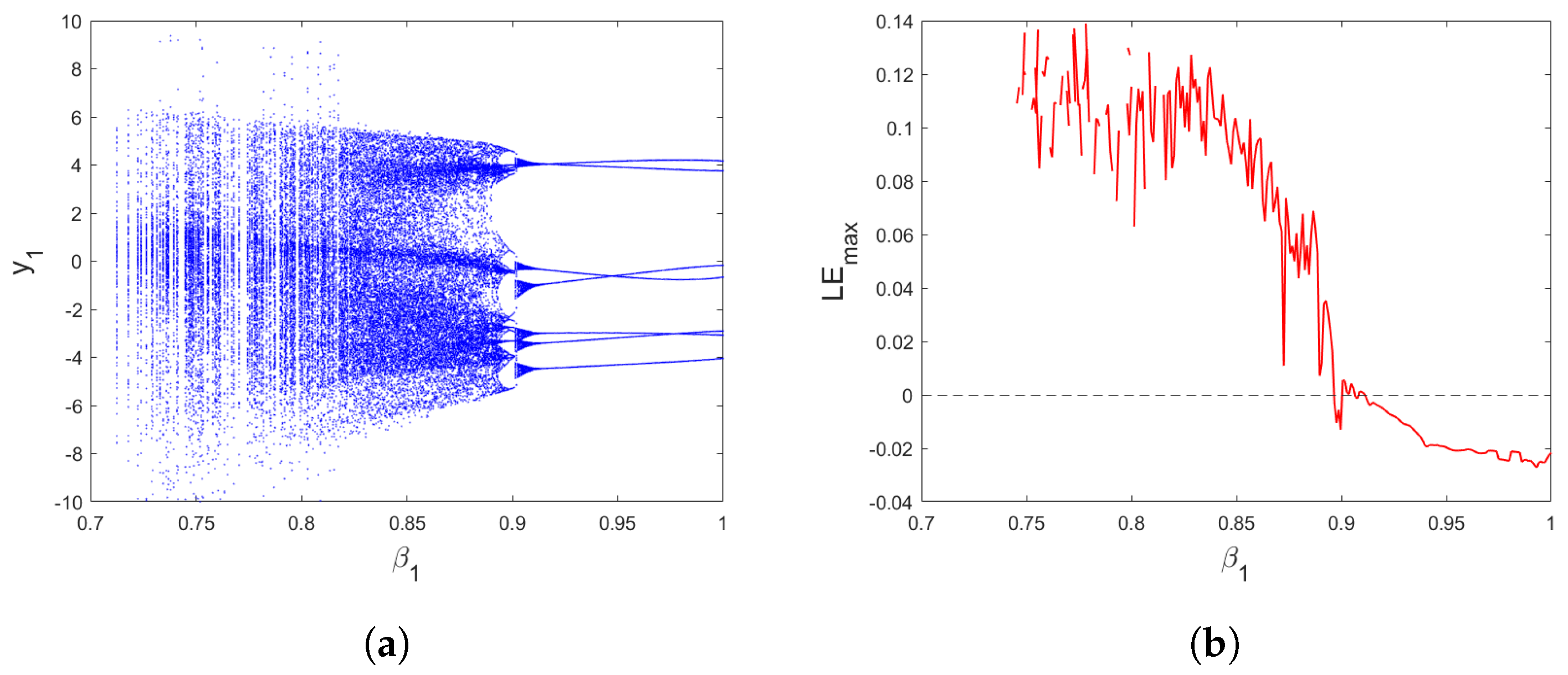
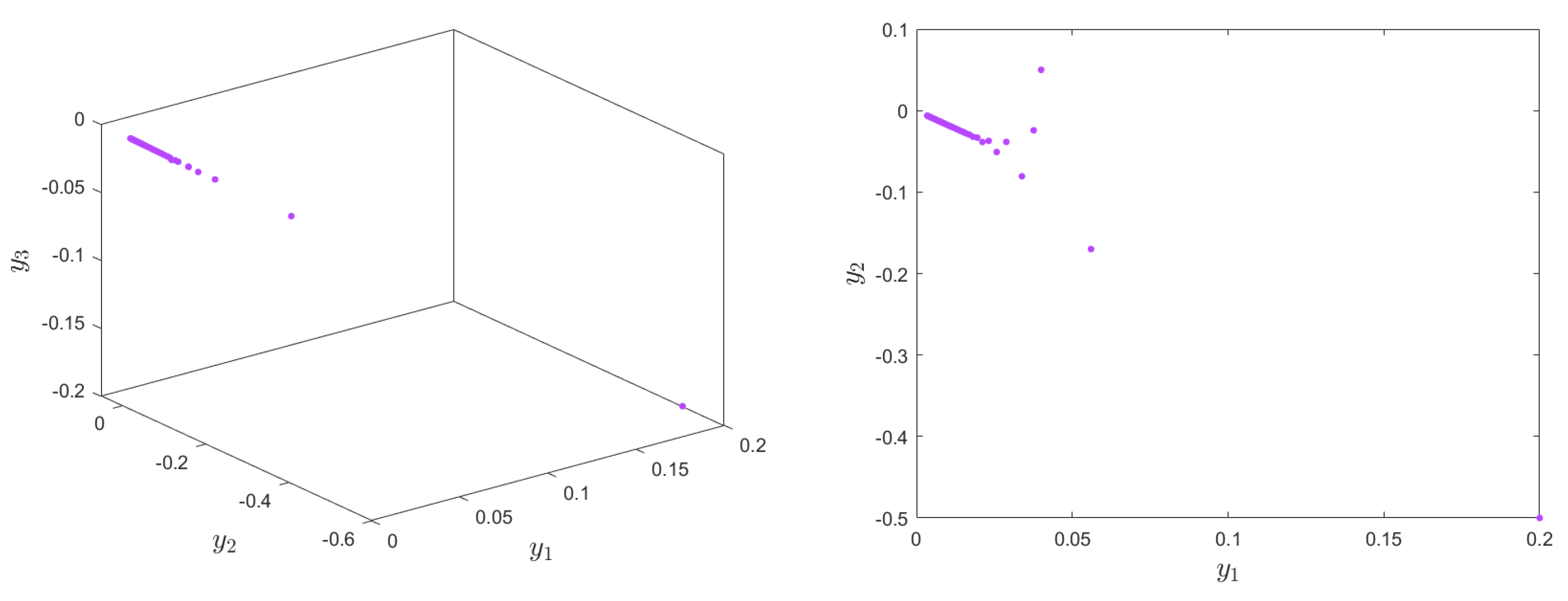
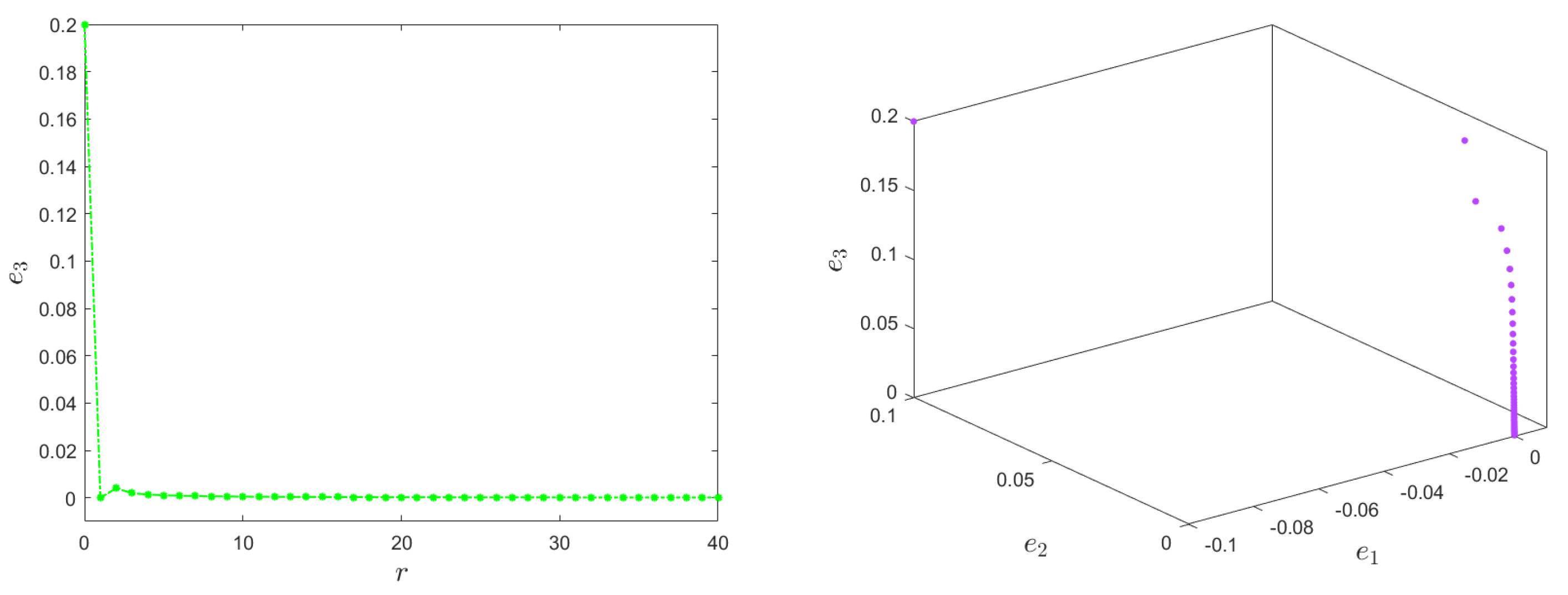
5. Control of Fractional Hénon-Based Memristor Map

In many real-world applications, it is essential to ensure that the system behaves in a stable and regulated manner. Control mechanisms are introduced to influence the system’s dynamics, guiding it towards desired states or trajectories. This is particularly important in applications where maintaining a specific behavior or avoiding chaotic outcomes is a priority. Chaotic systems often undergo bifurcations, leading to unpredictable and undesirable behavior. By incorporating control parameters into the map, we can exert influence over these bifurcations, stabilizing the system or steering it towards specific regions of the phase space. This is vital for controlling and mitigating chaotic behavior.

Control is frequently used in synchronization and communication systems to ensure that different parts of a system remain coordinated. By introducing control into our map, we can explore its utility in synchronization tasks, making it relevant to applications in secure communications and information transfer. In this section, we introduce nonlinear controllers designed for stabilizing and synchronizing the proposed fractional Hénon-based memristor map’s behavior, making it applicable to a wide range of practical scenarios.

5.1. Stabilization of Fractional Hénon-Based Memristor Map

Here, a stabilization controller is proposed to stabilize the suggested fractional Hénon-based memristor chaotic map. The main objective of the stabilization method is to design an effective adaptive controller that drives all states of the map towards zero asymptotically. To achieve this goal, we begin by revisiting the stability theorem for the fractional maps.

Theorem 2

([42]). Let $y\left(r\right)={(y_1\left(r\right),\dots ,y_n\left(r\right))}^T$ and $B\in {\mathcal{M}}_n\left(\mathbb{R}\right)$. The zero fixed point of the linear fractional-order map

$${}^C{\Delta }_b^{\beta }y\left(r\right)=By\left(\varrho \right),$$

(21)

$\forall r\in {\mathbb{N}}_{b+1-\beta }$ is asymptotically stable if

$${\lambda }_{\iota }\in \left\{\gamma \in \mathbb{C}:\left|\gamma \right|\le {\left(2cos\frac{|arg\gamma |-\pi }{2-\beta }\right)}^{\beta }\mathit{and}|arg\gamma |\ge \frac{\beta \pi }{2}\right\},$$

(22)

where ${\lambda }_{\iota }$ are the eigenvalues of the matrix B.

Now, the controlled fractional Hénon-based memristor map is given by

$$\left\{\begin{array}{cc}\hfill & {}^c{\Delta }_b^{\beta }{y}_1\left(\upsilon \right)=1-{\rho }_1{\left(y_1\left(\varrho \right)\right)}^2+y_2\left(\varrho \right)-y_1\left(\varrho \right)+C_1\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{\beta }{y}_2\left(\upsilon \right)={\rho }_2{y}_1\left(\varrho \right)+\left(\mu tanh\left(y_3\left(\varrho \right)\right)-1\right)y_2\left(\varrho \right)+C_2\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{\beta }{y}_3\left(\upsilon \right)=y_2\left(\varrho \right)+C_3\left(\varrho \right),\hfill \end{array}\right.$$

(23)

where $\varrho =\upsilon +\beta -1$ and $C={(C_1,C_2,C_3)}^T$ is the adaptive controller. The following theorem introduces control laws aimed at stabilizing the proposed novel fractional Hénon-based memristor map.

Theorem 3.

If suitable control laws are designed as follows,

$$\left\{\begin{array}{c}{C}_1\left(\varrho \right)=-1+{\rho }_1{\left(y_1\left(\varrho \right)\right)}^2-y_2\left(\varrho \right)-{\alpha }_1{y}_1\left(\varrho \right),\hfill \\ C_2\left(\varrho \right)=-{\rho }_2{y}_1\left(\varrho \right)-\mu y_2\left(\varrho \right)tanh\left(y_3\left(\varrho \right)\right)-{\alpha }_2{y}_2\left(\varrho \right),\hfill \\ C_3\left(\varrho \right)=-y_2\left(\varrho \right)-{\alpha }_3{y}_3\left(\varrho \right),\hfill \end{array}\right.$$

(24)

where $-1\le {\alpha }_1\le 2^{\beta }-1$, $-1\le {\alpha }_2\le 2^{\beta }-1$ and $0\le {\alpha }_3\le 2^{\beta }$, then the fractional Hénon-based memristor map can be stabilized at its equilibrium point.

Proof. 

Substituting $C_1$, $C_2$ and $C_3$ into (23) yields the following linear system:

$${}^C{\Delta }_b^{\beta }Y\left(r\right)=BY\left(\varrho \right),$$

(25)

where $Y={(y_1,y_2,q)}^T$ and

$$B=\left(\begin{array}{ccc}-(1+{\alpha }_1)& 0& 0\\ 0& -(1+{\alpha }_2)& 0\\ 0& 0& -{\alpha }_3\end{array}\right)$$

Since $-1\le {\alpha }_1\le 2^{\beta }-1$, $-1\le {\alpha }_2\le 2^{\beta }-1$ and $0\le {\alpha }_3\le 2^{\beta }$, it is easy to see that the eigenvalues of the matrix B satisfy

$$\left|{\lambda }_j\right|\le {\left(2cos\frac{|arg{\lambda }_j|-\pi }{2-\beta }\right)}^{\beta }\mathrm{and}|arg{\lambda }_j|=\pi \le \frac{\beta \pi }{2},j=1,2,3.$$

So, by employing Theorem 2, the controlled fractional Hénon-based memristor map is asymptotically stable. □

To validate the findings of Theorem 3, numerical simulations were performed. Figure 11 and Figure 12 present the time series of the controlled fractional Hénon-based memristor map (23) for $\beta =0.7$, ${\alpha }_1=-0.2$, ${\alpha }_2=0.1$ and ${\alpha }_3=0.8$. It is evident from the figures that the system’s states approach zero asymptotically, confirming the successful stabilization results.

5.2. Synchronization Scheme of Fractional Hénon-Based Memristor Map

In the following, nonlinear controllers for achieving synchronization of the fractional Hénon-based memristor map are presented. The synchronization process aims to minimize the error between the master map and the slave map, forcing it to converge toward zero. The commensurate fractional Hénon-based memristor map, represented by Equation (14), is considered the master map, while the slave Hénon-based memristor map is defined as follows:

$$\left\{\begin{array}{cc}\hfill & {}^c{\Delta }_b^{\beta }{y}_{1s}\left(\upsilon \right)=1-{\rho }_1{\left(y_{1s}\left(\varrho \right)\right)}^2+y_{2s}\left(\varrho \right)-y_{1s}\left(\varrho \right)+U_1\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{\beta }{y}_{2s}\left(\upsilon \right)={\rho }_2{y}_{1s}\left(\varrho \right)+\left(\mu tanh\left(y_{3s}\left(\varrho \right)\right)-1\right)y_{2s}\left(\varrho \right)+U_2\left(\varrho \right),\hfill \\ \hfill & {}^c{\Delta }_b^{\beta }{y}_{3s}\left(\upsilon \right)=y_{2s}\left(\varrho \right)+U_3\left(\varrho \right).\hfill \end{array}\right.$$

(26)

$U_1$, $U_2$ and $U_3$ represent the synchronization controllers. The fractional error map is defined as follows:

$$\left\{\begin{array}{cc}\hfill {}^C{\Delta }_b^{\beta }{e}_1\left(\upsilon \right)=& -e_1\left(\upsilon \right)\left({\rho }_1(y_{1s}+y_1)+1\right)+e_2\left(\upsilon \right)+U_1\left(\varrho \right),\hfill \\ \hfill {}^C{\Delta }_b^{\beta }{e}_2\left(\upsilon \right)=& {\rho }_2{e}_1\left(\upsilon \right)+\mu \left(y_{2s}tanh\left(y_{3s}\right)-y_{2}tanh\left(y_3\right)\right)-e_2\left(\upsilon \right)+U_2\left(\varrho \right),\hfill \\ \hfill {}^C{\Delta }_b^{\beta }{e}_3\left(\upsilon \right)=& e_2\left(\varrho \right)+U_3\left(\varrho \right)\hfill \end{array}\right.$$

(27)

The control rule proposed to establish this synchronization scheme is outlined in the theorem presented below.

Theorem 4.

Subject to

$$\left\{\begin{array}{c}{U}_1\left(\varrho \right)=e_1\left(\upsilon \right)\left({\rho }_1(y_{1s}+y_1)-{\gamma }_1\right)-e_2\left(\upsilon \right),\hfill \\ U_2\left(\varrho \right)=-{\rho }_2{e}_1\left(\upsilon \right)-\mu \left(y_{2s}tanh\left(y_{3s}\right)-y_{2}tanh\left(y_3\right)\right)-{\gamma }_2{e}_2\left(\varrho \right),\hfill \\ U_3\left(\varrho \right)=-e_2\left(\varrho \right)-{\gamma }_3{e}_3\left(\varrho \right)\hfill \end{array}\right.$$

(28)

where $0\le 1+{\gamma }_i\le 2^{\beta }$ ($i=1,2$) and $0\le {\gamma }_3\le 2^{\beta }$, the master Hénon-based memristor map (14) and slave Hénon-based memristor map (26) are synchronized.

Proof. 

Substituting the control law (28) into the fractional error map (27), we obtain

$${}^C{\Delta }_d^{\beta }{\left(e_1\left(\upsilon \right),e_2\left(\upsilon \right),e_3\left(\upsilon \right)\right)}^T=B\times (e_1\left(\varrho \right),e_2\left(\varrho \right),e_3\left(\varrho \right){)}^T,$$

(29)

where

$$B=\left(\begin{array}{ccc}-(1+{\gamma }_1)& 0& 0\\ 0& -(1+{\gamma }_2)& 0\\ 0& 0& -{\gamma }_3\end{array}\right)$$

The eigenvalues of the matrix B are ${\lambda }_1=-(1+{\gamma }_1)$, ${\lambda }_2=-(1+{\gamma }_2)$ and ${\lambda }_3=-{\gamma }_3$. It is easy to see that for $0\le 1+{\gamma }_i\le 2^{\beta }$ ($i=1,2$) and $0\le {\gamma }_3\le 2^{\beta }$, the eigenvalues satisfy the stability condition stated in Theorem 2, demonstrating that the zero solution of the fractional error map (27) is asymptotically stable, leading to the achieved synchronization of the master Hénon-based memristor map (14) and the slave Hénon-based memristor map (26). □

To confirm the validity of this result, numerical simulations are conducted using MATLAB. The values of the specific parameters chosen are $\beta =0.98$, ${\gamma }_1=0.1$, ${\gamma }_2=-0.3$, ${\gamma }_3=1$, and the initial values $(e_1\left(0\right),e_2\left(0\right),e_3\left(0\right))=(-0.1,0.1,0.2)$. Figure 13 presents the time evolution of the states of the fractional error map (27). The figure clearly illustrates that the errors tend to zero, validating the effectiveness of the earlier discussed synchronization process.

6. Conclusions

The presented article introduced a novel 3D fractional Hénon-based memristor map and thoroughly investigated its behavior under commensurate and incommensurate fractional orders. The analysis of the map revealed the absence of any fixed points, revealing that the map can exhibit intricate and diverse complex hidden dynamical behaviors. By employing a range of analytical methods, such as Lyapunov exponent calculations, bifurcation analysis, and phase portraits, the distinct behaviors of the proposed fractional Hénon-based memristor map are thoroughly explored across various scenarios. Furthermore, the sample entropy algorithm is utilized to quantitatively assess the model’s complexity. The results highlight the substantial influence exerted by the system parameters and fractional-orders on the states of the fractional Hénon-based memristor map. These parameters play a crucial role in shaping the system’s hidden dynamics and behavior, causing variations in trajectories within the map’s state space. Ultimately, the paper introduces effective control laws that ensure the stabilization and synchronization of the proposed map, driving its states towards asymptotic convergence to zero. Through the numerical simulations conducted, this research offers an extensive understanding of the system’s dynamics, revealing numerous intriguing and diverse hidden chaotic behaviors. These findings hold significant value in elucidating the implications of fractional memristive maps, further enriching the field of chaotic dynamics and nonlinear systems.