Filamentation of a Hollow Gaussian Beam in a Nonlinear Optical Medium
Abstract
1. Introduction
2. Theoretical Formulation
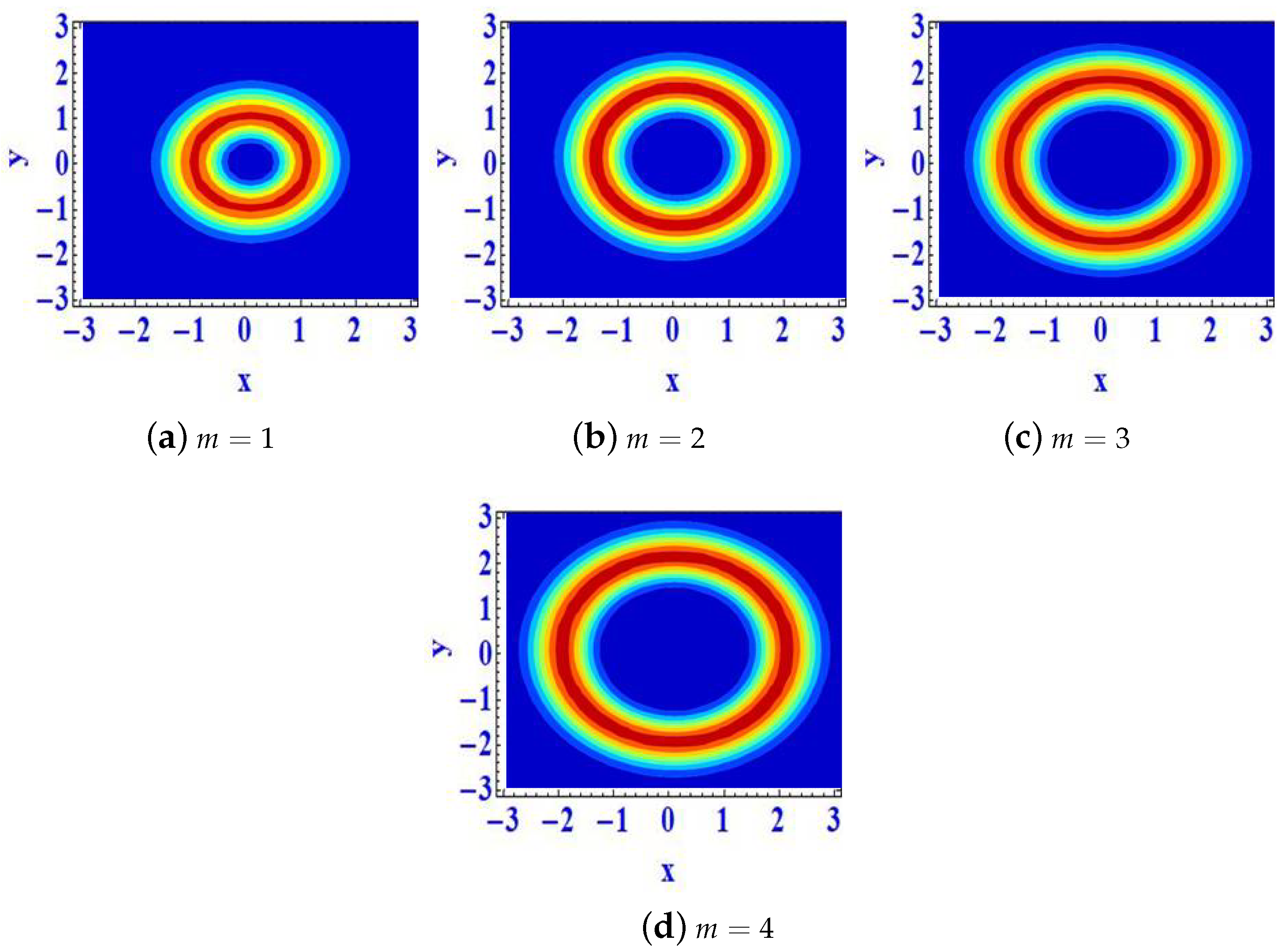
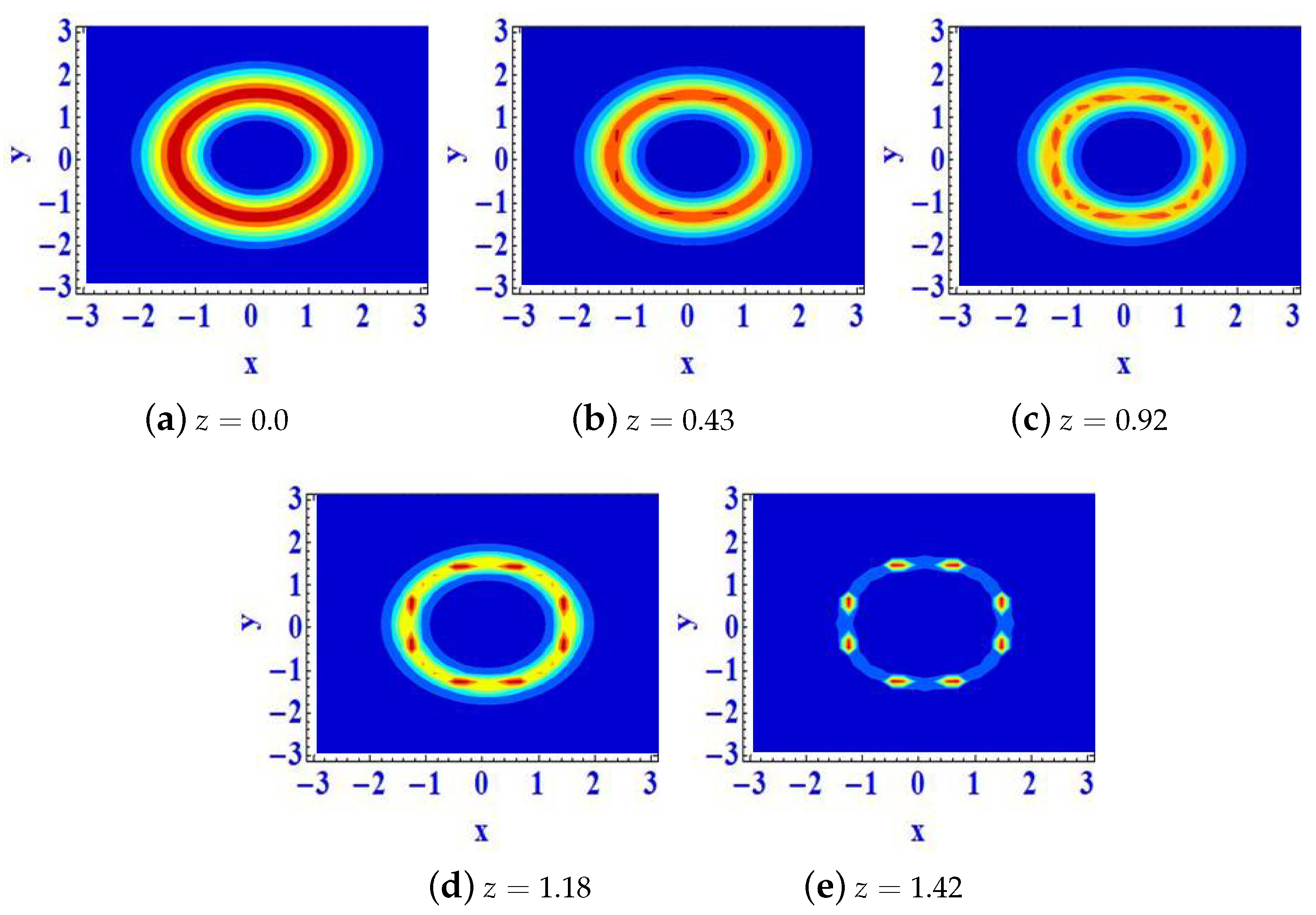
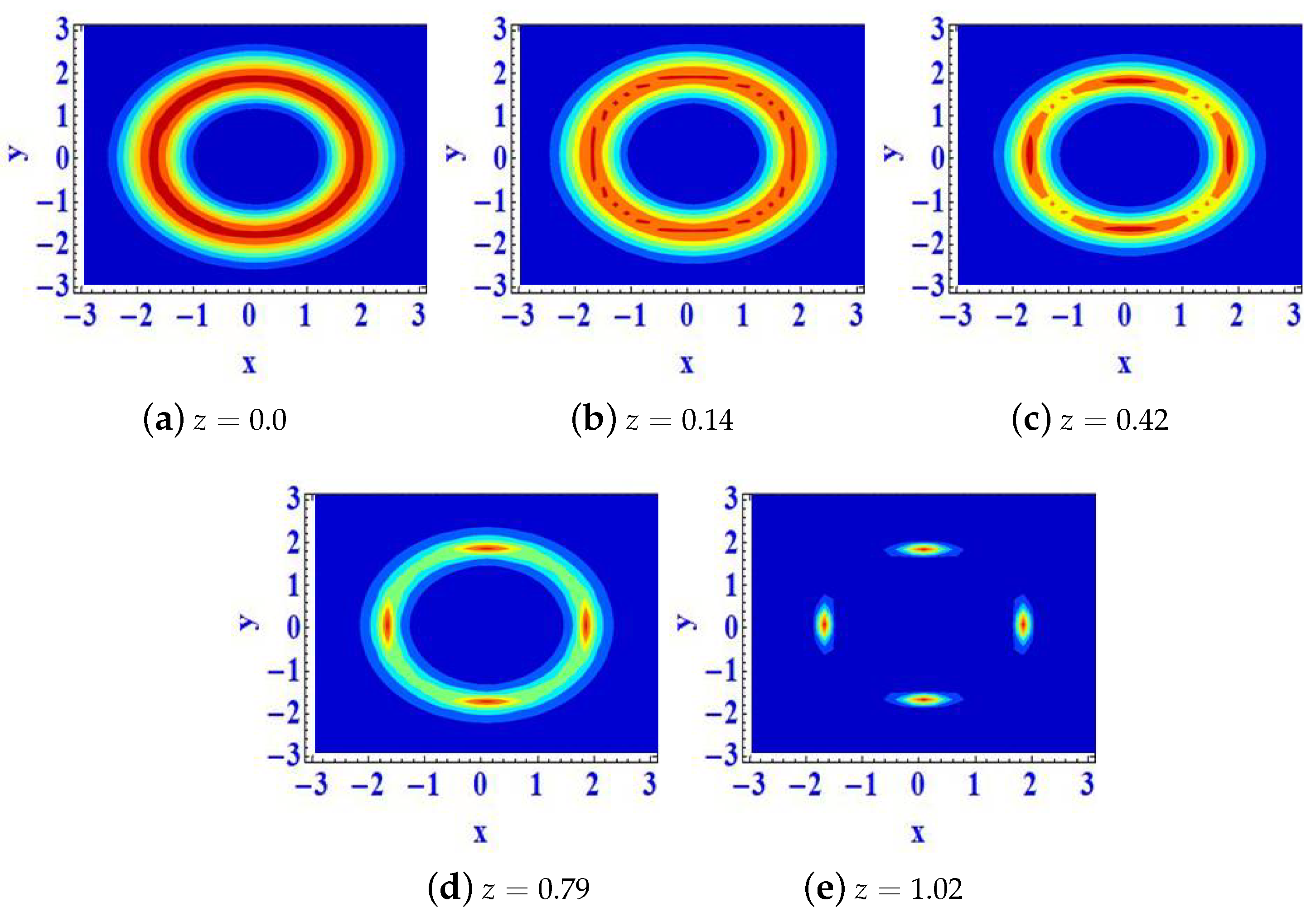
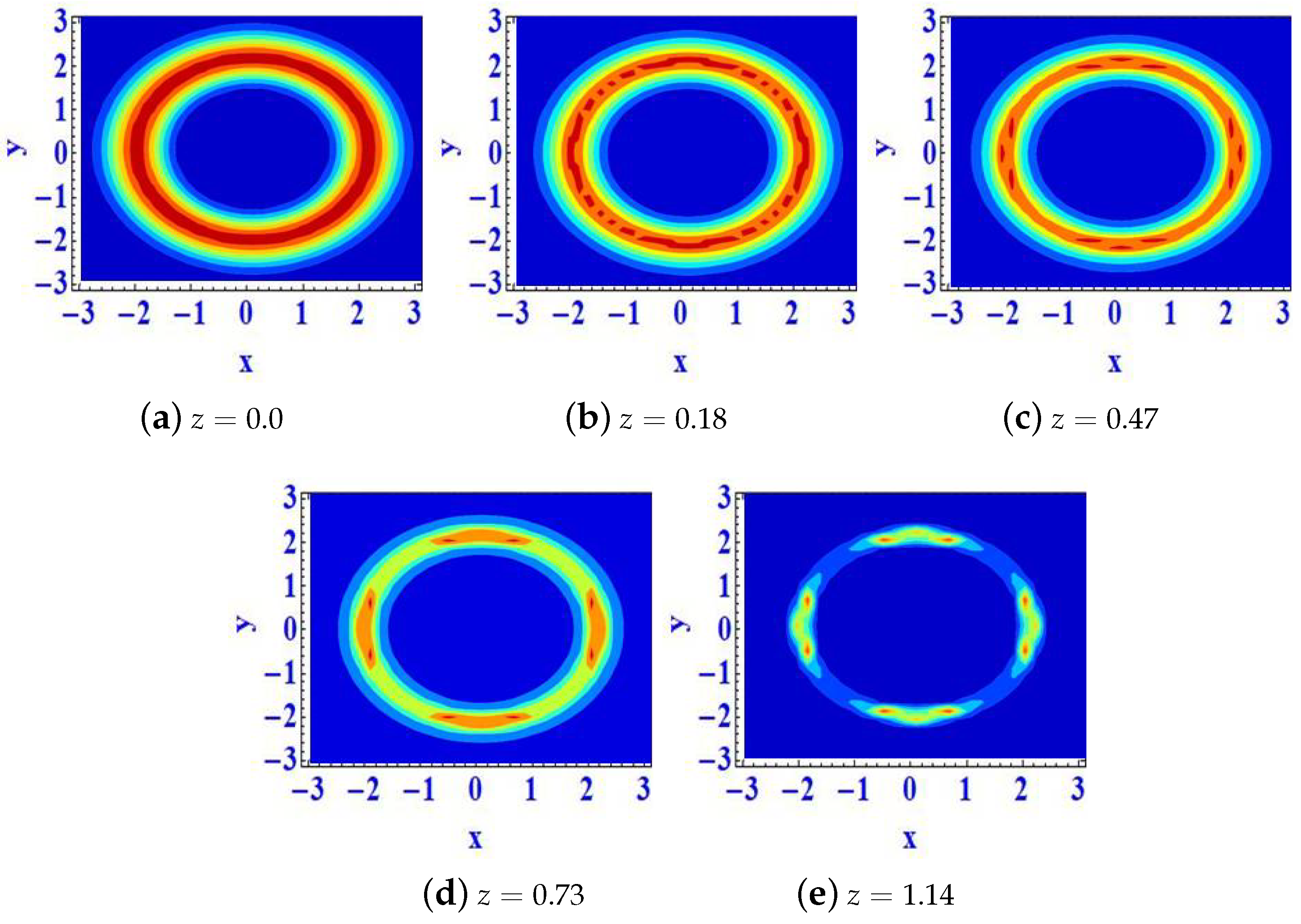
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Couairon, A.; Mysyrowicz, A. Femtosecond filamentation in transparent media. Phys. Rep. 2007, 441, 47. [Google Scholar] [CrossRef]
- Houard, A.; Franco, M.; Prade, B.; Durécu, A.; Lombard, L.; Bourdon, P.; Vasseur, O.; Fleury, B.; Robert, C.; Michau, V.; et al. Femtosecond filamentation in turbulent air. Phys. Rev. A 2008, 78, 033804. [Google Scholar] [CrossRef]
- Dubietis, A.; Tamossauskas, G.; Fibich, G.; Ilan, B. Multiple filamentation of intense laser beams. Opt. Lett. 2004, 29, 1126. [Google Scholar] [CrossRef] [PubMed]
- Maleshkov, G.; Neshev, D.N.; Petrova, E.; Dreischuh, A. Filamentation and supercontinuum generation by singular beams in self-focusing nonlinear media. J. Opt. 2011, 13, 064015. [Google Scholar] [CrossRef][Green Version]
- Rozina, C.; Tsintsade, N.L.; Maryam, N.; Komal, S. Effect of driving frequency on the electron energy distribution function and electron-sheath interaction in a low pressure capacitively coupled plasma. Phys. Plasmas 2016, 23, 112303. [Google Scholar] [CrossRef]
- Shafeeque Ali, A.K.; Govindarajan, A.; Lakshmanan, M. Self-trapped dynamics of a hollow Gaussian beam in metamaterials. Phys. Lett. A 2022, 451, 128416. [Google Scholar] [CrossRef]
- Dicaire, I.; Jukna, V.; Praz, C.; Milián, C.; Summerer, L.; Couairon, A. Spaceborne laser filamentation for atmospheric remote sensing. Lase Photonics Rev. 2016, 10, 481. [Google Scholar] [CrossRef]
- Chaitanya, N.A.; Jabir, M.V.; Banerji, J.; Samanta, G.K. Hollow Gaussian beam generation through nonlinear interaction of photons with orbital angular momentum. Sci. Rep. 2016, 6, 32464. [Google Scholar] [CrossRef]
- Liu, Z.; Dai, J.; Sun, X.; Liu, S. Propagation dynamics of an optical vortex imposed on an Airy beam. Opt. Express 2008, 16, 19926. [Google Scholar] [CrossRef]
- Anand, S. Generation of a hollow Gaussian beam and its anomalous behavior. Opt. Commun. 2009, 282, 1335–1339. [Google Scholar] [CrossRef]
- Cai, Y.; Lu, X.i.; Lin, Q. Propagation of various dark hollow beams in a turbulent atmosphere. Opt. Lett. 2003, 28, 1084–1086. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.K.S.; Lakshmanan, M. Self-trapped dynamics of a hollow Gaussian beam in metamaterials. Phys. Lett. A 2020, 384, 126527. [Google Scholar]
- Alkelly, A.A.; Nadary, H.A.; Alhijry, I.A. The intensity distribution of hollow Gaussian beams focused by a lens with spherical aberration. Opt. Commun. 2011, 284, 322–329. [Google Scholar] [CrossRef]
- Gerdova, I.; Zhang, X.; Hache, A. Optically tunable hollow Gaussian beams with thin metal films. J. Opt. Soc. Am. B 2006, 23, 1934–1937. [Google Scholar] [CrossRef]
- Dimitrevski, K.; Reimhult, E.; Svensson, E.; Öhgren, A.; Anderson, D.; Berntson, A.; Lisak, M.; Quiroga-Teixeiro, M.L. Analysis of stable self-trapping of laser beams in cubic-quintic nonlinear media. Phys. Lett. A 1998, 248, 369–376. [Google Scholar] [CrossRef]
- Konar, S.; Mishra, M.; Jana, S. Nonlinear evolution of cosh-Gaussian laser beams and generation of flat top spatial solitons in cubic quintic nonlinear media. Phys. Lett. A 2007, 362, 505–510. [Google Scholar] [CrossRef]
- Panagiotopoulos, P.; Efremidis, N.K.; Papazoglou, D.G.; Couairon, A.; Tzortzakis, S. Tailoring the filamentation of intense femtosecond laser pulses with periodic lattices. Phys. Rev. A. 2010, 82, 061803(R). [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Crasovan, L.C.; Malomed, B.A.; Lederer, F. Stable three-dimensional spinning optical solitons supported by competing quadratic and cubic nonlinearities. Phys. Rev. E 2000, 61, 7142. [Google Scholar] [CrossRef]
- Rajan, M.S.M.; Saravana, S. Veni Impact of external potential and non-isospectral functions on optical solitons and modulation instability in a cubic quintic nonlinear media. Chaos Solitons Fractals 2022, 159, 112186. [Google Scholar] [CrossRef]
- Ali, A.K.S.; Govindarajan, A.; Lakshmanan, M. Stabilization of light bullets in nonlinear metamaterial waveguides. Phys. Rev. A 2022, 105, 033516. [Google Scholar] [CrossRef]
- Ali, A.K.S.; Govindarajan, A.; Lakshmanan, M. Filamentation and stabilization of vortex solitons in nonlinear metamaterial waveguides. Phys. Lett. A 2022, 451, 128416. [Google Scholar]
- Zhang, J.; Wen, S.; Xiang, Y.; Wang, Y.; Luo, H. Spatiotemporal electromagnetic soliton and spatial ring formation in nonlinear metamaterials. Phys. Rev. A 2010, 81, 023829. [Google Scholar] [CrossRef]
- Adhikari, S.K. Elastic collision and breather formation of spatiotemporal vortex light bullets in a cubic-quintic nonlinear medium. Laser Phys. Lett. 2017, 14, 065402. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Gabitov, I.R.; Maimistov, A.I. Optical Bistability in a Nonlinear Optical Coupler with a Negative Index Channel. Phys. Rev. Lett. 2007, 99, 113902. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asma, M.; Ali, A.K.S.; Alzahrani, A.K.; Ullah, M.Z.; Shateyi, S. Filamentation of a Hollow Gaussian Beam in a Nonlinear Optical Medium. Mathematics 2023, 11, 4130. https://doi.org/10.3390/math11194130
Asma M, Ali AKS, Alzahrani AK, Ullah MZ, Shateyi S. Filamentation of a Hollow Gaussian Beam in a Nonlinear Optical Medium. Mathematics. 2023; 11(19):4130. https://doi.org/10.3390/math11194130
Chicago/Turabian StyleAsma, Mir, A. K. Shafeeque Ali, Abdullah Khamis Alzahrani, Malik Zaka Ullah, and Stanford Shateyi. 2023. "Filamentation of a Hollow Gaussian Beam in a Nonlinear Optical Medium" Mathematics 11, no. 19: 4130. https://doi.org/10.3390/math11194130
APA StyleAsma, M., Ali, A. K. S., Alzahrani, A. K., Ullah, M. Z., & Shateyi, S. (2023). Filamentation of a Hollow Gaussian Beam in a Nonlinear Optical Medium. Mathematics, 11(19), 4130. https://doi.org/10.3390/math11194130





