Some Results in Fuzzy b-Metric Space with b-Triangular Property and Applications to Fredholm Integral Equations and Dynamic Programming

Abstract

In this paper, we introduce the b-triangular property in fuzzy b-metric space. Furthermore, we give some new fixed point results in fuzzy b-metric space for non-continuous mappings. Our results generalize and expand some results from the related literature. Two applications of our results, to solving Fredholm integral equation and in dynamic programming, are also given.

1. Introduction and Preliminaries

The concept of continuous triangular norm was given by Schweizer and Sklar [1] in 1960. In 1965, the theory of fuzzy sets was given by Zadeh [2]. Later, in 1975, Kramosil and Michalek (see [3]), starting with the notion of fuzzy sets, defined the concept of fuzzy metric space with the continuous t-norms. The premise that there does not necessarily have to be a real number to describe the distance between two points is the basis for the fuzzy approach to distance. Then, in the same frame, George and Veeramani [4], in 1994, changed the definition of the fuzzy metric spaces. In [5], Grabeic gave the well-known Banach contraction principle in the case of fuzzy metric spaces, in the sense of Kramosil and Michalek. Starting with this generalization, many other researchers extended these results. One important case is that of Gregori and Sapena (see [6]), where the fuzzy Banach contraction theorem is translated in the case of fuzzy metric space in the sense of George and Veeramani [4]. Recently, were developed the fixed point theory fuzzy b-metric spaces. For example, see the generalizations of Sedghi and Shobe [7] and Abbas et al. [8]. The notion of the triangular property of the fuzzy metric in fuzzy metric spaces was given by Shamas et al. [9] in order to prove fixed point results losing the continuity condition. Moreover, many results on fuzzy metric spaces can be consulted in the following research works [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

Furthermore, we give some basic definitions below:

Definition 1

([7]). A 3-tuple $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ is said to be a fuzzy b-metric space (FBM space) if $\mathcal{U}$ is an arbitrary (non-empty) set, ∗ is a continuous ϑ-norm and ${\mathcal{M}}_{\mathfrak{r}}$ is a fuzzy set on ${\mathcal{U}}^2\times (0,+\infty )$, satisfying the following conditions:

(F1)

${\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )>0$,

(F2)

${\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )=1$ if and only if $\upsilon =\varpi$,

(F3)

${\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )={\mathcal{M}}_{\mathfrak{r}}(\varpi ,\upsilon ,\vartheta )$,

(F4)

${\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\mathfrak{s}(\vartheta +\mathfrak{g}))\ge {\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\xi ,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}(\xi ,\varpi ,\mathfrak{g})$,

(F5)

${\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,.):(0,+\infty )\to [0,1]$ is continuous,

for all $\upsilon ,\varpi ,\xi \in \mathcal{U}$, $\vartheta ,\mathfrak{g}>0$ and $\mathfrak{s}\ge 1$. The function ${\mathcal{M}}_{\mathfrak{r}}$ is said to be a fuzzy b-metric.

Definition 2

([8]). Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be a FBM space.

(D1)

A sequence $\left\{{\upsilon }_{\kappa }\right\}$ is convergent and converges to $\upsilon \in \mathcal{U}$ if ${lim}_{\kappa \to +\infty }{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },\upsilon ,\vartheta )=1$ for all $\vartheta >0$ and denoted ${\upsilon }_{\kappa }\to \upsilon$ as $\kappa \to +\infty$.

(D2)

If ${lim}_{\kappa ,\mathfrak{k}\to +\infty }{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\mathfrak{k}},\vartheta )=1$ and for any $\vartheta >0$ then $\left\{{\upsilon }_{\kappa }\right\}$ is said to be a Cauchy sequence in $\mathcal{U}$.

(D3)

If every Cauchy sequence is convergent in $\mathcal{U}$ then $\mathcal{U}$ is said to be a complete FBM space.

Definition 3.

Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be an FBM-space with $\mathfrak{s}\ge 1$ and a mapping $𝓁:\mathcal{U}\to \mathcal{U}$ is called fuzzy b-contraction if there exists ${\delta }_1\in (0,1)$ such that

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}-1& \le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right),\hfill \end{array}$$

(1)

for all ${\upsilon }_1,{\upsilon }^{*},\in \mathcal{U},\vartheta >0$.

Definition 4.

Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be an FBM-space with $\mathfrak{s}\ge 1$ and a mapping $𝓁:\mathcal{U}\to \mathcal{U}$ is said to be a rational type fuzzy b-contraction if there exists ${\delta }_1\in (0,1)$ and ${\delta }_2\ge 0$ s.t:

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}-1\le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )*{\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }_1,2\mathfrak{s}\vartheta )}-1\right),$$

(2)

for all ${\upsilon }_1,{\upsilon }^{*},\in \mathcal{U},\vartheta >0$.

In this manuscript, we prove some results of fixed points in the fuzzy b-metric spaces for non-continuous mappings. Motivated by the solutions of Shamas et al. [9] and Mani et al. [29] we recall the b-triangular property in fuzzy b-metric space, which is crucial for proving the new results here presented. Furthermore, we give some interesting applications of our results, the first result for proving the existence of a unique result of an integral Fredholm equation, and the other in dynamic programming.

2. Main Results

In this section, we recall first the b-triangular property given by Mani et al. in [29] and we discuss some new fixed point results involving this condition. We can say that it is an interesting way to prove the existence of a fixed point considering the b-triangular property, without having the property of continuity of the fuzzy b-metric. Then we give a result of fixed points for rational-type fuzzy b-contractions that satisfy condition (2).

First, let us recall the b-triangular property of a fuzzy b-metric in an $FBM$ space.

Definition 5

([29]). Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be an FBM space with $\mathfrak{s}\ge 1$. The fuzzy b-metric ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular if:

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )}-1& \le \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\xi ,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\xi ,\varpi ,\vartheta )}-1\right)\hfill \end{array}$$

Remark 1.

Note that, if $\mathfrak{s}=1$, we obtain the triangular property defined by Bari and Vetro [30].

Example 1

([29]). Let ${\mathcal{M}}_{\mathfrak{r}}:{\mathcal{U}}^2\times (0,+\infty )\to [0,1]$ be defined by:

$$\begin{array}{c}\hfill {\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )=\frac{\vartheta }{{\vartheta +|\upsilon -\varpi |}^2},\end{array}$$

for all $\upsilon ,\varpi \in \mathcal{U},\vartheta >0$.

Now,

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )}-1& =\frac{{|\upsilon -\varpi |}^2}{\vartheta }=\frac{{|\upsilon -\xi +\xi -\varpi |}^2}{\vartheta }\hfill \\ \hfill & \le 2\left(\frac{{|\upsilon -\xi |}^2}{\vartheta }+\frac{{|\xi -\varpi |}^2}{\vartheta }\right)\hfill \\ \hfill & =2\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\xi ,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\xi ,\varpi ,\vartheta )}-1\right)\hfill \end{array}$$

which implies that:

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )}-1& \le \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\xi ,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\xi ,\varpi ,\vartheta )}-1\right),\hfill \end{array}$$

for $\vartheta >0$, where $\mathfrak{s}=2$. So, ${\mathcal{M}}_{\mathfrak{r}}$ is fuzzy b-triangular.

Our first main result is the following.

Theorem 1

(Banach contraction principle in FBM). Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be a complete FBM-space with $\mathfrak{s}\ge 1$ s.t ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and a mapping $𝓁:\mathcal{U}\to \mathcal{U}$ is a fuzzy b-contraction satisfying (1). Then, ℓ has a UFP (unique fixed point) in $\mathcal{U}$.

Proof. 

Fix ${\upsilon }_0\in \mathcal{U}$ and ${\upsilon }_{\kappa +1}=𝓁{\upsilon }_{\kappa },\kappa \ge 0.$ Then, by (1), for $\vartheta >0,\kappa \ge 1$, we have:

$$\begin{array}{ccc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1& =& \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa },\vartheta )}-1\hfill \\ & \le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right).\hfill \end{array}$$

Then,

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right).$$

(3)

Now, from (3) using induction, we have:

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\le {\delta }_1^{\kappa }\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)$$

(4)

for $\vartheta >0$. So,

$$\underset{\kappa \to +\infty }{lim}\mathcal{M}({\upsilon }_{\kappa },{\upsilon }_{\kappa -1},\vartheta )=1,$$

(5)

for $\vartheta >0$. Since ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular, using (4) we obtain:

$$\begin{array}{ccc}& & \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\mathfrak{k}},\vartheta )}-1\le \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},{\upsilon }_{\mathfrak{k}},\vartheta )}-1\right)\hfill \\ & \le & \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\right)+{\mathfrak{s}}^2\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},{\upsilon }_{\kappa +2},\vartheta )}-1\right)\hfill \end{array}$$

$$\begin{array}{ccc}& +& \cdots +{\mathfrak{s}}^{\mathfrak{k}-\kappa -1}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\mathfrak{k}-1},{\upsilon }_{\mathfrak{k}},\vartheta )}-1\right)\hfill \\ & \le & (\mathfrak{s}{\delta }_1^{\kappa }+{\mathfrak{s}}^2{\delta }_1^{\kappa +1}+\cdots +{\mathfrak{s}}^{\mathfrak{k}-\kappa -1}{\delta }_1^{k-1})\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)\hfill \\ & \le & \frac{\mathfrak{s}{\delta }_1^{\kappa }}{1-\mathfrak{s}{\delta }_1}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)\to 0,\mathrm{as} \kappa \to +\infty .\hfill \end{array}$$

Therefore, $\left\{{\upsilon }_{\kappa }\right\}$ is a Cauchy sequence in $\mathcal{U}$. Since $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ is complete, there is ${\varpi }_1\in \mathcal{U}$ such that

$$\begin{array}{c}\hfill \underset{\kappa \to +\infty }{lim}{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )=1,\end{array}$$

(6)

for $\vartheta >0$. Since ${\mathcal{M}}_{\mathfrak{r}}$ is a b-triangular, from (1), (5) and (6), for $\vartheta >0$, we have:

$$\begin{array}{ccc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1& \le & \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},\vartheta )}-1\right)+\mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_{\kappa },𝓁{\varpi }_1,\vartheta )}-1\right)\hfill \\ & \le & \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},\vartheta )}-1\right)+\mathfrak{s}{\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}-1\right)\hfill \\ & =& \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},\vartheta )}-1\right)+\mathfrak{s}{\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}-1\right)\hfill \\ & \to & 0 \mathrm{as} \kappa \to +\infty .\hfill \end{array}$$

Hence,

$$\begin{array}{c}\hfill {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )=1.\end{array}$$

Therefore,

$$\begin{array}{c}\hfill 𝓁{\varpi }_1={\varpi }_1,\end{array}$$

for $\vartheta >0$. Let ${\mathfrak{z}}_1\in \mathcal{U}$ s.t $𝓁{\mathfrak{z}}_1={\mathfrak{z}}_1$ and $𝓁{\mathfrak{z}}_1\ne {\varpi }_1$; then, from (1) we obtain:

$$\begin{array}{ccc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1& =& \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\varpi }_1,𝓁{\mathfrak{z}}_1,\vartheta )}-1\hfill \\ & \le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)<\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1.\hfill \end{array}$$

This is a contradiction. So, ${\varpi }_1={\mathfrak{z}}_1$. □

Example 2.

Consider $\mathcal{U}=[0,+\infty )$, ∗ to be a continuous ϑ-norm and ${\mathcal{M}}_{\mathfrak{r}}:{\mathcal{U}}^2\times (0,+\infty )\to [0,1]$ by:

$${\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )=\frac{\vartheta }{\vartheta +|{\upsilon }_1-{\upsilon }^{*}{|}^2},$$

for all ${\upsilon }_1,{\upsilon }^{*}\in \mathcal{U},\vartheta >0$. Clearly, ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and $({\mathcal{M}}_{\mathfrak{r}},\ast )$ is a complete FBM space with $\mathfrak{s}=2$ (see Example 1). Define $𝓁:\mathcal{U}\to \mathcal{U}$ by:

$$𝓁\left({\upsilon }_1\right)=\frac{{\upsilon }_1}{\sqrt{3}},$$

for all ${\upsilon }_1\in \mathcal{U}$. Then we have:

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁\left({\upsilon }_1\right),𝓁\left({\upsilon }^{*}\right),\vartheta )}-1=\frac{1}{3}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right)$$

Thereby, all the axioms of Theorem 1 are fulfilled with ${\delta }_1=\frac{1}{3}\in (0,\frac{1}{2})$. Hence ℓ has a UFP ${\upsilon }_1=0$.

Our next main theorem is given below:

Theorem 2.

Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be a complete FBM-space with $\mathfrak{s}\ge 1$ s.t ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and a mapping $𝓁:\mathcal{U}\to \mathcal{U}$ is a rational-type fuzzy b-contraction satisfying (2) s.t ${\delta }_1\in (0,\frac{1}{\mathfrak{s}})$ and ${\delta }_2\ge 0$. Then, ℓ has a UFP in $\mathcal{U}$.

Proof. 

Fix ${\upsilon }_0\in \mathcal{U}$ and ${\upsilon }_{\kappa +1}=𝓁{\upsilon }_{\kappa },\kappa \ge 0.$ Then, by (2), for $\vartheta >0,\kappa \ge 1$, we have:

$$\begin{array}{ccc}& & \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1=\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa },\vartheta )}-1\hfill \\ & \le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa -1},\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa -1},2\mathfrak{s}\vartheta )}-1\right)\hfill \\ & =& {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa },2\mathfrak{s}\vartheta )}-1\right).\hfill \end{array}$$

Then,

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right).$$

(7)

Now, from (7) using induction, we have:

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\le {\delta }_1^{\kappa }\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)$$

(8)

for $\vartheta >0$. So,

$$\underset{\kappa \to +\infty }{lim}\mathcal{M}({\upsilon }_{\kappa },{\upsilon }_{\kappa -1},\vartheta )=1,$$

(9)

for $\vartheta >0$. Since ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular, using (8) we obtain:

$$\begin{array}{ccc}& & \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\mathfrak{k}},\vartheta )}-1\le \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},{\upsilon }_{\mathfrak{k}},\vartheta )}-1\right)\hfill \\ & \le & \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\right)+{\mathfrak{s}}^2\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},{\upsilon }_{\kappa +2},\vartheta )}-1\right)\hfill \\ & +& \cdots +{\mathfrak{s}}^{\mathfrak{k}-\kappa -1}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\mathfrak{k}-1},{\upsilon }_{\mathfrak{k}},\vartheta )}-1\right)\hfill \\ & \le & (\mathfrak{s}{\delta }_1^{\kappa }+{\mathfrak{s}}^2{\delta }_1^{\kappa +1}+\cdots +{\mathfrak{s}}^{\mathfrak{k}-\kappa -1}{\delta }_1^{k-1})\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)\hfill \\ & \le & \frac{\mathfrak{s}{\delta }_1^{\kappa }}{1-\mathfrak{s}{\delta }_1}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)\to 0,\mathrm{as} \kappa \to +\infty .\hfill \end{array}$$

Therefore, $\left\{{\upsilon }_{\kappa }\right\}$ is a Cauchy sequence in $\mathcal{U}$. Since $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ is complete, there is ${\varpi }_1\in \mathcal{U}$ such that:

$$\begin{array}{c}\hfill \underset{\kappa \to +\infty }{lim}{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )=1,\end{array}$$

(10)

for $\vartheta >0$. Since ${\mathcal{M}}_{\mathfrak{r}}$ is a b-triangular, from (2), (9) and (10), for $\vartheta >0$, we have:

$$\begin{array}{ccc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1& \le & \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},\vartheta )}-1\right)+\mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_{\kappa },𝓁{\varpi }_1,\vartheta )}-1\right)\hfill \\ & \le & \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},\vartheta )}-1\right)+\mathfrak{s}{\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}-1\right)\hfill \\ & +& \mathfrak{s}{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa },\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\upsilon }_{\kappa },2\mathfrak{s}\vartheta )}-1\right)\hfill \\ & =& \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},\vartheta )}-1\right)+\mathfrak{s}{\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}-1\right)\hfill \\ & +& \mathfrak{s}{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},2\mathfrak{s}\vartheta )}-1\right)\to 0 \mathrm{as} \kappa \to +\infty .\hfill \end{array}$$

Hence,

$$\begin{array}{c}\hfill {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )=1.\end{array}$$

Therefore,

$$\begin{array}{c}\hfill 𝓁{\varpi }_1={\varpi }_1,\end{array}$$

for $\vartheta >0$. Let ${\mathfrak{z}}_1\in \mathcal{U}$ s.t $𝓁{\mathfrak{z}}_1={\mathfrak{z}}_1$ and $𝓁{\mathfrak{z}}_1\ne {\varpi }_1$; then, from (2) we obtain:

$$\begin{array}{ccc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1& =& \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\varpi }_1,𝓁{\mathfrak{z}}_1,\vartheta )}-1\hfill \\ & \le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,𝓁{\varpi }_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ & \le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\varpi }_1,\vartheta )}-1\right)\hfill \\ & =& {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)<\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1.\hfill \end{array}$$

This is a contradiction. So, ${\varpi }_1={\mathfrak{z}}_1$. □

Next, let us give another fixed point result related to b-triangular property of the fuzzy metric.

Theorem 3.

Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be a complete FBM-space with $\mathfrak{s}\ge 1$, s.t ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and a mapping $𝓁:\mathcal{U}⟶\mathcal{U}$ that satisfies:

$$\begin{array}{cc}\hfill & \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}-1\le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }^{*},2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }^{*},2\mathfrak{s}\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }^{*},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }^{*},\vartheta )}-1\right),\hfill \end{array}$$

(11)

for all ${\upsilon }_1,{\upsilon }^{*}\in \mathcal{M},\vartheta >0,{\delta }_i\ge 0,i=1,2,3,4$ with ${\delta }_1+{\delta }_2+2{\delta }_3+2{\delta }_4<\frac{1}{\mathfrak{s}}$. Then ℓ has a UFP.

Proof. 

Fix ${\upsilon }_0\in \mathcal{U}$ and ${\upsilon }_{\kappa +1}=𝓁{\upsilon }_{\kappa },\kappa \ge 0$. Then, by (11), for $\vartheta >0,\kappa \ge 1$, we have:

$$\begin{array}{ccc}& & \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1=\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa },\vartheta )}-1\hfill \\ & \le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa },\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa -1},\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa },2\mathfrak{s}\vartheta )}-1\right)\hfill \\ & +& {\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa -1},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa },2\mathfrak{s}\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa },\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa },2\mathfrak{s}\vartheta )}-1\right)+{\delta }_4(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},𝓁{\upsilon }_{\kappa -1},\vartheta )}-1\hfill \\ & +& \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa },\vartheta )}-1)\hfill \\ & =& {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa +1},2\mathfrak{s}\vartheta )}-1\right)\hfill \\ & +& {\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa +1},2\mathfrak{s}\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa +1},2\mathfrak{s}\vartheta )}-1\right)+{\delta }_4(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\hfill \\ & +& \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1).\hfill \end{array}$$

By definition of the FBM space, ${\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa +1},2\mathfrak{s}\vartheta )\ge {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )$, for $\vartheta >0$, and after simplification, we have:

$$\begin{array}{c}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\le \beta \left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa -1},{\upsilon }_{\kappa },\vartheta )}-1\right),\end{array}$$

(12)

where $\beta =\frac{{\delta }_1+{\delta }_2+{\delta }_3+{\delta }_4}{1-{\delta }_3-{\delta }_4}<1$.

Now, from (12) using induction, we have:

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\le {\beta }^{\kappa }\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)$$

(13)

for $\vartheta >0$. Then,

$$\underset{\kappa \to +\infty }{lim}{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )=1,$$

(14)

for $\vartheta >0$. Notice that ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular; then, $\forall \mathfrak{k}>\kappa \ge {\kappa }_0$,

$$\begin{array}{cc}\hfill & \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\mathfrak{k}},\vartheta )}-1\le \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},{\upsilon }_{\mathfrak{k}},\vartheta )}-1\right)\hfill \\ \hfill & \le \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1\right)+{\mathfrak{s}}^2\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},{\upsilon }_{\kappa +2},\vartheta )}-1\right)\hfill \\ \hfill & +\cdots +{\mathfrak{s}}^{\mathfrak{k}-\kappa -1}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\mathfrak{k}-1},{\upsilon }_{\mathfrak{k}},\vartheta )}-1\right)\hfill \\ & \le (\mathfrak{s}{\beta }^{\kappa }+{\mathfrak{s}}^2{\beta }^{\kappa +1}+\cdots +{\mathfrak{s}}^{\mathfrak{k}-\kappa -1}{\beta }^{k-1})\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)\hfill \\ \hfill & \le \frac{\mathfrak{s}{\beta }^{\kappa }}{1-\mathfrak{s}\beta }\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_0,{\upsilon }_1,\vartheta )}-1\right)\to 0,as\kappa \to +\infty .\hfill \end{array}$$

Hence, $\left({\upsilon }_{\kappa }\right)$ is a Cauchy sequence. Since $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ is complete, then we can find ${\varpi }_1\in \mathcal{U}$ satisfying:

$$\begin{array}{c}\hfill \underset{\kappa \to \infty }{lim}{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )=1,\end{array}$$

(15)

for $\vartheta >0$. Since ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular,

$$\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\le \mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\upsilon }_{\kappa +1},\vartheta )}-1\right)+\mathfrak{s}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},𝓁{\varpi }_1,\vartheta )}-1\right),$$

(16)

for $\vartheta >0$. Now from (11), (14) and (15), for $\vartheta >0$,

$$\begin{array}{cc}& \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},𝓁{\varpi }_1,\vartheta )}-1=\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_{\kappa },𝓁{\varpi }_1,\vartheta )}-1\hfill \\ \hfill & \le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa },\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\varpi }_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa },\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\varpi }_1,2\mathfrak{s}\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\varpi }_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\upsilon }_{\kappa },\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\right)\hfill \\ \hfill & ={\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\varpi }_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\varpi }_1,2\mathfrak{s}\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\varpi }_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\right)\hfill \end{array}$$

By definition of the FBM space, we have ${\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },𝓁{\varpi }_1,2\mathfrak{s}\vartheta )\ge {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )\ast$${\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )$, for $\vartheta >0$. So, we obtain:

$$\begin{array}{c}\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},𝓁{\varpi }_1,\vartheta )}-1\le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )}-1\right)\hfill \\ +{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\right)\hfill \\ +{\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa +1},{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\right)\hfill \\ +{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_{\kappa },{\upsilon }_{\kappa +1},\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\right)\hfill \\ \to ({\delta }_3+{\delta }_4)\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\right)\mathrm{as}\kappa \to +\infty .\hfill \end{array}$$

(17)

Now, from (15)–(17), as $\kappa \to +\infty$, we derive that:

$$\begin{array}{c}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\le \mathfrak{s}({\delta }_3+{\delta }_4)\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1\right),\end{array}$$

for $\vartheta >0$, and $\mathfrak{s}({\delta }_3+{\delta }_4)<1$, where ${\delta }_1+{\delta }_2+2{\delta }_3+2{\delta }_4<\frac{1}{\mathfrak{s}}$ and hence ${\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )=1$, i.e., $𝓁{\varpi }_1={\varpi }_1$, for $\vartheta >0$. Let ${\mathfrak{z}}_1\in \mathcal{U}$ s.t $𝓁{\mathfrak{z}}_1={\mathfrak{z}}_1$. Then, from (11), we have:

$$\begin{array}{cc}& \frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1=\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\varpi }_1,𝓁{\mathfrak{z}}_1,\vartheta )}-1\hfill \\ \hfill & \le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,𝓁{\mathfrak{z}}_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\mathfrak{z}}_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\mathfrak{z}}_1,2\mathfrak{s}\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,𝓁{\mathfrak{z}}_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\mathfrak{z}}_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,𝓁{\varpi }_1,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,𝓁{\mathfrak{z}}_1,\vartheta )}-1\right)\hfill \\ \hfill & ={\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\delta }_3\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,2\mathfrak{s}\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,2\mathfrak{s}\vartheta )}-1\right)\hfill \\ \hfill & ={\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)+{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,{\mathfrak{z}}_1,\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_3\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,{\mathfrak{z}}_1,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\mathfrak{z}}_1,{\mathfrak{z}}_1,\vartheta )}-1\right)\hfill \\ \hfill & =({\delta }_1+2{\delta }_3)\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)=({\delta }_1+2{\delta }_3)\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\varpi }_1,𝓁{\mathfrak{z}}_1,\vartheta )}-1\right)\hfill \\ \hfill & \le {({\delta }_1+2{\delta }_3)}^2\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le {({\delta }_1+2{\delta }_3)}^{\kappa }\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )}-1\right)\to 0,\mathrm{as}\kappa \to +\infty ,\hfill \end{array}$$

where ${\delta }_1+2{\delta }_3<1$. Thereby, ${\mathcal{M}}_{\mathfrak{r}}({\varpi }_1,{\mathfrak{z}}_1,\vartheta )=1$. Hence, ${\varpi }_1={\mathfrak{z}}_1$, for $\vartheta >0$. □

Corollary 1.

Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be a complete FBM-space s.t ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and a map $𝓁:\mathcal{U}⟶\mathcal{U}$ satisfies:

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}-1\le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_2\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }^{*},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )\ast {\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }^{*},2\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }_1,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }^{*},\vartheta )}-1\right),\hfill \end{array}$$

$\forall {\upsilon }_1,{\upsilon }^{*}\in \mathcal{U},\vartheta >0,{\delta }_1,{\delta }_2,{\delta }_4\ge 0$ with ${\delta }_1+{\delta }_2+2{\delta }_4<\frac{1}{\mathfrak{s}}$. Then, ℓ has a UFP.

Corollary 2.

Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be a complete FBM-space with $\mathfrak{s}\ge 1$, in which ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and a mapping $𝓁:\mathcal{U}⟶\mathcal{U}$ satisfies:

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}-1\le & {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_3\left(\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }^{*},2\vartheta )}-1+\frac{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }^{*},\vartheta )}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }^{*},2\vartheta )}-1\right)\hfill \\ \hfill & +{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }^{*},\vartheta )}-1\right),\hfill \end{array}$$

$\forall {\upsilon }_1,{\upsilon }^{*}\in \mathcal{U},\vartheta >0,{\delta }_1,{\delta }_3,{\delta }_4\ge 0$ with ${\delta }_1+2{\delta }_3+2{\delta }_4<\frac{1}{\mathfrak{s}}$. Then, ℓ has a UFP.

Corollary 3.

Let $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ be a complete FBM-space with $\mathfrak{s}\ge 1$, s.t ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and a mapping $𝓁:\mathcal{U}⟶\mathcal{U}$ satisfies:

$$\begin{array}{c}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}-1\le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right)+{\delta }_4\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,𝓁{\upsilon }_1,\vartheta )}-1+\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }^{*},𝓁{\upsilon }^{*},\vartheta )}-1\right),\end{array}$$

$\forall {\upsilon }_1,{\upsilon }^{*}\in \mathcal{U},\vartheta >0,{\delta }_1,{\delta }_4\ge 0$ with ${\delta }_1+2{\delta }_4<\frac{1}{s}$. Then, ℓ has a UFP.

Example 3.

Let $\mathcal{U}=[0,+\infty )$, ∗ be a continuous ϑ-norm and ${\mathcal{M}}_{\mathfrak{r}}:{\mathcal{U}}^2\times (0,+\infty )\to [0,1]$ defined by:

$$\begin{array}{c}\hfill {\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )=\frac{\vartheta }{\vartheta +|{\upsilon }_1-{\upsilon }^{*}{|}^2}.\end{array}$$

Afterward, one may simply verify that ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and $({\mathcal{M}}_{\mathfrak{r}},\ast )$ is a complete FBM space with $\mathfrak{s}\ge 1$. Define $𝓁:\mathcal{U}\to \mathcal{U}$ by:

$$\begin{array}{c}\hfill 𝓁\left({\upsilon }_1\right)=sin\frac{{\upsilon }_1}{4},\end{array}$$

Let ${\upsilon }_1,{\upsilon }^{*}\in \mathcal{U}$ and $\vartheta >0$, then:

$$\begin{array}{c}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁\left({\upsilon }_1\right),𝓁\left({\upsilon }^{*}\right),\vartheta )}-1=\frac{|𝓁\left({\upsilon }_1\right)-𝓁\left({\upsilon }^{*}\right){|}^2}{\vartheta }=\frac{1}{16}\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right)\end{array}$$

Therefore, all the axioms of Theorem 3 are fulfilled with ${\delta }_1=\frac{1}{16},{\delta }_2={\delta }_3={\delta }_4=0$. Hence ℓ has a unique fixed point ${\upsilon }_1=0$.

3. Application to a Fredholm Inegral Equation

In this section, as an application of Theorem 2, we examine the existence and unique solution to a Fredholm integral problem. Let $\mathcal{U}=C\left(\right[0,\eta ],\mathbb{R})$ be the set of all real-valued continuous mappings on $[0,\eta ]$, where $\eta >0$. The Fredholm IE (integral equation) is:

$$\begin{array}{c}\hfill \upsilon \left(\pi \right)={\int }_0^{\eta }\mathcal{K}(\pi ,\wp ,\upsilon (\pi ))d\wp .\end{array}$$

(18)

The binary operation ∗ is defined by $\varphi \ast \varsigma =\varphi \varsigma$, for all $\varphi ,\varsigma \in [0,\eta ]$. Define ${\mathcal{M}}_{\mathfrak{r}}:\mathcal{U}\times \mathcal{U}\times (0,+\infty )\to [0,1]$ by:

$$\begin{array}{c}\hfill {\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )=\frac{\vartheta }{{\vartheta +|\upsilon -\varpi |}^2}.\end{array}$$

Then, ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$ is a complete FBM space with $\mathfrak{s}=2$.

Theorem 4.

Presume that:

(T1)

there is a mapping $\theta :[0,\eta ]\times [0,\eta ]\to [0,+\infty )$ be a continuous function s.t:

$$\begin{array}{c}\hfill |\mathcal{K}(\pi ,\wp ,\upsilon (\pi ))-\mathcal{K}(\pi ,\wp ,\varpi (\pi ))|\le \sqrt{\theta (\pi ,\wp )}|\upsilon (\pi )-\varpi (\pi )|,\end{array}$$

(T2)

${\int }_0^{\eta }\theta (\pi ,\wp )d\wp <\frac{1}{2}$.

Then, the Equation (18) has a unique solution in $\mathcal{U}$.

Proof. 

Define the mapping $𝓁:\mathcal{U}\to \mathcal{U}$ by:

$$\begin{array}{c}\hfill 𝓁\left(\upsilon (\pi )\right)={\int }_0^{\eta }\mathcal{K}(\pi ,\wp ,\upsilon (\pi ))d\wp .\end{array}$$

Then we have:

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁\upsilon (\pi ),𝓁\varpi (\pi )),\vartheta )}-1& =\frac{{|𝓁\upsilon (\pi )-𝓁\varpi (\pi )|}^2}{\vartheta }\hfill \\ \hfill & =\frac{{\left({\int }_0^{\eta }\mathcal{K}(\pi ,\wp ,\upsilon (\pi ))-\mathcal{K}(\pi ,\wp ,\varpi (\pi ))d\wp \right)}^2}{\vartheta }\hfill \\ \hfill & \le \frac{{\int }_0^{\eta }{|\mathcal{K}(\pi ,\wp ,\upsilon (\pi ))-\mathcal{K}(\pi ,\wp ,\varpi (\pi ))|}^{2}d\wp }{\vartheta }\hfill \\ \hfill & \le \frac{{\int }_0^{\eta }\theta (\pi ,\wp ){|\upsilon (\pi )-\varpi (\pi )|}^{2}d\wp }{\vartheta }\hfill \\ \hfill & \le {\delta }_1\frac{{|\upsilon (\pi )-\varpi (\pi )|}^2}{\vartheta }\hfill \\ \hfill & ={\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon (\pi ),\varpi (\pi )),\vartheta )}-1\right).\hfill \end{array}$$

Thereby, all the axioms of Theorem 2 are satisfied with ${\delta }_1={\int }_0^{\eta }\theta (\pi ,\wp )d\wp \in (0,\frac{1}{\mathfrak{s}})$ and ${\delta }_2=0$. Hence ℓ has a UFP in $\mathcal{U}$. □

Example 4.

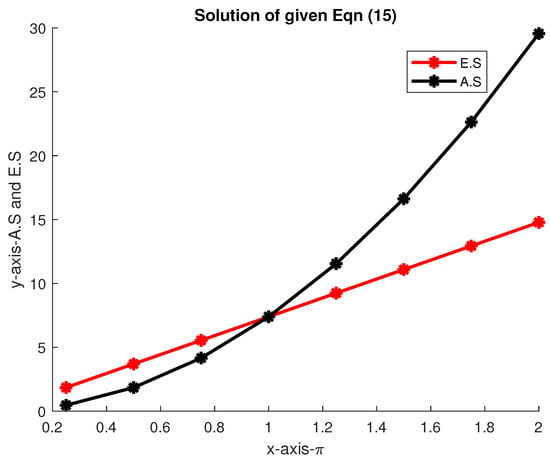
Consider the Fredholm IE as follows:

$$\begin{array}{c}\hfill \upsilon (\pi )={\int }_0^{\eta }\mathcal{K}(\pi ,\wp ,\upsilon (\wp ))d\wp ,\forall \eta >0.\end{array}$$

(19)

Let us take $\mathcal{K}(\pi ,\wp ,\upsilon (\wp ))={\mathit{e}}^{2\pi }$ as the exact solution of Equation (19).

Hence, the absolute solution of the given equation is $\pi {\mathit{e}}^{2\pi }$ for $\pi >0$. Table 1 shows the numerical results below:

Table 1. Numerical results for Example 4.

$\mathit{\pi }$	${\mathit{e}}^{2\mathit{\pi }}$	$\mathit{\pi }{\mathit{e}}^{2\mathit{\pi }}$	Error
0.25	1.8473	0.4618	1.0112
0.50	3.6945	1.8473	1.8473
0.75	5.5418	4.1563	1.3855
1.00	7.3891	7.3891	0.0000
1.25	9.2363	11.5454	2.3091
1.50	11.0836	16.6254	5.5418
1.75	12.9308	22.6289	9.6981
2.00	14.7781	29.5562	14.7781

The comparison between the approximate solution (A.S) and exact solutions (E.S) is shown in the following Figure 1.

Figure 1. Prove that the fixed point of $\pi$ is 1 and is unique.

4. Application to Dynamic Programming

Dynamic programming can be considered both a mathematical optimization and a computational programming method at the same time. It was formulated by the US mathematician Richard Bellman in the 1950s; see [31,32]. This algorithm was used to describe the problem-solving process in which the best decision is sought at each step. Dynamic programming is one of the most popular algorithms used in biocomputing. Moreover, it is used in a variety of processes, such as sequence comparison, physics phenomena, genetic recognition, social sciences analysis and many other problems.

The theory of dynamic programming extends to multi-stage decision processes. In these types of processes, some functional equations appear in a usual manner. In this section we use a couple functional equations which appear in some types of continuous multi-stage decision-making processes. Next, let us recall some main definitions of the continuous multi-stage decision-making theory.

Consider $\Delta \subset \mathcal{U}$, $\Omega \subset \mathcal{S}$ to be the state and decision space, respectively, where $\mathcal{U}$ and $\mathcal{S}$ are Banach spaces. We denote a state and decision vector by u and v. Let us consider the following given maps $𝓁:\Delta \times \Omega \to \Delta$, $\mathfrak{g}:\Delta \times \Omega \to \mathbb{R}$, and $\mathfrak{G}:\Delta \times \Omega \times \mathbb{R}\to \mathbb{R}$, where $\mathbb{R}$ denotes the set of real numbers. Let $\mathfrak{f}:\Delta \to \mathbb{R}$ be the return function of the continuous decision process; it is defined by the following functional equation:

$$\mathfrak{f}=\underset{\zeta \in \Omega }{sup}\{\mathfrak{g}(\lambda ,\zeta )+\mathfrak{G}(\lambda ,\zeta ,\mathfrak{f}\left(𝓁(\lambda ,\zeta )\right))\}, \mathrm{f}\mathrm{o}\mathrm{r} \lambda \in \Delta .$$

(20)

In accord with the previous facts, let us give the main outcome of this part.

Theorem 5.

Considering the previous conditions, we suppose the following to be true:

(i)

$\mathfrak{G}$ and $\mathfrak{g}$ are bounded;

(ii)

$|\mathfrak{G}(\lambda ,\zeta ,z_1)-\mathfrak{G}(\lambda ,\zeta ,z_2)|\le \sqrt{{\delta }_1}|z_1-z_2|$, for ${\delta }_1\in (0,\frac{1}{2})$,

for all $(\lambda ,\zeta ,z_1),(\lambda ,\zeta ,z_2)\in \Delta \times \Omega \times \mathbb{R}$.

Then the functional Equation (20) has a unique bounded solution on Δ.

Proof. 

Let $\mathcal{U}=\mathcal{B}(\Delta )$ be the space of bounded real-valued maps on $\Delta$ and let * be a binary operation defined by $\varphi \ast \varsigma =\varphi \varsigma$, for all $\varphi ,\varsigma \in [0,\eta ]$. We consider the fuzzy b-metric ${\mathcal{M}}_{\mathfrak{r}}:\mathcal{U}\times \mathcal{U}\times (0,+\infty )\to [0,1]$ defined as:

$$\begin{array}{c}\hfill {\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )=\frac{\vartheta }{{\vartheta +|\upsilon -\varpi |}^2}.\end{array}$$

Clearly, ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and $(\mathcal{B}\left(\mathcal{S}\right),{\mathcal{M}}_{\mathfrak{r}},\ast )$ is a complete FBM space with $\mathfrak{s}=2$. Next, let us define the mapping ℓ on $\mathcal{B}\left(\mathcal{S}\right)$ by $𝓁\upsilon =\xi$, where:

$$\xi \left(\lambda \right)=\underset{\zeta \in \Omega }{sup}\{\mathfrak{g}(\lambda ,\zeta )+\mathfrak{G}(\lambda ,\zeta ,\upsilon \left(𝓁(\lambda ,\zeta )\right))\}$$

By the hypothesis $\left(i\right)$ we obtain that $\xi \in \mathcal{B}\left(\mathcal{S}\right)$.

Let ${\upsilon }_1$ and ${\upsilon }^{*}$ be any two elements of $\mathcal{B}\left(\mathcal{S}\right)$, and we define ${\xi }_1=𝓁{\upsilon }_1$ and ${\xi }_2=𝓁{\upsilon }^{*}$. Then we have:

$${\xi }_1\left(\lambda \right)=\underset{\zeta \in \Omega }{sup}\{\mathfrak{g}(\lambda ,\zeta )+\mathfrak{G}(\lambda ,\zeta ,{\upsilon }_1\left(𝓁(\lambda ,\zeta )\right))\},$$

$${\xi }_2\left(\lambda \right)=\underset{\zeta \in \Omega }{sup}\{\mathfrak{g}(\lambda ,\zeta )+\mathfrak{G}(\lambda ,\zeta ,{\upsilon }^{*}\left(𝓁(\lambda ,\zeta )\right))\}.$$

We consider $\lambda \in \Delta$ and let $\eta >0$ be any positive real number. For any two elements ${\zeta }_1,{\zeta }_2\in \Omega$ we obtain:

$$\begin{array}{cc}\hfill & {\xi }_1\left(\lambda \right)<\mathfrak{g}(\lambda ,{\zeta }_1)+\mathfrak{G}(\lambda ,{\zeta }_1,{\upsilon }_1\left({\lambda }_1\right))+\eta ,\hfill \\ \hfill & {\xi }_2\left(\lambda \right)<\mathfrak{g}(\lambda ,{\zeta }_2)+\mathfrak{G}(\lambda ,{\zeta }_2,{\upsilon }^{*}\left({\lambda }_2\right))+\eta ,\hfill \end{array}$$

(21)

with ${\lambda }_i=𝓁(\lambda ,{\zeta }_i)$, for $i=\{1,2\}$.

In addition, we obtain:

$${\xi }_1\left(\lambda \right)\ge \mathfrak{g}(\lambda ,{\zeta }_2)+\mathfrak{G}(\lambda ,{\zeta }_2,{\upsilon }_1\left({\lambda }_2\right))+\eta ,$$

(22)

$${\xi }_2\left(\lambda \right)\ge \mathfrak{g}(\lambda ,{\zeta }_1)+\mathfrak{G}(\lambda ,{\zeta }_1,{\upsilon }^{*}\left({\lambda }_1\right))+\eta ,$$

(23)

By $\left(21\right)$ and $\left(23\right)$ we obtain:

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}\left({\xi }_1\left(\lambda \right)\right),{\xi }_2\left(\lambda \right)),\vartheta )}-1& =\frac{|{\xi }_1\left(\lambda \right))-{\xi }_2\left(\lambda \right){\left)\right|}^2}{\vartheta }\hfill \\ \hfill & <\frac{1}{\vartheta }{|\mathfrak{G}(\lambda ,{\zeta }_1,{\upsilon }_1\left({\lambda }_1\right))-\mathfrak{G}(\lambda ,{\zeta }_1,{\upsilon }^{*}\left({\lambda }_1\right))+\eta |}^2\hfill \\ \hfill & \le \frac{1}{\vartheta }\left[|\mathfrak{G}(\lambda ,{\zeta }_1,{\upsilon }_1\left({\lambda }_1\right))-\mathfrak{G}(\lambda ,{\zeta }_1,{\upsilon }^{*}\left({\lambda }_1\right)){|}^2+{\left|\eta \right|}^2\right]\hfill \\ \hfill & \le \frac{1}{\vartheta }\left({\delta }_1{|{\upsilon }_1\left({\lambda }_1\right)-{\upsilon }^{*}\left({\lambda }_1\right)|}^2+{\eta }^2\right)\hfill \\ \hfill & =\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1+\frac{{\eta }^2}{\vartheta }.\hfill \end{array}$$

(24)

By $\left(21\right)$ and $\left(22\right)$ and using the property $\left(F_3\right)$ we obtain:

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}\left({\xi }_2\left(\lambda \right)\right),{\xi }_1\left(\lambda \right)),\vartheta )}-1& =\frac{|{\xi }_2\left(\lambda \right))-{\xi }_1\left(\lambda \right){\left)\right|}^2}{\vartheta }\hfill \\ \hfill & <\frac{1}{\vartheta }{|\mathfrak{G}(\lambda ,{\zeta }_2,{\upsilon }^{*}\left({\lambda }_2\right))-\mathfrak{G}(\lambda ,{\zeta }_2,{\upsilon }_1\left({\lambda }_2\right))+\eta |}^2\hfill \\ \hfill & \le \frac{1}{\vartheta }\left[|\mathfrak{G}(\lambda ,{\zeta }_2,{\upsilon }^{*}\left({\lambda }_2\right))-\mathfrak{G}(\lambda ,{\zeta }_2,{\upsilon }_1\left({\lambda }_2\right)){|}^2+{\left|\eta \right|}^2\right]\hfill \\ \hfill & \le \frac{1}{\vartheta }\left({\delta }_1{|{\upsilon }^{*}\left({\lambda }_2\right)-{\upsilon }_1\left({\lambda }_2\right)|}^2+{\eta }^2\right)\hfill \\ \hfill & =\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1+\frac{{\eta }^2}{\vartheta }.\hfill \end{array}$$

(25)

Since $\eta ,\vartheta >0$ then $\frac{{\eta }^2}{\vartheta }>0$. Then, by (24) and (25) and using the definitions of ${\xi }_1$ and ${\xi }_2$ we obtain:

$$|\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁{\upsilon }_1,𝓁{\upsilon }^{*},\vartheta )}-1|\le {\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}({\upsilon }_1,{\upsilon }^{*},\vartheta )}-1\right).$$

Thus, all the axioms of Theorem 1 are accomplished. Then the map ℓ has a UFP. This gives that the functional Equation (20) has a unique bounded solution on $\Delta$. □

5. Application to Fractional Differential Equation

Consider the nonlinear fractional differential equation (NLFDE)

$$\begin{array}{c}\hfill {\mathcal{D}}_{0+}^{\omega }\upsilon \left(\vartheta \right)=\mathfrak{h}(\vartheta ,\upsilon \left(\vartheta \right)),0<\vartheta <1\end{array}$$

(26)

with $\upsilon \left(0\right)+\upsilon {}^{\prime }\left(0\right)=0,\upsilon \left(1\right)+\upsilon {}^{\prime }\left(1\right)=0$, where $1<\omega \le 2$ is a real number, ${\mathcal{D}}_{0+}^{\omega }$ is the Caputo fractional derivative and a continuous function $\mathfrak{h}$ from $[0,1]\times [0,\infty )$ to $[0,\infty )$. Let $\mathcal{U}=\mathcal{C}\left(\right[0,1],\mathbb{R})=\{\mathfrak{f}:[0,1]\to \mathbb{R}\mathrm{be}\mathrm{a}\mathrm{continuous}\mathrm{function}\}$. Define ${\mathcal{M}}_{\mathfrak{r}}:\mathcal{U}\times \mathcal{U}\times (0,+\infty )\to [0,1]$ by:

$$\begin{array}{c}\hfill {\mathcal{M}}_{\mathfrak{r}}(\upsilon ,\varpi ,\vartheta )=\frac{\vartheta }{\vartheta +{sup}_{\vartheta \in [0,1]}{|\upsilon \left(\vartheta \right)-\varpi \left(\vartheta \right)|}^2}.\end{array}$$

(27)

Then, ${\mathcal{M}}_{\mathfrak{r}}$ is b-triangular and $(\mathcal{U},{\mathcal{M}}_{\mathfrak{r}},\ast )$, where ∗ is defined by $\omega \ast \mathfrak{q}=\omega \mathfrak{q}$, for all $\omega ,\mathfrak{q}\in [0,1]$ is a complete FBM space with $\mathfrak{s}=2$. Notice that $\upsilon \in \mathcal{U}$ solves (26) whenever $\upsilon \in \mathcal{U}$ solves the following IE:

$$\begin{array}{cc}\hfill \upsilon \left(\vartheta \right)=& \frac{1}{\Gamma \left(\omega \right)}{\int }_0^1{(1-\iota )}^{\omega -1}(1-\vartheta )\mathfrak{h}(\iota ,\upsilon \left(\iota \right))\mathit{d}\iota +\frac{1}{\Gamma (\omega -1)}{\int }_0^1{(1-\iota )}^{\omega -1}(1-\vartheta )\mathfrak{h}(\iota ,\upsilon \left(\iota \right))\mathit{d}\iota \hfill \\ \hfill & +\frac{1}{\Gamma \left(\omega \right){\int }_0^{\vartheta }}{(\vartheta -\iota )}^{\omega -1}\mathfrak{h}(\iota ,\upsilon \left(\iota \right))\mathit{d}\iota .\hfill \end{array}$$

(28)

More details can be found in [33].

Theorem 6.

The integral operator $𝓁:\mathcal{U}\to \mathcal{U}$ is given by:

$$\begin{array}{cc}\hfill 𝓁\upsilon \left(\vartheta \right)=& \frac{1}{\Gamma \left(\omega \right)}{\int }_0^1{(1-\iota )}^{\omega -1}(1-\vartheta )\mathfrak{h}(\iota ,\upsilon \left(\iota \right))\mathit{d}\iota +\frac{1}{\Gamma (\omega -1)}{\int }_0^1{(1-\iota )}^{\omega -2}(1-\vartheta )\mathfrak{h}(\iota ,\upsilon \left(\iota \right))\mathit{d}\iota \hfill \\ \hfill & +\frac{1}{\Gamma \left(\omega \right)}{\int }_0^{\vartheta }{(\vartheta -\iota )}^{\omega -1}\mathfrak{h}(\iota ,\upsilon \left(\iota \right))\mathit{d}\iota ,\hfill \end{array}$$

(29)

where $\mathfrak{h}:[0,1]\times [0,\infty )\to [0,\infty )$ fulfills the following criteria:

(S1)

$|\mathfrak{h}(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right))|\le \frac{1}{3}|\upsilon \left(\iota \right)-\varpi \left(\iota \right)|\forall \upsilon ,\varpi \in \mathcal{U}$

(S2)

${sup}_{\vartheta \in [0,1]}\frac{1}{9}{\left[\frac{1-\vartheta }{\Gamma (\omega +1)}+\frac{1-\vartheta }{\Gamma \left(\omega \right)}+\frac{{\vartheta }^{\omega }}{\Gamma (\omega +1)}\right]}^2={\delta }_1<1$.

Then, NLFDE (26) has a unique solution in $\mathcal{U}$:

Proof. 

$$\begin{array}{cc}\hfill {|𝓁\upsilon \left(\vartheta \right)-𝓁\varpi \left(\vartheta \right)|}^2=& |\frac{1-\vartheta }{\Gamma \left(\omega \right)}{\int }_0^1{(1-\iota )}^{\omega -1}[\mathfrak{h}(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right))]\mathit{d}\iota \hfill \\ \hfill & +\frac{1-\vartheta }{\Gamma (\omega -1)}{\int }_0^1{(1-\iota )}^{\omega -1}[\mathfrak{h}(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right))]\mathit{d}\iota \hfill \\ \hfill & +\frac{1}{\Gamma \left(\omega \right)}{\int }_0^{\vartheta }{(\vartheta -\iota )}^{\omega -1}[\mathfrak{h}(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right))]\mathit{d}\iota {|}^2\hfill \\ \hfill \le & (\frac{1-\vartheta }{\Gamma \left(\omega \right)}{\int }_0^1{(1-\iota )}^{\omega -1}|\mathfrak{h}(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right))|\mathit{d}\iota \hfill \\ \hfill & +\frac{1-\vartheta }{\Gamma (\omega -1)}{\int }_0^1{(1-\iota )}^{\omega -1}|\mathfrak{h}(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right))|\mathit{d}\iota \hfill \\ \hfill & +\frac{1}{\Gamma \left(\omega \right)}{\int }_0^{\vartheta }{(\vartheta -\iota )}^{\omega -1}|\mathfrak{h}(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right))|\mathit{d}\iota {)}^2\hfill \\ \hfill \le & (\frac{1-\vartheta }{\Gamma \left(\omega \right)}{\int }_0^1{(1-\iota )}^{\omega -1}\frac{\left|\upsilon \right(\iota )-\varpi (\iota \left)\right|}{4}\mathit{d}\iota \hfill \\ \hfill & +\frac{1-\vartheta }{\Gamma (\omega -1)}{\int }_0^1{(1-\iota )}^{\omega -1}\frac{\left|\upsilon \right(\iota )-\varpi (\iota \left)\right|}{4}\mathit{d}\iota \hfill \\ \hfill & +\frac{1}{\Gamma \left(\omega \right)}{\int }_0^{\vartheta }{(\vartheta -\iota )}^{\omega -1}\frac{\left|\upsilon \right(\iota )-\varpi (\iota \left)\right|}{4}\mathit{d}\iota {)}^2\hfill \\ \hfill \le & \frac{1}{3^2}\underset{\vartheta \in [0,1]}{sup}{|\upsilon \left(\vartheta \right)-\varpi \left(\vartheta \right)|}^2(\frac{1-\vartheta }{\Gamma \left(\omega \right)}{\int }_0^1{(1-\iota )}^{\omega -1}\mathit{d}\iota \hfill \\ \hfill & +\frac{1-\vartheta }{\Gamma (\omega -1)}{\int }_0^1{(1-\iota )}^{\omega -2}\mathit{d}\iota +\frac{1}{\Gamma \left(\omega \right)}{\int }_0^{\vartheta }{(\vartheta -\iota )}^{\omega -1}\mathit{d}\iota {)}^2\hfill \\ \hfill \le & \frac{1}{9}\underset{\vartheta \in [0,1]}{sup}{|\upsilon \left(\vartheta \right)-\varpi \left(\vartheta \right)|}^2{\left[\frac{1-\vartheta }{\Gamma (\omega +1)}+\frac{1-\vartheta }{\Gamma \left(\omega \right)}+\frac{{\vartheta }^{\omega }}{\Gamma (\omega +1)}\right]}^2\hfill \\ \hfill =& {\delta }_1\underset{\vartheta \in [0,1]}{sup}{|\upsilon \left(\vartheta \right)-\varpi \left(\vartheta \right)|}^2.\hfill \end{array}$$

where ${\delta }_1={sup}_{\vartheta \in [0,1]}\frac{1}{9}{\left[\frac{1-\vartheta }{\Gamma (\omega +1)}+\frac{1-\vartheta }{\Gamma \left(\omega \right)}+\frac{{\vartheta }^{\omega }}{\Gamma (\omega +1)}\right]}^2$. Therefore, the above inequality becomes:

$$\begin{array}{cc}\hfill \underset{\vartheta \in [0,1]}{sup}{|𝓁\upsilon \left(\vartheta \right)-𝓁\varpi \left(\vartheta \right)|}^2& \le {\delta }_1\underset{\vartheta \in [0,1]}{sup}{|\upsilon \left(\vartheta \right)-\varpi \left(\vartheta \right)|}^2.\hfill \end{array}$$

Now,

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{M}}_{\mathfrak{r}}(𝓁\upsilon \left(\tau \right),𝓁\varpi \left(\tau \right)),\vartheta )}-1& =\frac{{sup}_{\vartheta \in [0,1]}{|𝓁\upsilon \left(\vartheta \right)-𝓁\varpi \left(\vartheta \right)|}^2}{\vartheta }\hfill \\ \hfill & \le \frac{{\delta }_1{sup}_{\vartheta \in [0,1]}{|\upsilon \left(\vartheta \right)-\varpi \left(\vartheta \right)|}^2}{\vartheta }\hfill \\ \hfill & ={\delta }_1\left(\frac{1}{{\mathcal{M}}_{\mathfrak{r}}(\upsilon \left(\tau \right),\varpi \left(\tau \right)),\vartheta )}-1\right).\hfill \end{array}$$

Thereby, all the axioms of Theorem 3 are fulfilled with ${\delta }_1<\frac{1}{\mathfrak{s}}$ and ${\delta }_2={\delta }_3={\delta }_4=0$. Hence ℓ has a UFP in $\mathcal{U}$. □

Example 5.

Consider the NLFDE:

$$\begin{array}{c}\hfill {\mathcal{D}}_{0+}^2\upsilon \left(\vartheta \right)=\mathfrak{h}(\vartheta ,\upsilon \left(\vartheta \right)),0<\vartheta <1,\end{array}$$

(30)

where $\mathfrak{h}$ is defined by:

$$\begin{array}{c}\hfill \mathfrak{h}(\vartheta ,\upsilon \left(\vartheta \right))=\frac{1}{3(1+\upsilon (\vartheta \left)\right)},\forall \upsilon \ge 0\end{array}$$

with:

$$\begin{array}{c}\hfill \upsilon \left(0\right)+\upsilon {}^{\prime }\left(0\right)=0,\upsilon \left(1\right)+\upsilon {}^{\prime }\left(1\right)=0.\end{array}$$

Proof. 

An integral operator $𝓁:\mathcal{U}\to \mathcal{U}$ is defined as in Theorem 6 and $\mathfrak{h}(\iota ,\upsilon \left(\iota \right))=\frac{1}{3(1+\upsilon (\iota \left)\right)}$, $\upsilon \left(\iota \right)\ge 0$ for $\iota \in [0,1]$.

(i)

Note that $\mathfrak{h}$ from $[0,1]\times [0,\infty )$ to $[0,\infty )$ is continuous and

$$\begin{array}{cc}\hfill \left|\mathfrak{h}\right(\iota ,\upsilon \left(\iota \right))-\mathfrak{h}(\iota ,\varpi \left(\iota \right)\left)\right|& =|\frac{1}{3(1+\upsilon (\iota \left)\right)}-\frac{1}{3(1+\varpi (\iota \left)\right)}|\hfill \\ \hfill & =\frac{\left|\upsilon \right(\iota )-\varpi (\iota \left)\right|}{3(1+\upsilon (\iota \left)\right)(1+\varpi (\iota \left)\right)}\le \frac{\left|\upsilon \right(\iota )-\varpi (\iota \left)\right|}{3}.\hfill \end{array}$$

(ii)

Here $\omega =2$. Hence,

$$\begin{array}{cc}\hfill {\delta }_1=\underset{\vartheta \in [0,1]}{sup}\frac{1}{9}{\left(\frac{1-\vartheta }{\Gamma (\omega +1)}+\frac{1-\vartheta }{\Gamma \left(\omega \right)}+\frac{{\vartheta }^{\omega }}{\Gamma (\omega +1)}\right)}^2& =\underset{\vartheta \in [0,1]}{sup}\frac{1}{9}{\left(\frac{1-\vartheta }{\Gamma \left(3\right)}+\frac{1-\vartheta }{\Gamma \left(2\right)}+\frac{{\vartheta }^2}{\Gamma \left(3\right)}\right)}^2\hfill \\ \hfill & =\underset{\vartheta \in [0,1]}{sup}\frac{1}{9}{\left(\frac{{\vartheta }^2-3\vartheta +3}{2}\right)}^2<1\hfill \end{array}$$

and ${\delta }_2={\delta }_3={\delta }_4=0$.

Therefore, all the axioms of Theorem 6 are fulfilled. Hence, the problem (30) has a solution on $\mathcal{U}$. □

Open problems:

(1)

It will be very interesting in future studies if the condition ${\delta }_1\in (0,\frac{1}{\mathfrak{s}})$ of the Theorem 2 can be replaced by the condition ${\delta }_1\in (0,1)$.

(2)

Moreover, the case of multivalued operators can raise other new results in this fixed point research direction.

6. Conclusions

In this manuscript, we proved the fixed point results without continuity and by using the b-triangular property on FBM-space. Moreover, we give some illustrative examples to sustain our results and two interesting and different applications, to show the variety of applicability of our main results in any other mathematics and computer sciences domains. Then, we give applications to prove the uniqueness and the existence of the solutions of a Fredholm IE and the second application is given for dynamic programming processes. In the end we give two open problems.