Some Common Fixed Point Results in Modular Ultrametric Space Using Various Contractions and Their Application to Well-Posedness
Abstract
1. Introduction
- First, we check for the existence and uniqueness of common fixed points in a modular ultrametric space using various contractions.
- The same is then investigated for fixed points in the above spaces.
- Finally, our main results utilize the application of well-posedness.
2. Preliminaries
- (i)
- iff ,
- (ii)
- ,
- (iii)
- , for every .
- A point is called a limit of if for each there exists such that for all . A sequence that has a limit is said to be convergent (or to converge to a), which is written as .
- A sequence in is said to be a Cauchy sequence if for each there exists such that for all .
- If every Cauchy sequence in E converges, E is said to be complete.
3. Main Results
3.1. Common Fixed Point Theorems in a Complete Modular Ultrametric Space
3.2. Fixed Point Theorems in Modular Ultrametric Spaces
- Let ; then,
- Let ; then,
- Let ; then,
- Let and ; then,
- Let and ; then,
- Let and ; then,
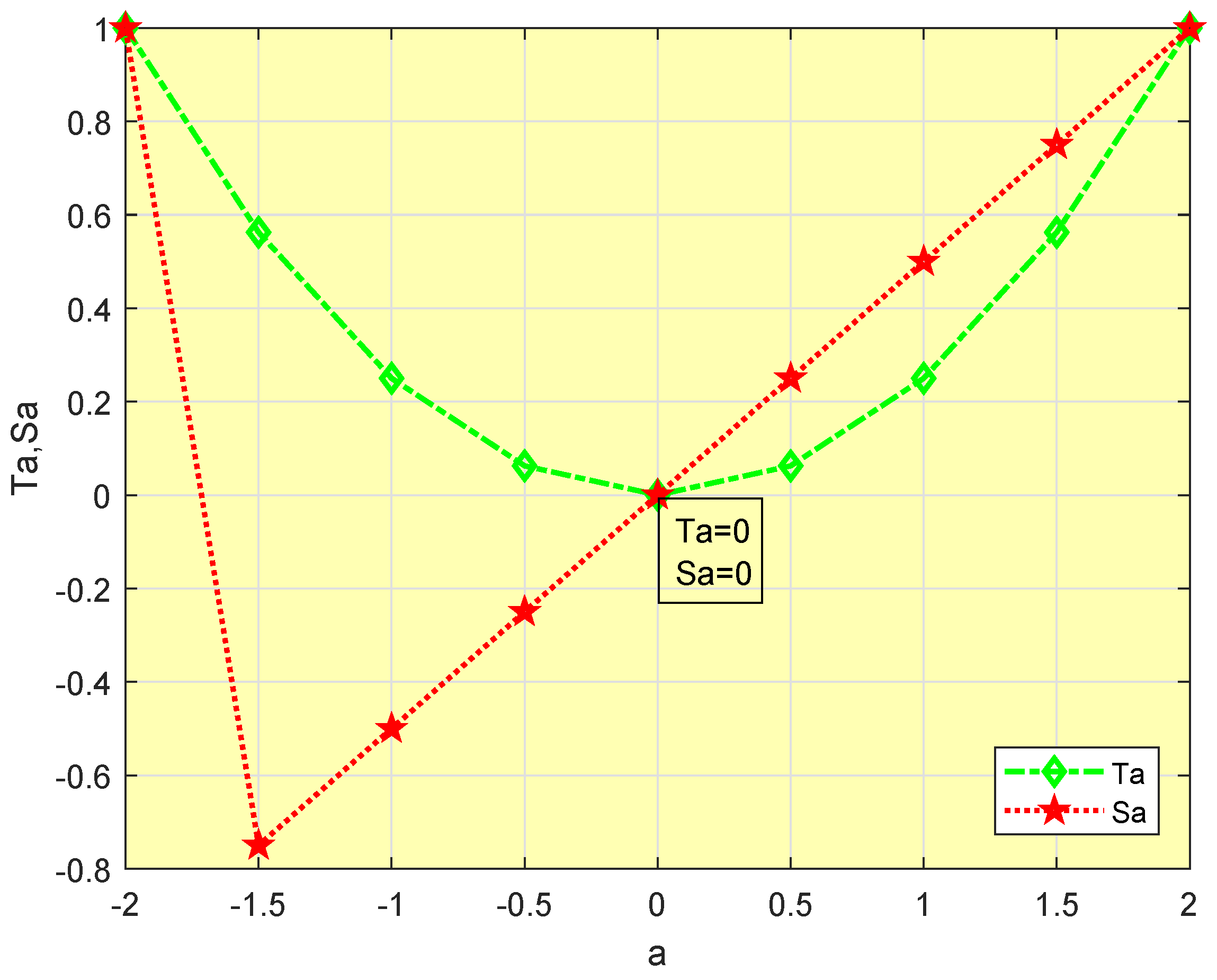
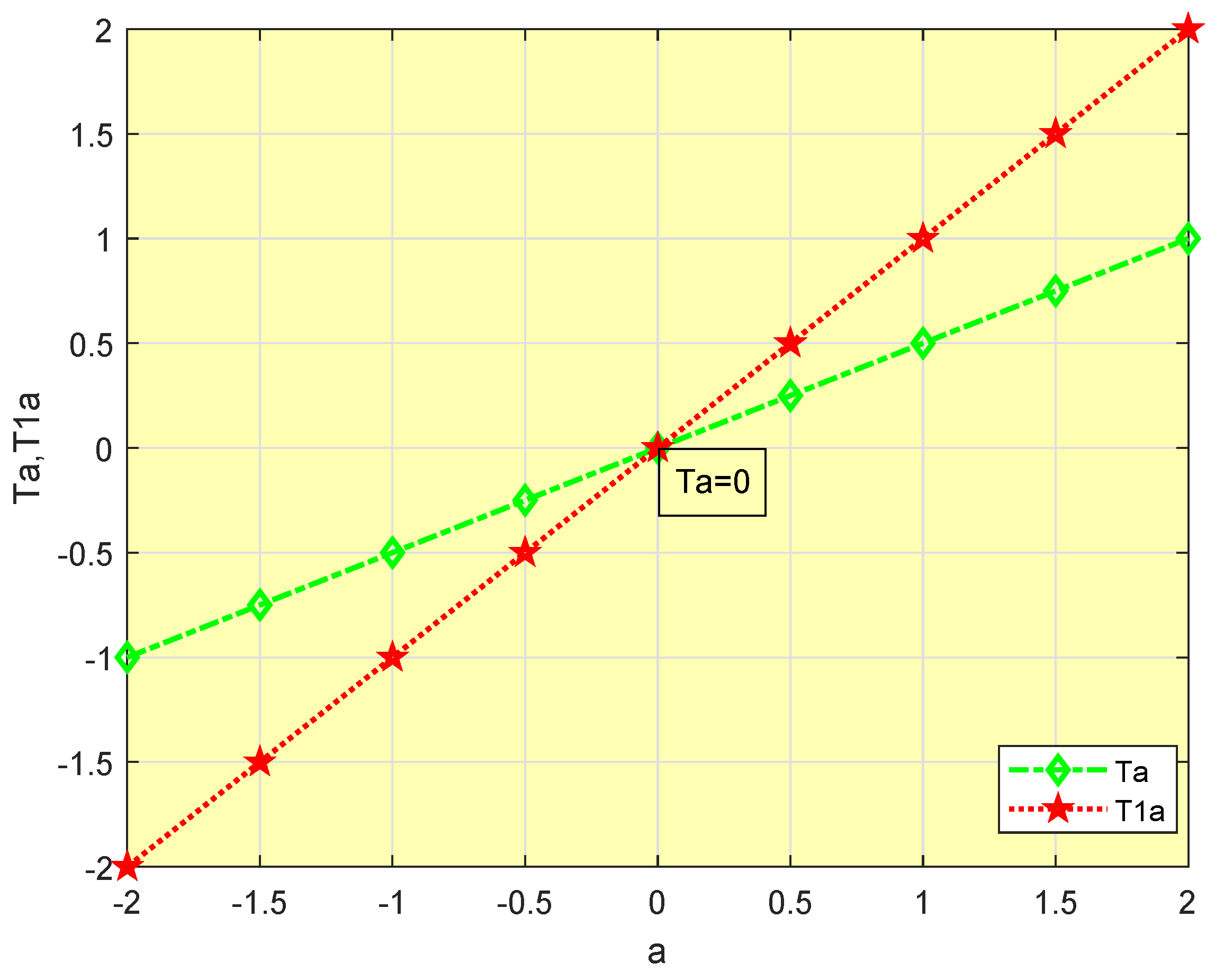
4. Applications
4.1. Application to Well-Posedness
- (1)
- T has precisely one fixed point
- (2)
- For every sequence, and , implying that .
- (1)
- For every sequence, with andimplying that
- (2)
- CFP is a singleton.
4.2. Application to Integral Equations
- (i)
- ;
- (ii)
- Define
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Amini-Harandi, A. Fixed point theory for generalized quasicontraction maps in vector modular spaces. Comput. Math. Appl. 2011, 61, 1891–1897. [Google Scholar] [CrossRef]
- Amnuaykarn, K.; Kumam, P.; Nantadilok, J. On the existence of best proximity points of multi-valued mappings in CAT (0) spaces. J. Nonlinear Funct. Anal. 2021, 25, 1–4. [Google Scholar]
- Aydi, H.; Nashine, H.K.; Samet, B.; Yazidi, H. Coincidence and Common fixed point results in partially ordered cone metric spaces and applications to integral equations. Nonlinear Anal. Theory Methods Appl. 2011, 74, 6814–6825. [Google Scholar] [CrossRef]
- Latif, A.; Al Subaie, R.F.; Alansari, M.O. Fixed points of generalized multi-valued contractive mappings in metric type spaces. J. Nonlinear Var. Anal. 2022, 6, 123–138. [Google Scholar]
- Mongkolkeha, C.; Kumam, P. Fixed point theorems for generalized asymptotic pointwise d-contraction mappings involving orbits in modular function spaces. Appl. Math. Lett. 2012, 25, 1285–1290. [Google Scholar] [CrossRef]
- Sintunavarat, W.; Cho, Y.J.; Kumam, P. Common fixed point theorems for c-distance in ordered cone metric spaces. Comput. Math. Appl. 2011, 62, 1969–1978. [Google Scholar] [CrossRef]
- Nakano, H. Modulared Semi-Ordered Linear Spaces; Maruzen Co., Ltd.: Tokyo, Japan, 1950. [Google Scholar]
- Musielak, J.; Orlicz, W. On modular spaces. Stud. Math. 1959, 18, 49–65. [Google Scholar] [CrossRef]
- Musielak, J.; Orlicz, W. Some remarks on modular spaces. Bull. Acad. Polon. Sci. 1959, 7, 661–668. [Google Scholar]
- Chistyakov, V.V. Modular metric spaces generated by F-modulars. Folia Math. 2008, 14, 3–25. [Google Scholar]
- Chistyakov, V.V. Modular metric spaces, I: Basic concepts. Nonlinear Anal. Theory Methods Appl. 2010, 72, 1–14. [Google Scholar] [CrossRef]
- Chistyakov, V.V. Fixed points of modular contractive maps. Dokl. Math. 2012, 86, 515–518. [Google Scholar] [CrossRef]
- Khamsi, M.A. Quasicontraction mappings in modular spaces without Δ2-condition. Fixed Point Theory Appl. 2008, 2008, 916187. [Google Scholar] [CrossRef]
- Azadifar, B.; Sadeghi, G.; Saadati, R.; Park, C. Integral type contractions in modular metric spaces. J. Inequal Appl. 2013, 2013, 483. [Google Scholar] [CrossRef]
- Hussain, N.; Salimi, P. Implicit contractive mappings in modular metric and fuzzy metric spaces. Sci. World J. 2014, 2014, 981578. [Google Scholar] [CrossRef] [PubMed]
- Mohiuddine, S.A.; Tamilvanan, K.; Mursaleen, M.; Alotaibi, T. Stability of quartic functional equation in modular spaces via Hyers and fixed-point methods. Mathematics 2022, 10, 1938. [Google Scholar] [CrossRef]
- Kilinc, E.; Alaca, C. A fixed point theorem in modular metric spaces. Adv. Fixed Point Theory 2014, 4, 199–206. [Google Scholar]
- Tamilvanan, K.; Alanazi, A.M.; Alshehri, M.G.; Kafle, J. Hyers-Ulam Stability of Quadratic Functional Equation Based on Fixed Point Technique in Banach Spaces and Non-Archimedean Banach Spaces. Mathematics 2021, 9, 2575. [Google Scholar] [CrossRef]
- Tamilvanan, K.; Alkhaldi, A.H.; Jakhar, J.; Chugh, R.; Jakhar, J.; Rassias, J.M. Ulam stability results of functional equations in modular spaces and 2-Banach spaces. Mathematics 2023, 11, 371. [Google Scholar] [CrossRef]
- Uthirasamy, N.; Tamilvanan, K.; Nashine, H.K.; George, R. Solution and stability of quartic functional equations in modular spaces by using fatou property. J. Funct. Spaces 2022, 2022, 5965628. [Google Scholar] [CrossRef]
- Ramakrishnan, K.; Uma, J.; Ponmana Selvan, A. Generalized Hyers-Ulam stability of a Bi-Quadratic mapping in non-Archimedean spaces. J. Math. Comput. Sci. 2023, 31, 393–402. [Google Scholar]
- Ramesh Kumar, D.; Pitchaimani, M. Set-valued contraction mappings of Prešić-Reich type in ultrametric spaces. Asian-Eur. J. Math. 2017, 10, 1750065. [Google Scholar] [CrossRef]
- Tamilvanan, K.; Mohiuddine, S.A.; Revathi, N. Ulam stability of mixed type functional equation in non-Archimedean IFN-Space. In Soft Computing; CRC Press: Boca Raton, FL, USA, 2023; pp. 167–178. [Google Scholar]
- Gajić, L. On ultrametric space. Novi Sad J. Math. 2001, 31, 69–71. [Google Scholar]
- Rao, K.P.R.; Kishore, G.N.V.; Ranga Rao, T. Some coincidence point theorems in ultra metric spaces. Int. J. Math. Anal. 2007, 1, 897–902. [Google Scholar]
- Kirk, W.A.; Shahzad, N. Some fixed point results in ultrametric spaces. Topol. Appl. 2012, 159, 3327–3334. [Google Scholar] [CrossRef][Green Version]
- Mishra, S.N.; Pant, R. Generalization of some fixed point theorems in ultrametric spaces. Adv. Fixed Point Theory 2013, 4, 41–47. [Google Scholar]
- Alaca, C.; Ege, M.E.; Park, C. Fixed point results for modular ultrametric spaces. J. Comput. Anal. Appl. 2016, 20, 1259–1267. [Google Scholar]
- Mamghaderi, H.; Masiha, H.P.; Hosseini, M. Some fixed point theorems for single valued strongly contractive mappings in partially ordered ultrametric and non-Archimedean normed spaces. Turk. J. Math. 2017, 41, 9–14. [Google Scholar] [CrossRef]
- Balaanandhan, R.; Uma, J. Fixed Point Results in Partially Ordered Ultrametric Space via p-adic Distance. IAENG Int. J. Appl. Math. 2023, 53, 772–778. [Google Scholar]
- Bogin, J. A generalization of a fixed point theorem of Goebel, Kirk and Shimi. Can. Math Bull. 1976, 9, 7–12. [Google Scholar] [CrossRef]
- Pitchaimani, M.; Ramesh Kumar, D. On Nadler type results in ultrametric spaces with application to well-posedness. Asian-Eur. J. Math. 2017, 10, 1750073. [Google Scholar] [CrossRef]
- Sarwar, M.; Rahman, M.U.; Ali, G. Some fixed point results in dislocated quasi metric (dq-metric) spaces. J. Inequal. Appl. 2014, 2014, 278. [Google Scholar] [CrossRef]
- Li, S.; Zada, A.; Shah, R.; Li, T. Fixed point theorems in dislocated quasi-metric spaces. J. Nonlinear Sci. Appl. 2017, 10, 4695–4703. [Google Scholar] [CrossRef]
- Kohli, M.; Shrivastava, R.; Sharma, M. Some results of fixed point theorem in dislocated quasi metric space. Int. J. Theoret. Appl. Sci. 2010, 2, 20–24. [Google Scholar]
- Van Rooij, A.C.M. Non-Archimedean Functional Analysis; Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker, Inc.: New York, NY, USA, 1978; Volume 51. [Google Scholar]
- Padcharoen, A.N.; Kumam, P.O.; Gopal, D.H. Coincidence and periodic point results in a modular metric spaces endowed with a graph and applications. Creat. Math. Inform. 2017, 26, 95–104. [Google Scholar] [CrossRef]
- De Blasi, F.S.; Myjak, J. Sur la porosité de l’ensemble des contractions sans point fixe. CR Acad. Sci. Paris 1989, 308, 51–54. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almalki, Y.; Radhakrishnan, B.; Jayaraman, U.; Tamilvanan, K. Some Common Fixed Point Results in Modular Ultrametric Space Using Various Contractions and Their Application to Well-Posedness. Mathematics 2023, 11, 4077. https://doi.org/10.3390/math11194077
Almalki Y, Radhakrishnan B, Jayaraman U, Tamilvanan K. Some Common Fixed Point Results in Modular Ultrametric Space Using Various Contractions and Their Application to Well-Posedness. Mathematics. 2023; 11(19):4077. https://doi.org/10.3390/math11194077
Chicago/Turabian StyleAlmalki, Yahya, Balaanandhan Radhakrishnan, Uma Jayaraman, and Kandhasamy Tamilvanan. 2023. "Some Common Fixed Point Results in Modular Ultrametric Space Using Various Contractions and Their Application to Well-Posedness" Mathematics 11, no. 19: 4077. https://doi.org/10.3390/math11194077
APA StyleAlmalki, Y., Radhakrishnan, B., Jayaraman, U., & Tamilvanan, K. (2023). Some Common Fixed Point Results in Modular Ultrametric Space Using Various Contractions and Their Application to Well-Posedness. Mathematics, 11(19), 4077. https://doi.org/10.3390/math11194077





