Real-Time Malfunction Detection of Maglev Suspension Controllers
Abstract
:1. Introduction
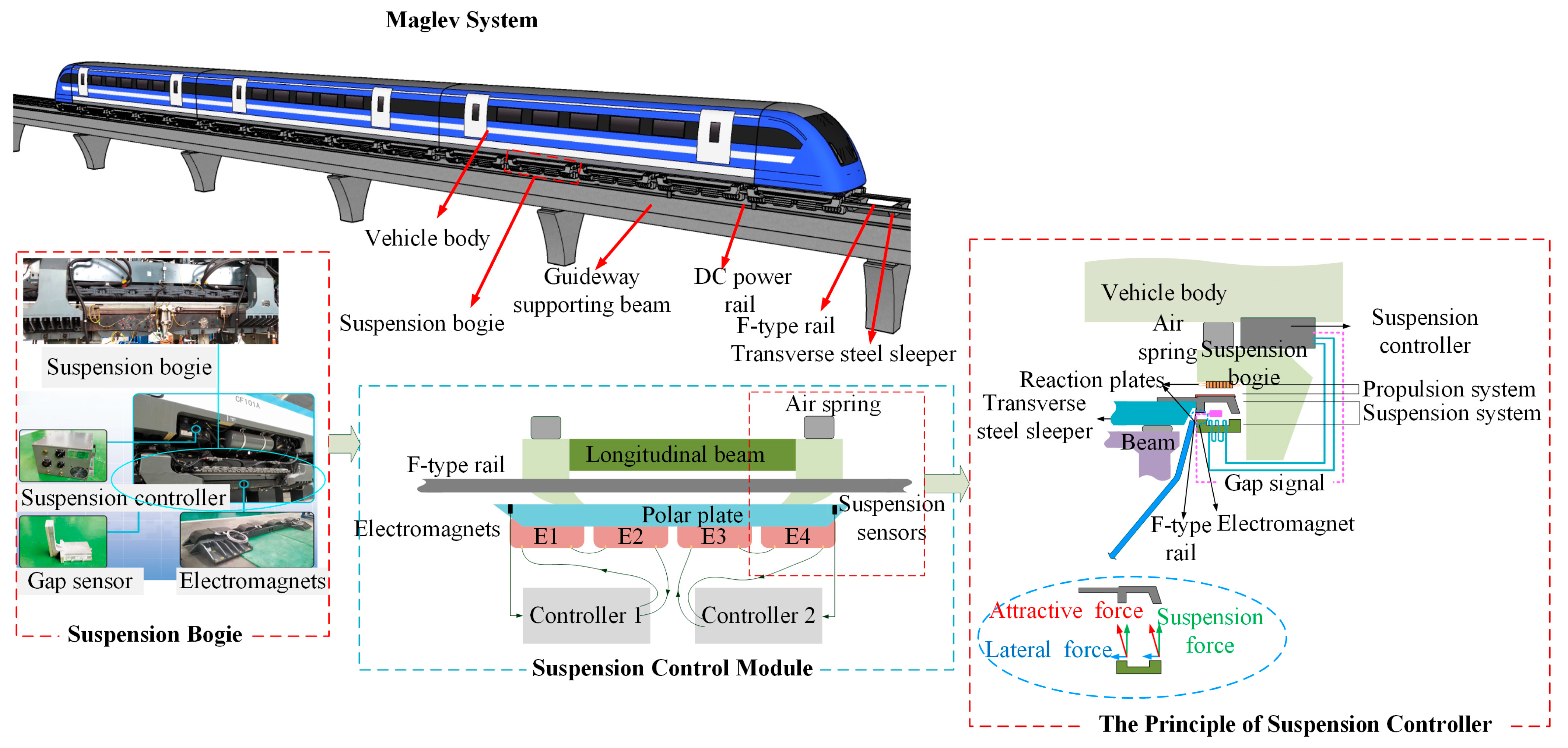
2. Overview of Maglev System
3. Track-Side Online Monitoring System
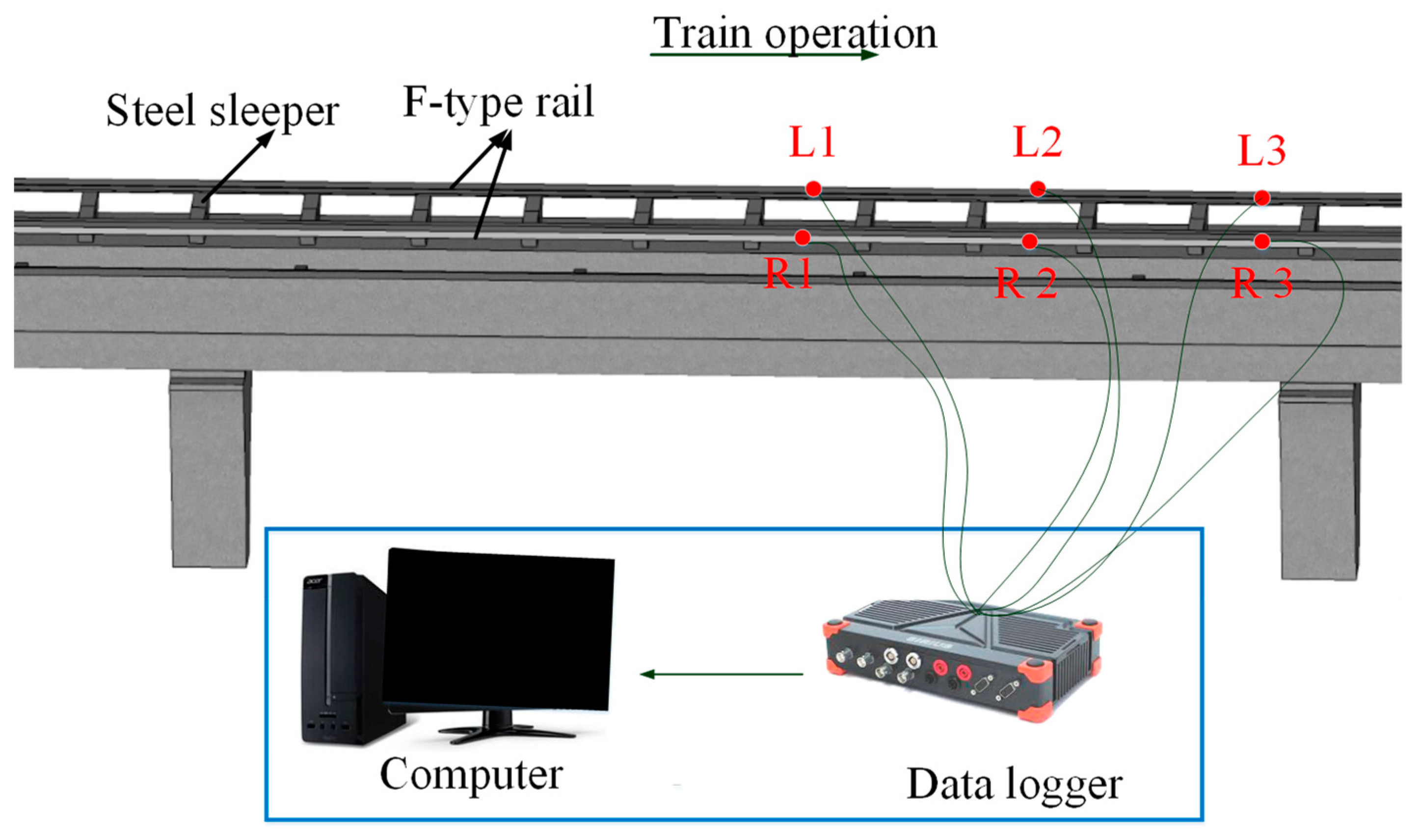
3.1. System Configuration
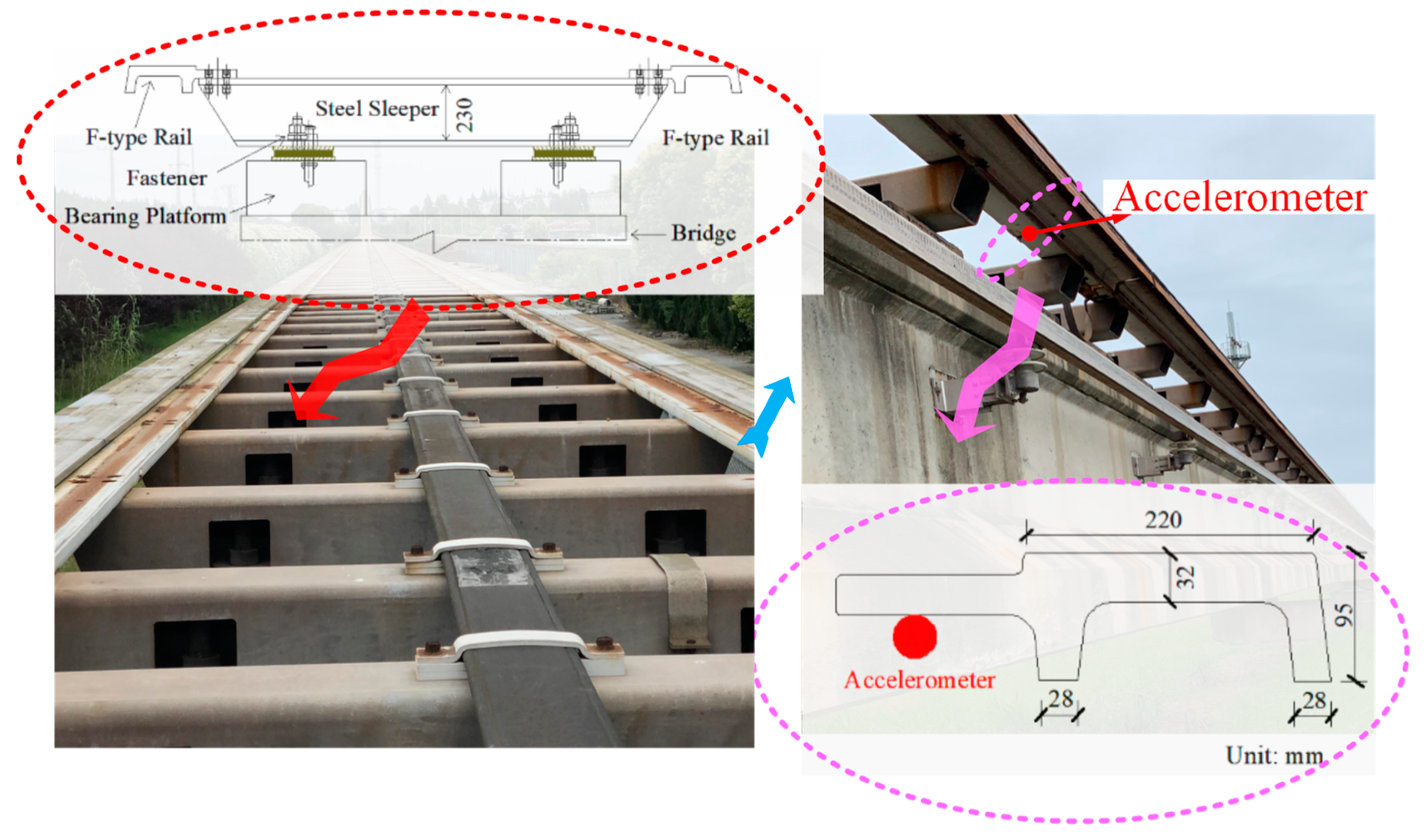
3.2. Deployment of Accelerometers
4. Track-Side Online Monitoring System Bayesian-Based Method for Online Malfunction Detection
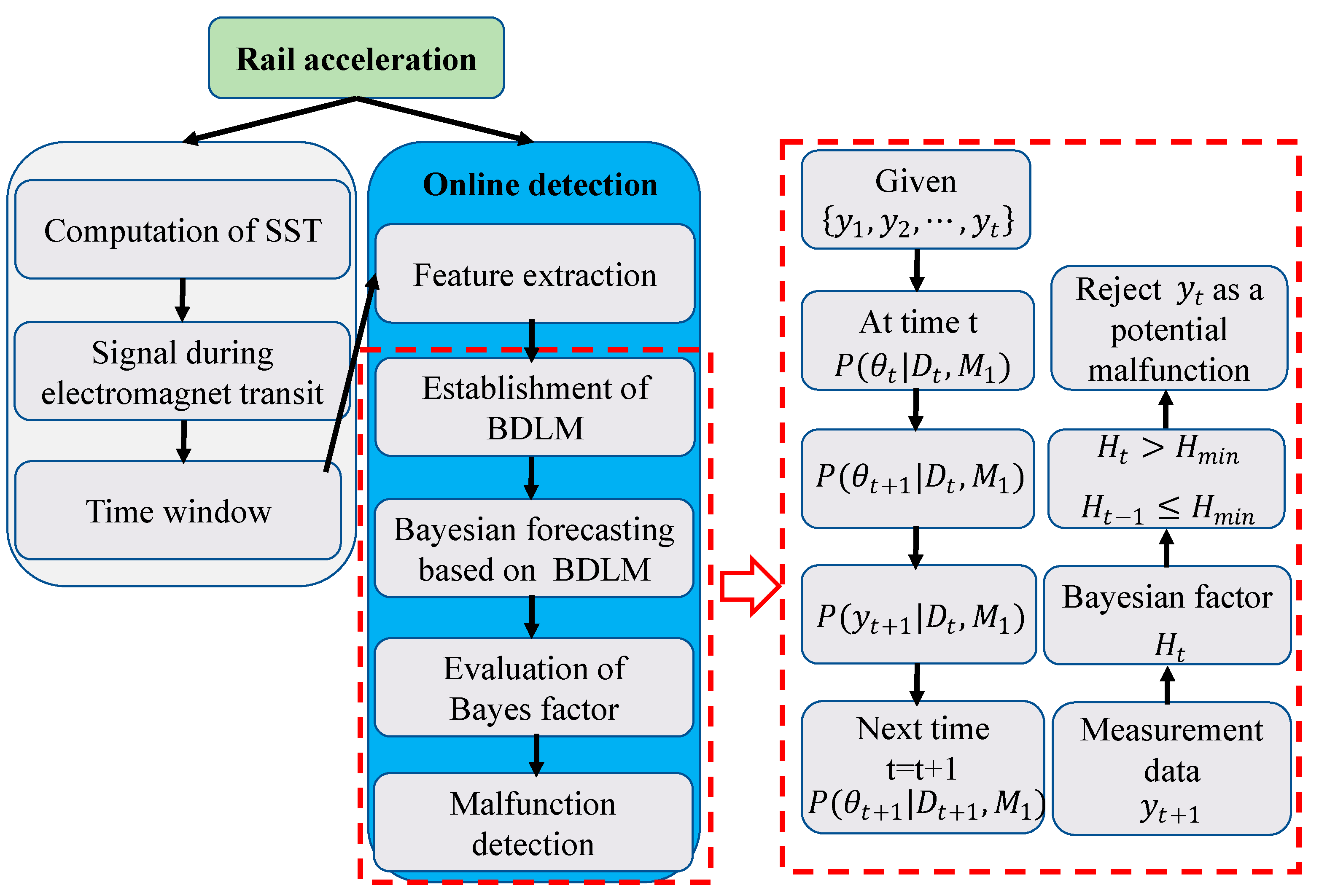
4.1. General Description
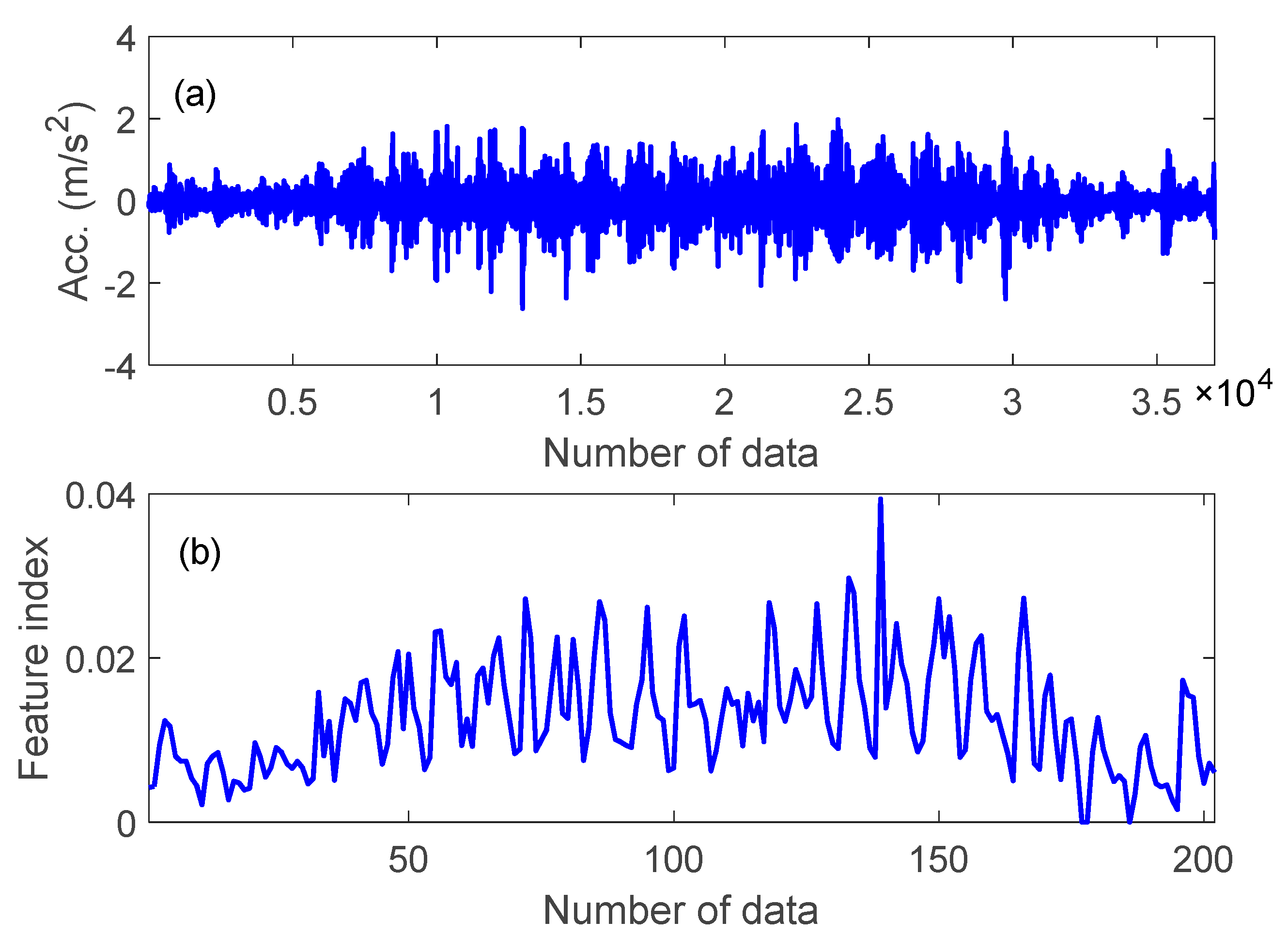
4.2. Identification of Time Intervals during Electromagnet Transit
4.3. Feature Index (FI)
4.4. BDLM for Malfunction Detection
5. In-Suit Verification
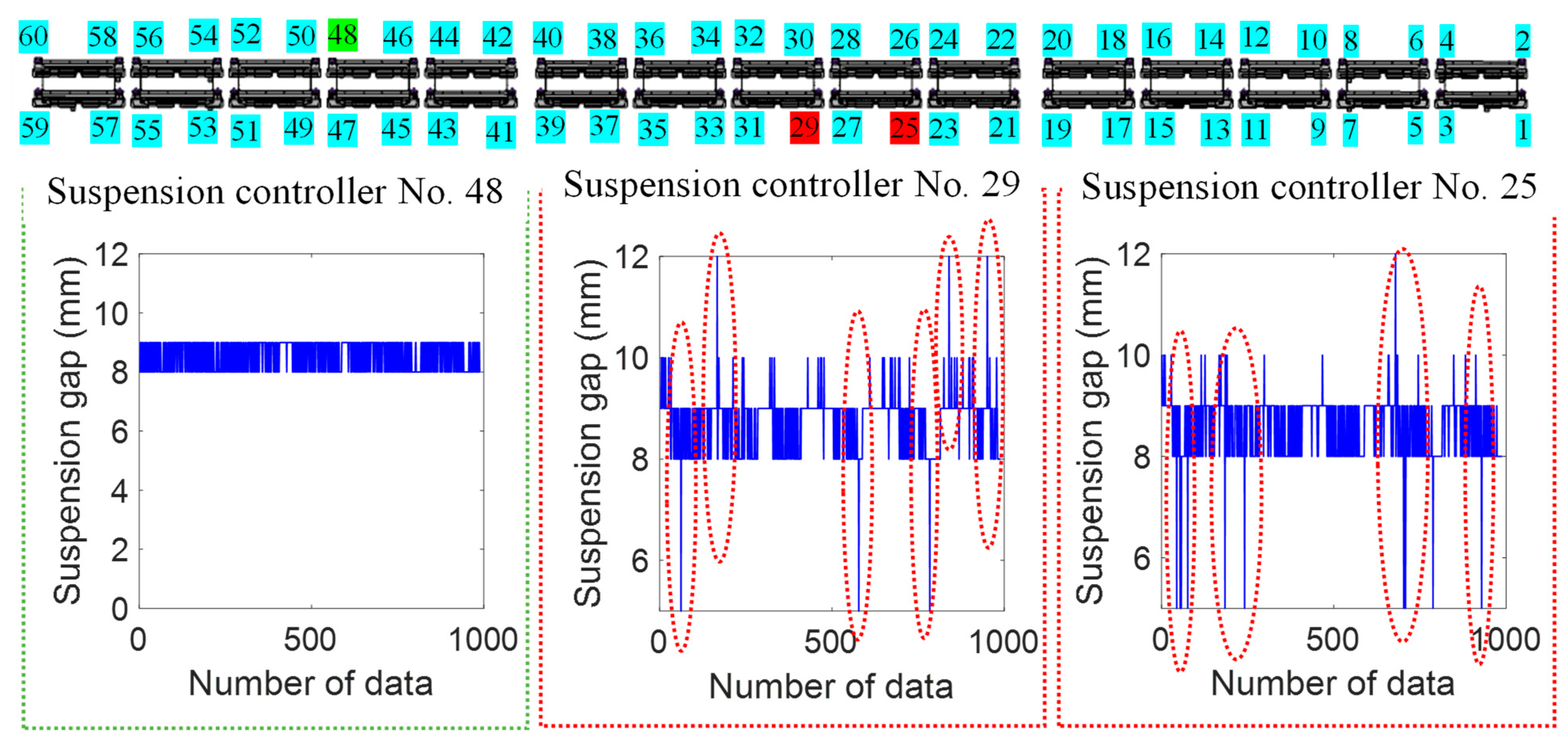
5.1. Full-Scale Tests
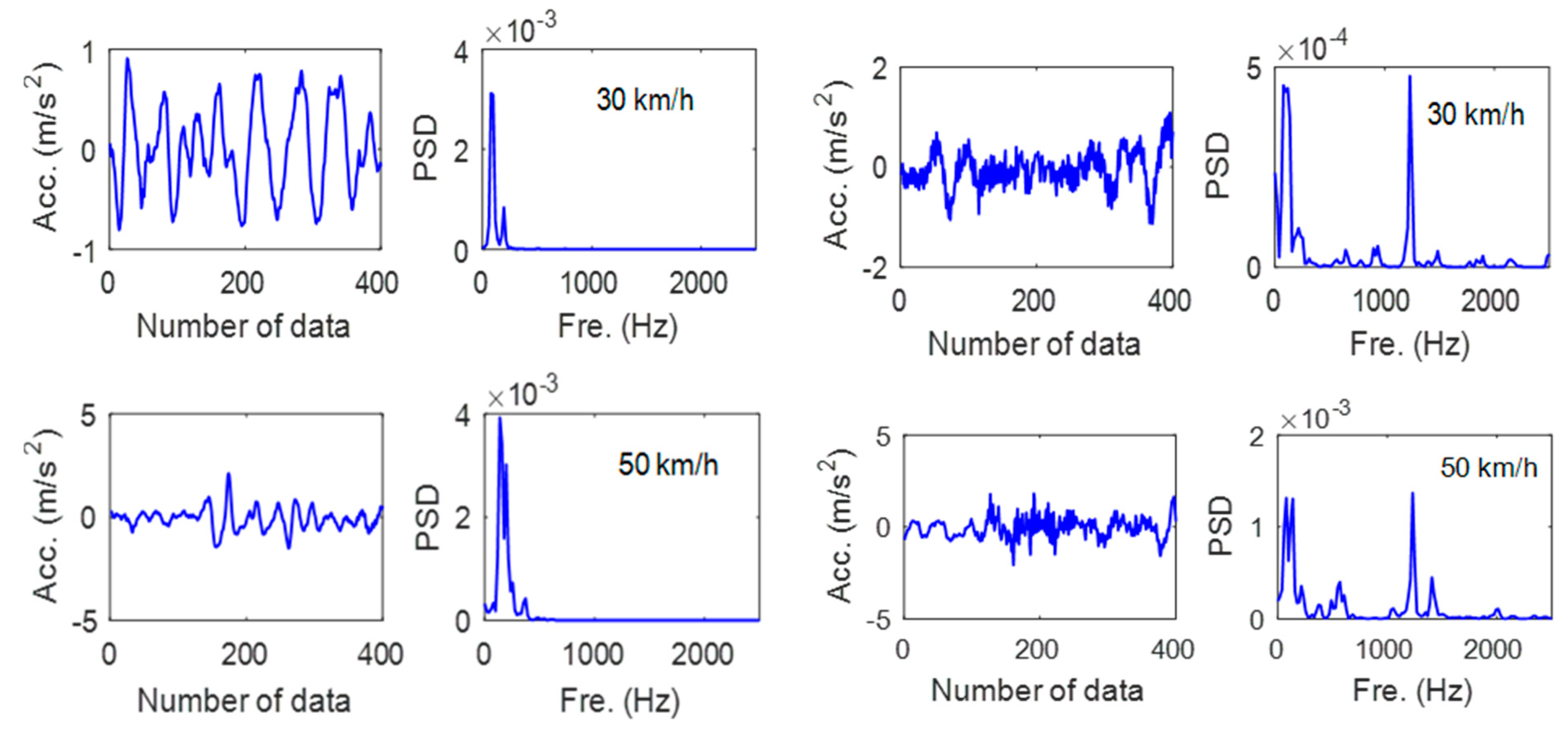
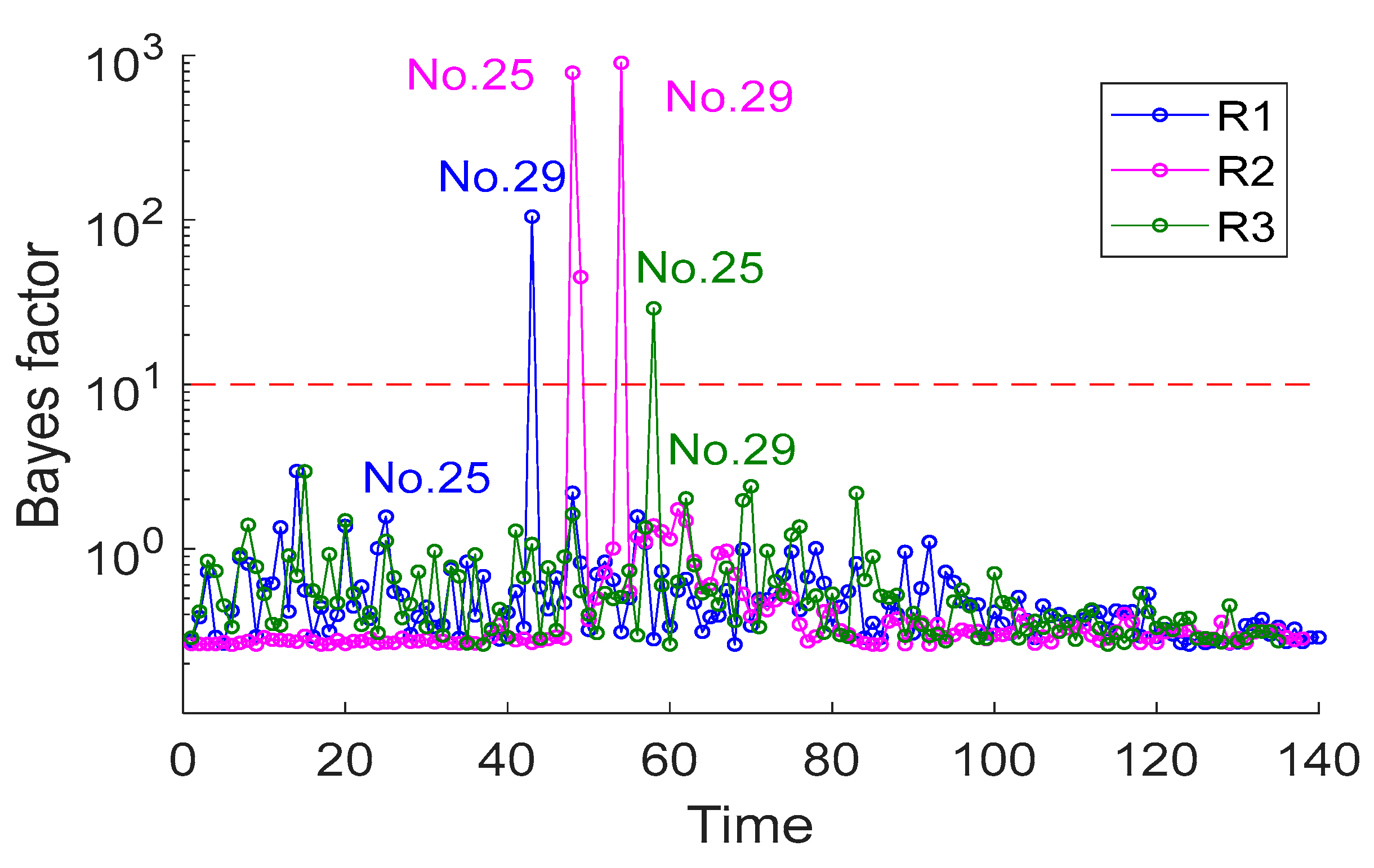
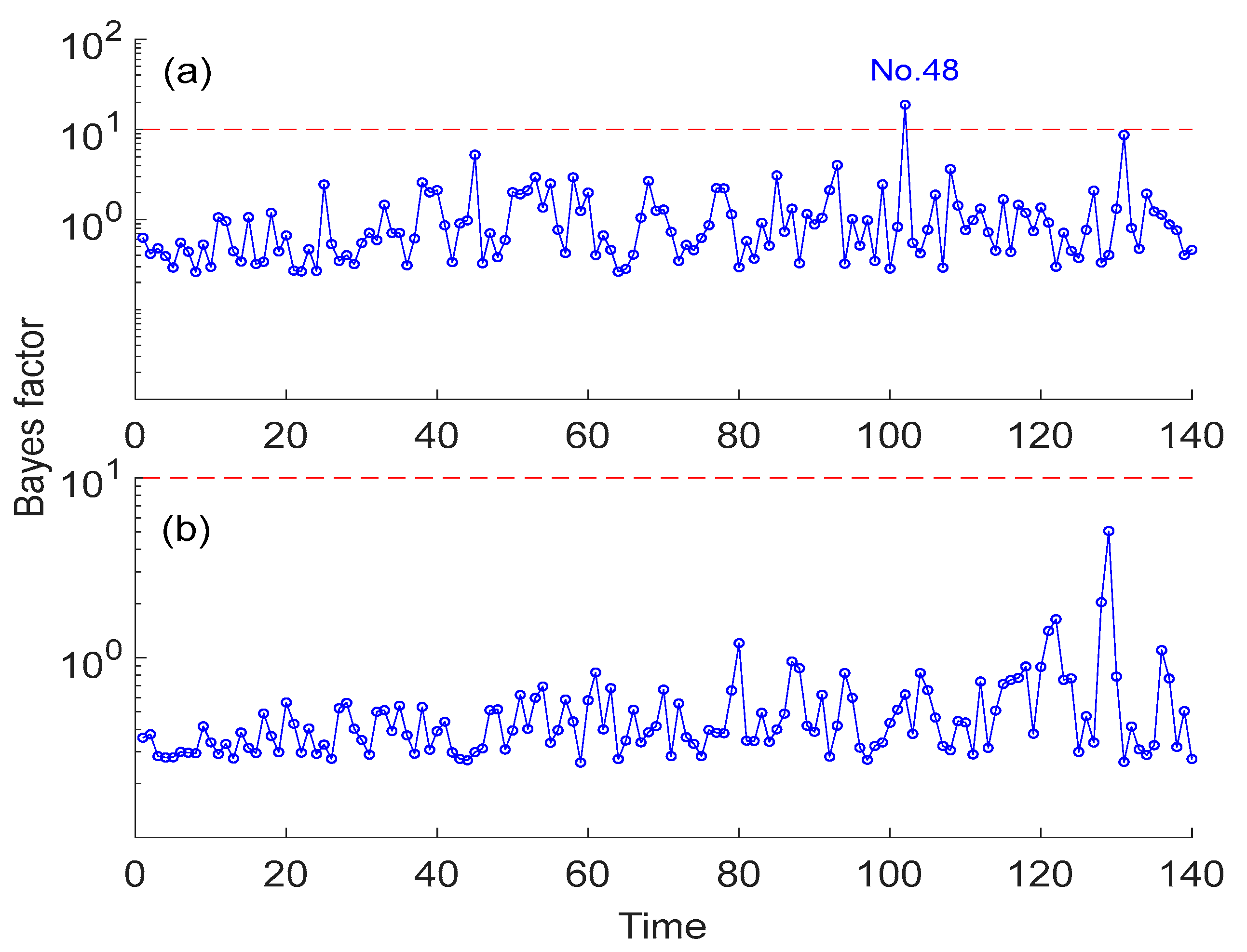
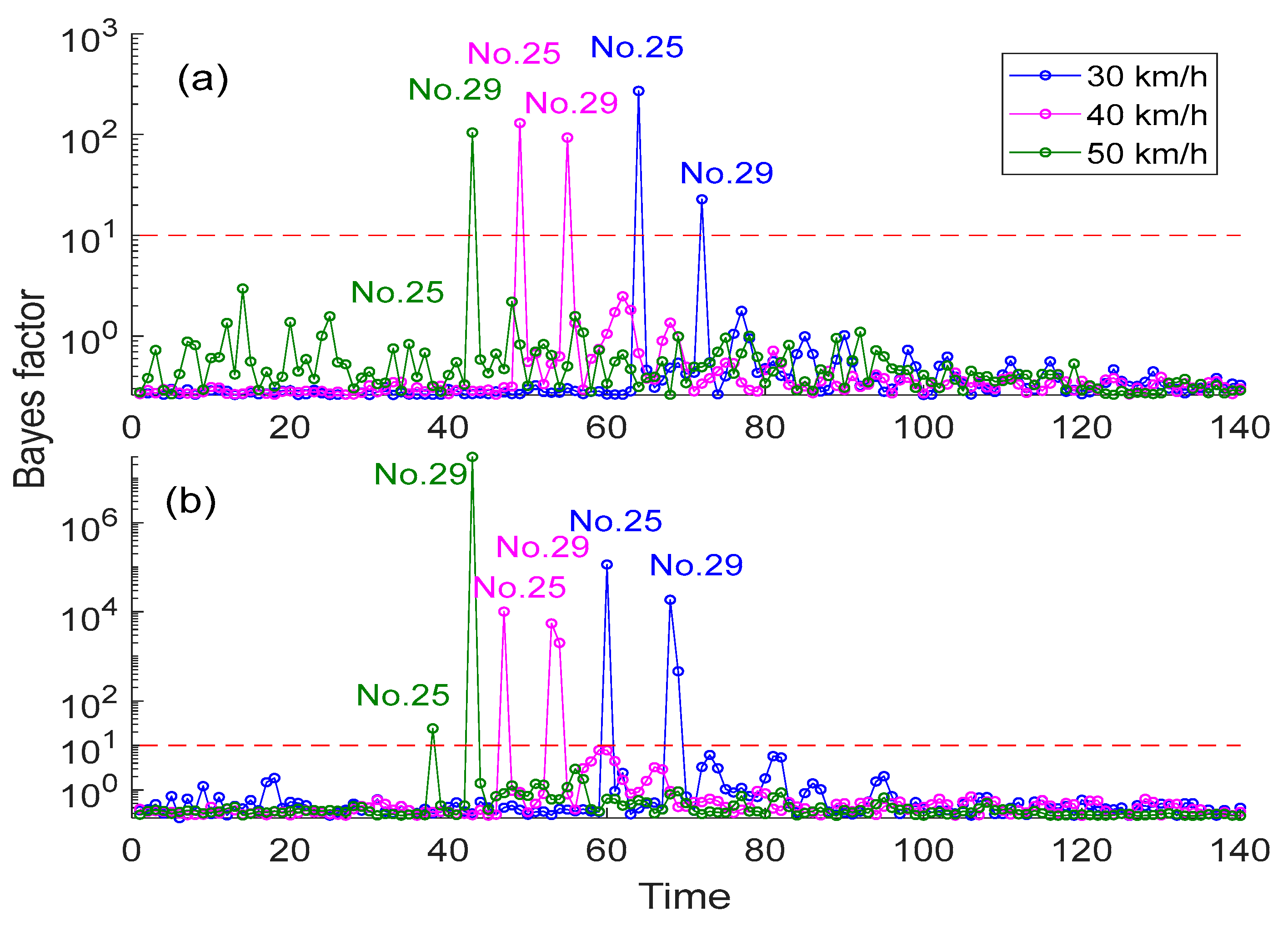
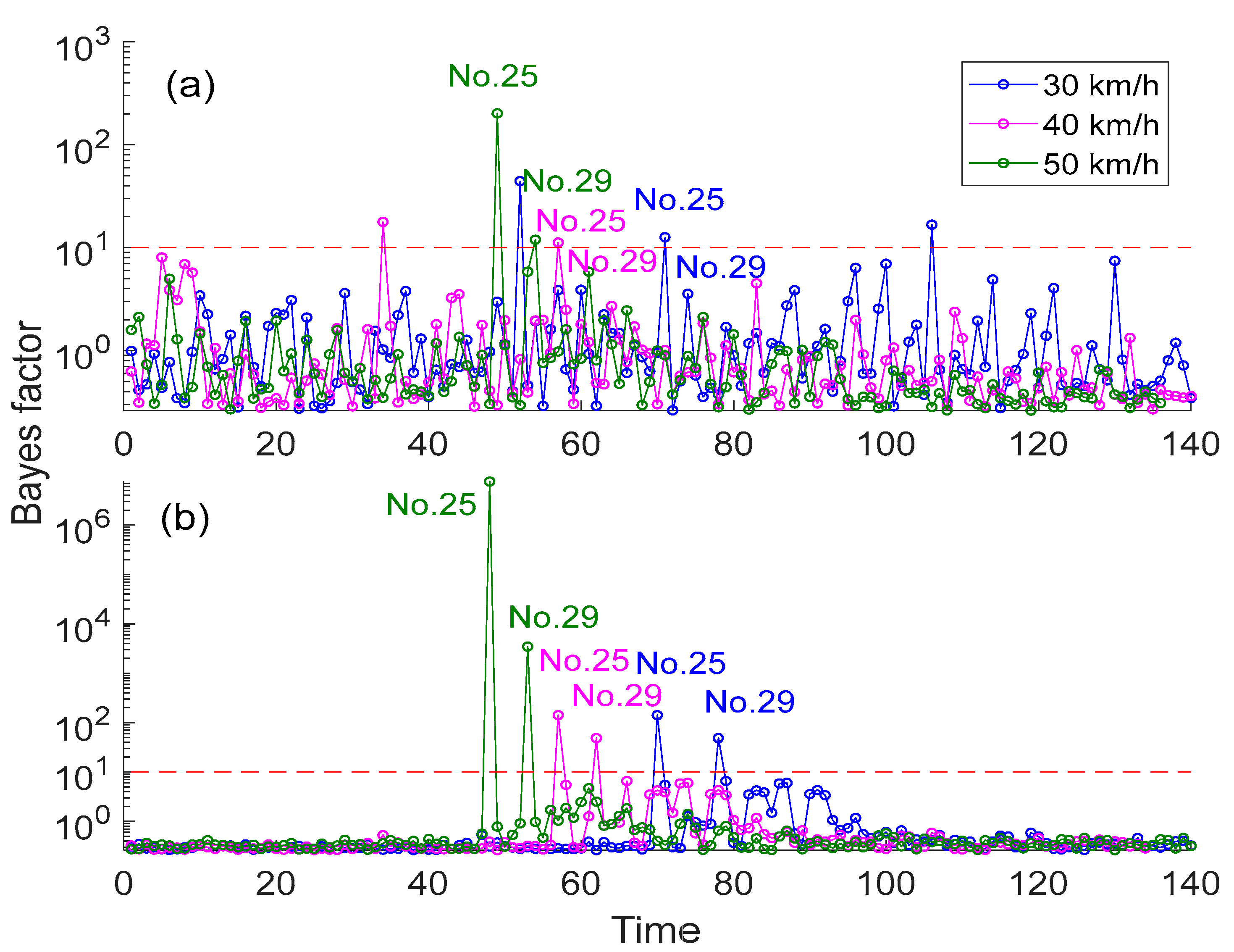
5.2. Malfunction Detection Results by Using Accelerations at Different Locations
5.3. Malfunction Detection Results by Using Accelerations at Different Running Speeds
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Long, Z.; Xue, S.; Zhang, Z.; Xie, Y. A new strategy of active fault-tolerant control for suspension system of maglev train. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 88–94. [Google Scholar]
- Ono, M.; Koga, S.; Ohtsuki, H. Japan’s superconducting maglev train. IEEE Instrum. Meas. Mag. 2002, 5, 9–15. [Google Scholar] [CrossRef]
- Huang, C.M.; Yen, J.Y.; Chen, M.S. Adaptive nonlinear control of repulsive maglev suspension systems. Control Eng. Pract. 2000, 8, 1357–1367. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Zhang, G.; Tian, W.J. Disturbance decoupled fault diagnosis for sensor fault of maglev suspension system. J. Cent. South Univ. 2013, 20, 1545–1551. [Google Scholar] [CrossRef]
- Zhou, D.; Li, J.; Hansen, C.H. Suppression of the stationary maglev vehicle-bridge coupled resonance using a tuned mass damper. J. Vib. Control 2013, 19, 191–203. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhou, D.; Cui, P.; Wang, L.; Yu, P. The active control of maglev stationary self-excited vibration with a virtual energy harvester. IEEE Trans. Ind. Electron. 2014, 62, 2942–2951. [Google Scholar] [CrossRef]
- Wai, R.J.; Lee, J.D. Adaptive fuzzy-neural-network control for maglev transportation system. IEEE Trans. Neural Netw. 2008, 19, 54–70. [Google Scholar] [PubMed]
- Zhou, D.; Li, J.; Zhang, K. Amplitude control of the track-induced self-excited vibration for a maglev system. ISA Trans. 2014, 53, 1463–1469. [Google Scholar] [CrossRef]
- Xu, Y.L.; Wang, Z.L.; Li, G.Q.; Chen, S.; Yang, Y.B. High-speed running maglev trains interacting with elastic transitional viaducts. Eng. Struct. 2019, 183, 562–578. [Google Scholar] [CrossRef]
- Wang, Z.L.; Xu, Y.L.; Li, G.Q.; Yang, Y.B.; Chen, S.W.; Zhang, X.L. Modelling and validation of coupled high-speed maglev train-and-viaduct systems considering support flexibility. Veh. Syst. Dyn. 2019, 57, 161–191. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, Y. A nonlinear control method for the electromagnetic suspension system of the maglev train. J. Mod. Transp. 2011, 19, 176–180. [Google Scholar] [CrossRef]
- Wang, P.; Long, Z.; Dang, N. Multi-model switching based fault detection for the suspension system of maglev train. IEEE Access 2018, 7, 6831–6841. [Google Scholar] [CrossRef]
- Wang, L.; Yu, P.; Li, J.; Zhou, D.; Li, J. Suspension system status detection of maglev train based on machine learning using levitation sensors. In Proceedings of the 2017 29th Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017; pp. 7579–7584. [Google Scholar]
- Long, Z.Q.; Chen, X.Y.; Fan, C.X. Middle-low speed maglev train suspension control system common cause failure risk analysis. In Proceedings of the 2017 36th Chinese Control Conference, Dalian, China, 26–28 July 2017; pp. 7218–7224. [Google Scholar]
- Sun, Y.; Xu, J.; Qiang, H.; Chen, C.; Lin, G.B. Adaptive sliding mode control of maglev system based on RBF neural network minimum parameter learning method. Measurement 2019, 141, 217–226. [Google Scholar] [CrossRef]
- Zhou, D.; Yu, P.; Wang, L.; Li, J. An adaptive vibration control method to suppress the vibration of the maglev train caused by track irregularities. J. Sound Vib. 2017, 408, 331–350. [Google Scholar] [CrossRef]
- Hou, Z.; Gan, W.; Xu, S.; Guo, W.; Chen, Q.; Wang, W.; Chen, K. Fault detection of accelerometer and fault-tolerant control for maglev. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference, Hanoi, Vietnam, 14–17 October 2019; pp. 1–5. [Google Scholar]
- Yin, S.; Rodriguez-Andina, J.J.; Jiang, Y. Real-time monitoring and control of industrial cyberphysical systems: With integrated plant-wide monitoring and control framework. IEEE Ind. Electron. Mag. 2019, 13, 38–47. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ni, Y.Q.; Wang, S.M. Structural health monitoring of railway bridges using innovative sensing technologies and machine learning algorithms: A concise review. Intell. Transp. Infrastruct. 2022, 1, liac009. [Google Scholar] [CrossRef]
- Sun, Y.; Qiang, H.; Xu, J.; Lin, G. Internet of Things-based online condition monitor and improved adaptive fuzzy control for a medium-low-speed maglev train system. IEEE Trans. Ind. Inform. 2019, 16, 2629–2639. [Google Scholar] [CrossRef]
- Kang, D.; Chung, W. Integrated monitoring scheme for a maglev guideway using multiplexed FBG sensor arrays. NDT E Int. 2009, 42, 260–266. [Google Scholar] [CrossRef]
- He, Q.; Wang, J.; Hu, F.; Kong, F. Wayside acoustic diagnosis of defective train bearings based on signal resampling and information enhancement. J. Sound Vib. 2013, 332, 5635–5649. [Google Scholar] [CrossRef]
- Ngigi, R.W.; Pislaru, C.; Ball, A.; Gu, F. Modern techniques for condition monitoring of railway vehicle dynamics. J. Phys. Conf. Ser. 2012, 364, 012016. [Google Scholar] [CrossRef]
- Filograno, M.L.; Corredera, P.; Rodriguez-Plaza, M.; Andres-Alguacil, A.; Gonzalez-Herraez, M. Wheel flat detection in high-speed railway systems using fiber Bragg gratings. IEEE Sens. J. 2013, 13, 4808–4816. [Google Scholar] [CrossRef]
- Liu, X.Z.; Ni, Y.Q. Wheel tread defect detection for high-speed trains using FBG-based online monitoring techniques. Smart Struct. Syst. 2018, 21, 687–694. [Google Scholar]
- Wei, C.; Xin, Q.; Chung, W.H.; Liu, S.Y.; Tam, H.Y.; Ho, S.L. Real-time train wheel condition monitoring by fiber Bragg grating sensors. Int. J. Distrib. Sens. Netw. 2011, 8, 409048. [Google Scholar] [CrossRef]
- Han, H.S.; Kim, D.S. Magnetic Levitation: Maglev Technology and Applications; Springer: Dordrecht The Netherlands, 2016. [Google Scholar]
- Frank, P.M. Analytical and qualitative model-based fault diagnosis—A survey and some new results. Eur. J. Control 1996, 2, 6–28. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Kaynak, O. Optimized design of parity relation-based residual generator for fault detection: Data-driven approaches. IEEE Trans. Ind. Inform. 2021, 17, 1449–1458. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H. A review on basic data-driven approaches for industrial process monitoring. IEEE Trans. Ind. Electron. 2014, 61, 6418–6428. [Google Scholar] [CrossRef]
- Zang, Y.; Shang, G.W.; Cai, B.; Wang, H.; Pecht, M.G. Methods for fault diagnosis of high-speed railways: A review. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 233, 908–922. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Ding, S.X.; Huang, B. Data-driven fault diagnosis for traction systems in high-speed trains: A survey, challenges, and perspectives. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1700–1716. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Ding, S.X. A broad learning aided data-driven framework of fast fault diagnosis for high-speed trains. IEEE Intell. Transp. Syst. Mag. 2020, 13, 83–88. [Google Scholar] [CrossRef]
- Davari, N.; Veloso, B.; Costa, G.D.A.; Pereira, P.M.; Ribeiro, R.P.; Gama, J. A survey on data-driven predictive maintenance for the railway industry. Sensors 2021, 21, 5739. [Google Scholar] [CrossRef]
- Wang, S.M.; Jiang, G.F.; Ni, Y.Q.; Lu, Y.; Lin, G.B.; Pan, H.L.; Xu, J.Q.; Hao, S. Multiple damage detection of maglev rail joints using time-frequency spectrogram and convolutional neural network. Smart Struct. Syst. 2022, 29, 625–640. [Google Scholar]
- Li, H.W.; Yang, D.S.; Sun, Y.L.; Han, J. Study review and prospect of intelligent fault diagnosis technique. Comput. Eng. Des. 2013, 34, 632–637. [Google Scholar]
- Ni, Y.Q.; Wang, Y.W.; Zhang, C. A Bayesian approach for condition assessment and damage alarm of bridge expansion joints using long-term structural health monitoring data. Eng. Struct. 2020, 212, 110520. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ni, Y.Q.; Wang, X. Real-time defect detection of high-speed train wheels by using Bayesian forecasting and dynamic model. Mech. Syst. Signal Process. 2020, 139, 106654. [Google Scholar] [CrossRef]
- Vagnoli, M.; Remenyte-Prescott, R.; Andrews, J. A fuzzy-based Bayesian belief network approach for railway bridge condition monitoring and fault detection. In Proceedings of the 2017 ESREL Conference on Safety and Reliability—Theory and Application, Portoroz, Slovenia, 18–22 June 2017. [Google Scholar]
- West, M.; Harrison, J. Bayesian Forecasting and Dynamic Models; Chapman and Hall: New York, NY, USA, 2006. [Google Scholar]
- Lipowsky, H.; Staudacher, S.; Bauer, M.; Schmidt, K.J. Application of Bayesian forecasting to change detection and prognosis of gas turbine performance. J. Eng. Gas Turbines Power 2012, 134, 031602. [Google Scholar]
- Wang, Y.W.; Ni, Y.Q. Bayesian dynamic forecasting of structural strain response using structural health monitoring data. Struct. Control. Health Monit. 2020, 27, e2575. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosquee zed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Meignen, S.; Oberlin, T.; Pham, D.H. Synchrosqueezing transforms: From low-to high-frequency modulations and perspectives. Comptes Rendus Phys. 2019, 20, 449–460. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability; Oxford Clarendon Press: Oxford, UK, 1961. [Google Scholar]




| For t = 1→T | |
| Calculate through (14) and (15) | |
| Sample from | |
| Calculate through (8) | |
| Update by adding new data through (18) and (19) | |
| Calculate through (20) | |
| End | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-M.; Wang, Y.-W.; Ni, Y.-Q.; Lu, Y. Real-Time Malfunction Detection of Maglev Suspension Controllers. Mathematics 2023, 11, 4045. https://doi.org/10.3390/math11194045
Wang S-M, Wang Y-W, Ni Y-Q, Lu Y. Real-Time Malfunction Detection of Maglev Suspension Controllers. Mathematics. 2023; 11(19):4045. https://doi.org/10.3390/math11194045
Chicago/Turabian StyleWang, Su-Mei, You-Wu Wang, Yi-Qing Ni, and Yang Lu. 2023. "Real-Time Malfunction Detection of Maglev Suspension Controllers" Mathematics 11, no. 19: 4045. https://doi.org/10.3390/math11194045
APA StyleWang, S.-M., Wang, Y.-W., Ni, Y.-Q., & Lu, Y. (2023). Real-Time Malfunction Detection of Maglev Suspension Controllers. Mathematics, 11(19), 4045. https://doi.org/10.3390/math11194045







